Fractal Analysis for Fatigue Crack Growth Rate Response of Engineering Structures with Complex Geometry
Abstract
1. Introduction
2. Multifractal Fatigue Crack Growth Model
3. Materials and Experimental Methods
4. Results and Discussion
4.1. Fatigue Crack Growth Behavior
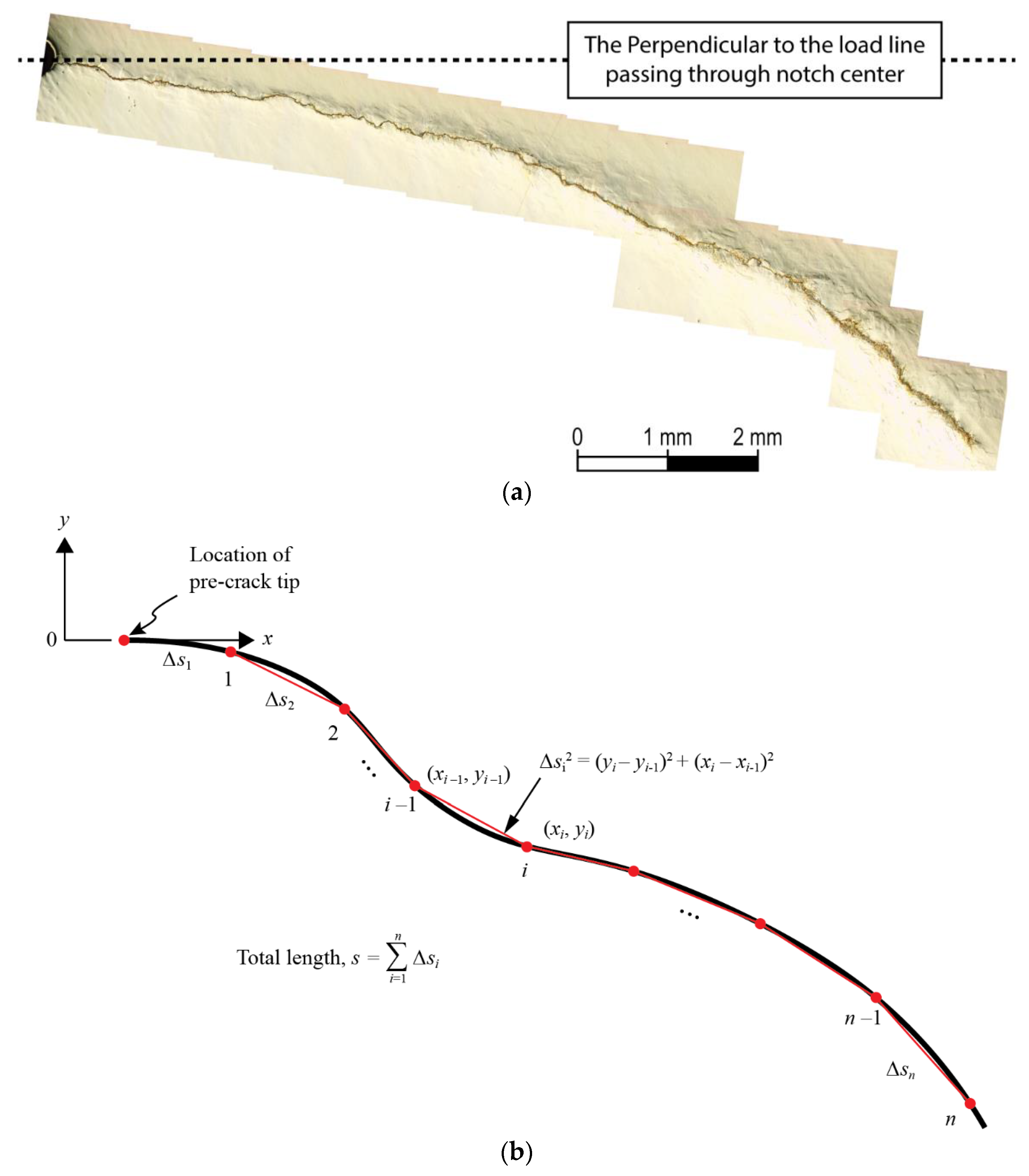
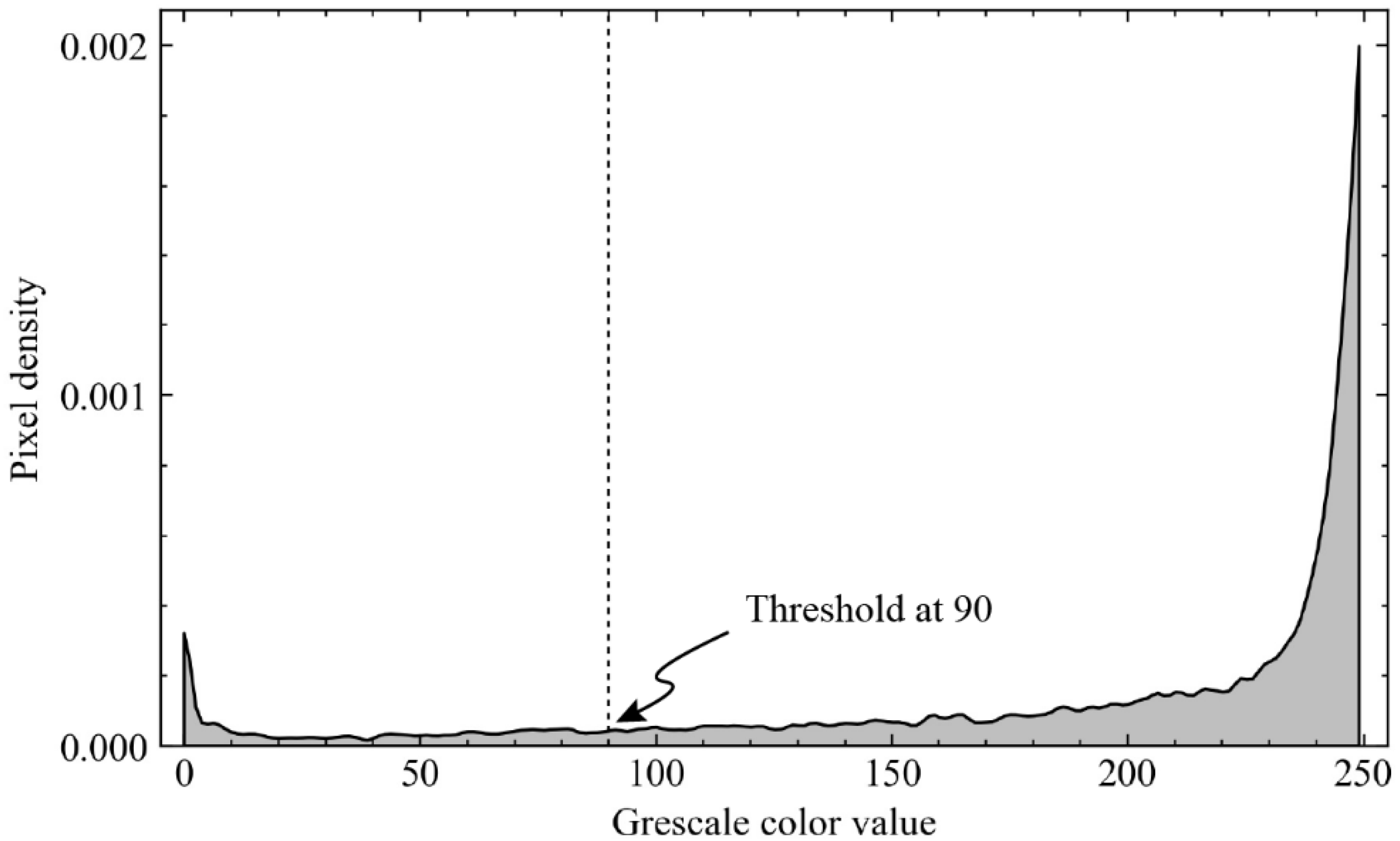
4.2. Fractal Dimensions of the Fatigue Crack
4.3. Multifractal Fatigue Crack Growth Rate
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tada, H.; Paris, P.; Irwin, G. The Analysis of Cracks Handbook; ASME Press: New York, NY, USA, 2000; Volume 2, p. 1. [Google Scholar]
- Rooke, D.P.; Cartwright, D.J. Compendium of Stress Intensity Factors; H.M.S.O.: London, UK, 1976; p. 330.
- Sherry, A.H.; France, C.; Goldthorpe, M. Compendium of T-stress solutions for two and three dimensional cracked geometries. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 141–155. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- de Morais, A.B.; de Moura, M.F.; Gonçalves, J.P.M.; Camanho, P.P. Analysis of crack propagation in double cantilever beam tests of multidirectional laminates. Mech. Mater. 2003, 35, 641–652. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Heidari-Rarani, M.; Rahimi, S. Influence of curved delamination front on toughness of multidirectional DCB specimens. Compos. Struct. 2012, 94, 1359–1365. [Google Scholar] [CrossRef]
- Orifici, A.C.; Krueger, R. Benchmark assessment of automated delamination propagation capabilities in finite element codes for static loading. Finite Elem. Anal. Des. 2012, 54, 28–36. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Rajabpour-Shirazi, H.; Heidari-Rarani, M.; Haghpanahi, M. Simulation of mode I delamination propagation in multidirectional composites with R-curve effects using VCCT method. Comput. Mater. Sci. 2012, 65, 66–73. [Google Scholar] [CrossRef]
- Pereira, A.B.; de Morais, A.B. Mode I interlaminar fracture of carbon/epoxy multidirectional laminates. Compos. Sci. Technol. 2004, 64, 2261–2270. [Google Scholar] [CrossRef]
- Robinson, P.; Javidrad, F.; Hitchings, D. Finite element modelling of delamination growth in the DCB and edge delaminated DCB specimens. Compos. Struct. 1995, 32, 275–285. [Google Scholar] [CrossRef]
- Samborski, S. Numerical analysis of the DCB test configuration applicability to mechanically coupled Fiber Reinforced Laminated Composite beams. Compos. Struct. 2016, 152, 477–487. [Google Scholar] [CrossRef]
- Jimenez, M.A.; Miravete, A. Application of the Finite-Element Method to Predict the Onset of Delamination Growth. J. Compos. Mater. 2004, 38, 1309–1335. [Google Scholar] [CrossRef]
- Hashmi, M.H.; Koloor, S.S.R.; Abdul-Hamid, M.F.; Tamin, M.N. Exploiting fractal features to determine fatigue crack growth rates of metallic materials. Eng. Fract. Mech. 2022, 270, 108589. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Walker, K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum. In Effects of Environment and Complex Load History on Fatigue Life; ASTM International: West Conshohocken, PA, USA, 1970. [Google Scholar]
- Forman, R.G. Study of fatigue crack initiation from flaws using fracture mechanics theory. Eng. Fract. Mech. 1972, 4, 333–345. [Google Scholar] [CrossRef]
- Collipriest, J., Jr. An experimentalist’s view of the surface flaw problem. In The Surface Crack-Physical Problems and Computational Solutions; ASME: New York, NY, USA, 1972; pp. 43–61. [Google Scholar]
- McEvily, A. Phenomenological and microstructural aspects of fatigue. In The Microstructure and Design of Alloys; Iron and Steel Institute: Cambridge, UK, 1973; pp. 204–225. [Google Scholar]
- McEvily, A.J.; Groeger, J. On the threshold for fatigue crack growth. In Advances in Research on the Strength and Fracture of Materials; Taplin, D.M.R., Ed.; Pergamon: Amsterdam, The Netherlands, 1978; pp. 1293–1298. [Google Scholar] [CrossRef]
- Frost, N.; Pook, L.; Denton, K. A fracture mechanics analysis of fatigue crack growth data for various materials. Eng. Fract. Mech. 1971, 3, 109–126. [Google Scholar] [CrossRef]
- Xiulin, Z.; Hirt, M.A. Fatigue crack propagation in steels. Eng. Fract. Mech. 1983, 18, 965–973. [Google Scholar] [CrossRef]
- Wang, W.; Hsu, C.-T.T. Fatigue crack growth rate of metal by plastic energy damage accumulation theory. J. Eng. Mech. 1994, 120, 776–795. [Google Scholar] [CrossRef]
- Miller, M.; Gallagher, J. An analysis of several fatigue crack growth rate (FCGR) descriptions. Fatigue Crack Growth Meas. Data Anal. ASTM STP 1981, 738, 205–251. [Google Scholar]
- Dowling, N.; Begley, J. Fatigue Crack Growth during Gross Plasticity and the J-Integral; ASTM International: West Conshohocken, PA, USA, 1976. [Google Scholar]
- Pugno, N.M.; Ruoff, R.S. Quantized fracture mechanics. Philos. Mag. 2004, 84, 2829–2845. [Google Scholar] [CrossRef]
- Broek, D. The Practical Use of Fracture Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wen, P.H.; Aliabadi, M.H.; Rooke, D.P. A contour integral for the evaluation of stress intensity factors. Appl. Math. Model. 1995, 19, 450–455. [Google Scholar] [CrossRef]
- Berer, M.; Mitev, I.; Pinter, G. Finite element study of mode I crack opening effects in compression-loaded cracked cylinders. Eng. Fract. Mech. 2017, 175, 1–14. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Daux, C.; Moës, N.; Dolbow, J.; Sukumar, N.; Belytschko, T. Arbitrary branched and intersecting cracks with the extended finite element method. Int. J. Numer. Methods Eng. 2000, 48, 1741–1760. [Google Scholar] [CrossRef]
- Mariano, P.M.; Stazi, F.L. Strain localization due to crack–microcrack interactions: X-FEM for a multifield approach. Comput. Methods Appl. Mech. Eng. 2004, 193, 5035–5062. [Google Scholar] [CrossRef]
- Elguedj, T.; Gravouil, A.; Combescure, A. Appropriate extended functions for X-FEM simulation of plastic fracture mechanics. Comput. Methods Appl. Mech. Eng. 2006, 195, 501–515. [Google Scholar] [CrossRef]
- Dumstorff, P.; Meschke, G. Crack propagation criteria in the framework of X-FEM-based structural analyses. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 239–259. [Google Scholar] [CrossRef]
- Legrain, G.; Moes, N.; Verron, E. Stress analysis around crack tips in finite strain problems using the extended finite element method. Int. J. Numer. Methods Eng. 2005, 63, 290–314. [Google Scholar] [CrossRef]
- Li, L.; Sun, H.-X.; Zhang, Y.; Yu, B. Surface Cracking and Fractal Characteristics of Bending Fractured Polypropylene Fiber-Reinforced Geopolymer Mortar. Fractal Fract. 2021, 5, 142. [Google Scholar] [CrossRef]
- Hashmi, M.H.; Abdul-Hamid, M.F.; Abdul-Latif, A.; Tamin, M.N.; Khattak, M.A. Fractal Dimensions of a Propagating Fatigue Crack in Metallic Materials. J. Fail. Anal. Prev. 2021, 21, 1644–1651. [Google Scholar] [CrossRef]
- Ma, G.; Li, J.; Zhou, X.; Zhang, L.; Qiu, P.; Yu, Y. Application of Asymmetric Notched Semi-Circular Bending Specimen to Evaluate Mixed-Mode I-II Fracture Behaviors of Sandstone. Fractal Fract. 2022, 6, 336. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Liu, B.; Zhao, F.; Tang, S.; Jin, M. Effects of Fly Ash Dosage on Shrinkage, Crack Resistance and Fractal Characteristics of Face Slab Concrete. Fractal Fract. 2022, 6, 335. [Google Scholar] [CrossRef]
- Li, W.; Wu, M.; Shi, T.; Yang, P.; Pan, Z.; Liu, W.; Liu, J.; Yang, X. Experimental Investigation of the Relationship between Surface Crack of Concrete Cover and Corrosion Degree of Steel Bar Using Fractal Theory. Fractal Fract. 2022, 6, 325. [Google Scholar] [CrossRef]
- Wang, L.; Song, X.; Yang, H.; Wang, L.; Tang, S.; Wu, B.; Mao, W. Pore Structural and Fractal Analysis of the Effects of MgO Reactivity and Dosage on Permeability and F–T Resistance of Concrete. Fractal Fract. 2022, 6, 113. [Google Scholar] [CrossRef]
- An, Q.; Chen, X.; Wang, H.; Yang, H.; Yang, Y.; Huang, W.; Wang, L. Segmentation of Concrete Cracks by Using Fractal Dimension and UHK-Net. Fractal Fract. 2022, 6, 95. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, X.; Yang, H.; Lv, X.; Guo, F.; Shi, Y.; Hanif, A. Investigation and Application of Fractal Theory in Cement-Based Materials: A Review. Fractal Fract. 2021, 5, 247. [Google Scholar] [CrossRef]
- Balankin, A.S.; Susarrey, O.; Paredes, R.G.; Morales, L.; Samayoa, D.; López, J.A. Intrinsically anomalous roughness of admissible crack traces in concrete. Phys. Rev. E 2005, 72, 065101. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Liebovitch, L.S.; Toth, T. A fast algorithm to determine fractal dimensions by box counting. Phys. Lett. A 1989, 141, 386–390. [Google Scholar] [CrossRef]
- Gonzato, G. A practical implementation of the box counting algorithm. Comput. Geosci. 1998, 24, 95–100. [Google Scholar] [CrossRef]
- ASTM E647-15e1; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2015.






| Property | ν | |||||
|---|---|---|---|---|---|---|
| Value | 200 | 620 | 657 | 0.30 | 55.0 | 15.2 (min.) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashmi, M.H.; Koloor, S.S.R.; Abdul-Hamid, M.F.; Tamin, M.N. Fractal Analysis for Fatigue Crack Growth Rate Response of Engineering Structures with Complex Geometry. Fractal Fract. 2022, 6, 635. https://doi.org/10.3390/fractalfract6110635
Hashmi MH, Koloor SSR, Abdul-Hamid MF, Tamin MN. Fractal Analysis for Fatigue Crack Growth Rate Response of Engineering Structures with Complex Geometry. Fractal and Fractional. 2022; 6(11):635. https://doi.org/10.3390/fractalfract6110635
Chicago/Turabian StyleHashmi, Mudassar Hussain, Seyed Saeid Rahimian Koloor, Mohd Foad Abdul-Hamid, and Mohd Nasir Tamin. 2022. "Fractal Analysis for Fatigue Crack Growth Rate Response of Engineering Structures with Complex Geometry" Fractal and Fractional 6, no. 11: 635. https://doi.org/10.3390/fractalfract6110635
APA StyleHashmi, M. H., Koloor, S. S. R., Abdul-Hamid, M. F., & Tamin, M. N. (2022). Fractal Analysis for Fatigue Crack Growth Rate Response of Engineering Structures with Complex Geometry. Fractal and Fractional, 6(11), 635. https://doi.org/10.3390/fractalfract6110635









