Author Contributions
Conceptualization, H.L. (Hongju Li) and Y.L.; methodology, H.L. (Hongju Li) and Y.W.; software, H.L. (Hongju Li); validation, H.L. (Hongju Li) and H.L. (Haoran Liao); formal analysis, H.L. (Hongju Li); investigation, H.L. (Hongju Li), Y.W. and H.L. (Haoran Liao); resources, Y.L.; data curation, H.L. (Hongju Li); writing-original draft preparation, H.L. (Hongju Li); writing-review and editing, H.L. (Hongju Li), Y.L., Y.W. and H.L. (Haoran Liao); visualization, H.L. (Hongju Li), Y.W. and H.L. (Haoran Liao); supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Figure 1.
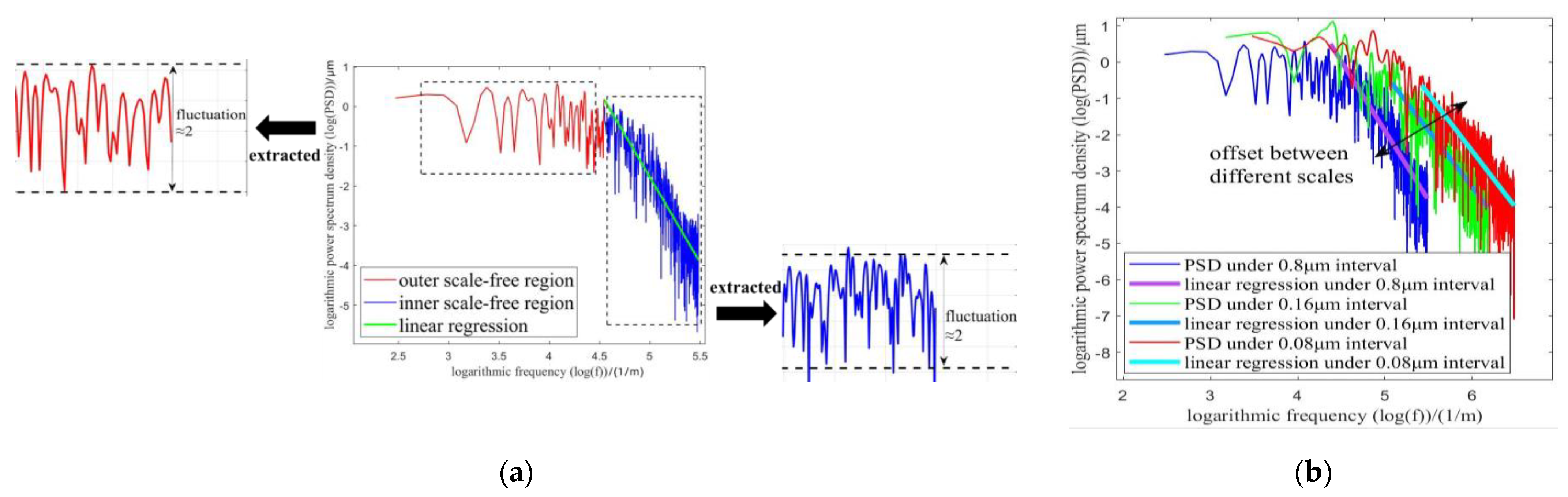
The basic concepts of fractals and scale dependence. (a) the scale-free region; (b) the scale-dependence phenomenon.
Figure 1.
The basic concepts of fractals and scale dependence. (a) the scale-free region; (b) the scale-dependence phenomenon.
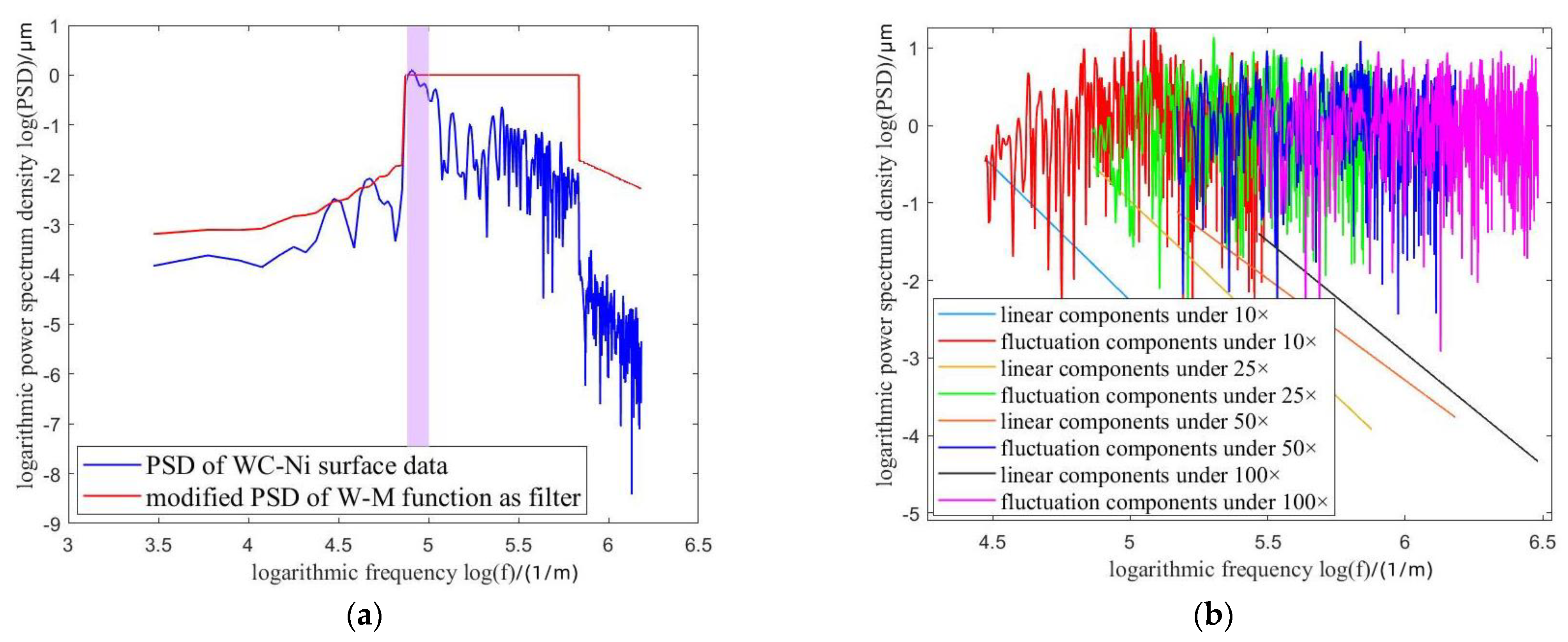
Figure 2.
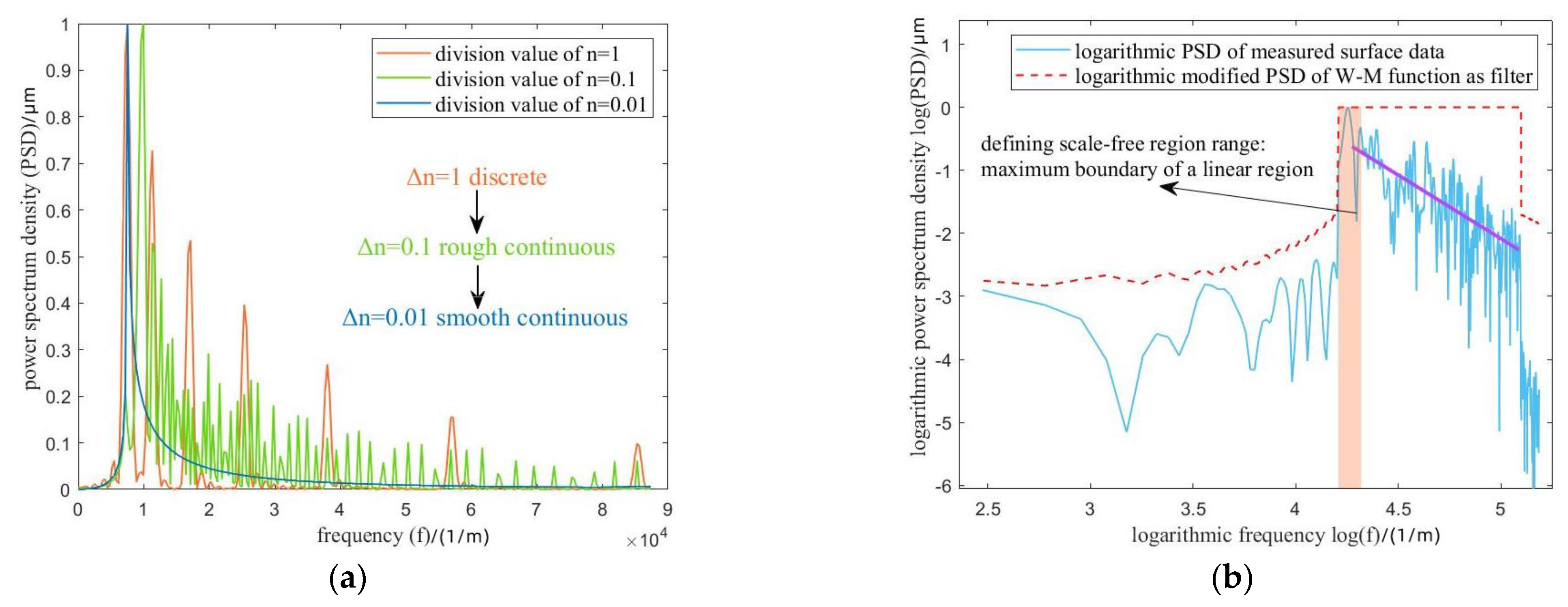
Determination method for the scale-free region based on modified W–M function. (a) introduction of non-integer frequency index; (b) results in log-log PSD.
Figure 2.
Determination method for the scale-free region based on modified W–M function. (a) introduction of non-integer frequency index; (b) results in log-log PSD.
Figure 3.
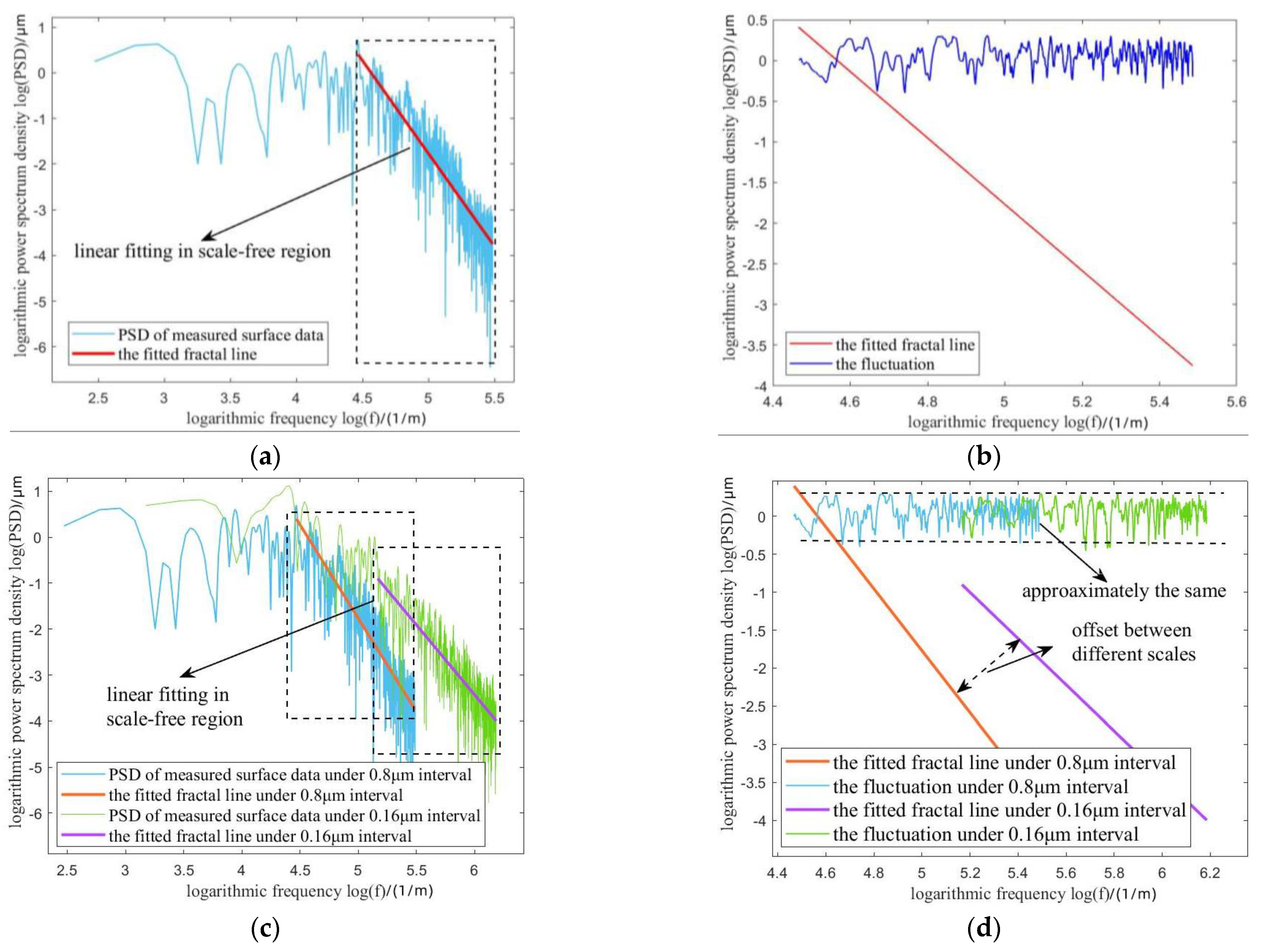
Separation of three components in linear log-log PSD. (a) linear function under a single scale; (b) the fractal components and fluctuation components under a single scale; (c) linear function under multi-scales; (d) the fractal components, fluctuation components, and offset components under multi-scales.
Figure 3.
Separation of three components in linear log-log PSD. (a) linear function under a single scale; (b) the fractal components and fluctuation components under a single scale; (c) linear function under multi-scales; (d) the fractal components, fluctuation components, and offset components under multi-scales.
Figure 4.
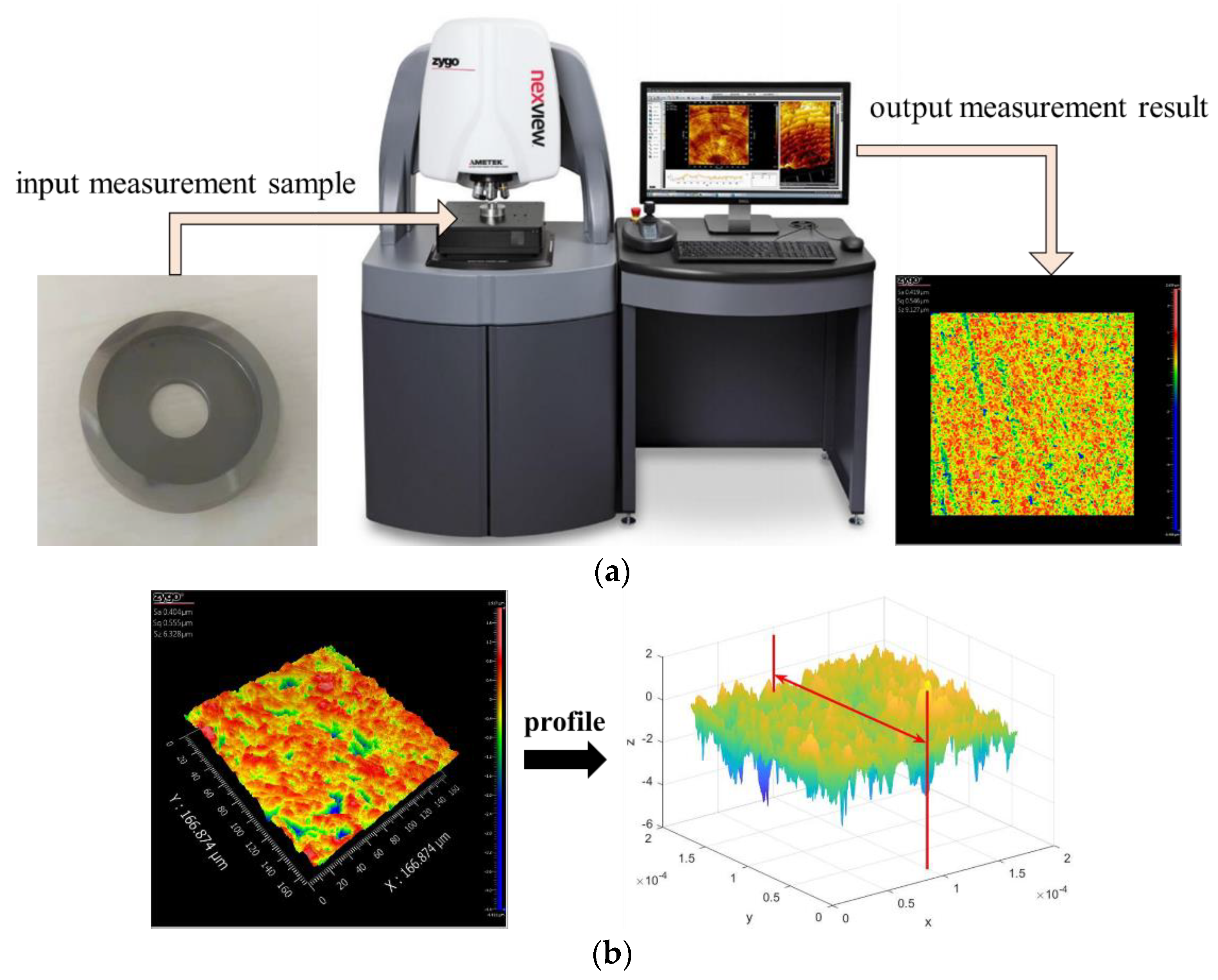
Measurement process of the experiment. (a) measurement instrument; (b) roughness profiles.
Figure 4.
Measurement process of the experiment. (a) measurement instrument; (b) roughness profiles.
Figure 5.
Operation processes on the measured data. (a) determination of scale-free region; (b) component decomposition and filtering fluctuation components.
Figure 5.
Operation processes on the measured data. (a) determination of scale-free region; (b) component decomposition and filtering fluctuation components.
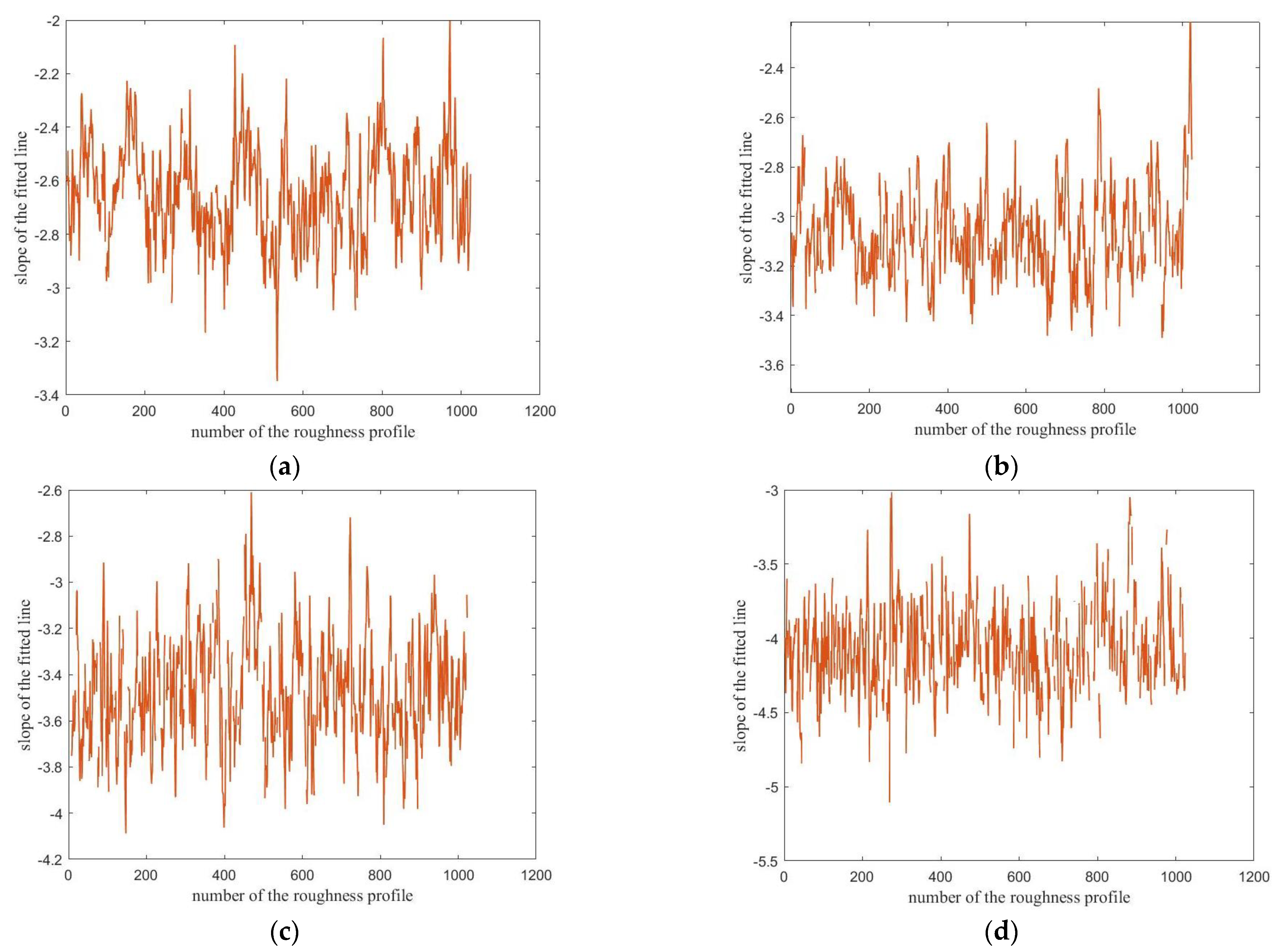
Figure 6.
Results of 1024 slopes under each scale (WC-Ni). (a) 100; (b) 50; (c) 25; (d) 10.
Figure 6.
Results of 1024 slopes under each scale (WC-Ni). (a) 100; (b) 50; (c) 25; (d) 10.
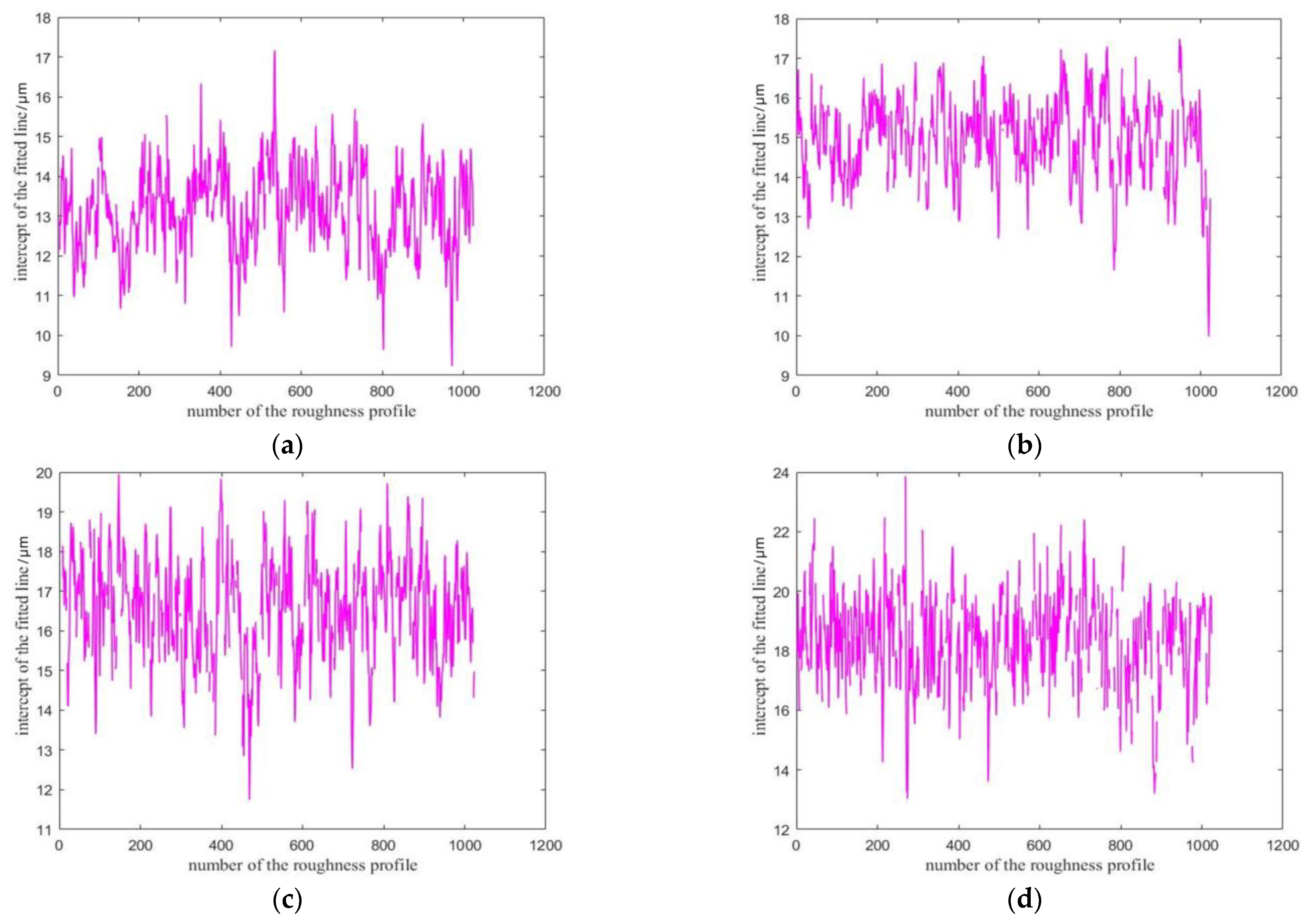
Figure 7.
Results of 1024 intercepts under each scale (WC-Ni). (a) 100; (b) 50; (c) 25; (d) 10.
Figure 7.
Results of 1024 intercepts under each scale (WC-Ni). (a) 100; (b) 50; (c) 25; (d) 10.
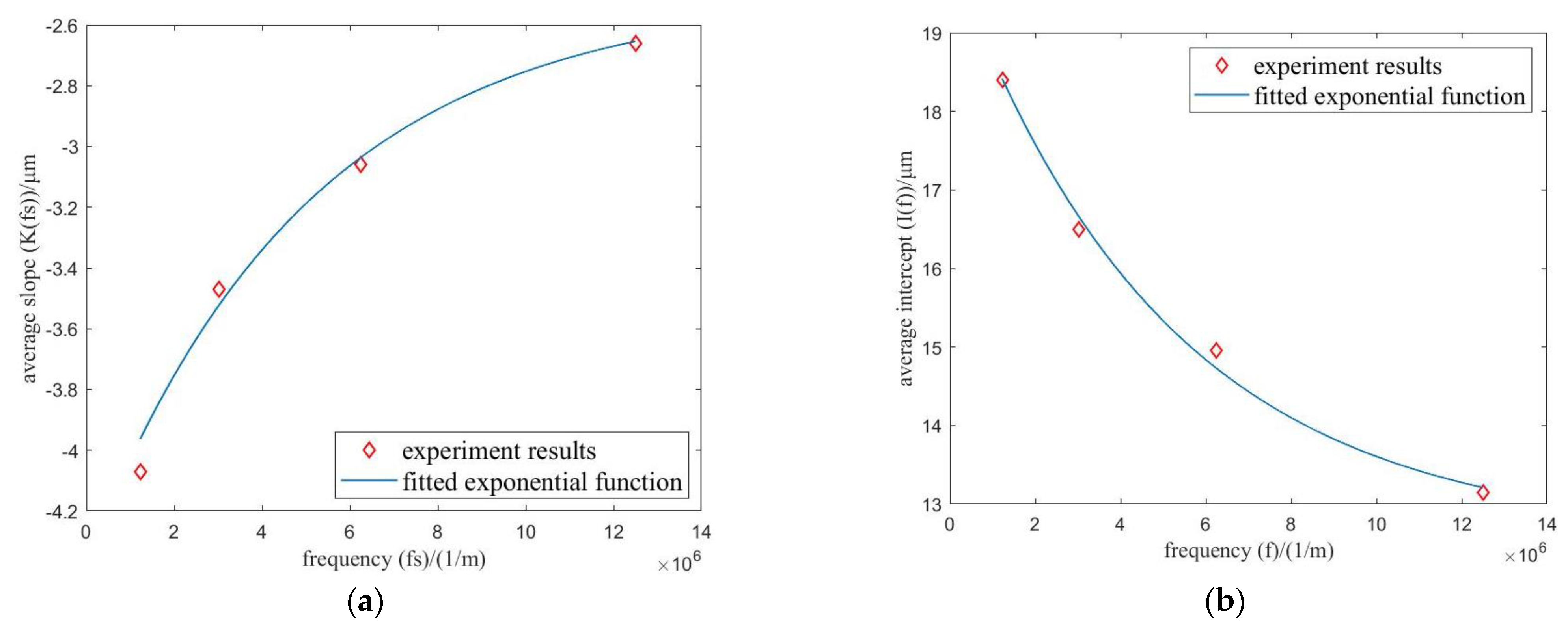
Figure 8.
Experiment results and fitted exponential function (WC-Ni). (a) slopes; (b) intercepts.
Figure 8.
Experiment results and fitted exponential function (WC-Ni). (a) slopes; (b) intercepts.
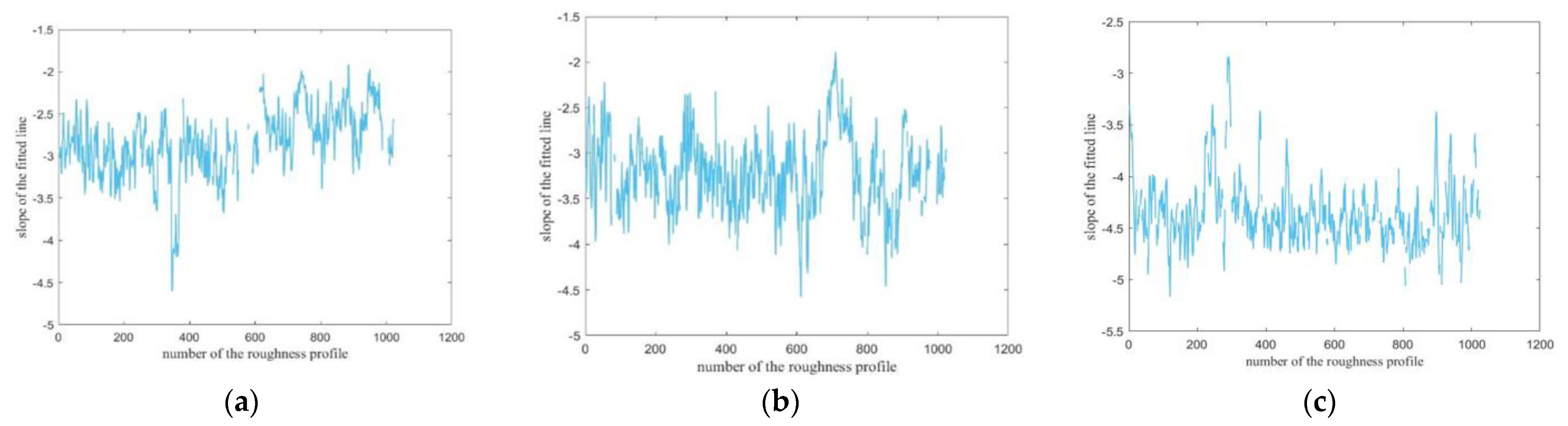
Figure 9.
Results of 1024 slopes under each scale (9Cr18Mo). (a) 100; (b) 50; (c) 10.
Figure 9.
Results of 1024 slopes under each scale (9Cr18Mo). (a) 100; (b) 50; (c) 10.
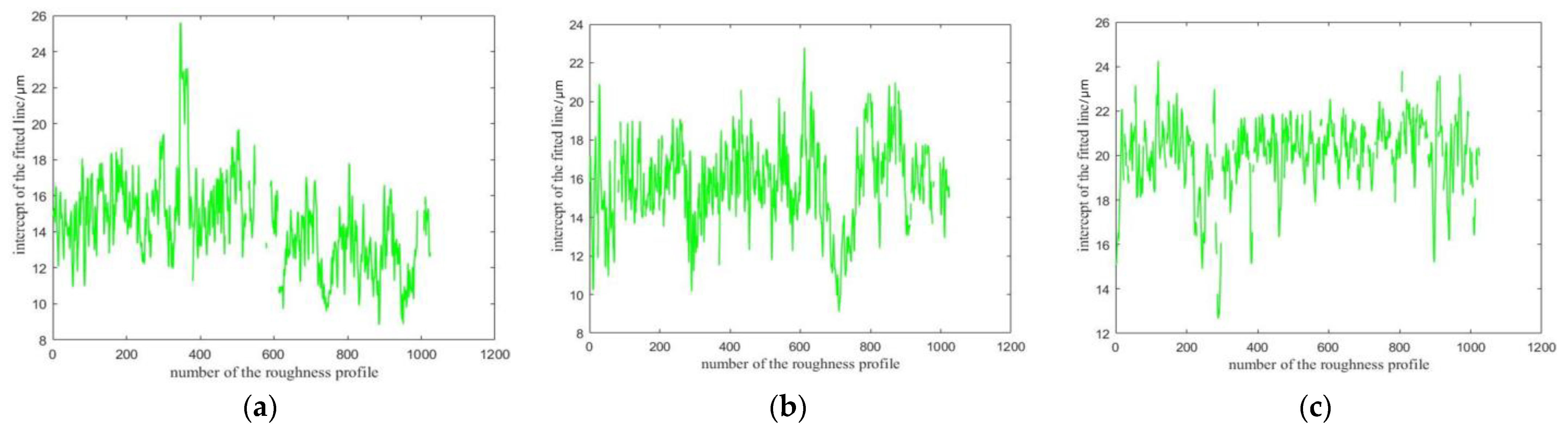
Figure 10.
Results of 1024 intercepts under each scale (9Cr18Mo). (a) 100; (b) 50; (c) 10.
Figure 10.
Results of 1024 intercepts under each scale (9Cr18Mo). (a) 100; (b) 50; (c) 10.
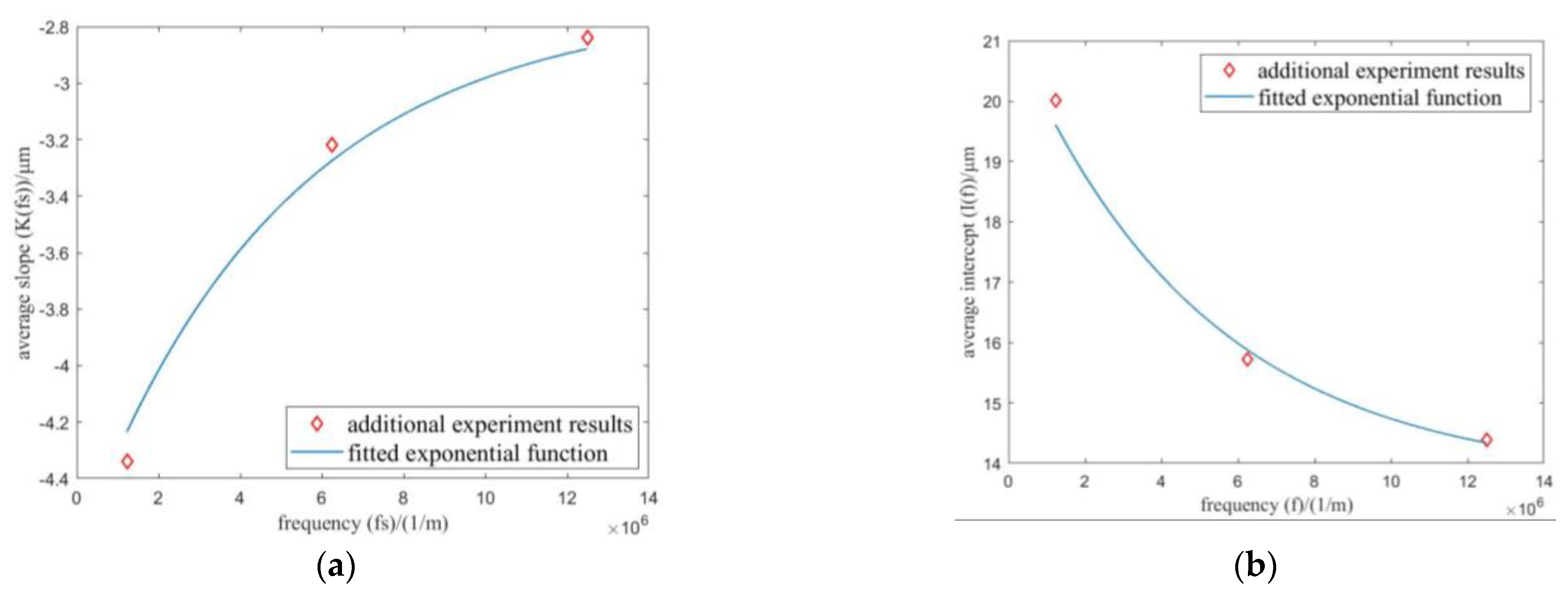
Figure 11.
Experiment results and fitted exponential function (9Cr18Mo). (a) slopes; (b) intercepts.
Figure 11.
Experiment results and fitted exponential function (9Cr18Mo). (a) slopes; (b) intercepts.
Figure 12.
Fluctuation components of WC-Ni surface under different scales. (a) WC-Ni surface; (b) 9Cr18Mo surface.
Figure 12.
Fluctuation components of WC-Ni surface under different scales. (a) WC-Ni surface; (b) 9Cr18Mo surface.
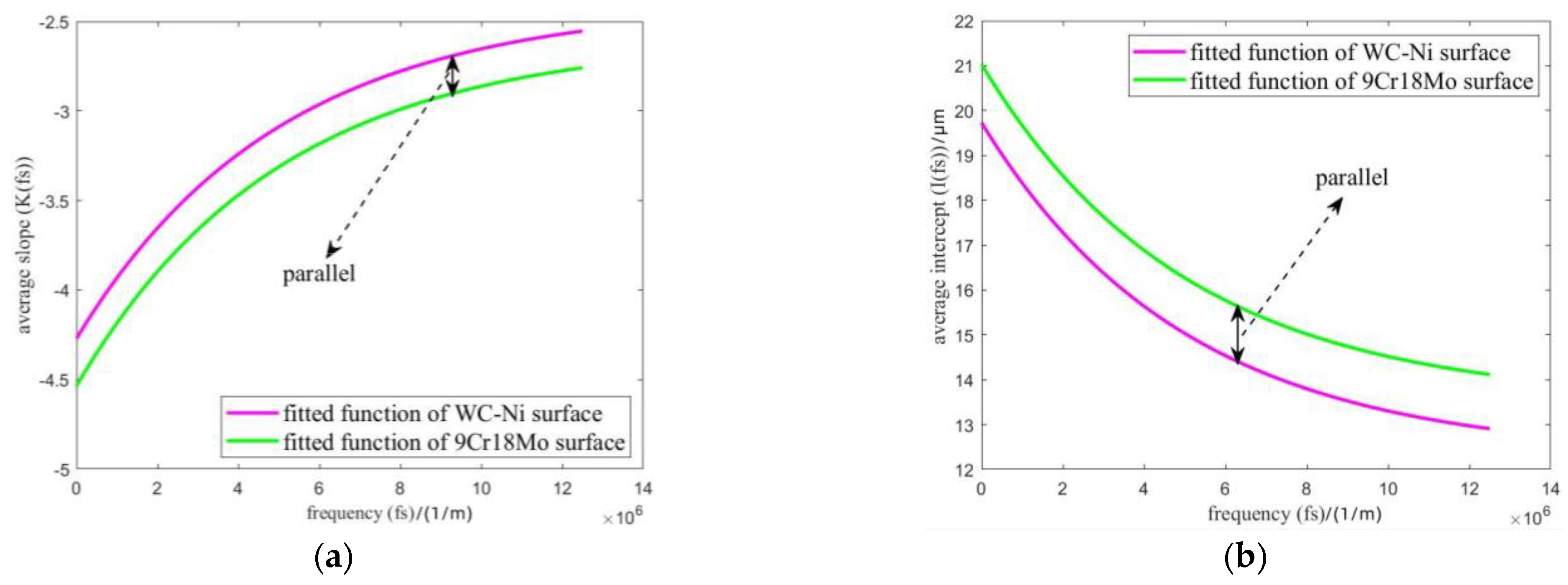
Figure 13.
Comparison of the two experimental results. (a) slopes; (b) intercepts.
Figure 13.
Comparison of the two experimental results. (a) slopes; (b) intercepts.
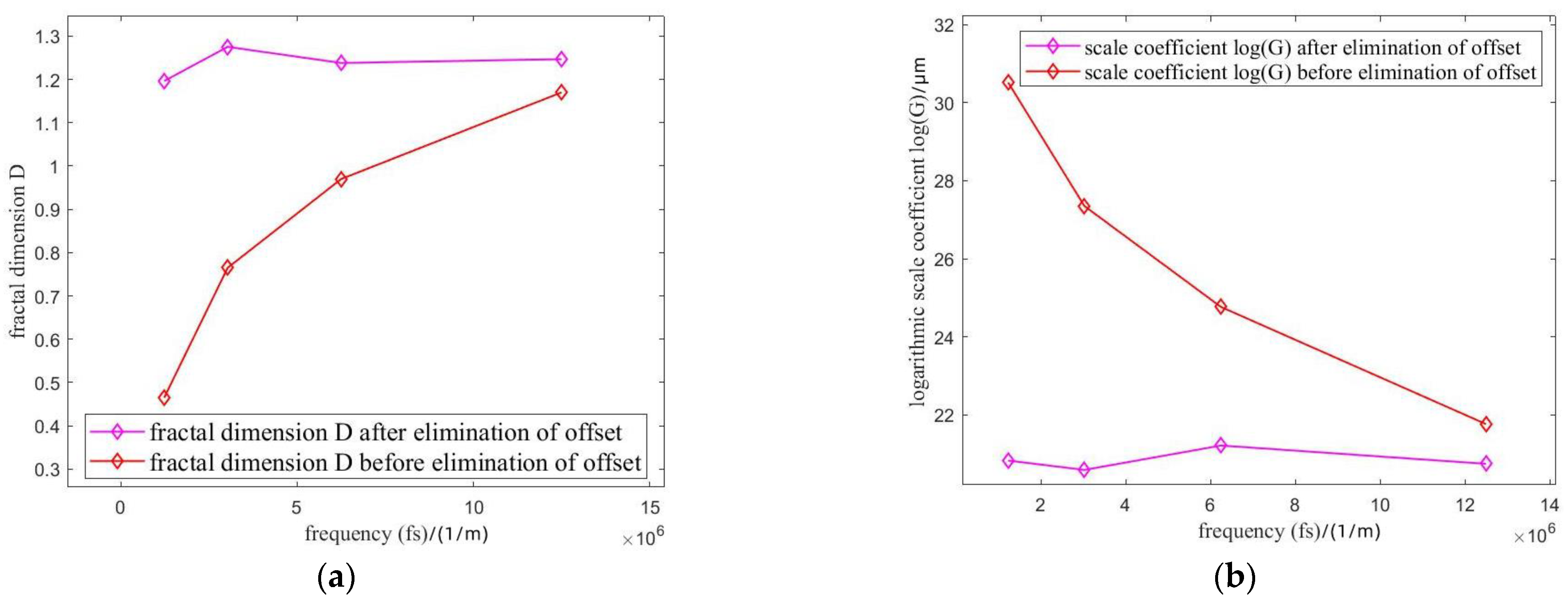
Figure 14.
Comparison of fractal dimension D and scale coefficient G of fractal components before and after eliminating offset components. (a) D; (b) G.
Figure 14.
Comparison of fractal dimension D and scale coefficient G of fractal components before and after eliminating offset components. (a) D; (b) G.
Table 1.
Detailed parameters under the two scales.
Table 1.
Detailed parameters under the two scales.
| Slopes of the Linear Function | | | |
|---|
| 0.8 | −4.0748 | 18.6051 | 0 | 0.3001 |
| 0.16 | −3.0414 | 14.8144 | 0 | 0.2815 |
Table 2.
Machining information of experiment sample surface of WC-Ni.
Table 2.
Machining information of experiment sample surface of WC-Ni.
| | Step1: Rough Lapping | Step2: Fine Grinding | Step3: Polishing |
|---|
| Abradant | W20 boron carbide/oil | W3.5 artificial diamond/water | W7 artificial diamond/water |
| Lapping duration | 20 min | 15 min | 7 min |
| Grinding miller | Cast iron plate | Brass plate | Nylon cloth |
Table 3.
Machining information of additional experiment sample surface of 9Cr18Mo.
Table 3.
Machining information of additional experiment sample surface of 9Cr18Mo.
| | Step 1: Original Grinding | Step 2: Rough Lapping | Step 3: Polishing |
|---|
| Abradant | 10# abrasive sand | W20 boron nitride | Polishing lint |
| Lapping duration | N/A | 20 min | 5 min |
| Grinding miller | Cast iron plate | Cast iron plate | Nylon cloth |
Table 4.
Measurement information of experiment sample surface.
Table 4.
Measurement information of experiment sample surface.
| Times of Scopes | | | |
|---|
|
100 | 84 | 0.08 | |
|
50 | 167 | 0.16 | |
|
25 | 336 | 0.33 | |
|
10 | 833 | 0.81 | |
Table 5.
Average slopes and intercepts under different measurement frequencies (WC-Ni).
Table 5.
Average slopes and intercepts under different measurement frequencies (WC-Ni).
| Times of Scopes | | Average Slope | |
|---|
|
100 | | −2.66 | 13.15 |
|
50 | | −3.07 | 14.95 |
|
25 | | −3.47 | 16.50 |
|
10 | | −4.07 | 18.40 |
Table 6.
Average slopes and intercepts under different measurement frequencies (9Cr18Mo).
Table 6.
Average slopes and intercepts under different measurement frequencies (9Cr18Mo).
| Times of Scopes | | Average Slope | |
|---|
|
100 | | −2.84 | 14.39 |
|
50 | | −3.22 | 15.72 |
|
10 | | −4.34 | 20.01 |
Table 7.
Detailed values of fluctuation components in WC-Ni surfaces.
Table 7.
Detailed values of fluctuation components in WC-Ni surfaces.
| Times of Scopes | | | |
|---|
|
10 | | 0 | 0.3688 |
|
25 | | 0 | 0.3280 |
|
50 | | 0 | 0.2750 |
|
100 | | 0 | 0.2985 |
Table 8.
Detailed values of fluctuation components on 9Cr18Mo surfaces.
Table 8.
Detailed values of fluctuation components on 9Cr18Mo surfaces.
| Times of Scopes | | | |
|---|
|
10 | | 0 | 0.3001 |
|
50 | | 0 | 0.2815 |
|
100 | | 0 | 0.3440 |
Table 9.
Fractal dimension D obtained by different methods and their relative errors between the ideal D.
Table 9.
Fractal dimension D obtained by different methods and their relative errors between the ideal D.
| Ideal Fractal Dimension | Estimated Fractal Dimension | Relative Errors | Original Fractal Dimension | Relative Errors |
|---|
| 1.3 | 1.1963 | 7.98% | 0.465 | 64.23% |
| 1.2752 | 1.91% | 0.765 | 41.15% |
| 1.2380 | 4.77% | 0.97 | 25.38% |
| 1.2468 | 4.09% | 1.17 | 10% |
Table 10.
Scale coefficient logG obtained by different methods and their relative errors between the ideal logG.
Table 10.
Scale coefficient logG obtained by different methods and their relative errors between the ideal logG.
| | | Relative Errors | | Relative Errors |
|---|
| 20.3483 | 20.8309 | 2.37% | 30.5150 | 49.96% |
| 20.5919 | 1.20% | 27.3483 | 34.40% |
| 21.2166 | 4.27% | 24.7650 | 21.71% |
| 20.7483 | 1.97% | 21.7650 | 6.96% |