Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique
Abstract
1. Introduction
2. Materials and Methods
3. Basic Concepts on Fractional and Laplace Operators
- (i)
- .
- (ii)
- .
- (iii)
- .
- (i)
- .
- (ii)
- .
- (iii)
- .
- (iv)
- (v)
4. Constructing the L-RPS Solutions for Nonlinear T-FCB-BEs
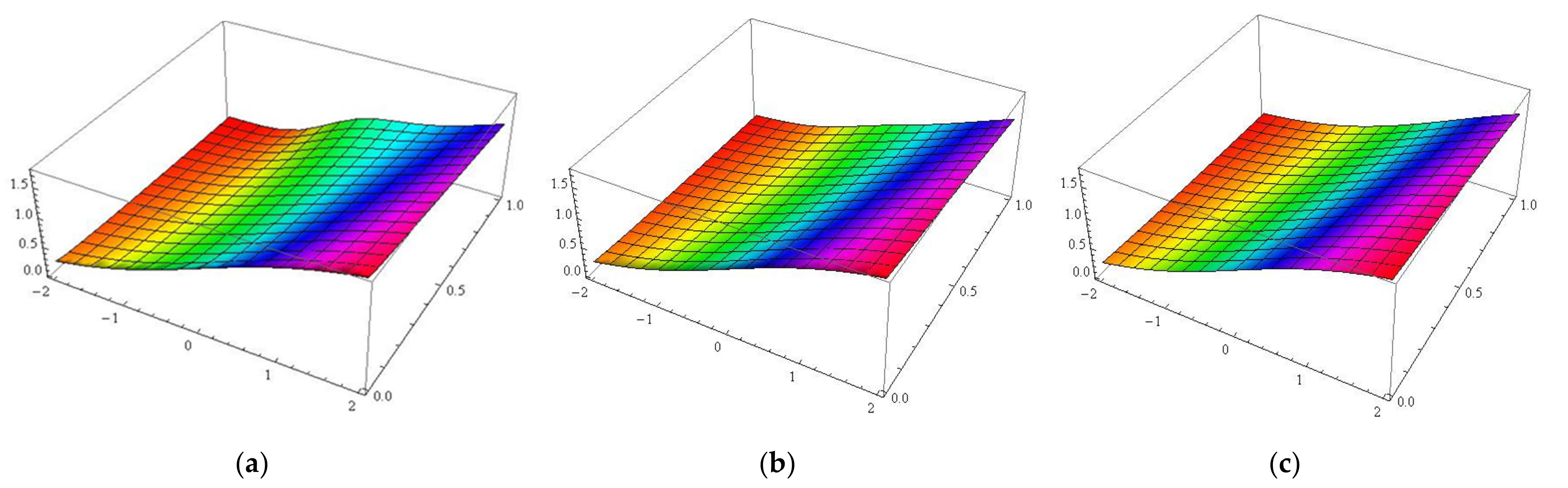
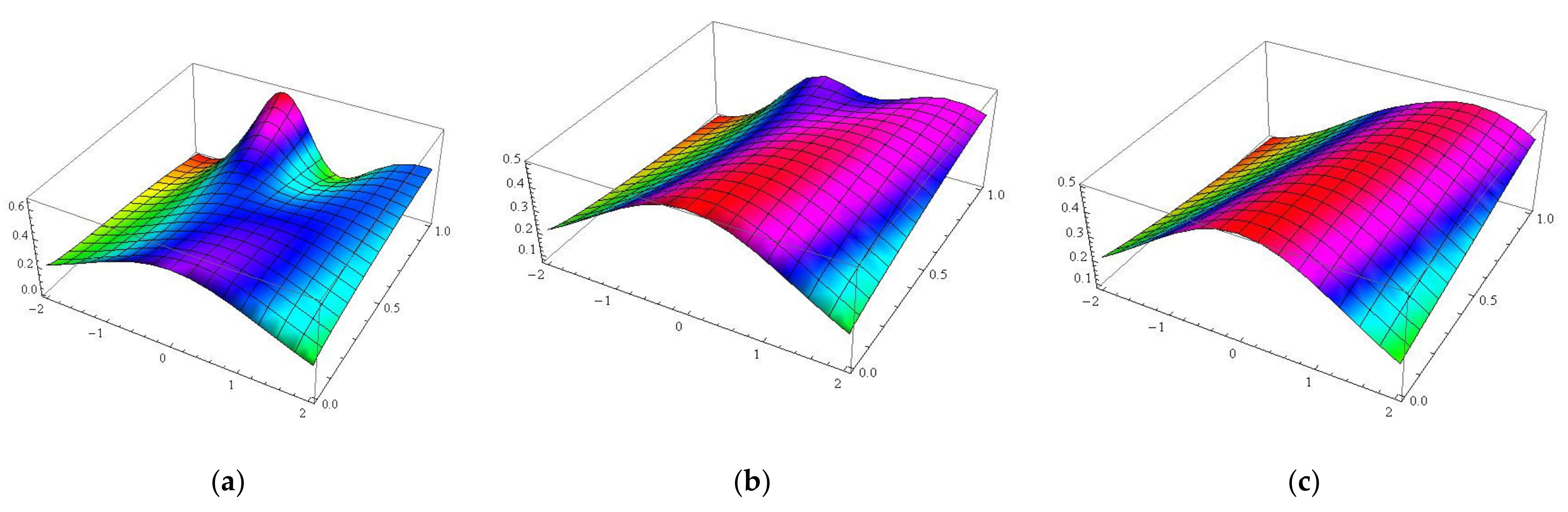
5. Application with Graphical Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El-Ajou, A.; Abu Arqub, O. Solving fractional two-point boundary value problems using continuous analytic method. Ain Shams Eng. J. 2013, 4, 539–547. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Comparison between the homotopy perturbation method and the variational iteration method for linear fractional partial differential equations. Comput. Math. Appl. 2007, 54, 910–919. [Google Scholar] [CrossRef]
- Gupta, A.K.; Saha Ray, S. Comparison between homotopy perturbation method and optimal homotopy asymptotic method for the soliton solutions of Boussinesq–Burger equations. Comput. Fluids 2014, 103, 34–41. [Google Scholar] [CrossRef]
- Das, S. Analytical solution of a fractional diffusion equation by variational iteration method. Comput. Math. Appl. 2009, 57, 483–487. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Ali, N.M. Application of optimal Homotopy asymptotic method to some well-known linear and nonlinear two-point boundary value problems. Int. J. Differ. Equ. 2018, 2018, 8725014. [Google Scholar] [CrossRef]
- Kazem, S. Exact solution of some linear fractional differential equations by Laplace transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Arikoglu, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar] [CrossRef]
- Momani, S. Non-perturbative analytical solutions of the space-and time-fractional Burger’s equations. Chaos Solitons Fractals 2006, 28, 930–937. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Smadi, M.; Oqielat, M.; Momani, S.; Hadid, S. Smooth expansion to solve high-order linear conformable fractional PDEs via residual power series method: Applications to physical and engineering equations. Ain Shams Eng. J. 2020, 11, 1243–1254. [Google Scholar] [CrossRef]
- El-Ajou, A.; Oqielat, M.; Al-Zhour, Z.; Momani, S. A class of linear non-homogenous higher order matrix fractional differential equations: Analytical solutions and new technique. Fract. Calc. Appl. Anal. 2020, 23, 356–377. [Google Scholar] [CrossRef]
- Shqair, M.; El-Ajou, A.; Nairat, M. Analytical solution for multi-energy groups of neutron diffusion equations by a residual power series method. Mathematics 2019, 7, 633. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Zhour, Z.; Oqielat, M.; Momani, S.; Hayat, T. Series solutions of non- linear conformable fractional KdV-Burgers equation with some applications. Eur. Phys. J. Plus 2019, 134, 402. [Google Scholar] [CrossRef]
- Oqielat, M.; El-Ajou, A.; Al-Zhour, Z.; Alkhasawneh, R.; Alrabaiah, H. Series solutions for nonlinear time-fractional Schrödinger equations: Comparisons between conformable and Caputo derivatives. Alex. Eng. J. 2020, 59, 2101–2114. [Google Scholar] [CrossRef]
- El-Ajou, A.; Oqielat, M.; Al-Zhour, Z.; Momani, S. Analytical numerical solutions of the fractional multi-pantograph system: Two attractive methods and comparisons. Results Phys. 2019, 14, 102500. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Oqielat, M.N.; Al-Zhour, Z.; Momani, S. A New attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos Solitons Fractals 2020, 138, 109957. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alex. Eng. J. 2022, 61, 1069–1077. [Google Scholar] [CrossRef]
- Saadeh, R.; Burqan, A.; El-Ajou, A. Reliable solutions to fractional Lane-Emden equations via Laplace transform and residual error function. Alex. Eng. J. 2022, 61, 10551–10562. [Google Scholar] [CrossRef]
- Khan, H.; Kumam, P.; Khan, Q.; Khan, S.; Hajira Arshad, M.; Sitthithakerngkiet, K. The solution comparison of time-fractional non-linear dynamical systems by using different techniques. Front. Phys. 2022, 11, 863551. [Google Scholar] [CrossRef]
- Alaroud, M. Application of Laplace residual power series method for approximate solutions of fractional IVP’s. Alex. J. 2022, 61, 1585–1595. [Google Scholar] [CrossRef]
- Khan, M.R.; AbidI, A.; Madioul, I.J.; Guedri, K.; Al-Bugami, A.M.; Al-arabi, T.H.; Al-Zhour, Z.; Galal, A.M. Impact of Joule heating and viscous dissipation on magnetohydrodynamics boundary layer flow of viscous nanofluid subject to the stretched surface. Proc. IMechE Part E J. Process Mech. Eng. 2021, 1–8. [Google Scholar] [CrossRef]
- Boussinesq, J. Thorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 1872, 17, 55–108. [Google Scholar]
- Malfliet, W. Solitary wave solutions of nonlinear wave equations. Am. J. Phys. 1992, 60, 650–654. [Google Scholar] [CrossRef]
- Tasbozan, O.; Senol, M.; Kurt, A.; Özkan, O. New solutions of fractional Drinfeld-Sokolov-Wilson system in shallow water waves. Ocean Eng. 2018, 161, 62–68. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Proc. R. Soc. A Math. Phys. Eng. Sci. 1967, 299, 6–25. [Google Scholar]
- Yokus, A.; Kaya, D. Numerical and exact solutions for time fractional Burgers’ equation. J. Nonlinear Sci. Appl. 2017, 10, 3419–3428. [Google Scholar] [CrossRef]
- Yoku¸s, A.; Kaya, D. Conservation laws and a new expansion method for sixth order Boussinesq equation. AIP Conf. Proc. 2015, 1676, 020062. [Google Scholar]
- Durur, H.; Tasbozan, O.; Kurt, A. New analytical solutions of conformable time fractional bad and good modified Boussinesq equations. Appl. Math. Nonlinear Sci. 2020, 5, 447–454. [Google Scholar] [CrossRef]
- Bateman, H. Some Recent Research on the Motion of Fluids. Mon. Weather Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves, 42; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Khanin, K.; Mazel, A.; Sinai, Y. Invariant measures for Burger’s equation with stochastic forcing. Ann. Math. 2000, 151, 877–960. [Google Scholar]
- Basto, M.; Semiao, V.; Calheiros, F. Dynamics and synchronization of numerical solutions of the Burgers equation. J. Comput. Appl. Math. 2009, 231, 793–806. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Erfani, E. New Analytical Method for Solving Burgers’ and nonlinear heat transfer equations and comparison with HAM. Comput. Phys. Commun. 2009, 180, 1539–1544. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Ozis, T.; Ozdes, A. A Direct variational method applied to Burger’s equation. J. Comput. Appl. Math. 1996, 71, 163–175. [Google Scholar] [CrossRef][Green Version]
- Evans, D.J.; Abdullah, A.R. The Group explicit method for the solution of Burger’s equation. Computing 1984, 32, 239–253. [Google Scholar] [CrossRef]
- Mittal, R.C.; Singhal, P. Numerical Solution of Burger’s equation. Commun. Numer. Methods Eng. 1993, 9, 397–406. [Google Scholar] [CrossRef]
- Caldwell, J.; Wanless, P.; Cook, A.E. A Finite element approach to burger’s equation. Appl. Math. Model. 1981, 5, 189–193. [Google Scholar] [CrossRef]
- Kurt, A.; Cenesiz, Y.; Tasbozan, O. Exact solution for the conformable Burger’s equation by the Hopf-Cole transform. Cankaya Univ. J. Sci. Eng. 2016, 13, 18–23. [Google Scholar]
- Inc, M. The approximate and exact solutions of the space- and time-fractional Burger’s equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345, 476–484. [Google Scholar] [CrossRef]
- Esen, A.; Yagmurlu, N.M.; Tasbozan, O. Approximate analytical solution to time-fractional damped Burger and Cahn-Allen equations. Appl. Math. Inf. Sci. 2013, 7, 1951–1966. [Google Scholar] [CrossRef]
- Esen, A.; Tasbozan, O. Numerical Solution of Time Fractional Burgers Equation by Cubic B-Spline Finite Elements. Mediterr. J. Math. 2016, 13, 1325–1337. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Y.; Li, X. Quasi-periodic solution of the (2+1)-dimensional Boussinesq–Burger’s soliton equation. Phys. A Stat. Mech. Appl. 2003, 319, 213–232. [Google Scholar] [CrossRef]
- Chen, A.; Li, X. Darboux transformation and soliton solutions of Boussinesq–Burger’s equation. Chaos Solitons Fractals 2006, 27, 43–52. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.F.; Li, C. Some new exact solutions of Jacobian elliptic function about the generalized Boussinesq equation and Boussinesq-Burgers equation. Chin. Phys. B 2008, 17, 403–410. [Google Scholar]
- Rady AS, A.; Khalfallah, M. On soliton solutions for Boussinesq-Burgers equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 886–894. [Google Scholar] [CrossRef]
- Wang, P.; Tian, B.; Liu, W.; Lü, X.; Jiang, Y. Lax pair, Bäcklund transformation and multi-soliton solutions for the Boussinesq-Burgers equations from shallow water waves. Appl. Math. Comput. 2011, 218, 1726–1734. [Google Scholar] [CrossRef]
- Ravi LK Ray, S.S.; Sahoo, S. New exact solutions of coupled Boussinesq–Burgers equations by Exp-function method. J. Ocean Eng. Sci. 2017, 2, 34–46. [Google Scholar] [CrossRef]
- Al-Amr, M.O. Solution of the coupled Boussinesq–Burger’s equations by reduced differential transform method. In Proceedings of the 15th International Conference for Informatics and Information Technology (CIIT 2018), Mavrovo, North Macedonia, 20–22 April 2018; pp. 83–87. [Google Scholar]
- Alrawashdeh MS Bani-Issa, S. An efficient technique to solve coupled–time fractional Boussinesq–Burger equation using fractional decomposition method. Adv. Mech. Eng. 2021, 13, 1–10. [Google Scholar] [CrossRef]
- Javeed, S.; Saif, S.; Waheed, A.; Baleanu, D. Exact solutions of fractional mBBM equation and coupled system of fractional Boussinesq-Burgers. Results Phys. 2018, 9, 1275–1281. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M.K. A generalized definition of the fractional derivative with applications. Math. Probl. Eng. 2021, 2021, 9444803. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M.K. A novel computational tool for the fractional-order special functions arising from modeling scientific phenomena via Abu-Shady–Kaabar fractional derivative. Comput. Math. Methods Med. 2022, 2022, 2138557. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Geng, L.L.; Yu, X.J. On fractional symmetry group scheme to the higher-dimensional space and time fractional dissipative Burgers equation. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250173. [Google Scholar] [CrossRef]
- Eyube, E.S.; Notani, P.P.; Dikko, A.B. Modeling of diatomic molecules with modified hyperbolical-type potential. Eur. Phys. J. Plus 2022, 137, 329. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarhan, A.; Burqan, A.; Saadeh, R.; Al-Zhour, Z. Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique. Fractal Fract. 2022, 6, 631. https://doi.org/10.3390/fractalfract6110631
Sarhan A, Burqan A, Saadeh R, Al-Zhour Z. Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique. Fractal and Fractional. 2022; 6(11):631. https://doi.org/10.3390/fractalfract6110631
Chicago/Turabian StyleSarhan, Aref, Aliaa Burqan, Rania Saadeh, and Zeyad Al-Zhour. 2022. "Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique" Fractal and Fractional 6, no. 11: 631. https://doi.org/10.3390/fractalfract6110631
APA StyleSarhan, A., Burqan, A., Saadeh, R., & Al-Zhour, Z. (2022). Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique. Fractal and Fractional, 6(11), 631. https://doi.org/10.3390/fractalfract6110631








