Fractal Analysis for Wave Propagation in Combustion–Explosion Fracturing Shale Reservoir
Abstract
1. Introduction
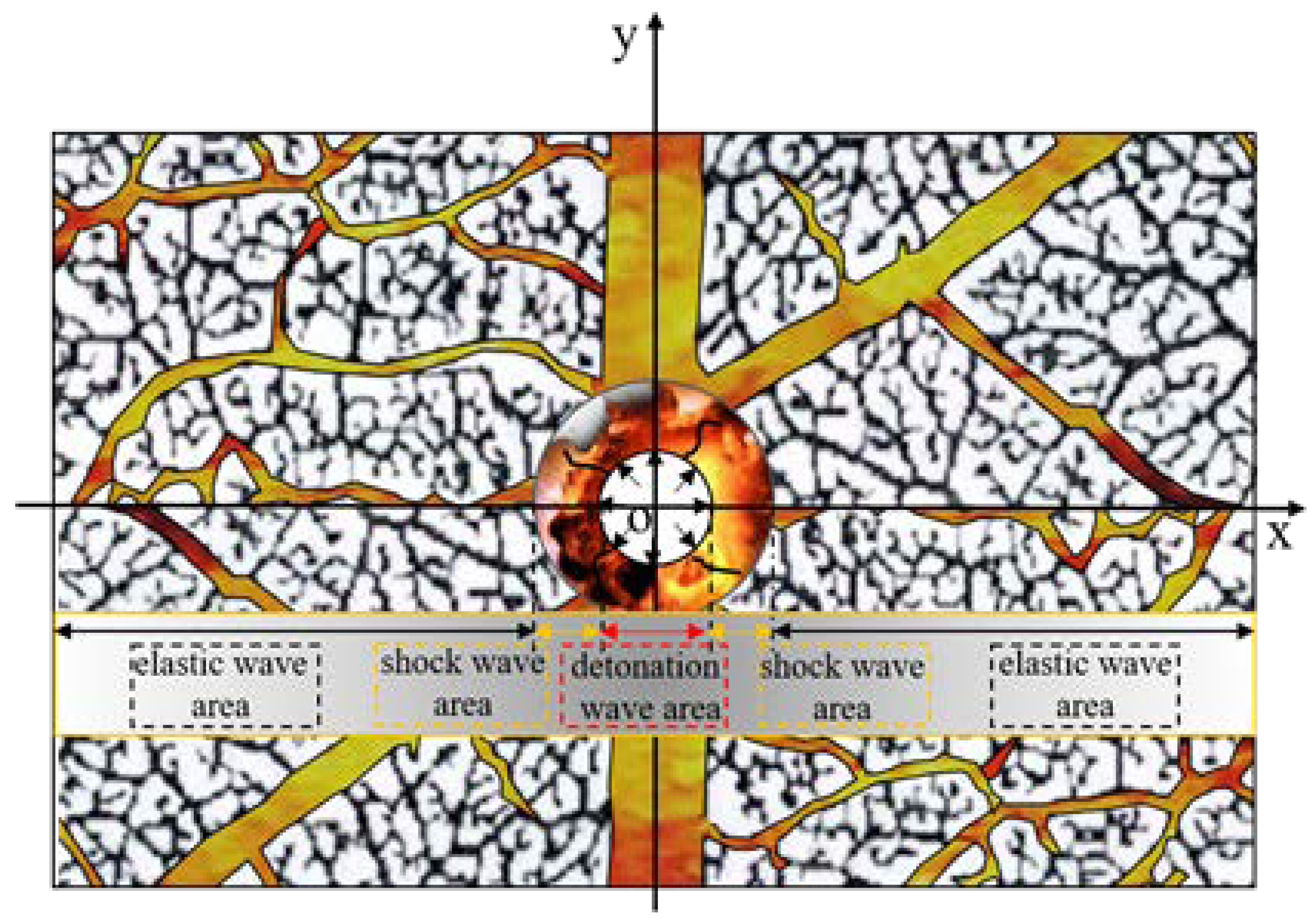
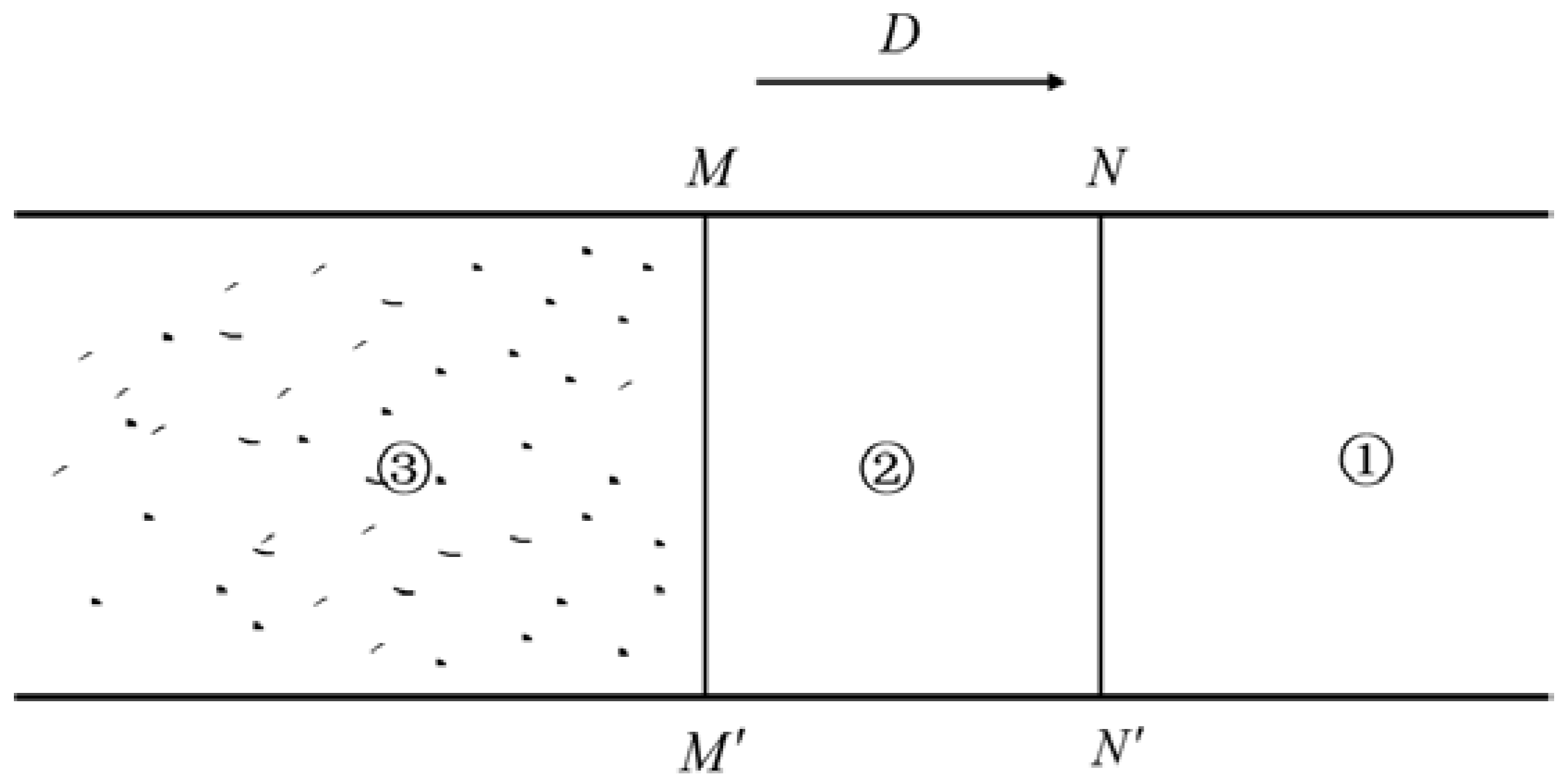
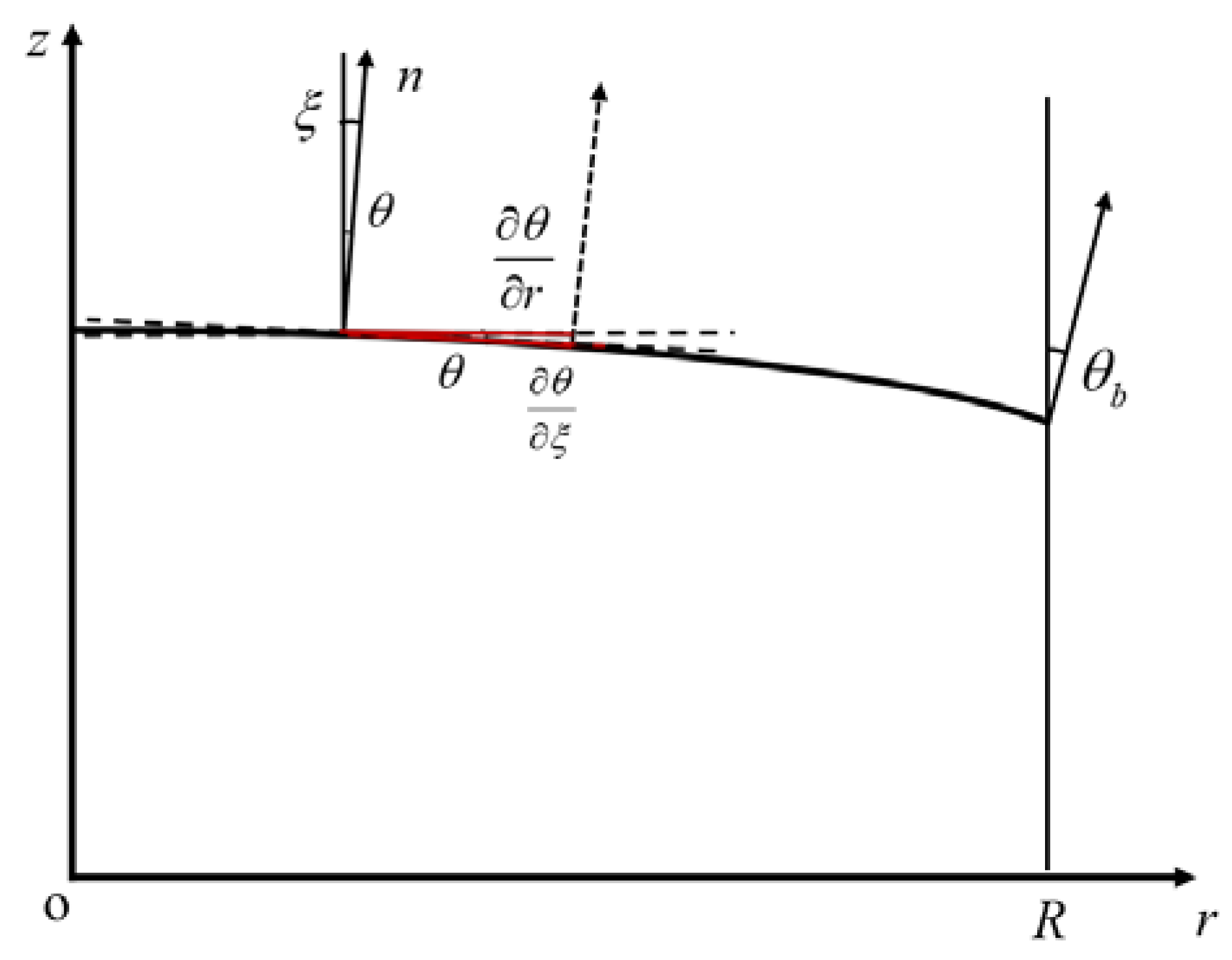
2. Transformation Mechanism of Local Rotational Failure from Detonation Wave Stage to Shock Wave Stage
- (a)
- The fractured rock is a heterogeneous, anisotropic, rigorous, porous continuum;
- (b)
- The wave flows in the same plane, and the density and viscosity of the fluid are independent of temperature;
- (c)
- The shock front of a plane blasting wave is a strong discontinuity, and the chemical reaction is instantaneous. The chemical reaction region is so thin that it can be treated as a mathematical plane;
- (d)
- The strong discontinuity is stable, and no dissipative effects, such as viscosity and heat conduction, happen during its propagation.
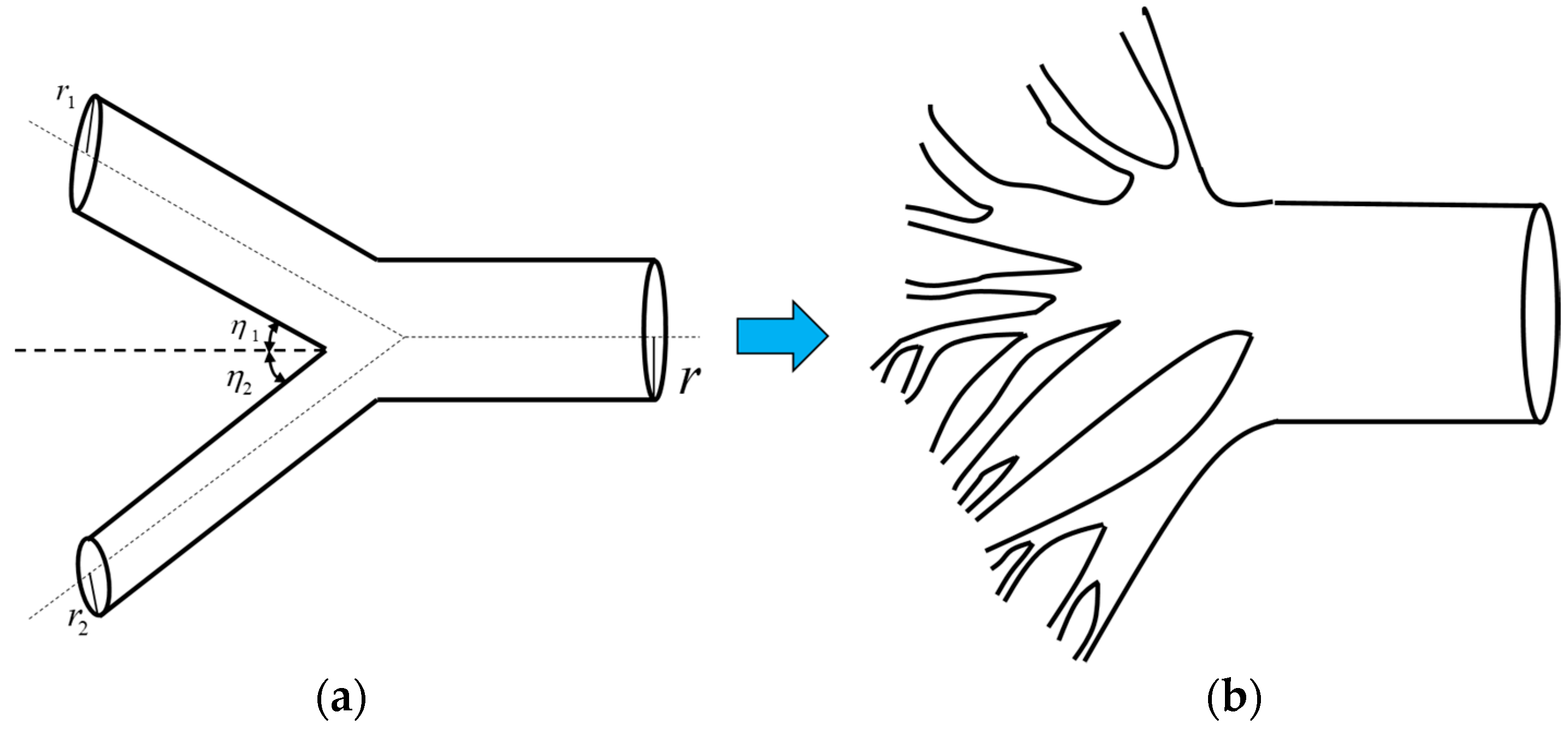
2.1. Governing Equation of Rotation Angle
2.2. Analytical Solutions of Rotation Angle
2.3. Discussion
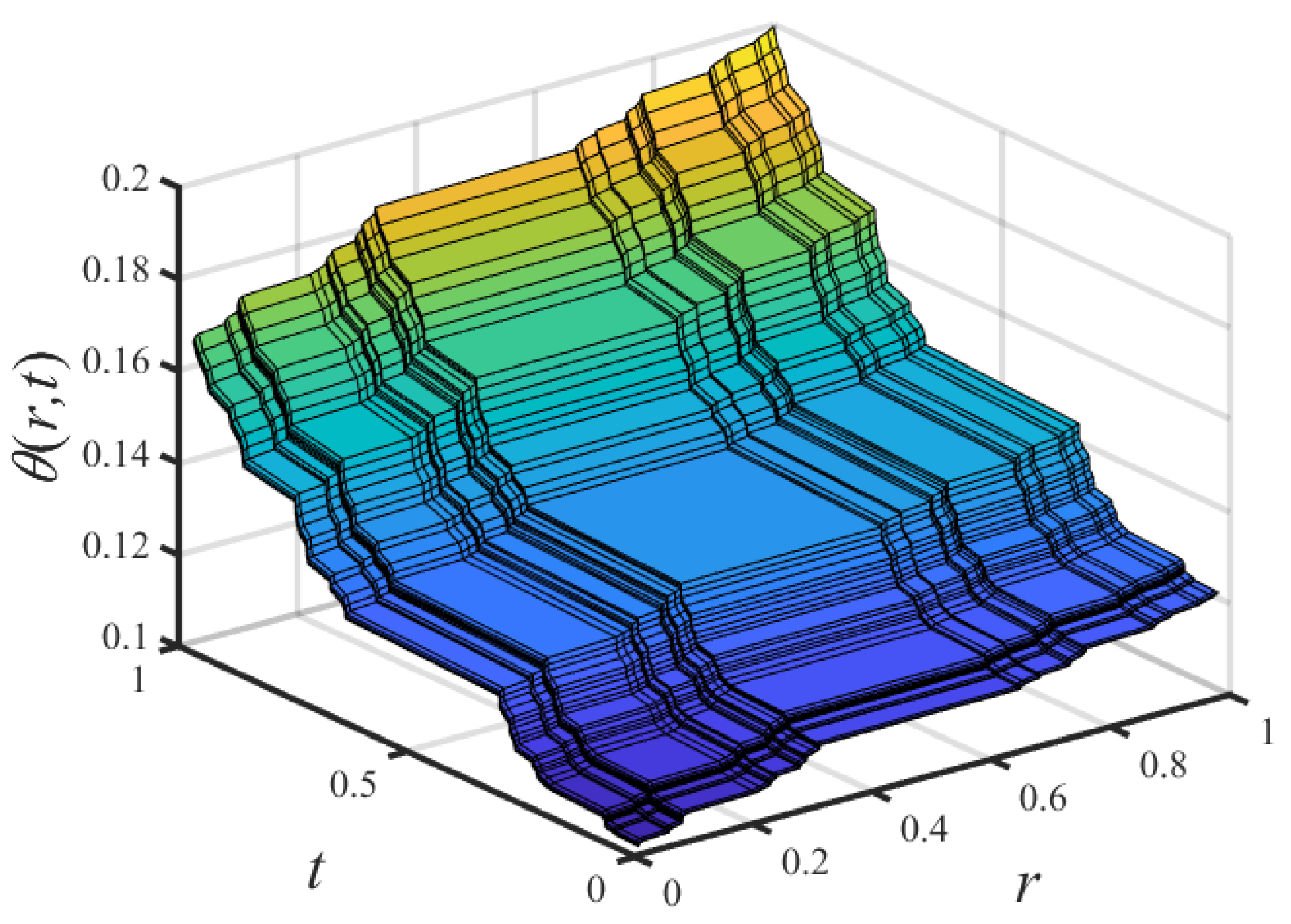
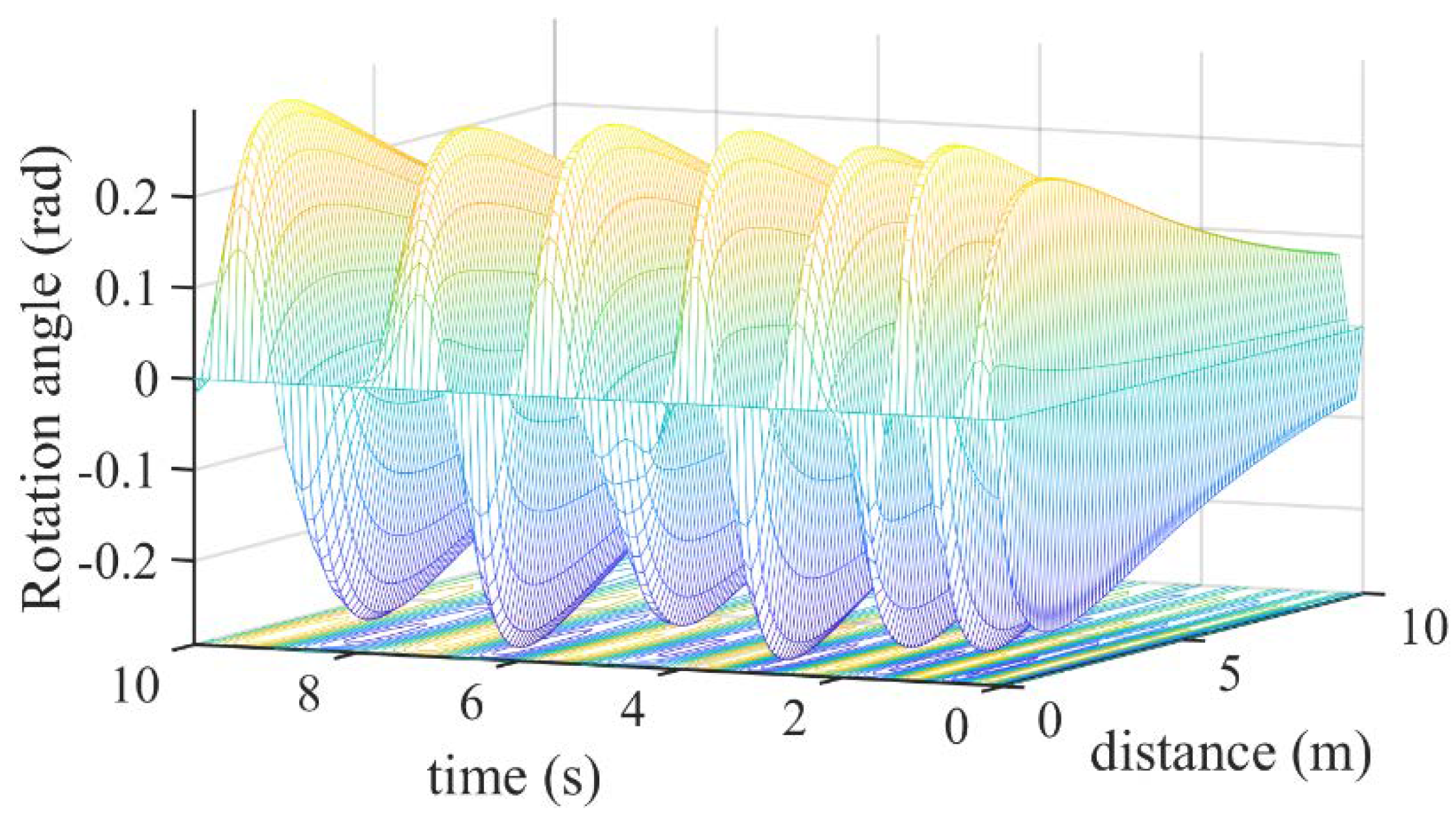
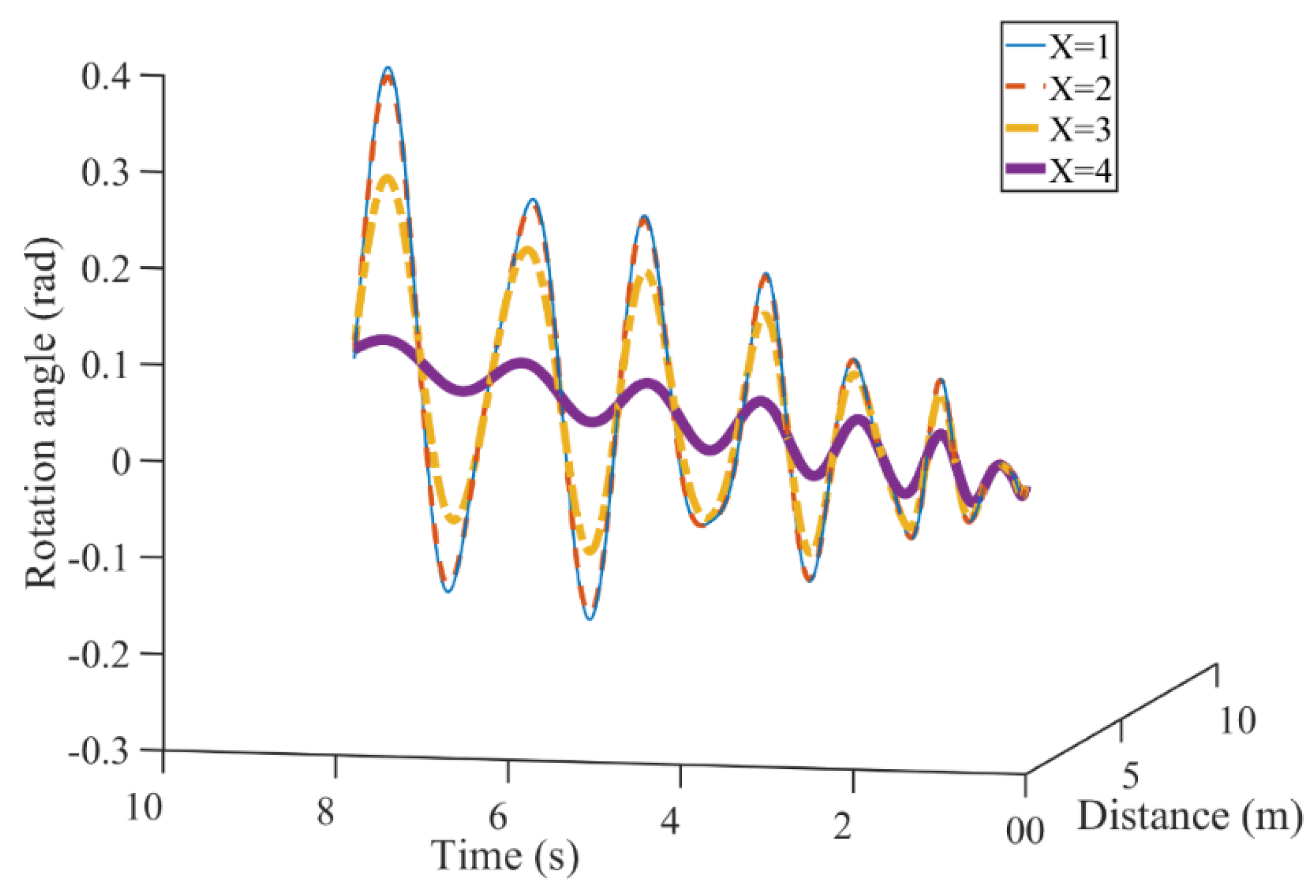
2.3.1. General Change of Rotation Angle
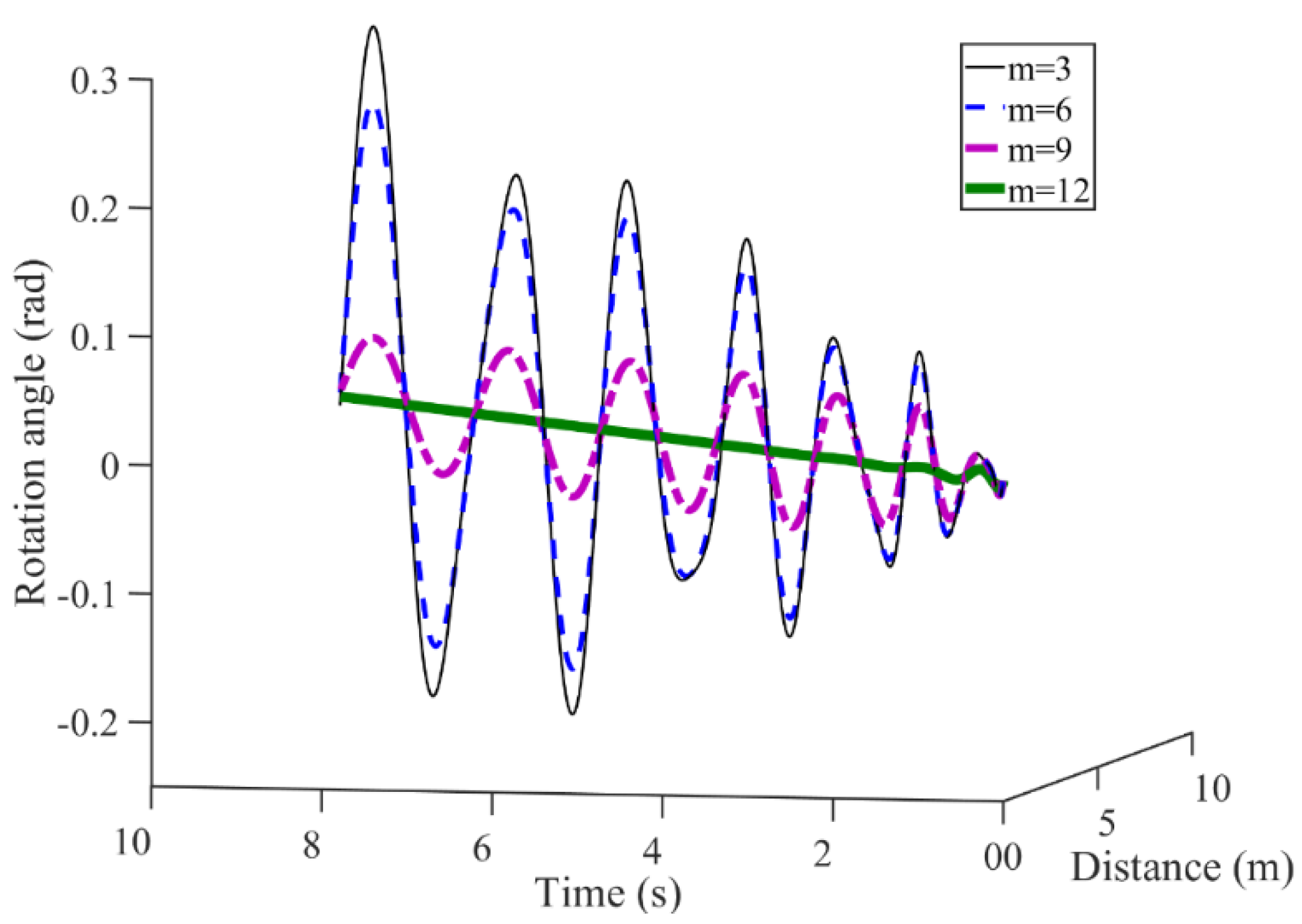
2.3.2. Sensitive Analysis of Branching Parameter
2.3.3. Sensitive Analysis of Aggregation Order
2.3.4. Sensitive Analysis of Explosive Type
3. Wave Propagation Mechanism from Shock Wave Stage to Elastic Wave Stage
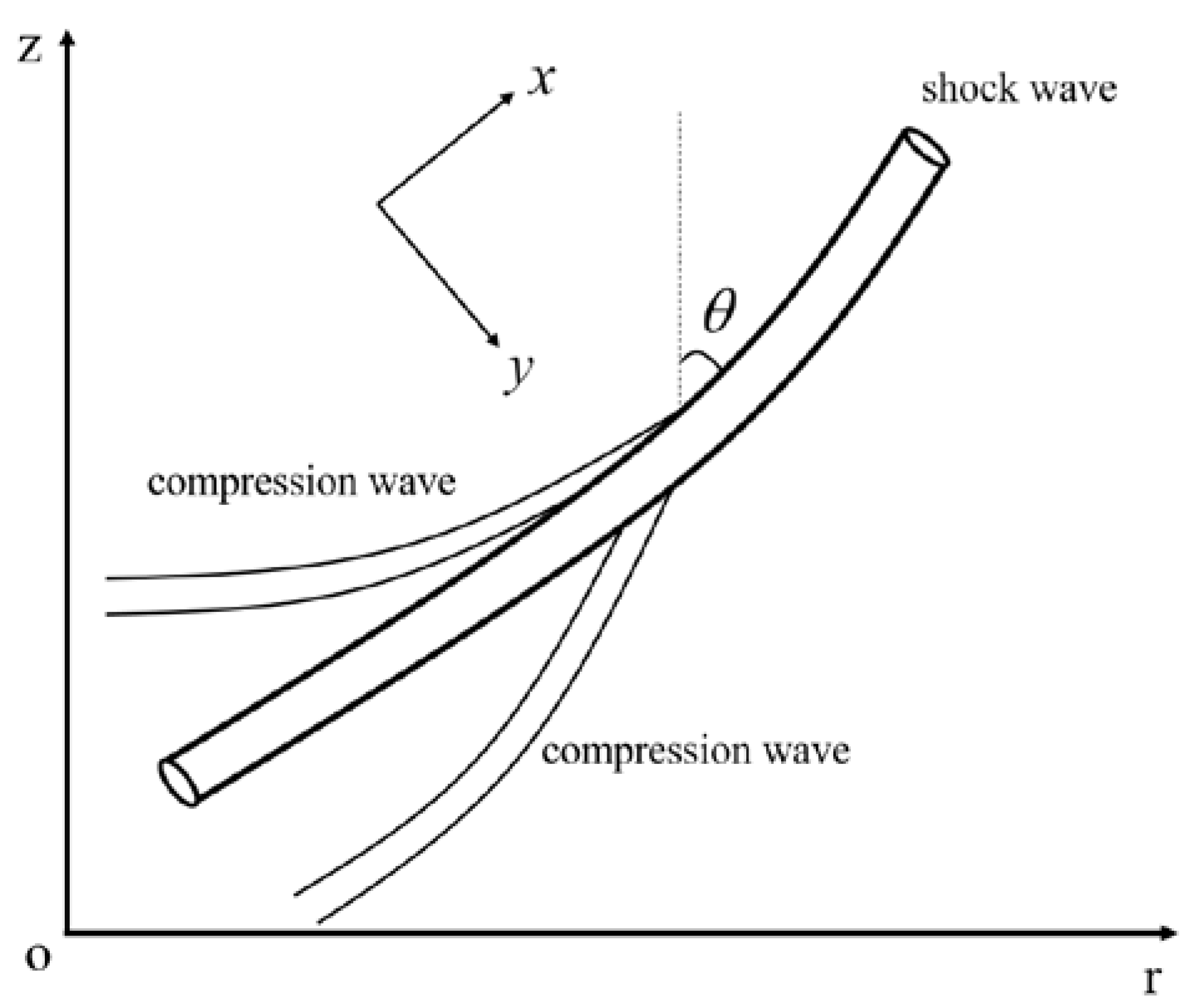
3.1. Governing Equation of P-Wave Displacement
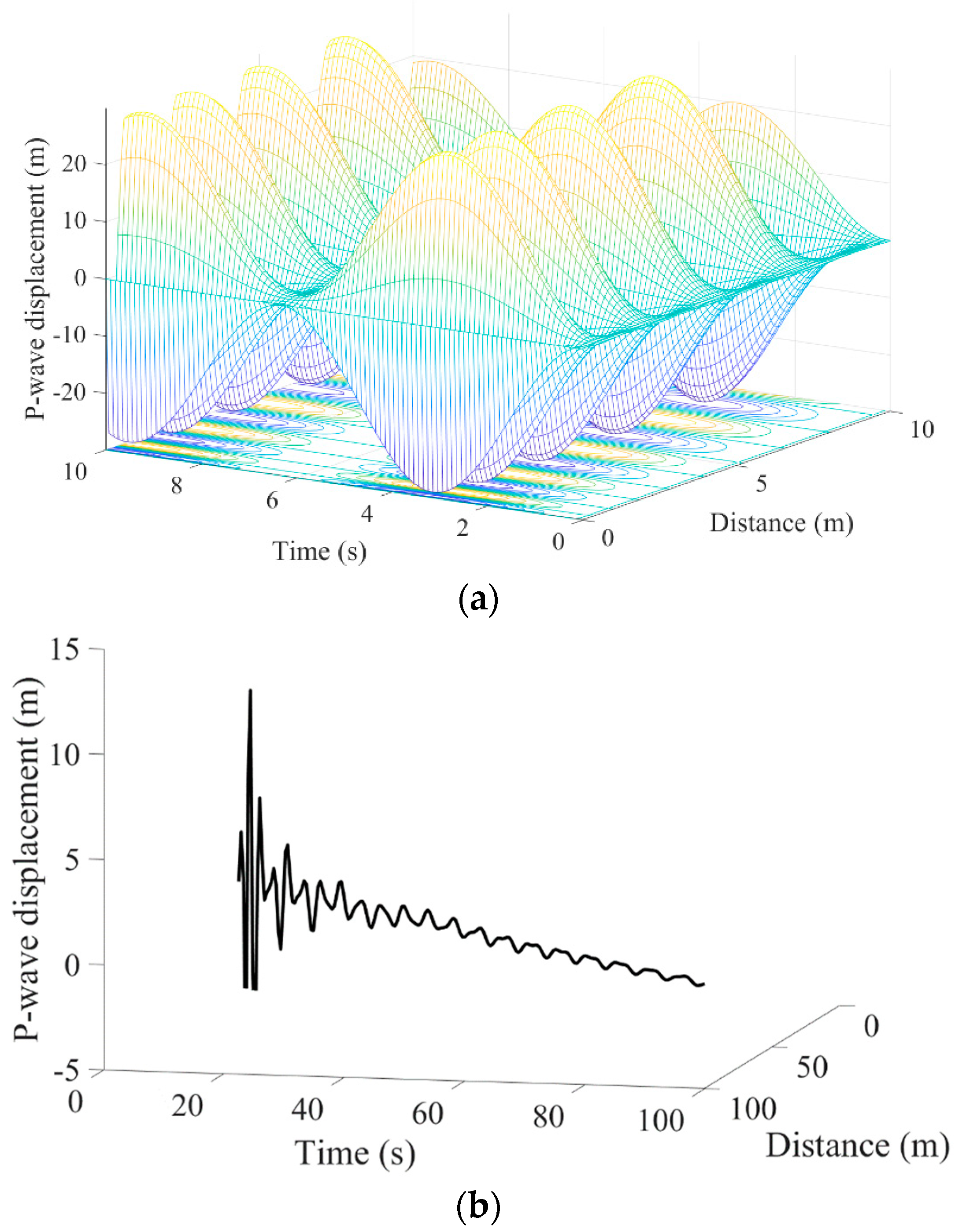
3.2. Analytical Solutions of P-Wave Displacement
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hughes, J.D. Energy: A reality check on the shale revolution. Nature 2013, 494, 307–308. [Google Scholar] [CrossRef]
- Wu, J.J.; Liu, L.C.; Zhao, G.H.; Chu, X.S. Research and exploration of high energy gas fracturing stimulation integrated technology in Chinese shale gas reservoir. Adv. Mater. Res. 2012, 524–527, 1532–1536. [Google Scholar]
- Mahdaviara, M.; Sharifi, M.; Ahmadi, M. Toward evaluation and screening of the enhanced oil recovery scenarios for low permeability reservoirs using statistical and machine learning techniques. Fuel 2022, 325, 124795. [Google Scholar] [CrossRef]
- Wu, J.J.; Liu, J.; Zhao, J.Z.; Du, F. Research on explosive fracturing technology of liquid explosives in micro-cracks in low permeability reservoirs. Mater. Sci. Eng. 2019, 592, 4–6. [Google Scholar] [CrossRef]
- Wu, F.P.; Wei, X.M.; Chen, Z.X.; Rahman, S.S.; Pu, C.S.; Li, X.J.; Zhang, Y.Y. Numerical simulation and parametric analysis for designing high energy gas fracturing. J. Nat. Gas Sci. Eng. 2018, 53, 218–236. [Google Scholar] [CrossRef]
- Roberts, L.N. Liquid Explosive for Well Fracturing; U.S.P.: Rockville, MD, USA, 1974; p. 3825452. [Google Scholar]
- Ye, Q.; Lin, B.Q.; Jia, Z.Z.; Zhu, C.J. Propagation law and analysis of gas explosion in bend duct. Procedia Earth Planet. Sci. 2009, 1, 316–321. [Google Scholar]
- Shang, X.J.; Wang, J.G.; Zhang, Z.Z.; Gao, F. A three-parameter permeability model for the cracking process of fractured rocks under temperature change and external loading. Int. J. Rock Mech. Min. 2019, 123, 104106. [Google Scholar] [CrossRef]
- Wang, F.; Cheng, H. A fractal permeability model for 2D complex tortuous fractured porous media. J. Petrol. Sci. Eng. 2020, 188, 106938. [Google Scholar] [CrossRef]
- Ma, C.; Zhu, C.J.; Zhou, J.X.; Ren, J.; Yu, Q. Dynamic response and failure characteristics of combined rocks under confining pressure. Sci. Rep. 2022, 12, 12187. [Google Scholar] [CrossRef]
- Smoller, J. Shock Waves and Reaction-Diffusion Equations; Springer: New York, NY, USA, 1983; pp. 337–358. [Google Scholar]
- Tahir, S.I.; Tounsi, A.; Chikh, A.; Al-Osta, M.A.; Al-Dulaijan, S.U.; Al-Zahrani, M.M. The effect of three-variable viscoelastic foundation on the wave propagation in functionally graded sandwich plates via a simple quasi-3D HSDT. Stell Compos. Struct. 2022, 42, 501–511. [Google Scholar]
- Tahir, S.I.; Chikh, A.; Tounsi, A.; Al-Osta, M.A.; Al-Dulaijan, S.U.; Al-Zahrani, M.M. Wave propagation analysis of a ceramic-metal functionally graded sandwich plate with different porosity distributions in a hygro-thermal environment. Compos. Struct. 2021, 269, 114030. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.J.; Huang, Y.B.; Xia, Y. Experimental study of fracture evolution in enhanced geothermal systems based on fractal theory. Geothermics 2022, 102, 102406. [Google Scholar] [CrossRef]
- Mustafa, S.; Hajira; Khan, H.; Shah, R.; Masood, S. A novel analytical approach for the solution of fractional-order diffusion-wave equations. Fractal Fract. 2021, 5, 206. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. Approximate solutions of the damped wave equation and dissipative wave equation in fractal strings. Fractal Fract. 2019, 3, 26. [Google Scholar] [CrossRef]
- Yang, Y.J.; Baleanu, D.; Yang, X.J. A local fractional variational iteration method for Laplace equation within local fractional operators. Abstr. Appl. Anal. 2013, 2013, 202650. [Google Scholar] [CrossRef]
- Shang, X.J.; Wang, J.G.; Zhang, Z.Z. Analytical solutions of fractal-hydro-thermal model for two-phase flow in thermal stimulation enhanced coalbed methane recovery. Therm. Sci. 2019, 23, 1345–1353. [Google Scholar] [CrossRef]
- Shang, X.J.; Wang, J.G.; Yang, X.J. Fractal analysis for heat extraction in geothermal system. Therm. Sci. 2017, 21, S25–S31. [Google Scholar] [CrossRef]
- Hou, R.; Xu, W.B. The Traveling Wave Solutions in a Mixed-Diffusion Epidemic Model. Fractal Fract. 2022, 6, 217. [Google Scholar] [CrossRef]
- Hong, T.; Wang, H. Analytical solution for unsteady two-dimensional detonation two-dimensional detonation wave with DSD method. Explo. Shock Waves 1996, 16, 317–325. (In Chinese) [Google Scholar]
- Jones, J. The spherical detonation. Adv. Appl. Math. 1991, 12, 147–186. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, F.L.; Wu, Y.Q.; Long, R.R. Explosion Physics; Beijing Institute of Technology Press: Beijing, China, 2019; pp. 60–68. [Google Scholar]
- Yu, B.B.; Xu, P.; Zou, M.Q.; Cai, J.C.; Zheng, Q. Transport Physics of Fractal Porous Media; Science Press: Beijing, China, 2014; pp. 131–149. [Google Scholar]
- Bdzil, J.B. Modeling two-dimension with detonation shock dynamics. Phy. Fluids 1989, 1, 1261–1267. [Google Scholar] [CrossRef]
- Lambourn, B.D. Application of Whitham’s shock dynamics theory to the propagation of divergent detonation waves, In 9th Symp (Intern) on Detonation; Office of Naval Research: Portland, OR, USA, 1989; pp. 784–797. [Google Scholar]
- Chen, Y.; Huang, T.F.; Liu, E.R. Rock Physics; University of Science and Technology of China Press: Hefei, China, 2009; pp. 79–85. [Google Scholar]
- Wei, Y.Z. Detonation and propagation behavior of TATB explosive. In Internal Report of Institute of Fluid Physics; CAEP: Mianyang, China, 1991. [Google Scholar]
- Shang, X.J.; Wang, J.G.; Zhang, Z.Z. Iterative analytical solutions for nonlinear two-phase flow with gas solubility in shale gas reservoirs. Geofluids 2019, 2019, 4943582. [Google Scholar] [CrossRef]

| Parameter | Unit | Value | Physical Meanings |
|---|---|---|---|
| 4 | branching parameter of fractured shale | ||
| 10 | grades of bifurcated pipes | ||
| 6209 | compression wave velocity of the 0-th pipe | ||
| 0.875 | constant related to nature of the explosive | ||
| m | 0.108 | radius of detonation wave area | |
| ln2/ln3 | fractional order | ||
| E | MPa | 7500 | Young’s modulus of shale |
| 0.25 | Poisson’s ratio of shale | ||
| 2600 | density of shale | ||
| m | 0.108 | initial displacement of shock wave |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, X.; Zhang, Z.; Yang, W.; Wang, J.G.; Zhai, C. Fractal Analysis for Wave Propagation in Combustion–Explosion Fracturing Shale Reservoir. Fractal Fract. 2022, 6, 632. https://doi.org/10.3390/fractalfract6110632
Shang X, Zhang Z, Yang W, Wang JG, Zhai C. Fractal Analysis for Wave Propagation in Combustion–Explosion Fracturing Shale Reservoir. Fractal and Fractional. 2022; 6(11):632. https://doi.org/10.3390/fractalfract6110632
Chicago/Turabian StyleShang, Xiaoji, Zhizhen Zhang, Weihao Yang, J. G. Wang, and Cheng Zhai. 2022. "Fractal Analysis for Wave Propagation in Combustion–Explosion Fracturing Shale Reservoir" Fractal and Fractional 6, no. 11: 632. https://doi.org/10.3390/fractalfract6110632
APA StyleShang, X., Zhang, Z., Yang, W., Wang, J. G., & Zhai, C. (2022). Fractal Analysis for Wave Propagation in Combustion–Explosion Fracturing Shale Reservoir. Fractal and Fractional, 6(11), 632. https://doi.org/10.3390/fractalfract6110632











