Abstract
In this paper, the global attractive set (GAS) and positive invariant set (PIS) of the five-dimensional Lorenz model with the fractional order derivative are studied. Using the Mittag-Leffler function and Lyapunov function method, the ultimate boundedness of the proposed system are estimated. An effective control strategy is also designed to achieve the finite time stability of this fractional chaotic system. The corresponding boundedness and control scheme are numerically verified to show the effectiveness of the theoretical analysis.
1. Introduction
In recent years, interest in studying fractional-order dynamical systems has increased. Modeling many systems with fractional order equations is a necessity to study the behavior of dynamical systems in more realistic applications [1,2,3,4,5,6,7,8]. Integer order calculus is a special case in fractional calculus that is approximate to the real system in the mathematical model. Viscoelastic systems [9], distributed-order dynamical systems [10], hydro-turbine governing systems [11], and glucose-insulin regulatory system [12] are described by fractional order equations. Investigating the stability, control, and synchronization of chaotic fractional dynamical systems are three important issues that have been considered by researchers. Some physical systems exhibit fractional dynamic behavior due to their special properties. Since fractional calculus provides an accurate way to describe, predict, and control physical systems, it is used for these goals. The adaptive fuzzy control scheme, sliding-mode control, linear, nonlinear, active, feedback, and adaptive control method have been applied for the global stability and projective synchronization of chaotic fractional systems [13,14,15,16,17].
Chaos in dynamical systems presented with two-dimensional equations, including forced, dissipative Rayleigh-Benard convection. This system was named the 3-dimensional Lorenz model (3DLM) [18,19,20,21]. Lorenz showed that accurate weather predictions are impossible and numerical calculations indicated that the behavior of 3DLM becomes chaotic due to certain parameters and initial conditions.
Shen [22,23] studied the three-dimensional Lorenz model (3DLM) and developed it into a five-dimensional Lorenz model (5DLM). Many interesting properties of this system, which include improving the stability of the solutions [24], were investigated by Shen. He fully articulated the role of modes in the behavior of solutions and their stability. Additionally, the effect of some parameters in increasing the stability of system solutions was another highlight of his research. The Lorenz equations of 3, 5, and higher dimensions are derived from the Rayleigh-Benard convection equations, which have three physical processes, namely heating, dissipative, and nonlinear advection. Faghihi-Naini and Shen [25] examined the non-dissipative version of the 5DLM from another perspective. They proposed an analytical method for solving the 5DLM and thus were able to produce the quasi-periodic solutions to the system using the nonlinear feedback loop (NFL). These studies showed that by further expanding the NFL and introducing Lorenz systems with higher dimensions, interesting and practical results can be achieved.
Estimation of boundaries and attractive sets in dynamical systems is one of the important and practical issues in chaos control, chaos synchronization, Hausdorff dimension, and finding the system’s hidden attractors [26,27,28,29,30,31,32,33,34]. In fact, if one can calculate ultimate bound set (UBS) or globally attractive set (GAS) for a system, then one can claim that this system will not have any chaotic attractors, equilibrium points, periodic solutions, quasi-periodic solutions, etc., outside of these sets. This issue has a great application in controlling systems and preventing their possible problems [35,36,37,38]. In this paper, we will introduce the five-dimensional Lorenz model with the fractional order derivative. To the best of our knowledge, the GAS and the UBS for the fractional five-dimensional Lorenz model have not been investigated. As an innovation, in addition to proving the global boundness of the proposed system, we calculate a family of GASs. In fact, by changing system parameters and other conditions, we can create a variety of attractive sets. Furthermore, a controller is designed so that the controlled system can be stabilized in a finite time.
This article is organized in the following sections. Section 2 presents the integer and fractional model of five-dimensional Lorenz model (5DLM). In Section 3, we will study the Mittag-Leffler GASs of the fractional five-dimensional Lorenz model. Section 4 discusses the finite-time stability of the proposed system. Conclusions are drawn in Section 5.
2. Mathematical Model
In this section, we first review the process of generalizing the 3D Lorenz model to 5DLM and then introduce the fractional order five-dimensional Lorenz model.
2.1. Integer Order Five-Dimensional Lorenz Model
The flow occurred in a layer of fluid with uniform H depth was studied by Rayleigh [21]. Lorenz, in 1963 [18], introduced Rayleigh-Bennard equations for two-dimensional, forced, and dissipative convection:
where is a stream function, is temperature perturbation, and the constants and denote the acceleration of gravity, the coefficient of thermal expansion, the kinematic viscosity, and the thermal diffusivity, respectively. Additionally, is the difference in temperature between the top and bottom boundaries.
The chaotic system that Lorenz introduced is expressed as the following equations:
Although the 3DLM demonstrates solution dependence on initial conditions for chaotic solutions, the generalized Lorenz models (LMs) were derived for understanding the impact of mode truncations on solution stability and the route to chaos. Shen et al. [22] extended the 3DLM to the five-dimensional LM (5DLM) by including two additional Fourier modes with two additional vertical wave numbers. They used the five Fourier modes and rewrote and as the following:
where is Rayleigh number, is the critical value of free-slip Rayleigh-Benard problem, a is a ratio of the vertical scale of the convection cell to its horizontal scale, and
An additional mode is included to derive the 6DLM. Here, l and m are defined as and representing the horizontal and vertical wave numbers, respectively, and a is a ratio of the vertical scale of the convection cell to its horizontal scale. The term H is the domain height and represents the domain width.
By coordinate transformation, the original equation can be reduced to the following five-dimensional nonlinear dynamics:
where are constant parameters. The dynamic properties and conditions of the new five-dimensional Lorenz model (6) were investigated in [22,25,39,40,41]. They discussed in detail the numerical solutions, which included chaotic, periodic, and quasi-periodic responses.
2.2. Basic Definitions of Fractional Calculus
Definition 1.
The Riemann-Liouville fractional integral function is
is the gamma function:
Definition 2.
The Caputo fractional-order derivative of function is
Definition 3.
The Mittag-Leffler function with two parameters is defined as
where and m is a complex number. It is clear that
Let us consider the following fractional-order system
where , is sufficiently smooth and is the solution.
Definition 4.
For a given Lyapunov function with , if there exists constants and such that
for , then is said to be the Mittag-Leffler GAS of system (11). If for any and any , then is said to be a Mittag-Leffler PISs, where
2.3. Fractional Five-Dimensional Lorenz Model
Let us introduce the fractional calculus into the system (6). The fractional-order of the five-dimensional Lorenz model can be written as follows:
when , and , the chaotic behavior of system (6), are shown in Figure 1 and Figure 2. It is noteworthy that changing the order of fractional derivative changes the behavior of the system from chaotic to steady-state, which is shown in Figure 3. The time responses and phase portraits of system (13), with , and , are shown in Figure 4 and Figure 5.
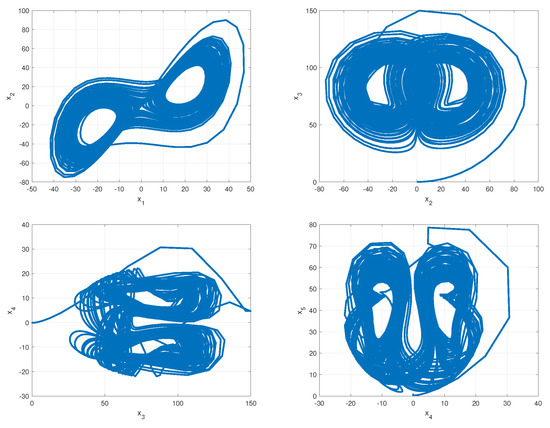
Figure 1.
The phase portraits of system (13), where , and .
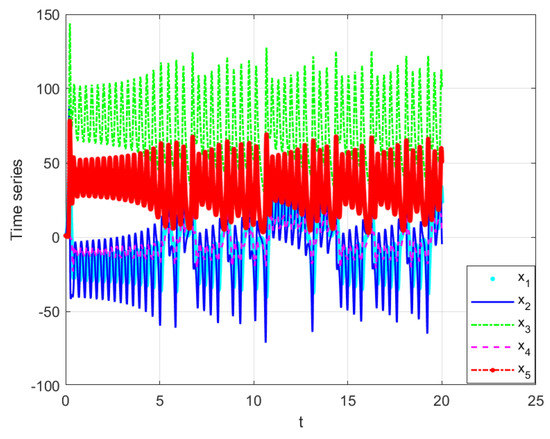
Figure 2.
Time responses of the states (13), where , and .
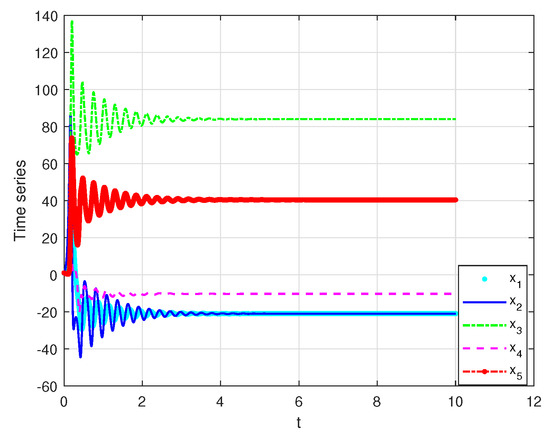
Figure 3.
Time responses of the states (13), where and .
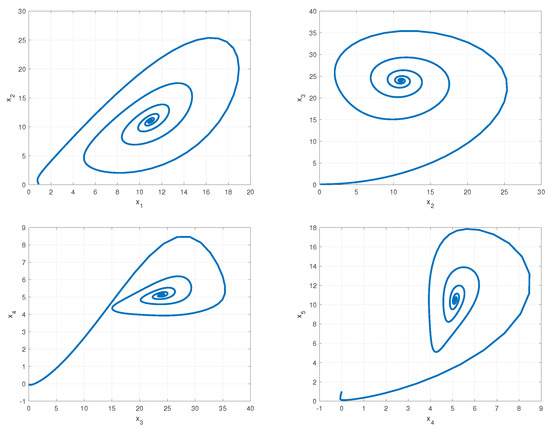
Figure 4.
Phase portrait for (13) with , and .
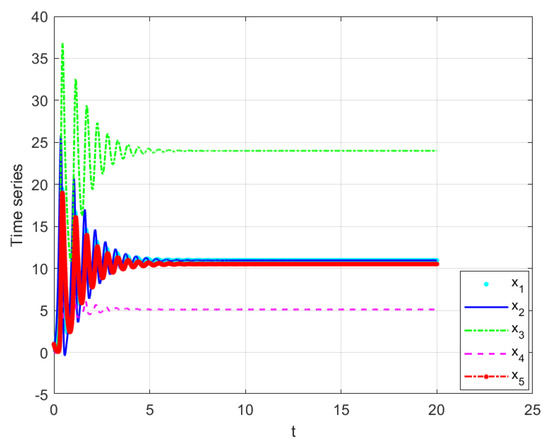
Figure 5.
Time responses of the states (13), where , and .
3. Mittag-Leffler GAS Estimation of the Fractional Five-Dimensional Lorenz Model
In this section, we will calculate the Mittag-Leffler GASs for the fractional-order of five-dimensional Lorenz model (13).
Lemma 1
([42]). If is a continuous and differentiable function, then
Lemma 2
([42]). For and constant , if a continuous function meets
then
The following theorem investigated the Mittag-Leffler GASs and the Mittag-Leffler PISs of the system (13):
Theorem 1.
Let and denote
Then is the Mittag-Leffler GASs and the Mittag-Leffler PISs of system (13), where
and
Proof.
Define the following generalized positively definite and radically unbounded Lyapunov function
where Computing the derivative of along the trajectory of system (13), we have
where
It is obvious that
Remark 1.
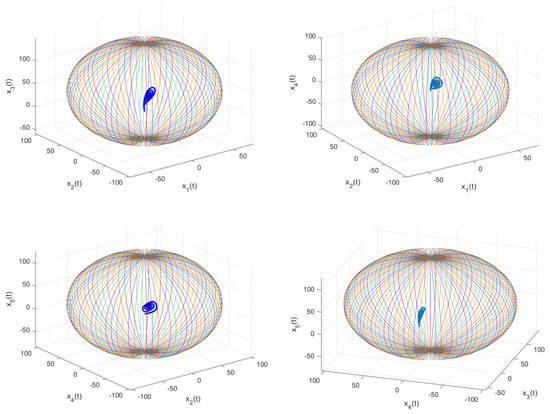
When and we have
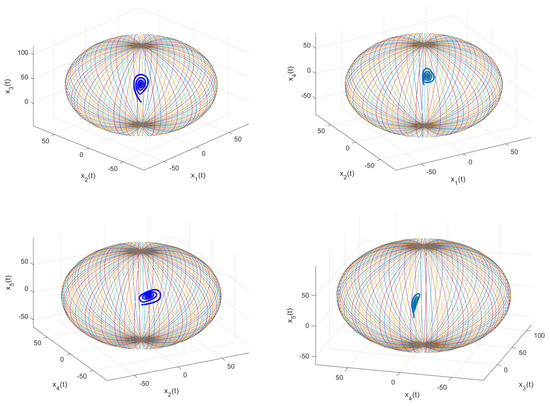
Figure 6 shows the phase portraits and the Mittag-Leffler GAS of system (13) in the different spacess defined by

Figure 6.
The phase portraits and the Mittag-Leffler GAS () of system (13), where , , and
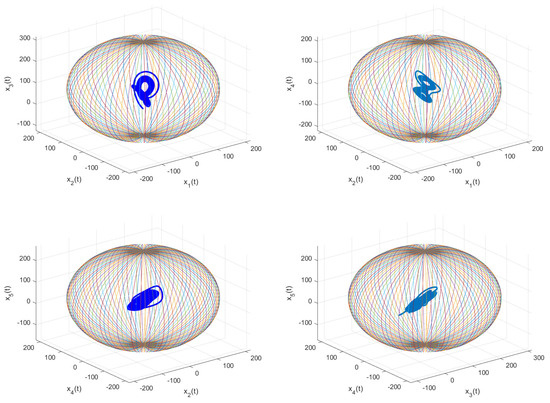
By considering the value of the solutions of (13) change from steady-state to chaotic. Figure 7 shows chaotic attractors of system (13) in the different spacess defined by (ii) Let us take then we get that the set
is the Mittag-Leffler GAS of system (6).

Figure 7.
The phase portraits and the Mittag-Leffler GAS of system (13), where and
When and we have
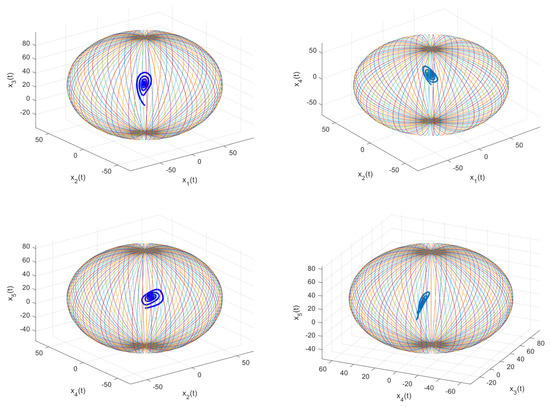
Figure 8 shows the phase portraits and the Mittag-Leffler GAS of system (13) in the different spacess defined by

Figure 8.
The phase portraits and the Mittag-Leffler GAS () of system (13), where , and
When and we have
Figure 9 shows the phase portraits and the Mittag-Leffler GAS of system (13) in the different spacess defined by

Figure 9.
The phase portraits and the Mittag-Leffler GAS () of system (13), where , and
4. Finite-Time Stabilization of Fractional Order System
In this section, we design an effective control scheme to stabilize the fractional-order five-dimensional Lorenz model in a finite time. The controlled fractional order system is given as
where , and are control parameters of the system (23). Now the control goal is to design a suitable robust controller to stabilize system (23) around zero in finite time.
Lemma 3
([43]). If are positive real numbers, and then we have the following inequality:
Theorem 2
([43]). Assume that is a domain containing the origin and is a continuously differentiable function and locally Lipschitz, so that
where then the system (23) is called Mittag-Leffler stable.
In the previous section, we have derived the Mittag-Leffler GAS and Mittag-Leffler PIS for the system (13):
where was given in (17). This implies that there exists constants and such that
Theorem 3.
The controlled chaotic system (23) can be finite-timely stabilized by the controller,
where , and the finite time T is estimated by:
Proof.
To prove the stability of system (23), let us use the classic Lyapunov direct method, proposing the quadratic function as a Lyapunov candidate, which is positive definite
Substituting (27) into (23), calculating the -order fractional derivative of the Lyapunov function and using Lemma 1, one can get
then,
It is obvious that the Lyapunov function defined in (29) satisfies conditions (25) and (26) in Theorem 2. Thus, the system (23) is Mittag-Leffler stable. Based on the property of Caputo fractional derivatives,
we have
therefore, we obtain from (30) and (32)
and one may take integral of both sides of (33) from 0 to T as follows:
The time is expressed as
□
Numerical results are presented to show the effectiveness of the designed controller in the fractional order 5DLM. We set the time step size to 0.001, and the order of fractional derivative is selected as and The states of the system under the controller are depicted in Figure 10 and Figure 11, which indicate that the trajectories of the system can be stabilized to the origin in a finite time. In addition, the chaotic behavior is suppressed. Numerical results show that changing and k causes the system converges to zero quickly.
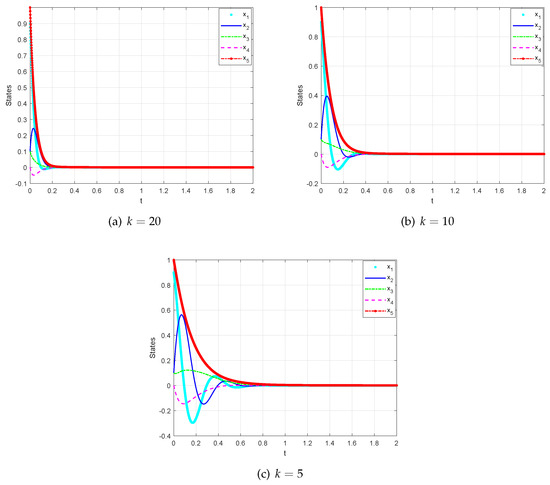
Figure 10.
State trajectories of the controlled system (23) with , and 5.
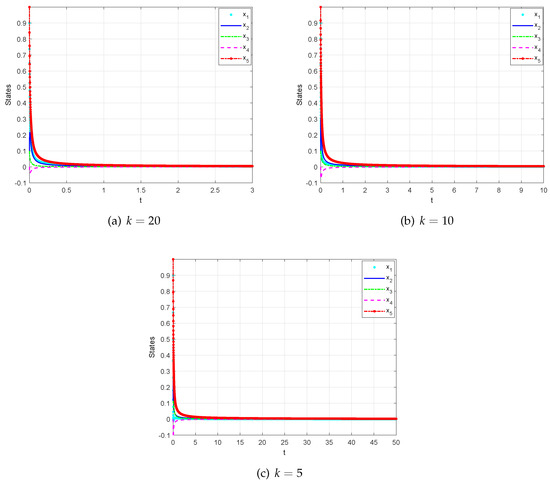
Figure 11.
State trajectories of the controlled system (23) with , and 5.
5. Conclusions
In this paper, we introduced the fractional-order five-dimensional Lorenz model. Using the Lyapunov function and fractional-order derivative, the Mittag-Leffler GASs and Mittag-Leffler PISs for this system are obtained. Furthermore, we investigated finite-time stabilization of the fractional-order five-dimensional Lorenz model. Finally, simulation results were given to show the validity of the proposed scheme. The estimation of the bound sets of fractional-order chaotic systems was not seriously investigated due to their specific complexities. Therefore, the calculation of global attractive set (GAS) and positive invariant set (PIS) for fractional 5DLM can encourage us to provide new methods for estimating the bounds of various fractional order systems.
Author Contributions
M.H., S.L., S.S. and H.S.-N. contributed equally to conceptualization, formal analysis, and writing–original draft preparation; S.S. and H.S.-N. contributed equally to methodology, software, and numerical simulation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was sponsored in part by Social Science Planning Fundation of Liaoning Province (L21BSH004) Project Name: Study on public risk perception and behavior decision-making in urban-rural fringe under public health emergencies.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this article.
References
- Rahimi, M.A.; Salarieh, H.; Alasty, A. Stabilizing periodic orbits of fractional order chaotic systems via linear feedback theory. Appl. Math. Model. 2012, 36, 863–877. [Google Scholar] [CrossRef]
- Pham, V.T.; Kingni, S.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- He, Y.; Peng, J.; Zheng, S. Fractional-order financial fystem and fixed-time synchronization. Fractal Fract. 2022, 6, 507. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and dsp implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Li, C.L.; Zhang, J. Synchronisation of a fractional-order chaotic system using finite-time input-to-state stability. Int. J. Syst. Sci. 2016, 47, 2440–2448. [Google Scholar] [CrossRef]
- Li, C.L.; Su, K.L.; Wu, L. Adaptive sliding mode control for synchronization of a fractional-order chaotic system. J. Comput. Nonlinear Dyn. 2013, 8, 031005–031011. [Google Scholar] [CrossRef]
- Al-sawalha, M.M. Synchronization of different order fractional-order chaotic systems using modify adaptive sliding mode control. Adv. Differ. Equ. 2020, 2020, 417. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Liu, D. Response of fractional oscillators with viscoelastic term under random excitation. J. Comput. Nonlinear Dyn. 2014, 9, 031015. [Google Scholar] [CrossRef]
- Jiao, Z.; Chen, Y.Q.; Podlubny, I. Distributed-Order Dynamic Systems; Springer: New York, NY, USA, 2012. [Google Scholar]
- Xu, B.; Chen, D.; Zhang, H.; Wang, F. Modeling and stability analysis of a fractional-order Francis hydro-turbine governing system. Chaos Solitons Fractals 2015, 75, 50–61. [Google Scholar] [CrossRef]
- Rajagopal, K.; Bayani, A.; Jafari, S.; Karthikeyan, A.; Hussain, I. Chaotic dynamics of a fractional order glucoseinsulin regulatory system. Front. Inf. Technol. Electron. Eng. 2019, 21, 1108–1118. [Google Scholar] [CrossRef]
- Ardehaei, M.F.; Farahi, M.H.; Effati, S. Finite time synchronization of fractional chaotic systems with several slaves in an optimal manner. Phys. Scr. 2020, 95, 035219. [Google Scholar] [CrossRef]
- Aghababa, M.P. Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dyn. 2012, 69, 247–261. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Synchronization of different fractional order chaotic systems using active control. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3536–3546. [Google Scholar] [CrossRef]
- Behinfaraz, R.; Badamchizadeh, M.A. Optimal synchronization of two different in-commensurate fractional-order chaotic systems with fractional cost function. Complexity 2016, 21, 401–416. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Synchronization of chaotic fractional-order systems via active sliding mode controller. Phys. A 2008, 387, 57–70. [Google Scholar] [CrossRef]
- Lorenz, E. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lorenz, E. The predictability of hydrodynamic flow. Trans. N. Y. Acad. Sci. 1963, 25, 409–432. [Google Scholar] [CrossRef]
- Saltzman, B. Finite amplitude free convection as an initial value problem. J. Atmos. Sci. 1962, 19, 329–341. [Google Scholar] [CrossRef]
- Rayleigh, L. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 1916, 32, 529–546. [Google Scholar] [CrossRef]
- Shen, B.W. Nonlinear feedback in a five-dimensional Lorenz model. J. Atmos. Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Shen, B.W. Nonlinear feedback in a six-dimensional Lorenz model. Impact of an additional heating term. Nonlinear Process. Geophys. 2015, 22, 749–764. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Faghih-Naini, S.; Shen, B.W. Quasi-periodic orbits in the five-dimensional non-dissipative Lorenz model: The role of the extended nonlinear feedback loop. Int. J. Bifurc. Chaos 2018, 28, 1850072. [Google Scholar] [CrossRef]
- Leonov, G.; Bunin, A.; Koksch, N. Attractor localization of the Lorenz system. Z. Angew. Math. Mech. 1987, 67, 649–656. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Liao, X. On the global basin of attraction and positively invariant set for the Lorenz chaotic system and its application in chaos control and synchronization. Sci. China Ser. E Inform. Sci. 2004, 34, 1404–1419. [Google Scholar]
- Wang, P.; Zhang, Y.; Tan, S.; Wan, L. Explicit ultimate bound sets of a new hyper-chaotic system and its application in estimating the Hausdorff dimension. Nonlinear Dyn. 2013, 74, 133–142. [Google Scholar] [CrossRef]
- Jian, J.; Zhao, Z. New estimations for ultimate boundary and synchronization control for a disk dynamo system. Nonlinear Anal. Hybrid Syst. 2013, 9, 56–66. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Chen, Z.; Li, H. Ultimate bound of a 3D chaotic system and its application in chaos synchronization. Abstr. Appl. Anal. 2014, 2014, 781594. [Google Scholar] [CrossRef]
- Saberi-Nik, H.; Effati, S.; Saberi-Nadjafi, J. New ultimate bound sets and exponential finite-time synchronization for the complex Lorenz system. J. Complex. 2015, 31, 715–730. [Google Scholar] [CrossRef]
- Gao, W.; Yan, L.; Saeedi, M.; Saberi-Nik, H. Ultimate bound estimation set and chaos synchronization for a financial risk system. Math. Comput. Simul. 2018, 154, 19–33. [Google Scholar] [CrossRef]
- Zhang, X. Dynamics of a class of non-autonomous Lorenz-type systems. Int. J. Bifurc. Chaos 2016, 28, 1650208. [Google Scholar] [CrossRef]
- Zhang, F.; Liao, X.; Chen, Y.-A. On the Dynamics of the Chaotic General Lorenz System. Int. J. Bifurc. Chaos 2017, 27, 1750075. [Google Scholar] [CrossRef]
- Chien, F.; Chowdhury, A.R.; Saberi-Nik, H. Competitive modes and estimation of ultimate bound sets for a chaotic dynamical financial system. Nonlinear Dyn. 2021, 106, 3601–3614. [Google Scholar] [CrossRef]
- Chien, F.; Inc, M.; Yosefzade, H.-R.; Saberi-Nik, H. Predicting the chaos and solution bounds in a complex dynamical system. Chaos Solitons Fractals 2021, 153, 111474. [Google Scholar] [CrossRef]
- Wang, H.; Dong, G. New dynamics coined in a 4-D quadratic autonomous hyper-chaotic system. Appl. Math. Comput. 2019, 346, 272–286. [Google Scholar] [CrossRef]
- Felicio, C.C.; Rech, P.C. On the dynamics of five and six-dimensional Lorenz models. J. Phys. Commun. 2018, 2, 025028. [Google Scholar] [CrossRef]
- Zhang, D.; Deng, D. Dynamical transition and chaos for a five-dimensional Lorenz model. Math. Methods Appl. Sci. 2022, 45, 1612–1631. [Google Scholar] [CrossRef]
- Pati, N.C.; Rech, P.C. Dynamics of a high-order generalized Lorenz model for magnetoconvection. Int. J. Bifurc. Chaos 2020, 30, 2050187. [Google Scholar] [CrossRef]
- Camacho, N.A.; Mermoud, M.A.D.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Pan, W.; Li, T.; Sajid, M.; Ali, S.; Pu, L. Parameter identification and the finite-time combination-combination synchronization of fractional-order chaotic systems with different structures under multiple stochastic disturbances. Mathematics 2022, 10, 712. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).