Fractional-Order PD Attitude Control for a Type of Spacecraft with Flexible Appendages

Abstract

As large-sized spacecraft have been developed, they have been equipped with flexible appendages, such as solar cell plates and mechanical flexible arms. The attitude control of spacecraft with flexible appendages has become more complex, with higher requirements. In this paper, a fractional-order PD attitude control method for a type of spacecraft with flexible appendages is presented. Firstly, a lumped parameter model of a spacecraft with flexible appendages is constructed, which provides the transfer function of the attitude angle and external moment. Then, a design method for the fractional-order PD controller for the attitude control of a spacecraft with flexible appendages is provided. Based on the designed steps, a numerical example is provided to compare the control performances between the fractional-order and integer-order PD controllers. Finally, the obtained numerical results are presented to verify the effectiveness of the proposed control method.

1. Introduction

Spacecraft are the main carriers of space exploration missions, which have become complex and large-scale in recent years [1,2]. The spacecraft’s capacity and launch cost limit the spacecraft weight, such that large spacecraft always use lightweight materials to reduce the overall mass of the spacecraft. In general, large spacecraft with lightweight materials have strong flexibility.

In the modeling process of flexible spacecraft, the commonly used methods include the lumped parameter method, the distributed parameter method, and the finite element method. The lumped parameter method regards the spacecraft structure as a rigid body system composed of several springs and rigid bodies [3]. Moreover, the flexible appendages of the spacecraft structure are expressed by adjusting the stiffness of the spring. Then, the spacecraft dynamical model can be established according to the multi-rigid-body dynamics. Some researchers have studied the modeling and dynamics of spacecraft with flexible appendages. Liu et al. [4] studied the dynamic characteristics of the dual solar panel flexible spacecraft and discussed the rigid–flexible coupling effect between the attitude motion, structural deformation, and thermal load. Gasbarri et al. [5] used the finite element method to study the modeling of multibody flexible spacecraft and the spacecraft dynamics in the form of the attitude coupling of complex spacecraft.

In the space environment, the spacecraft should be able to adjust its attitude to meet the stated mission. Attitude control of the spacecrafts is one of the most important aspects [6]. The design of the attitude control indirectly determines the normal operation of a spacecraft in orbit. For example, a spacecraft equipped with flexible solar panels is a typical rigid–flexible coupling system [7]. During the attitude adjustment of the spacecraft, the flexible solar panels vibrate and affect the spacecraft. If this rigid–flexible combination is not properly controlled, the normal operation of the spacecraft could be affected. Compared with rigid spacecraft, flexible spacecraft are more complicated to control because of the vibration of the flexible structure and the coupling between the central rigid bodies. Thus, the influence of the flexible appendages in spacecraft attitude control should be considered.

The spacecraft attitude control algorithm mainly uses relatively common algorithms, such as the PD control [8,9,10]. The impact analysis of the external interference and flexible structure vibration is not comprehensive. With the increasing complexity of the spacecraft structure, it is difficult for the conventional PD control to meet the control requirements of the spacecraft. Without considering the influence of the flexible appendages’ vibration on the attitude of the spacecraft, the attitude control design could affect the operating state of the spacecraft and even lead to the instability of the spacecraft.

Fractional calculus is a generalization of the traditional integer calculus [11,12,13]. To improve the control performance of the PD control, fractional calculus has been introduced into the traditional PD control. Safikhani et al. designed a non-overshooting fractional-order PD for special case of fractional-order plants [14]. Saleem et al. proposed an intelligently optimized fractional-order PD controller of a rotary inverted pendulum [15]. Celik provided a new fractional-order PD cascade controller for the advanced load frequency control of a power system [16]. These references show the superiority of the fractional-order PD controller, which encourages the study of fractional-order PD attitude control for spacecraft with flexible appendages.

Motivated by the above discussion, this paper focuses on the design of a fractional-order PD controller for spacecraft with flexible appendages. Based on the lumped parameter method, the dynamical model of spacecraft with flexible appendages is discussed, as well as the transfer function of the attitude angle and external moment. Then, the fractional-order PD controller is designed according to the given gain crossover frequency and phase margin. In addition, the effectiveness of the obtained results is verified by a numerical simulation.

The rest of this paper is organized as follows: in Section 2, some preliminaries are introduced, including the fractional derivative and fractional-order PD controller; then, the attitude control modeling of spacecraft with flexible appendages is proposed in Section 3; a fractional-order PD controller and its design steps are given in Section 4; an example is provided to verify the obtained results in Section 5; finally, the conclusions are listed in Section 6.

2. Preliminaries

2.1. Fractional Derivative

The fractional derivative is a generalization of the integer-order derivatives, which have been widely applied in different fields, such as dynamics, engineering, computer science, etc. In particular, fractional derivative damping is utilized to describe the viscoelastic damping model. The fractional derivative has three common definitions, the Grunwald–Letnikov [17], Riemann–Liouville [18], and Caputo [19]. Let us introduce these definitions.

Definition 1

([17]). In the Grunwald–Letnikov definition, the fractional integration and derivative of a function $x:(0,+\infty )⟶\mathrm{R}$ with order q is described by

$$\begin{array}{c}\hfill {}_a^G{D}_t^{q}x\left(t\right)=\underset{h\to 0^{+}}{lim}\frac{1}{h^q}\sum _{i=0}^{\left[\frac{t-a}{h}\right]}{(-1)}^i\left(\begin{array}{c}q\\ i\end{array}\right)x(t-ih),\end{array}$$

(1)

where $\left[\frac{t-a}{h}\right]$ is the maximum integer, which is less than $\frac{t-a}{h}$ and

$$\left(\begin{array}{c}q\hfill \\ i\hfill \end{array}\right)=\frac{q(q-1)(q-2)\dots (q-i+1)}{i!}.$$

When $q>0$, Equation (1) denotes the Grunwald–Letnikov fractional derivative definition. When $q<0$, Equation (1) is the Grunwald–Letnikov fractional integration definition. Due to its discreteness, the Grunwald–Letnikov definition is always employed in numerical simulations.

In the theoretical analysis, Riemann–Liouville and Caputo definitions are commonly used.

Definition 2

([18]). The Riemann–Liouville fractional integration of a continuous function $x:(0,+\infty )⟶\mathrm{R}$ is defined as:

$${}_a^R{D}_{t^{}}^{-q}x\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(q\right)}{\int }_a^t{(t-s)}^{q-1}x\left(s\right)\mathrm{ds},$$

(2)

where $q>0$, and $\mathrm{\Gamma }\left(q\right)$ is the Gamma function described by

$$\mathrm{\Gamma }\left(q\right)={\int }_0^{+\infty }{\tau }^{q-1}{e}^{-\tau }\mathrm{d}\tau .$$

Definition 3

([18]). The Riemann–Liouville fractional derivative of a continuous function $x:(0,+\infty )⟶\mathrm{R}$ with order $\alpha >0$ is defined as:

$${}_0^R{D}_{t^{}}^{\alpha }x\left(t\right)=\frac{1}{\mathrm{\Gamma }(r-\alpha )}\frac{{\mathrm{d}}^r}{\mathrm{d}{\mathrm{t}}^r}{\int }_0^t\frac{x\left(s\right)}{{(t-s)}^{\alpha -r+1}}\mathrm{ds},$$

(3)

where r is a positive integer, and $r-1\le \gamma \le r$.

The Laplace transforms of the Riemann–Liouville fractional integration and derivative are given respectively, i.e.,

$$L\left\{{}_a^R{D}_t^{-q}x\left(t\right)\right\}=s^{-q}X\left(s\right),$$

(4)

$$L\left\{{}_a^R{D}_t^{\alpha }x\left(t\right)\right\}=s^{\alpha }X\left(s\right)-\sum _{i=0}^{r-1}{s}^i{\left.{}_a^R{D}_t^{\alpha -i-1}x\left(t\right)\right|}_{t=a},$$

(5)

where $L\{·\}$ is a Laplace transform operator $X\left(s\right)=L\left\{x\right(t\left)\right\}$, and r is a positive integer with $r-1\le \alpha \le r$.

According to Equation (5), the initial conditions of the Riemann–Liouville fractional derivative are complex and have unclear physical meanings. To improve this problem, the Caputo definition of a fractional derivative is introduced.

Definition 4

([19]). The Caputo fractional derivative of a continuous function $x:(0,+\infty )⟶\mathrm{R}$ with order $\alpha >0$ is defined as:

$${}_a^C{D}_{t^{}}^{\alpha }x\left(t\right)=\frac{1}{\mathrm{\Gamma }(r-\alpha )}{\int }_a^t\frac{x^{\left(r\right)}\left(s\right)}{{(t-s)}^{\alpha -r+1}}\mathrm{ds},$$

(6)

where r is a positive integer, and $r-1\le \alpha \le r$.

In addition, the Laplace transformation of the Caputo fractional derivative is obtained,

$$L\left\{{}_a^C{D}_t^{\alpha }x\left(t\right)\right\}=s^{\alpha }X\left(s\right)-\sum _{i=0}^{r-1}{s}^{\alpha -i-1}{x}^{\left(i\right)}\left(a\right),$$

(7)

where r is a positive integer with $r-1\le \alpha \le r$.

According to Equation (7), the initial values of the Caputo fractional derivative are integer-order and have practical physical meanings. We note that the Laplace transforms of the Riemann–Liouville and Caputo fractional derivative are the same with null initial conditions, i.e.,

$$L\left\{{}_a^{R,C}{D}_t^{\alpha }x\left(t\right)\right\}=s^{\alpha }X\left(s\right),$$

(8)

when $x^{\left(i\right)}\left(a\right)=0$ for $i=0,\dots ,r-1$.

2.2. Fractional-Order PD Controller

The classical PD controller contains a proportion controller and a differentiation controller and is described by

$$u\left(t\right)=\left[K_p+K_d\frac{d}{dt}\right]e\left(t\right),$$

(9)

where $u\left(t\right)$ is the control signal, $e\left(t\right)$ is the input of the PD controller, $K_p$ is the proportion coefficient, and $K_d$ is the differentiation coefficient.

The fractional-order PD controller improves the classical integer-order differentiation controller using a Caputo fractional derivative. Then, the fractional-order PD controller is obtained as

$$u\left(t\right)=\left[K_p+K_d{}_0^C{D}_{t^{}}^{\alpha }\right]e\left(t\right),$$

(10)

where ${}_a^C{D}_{t^{}}^{\alpha }$ is the Caputo fractional derivative operation, which is defined in Definition 4. The Caputo fractional order $\alpha$ in the fractional-order PD controller is always set as $\alpha \in (0,2)$.

With null initial conditions, the Laplace transform of the fractional-order PD controller (10) can be provided:

$$C\left(s\right)=L\left\{\frac{u\left(t\right)}{e\left(t\right)}\right\}=K_p+K_d{s}^{\alpha }.$$

(11)

In the rest of this paper, the fractional-order PD controller (11) is used in the attitude control of a type of spacecraft with flexible attachments.

3. Attitude Control Modeling of Spacecraft with Flexible Appendages

In this section, a lumped parameter model of spacecraft with flexible appendages is proposed. Then, the corresponding attitude control model is constructed.

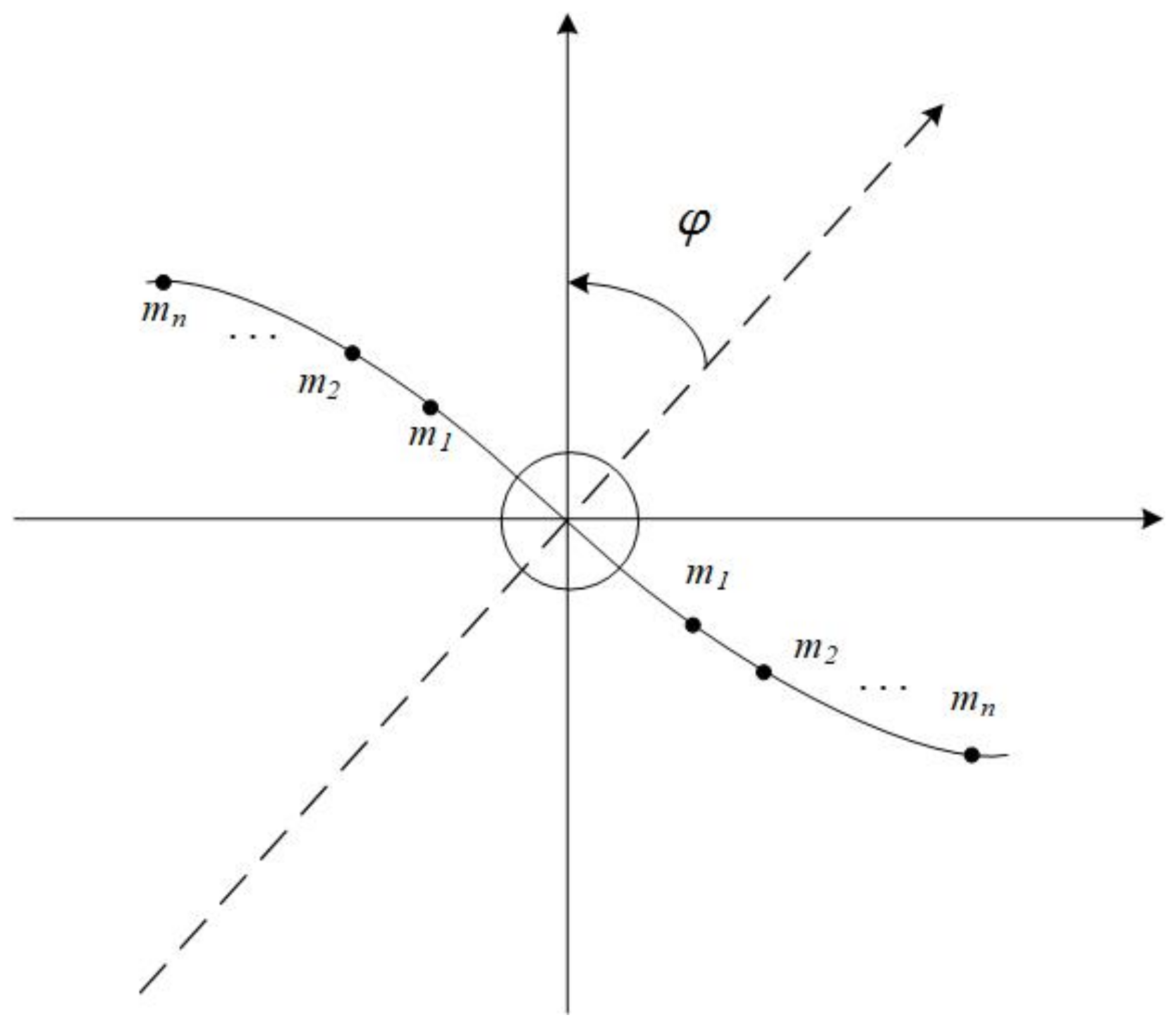
Figure 1 is the lumped parameter model of a spacecraft with flexible appendages, which assumes that one side of the flexible appendages has n mass points $m_i$$(i=1,\dots ,n)$ satisfying

$$V_i=\dot{\phi }{l}_i+{\dot{\mu }}_i,i=1,\dots ,n.$$

(12)

where $\phi$ is the attitude angle of the spacecraft, and $V_i$, $l_i$, and ${\mu }_i$ are the velocity, position, and the elastic deformation of the mass point $m_i$, respectively.

Figure 1. The lumped parameter model of spacecraft with flexible appendages.

According to the angular momentum theorem, we have

$$\dot{H}=I\ddot{\phi }+2\sum _{i=1}^n{m}_i{l}_i{\ddot{\mu }}_i=T,$$

(13)

where H is the angular momentum of the centroid of the spacecraft system, T is the external moment, and I is the moment of inertia of the spacecraft system satisfying $I=I_0+2{\displaystyle \sum _{i=1}^n}{m}_i{l}_i^2$.

In addition, spacecraft with flexible appendages have a motion equation. For example, large-size solar panels always have flexibility due to the special material of metal–silicide composites. Given the bending rigidity $EI$ and structure distribution, the motion equation of the spacecraft system can be obtained as

$$M\ddot{\mu }+C\mu +Ml\ddot{\phi }=0,$$

(14)

where $\mu ={({\mu }_1,{\mu }_2,\dots ,{\mu }_n)}^T$, $l={(l_1,l_2,\dots ,l_n)}^T$, $C=diag\{m_1,m_2,\dots ,m_n\}$ is the mass matrix of the flexible appendages, and $C>0$ is always symmetric and denotes the stiffness matrix of the flexible appendages. In addition, the flexible appendages are assumed to be undamped.

Equations (13) and (14) imply

$$M\ddot{\mu }+C\mu +Ml\left(\frac{T}{I}-\frac{2}{I}{l}^{\mathrm{T}}M\ddot{\mu }\right)=0.$$

(15)

Equivalently, we obtain

$$Q\ddot{\mu }+C\mu +\frac{T}{I}Ml=0,$$

(16)

where Q is also a real symmetric matrix satisfying

$$Q=M-\frac{2}{I}Ml{l}^{\mathrm{T}}M.$$

Because Q and C are both real symmetric invertible matrices, there exists a matrix K, which is able to diagonalize Q and C, i.e.,

$$\left\{\begin{array}{c}{K}^{T}QK=I_n,\\ K^{T}CK=\mathrm{diag}\left\{{\rho }_1^2,{\rho }_2^2,\dots ,{\rho }_n^2\right\}\triangleq \mathrm{\Omega }.\end{array}\right.$$

(17)

Substituting an alternative, $\mu =K\delta$, Equations (13) and (17) can be respectively rewritten as

$$I\ddot{\phi }+2\mathrm{\Theta }\ddot{\delta }=T,$$

(18)

$$\ddot{\delta }+\mathrm{\Omega }\delta +\frac{T}{I}{\mathrm{\Theta }}^T=0,$$

(19)

where $\mathrm{\Theta }=l^{T}MK\in R^{1\times n}$. Then, the Laplace transforms of Equations (18) and (19) are obtained;

$$I{s}^2\phi \left(s\right)=T\left(s\right)-2s^2\mathrm{\Theta }\delta \left(s\right),$$

(20)

$$\delta \left(s\right)=-{\left(\frac{{\mathrm{\Theta }}_1}{s^2+{\rho }_1^2},\frac{{\mathrm{\Theta }}_2}{s^2+{\rho }_2^2},\dots ,\frac{{\mathrm{\Theta }}_n}{s^2+{\rho }_n^2}\right)}^T\frac{T\left(s\right)}{I}.$$

(21)

Obviously, the transfer function of the attitude angle $\phi$ and external moment T is given as

$$G\left(s\right)=\frac{\phi \left(s\right)}{T\left(s\right)}=\frac{1}{I{s}^2}\left(1+\frac{2}{I}\sum _{i=1}^n\frac{{\mathrm{\Theta }}_i^2{s}^2}{s^2+{\rho }_i^2}\right)\triangleq \frac{N\left(s\right)}{D\left(s\right)},$$

(22)

where $N\left(s\right)$ and $D\left(s\right)$ are both polynomial functions of s.

According to the fractional-order PD controller (11), the open-loop $P_o\left(s\right)$ and closed-loop $P_c\left(s\right)$ transfer functions of the controlled system are proposed, respectively,

$$P_o\left(s\right)=G\left(s\right)C\left(s\right)=\frac{\left(K_p+K_d{s}^{\alpha }\right)N\left(s\right)}{D\left(s\right)},$$

(23)

$$P_c\left(s\right)=\frac{G\left(s\right)C\left(s\right)}{1+G\left(s\right)C\left(s\right)}=\frac{(K_p+K_d{s}^{\alpha })N\left(s\right)}{D\left(s\right)+(K_p+K_d{s}^{\alpha })N\left(s\right)}.$$

(24)

The attitude control model of spacecraft with flexible appendages is given as the above Equations (23) and (24). How to design the control parameters $K_p$, $K_d$, and $\alpha$ of the fractional-order PD controller (11) is discussed in the next section.

4. Fractional-Order PD Controller Design

In this section, a design method for the fractional-order PD controller for the attitude control of spacecraft with flexible appendages is presented. As we know, the gain crossover frequency and phase margin are the two main indices for a controlled system. The gain crossover frequency is the frequency at which the amplitude frequency curve intersects the 0dB. When the crossing frequency is higher, the response speed becomes faster. The phase margin is the maximum phase allowed to increase through the frequency point. The ideal value of the phase margin is from $\frac{\pi }{6}$ to $\frac{\pi }{3}$. To achieve the desired control performance, the gain crossover frequency ${\omega }_c$ and phase margin ${\varphi }_m$ should be set in advance, whose definitions are described by

$$\left\{\begin{array}{c}|P_o\left(s\right){|}_{s=j{\omega }_c}=1,\hfill \\ arg\left(P_o\left(s\right){|}_{s=j{\omega }_c}\right)=-\pi +{\varphi }_m.\hfill \end{array}\right.$$

(25)

Then, according the the open-loop (23) and closed-loop (24) transfer functions of the controlled system, we have

$${\left.D\left(s\right)+(K_p+K_d{s}^{\alpha })N\left(s\right)e^{-j{\varphi }_m}\right|}_{s=j{\omega }_c}=0.$$

(26)

Due to Equation (22), $N\left(s\right)$ and $D\left(s\right)$ are rewritten, respectively, as

$$\left\{\begin{array}{c}N\left(s\right)=c_{2n}{s}^{2n}+c_{2n-2}{s}^{2n-2}+\dots +c_2{s}^2+c_0,\\ D\left(s\right)=d_{2n+2}{s}^{2n+2}+d_{2n}{s}^{2n}+\dots +d_4{s}^4+d_2{s}^2.\end{array}\right.$$

(27)

Substituting Equation (27) into Equation (26), we have

$$D_{\omega }+N_{\omega }{K}_p\left[cos\left({\varphi }_m\right)-jsin\left({\varphi }_m\right)\right]+N_{\omega }{K}_d{\omega }_c^{\alpha }\left[cos\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)+jsin\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)\right]=0,$$

(28)

where

$$\left\{\begin{array}{c}{N}_{\omega }={\left(-1\right)}^n{c}_{2n}{\omega }_c^{2n}+{\left(-1\right)}^{n-1}{c}_{2n-2}{\omega }_c^{2n-2}+\dots +{\left(-1\right)}^1{c}_2{\omega }_c^2+c_0,\\ D_{\omega }={\left(-1\right)}^{n+1}{d}_{2n+2}{\omega }_c^{2n+2}+{\left(-1\right)}^n{d}_{2n}{\omega }_c^{2n}+\dots +{\left(-1\right)}^2{d}_4{\omega }_c^4+{\left(-1\right)}^1{d}_2{\omega }_c^2.\end{array}\right.$$

(29)

Equivalently, Equation (28) gives

$$\left\{\begin{array}{c}{K}_{p}cos\left({\varphi }_m\right)+K_d{\omega }_c^{\alpha }cos\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)+\frac{D_{\omega }}{N_{\omega }}=0,\\ -K_{p}sin\left({\varphi }_m\right)+K_d{\omega }_c^{\alpha }sin\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)=0,\end{array}\right.$$

(30)

which obtains the solutions of $K_p$ and $K_d$:

$$\left\{\begin{array}{c}{K}_p=-\frac{D_{\omega }}{N_{\omega }}·\frac{sin\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)}{cos\left({\varphi }_m\right)sin\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)+sin\left({\varphi }_m\right)cos\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)},\\ K_d=-\frac{D_{\omega }}{{\omega }_c^{\alpha }{N}_{\omega }}·\frac{sin\left({\varphi }_m\right)}{cos\left({\varphi }_m\right)sin\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)+sin\left({\varphi }_m\right)cos\left(\frac{\alpha \pi }{2}-{\varphi }_m\right)}.\end{array}\right.$$

(31)

Based on Equation (31), the proportion coefficient $K_p$ and differentiation coefficient $K_d$ both depend on the fractional order $\alpha$ given the gain crossover frequency ${\omega }_c$ and phase margin ${\varphi }_m$. Then, the fractional order $\alpha$ should be determined. The use of the fractional order $\alpha$ instead of the integer order leads to better results, since the fractional order has an extra degree of freedom. Thus, an additional error evaluation method is given. To obtain better control performance, an error evaluation method is always used to minimize the control error. The common error evaluation methods include the maximum absolute error (MAE), integral absolute error (IAE), integral time-weighted absolute error (ITAE), integral squared error (ISE), and the integral time-weighted squared error (ITSE), and the corresponding objective functions are listed as follows:

$$\left\{\begin{array}{c}\mathrm{MAE}:J=\underset{t}{max}\left|e\left(t\right)\right|,\\ \mathrm{IAE}:J={\int }_0^T\left|e\right(t\left)\right|dt,\\ \mathrm{ITAE}:J={\int }_0^{T}t\left|e\left(t\right)\right|dt,\\ \mathrm{ISE}:J={\int }_0^T{\left[e\left(t\right)\right]}^{2}dt,\\ \mathrm{ITSE}:J={\int }_0^{T}t{\left[e\left(t\right)\right]}^{2}dt,\end{array}\right.$$

(32)

where $e\left(t\right)$ is the control error. In this paper, the ITAE is utilized to calculate the optimal fractional order $\alpha$. Then, combining Equation (31), all the control parameters $K_p$, $K_d$, and $\alpha$ can be determined. The detailed design steps are given as follows.

The design method of the fractional-order PD controller for the attitude control of spacecraft with flexible appendages has three steps.

• According to Equations (12)–(22), we calculate the open loop $P_o\left(s\right)$ in Equation (23) and $N\left(s\right),D\left(s\right)$ in Equation (27). Then, we obtain the parameters $c_0$, $c_2$, …, $c_{2n}$ and $d_2$, $d_4$, …, $d_{2n+2}$.
• Given the gain crossover frequency ${\omega }_c$ and the phase margin ${\varphi }_m$, we determine the expressions of $K_p$ and $K_d$ based on Equation (31). We substitute Equation (31) into Equation (24) and obtain the closed-loop transfer function with only one independent variable $\alpha$.
• We select the ITAE in Equation (32) and calculate the optimal $\alpha$, which can obtain the minimum of the ITAE objective function. We determine $K_p$ and $K_d$ according to Equation (31).

5. Numerical Simulation

In this section, a numerical example is given to demonstrate the effectiveness of the proposed fractional-order PD attitude control method of spacecraft with flexible appendages.

We assumed that the flexible appendages had two mass points, i.e., $n=2$ in Equation (12). The two mass points were both $m_1=m_2=1$ kg. The length of the flexible appendages on one side was $L=4$ m, and the positions of the two mass points $m_1$, $m_2$ were $l_1=2$ m and $l_2=4$ m, respectively. The bending rigidity was selected as $EI=1.6e7$ N·m${}^2$, and the moment of inertia of the spacecraft system was I = 50 kg·m${}^2$. Obviously, Equation (13) became

$$\dot{H}=I\ddot{\phi }+2\left(m_1{l}_1{\ddot{\mu }}_1+m_2{l}_2{\ddot{\mu }}_2\right)=T,$$

and the mass matrix M of the flexible appendages was

$$M=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].$$

The bending equations in $O{m}_1$ and $m_1{m}_2$ were listed, respectively, as

$$\left\{\begin{array}{c}EI\ddot{\mu }=F_1\left(\frac{L}{2}-l\right)+F_2(L-l),\\ EI\ddot{\mu }=-F_2(L-l).\end{array}\right.$$

Combined with the initial value conditions, we obtained

$$\left\{\begin{array}{c}{F}_1=\frac{48EI}{7L^3}\left(-16{\mu }_1+5{\mu }_2\right),\\ F_2=\frac{48EI}{7L^3}\left(5{\mu }_1-2{\mu }_2\right).\end{array}\right.$$

Then, the stiffness matrix of the flexible appendages was calculated as

$$C={10}^7\times \left[\begin{array}{cc}2.7429& -0.8571\\ -0.8571& 0.3429\end{array}\right].$$

Thus, the motion equation of the spacecraft system (14) became

$$\left[\begin{array}{c}{\ddot{\mu }}_1\hfill \\ {\ddot{\mu }}_2\hfill \end{array}\right]+{10}^7\times \left[\begin{array}{cc}2.7429& -0.8571\\ -0.8571& 0.3429\end{array}\right]\times \left[\begin{array}{c}{\mu }_1\hfill \\ {\mu }_2\hfill \end{array}\right]+\left[\begin{array}{c}2\hfill \\ 4\hfill \end{array}\right]\ddot{\phi }=0.$$

The equivalent Equation (16) was obtained, and the corresponding parameters were

$$Q=\left[\begin{array}{cc}0.84& -0.32\\ -0.32& 0.36\end{array}\right],K=\left[\begin{array}{cc}1.19& 0.6195\\ 0.2882& 2.029\end{array}\right],\mathrm{\Omega }={10}^7\times \left[\begin{array}{cc}3.325& 0\\ 0& 0.3093\end{array}\right].$$

In this case, the parameter B in Equation (18) was determined as

$$\mathrm{\Theta }=\left[\begin{array}{cc}3.5328& 9.3548\end{array}\right].$$

According to Equation (22), the transfer function of the attitude angle and external moment was given as

$$G\left(s\right)=\frac{1}{50s^2}\left(1+\frac{2}{50}\left[\frac{3.5328^2\times s^2}{s^2+3.325\times {10}^7}+\frac{9.3548^2\times s^2}{s^2+0.3093\times {10}^7}\right]\right).$$

Equivalently, the polynomial functions $D\left(s\right)$ and $N\left(s\right)$ were obtained as

$$G\left(s\right)=\frac{0.1\times s^4+3.086\times {10}^6\times s^2+2.057\times {10}^{12}}{s^6+3.634\times {10}^7\times s^4+1.029\times {10}^{14}\times s^2}\triangleq \frac{N\left(s\right)}{D\left(s\right)}.$$

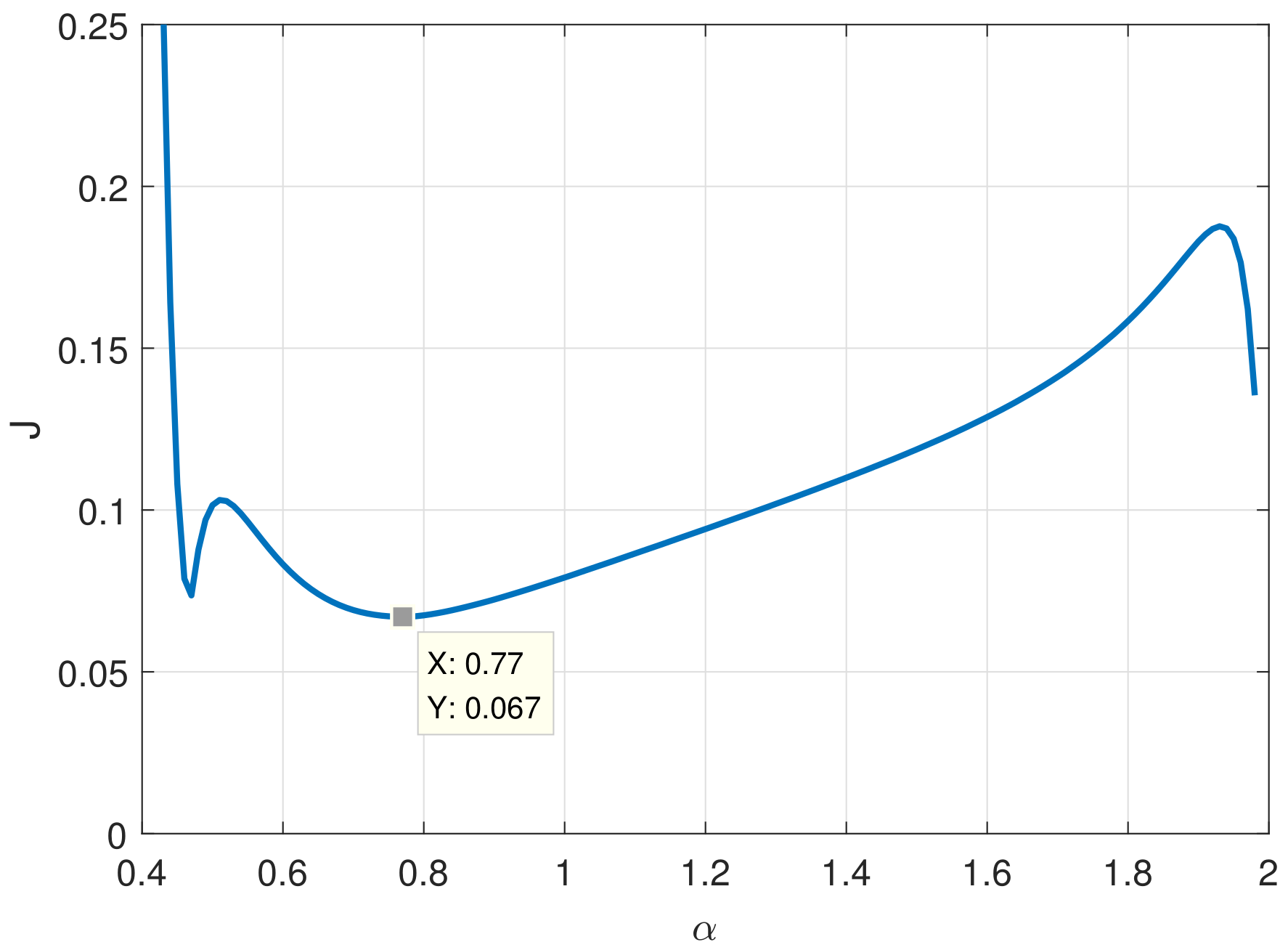
According to the steps of the proposed fractional-order PD controller, we chose the gain crossover frequency ${\omega }_c=8Hz$ and phase margin ${\varphi }_m=\frac{\pi }{4}rad$. We selected the ITAE in Equation (32) and calculated the optimal $\alpha$; the relationship between the ITAE and order $\alpha$ is shown in Figure 2. The minimum of the ITAE objective function was 0.067 with the optimal order $\alpha =0.77$. Based on Equation (31), the optimal control parameters were obtained as

$$K_p=1408.5,K_d=488.1,\alpha =0.77.$$

Figure 2. The relationship between the ITAE and order $\alpha$.

To compare the control performance, the traditional integer-order PD controller was used as a reference. The fractional-order PD control process was numerically simulated by the FOTF Toolbox in MATLAB Simulink. From Equation (31), the corresponding parameters of the integer-order PD controller were $K_p^{IO}=2264$ and $K_d^{IO}=283$ with $\alpha =1$. The Bode diagrams under fractional-order and integer-order PD controllers are both shown in Figure 3 and Figure 4. Obviously in Figure 3 and Figure 4, the proposed PD controller satisfied the given gain crossover frequency ${\omega }_c=8$ Hz and phase margin ${\varphi }_m=\frac{\pi }{4}$ rad.

Figure 3. The Bode diagram under the fractional-order PD controller $K_p=1408.5,K_d=488.1,\alpha =0.77$.

Figure 4. The Bode diagram under the integer-order PD controller $K_p^{IO}=2264,K_d^{IO}=283$.

To check the stability of the closed-loop system under the fractional-order PD controller, the corresponding root locus is shown in Figure 5. Obviously, the whole root locus was located in the lefthalf plane, which ensures the stability of the controlled system. In addition, the Nyquist diagram under the fractional-order PD controller is given in Figure 6. The Nyquist curve did not circle the critical point $(-1,0)$, which benefits the dynamics analysis of the closed control loop.

Figure 5. Root locus under the fractional-order PD controller $K_p=1408.5,K_d=488.1,\alpha =0.77$.

Figure 6. Nyquist diagram under the fractional-order PD controller $K_p=1408.5,K_d=488.1,\alpha =0.77$.

Moreover, the step responses under the fractional-order and integer-order PD controllers are given in Figure 7. According to Figure 7, the control performance under the fractional-order PD controller had higher error precision, smaller overshoot, and a faster response time, which verified the effectiveness of the proposed fractional-order PD attitude control for spacecraft with flexible appendages.

Figure 7. Step responses under fractional-order and integer-order PD controllers (abbreviated as FOPD and PD, respectively).

6. Conclusions

In this paper, a fractional-order PD attitude control method for spacecraft with flexible appendages was proposed. Firstly, a lumped parameter model of spacecraft with flexible appendages was obtained based on the angular momentum theorem and motion equation. Then, the transfer function of the attitude angle and external moment was determined according to the lumped parameter model. The design steps of the fractional-order PD control were listed. With the given gain crossover frequency and phase margin, the relationships of the control parameters were obtained. In addition, the optimal control parameters were calculated by choosing the minimum of the ITAE objective function. Finally, a numerical example was given to illustrate the effectiveness of the obtained control method. The numerical results showed that the fractional-order PD had higher error precision, a smaller overshoot, and a faster response time, which would improve the attitude control performance of spacecrafts with flexible appendages.