Scale-Free Fractal Interpolation

Abstract

An iterated function system that defines a fractal interpolation function, where ordinate scaling is replaced by a nonlinear contraction, is investigated here. In such a manner, fractal interpolation functions associated with Matkowski contractions for finite as well as infinite (countable) sets of data are obtained. Furthermore, we construct an extension of the concept of $\alpha$-fractal interpolation functions, herein called R-fractal interpolation functions, related to a finite as well as to a countable iterated function system and provide approximation properties of the R-fractal functions. Moreover, we obtain smooth R-fractal interpolation functions and provide results that ensure the existence of differentiable R-fractal interpolation functions both for the finite and the infinite (countable) cases.

1. Introduction

The concept of a fractal interpolation function, or FIF for short, introduced by Barnsley in [1] gained a lot of attention from researchers and has been intensively studied in recent years; see, for instance, [2,3,4,5,6,7,8,9]. The interest in this type of interpolation is motivated by the significant applicability of fractal interpolation to model real-life data. FIFs have various applications, among which we mention curve fitting (see [10]), image data reconstruction (see [11]), image compression (see [12]), reconstruction of epidemic curves (see [13]) and others.

Nowadays, the development of technology, digital transformation and data science make artificial intelligence a basic tool in engineering and in the treatment and processing of complicated systems that involve a huge quantity of inputs and outputs. The relation between artificial intelligence and fractal geometry has two aspects: how to deal with data owning a self-similar structure, and how to add fractal characteristics to the models in order to capture hidden structures not well fitted by Euclidean objects (see [14,15], for instance). There are interesting contributions linking fractal geometry and artificial intelligence to modern scientific and technological fields, such as image encoding ([16]), wind speed fluctuation ([17]), concrete crack ([18]), fractal antennas ([19]), surface roughness ([20]), etc. One of the main fields of application of artificial intelligence is health diagnoses, where bioelectric signals play an essential role. This kind of data shows an unequivocal fractal character, reported by a huge quantity of bibliographical references. For the processing of these computerized data, fractal functions are a key tool. This fact makes the development of the theory of fractal maps a must in order to understand the rich self-similar structure of the recorded data. Our work follows this need, enlarging the field of the now classic fractal interpolation. The article we present constructs a more general model for the iterated function system involved in the definition of a fractal interpolant. Thus, the schematic scaling term in the y-ordinate, is replaced by a more general contraction. The model we present here provides a wider framework for dealing with fractal interpolation of data, enlarging the possibilities of this methodology.

In [21], Navascués proved that for any continuous function f defined on a compact interval, there can be a family of fractal interpolation functions $f^{\alpha }$ associated that interpolate and approximate f, thus obtaining $\alpha$-fractal functions, which pioneered a novel direction for research. Various properties of the $\alpha$-fractal function have been studied (see [22,23,24] et al.) and several extensions of the $\alpha$-fractal functions were introduced, among which we mention variable scaling factors $\alpha$-FIFs, hidden-variable, etc. (see, for instance, [25,26,27,28,29]).

A recent direction of research to obtain more general FIF is to replace the classical Banach contraction principle with more relaxed fixed point results, thus obtaining a wider spectrum of FIFs. In this respect, the reader is encouraged to refer to [30,31,32], for instance. The concept of FIF has been extended by Secelean (see [33]) to countable systems of data by using countable iterated function systems, or CIFS, for short. For more detailed information on CIFS, see [34]. More recently, Pacurar combined the idea of using different types of contractions with countable FIFs (see [35]) and Miculescu et al. introduced a fractal interpolation scheme for a possible sizable set of data (see [36]).

The first part of the article is devoted to the study of an iterated function system, or IFS for short, defined on $I\times \mathbb{R}$, where $I\subseteq \mathbb{R}$ is compact, which defines a FIF, where the ordinate scaling is replaced by a nonlinear contraction. In this way, we obtain Matkowski-FIFs for finite real data and extend our results to the case where we have an infinite (countable) amount of data. Our scheme can be used for any contraction that allows a fixed point theorem on a metric space, which emphasizes the significance to the field of the generalizations brought by the results in the current paper. The second part of the paper provides an extension of the concept of $\alpha$-FIF by defining a class of interpolation functions $f^R$ associated with a continuous function f, called R-FIF. We define the R-FIF for both finite and infinite (countable) collections of data. Moreover, for the infinite case, we provide different conditions than in [35] for the existence of FIF. In the final part of the paper, we construct R-smooth fractal interpolation functions and extend the results (see, for instance, [37]) that prove the existence of differentiable and smooth FIF with any order of regularity.

2. Preliminaries

Let $(X,d)$ be a metric space.

Definition 1.

For the function $\phi :[0,\infty )\to [0,\infty )$ (called comparison function), a map $f:X\to X$ is:

(i) 

φ-contraction if

$$d\left(f\right(x),f(y\left)\right)\le \phi \left(d\right(x,y\left)\right)$$

for every $x,y\in X$.

(ii) 

Rakotch contraction if it is a φ-contraction where the function φ satisfies: $t\to \frac{\phi \left(t\right)}{t}$ is non-increasing and $\frac{\phi \left(t\right)}{t}<1$, for every $t>0$.

(iii) 

Matkowski contraction if it is a φ-contraction where the function φ is non-decreasing and the following limit holds $\underset{n\to \infty }{lim}{\phi }^n\left(t\right)=0$, for every $t>0$.

Remark 1.

Each Banach contraction is a Rakotch contraction with the function $\phi \left(t\right)=Ct$, for every $t>0$, where $C\in [0,1)$.

Remark 2.

Each Rakotch contraction is a Matkowski contraction.

Theorem 1.

(see [38]) For the complete metric space $(X,d)$, if the function $F:X\to X$ is a Matkowski contraction, then F has a unique fixed point $x_0\in X$ and $\underset{n\to \infty }{lim}{F}^n\left(x\right)=x_0$ for every $x\in X$.

Definition 2.

(see [39]) The system of functions ${\left\{f_n\right\}}_{n\in J}$ is called an iterated function system, or IFS, for short, if:

(i) 

J is finite;

(ii) 

$f_n:X\to X$ are continuous functions;

(iii) 

$(X,d)$ is a complete metric space.

Remark 3.

(see [40]) If the set J in Definition 2 is countable, then the IFS is called a countable iterated function system, or CIFS, for short.

Definition 3.

For $x_1,x_2,\dots ,x_{n-k+1}\in \mathbb{R}$, we consider the partial or incomplete Bell polynomial ([41]) given by

$$B_{n,k}(x_1;\dots ;x_{n-k+1})=\sum _{\underset{j_1+2j_2+\cdots +(n-k+1)j_{n-k+1}=n}{j_1+j_2+\cdots +j_{n-k+1}=k}}{\displaystyle \frac{n!}{j_1!\dots j_{n-k+1}!}}{\left({\displaystyle \frac{x_1}{1!}}\right)}^{j_1}\cdots {\left({\displaystyle \frac{x_{n-k+1}}{(n-k+1)!}}\right)}^{j_{n-k+1}}.$$

3. Fractal Interpolation Associated with Matkowski Contractions

We consider a general IFS, defined on the set $I\times \mathbb{R}$, where I is a compact real interval, related to a partition of it. This system will define a FIF of a set of real data. Firstly, we study the case where the partition has a finite number of points.

3.1. Finite Number of Data

Let $\Delta$ be a partition of I, $\Delta :x_0<x_1<\cdots <x_N$, where $N>1$, and a finite set of data ${\left\{(x_i,y_i)\right\}}_{i=0}^N$. We define an IFS through a collection of contractive homeomorphisms $l_n:I\to I_n$, where $I_n=[x_{n-1},x_n]$, satisfying the conditions

$$l_n\left(x_0\right)=x_{n-1};l_n\left(x_N\right)=x_n,$$

(1)

for $n=1,2,\dots ,N$ and the family of continuous functions $W_n:I\times \mathbb{R}\to \mathbb{R}$ satisfying the “join-up” conditions:

$$W_n(x_0,y_0)=y_{n-1};W_n(x_N,y_N)=y_n,$$

(2)

for $n=1,2,\dots ,N$. Let us consider the space

$${\mathcal{C}}_0\left(I\right)=\{g\in \mathcal{C}\left(I\right):g\left(x_0\right)=y_0,g\left(x_N\right)=y_N\}.$$

${\mathcal{C}}_0\left(I\right)$ is a closed set of the complete subspace of continuous functions $\mathcal{C}\left(I\right)$ and thus, a complete space with respect to the supremum norm. Let T be the usual operator for fractal interpolation $T:{\mathcal{C}}_0\left(I\right)\to {\mathcal{C}}_0\left(I\right)$ defined as

$$Tg\left(x\right)=W_n(l_n^{-1}\left(x\right),(g\circ l_n^{-1})\left(x\right)),$$

(3)

if $x\in I_n$. Using the conditions (1) and (2), it is easy to check that $Tg$ is well-defined and further,

$$Tg\left(x_i\right)=y_i,$$

for all $i=0,1,2,\dots ,N$.

Lemma 1.

Let us define $\phi \left(t\right)={sup}_n{\phi }_n\left(t\right)$, for $t\in D\subseteq \mathbb{R}$ and $n\in J$. If ${\phi }_n$ is non-decreasing for any $n\in J$, then φ is also non-decreasing.

Proof. 

It is based on the fact that $a_n\le b_n$ for any $n\in J$ implies that ${sup}_n{a}_n\le {sup}_n{b}_n$. □

The next result ensures the existence of a fractal interpolant of the given data under some conditions on the maps $W_n$. From here on, we consider functions ${\phi }_n:[0,\infty )\to [0,\infty )$ non-decreasing, such that ${lim}_{m\to \infty }{\phi }_n^m\left(t\right)=0$ for every $t>0$, where ${\phi }_n^m$ denotes the composition of ${\phi }_n$ with itself m times.

Theorem 2.

Let $W_n$ be a Matkowski contraction in the second variable, i.e., there exist functions ${\phi }_n:[0,\infty )\to [0,\infty )$ satisfying the conditions of item (iii) of Definition 1 such that

$$|W_n(x,y)-W_n(x,y^{\prime })|\le {\phi }_n\left(\right|y-y^{\prime }\left|\right),$$

for all $n=1,2,\dots ,N$ and $y,y^{\prime }\in \mathbb{R}$. We assume further that the map defined as $\phi \left(t\right)={sup}_n{\phi }_n\left(t\right)$ is such that ${lim}_{m\to \infty }{\phi }^m\left(t\right)=0$. Then the operator T defined in (3) is a Matkowski contraction, and consequently, it has a fixed point $f_{*}\in {\mathcal{C}}_0\left(I\right)$. The map $f_{*}$ is an interpolant of the data $(x_i,y_i)$, $i=0,1,\dots ,N$.

Proof. 

The operator T satisfies the following equality, for $x\in I_n$, $g,h\in {\mathcal{C}}_0\left(I\right):$

$$|Tg\left(x\right)-Th\left(x\right)|=|W_n(l_n^{-1}\left(x\right),g\circ l_n^{-1}\left(x\right))-W_n(l_n^{-1}\left(x\right),h\circ l_n^{-1}\left(x\right))|$$

and by hypothesis,

$$|Tg\left(x\right)-Th\left(x\right)|\le {\phi }_n\left(\right|g\left(\tilde{x}\right)-h\left(\tilde{x}\right)\left|\right)\le \phi \left(\right||g-{h\left|\right|}_{\infty }),$$

where $\tilde{x}=l_n^{-1}\left(x\right)$. Consequently

$$\left|\right|Tg-{Th\left|\right|}_{\infty }\le \phi \left(\right||g-{h\left|\right|}_{\infty }),$$

and T is a Matkowski contraction. According to Theorem 1, it has a unique fixed point $f_{*}$. As said previously, all the images of T are interpolant of the data and, in particular, $f_{*}$. □

Definition 4.

The map $f_{*}=T{f}_{*}$ defined in Theorem 2 is a Matkowski fractal interpolation function of the considered data.

The usual approach to construct a FIF is to obtain a curve that is the attractor of the IFS ${\left\{(l_n,W_n)\right\}}_{n\in J}$ with $W_n(x,y)={\alpha }_{n}y+q_n\left(x\right)$, where ${\alpha }_n$ is lower than 1 in modulus. However, in this paper, we consider nonlinear contractions instead of the scaling term in the y-coordinate.

Corollary 1.

If the maps $W_n:I\times \mathbb{R}\to \mathbb{R}$ are defined as $W_n(x,y)=U_n\left(x\right)+R_n\left(y\right)$, where $U_n:I\to \mathbb{R}$ is continuous on $I$, $R_n:\mathbb{R}\to \mathbb{R}$ is a Matkowski contraction whose comparison function ${\phi }_n$ satisfies the conditions described in Theorem 2 and the maps $U_n\left(x\right)$, $R_n\left(y\right)$ satisfy the join-up conditions prescribed in (2), then the IFS $\left\{(l_n,W_n)\right\}$ defines a Matkowski FIF.

Proof. 

It is a straightforward consequence of Theorem 2. □

Remark 4.

The maps $W_n$ can be made more general taking $W_n(x,y)=U_n\left(x\right)+R_n(x,y)$ such that $R_n:I\times \mathbb{R}\to \mathbb{R}$ is a Matkowski contraction in the second variable. In this case, we also obtain a Matkowski FIF. For instance, $R_n\left(y\right)={\alpha }_n\left(x\right)y$ satisfies the condition, for ${\phi }_n\left(t\right)={\parallel {\alpha }_n\parallel }_{\infty }t$, if $\parallel {\alpha }_n{\parallel }_{\infty }<1$.

Example 1.

Let us consider the set of data $D=\left\{\right(0,0),(1/3,3),(2/3,6),(1,5\left)\right\}$ in the interval $I=[0,1]$ and the maps:

$$l_1\left(x\right)=x/3;l_2\left(x\right)=(x+1)/3;l_3\left(x\right)=(x+2)/3$$

for the first coordinate, and

$$\begin{array}{c}{W}_1(x,y)=13x/6+xy/(1+y);W_2\left(x\right)=17/6x+3+x/(1+y);W_3\left(x\right)=-x+6+\frac{xsin\left(\pi y\right)}{3\pi }.\end{array}$$

It is an easy exercise to prove that $l_n$, $W_n$ satisfy the prescribed join-up conditions (1) and (2). Since

$$|W_1(x,y)-W_1(x,y^{\prime })|\le |\frac{y}{1+y}-\frac{y^{\prime }}{1+y^{\prime }}|\le \frac{|y-y^{\prime }|}{1+|y-y^{\prime }|},$$

$$|W_2(x,y)-W_2(x,y^{\prime })|\le |\frac{1}{1+y}-\frac{1}{1+y^{\prime }}|\le \frac{|y-y^{\prime }|}{1+|y-y^{\prime }|},$$

for $y,y^{\prime }\ge 0$, $W_1,W_2$ are Matkowski contractions in the second variable, with comparison functions ${\phi }_1\left(t\right)={\phi }_2\left(t\right)=t/(1+t)$. Moreover

$$|W_3(x,y)-W_3(x,y^{\prime })|\le \frac{1}{3}|y-y^{\prime }|,$$

and $W_3$ is a Matkowski contraction with comparison function ${\phi }_3\left(t\right)=t/3$. Thus, the operator T defined by the expression (3) satisfies the inequality

$$\left|\right|Tg-{Th\left|\right|}_{\infty }\le \phi \left(\right||g-{h\left|\right|}_{\infty }),$$

where $\phi \left(t\right)=max\{{\phi }_1\left(t\right),{\phi }_3\left(t\right)\}$. Consequently, T owns a fixed point defining a fractal function $f_{*}$ that interpolates the set of data $D$.

3.2. Infinite Number of Data

Consider the countable system of data

$$\Delta =\{(x_n,y_n)\in I\times \mathbb{R},n\ge 0\},$$

where ${\left(x_n\right)}_{n\ge 0}$ is a strictly increasing and bounded sequence with $x_0=a$, $\underset{n\to \infty }{lim}{x}_n=b$ and ${\left(y_n\right)}_{n\ge 0}$ is a convergent sequence with $\underset{n\to \infty }{lim}{y}_n=M$, and $I=[a,b]$. Let us denote $m=y_0$.

We define a family of contractive homeomorphisms ${\left(l_n\right)}_{n\ge 1}$, $l_n:I\to I_n$, for every $n\ge 1$, such that

$$l_n\left(a\right)=x_{n-1},l_n\left(b\right)=x_n.$$

We consider a countable family of continuous functions ${\left(W_n\right)}_{n\ge 1}$, $W_n:I\times \mathbb{R}\to \mathbb{R}$, such that

$$W_n(a,m)=y_{n-1},W_n(b,M)=y_n.$$

Let us define the subspace of continuous functions

$${\mathcal{C}}_{m,M}\left(I\right)=\{g\in \mathcal{C}\left(I\right):g\left(a\right)=m,g\left(b\right)=M\}$$

(4)

and the operator $T:{\mathcal{C}}_{m,M}\left(I\right)\to {\mathcal{C}}_{m,M}\left(I\right)$ defined as

$$Tg\left(x\right)=W_n(l_n^{-1}\left(x\right),g\circ l_n^{-1}\left(x\right)),$$

(5)

if $x\in I_n$, and $Tg\left(b\right)=M$. Using the “join-up” conditions on $l_n$ and $W_n$, it is easy to prove that $Tg\left(x_n\right)=y_n$ for any $n\ge 0$. The only different issue with respect to the finite case is that one has to prove that $Tg$ is (left) continuous at $b$. This is proved in the reference [35] assuming the hypothesis that $diam\left(Im\left(W_n\right)\right)$ tends to zero when n goes to infinity ($diam\left(Im\left(W_n\right)\right)$ means the diameter of the image of $W_n$). Thus, we propose the next theorem as a generalization of Theorem 3 of the same reference.

Theorem 3.

Let $W_n$ be Matkowski contractions in the second variable, that is to say, there exist functions ${\phi }_n:[0,\infty )\to [0,\infty )$ satisfying the conditions of item (iii) of Definition 1 such that

$$|W_n(x,y)-W_n(x,y^{\prime })|\le {\phi }_n\left(\right|y-y^{\prime }\left|\right),$$

for all $n=1,\dots ,N$ and $y,y^{\prime }\in \mathbb{R}$. We assume further that the map defined as $\phi \left(t\right)={sup}_n{\phi }_n\left(t\right)$ is such that $\phi \left(t\right)<\infty$ for any $t>0$ and ${lim}_{m\to \infty }{\phi }^m\left(t\right)=0$, for any $t>0$. Then if $diam\left(Im\left(W_n\right)\right)$ tends to zero when n goes to infinity, the operator T defined in (5) is a Matkowski contraction and, consequently, has a fixed point $f_{*}\in {\mathcal{C}}_0\left(I\right)$. The map $f_{*}$ is an interpolant of the data $(x_n,y_n)$, for any $n\ge 0$.

Proof. 

Take $\phi \left(t\right)={sup}_n{\phi }_n\left(t\right)$ in the proof of the quoted theorem. □

Definition 5.

The map $f_{*}=T{f}_{*}$ defined in Theorem 3 is a Matkowski FIF of the countable collection of data ${\left\{(x_n,y_n)\right\}}_{n\ge 0}$.

Corollary 2.

If the maps $W_n:I\times \mathbb{R}\to \mathbb{R}$ are defined as $W_n(x,y)=U_n\left(x\right)+R_n\left(y\right)$, where $U_n:I\to \mathbb{R}$ is continuous on I and $R_n:\mathbb{R}\to \mathbb{R}$ is a Matkowski contraction whose function ${\phi }_n$ satisfies the conditions described in Theorem 3, the IFS ${\left\{(l_n,W_n)\right\}}_{n\ge 0}$ defines a Matkowski FIF for a countable collection of data.

Proof. 

It is a straightforward consequence of Theorem 3. □

Remark 5.

$R_n$ (respectively $W_n$) can be Banach and Rakotch contractions, as particular cases of Matkowski contractions.

Remark 6.

$R_n$ can be defined as $R_n(x,y)$ where $R_n$ is Matkowski in the second variable, and it also defines a FIF of a countable set of data. For instance, $R_n\left(y\right)={\alpha }_n\left(x\right)y$ satisfies the condition, for ${\phi }_n\left(t\right)={\parallel {\alpha }_n\parallel }_{\infty }t$, if ${sup}_n{\parallel {\alpha }_n\parallel }_{\infty }<1$.

Remark 7.

The arguments in this section may serve for any contraction admitting a fixed point theorem on a complete metric space.

4. R-Fractal Interpolation Functions

Let us consider again the finite case associated with the set ${\left\{(x_i,y_i)\right\}}_{i=0}^N$. Let for $n=1,2,\dots ,N$, $l_n$ be defined as in Section 3.1, and define $W_n$ as

$$W_n(x,y)=f\circ l_n\left(x\right)-S_n\left(x\right)+R_n\left(y\right),$$

for $x\in I_n$, where $f:I\to \mathbb{R}$ is a continuous function such that

$$f\left(x_i\right)=y_i$$

for $i=0,1,\dots ,N$, $S_n:I\to \mathbb{R}$ is also continuous, $R_n$ is a Matkowski contraction and

$$S_n\left(x_0\right)=R_n\left(y_0\right),S_n\left(x_N\right)=R_n\left(y_N\right).$$

With these conditions we have

$$W_n(x_0,y_0)=y_{n-1},W_n(x_N,y_N)=y_n$$

and the IFS $\left\{(l_n,W_n)\right\}$ satisfies the conditions of Theorem 2. Consequently, there is a fractal interpolant to the data.

Definition 6.

We call the fractal interpolant $f^R$ defined by the IFS described above the R-fractal interpolation function associated with f.

Remark 8.

This definition generalizes the concept of α-fractal function ([21]), taking $R_n\left(y\right)={\alpha }_{n}y$ and $S_n\left(x\right)={\alpha }_{n}b\left(t\right)$, where $b\left(x_0\right)=f\left(x_0\right)$ and $b\left(x_N\right)=f\left(x_N\right)$.

Remark 9.

One can consider different types of contractions $R_n$ to define the R-fractal function, so the results are more general than they appear.

Remark 10.

We can generalize the model to $W_n(x,y)=f\circ l_n\left(x\right)-S_n\left(x\right)+R_n(x,y)$, where $R_n$ is a Matkowski contraction in the second variable. This is the case for α-fractal functions with α depending on $x:$$R_n(x,y)={\alpha }_n\left(x\right)y$. The function would be ${\phi }_n\left(t\right)=\left|\right|{\alpha }_n{\left|\right|}_{\infty }t$, and $\phi \left(t\right)={sup}_n\left|\right|{\alpha }_n{\left|\right|}_{\infty }t$, which satisfies the condition required in Theorem 2.

Let us consider now an infinite collection of data

$$\Delta =\{(x_n,y_n)\in I\times \mathbb{R},n\ge 0\},$$

where ${\left(x_n\right)}_{n\ge 0}$ is a strictly increasing and bounded sequence with $x_0=a$, $\underset{n\to \infty }{\lim }{x}_n=b$, ${\left(y_n\right)}_{n\ge 0}$ is a convergent sequence with $\underset{n\to \infty }{lim}{y}_n=M$ and $I=[a,b]$. Let us denote $m=y_0$.

Let ${\left(l_n\right)}_{n\ge 1}$, $l_n:I\to I_n$, be contractive homeomorphisms for every $n\ge 1$, such that

$$l_n\left(a\right)=x_{n-1},l_n\left(b\right)=x_n.$$

Let $f\in \mathcal{C}\left(I\right)$ such that $f\left(x_n\right)=y_n$ for all $n\ge 0$. For continuity $f\left(b\right)=M$. We also define in this case for every $n\in \mathbb{N}$:

$$W_n(x,y)=(f\circ l_n)\left(x\right)-S_n\left(x\right)+R_n\left(y\right),$$

(6)

satisfying, for any natural $n$, the matching conditions

$$W_n(x_0,y_0)=y_{n-1},W_n(b,M)=y_n.$$

The operator T is defined as the infinite case of the previous section on the space ${\mathcal{C}}_{m,M}\left(I\right)$ (4). In the next theorem, we prove that T is well-defined. Now we consider different hypotheses to provide a fractal interpolant of the sequence since the (sufficient) condition $diam\left(Im\left(W_n\right)\right)\to 0$ as n tends to infinity is sometimes difficult to check. Therefore, we propose the following result.

Theorem 4.

For the IFS whose map $W_n$ is defined by (6), let $R_n$ be a Matkowski contraction, that is to say, there exists a function ${\phi }_n:[0,\infty )\to [0,\infty )$ satisfying the conditions of item (iii) of Definition 1 such that

$$|R_n\left(y\right)-R_n\left(y^{\prime }\right)|\le {\phi }_n\left(\right|y-y^{\prime }\left|\right),$$

for all $n=1,\dots ,N$ and $y,y^{\prime }\in \mathbb{R}$. We assume further that the map defined as $\phi \left(t\right)={sup}_n{\phi }_n\left(t\right)$ is such that $\phi \left(t\right)<\infty$ for any $t>0$ and ${lim}_{m\to \infty }{\phi }^m\left(t\right)=0$. Let us choose $R_n$, $S_n$ such that ${lim}_{n\to \infty }{R}_n\left(y\right)={lim}_{n\to \infty }{S}_n\left(x\right)=0$ uniformly. Then the operator T is a Matkowski contraction and, consequently, has a fixed point $f_{*}\in {\mathcal{C}}_0\left(I\right)$. The map $f_{*}$ is an interpolant of the data $(x_n,y_n)$, for any $n\ge 0$.

Proof. 

Let us prove that $Tg$ is continuous at b. For $x\in I_n$,

$$Tg\left(x\right)-Tg\left(b\right)=f\left(x\right)+R_n\circ g\circ l_n^{-1}\left(x\right)-S_n\circ l_n^{-1}\left(x\right)-f\left(b\right).$$

Given $ϵ>0$, the left continuity of f at b implies that there exists $\delta >0$ such that $b-x<\delta$ implies

$$|f\left(x\right)-f\left(b\right)|<\frac{ϵ}{3}.$$

Now, the convergence to zero of $R_n$, $S_n$ implies that there are $n_1,n_2\in \mathbb{N}$ such that

$$|R_n\circ g\left(\tilde{x}\right)|<\frac{ϵ}{3},$$

$$|S_n\left(\tilde{x}\right)|<\frac{ϵ}{3},$$

where $\tilde{x}=l_n^{-1}\left(x\right)$, $n\ge max\{n_1,n_2\}$. Taking x close enough to b, we obtain

$$\left|Tg\right(x)-Tg(b\left)\right|<ϵ.$$

The rest is similar to the finite case. □

Remark 11.

For the case of α-fractal functions, the conditions on the function imply ${\alpha }_n\to 0$ when n tends to infinity. In the case of variable scaling, the condition is $\left|\right|{\alpha }_n{\left|\right|}_{\infty }\to 0$.

4.1. Properties of R-Fractal Interpolation Functions

The operator T in the n-th interval is defined as,

$$Tg\left(x\right)=f\left(x\right)+R_n\circ g\left(l_n^{-1}\left(x\right)\right)-S_n\left(l_n^{-1}\left(x\right)\right)$$

and consequently

$$\left|\right|Tg-{f\left|\right|}_{\infty }\le \underset{n}{sup}\left|\right|R_n\circ g-S_n{\left|\right|}_{\infty }\le \underset{n}{sup}\left(\right||R_n{\left|\right|}_{\infty }+\left|\right|S_n{\left|\right|}_{\infty }),$$

assuming that the suprema are finite.

In particular, for $g=f^R$, we have

$$\left|\right|f^R-{f\left|\right|}_{\infty }\le \underset{n}{sup}\left|\right|R_n\circ f^R-S_n{\left|\right|}_{\infty }.$$

(7)

Moreover, defining $\tilde{x}=l_n^{-1}\left(x\right)$, for $x\in I_n$,

$$|Tg\left(x\right)-Th\left(x\right)|=|R_n\circ g\left(\tilde{x}\right)-R_n\circ h\left(\tilde{x}\right)|\le {\phi }_n\left(\right|g\left(\tilde{x}\right)-h\left(\tilde{x}\right)\left|\right)\le {\phi }_n\left(\right||g-{h\left|\right|}_{\infty }),$$

since ${\phi }_n$ is non-decreasing.

If $R_n$ is a Rakotch contraction:

$$|Tg\left(x\right)-Th\left(x\right)|<|g\left(\tilde{x}\right)-h\left(\tilde{x}\right)|$$

if $g\left(\tilde{x}\right)\ne h\left(\tilde{x}\right)$. If $g\left(\tilde{x}\right)=h\left(\tilde{x}\right)$ then $Tg\left(x\right)=Th\left(x\right)$ and consequently

$$\left|\right|Tg-{Th\left|\right|}_{\infty }\le \left|\right|g-{h\left|\right|}_{\infty }.$$

In general:

$$\left|\right|Tg-{Th\left|\right|}_{\infty }\le \underset{n}{sup}{\phi }_n\left(\right||g-{h\left|\right|}_{\infty }).$$

The fixed point equation for $f^R$ in the interval $I_n$ is:

$$f^R\left(x\right)=f\left(x\right)+(R_n\circ f^R-S_n)\circ l_n^{-1}\left(x\right).$$

(8)

An emerging question is if $f^R$ may agree with f. The answer is given in the next result.

Proposition 1.

$f^R\ne f$ if and only if there exist n and $x\in I$ such that $R_n\circ f\left(x\right)\ne S_n\left(x\right)$.

Proof. 

It is a consequence of the Equation (8), taking $f^R=f$. □

4.2. Case $S_n=R_n\circ B$

Let us consider the particular case where $S_n=R_n\circ B$, and $B\left(a\right)=m$, $B\left(b\right)=M$. Then for $x\in I_n$

$$|f^R\left(x\right)-f\left(x\right)|=|R_n\circ f^R\left(\tilde{x}\right)-R_n\circ B\left(\tilde{x}\right)|\le {\phi }_n\left(\right|f^R\left(\tilde{x}\right)-B\left(\tilde{x}\right)\left|\right)\le {\phi }_n\left(\right||f^R-{B\left|\right|}_{\infty }).$$

Thus, if $R_n$ is a Rakotch contraction, we have

$$\left|\right|f^R-{f\left|\right|}_{\infty }\le \underset{n}{sup}{\phi }_n\left(\right||f^R-{B\left|\right|}_{\infty })\le ||f^R-B{\left|\right|}_{\infty }.$$

In this case, we can define a binary internal operation in the space ${\mathcal{C}}_{m,M}\left(I\right)$ as:

$$f\ast B=f^R$$

that generalizes the fractal convolution defined in ([42]). If we take $B=f$ in the operator T, for $x\in I_n$, then

$$Tf\left(x\right)=f\left(x\right)+R_n\circ f\left(l_n^{-1}\left(x\right)\right)-R_n\circ f\left(l_n^{-1}\left(x\right)\right).$$

Thus, we obtain that $Tf\left(x\right)=f\left(x\right)$. Consequently, f is the fixed point of T and $f^R=f$. The conclusion is that

$$f\ast f=f,$$

and the operation is idempotent.

If $S_n=R_n\circ B$ and $R_n$ are Banach contractions with contractivity ratio $k_n$, the inequality (7) becomes:

$$\left|\right|f^R-{f\left|\right|}_{\infty }\le k\left|\right|f^R-B{\left|\right|}_{\infty },$$

where $k={sup}_n{k}_n$, assuming that $k<\infty$. Inserting in the last norm the map f, we obtain:

$$\left|\right|f^R-{f\left|\right|}_{\infty }\le \frac{k}{1-k}\left|\right|f-{B\left|\right|}_{\infty }.$$

For $\alpha$-fractal functions ([21]) $R_n\left(y\right)={\alpha }_{n}y$ and $S_n\left(x\right)={\alpha }_{n}b\left(x\right)=R_n\circ b\left(x\right)$. The last inequality provides the classical bounding error formula for $\alpha$-fractal functions ($k={\left|\alpha \right|}_{\infty }$ assuming that ${\left|\alpha \right|}_{\infty }={sup}_n\left|{\alpha }_n\right|<1$), and the inequality holds for an infinite set of data as well.

4.3. Linear Case

Let us consider a different case, where $R_n$ and $S_n$ are linearly dependent of f, that is to say: there exist two sequences of linear operators such that $R_n=L_{n}f$ and $S_n=L_n^{\prime }f$. Then arguing as in ([21]) the operator $\mathcal{L}:\mathcal{C}\left(I\right)\to \mathcal{C}\left(I\right)$ defined as

$$\mathcal{L}\left(f\right)=f^R$$

is linear. Moreover, if $L_n,L_n^{\prime }$ are bounded,

$$\left|\right|\mathcal{L}\left(f\right)-{f\left|\right|}_{\infty }\le \underset{n}{sup}\left|\right|L_n\left(f\right)\circ f^R-L_n^{\prime }{\left(f\right)\left|\right|}_{\infty }\le (s+s^{\prime }){\left|\right|f\left|\right|}_{\infty },$$

assuming that $s={sup}_n\left|\right|L_n\left|\right|$ and $s^{\prime }={sup}_n\left|\right|L_n^{\prime }\left|\right|$ are finite. The operator $\mathcal{L}$ is also bounded and

$$\left|\right|\mathcal{L}\left|\right|\le (1+s+s^{\prime }).$$

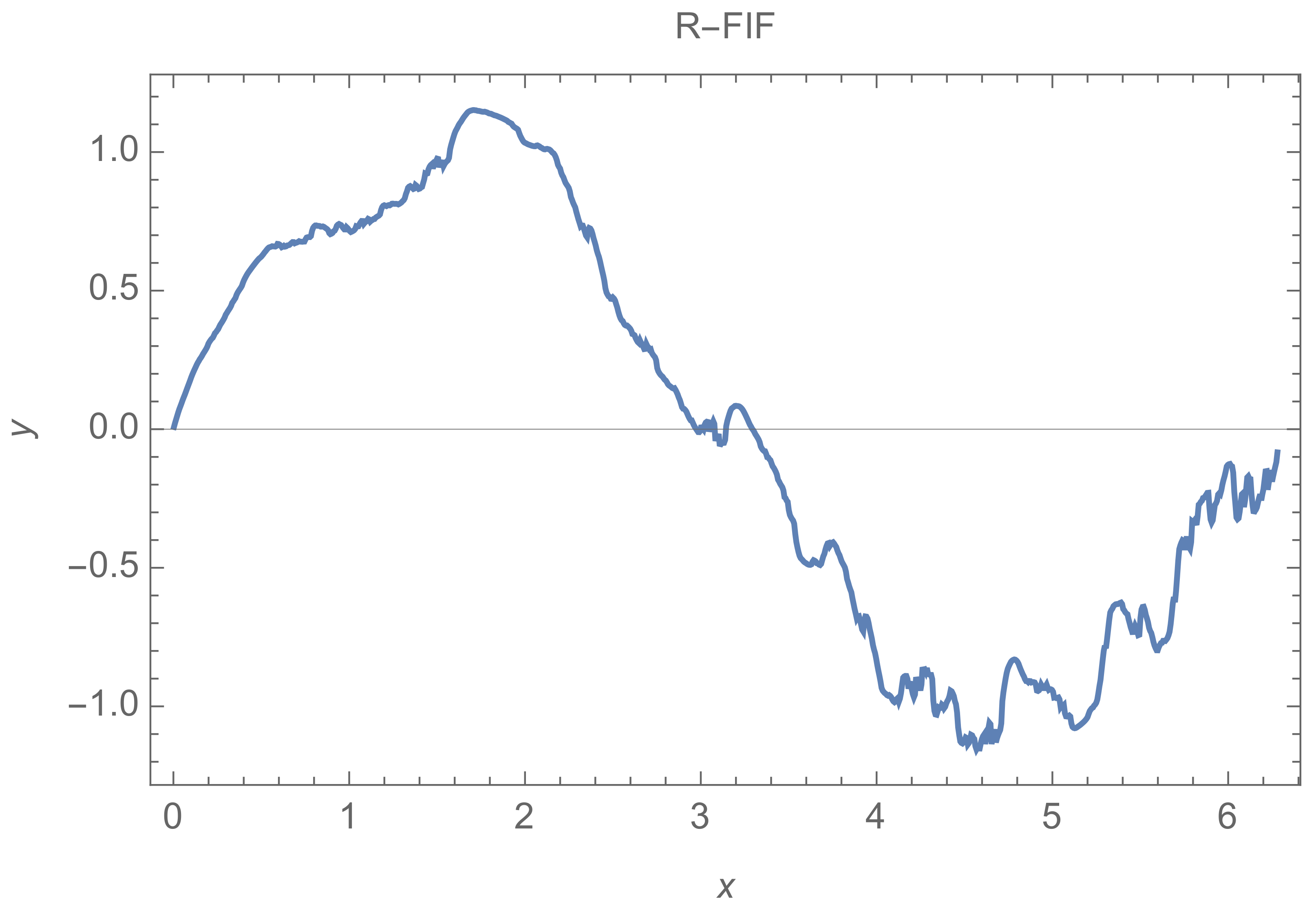
Figure 1 represents an R-fractal function corresponding to a uniform partition of the interval $I=[0,2\pi ]$ with five data, function $f=sin\left(x\right)$ and maps $R_n\left(y\right)=sin\left(ny\right)/6$ for $n=1,\dots ,4$ with comparison functions ${\phi }_n\left(t\right)=nt/6$, $\phi \left(t\right)=2t/3$, and $S_n\left(x\right)=0$ for all n.

5. Smooth R-Fractal Interpolation Functions

Let $I=[a,b]$, and a partition of it $\Delta :a=x_0<x_1<\cdots <x_N=b$, ($N>1$). Let $I_i=[x_{i-1},x_i]$ and $J_N=\{0,1,\dots ,N\}$. We consider the finite system of data

$${\Delta }^{\prime }=\{(x_i,y_{i,p})\in I\times \mathbb{R},i\in J_N,0\le p\le k\}.$$

Let a finite family of contractive homeomorphisms $l_i:I\to I_i$ be such that

$$l_i\left(a\right)=x_{i-1}\mathrm{and}{l}_i\left(b\right)=x_i$$

for every $i\in J_N\backslash \left\{0\right\}$ and $l_i\left(x\right)=a_{i}x+b_i$.

Let us consider the maps $W_i:I\times Y\to Y$, where Y is a compact subset of $\mathbb{R}$, defined as

$$W_i(x,y)=f\left(l_i\left(x\right)\right)+R_i\left(y\right)-S_i\left(x\right),$$

where $f\in {\mathcal{C}}^k\left(I\right)$, and $f^{\left(p\right)}\left(x_i\right)=y_{i,p}$ for all $i,p$ in their ranges. Let us assume that $S_i\in {\mathcal{C}}^k\left(I\right)$ and $R_i\in {\mathcal{C}}^k\left(Y\right)$.

Let us define

$${\mathcal{A}}^k\left(I\right)=\{g\in {\mathcal{C}}^k\left(I\right):g^{\left(p\right)}\left(a\right)=y_{0,p}\mathrm{and}{g}^{\left(p\right)}\left(b\right)=y_{N,p},\mathrm{for}0\le p\le k\},$$

and the norm ${\parallel g\parallel }_k=\underset{p\in J_k}{\max }\{\parallel g^{\left(p\right)}{\parallel }_{\infty }\}$. Then $({\mathcal{A}}^k\left(I\right),\parallel ·{\parallel }_k)$ is a complete metric space.

Let the operator $T:{\mathcal{A}}^k\left(I\right)\to {\mathcal{A}}^k\left(I\right)$ be defined as usual

$$Tg\left(x\right)=W_i(l_i^{-1}\left(x\right),g\left(l_i^{-1}\left(x\right)\right)),$$

for every $x\in I_i$.

Theorem 5.

For the data ${\Delta }^{\prime }$, the functions $l_i$ and $W_i$ defined as above let us assume that for every $i\in J_N$ and $1\le p\le k$ the following join-up conditions are satisfied:

$$S_i^{\left(p\right)}\left(a\right)=\sum _{j=1}^p{R}_i^{\left(j\right)}\left(y_0\right)B_{p,j}(y_{0,1};y_{0,2}\dots ;y_{0,p-j+1}),$$

(9)

$$S_i^{\left(p\right)}\left(b\right)=\sum _{j=1}^p{R}_i^{\left(j\right)}\left(y_N\right)B_{p,j}(y_{N,1};y_{N,2}\dots ;y_{N,p-j+1})$$

(10)

and $S_i\left(a\right)=R_i\left(y_0\right)$, $S_i\left(b\right)=R_i\left(y_N\right)$. Let us define the operator $V_{i,p}:{\mathcal{C}}^k\left(I\right)\to \mathcal{C}\left(I\right),$ for $p\in J_k$ as $V_{i,p}\left(g\right)={(R_i\circ g)}^{\left(p\right)},$ and assume that $V_{i,p}$ is a Matkowski contraction for any $i,p$ with comparison function ${\phi }_{i,p}$ such that $\phi \left(t\right)=sup\{a_i^{-p}{\phi }_{i,p}\left(t\right):1\le i\le N,p\in J_k\}$ satisfies the condition ${\phi }^m\left(t\right)$ and tends to zero as m tends to infinity.

Then there exists a smooth R-FIF $f^R\in {\mathcal{C}}^k\left(I\right)$ satisfying the following functional equations, for every $p\in J_k$:

$$\begin{array}{cc}\hfill & {\left(f^R\right)}^{\left(p\right)}\left(l_i\left(x\right)\right)=f^{\left(p\right)}\left(l_i\left(x\right)\right)+\hfill \\ & +a_i^{-p}\sum _{j=1}^p{R}_i^{\left(j\right)}\left(f^R\left(x\right)\right)B_{p,j}({\left(f^R\right)}^{\prime }\left(x\right);{\left(f^R\right)}^{\left(2\right)}\left(x\right);\dots ;{\left(f^R\right)}^{(p-j+1)}\left(x\right))-a_i^{-p}{S}_i^{\left(p\right)}\left(x\right)=\hfill \\ & f^{\left(p\right)}\left(l_i\left(x\right)\right)+a_i^{-p}{(R_i\circ f^R)}^{\left(p\right)}\left(x\right)-a_i^{-p}{S}_i^{\left(p\right)}\left(x\right),\hfill \end{array}$$

(11)

for $1\le p\le k$, $x\in I,$ and

$$f^R\left(x\right)=f\left(x\right)+(R_i\circ f^R-S_i)\circ l_i^{-1}\left(x\right),$$

(12)

for $x\in I_i$. The function $f^R$ interpolates the data up to the order p: ${\left(f^R\right)}^{\left(p\right)}\left(x_{i,p}\right)=y_{i,p}$ for any $i,p$ in their ranges.

Proof. 

Let $T:{\mathcal{A}}^k\left(I\right)\to {\mathcal{A}}^k\left(I\right)$ defined for $x\in I_i$ as

$$\left(Tg\right)\left(x\right)=f\left(x\right)+R_i\left(g\left(l_i^{-1}\right)\left(x\right)\right)-S_i\left(l_i^{-1}\left(x\right)\right)$$

The Faà di Bruno formula for the derivative of a composition of functions provides

$$a_i^p{\left(Tg\right)}^{\left(p\right)}\left(l_i\left(x\right)\right)=a_i^p{f}^{\left(p\right)}\left(l_i\left(x\right)\right)+\sum _{j=1}^p{R}_i^{\left(j\right)}\left(g\left(x\right)\right)B_{p,j}(g^{\prime }\left(x\right);g^{\left(2\right)}\left(x\right);\dots ;g^{(p-j+1)}\left(x\right))-S_i^{\left(p\right)}\left(x\right)$$

and since $l_i$ satisfy $l_i\left(a\right)=l_{i-1}\left(b\right)$, we have

$$a_i^p{\left(Tg\right)}^{\left(p\right)}\left(x_i^{+}\right)=a_i^p{f}^p\left(x_i^{+}\right)+\sum _{j=1}^p{R}_i^{\left(j\right)}\left(y_0\right)B_{p,j}(g^{\prime }\left(a\right);g^{\left(2\right)}\left(a\right);\dots ;g^{(p-j+1)}\left(a\right))-S_i^{\left(p\right)}\left(a\right),$$

$$a_{i-1}^p{\left(Tg\right)}^{\left(p\right)}\left(x_i^{-}\right)=a_{i-1}^p{f}^{\left(p\right)}\left(x_i^{-}\right)+\sum _{j=1}^p{R}_{i-1}^{\left(j\right)}\left(y_N\right)B_{p,j}(g^{\prime }\left(b\right);g^{\left(2\right)}\left(b\right);\dots ;g^{(p-j+1)}\left(b\right))-S_{i-1}^{\left(p\right)}\left(b\right).$$

Using the fact that

$$f^{\left(p\right)}\left(x_i^{-}\right)=f^{\left(p\right)}\left(x_i^{+}\right),\mathrm{for}\mathrm{every}p\in J_k$$

and from (9) and (10), we obtain

$${\left(Tg\right)}^{\left(p\right)}\left(x_i^{+}\right)={\left(Tg\right)}^{\left(p\right)}\left(x_i^{-}\right),p\in J_k.$$

Moreover,

$${\left(Tg\right)}^{\left(p\right)}\left(a\right)=f^{\left(p\right)}\left(a\right)=y_{0,p},p\in J_k,$$

$${\left(Tg\right)}^{\left(p\right)}\left(b\right)=f^{\left(p\right)}\left(b\right)=y_{N,p},p\in J_k,$$

which proves that T is well defined. Further, for any $g\in {\mathcal{A}}^k\left(I\right)$

$${\left(Tg\right)}^{\left(p\right)}\left(x_i\right)=y_{i,p},p\in J_k.$$

On the other hand, for $g,h\in {\mathcal{A}}^k\left(I\right)$, $x\in I_i$ and $p\in J_k$, we have

$$\begin{array}{cc}\hfill {|\left(Tg\right)}^{\left(p\right)}\left(x\right)& -{\left(Th\right)}^{\left(p\right)}\left(x\right)|=a_i^{-p}|{(R_i\circ g)}^{\left(p\right)}\left(x\right)-{(R_i\circ h)}^{\left(p\right)}\left(x\right)|\hfill \\ & \le a_i^{-p}|V_{i,p}g\left(x\right)-V_{i,p}h\left(x\right)|\hfill \\ & \le a_i^{-p}\left|\right|V_{i,p}g-V_{i,p}h{\left|\right|}_{\infty }\hfill \\ & \le a_i^{-p}{\phi }_{i,p}\left(\right||g-{h\left|\right|}_k{)\le \phi (\left|\right|g-h\left|\right|}_k)\hfill \end{array}$$

This proves that T is a Rakotch contraction on ${\mathcal{A}}^k\left(I\right)$. Thus, by Theorem 1, we obtain that T has a unique fixed point $f^R\in {\mathcal{A}}^k\left(I\right)$ and ${\left(T{f}^R\right)}^{\left(p\right)}\left(x\right)={\left(f^R\right)}^{\left(p\right)}\left(x\right)$, which proves the functional Equations (11) and (12). The function $f^R$ interpolates f at the nodes up to the order k. □

Remark 12.

In the case of α-fractal functions, $R_i\left(y\right)={\alpha }_{i}y$ and ${(R_i\circ g)}^{\left(p\right)}\left(x\right)={\alpha }_i{g}^{\left(p\right)}\left(x\right)$. Consequently

$$\left|\right|{(R_i\circ g)}^{\left(p\right)}-{(R_i\circ h)}^{\left(p\right)}{\left|\right|}_{\infty }\le |{\alpha }_i\left|\right||g^{\left(p\right)}-h^{\left(p\right)}{\left|\right|}_{\infty }\le |{\alpha }_i\left|\right||g-{h\left|\right|}_k.$$

The comparison function of the operator $V_{i,p}$ defined as $V_{i,p}\left(g\right)={(R_i\circ g)}^{\left(p\right)}$, is ${\phi }_{i,p}\left(t\right)=\left|{\alpha }_i\right|t$. The function defined in the Theorem is $\phi \left(t\right)={max}_{i,p}{a}_i^{-p}\left|{\alpha }_i\right|t$. The hypothesis required on φ holds if $a_i^{-k}\left|{\alpha }_i\right|<1$ for any $i\in J_N$.

Let us consider now the smooth case with an infinite number of data ${\left\{(x_i,y_i)\right\}}_{i=0}^{\infty }$ such that $a=x_0$, $\left(x_n\right)$ is strictly increasing and $b={lim}_{i\to \infty }{x}_i$. Let $I_i=[x_{i-1},x_i]$. We consider the system of data, for $p\ge 0:$

$${\Delta }^{\prime }=\{(x_i,y_{i,p})\in I\times \mathbb{R},i\ge 0,0\le p\le k\},$$

such that ${lim}_{i\to \infty }{y}_{i,p}=M_p\in \mathbb{R}$ for every p.

Let an infinite family of contractive homeomorphisms $l_i:I\to I_i$ be such that

$$l_i\left(a\right)=x_{i-1}\mathrm{and}{l}_i\left(b\right)=x_i$$

for every $i\ge 1$ and $l_i\left(x\right)=a_{i}x+b_i$, $I=[a,b]$.

Let us consider the maps $W_i:I\times Y\to Y$, where Y is a compact subset of $\mathbb{R}$, be defined as

$$W_i(x,y)=f\left(l_i\left(x\right)\right)+R_i\left(y\right)-S_i\left(x\right),$$

where $f\in {\mathcal{C}}^k\left(I\right)$, and $f^{\left(p\right)}\left(x_i\right)=y_{i,p}$ for all $i,p$. The k-continuity of f implies that $f^{\left(p\right)}\left(b\right)=M_p$ for $0\le p\le k$. Let us assume that $S_i\in {\mathcal{C}}^k\left(I\right)$, $R_i\in {\mathcal{C}}^k\left(Y\right)$.

Let

$${\mathcal{A}}^k\left(I\right)=\{g\in {\mathcal{C}}^k\left(I\right):g^{\left(p\right)}\left(a\right)=y_{0,p}\mathrm{and}{g}^{\left(p\right)}\left(b\right)=M_p,\mathrm{for}0\le p\le k\},$$

and the norm ${\parallel g\parallel }_k=\underset{p\in J_k}{\max }\{\parallel g^{\left(p\right)}{\parallel }_{\infty }\}$, then $({\mathcal{A}}^k\left(I\right),\parallel ·{\parallel }_k)$ is a complete metric space.

Let the operator $T:{\mathcal{A}}^k\left(I\right)\to {\mathcal{A}}^k\left(I\right)$ be defined as usual

$$Tf\left(x\right)=W_i(l_i^{-1}\left(x\right),f\left(l_i^{-1}\left(x\right)\right)),$$

for every $x\in I_i$.

Theorem 6.

For the data ${\Delta }^{\prime }$, let the functions $l_i$ and $W_i$ be defined as above for every $i\ge 0$. Let us assume that the following join-up conditions are satisfied:

$$S_i^{\left(p\right)}\left(a\right)=\sum _{j=1}^p{R}_i^{\left(j\right)}\left(y_0\right)B_{p,j}(y_{0,1};y_{0,2}\dots ;y_{0,p-j+1}),$$

$$S_i^{\left(p\right)}\left(b\right)=\sum _{j=1}^p{R}_i^{\left(j\right)}\left(M_0\right)B_{p,j}(M_1;M_2\dots ;M_{p-j+1}),$$

for $1\le p\le k$, and $S_i\left(a\right)=R_i\left(y_0\right)$, $S_i\left(b\right)=R_i\left(M_0\right)$. Let us define the operator $V_{i,p}:{\mathcal{C}}^k\left(I\right)\to \mathcal{C}\left(I\right)$, for $p\in J_k$ defined as $V_{i,p}\left(g\right)={(R_i\circ g)}^{\left(p\right)}$, and assume that $V_{i,p}$ is a Matkowski contraction for any $i,p$ with comparison function ${\phi }_{i,p}$ such that $\phi \left(t\right)=sup\{a_i^{-p}{\phi }_{i,p}\left(t\right):i\in \mathbb{N},p\in J_k\}$ satisfies the conditions $\phi \left(t\right)<\infty$ for all t and ${\phi }^i\left(t\right)$ tends to zero as i tends to infinity. Additionally, let us assume that $\left|\right|R_i{\left|\right|}_k\to 0$ and $\left|\right|S_i{\left|\right|}_k\to 0$ when $i\to \infty$.

Then there exists a smooth R-FIF $f^R\in {\mathcal{C}}^k\left(I\right),$ such that for every $p\ge 1$, it satisfies the following functional equations:

$$\begin{array}{cc}\hfill & {\left(f^R\right)}^{\left(p\right)}\left(l_i\left(x\right)\right)=f^{\left(p\right)}\left(l_i\left(x\right)\right)+\hfill \\ & +a_i^{-p}\sum _{k=1}^p{R}_i^{\left(k\right)}\left(f^R\left(x\right)\right)B_{p,k}({\left(f^R\right)}^{\prime }\left(x\right);{\left(f^R\right)}^{\left(2\right)}\left(x\right);\dots ;{\left(f^R\right)}^{(p-k+1)}\left(x\right))-a_i^{-p}{S}_i^{\left(p\right)}\left(x\right)=\hfill \\ & f^{\left(p\right)}\left(l_i\left(x\right)\right)+a_i^{-p}{(R_i\circ f^R)}^{\left(p\right)}\left(x\right)-a_i^{-p}{S}_i^{\left(p\right)}\left(x\right),\hfill \end{array}$$

for $x\in I$ and

$$f^R\left(x\right)=f\left(x\right)+(R_i\circ f^R-S_i)\circ l_i^{-1}\left(x\right),$$

for $x\in I_i$. The function $f^R$ interpolates the data up to the order p: ${\left(f^R\right)}^{\left(p\right)}\left(x_{i,p}\right)=y_{i,p}$ for any $i,p$.

Proof. 

The arguments are analogous to those of Theorems 4 and 5. □

Remark 13.

For α-fractal functions, the operators $V_{i,p}$ are defined as in the finite case (Remark 12). However, the conditions to be held here are: If $c_i=a_i^{-k}\left|{\alpha }_i\right|$ then $c={sup}_i{c}_i<1$ and $c_i\to 0$ as i tends to infinity.

6. Conclusions

The main result of this paper concerns IFSs that define FIFs associated with a set of interpolation data, typically defined as

$$F_n(x,y)=(l_n\left(x\right),W_n(x,y)),$$

where the maps $l_n$ are homeomorphisms, $W_n$ are continuous and both satisfy the join-up conditions (1), (2). We have proved that for maps $W_n$ of type $W_n(x,y)=U_n\left(x\right)+R_n\left(y\right)$, or $W_n(x,y)=U_n\left(x\right)+R_n(x,y)$, where $U_n$ is continuous and $R_n$ is a Matkowski contraction, or a Matkowski contraction in the second variable, respectively, the IFS defines a continuous FIF interpolating the data. More precisely, we have proved that the classical vertical scaling term ${\alpha }_{n}y$ (or ${\alpha }_n\left(x\right)y$) may be substituted by a general Matkowski contraction in the y-variable. This result is true for a finite set and for a countable family of nodal data.

In particular, we have generalized the concept of $\alpha$-fractal function to R-fractal function when the described change in the y-coordinate of $W_n$ is performed. Thus, we have defined more general fractal perturbations of continuous functions. In the last part of the paper, we construct smooth R-fractal functions in the framework of the IFS described above.