New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
- (i)
- (ii)
- (iii)
3. Main Results
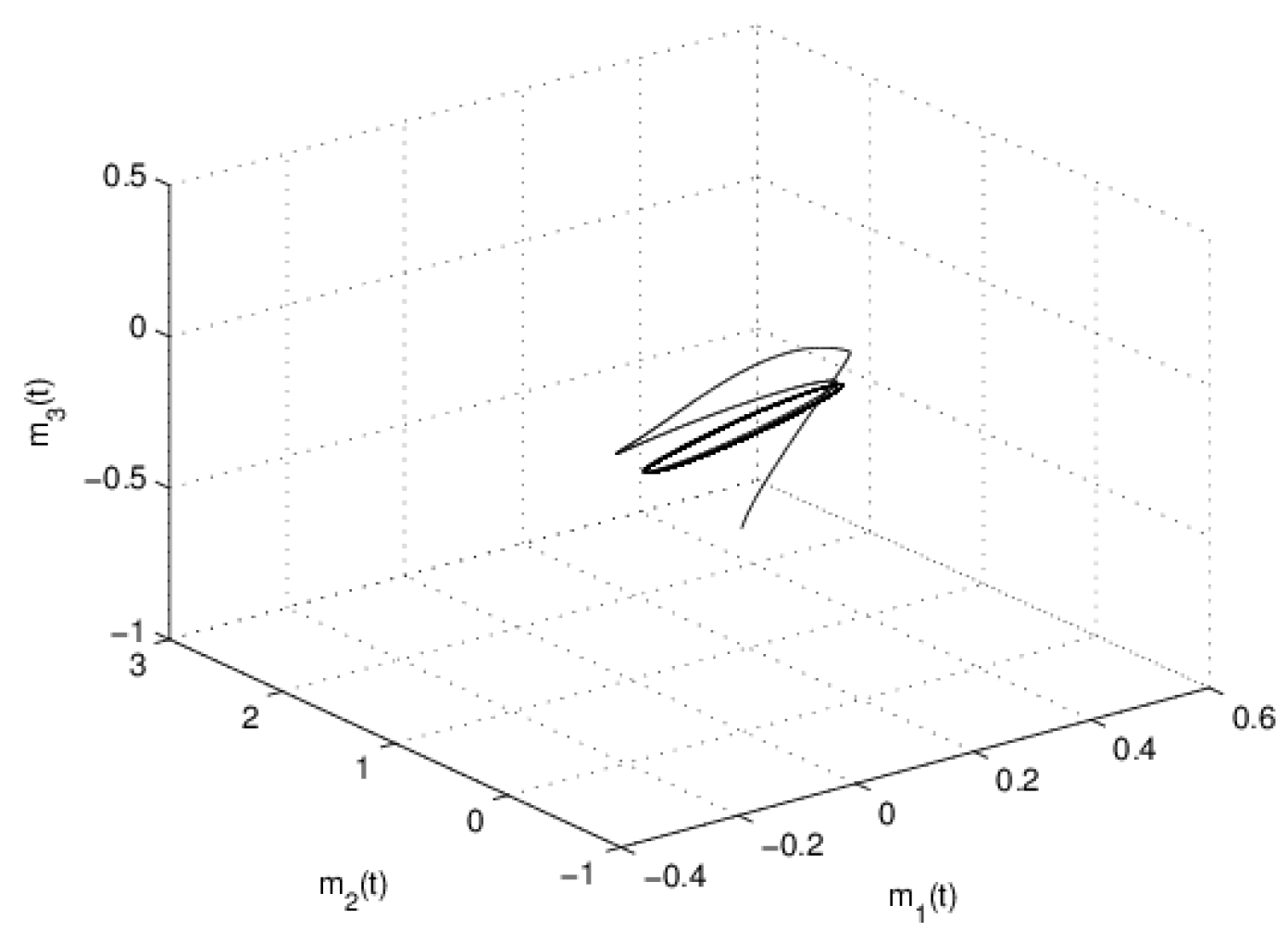
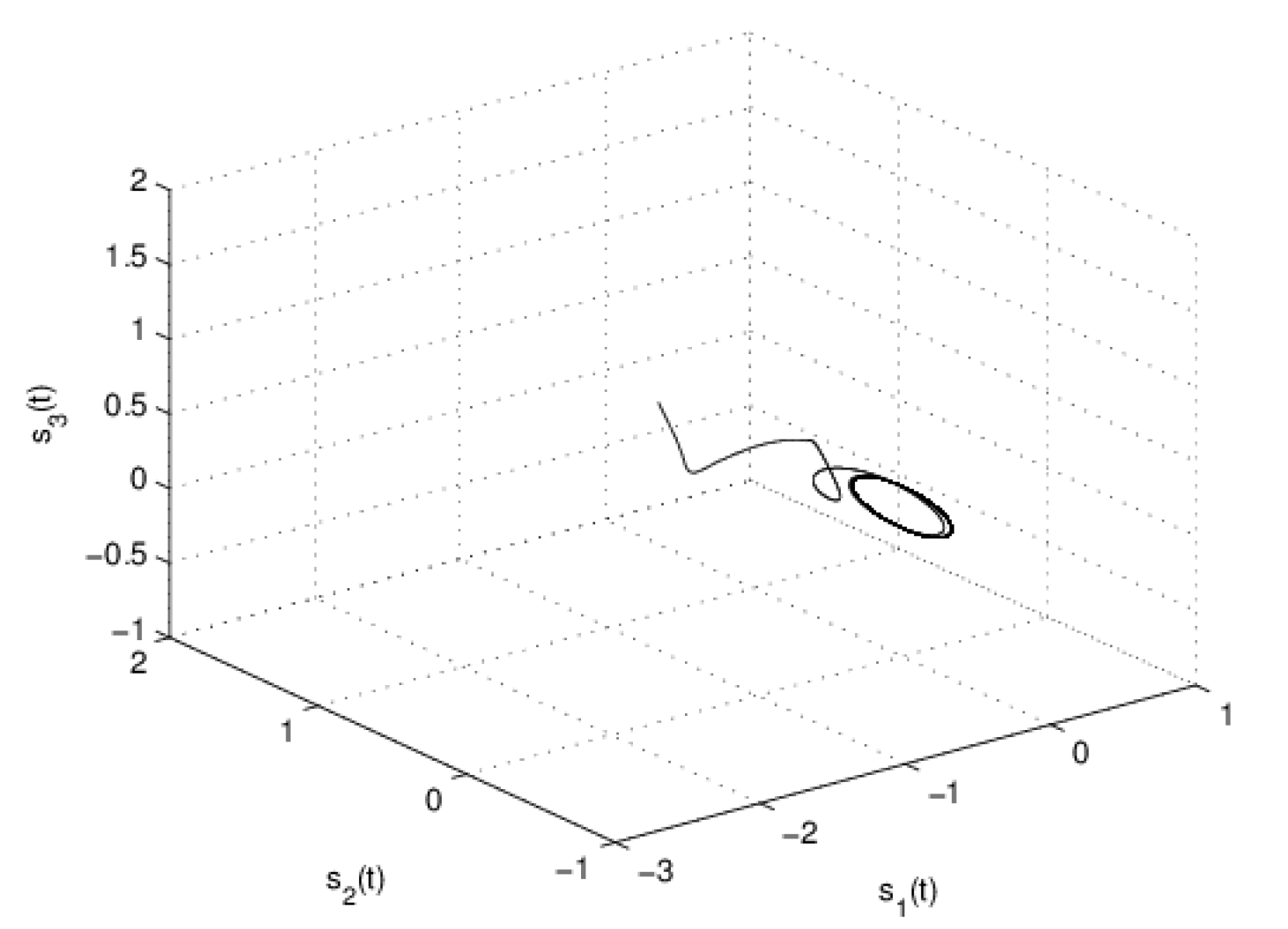
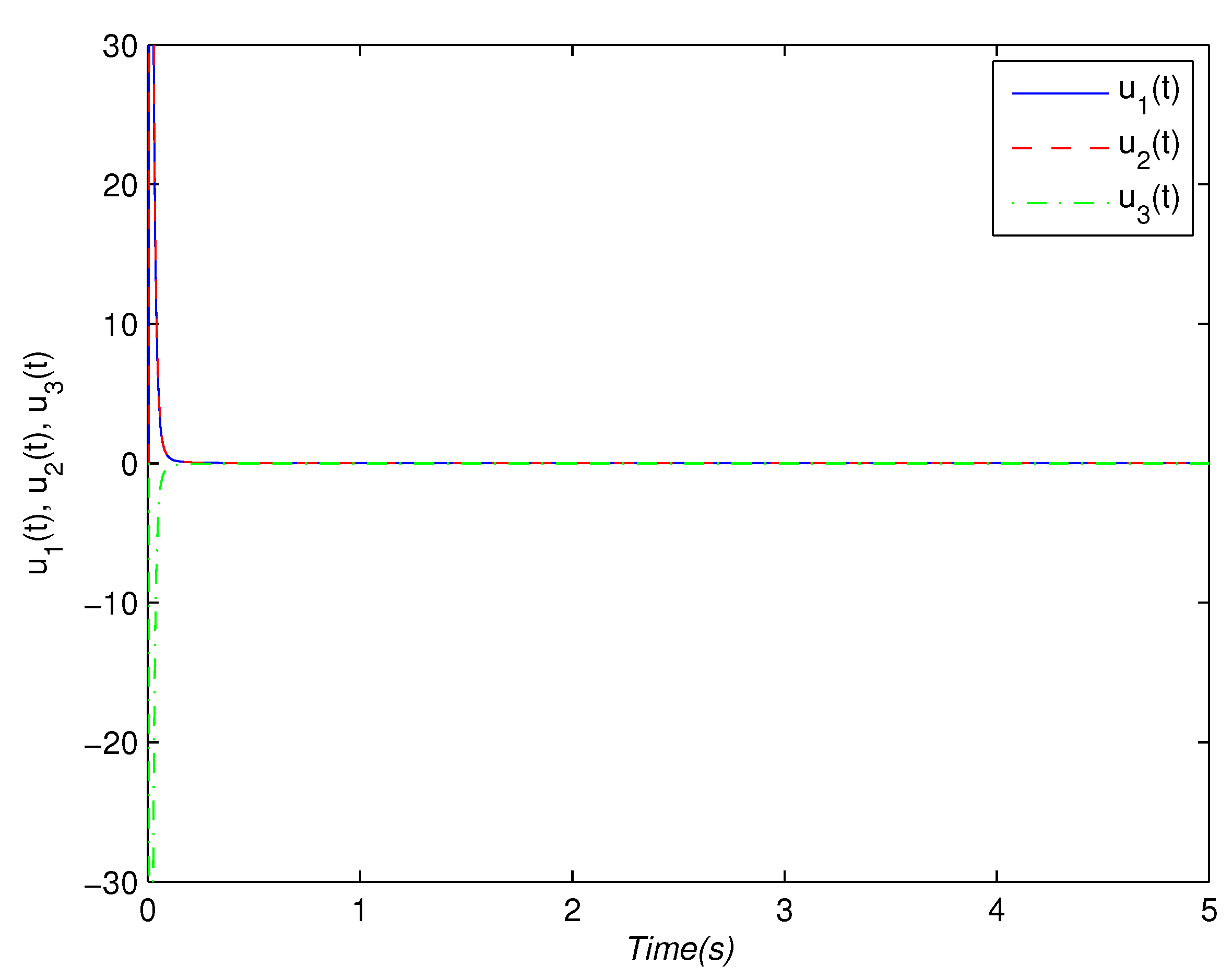
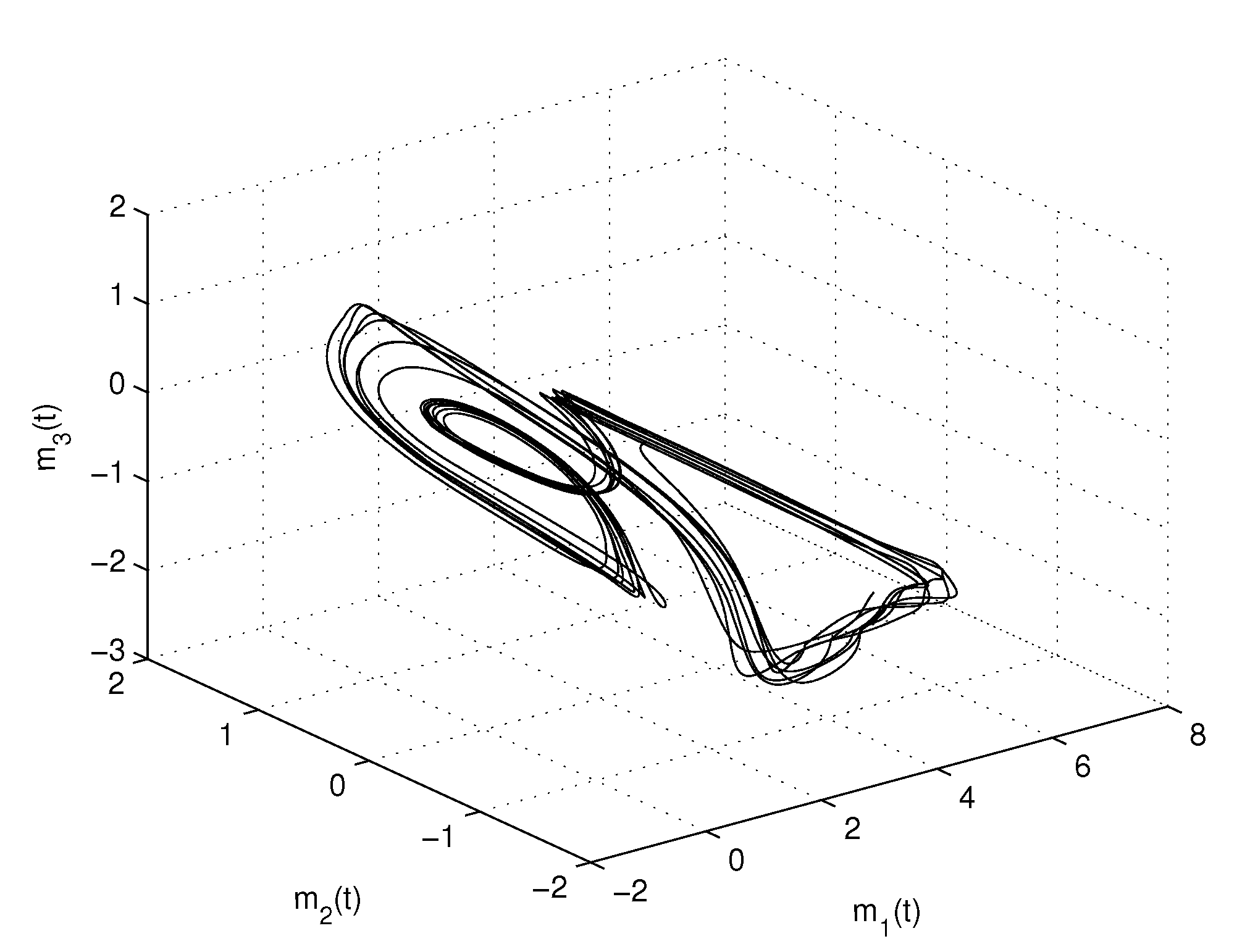
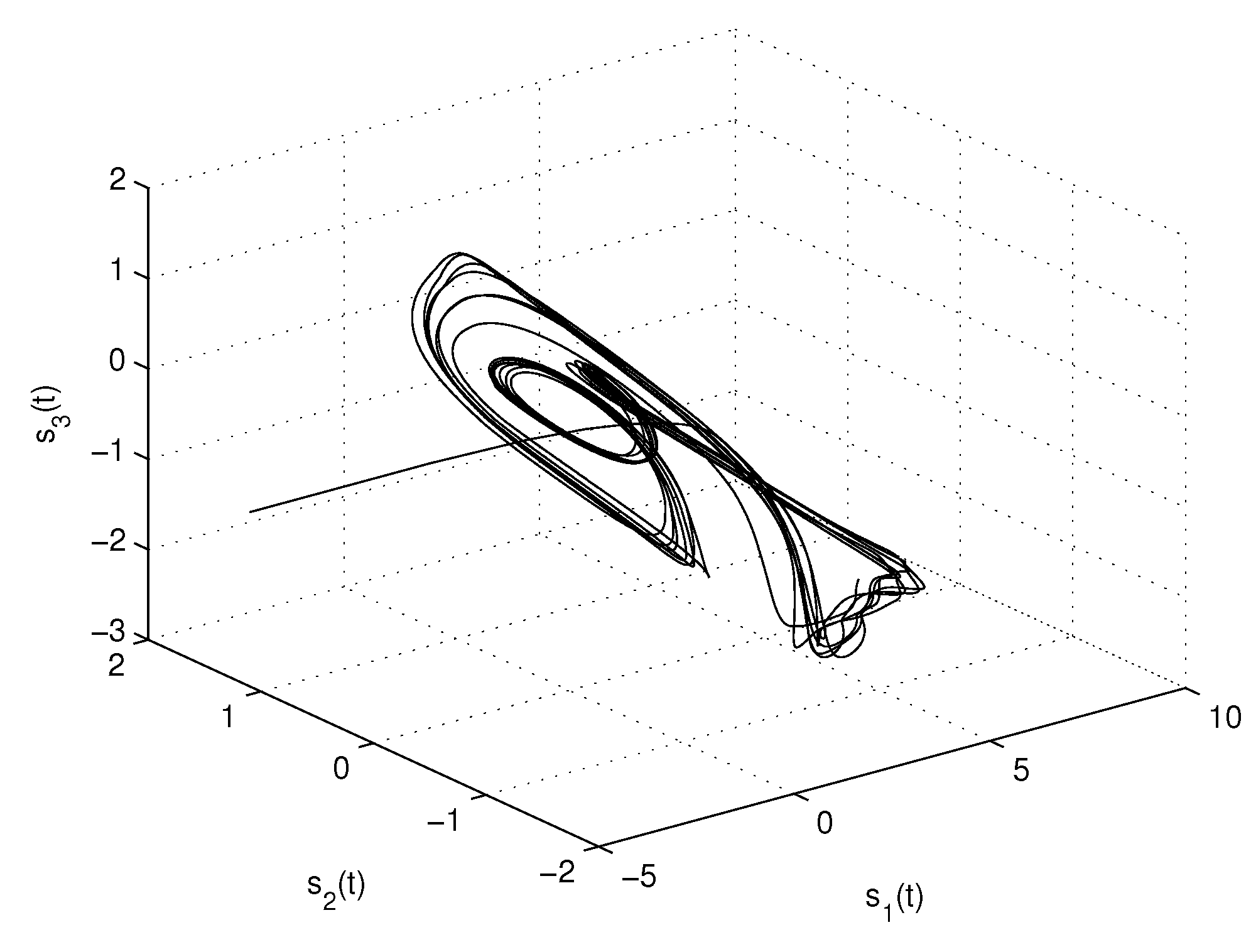
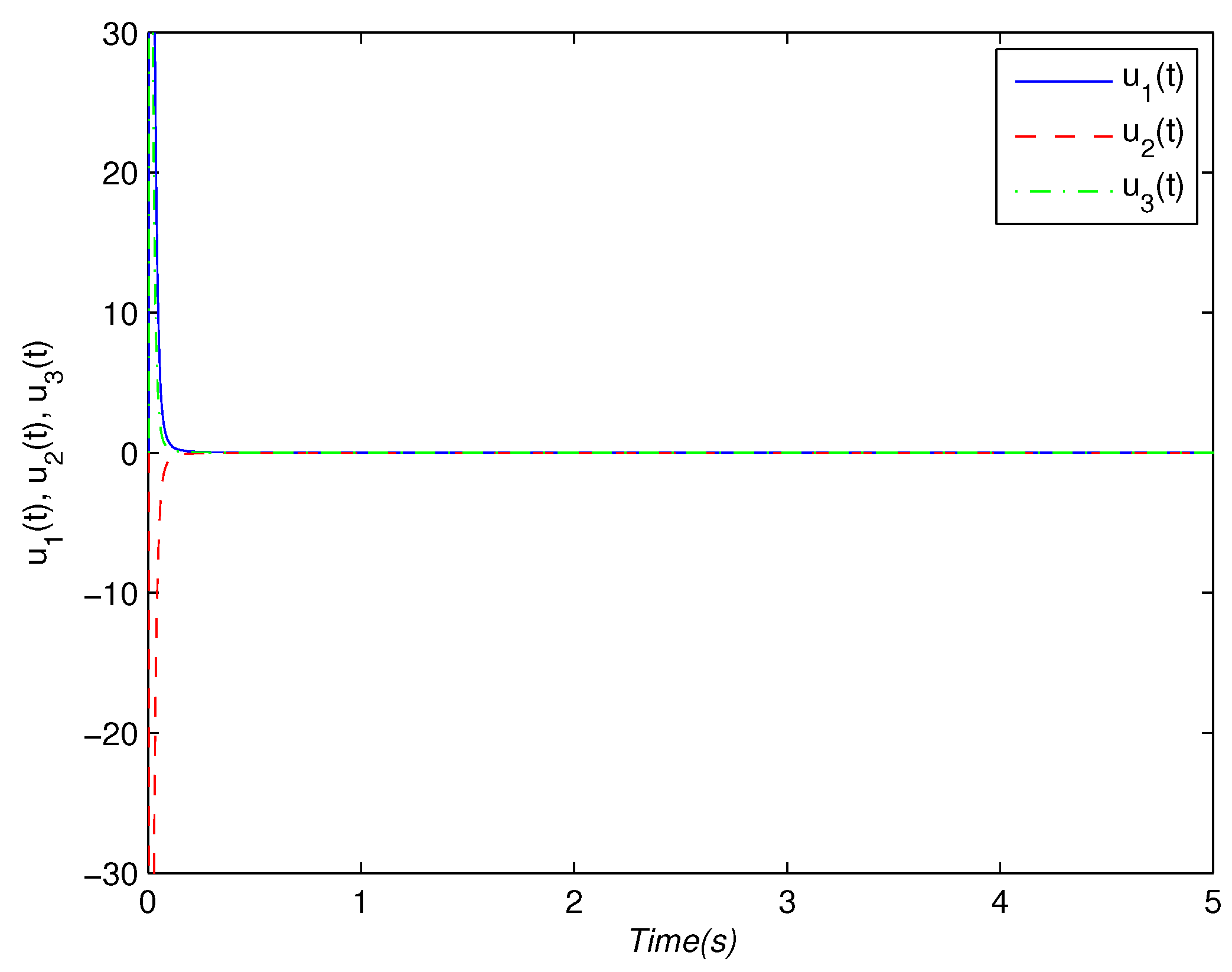
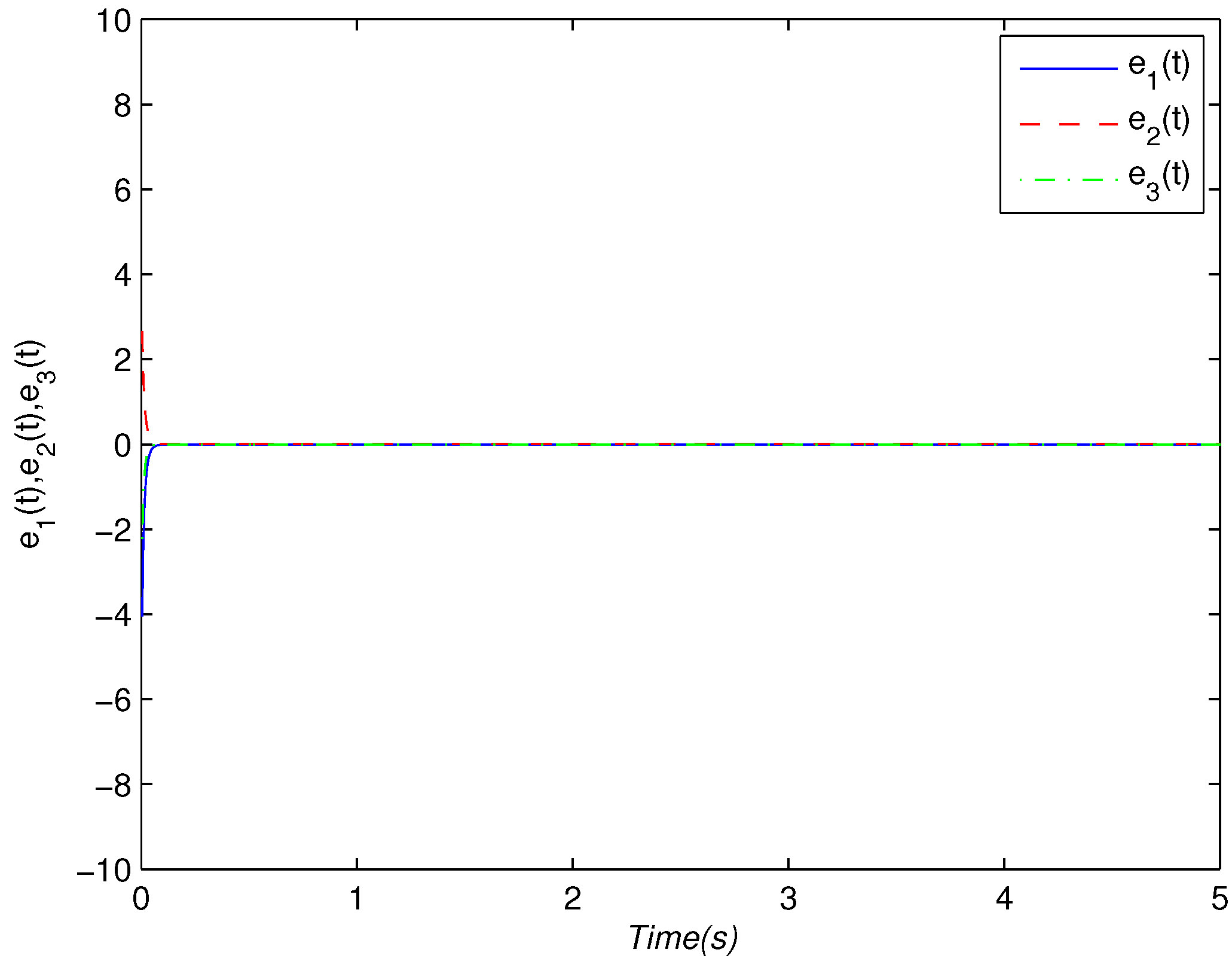
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cafagna, D. Fractional calculus: A mathematical tool from the past for present engineers. IEEE Ind. Electron. Mag. 2007, 1, 35–40. [Google Scholar] [CrossRef]
- Ortigueira, M. An introduction to the fractional continuous time linear systems: The 21st century systems. IEEE Circuits Syst. Mag. 2008, 8, 19–26. [Google Scholar] [CrossRef]
- West, B. Fractional Calculus View of Complexity; CRC Press, Talyor Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Stamova, I. Global Mittag-Leffler stability and synchronization of impulsive fractional-order neural networks with time-varying delays. Nonlinear Dyn. 2014, 77, 1251–1260. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Fardoun, H. Stability and synchronization criteria for fractional order competitive neural networks with time delays: An asymptotic expansion of Mittag Leffler function. J. Frankl. Inst. 2019, 356, 2212–2239. [Google Scholar] [CrossRef]
- Cao, J.; Stamov, G.; Stamova, I.; Simeonov, S. Almost periodicity in impulsive fractional-order reaction-diffusion neural networks with time-varying delays. IEEE Trans. Cybern. 2020, 51, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Balamash, A.; Bettayeb, M.; Djennoune, S.; Al-Saggaf, U.M.; Moinuddin, M. Fixed-time terminal synergetic observer for synchronization of fractional-order chaotic systems. Chaos 2020, 30, 073124. [Google Scholar] [CrossRef] [PubMed]
- Stamov, G.; Stamova, I.; Martynyuk, A.; Stamov, T. Almost periodic dynamics in a new class of impulsive reaction-diffusion neural networks with fractional-like derivatives. Chaos Solitons Fractals 2021, 143, 110647. [Google Scholar] [CrossRef]
- Aadhithiyan, S.; Raja, R.; Zhu, Q.; Alzabut, J.; Niezabitowski, M.; Lim, C. Modified projective synchronization of distributive fractional order complex dynamic networks with model uncertainty via adaptive control. Chaos Solitons Fractals 2021, 147, 110853. [Google Scholar] [CrossRef]
- Stamov, T.; Stamova, I. Design of impulsive controllers and impulsive control strategy for the Mittag-Leffler stability behavior of fractional gene regulatory networks. Neurocomputing 2021, 424, 54–62. [Google Scholar] [CrossRef]
- Cao, J.; Udhayakumar, K.; Rakkiyappan, R.; Li, X.; Lu, J. A comprehensive review of continuous-/discontinuous-time fractional-order multidimensional neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Makhlouf, A.B.; Baleanu, D. Finite time stability of fractional order systems of neutral type. Fractal Fract. 2022, 6, 289. [Google Scholar] [CrossRef]
- Lundstrom, B.; Higgs, M.; Spain, W.; Fairhall, A. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335–1342. [Google Scholar] [CrossRef] [PubMed]
- Trigeassou, J.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Boroujeni, E.; Momeni, H. Non-fragile nonlinear fractional order observer design for a class of nonlinear fractional order systems. Signal Process. 2012, 92, 2365–2370. [Google Scholar] [CrossRef]
- Lan, Y.; Zhou, Y. Non-fragile observer-based robust control for a class of fractional-order nonlinear systems. Syst. Control Lett. 2013, 62, 1143–1150. [Google Scholar] [CrossRef]
- Lan, Y.; Gu, H.; Chen, C.; Zhou, Y.; Luo, Y. An indirect Lyapunov approach to the observer-based robust control for fractional-order complex dynamic networks. Neurocomputing 2014, 136, 235–242. [Google Scholar] [CrossRef]
- Yin, C.; Cheng, Y.; Chen, Y.; Stark, B.; Zhong, S. Adaptive fractional-order switching-type control method design for 3D fractional-order nonlinear systems. Nonlinear Dyn. 2015, 82, 39–52. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, S.; Moura, S.; Peng, H. State-of-charge estimation for lithium-ion batteries based on a nonlinear fractional model. IEEE Trans. Control Syst. Technol. 2017, 25, 3–11. [Google Scholar] [CrossRef]
- Sakthivel, R.; Mohanapriya, S.; Ahn, C.K.; Karimi, H.R. Output tracking control for fractional-order positive switched systems with input time delay. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1013–1017. [Google Scholar] [CrossRef]
- Tan, Y.; Xiong, M.; Du, D.; Fei, S. Observer-based robust control for fractional-order nonlinear uncertain systems with input saturation and measurement quantization. Nonlinear Anal. Hybrid Syst. 2019, 34, 45–57. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H.; Fan, X. Projective synchronization for fractional neural networks. Neural Netw. 2014, 49, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Cao, J. Dynamics in fractional-order neural networks. Neurocomputing 2014, 142, 494–498. [Google Scholar] [CrossRef]
- Maiti, M.; Sunder, M.; Abishek, R.; Bingi, K.; Shaik, N.; Benjapolakul, W. Recent advances and applications of fractional-order neural networks. Eng. J. 2022, 26, 49–67. [Google Scholar]
- Priya, B.; Thakur, G.K.; Ali, M.; Stamov, G.; Stamova, I.; Sharma, P. On the finite-time boundedness and finite-time stability of Caputo-type fractional order neural networks with time delay and uncertain terms. Fractal Fract. 2022, 6, 368. [Google Scholar] [CrossRef]
- Xu, S.; Liu, H.; Han, Z. The passivity of uncertain fractional-order neural networks with time-varying delays. Fractal Fract. 2022, 6, 375. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Wang, Z. Local stabilization of delayed fractional-order neural networks subject to actuator saturation. Fractal Fract. 2022, 6, 451. [Google Scholar] [CrossRef]
- Han, X.; Cheng, F.; Tang, S.; Zhang, Y.; Fu, Y.; Cheng, W.; Xu, L. Synchronization analysis of fractional-order neural networks with adaptive intermittent-active control. IEEE Access 2022, 10, 75097–75104. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Castillo, O. Application of variable-order fractional calculus in neural networks: Where do we stand? Eur. Phys. J. Spec. Top. 2022, 231, C1753–C1756. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Z.; Jiang, P. Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 2014, 51, 1–8. [Google Scholar] [CrossRef]
- Chen, L.; Wu, R.; Cao, J.; Liu, J. Stability and synchronization of memristor-based fractional-order delayed neural networks. Neural Netw. 2015, 71, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Park, J.; Cao, J. Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 2015, 82, 1343–1354. [Google Scholar] [CrossRef]
- Gu, Y.; Yu, Y.; Wang, H. Synchronization for fractional-order time-delayed memristor-based neural networks with parameter uncertainty. J. Frankl. Inst. 2016, 353, 3657–3684. [Google Scholar] [CrossRef]
- Bao, H.; Cao, J.; Kurths, J. State estimation of fractional-order delayed memristive neural networks. Nonlinear Dyn. 2018, 94, 1215–1225. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.; Cao, J. Non-fragile state estimation for fractional-order delayed memristive BAM neural networks. Neural Netw. 2019, 119, 190–199. [Google Scholar] [CrossRef]
- Li, R.; Gao, X.; Cao, J. Non-fragile state estimation for delayed fractional-order memristive neural networks. Appl. Math. Comput. 2019, 340, 221–233. [Google Scholar] [CrossRef]
- Vivekanandan, G.; Mehrabbeik, M.; Natiq, H.; Rajagopal, K.; Tlelo-Cuautle, E. Fractional-order memristive wilson neuron model: Dynamical analysis and synchronization patterns. Mathematics 2022, 10, 2827. [Google Scholar] [CrossRef]
- Sakthivel, R.; SA, K.; Wang, C. Finite-time reliable sampled-data control for fractional-order memristive neural networks with quantisation. J. Exp. Theor. Artif. Intell. 2022, 1–19. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Liu, L. Asymptotic and finite-time synchronization of fractional-order memristor-based inertial neural networks with time-varying delay. Fractal Fract. 2022, 6, 350. [Google Scholar] [CrossRef]
- Wang, G.; Ding, Z.; Li, S.; Yang, L.; Jiao, R. Finite-time Mittag-Leffler synchronization of fractional-order complex-valued memristive neural networks with time delay. Chin. Phys. B 2022, in press. [Google Scholar] [CrossRef]
- Petersen, I.; Tempo, R. Robust control of uncertain systems: Classical results and recent developments. Automatica 2014, 50, 1315–1335. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equation; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Boyd, S.; Ghaoui, L.; Feron, E. Linear Matrix Inequalities in System and Control Theory; SIAM Studies in Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Aubin, J.; Cellina, A. Differential Inclusions; Springer: Berlin, Germany, 1984. [Google Scholar]
- Filippov, A. Differential Equations with Discontinuous Right-Hand Side; Kluwer Academic: Boston, MA, USA, 1988. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Cao, J.; Abdel-Aty, M. New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality. Fractal Fract. 2022, 6, 585. https://doi.org/10.3390/fractalfract6100585
Song C, Cao J, Abdel-Aty M. New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality. Fractal and Fractional. 2022; 6(10):585. https://doi.org/10.3390/fractalfract6100585
Chicago/Turabian StyleSong, Chao, Jinde Cao, and Mahmoud Abdel-Aty. 2022. "New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality" Fractal and Fractional 6, no. 10: 585. https://doi.org/10.3390/fractalfract6100585
APA StyleSong, C., Cao, J., & Abdel-Aty, M. (2022). New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality. Fractal and Fractional, 6(10), 585. https://doi.org/10.3390/fractalfract6100585








