The Effect of Caputo Fractional Variable Difference Operator on a Discrete-Time Hopfield Neural Network with Non-Commensurate Order

Abstract

In this work, we recall some definitions on fractional calculus with discrete-time. Then, we introduce a discrete-time Hopfield neural network (D.T.H.N.N) with non-commensurate fractional variable-order (V.O) for three neurons. After that, phase-plot portraits, bifurcation and Lyapunov exponents diagrams are employed to verify that the proposed discrete time Hopfield neural network with non-commensurate fractional variable order has chaotic behavior. Furthermore, we use the 0-1 test and $C_0$ complexity algorithm to confirm and prove the results obtained about the presence of chaos. Finally, simulations are carried out in Matlab to illustrate the results.

1. Introduction

Recently, due to its multiple applications, particularly in the context of secure communication [1,2,3,4] and control [5,6], chaotic discrete-time systems have gained a lot of attention. Lozi map [7], 2-D Hénon system [8], Zeraoulia-Sprott map [9], Baier–Klein map [10], the generalized Hénon system [11] and the discrete Rössler system [12] are a few examples of chaotic discrete-time systems with integer order that have been presented over time. Researchers have lately become more interested in the systems with fractional order that correspond to the previous chaotic systems with integer order [13].

Fractional-order derivatives are more precise than integer-order derivatives because they are a great tool for describing the memory effect in a variety of materials and processing [14].

Discrete fractional calculus and fractional difference operators have received the attention of mathematicians [15,16,17]. Refs. [18,19] introduced the concept of discrete fractional calculus to chaotic maps and showed that chaos characteristics remain. For instance, in [20], the authors analysed the existence of chaos in 2D maps with fractional order, the chaotic behavior of Ikeda map with a non-integer order was studied in [21], in [22], fractional chaotic systems with discrete time and without equilibrium points were introduced, and, in [23], bifurcation and dynamics of systems with fractional and various closed curve equilibrium points were investigated, while control and dynamics of fractional quadratic map with no equilibrium points were analysed in [24].

The great interest of taking into account a Caputo fractional difference operator [25] in the modeling of dynamical systems with discrete time was demonstrated by the pertinent publications cited above.

Since fractional calculus has more advantages than an integer one, it makes sense for us to use this approach in studying neural networks’ systems [26,27,28,29]. The modeling of neural networks with fractional order is used to investigate biological neurons for two reasons. First, by increasing one degree of freedom, the fractional order increases the performance of the system. Second, the modeling of neural networks with fractional order has an infinite memory. Fractional-order neural networks hope to play an important role in the field of parameter estimation. Neural networks approximation showed higher rates of approximation at a fractional level [30].

A lot of attention has been paid to the analysis of the dynamics of neural networks with fractional order, and significant results have been achieved. For instance, in [31], LMI conditions for global stability of fractional-order neural networks were studied; in Ref. [32], the authors presented an adaptive model-free synchronization of different fractional-order neural networks with an application in cryptography, the stability, bifurcation, and chaos of Hopfield neural networks with a non-integer order were analysed. In [33,34,35,36,37], the stability of the Hopfield neural networks with fractional order was investigated, in [38], complexity, chaos and multi-stability of a discrete time Hopfield neural network with variable order and short memory were studied, whereas, in [39], the dynamics of the fractional order neural network were analysed. Recently, in [40], a study of discrete time Hopfield neural network with incommensurate fractional order was presented.

The major purpose of this research is to study the effect of using the non-commensurate fractional variable-order on the system studied in [40]. The fractional variable-order form is likely to exhibit even more complex dynamics.

Inspired by the research cited above, firstly, a discrete time Hopfield neural network with a non-commensurate fractional variable order is proposed. Then, the dynamics of the presented model are analysed via phase-plot portraits, bifurcation and maximum Lyapunov exponent (MLE) diagrams. After that, 0-1 test and the $C_0$ complexity algorithm are used to confirm the chaotic behavior of the system. Finally, the corresponding simulations are performed.

2. Preliminaries on Discrete Fractional Calculus

In this section, we present some definitions according to fractional discrete calculus to describe the discrete time Hopfield neural network (D.T.H.N.N.) with an incommensurate fractional variable-order.

Discrete Fractional Calculus

Let h be a function defined on a time scale ${\mathbb{N}}_{\beta }=\left\{\beta ,\beta +1,\beta +2,\dots \right\}$.

• The $\eta$-th fractional sum for the function h is defined as [16]:

  $${\mathsf{\Delta }}_{\beta }^{-\eta }h\left(r\right)=\frac{1}{\mathsf{\Gamma }\left(\eta \right)}\sum _{\rho =\beta }^{r-\eta }{(r-\rho -1)}^{(\eta -1)}h\left(\rho \right),r\in {\mathbb{N}}_{\beta +\eta },\eta >0,$$

  (1)

  where

  $${(r-\rho -1)}^{(\eta -1)}=\frac{\mathsf{\Gamma }(r-\rho )}{\mathsf{\Gamma }(r-\rho -\eta +1)},$$

  (2)

  which represents the falling factorial function.
• The $\eta$-Caputo fractional difference operator for the function h is defined as [25]:

  $${}^C{\mathsf{\Delta }}_{\beta }^{\eta }h\left(r\right)={\mathsf{\Delta }}_a^{-(k-\eta )}{\mathsf{\Delta }}^{k}h\left(r\right),$$

  (3)

  where $k=\left[\eta \right]+1$, $r\in {\mathbb{N}}_{\beta +k-\eta },$ and $\eta \notin \mathbb{N}$.
  Using the Formulas (1) and (2), we obtain:

  $${}^C{\mathsf{\Delta }}_{\beta }^{\eta }h\left(r\right)=\frac{1}{\mathsf{\Gamma }(k-\eta )}{\displaystyle \sum _{\rho =\beta }^{r-(k-\eta )}}\frac{\mathsf{\Gamma }(r-\rho )}{\mathsf{\Gamma }(r-\rho -k-\eta +1)}{\mathsf{\Delta }}_{\rho }^{k}h\left(\rho \right),$$

  (4)

  where ${\mathsf{\Delta }}_{\rho }^k$ is the k-th integer difference operator defined as:

$${\mathsf{\Delta }}^{k}h\left(r\right)=\mathsf{\Delta }\left({\mathsf{\Delta }}^{k-1}h\left(r\right)\right)=\sum _{j=0}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right){(-1)}^{k-j}h(r+j),r\in {\mathbb{N}}_{\beta }.$$

(5)

3. The Discrete-Time Neural Network with an Incommensurate Fractional Variable Order

Sivasundaram and Kaslik [41] described the model of the Hopfield fractional neural network consisting of m neurons as follows:

$${}^c{D}^{{\gamma }_j}{x}_j\left(r\right)=-{\alpha }_j{x}_j\left(r\right)+\sum _{j=1}^m{A}_{j,i}{h}_j\left(x_i\left(r\right)\right)+E_j,\forall r>0,\forall j=1,2,\dots ,m.$$

(6)

Given that:

• $h_j:\mathbb{R}\to \mathbb{R}$ represents the activation function of the neurons;
• $A={\left(A_{ji}\right)}_{m\times m}$ denotes the weights matrix which describes the connection between i and j neurons;
• ${\alpha }_j>0$ represents the self-regulating neurons’ parameters;
• $E_j$ are the external inputs; in our work, they are equal to 0.

Note that ${}^c{D}^{{\gamma }_j}$ is the Caputo fractional order derivative defined as:

$${}^c{D}^{{\gamma }_j}h\left(r\right)=\frac{1}{\mathsf{\Gamma }(1-{\gamma }_j)}{\int }_{r_0}^r{(r-\rho )}^{-{\gamma }_j}h\left(\rho \right)d\rho ,$$

(7)

where the fractional order ${\gamma }_j\in (0,1]$.

Here, we consider a system with three neurons. To simplify calculations, herein choose $h_j\left(x_i\right)=tanh\left(x_i\right)$, ${\alpha }_j=1$, and the matrix A is chosen as:

$$A=\left. [\begin{array}{ccc}-1.4& 1.2& -7\\ 1.1& 0& 2.8\\ P& -2& 4\end{array}\right].$$

(8)

As a result, we obtain the following Hopfield neural network with continuous time:

$$\left\{\begin{array}{ccc}{}^c{D}^{{\gamma }_1}{x}_1\left(r\right)\hfill & =& -x_1\left(r\right)-1.4tanh\left(x_1\left(r\right)\right)+1.2tanh\left(x_2\left(r\right)\right)-7tanh\left(x_3\left(r\right)\right),\hfill \\ {}^c{D}^{{\gamma }_2}{x}_2\left(r\right)\hfill & =& -x_2\left(r\right)+1.1tanh\left(x_1\left(r\right)\right)+2.8tanh\left(x_3\left(r\right)\right),\hfill \\ {}^c{D}^{{\gamma }_3}{x}_3\left(r\right)\hfill & =& -x_3\left(r\right)+Ptanh\left(x_1\left(r\right)\right)-2tanh\left(x_2\left(r\right)\right)+4tanh\left(x_3\left(r\right)\right).\hfill \end{array}\right.$$

(9)

From system (9), we obtain a new D.T.H.N.N with incommensurate fractional variable-order by replacing the operator ${}^c{D}^{{\gamma }_i}$ with the Caputo-like difference operator with fractional variable-order ${}^c{\mathsf{\Delta }}^{{\gamma }_i\left(r\right)}$, which can be given by:

$$\left\{\begin{array}{ccc}{ }^c{\mathsf{\Delta }}^{{\gamma }_1\left(r\right)}{x}_1\left(r\right)& =& -x_1(r+{\gamma }_1\left(r\right)-1)-1.4tanh\left(x_1(r+{\gamma }_1\left(r\right)-1)\right)+1.2tanh\left(x_2(r+{\gamma }_1\left(r\right)-1)\right)\\ & & -7tanh\left(x_3(r+{\gamma }_1\left(r\right)-1)\right),\\ { }^c{\mathsf{\Delta }}^{{\gamma }_2\left(r\right)}{x}_2\left(r\right)& =& -x_2(r+{\gamma }_2\left(r\right)-1)+1.1tanh\left(x_1(r+{\gamma }_2\left(r\right)-1)\right)+2.8tanh\left(x_3(r+{\gamma }_2\left(r\right)-1)\right),\\ { }^c{\mathsf{\Delta }}^{{\gamma }_3\left(r\right)}{x}_3\left(r\right)& =& -x_3(r+{\gamma }_3\left(r\right)-1)+Ptanh\left(x_1(r+{\gamma }_3\left(r\right)-1)\right)-2tanh\left(x_2(r+{\gamma }_3\left(r\right)-1)\right)\hfill \\ & & +4tanh\left(x_3(\tau +{\gamma }_3\left(r\right)-1)\right),\end{array}\right.$$

(10)

with $r\in {\mathbb{N}}_{\beta +1-{\gamma }_j\left(r\right)}$, ${\gamma }_j\left(r\right)$ being the variable order and ${\gamma }_j\left(r\right)\in (0,1]$, $j=1,2,3.$

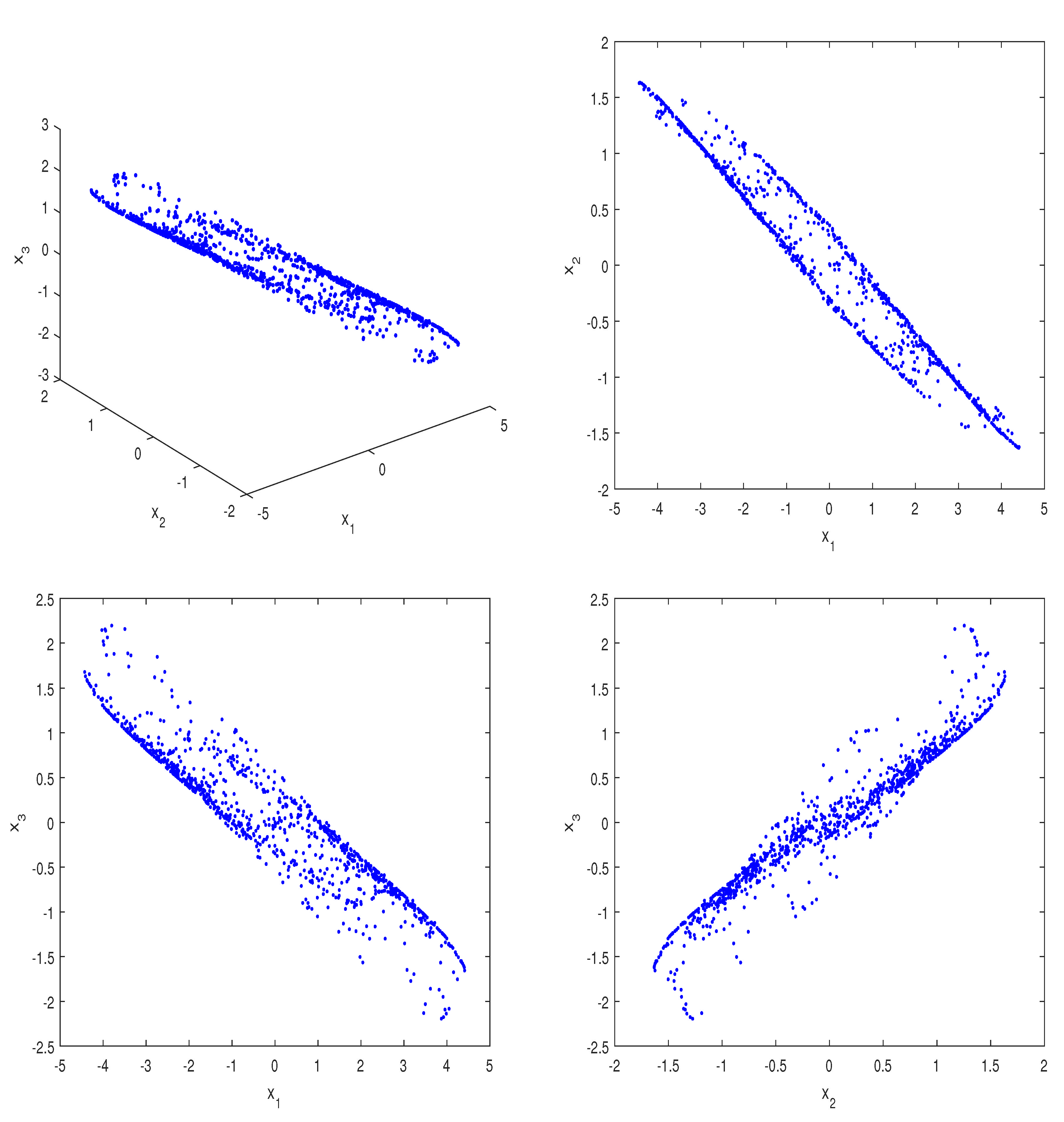
3.1. Dynamical Analysis and Numerical Simulations

The goal of this section is to illustrate the dynamics of the D.T.H.N.N with incommensurate fractional variable order (10) via numerical simulation.

Now, according to the theorem cited in [42], the unique solution of the system (10) is given by:

$$\left\{\begin{array}{cc}{x}_1\left(r\right)& =x_1\left(\beta \right)+\frac{1}{\mathsf{\Gamma }\left({\gamma }_1\left(r\right)\right)}{\displaystyle \sum _{\tau =\beta +1-{\gamma }_1\left(r\right)}^{r-{\gamma }_1\left(r\right)}}{(r-\tau -1)}^{({\gamma }_1\left(r\right)-1)}\{-x_1(\tau +{\gamma }_1\left(r\right)-1)\\ & -1.4tanh\left(x_1(\tau +{\gamma }_1\left(r\right)-1)\right)+1.2tanh\left(x_2(\tau +{\gamma }_1\left(r\right)-1)\right)-7tanh\left(x_3(\tau +{\gamma }_1\left(r\right)-1)\right)\},\\ x_2\left(r\right)& =x_2\left(\beta \right)+\frac{1}{\mathsf{\Gamma }\left({\gamma }_2\left(r\right)\right)}{\displaystyle \sum _{\tau =\beta +1-{\gamma }_2\left(r\right)}^{r-{\gamma }_2\left(r\right)}}{(r-\tau -1)}^{({\gamma }_2\left(r\right)-1)}\{-x_2(\tau +{\gamma }_2\left(r\right)-1)\\ & +1.1tanh\left(x_1(\tau +{\gamma }_2\left(r\right)-1)\right)+2.8tanh\left(x_3(\tau +{\gamma }_2\left(r\right)-1)\right)\},\\ x_3\left(r\right)& =x_3\left(\beta \right)+\frac{1}{\mathsf{\Gamma }\left({\gamma }_3\left(r\right)\right)}{\displaystyle \sum _{\tau =\beta +1-{\gamma }_3\left(r\right)}^{r-{\gamma }_3\left(r\right)}}{(r-\tau -1)}^{({\gamma }_3\left(r\right)-1)}\{-x_3(\tau +{\gamma }_3\left(r\right)-1)\\ & +Ptanh\left(x_1(\tau +{\gamma }_3\left(r\right)-1)\right)-2tanh\left(x_2(\tau +{\gamma }_3\left(r\right)-1)\right)+4tanh\left(x_3(\tau +{\gamma }_3\left(r\right)-1)\right)\},\end{array}\right.$$

(11)

Take $\beta =0$ and since ${(r-\tau -1)}^{({\gamma }_j\left(r\right)-1)}=\frac{\mathsf{\Gamma }(r-\tau )}{\mathsf{\Gamma }(r-\tau -{\gamma }_j\left(r\right)+1)}$, and the numerical formula of the system (10) is designed as:

$$\left\{\begin{array}{ccc}{x}_{n+1}^1\hfill & =& x_0^1+{\displaystyle \sum _{j=0}^n}\frac{\mathsf{\Gamma }(n-j+{\gamma }_1\left(j\right))}{\mathsf{\Gamma }\left({\gamma }_1\left(j\right)\right)\mathsf{\Gamma }(n-j+1)}\{-x_j^1-1.4tanh\left(x_j^1\right)+1.2tanh\left(x_j^2\right)-7tanh\left(x_j^3\right)\},\hfill \\ x_{n+1}^2\hfill & =& x_0^2+{\displaystyle \sum _{j=0}^n}\frac{\mathsf{\Gamma }(n-j+{\gamma }_2\left(j\right))}{\mathsf{\Gamma }\left({\gamma }_2\left(j\right)\right)\mathsf{\Gamma }(n-j+1)}\{-x_j^2+1.1tanh\left(x_j^1\right)+2.8tanh\left(x_j^3\right)\},\hfill \\ x_{n+1}^3\hfill & =& x_0^3+{\displaystyle \sum _{j=0}^n}\frac{\mathsf{\Gamma }(n-j+{\gamma }_3\left(j\right))}{\mathsf{\Gamma }\left({\gamma }_3\left(j\right)\right)\mathsf{\Gamma }(n-j+1)}\{-x_j^3+Ptanh\left(x_j^1\right)-2tanh\left(x_j^2\right)+4tanh\left(x_j^3\right)\},\hfill \end{array}\right.$$

(12)

with the known initial condition $x_0^1=x_1\left(0\right)$, $x_0^2=x_2\left(0\right)$, $x_0^3=x_3\left(0\right)$.

To study the effect of the fractional variable order on the D.T.H.N.N (10), we take $P=0.57$ and the initial condition $(x_0^1,x_0^2,x_0^3)=(0,0.01,0)$, where the fractional variable order is chosen as: ${\gamma }_1\left(r\right)=tanh\left(r\right)$, ${\gamma }_2\left(r\right)=\frac{1}{1+e^{-r}}$ and ${\gamma }_3\left(r\right)=\frac{r}{1+r}$.

Firstly, we draw the discrete time evolution of the states as shown in Figure 1.

We observe that the states $x_1$, $x_2$ and $x_3$ of the system (10) exhibit chaotic behaviour, but we do not rely on it to determine the nature of the dynamic; for this reason, we need to plot the trajectories in the state space.

Figure 2 depicts the plot of phase portraits of our system (10), which displays a chaotic attractor.

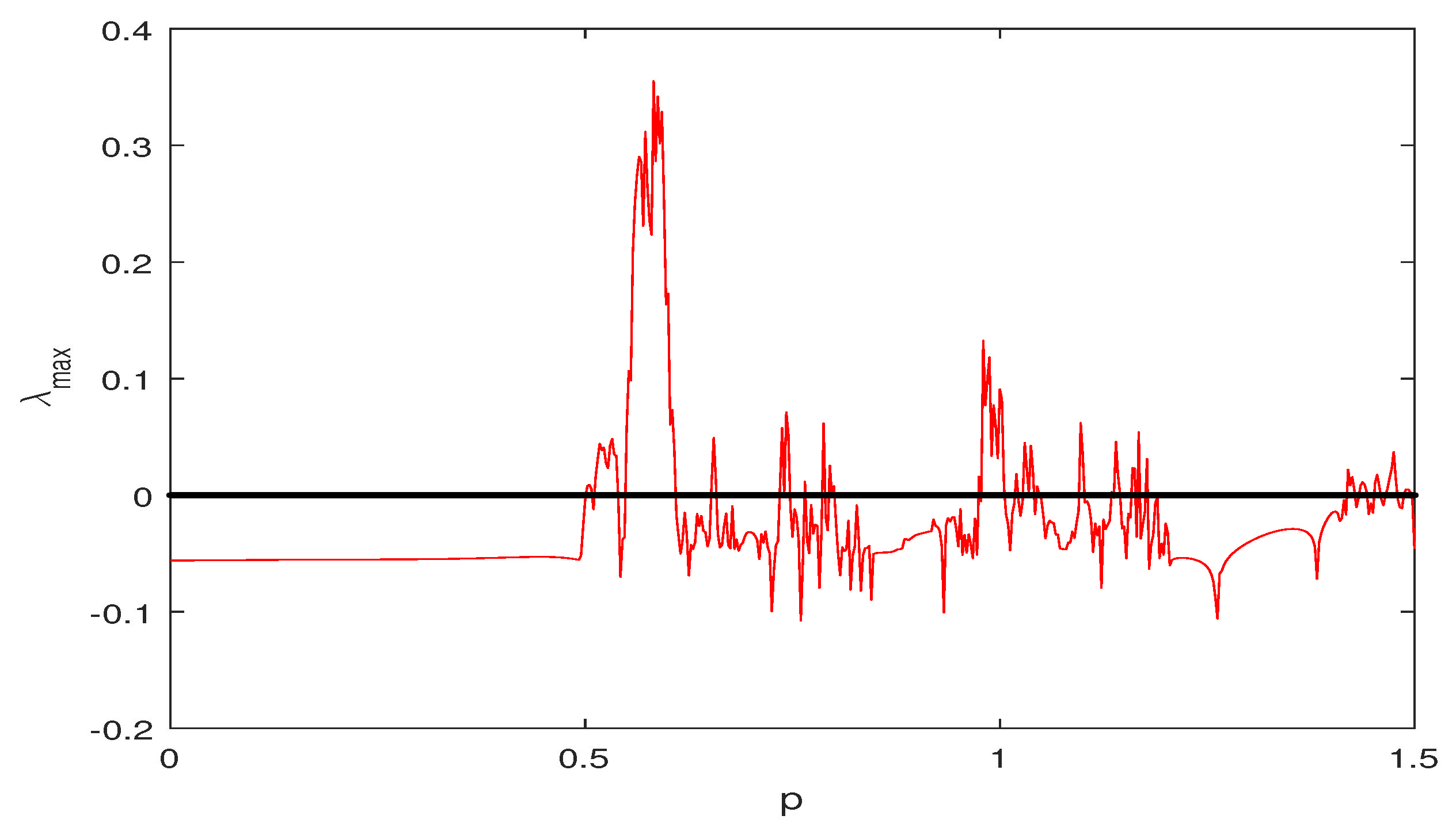
3.2. Bifurcation Diagram and Maximum Lyapunov Exponents

Now, in order to explore the presence of chaos, we consider the bifurcation diagram and maximum Lyapunov exponents of the state $x_1$ by varying the parameter P in the interval $[0,1.5]$ with the step $\mathsf{\Delta }P=0.0025$. Note that we calculate the maximum L.E using the algorithm of Jacobian matrix [43].

In our case, the matrix $J_j$ of the system (10) is given by:

$$J_j=\left. [\begin{array}{ccc}{\alpha }_i^1& {\alpha }_i^2& {\alpha }_i^3\\ \\ {\beta }_i^1& {\beta }_i^2& {\beta }_i^3\\ \\ {\gamma }_i^1& {\gamma }_i^2& {\gamma }_i^3\end{array}\right],$$

(13)

where

$$\left\{\begin{array}{c}{\alpha }_i^j={\alpha }_0^j+{\displaystyle \sum _{i=0}^n}\frac{\mathsf{\Gamma }(n-i+q_1\left(i\right))}{\mathsf{\Gamma }(n-i+1)\mathsf{\Gamma }\left(q_1\left(i\right)\right)}(-{\alpha }_i^j-1.4{\alpha }_i^j(1-{\left(tanh\left(x_1\left(i\right)\right)\right)}^2)+1.2{\beta }_i^j(1-{\left(tanh\left(x_2\left(i\right)\right)\right)}^2)\hfill \\ -7{\gamma }_i^j(1-{\left(tanh\left(x_3\left(i\right)\right)\right)}^2)),\hfill \\ {\beta }_i^j={\beta }_0^j+{\displaystyle \sum _{i=0}^n}\frac{\mathsf{\Gamma }(n-i+q_2\left(i\right))}{\mathsf{\Gamma }(n-i+1)\mathsf{\Gamma }\left(q_2\left(i\right)\right)}(-{\beta }_i^j+1.1{\alpha }_i^j(1-{\left(tanh\left(x_1\left(i\right)\right)\right)}^2)+2.8{\gamma }_i^j(1-{\left(tanh\left(x_3\left(i\right)\right)\right)}^2)),\hfill \\ {\gamma }_i^j={\gamma }_0^j+{\displaystyle \sum _{i=0}^n}\frac{\mathsf{\Gamma }(n-i+q_3\left(i\right))}{\mathsf{\Gamma }(n-i+1)\mathsf{\Gamma }\left(q_3\left(i\right)\right)}(-{\gamma }_i^j+P{\alpha }_i^j(1-{\left(tanh\left(x_1\left(i\right)\right)\right)}^2)-2{\beta }_i^j(1-{\left(tanh\left(x_2\left(i\right)\right)\right)}^2)\hfill \\ +4{\gamma }_i^j(1-{\left(tanh\left(x_3\left(i\right)\right)\right)}^2)),\hfill \end{array}\right.$$

(14)

$j=1,2,3.$

Finally, the maximum L.E has the following formula:

$${\lambda }_k\left(x_0\right)=\underset{i\to \infty }{lim}\frac{1}{i}ln\mid {\lambda }_k^{\left(i\right)}\mid ,fork=1,2,3.$$

(15)

Note that ${\lambda }_k$ are the eigenvalues of the matrix $J_j$.

As can be observed in the bifurcation and the Maximum L.E represented in Figure 3 and Figure 4, respectively, upon varying the parameter P, system (10) exhibits complex dynamics which include chaos and quasi-periodic behavior. In particular, system (10) is chaotic when the parameter $P\in [0.56,0.61]$, where the value of the maximum Lyapunov exponents is positive, while for the rest of values of the parameter P, the system is quasi-periodic since it can not be periodic because fractional order systems cannot have periodic non-constant solutions (for more details, see [44,45,46]), where the value of the maximum Lyapunov exponents is negative.

3.3. $C_0$ Complexity

To analyse the complex behaviour of systems, the $C_0$ complexity [47] is used based on the inverse Fourier transform.

For a sequence $\left[\varphi \right(0),\dots ,\varphi (M-1\left)\right]$, the algorithm of the $C_0$ complexity is given as follows:

• We calculate the discrete Fourier transform of the sequence $\left[\varphi \right(0),\dots ,\varphi (M-1\left)\right]$ as:

  $${\mathsf{\Phi }}_M\left(m\right)=\sum _{j=0}^{M-1}\varphi \left(j\right){exp}^{-2\pi i(jm/M)},m=0,\dots ,M-1.$$

  (16)
• The mean square value is given as:

  $$G_M=\frac{1}{M}\sum _{m=0}^{M-1}{\left|{\mathsf{\Phi }}_M\left(m\right)\right|}^2.$$

  (17)
• We set

  $${\overline{\mathsf{\Phi }}}_M\left(m\right)=\left\{\begin{array}{ccc}{\mathsf{\Phi }}_M\left(m\right)\hfill & if& |{\mathsf{\Phi }}_M{\left(m\right)|}^2>r{G}_M,\hfill \\ 0\hfill & if& |{\mathsf{\Phi }}_M{\left(m\right)|}^2\le r{G}_M.\hfill \end{array}\right.$$

  (18)
• We define the inverse Fourier transform of ${\overline{\mathsf{\Phi }}}_M$ as follows:

  $$\overline{\varphi }\left(j\right)=\frac{1}{M}\sum _{m=0}^{M-1}\overline{\mathsf{\Phi }}\left(m\right){exp}^{2\pi i(jm/M)},j=0,\dots ,M-1.$$

  (19)
  Finally, the formula of the $C_0$ complexity is defined as:

  $$C_0=\frac{{\displaystyle \sum _{j=0}^{M-1}}{|\varphi \left(j\right)-\overline{\varphi }\left(j\right)|}^2}{{\displaystyle \sum _{j=0}^{M-1}}{\left|\varphi \left(j\right)\right|}^2}.$$

  (20)

The plot of $C_0$ complexity is shown in Figure 5, and we can observe that the value of the $C_0$ complexity of the proposed system (10) increases when the parameter P passes through the range [0.56, 0.61], which confirms that the proposed system is chaotic in this range, so the $C_0$ algorithm measures the complexity effectively.

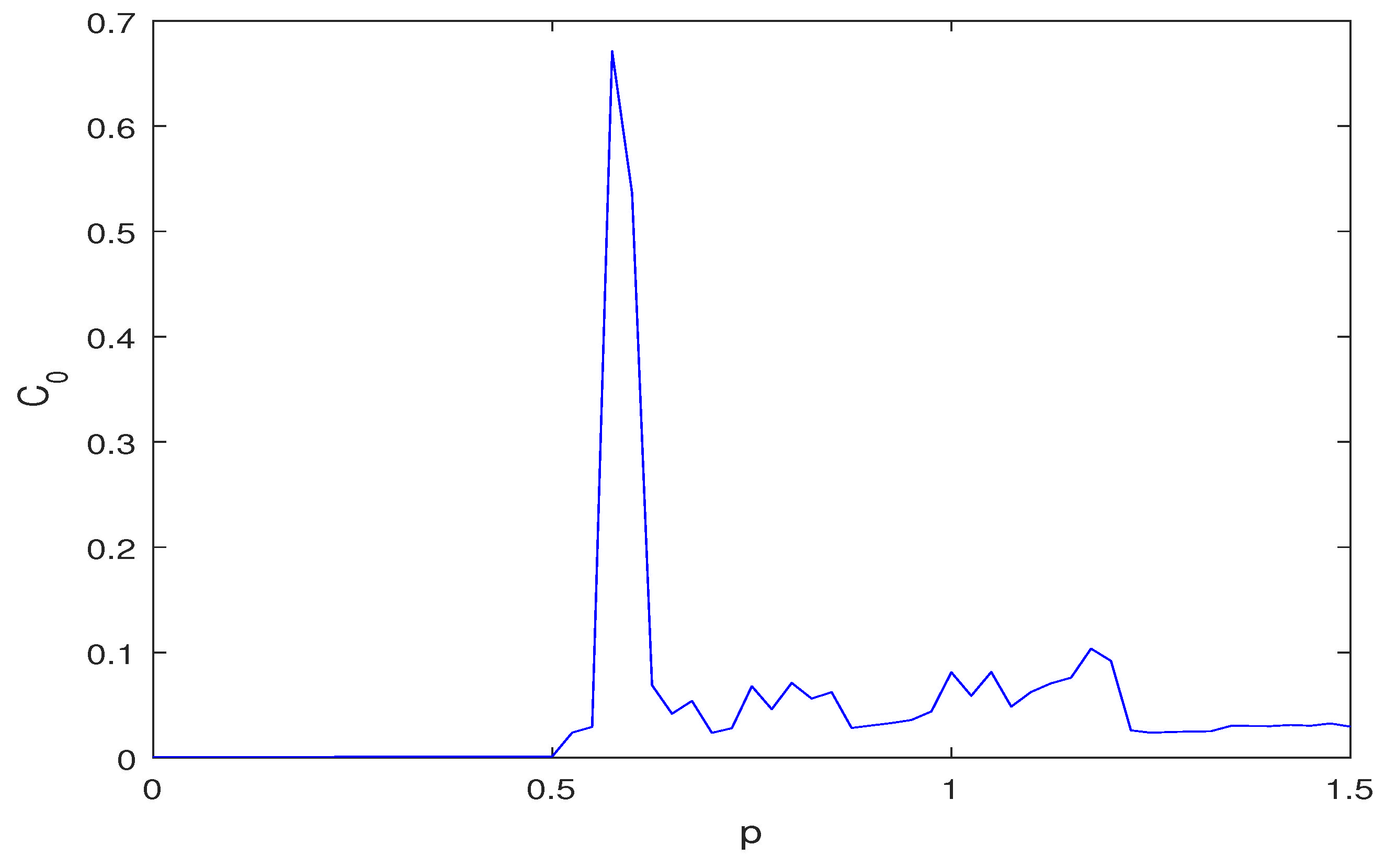
3.4. The 0-1 Test Method for Chaos

Another method that can be used to test chaos of the proposed D.T.H.N.N with incommensurate fractional V.O is a "0–1 test", which was first presented by Gottwald and Melbourne [48] to detect the existence of chaos from a time series.

Firstly, we consider a time series ${\left(w\left(i\right)\right)}_{i=1,\dots ,N}$ and c a random constant in the interval $(0,\pi )$. Then, we define two translation variables as follows:

$$p_c\left(m\right)=\sum _{i=1}^{m}w\left(i\right)cos\left(ic\right),q_c\left(m\right)=\sum _{i=1}^{m}w\left(i\right)sin\left(ic\right),m=1,2,\dots ,N.$$

(21)

In addition, we present the formula of the mean square displacement:

$$M_c\left(m\right)=\frac{1}{N}\sum _{i=1}^N({(p_c(i+m)-p_c\left(i\right))}^2+{(q_c(i+m)-q_c\left(i\right))}^2),m<\frac{N}{10}.$$

(22)

Finally, the asymptotic growth rate is defined by:

$$K_c=\underset{m\to \infty }{lim}\frac{log{M}_c}{logm}.$$

(23)

Now, in order to determine the presence of chaos, we need the plot of the asymptotic growth rate $K=median\left(K_c\right)$ and the plot of $q_c$ and $p_c$ in the $p-q$ plane. When K is closer to 1 and the trajectories of $q_c$ and $p_c$ are Brownian, the map is chaotic, whereas, when K is closer to 0 and the trajectories of $q_c$ and $p_c$ are bounded, the map is regular.

Figure 6 depicts the 0–1 test versus P of the D.T.H.N.N with an incommensurate fractional variable order (10). One can observe that, when $P\in [0.56,0.61]$, the value of the growth rate K is closer to 1, which indicates the presence of chaos, while the value of the growth rate K is closer to 0 for the rest of values of the system parameter P, which proves that the proposed system (10) is quasi-periodic.

The $p_c-q_c$ plots are shown in Figure 7 for different values of the parameter P with the same initial conditions used previously. In particular, when $P=0.1$ and $P=0.7$, the trajectories of $q_c$ and $p_c$ are bounded, and the system (10) is quasi-periodic. When $P=0.59$ and $P=0.6$ the trajectories of $q_c$ and $p_c$ are Brownian and the system (10) is chaotic, which is extremely similar to the results obtained in Figure 6.

We observe that the results of the 0-1 test agree well with the results obtained in bifurcation and the largest Lyapunov exponents’ diagrams and the $C_0$ complexity algorithm.

4. Conclusions and Future Research Directions

Based on the discrete time Hopfield neural network with incommensurate fractional order, this research has presented a Caputo-difference form of the discrete time Hopfield neural network with an incommensurate fractional variable-order. Phase-plot portraits, bifurcation and maximum Lyapunov exponents diagrams have shown the complexity of the dynamics of the proposed model. In addition, the 0-1 test and $C_0$ complexity algorithm have been employed to prove and confirm the presence of chaos in a small interval. The obtained results give us insight into the behavior of the discrete time Hopfield neural network system when using fractional variable order.

The future research directions that will depend on the results obtained in this work are in two directions: the first is theoretical and the second is practical. The theoretical aspect lies in the formulation of discrete time neural networks with strong and appropriate fractional operators, whether from an analytical or numerical point of view, while the practical aspect lies in the actual application of this type of network, especially in encryption and secure communications; the authors also aim to find electrical circuits that represent this type of network, due to the dynamic property of these neural networks proven to be suitable for these types of applications.