Mixed Convection of Fractional Nanofluids Considering Brownian Motion and Thermophoresis
Abstract
1. Introduction
2. Mathematical Formulation
3. Numerical Technique
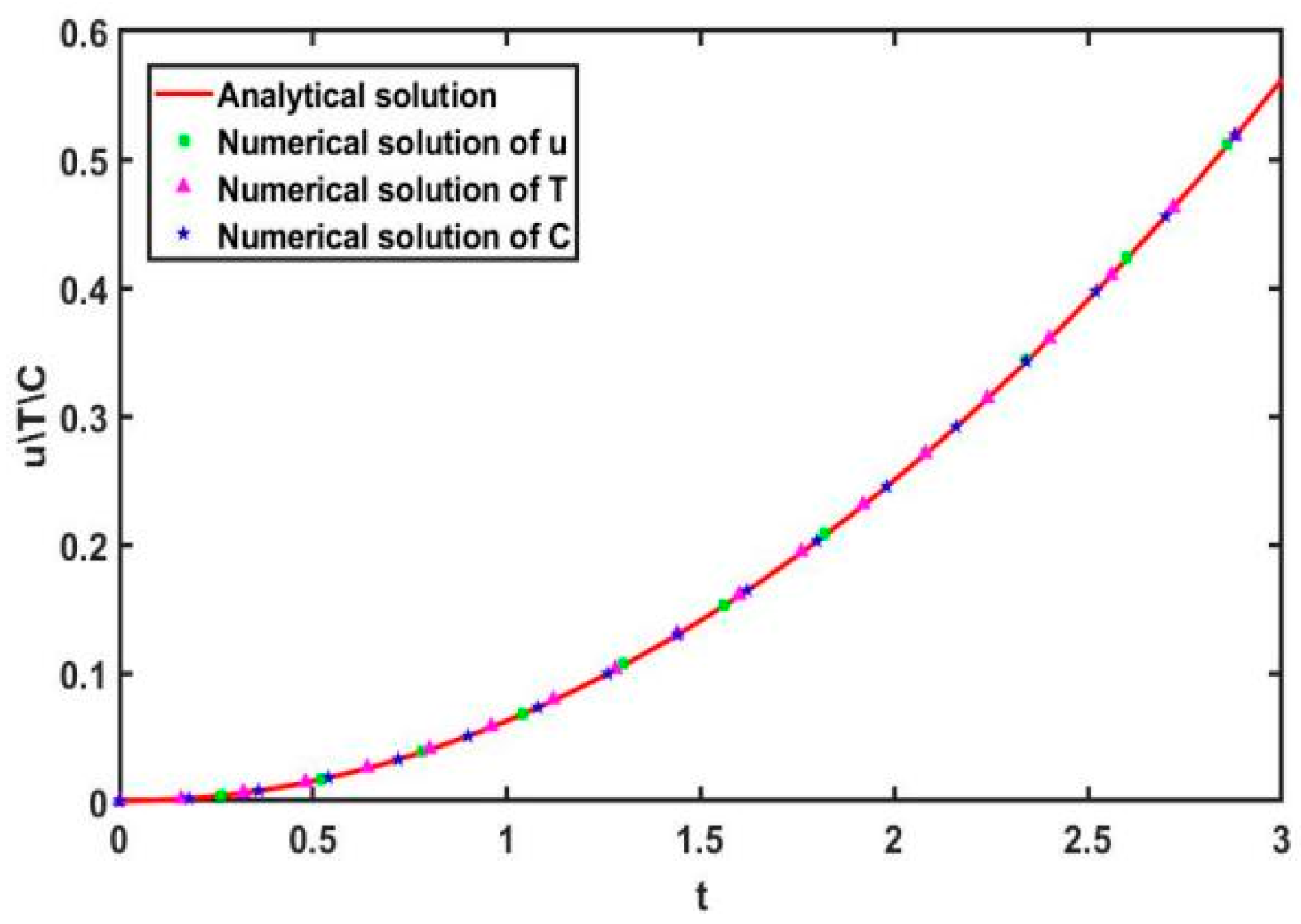
4. Validation of the Numerical Method
5. Results and Discussion
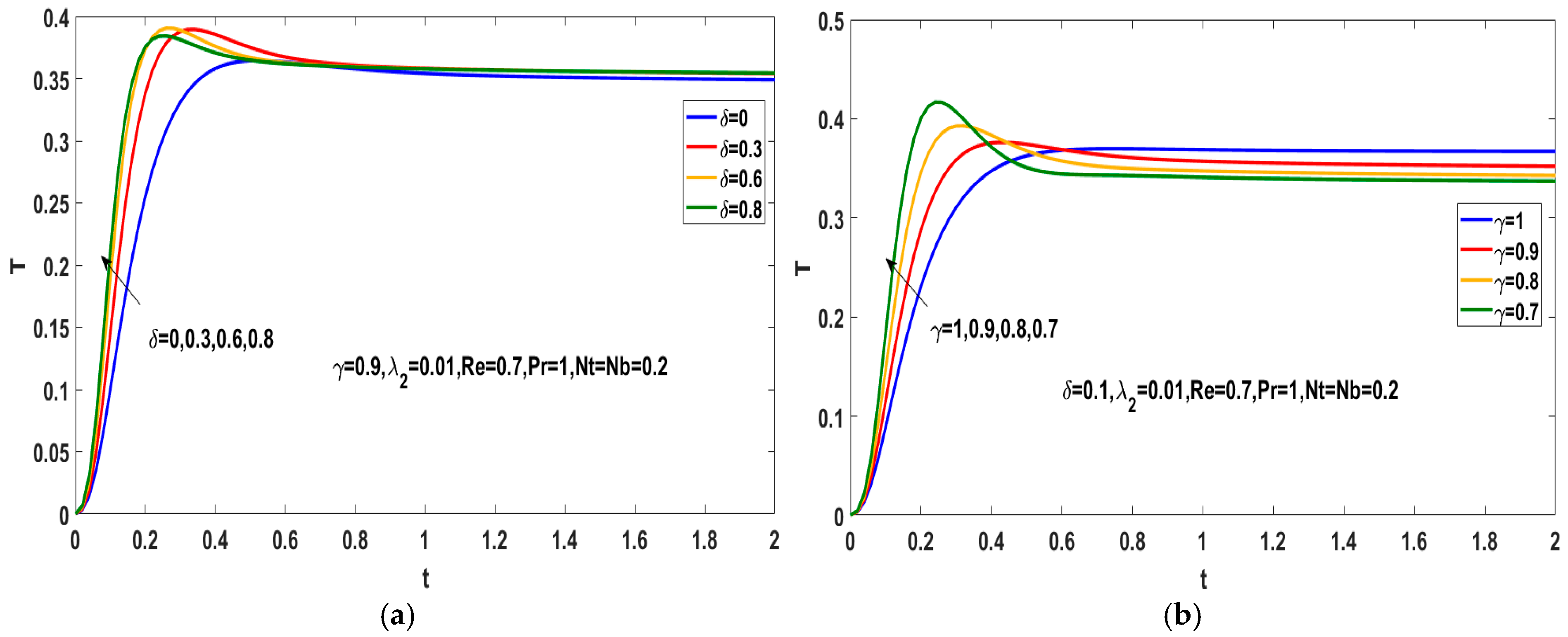
5.1. Effects of the Fractional Parameters on the Temperature Field
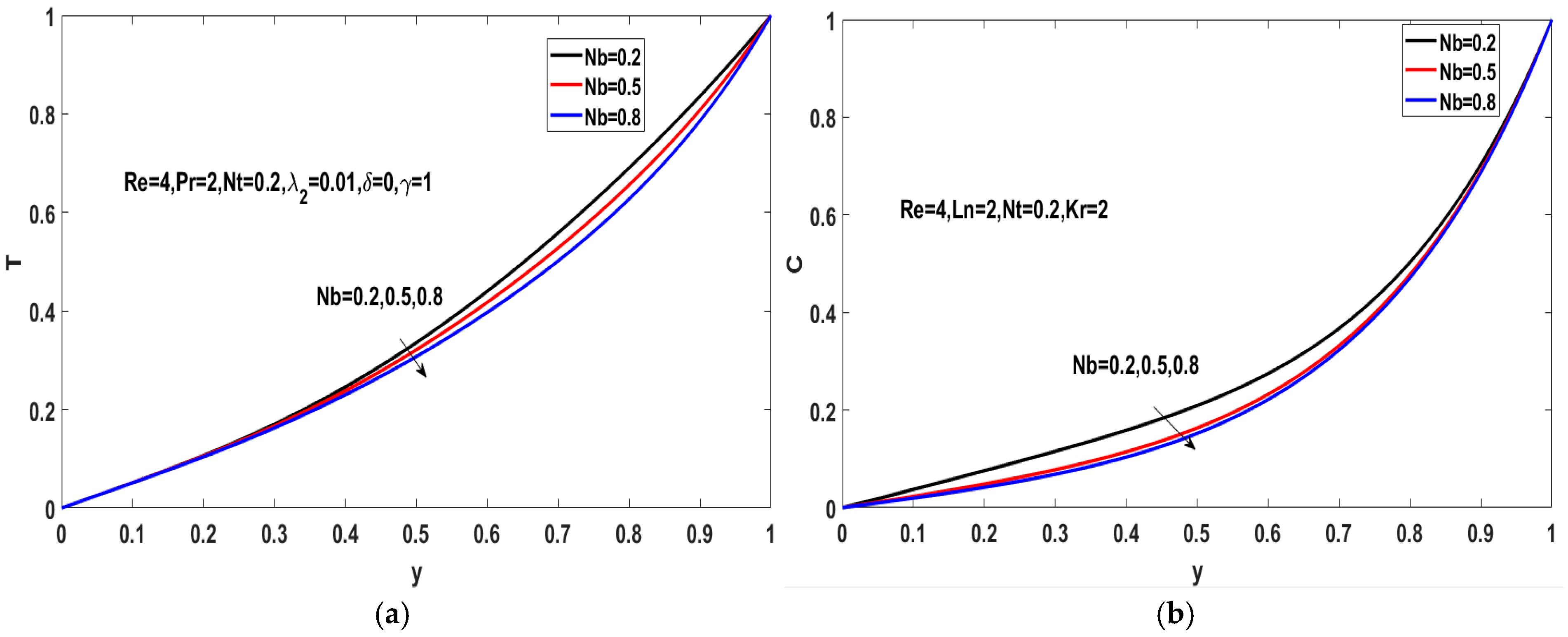
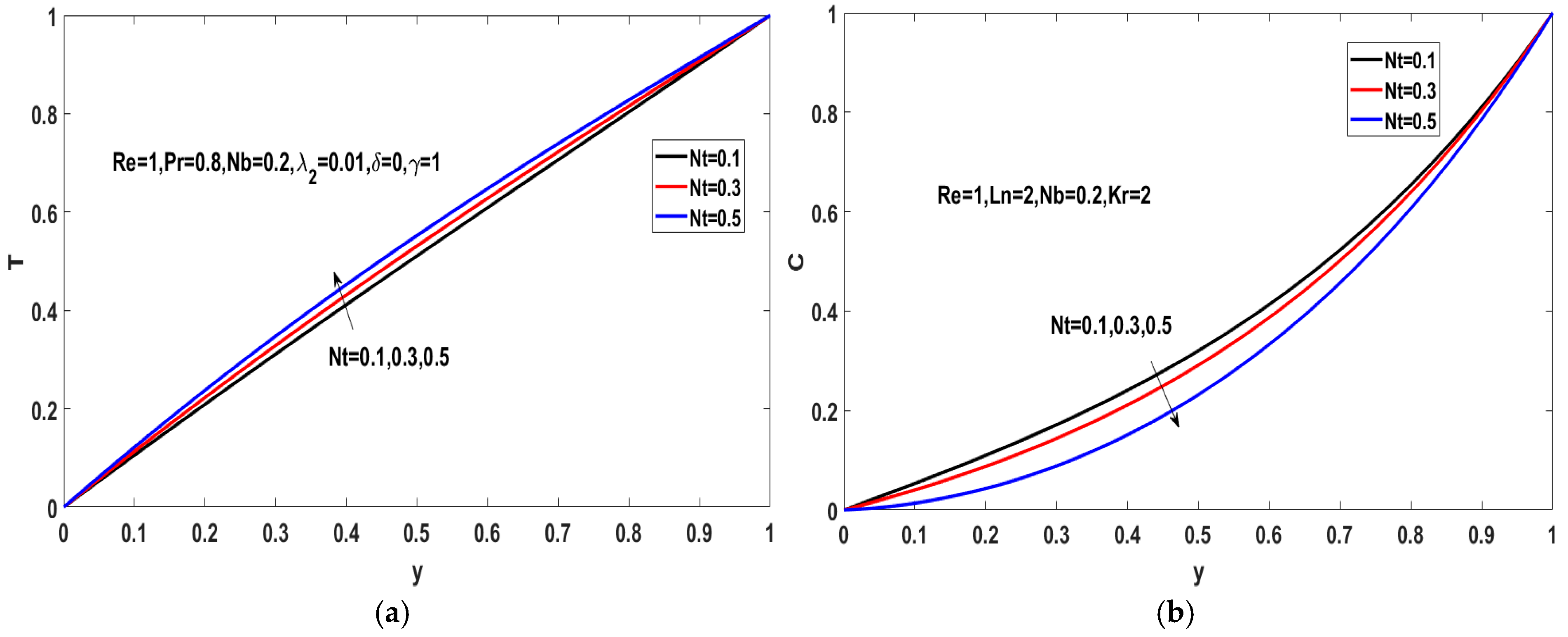
5.2. Effects of the Fractional Parameters on the Concentration Field
5.3. Effects of and
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Heat flux | |
| Thermal conductivity | |
| Permeability | |
| Specific enthalpy | |
| Nanofluids temperature | |
| Diffusion mass flux | |
| Brownian diffusion coefficient | |
| Thermophoresis diffusion coefficient | |
| Shear modulus | |
| Pressure | |
| Gravitational acceleration | |
| Chemical reaction parameter | |
| Reynolds number | |
| Grashof number | |
| Generalized Prandtl number | |
| Thermophoresis parameter | |
| Brownian motion parameter | |
| Lewis number | |
| Greek Symbols | |
| Time fractional derivative parameters | |
| Shear stress | |
| Shear strain | |
| Dynamic viscosity | |
| Relaxation time | |
| Temperature relaxation time | |
| Mass density | |
| Density of the nanofluids | |
| Thermal expansion coefficient | |
| Capacitance | |
| Heat capacity of nanoparticle materials | |
| Kinematic viscosity | |
| Gamma function | |
| Subscripts | |
| Nanofluids | |
| Nanoparticles | |
| Wall condition | |
| Superscript | |
| Dimensionless form |
References
- Fan, T.; Xu, H.; Pop, I. Mixed convection heat transfer in horizontal channel filled with nanofluids. Appl. Math. Mech. 2013, 34, 339–350. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Chamkha, A.J. Mixed convection flow of a nanofluid in a lid-driven cavity with a wavy wall. Int. Commun. Heat Mass Transf. 2014, 57, 36–47. [Google Scholar] [CrossRef]
- Aaiza, G.; Khan, I.; Shafie, S. Energy transfer in mixed convection MHD flow of nanofluid containing different shapes of nanoparticles in a channel filled with saturated porous medium. Nanoscale Res. Lett. 2015, 10, 490. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z. Impacts of gold nanoparticles on MHD mixed convection Poiseuille flow of nanofluid passing through a porous medium in the presence of thermal radiation, thermal diffusion and chemical reaction. Neural Comput. Appl. 2018, 30, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Chakravarty, A.; Datta, P.; Ghosh, K.; Sen, S.; Mukhopadhyay, A. Mixed convective heat transfer in an enclosure containing a heat-generating porous bed under the influence of bottom injection. Int. J. Heat Mass Transf. 2018, 117, 645–657. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. Double-diffusive mixed convection in a lid-driven enclosure filled with a fluid-saturated porous medium. Numer. Heat Transf. 2002, 42, 465–486. [Google Scholar] [CrossRef]
- Moolya, S.; Anbalgan, S. Optimization of the effect of Prandtl number, inclination angle, magnetic field, and Richardson number on double-diffusive mixed convection flow in a rectangular domain. Int. Commun. Heat Mass Transf. 2021, 126, 105358. [Google Scholar] [CrossRef]
- Shankar, B.M.; Kumar, J.; Shivakumara, I.S. Magnetohydrodynamic instability of mixed convection in a differentially heated vertical channel. Eur. Phys. J. Plus. 2019, 134, 53. [Google Scholar] [CrossRef]
- Shankar, B.M.; Kumar, J.; Shivakumara, I.S. Stability of mixed convection in a differentially heated vertical fluid layer with internal heat sources. Fluid Dyn. Res. 2019, 51, 055501. [Google Scholar] [CrossRef]
- Mahian, O.; Bellos, E.; Markides, C.N.; Taylor, R.A.; Wongwises, S. Recent advances in using nanofluids in renewable energy systems and the environmental implications of their uptake. Nano Energy 2021, 86, 106069. [Google Scholar] [CrossRef]
- Esfe, M.H.; Bahiraei, M.; Mir, A. Application of conventional and hybrid nanofluids in different machining processes: A critical review. Adv. Colloid Interface Sci. 2020, 282, 102199. [Google Scholar] [CrossRef]
- Nikolov, A.; Wu, P.K.; Wasan, D. Structure and stability of nanofluid films wetting solids: An overview. Adv. Colloid. Interface Sci. 2019, 264, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. Asme. Fed. 1995, 231, 99–105. [Google Scholar]
- Xuan, Y.M.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Rashed, Z.Z. MHD natural convection in a heat generating porous medium-filled wavy enclosures using Buongiorno’s nanofluid model. Case Stud. Therm. Eng. 2019, 14, 100430. [Google Scholar] [CrossRef]
- Bänsch, E.; Faghih-Naini, S.; Morin, P. Convective transport in nanofluids: The stationary problem. J. Math. Anal. Appl. 2020, 489, 124151. [Google Scholar] [CrossRef]
- Sohail, N.; Wang, F.Z.; Fahad, M.A.; Farrah, S. Numerical computations for Buongiorno nano fluid model on the boundary layer flow of viscoelastic fluid towards a nonlinear stretching sheet. Alex. Eng. J. 2022, 61, 1769–1778. [Google Scholar]
- Rana, P.; Gupta, G. Numerical and sensitivity computations of three-dimensional flow and heat transfer of nanoliquid over a wedge using modified Buongiorno model. Comput. Math. Appl. 2021, 101, 51–62. [Google Scholar] [CrossRef]
- Puneeth, V.; Anandika, R.; Manjunatha, S. Implementation of modified Buongiorno’s model for the investigation of chemically reacting ternary nanofluid jet flow in the presence of bio-active mixers. Chem. Phys. Lett. 2022, 786, 139194. [Google Scholar] [CrossRef]
- Kulish, V.V.; Lage, J.L. Application of fractional calculus to fluid mechanics. J. Fluids Eng. 2002, 124, 803–806. [Google Scholar] [CrossRef]
- Liu, F.; Turner, I.; Anh, V. An unstructured mesh finite volume method for modelling saltwater intrusion into coastal aquifers. J. Comput. Appl. Math. 2002, 9, 391–407. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Tlili, I. A new caputo time fracional model for heat transfer enhancement of water based graphene nanofluid: An application to solar energy. Results Phys. 2018, 9, 1352–1362. [Google Scholar] [CrossRef]
- Zhao, J.H.; Zheng, L.C.; Zhang, X.X.; Liu, F.W. Unsteady natural convection boundary layer heat transfer of fractional Maxwell viscoelastic fluid over a vertical plate. Int. J. Heat Mass Transf. 2016, 97, 760–766. [Google Scholar] [CrossRef]
- Chen, X.H.; Ye, Y.F.; Zhang, X.R.; Zheng, L.C. Lie-group similarity solution and analysis for fractional viscoelastic MHD fluid over a stretching sheet. Comput. Math. Appl. 2018, 75, 3002–3011. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.C.; Liu, F.W.; Zhang, X.X. Heat conduction with fractional Cattaneo-Christov upper-convective derivative flux model. Int. J. Therm. Sci. 2017, 112, 421–426. [Google Scholar] [CrossRef]
- Cao, Z.; Zhao, J.H.; Wang, Z.J.; Liu, F.W.; Zheng, L.C. MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid over a moving plate. J. Mol. Liq. 2016, 222, 1121–1127. [Google Scholar] [CrossRef]
- Zhao, J.H.; Zheng, L.C.; Chen, X.H.; Zhang, X.X.; Liu, F.W. Unsteady marangoni convection heat transfer of fractional Maxwell fluid with Cattaneo heat flux. Appl. Math. Model. 2017, 44, 497–507. [Google Scholar] [CrossRef]
- Chen, X.H.; Yang, W.D.; Zhang, X.R.; Liu, F.W. Unsteady boundary layer flow of viscoelastic MHD fluid with a double fractional Maxwell model. Appl. Math. Lett. 2019, 95, 143–149. [Google Scholar] [CrossRef]
- Tan, W.C.; Pan, W.X.; Xu, M.Y. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. Int. J. Non-Linear Mech. 2003, 38, 645–650. [Google Scholar]
- Yang, W.D.; Chen, X.H.; Zhang, X.R.; Zheng, L.C.; Liu, F.W. Flow and heat transfer of double fractional Maxwell fluids over a stretching sheet with variable thickness. Appl. Math. Model. 2020, 80, 204–216. [Google Scholar] [CrossRef]
- Yang, W.D.; Chen, X.H.; Jiang, Z.Y.; Zhang, X.R.; Zheng, L.C. Effect of slip boundary condition on flow and heat transfer of a double fractional Maxwell fluid. Chin. J. Phys. 2020, 68, 214–223. [Google Scholar] [CrossRef]
- Shen, M.; Chen, L.L.; Zhang, M.C.; Liu, F.W. A renovated Buongiorno’s model for unsteady sisko nanofluid with fractional Cattaneo heat flux. Int. J. Heat Mass Transf. 2018, 126, 277–286. [Google Scholar] [CrossRef]
- Zhang, M.C.; Shen, M.; Liu, F.W.; Zhang, H.M. A new time and spatial fractional heat conduction model for Maxwell nanofluid in porous medium. Comput. Math. Appl. 2019, 78, 1621–1636. [Google Scholar] [CrossRef]
- Shen, M.; Chen, S.R.; Liu, F.W. Unsteady MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid with Cattaneo heat flux and different particle shapes. Chin. J. Phys. 2018, 56, 1199–1211. [Google Scholar] [CrossRef]
- Sayehvand, H.O.; Parsa, A.B. A new numerical method for investigation of thermophoresis and Brownian motion effects on MHD nanofluid flow and heat transfer between parallel plates partially filled with a porous medium. Results Phys. 2017, 7, 1595–1607. [Google Scholar] [CrossRef]




| Error | Order | Error | Order | |
|---|---|---|---|---|
| 0.1 | 3.0723 × 10−3 | - | 4.4143 × 10−3 | - |
| 0.05 | 1.5496 × 10−3 | 0.9874 | 2.2262 × 10−3 | 0.9876 |
| 0.025 | 7.7837 × 10−4 | 0.9934 | 1.1181 × 10−3 | 0.9935 |
| 0.0125 | 3.9022 × 10−4 | 0.9962 | 5.6051 × 10−4 | 0.9962 |
| Error | Order | Error | Order | |
|---|---|---|---|---|
| 0.1 | 1.8800 × 10−3 | - | 2.7568 × 10−3 | - |
| 0.05 | 9.6757 × 10−4 | 0.9583 | 1.4177 × 10−3 | 0.9594 |
| 0.025 | 4.9147 × 10−4 | 0.9773 | 7.1997 × 10−4 | 0.9775 |
| 0.0125 | 2.4796 × 10−4 | 0.9870 | 3.6353 × 10−4 | 0.9859 |
| Error | Order | Error | Order | |
|---|---|---|---|---|
| 0.1 | 4.0470 × 10−4 | - | 5.4928 × 10−4 | - |
| 0.05 | 1.8991 × 10−4 | 1.0915 | 2.5773 × 10−4 | 1.0917 |
| 0.025 | 9.1774 × 10−5 | 1.0492 | 1.2564 × 10−4 | 1.0366 |
| 0.0125 | 4.5249 × 10−5 | 1.0202 | 6.3692 × 10−5 | 0.9801 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Tian, Y.; Yang, W.; Chen, X. Mixed Convection of Fractional Nanofluids Considering Brownian Motion and Thermophoresis. Fractal Fract. 2022, 6, 584. https://doi.org/10.3390/fractalfract6100584
Chen M, Tian Y, Yang W, Chen X. Mixed Convection of Fractional Nanofluids Considering Brownian Motion and Thermophoresis. Fractal and Fractional. 2022; 6(10):584. https://doi.org/10.3390/fractalfract6100584
Chicago/Turabian StyleChen, Mingwen, Yefan Tian, Weidong Yang, and Xuehui Chen. 2022. "Mixed Convection of Fractional Nanofluids Considering Brownian Motion and Thermophoresis" Fractal and Fractional 6, no. 10: 584. https://doi.org/10.3390/fractalfract6100584
APA StyleChen, M., Tian, Y., Yang, W., & Chen, X. (2022). Mixed Convection of Fractional Nanofluids Considering Brownian Motion and Thermophoresis. Fractal and Fractional, 6(10), 584. https://doi.org/10.3390/fractalfract6100584







