A Fourth-Order Time-Stepping Method for Two-Dimensional, Distributed-Order, Space-Fractional, Inhomogeneous Parabolic Equations

Abstract

Distributed-order, space-fractional diffusion equations are used to describe physical processes that lack power-law scaling. A fourth-order-accurate, A-stable time-stepping method was developed, analyzed, and implemented to solve inhomogeneous parabolic problems having Riesz-space-fractional, distributed-order derivatives. The considered problem was transformed into a multi-term, space-fractional problem using Simpson’s three-eighths rule. The method is based on an approximation of matrix exponential functions using fourth-order diagonal Padé approximation. The Gaussian quadrature approach is used to approximate the integral matrix exponential function, along with the inhomogeneous term. Partial fraction splitting is used to address the issues regarding stability and computational efficiency. Convergence of the method was proved analytically and demonstrated through numerical experiments. CPU time was recorded in these experiments to show the computational efficiency of the method.

1. Introduction

Complex processes which obey a mixture of power laws and flexible variations in space are modeled by distributed-order, space-fractional differential equations. Distributed-order, space-fractional differential equations are used to model the phenomena where the order of differentiation varies in a given range [1,2]. Due to their nonlocal properties, the distributed-order differentials can model more complex dynamical systems than the fractional-order or classical models.

Consider the following two-dimensional Riesz-space, distributed-order, fractional, inhomogeneous diffusion equation:

$$\frac{\partial u}{\partial t}=K_x\underset{1}{\overset{2}{\int }}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{{\partial \left|x\right|}^{\alpha }} d\alpha +K_y\underset{1}{\overset{2}{\int }}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{{\partial \left|y\right|}^{\beta }} d\beta +f(x,y,t),\hspace{1em}(x,y,t)\in \mathsf{\Omega }\times (0,T],$$

(1)

with initial condition

$$\begin{array}{c}\hfill u(x,y,0)=u_0(x,y),\hspace{1em}(x,y)\in \mathsf{\Omega },\end{array}$$

and boundary condition

$$\begin{array}{c}\hfill u(x,y,t)=0,\hspace{1em}(x,y)\in \partial \mathsf{\Omega },\end{array}$$

where $\mathsf{\Omega }=(a,b)\times (c,d)$. The coefficients P and Q are non-negative functions defined on $(1,2]$, that are not identically zero and satisfy

$$0<\underset{1}{\overset{2}{\int }}P\left(\alpha \right)d\alpha <\infty ,\hspace{1em}0<\underset{1}{\overset{2}{\int }}Q\left(\beta \right)d\beta <\infty .$$

The inhomogeneous source term f is assumed to be sufficiently smooth. The distributed-order, space-fractional derivative terms are approximated using Simpson’s three-eighth rule. For any $1<{\alpha }_i\le 2$, the two-sided, Riesz-space-fractional derivative operator $\frac{{\partial }^{{\alpha }_i}}{{\partial \left|x\right|}^{{\alpha }_i}}$ on a finite interval $(a,b)$ is given by

$$\frac{{\partial }^{{\alpha }_i}}{{\partial \left|x\right|}^{{\alpha }_i}}=-\frac{1}{2cos\frac{\pi {\alpha }_i}{2}} \left[{}_a{D}_x^{{\alpha }_i}+{}_x{D}_b^{{\alpha }_i}\right],\hspace{1em}1<{\alpha }_i\le 2,$$

(2)

where ${}_a{D}_x^{{\alpha }_i}$ is the left Riemann–Liouville and ${}_x{D}_b^{{\alpha }_i}$ is the right Riemann–Liouville fractional derivatives, which are, respectively,

$${}_a{D}_x^{{\alpha }_i}u(x,y,t)=\frac{1}{\mathsf{\Gamma }(2-{\alpha }_i)} \frac{{\partial }^2}{\partial x^2}{\int }_a^x{(x-\chi )}^{1-{\alpha }_i} u(\chi ,y,t) d\chi ,$$

$${}_x{D}_b^{{\alpha }_i}u(x,y,t)=\frac{1}{\mathsf{\Gamma }(2-{\alpha }_i)} \frac{{\partial }^2}{\partial x^2}{\int }_x^b{(\chi -x)}^{1-{\alpha }_i} u(\chi ,y,t) d\chi .$$

The Riesz-space-fractional derivative operator $\frac{{\partial }^{{\beta }_j}}{{\partial \left|y\right|}^{{\beta }_j}}$ on $(c,d)$ is defined similarly.

A recent review article [3] provided a state-of-the-art introduction to the mathematics of distributed-order fractional calculus, along with analytical and numerical methods. An extensive overview of the applications of distributed-order fractional calculus with applications to viscoelasticity, transport processes, and control theory have been discussed.

Anomalous diffusion phenomena take place in many complex systems, such as subsurface flows, human tissues, viscoelastic material, and plasma. In such systems, the diffusion is slower or faster than normal, the probability density function is not anymore Gaussian, and the mean-square displacement is not linear in time; see, for example, [4] and references therein. As such, the predictions obtained through integer-order local models do not match the collected data and observed behaviors. Riesz-space-fractional diffusion equations provide a powerful mathematical tool for modeling such phenomena. In these models, the diffusion rate depends on the global state of the field. In particular, the order of the Riesz fractional derivatives identifies the power-law scaling of the physical process.

Many physical processes, however, lack power-law scaling and cannot be characterized by specific scaling exponents. Among these processes are several cases of accelerating super diffusion [5,6,7]. These processes can easily be described by Riesz-space distributed-order fractional diffusion equations.

There are many applications of the distributed-order fractional operators. For example, applications to fields such as viscoelasticity, transport processes, and control theory were discussed by Ding et al. in [3], and Patnaik et al. [8] discussed applications of variable- and distributed-order fractional operators to the dynamic analysis of nonlinear oscillators.

Analytical solutions for some problems were constructed by Caputo [5] and Sokolov et al. [6]. The well-posedness of particular classes of such problems were studied by Jia et al. [9]. Numerical solutions for distributed-order space-fractional models on bounded domains are in high demand, since analytical solutions are not in general available. Wang et al. [2] developed a second-order-accurate, implicit numerical method for one- and two-dimensional Riesz-space, distributed-order fractional advection–dispersion equations. Their method is based on use of a midpoint quadrature rule for the Riesz space distributed-order term. Li et al. [10] proposed an unconditionally stable second-order Crank–Nicolson method for a one-dimensional Riesz space distributed-order diffusion equation. The method is based on midpoint quadrature and the finite volume method. For the two-dimensional Riesz-space, distributed-order advection–diffusion equation, a Crank–Nicolson ADI, Galerkin–Legendre spectral method was developed by Zhang et al. [11]. Jia and Wang [12] designed a fast finite difference method for distributed-order, space-fractional partial differential equations on convex domains. Qiao et al. [13] analyzed the velocity distributions of the distributed/variable-order fractional Maxwell governing equations under specific conditions, and discussed the effects of different parameters on the solution.

The time-stepping methods mentioned in all the above-mentioned references are of second order. The purpose of this work was to develop a computationally efficient, strongly stable, fourth-order time-stepping method that is suitable for solving problems such as (1). The numerical method is obtained by first applying the three-eighth Simpson’s rule to the distributed-order space-fractional derivative term. Then, the multi-term fractional derivative equation is discretized in space by using the fractional centered-difference formulas introduced by Ortigueira [14]. The exact solution of the resulting semi-discretized system is written using the Duhamel’s principle [15]. This exact solution involves a matrix exponential function and the integral of a matrix exponential function, along with the inhomogeneous term. Matrix exponential functions are approximated by diagonal (2,2)-Padé approximation. The rationale behind using a diagonal (2,2)-Padé approximation is that only one algebraic system needs to be solved at each time step. Therefore, we can implement this fourth-order method with the same computational complexity as a first-order method. We utilize an approach with a class of single-step, fully discrete numerical methods developed by Brenner et al. [16], and the same approach is summarized in the book by Thomée [15].

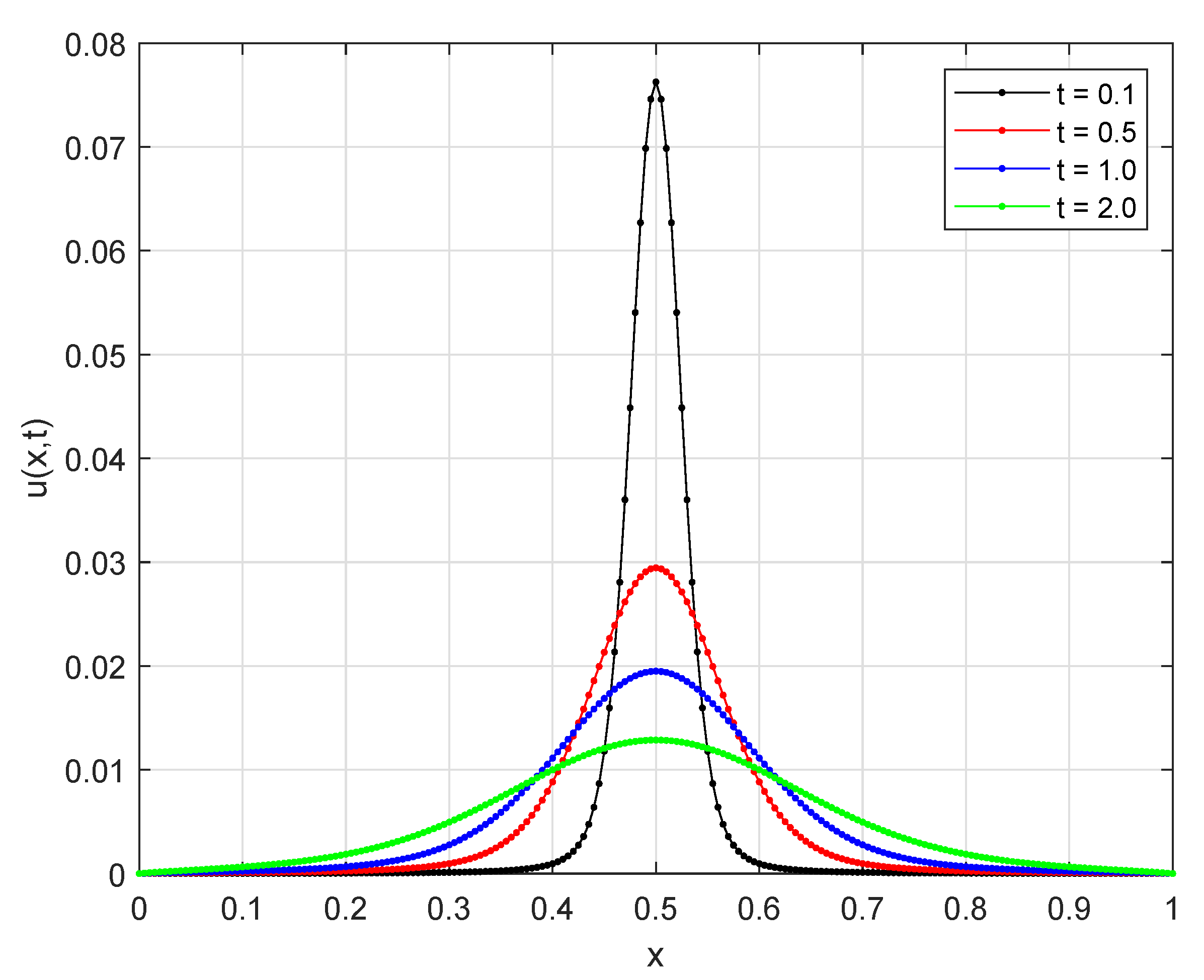
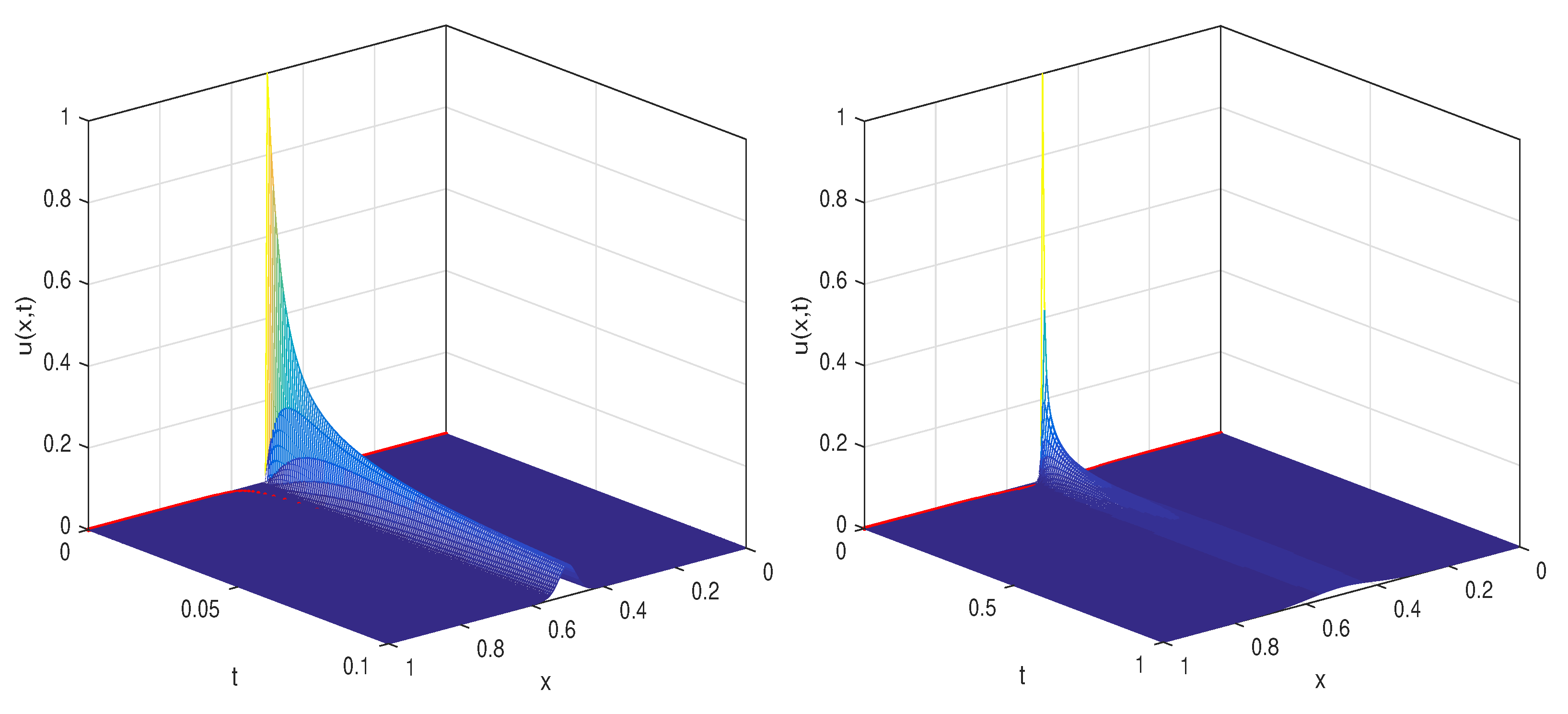
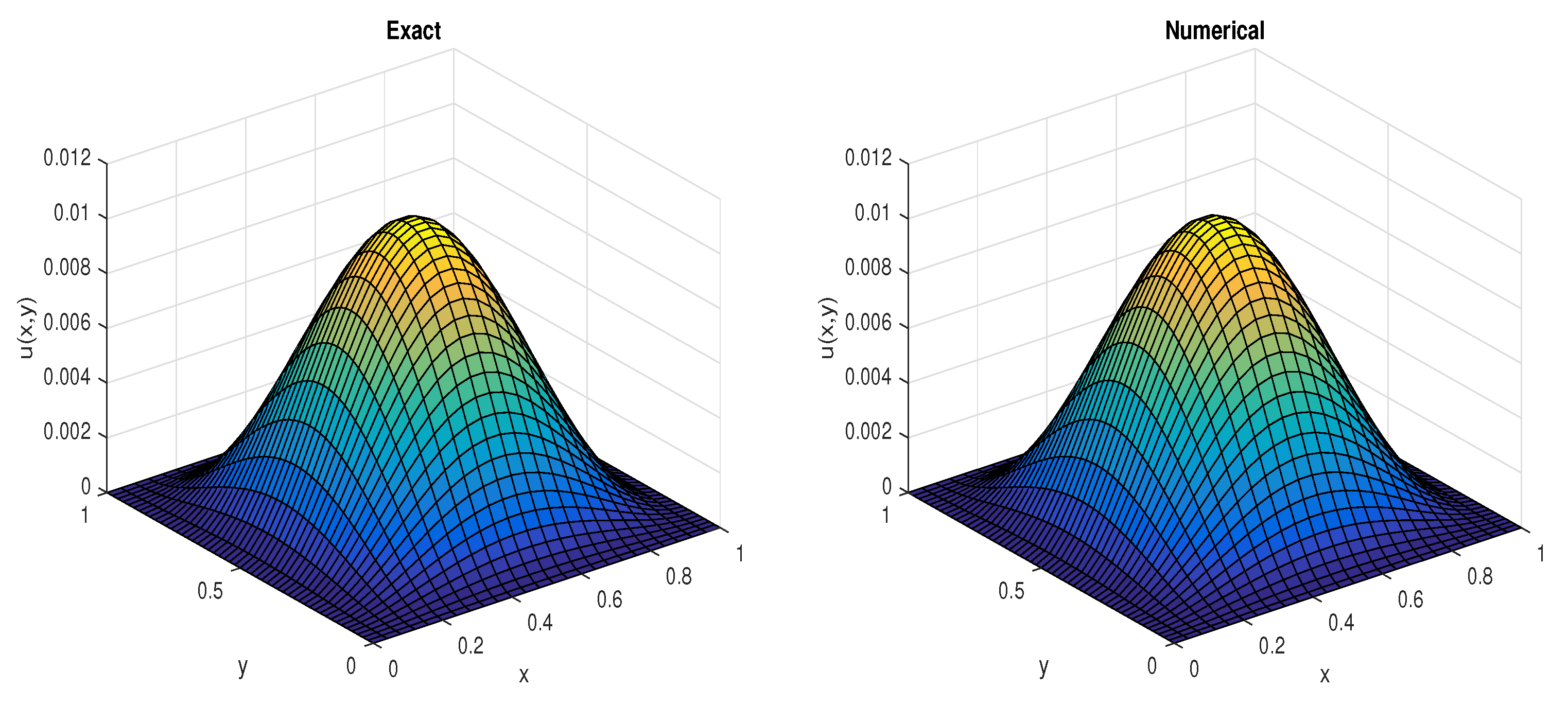
The paper is organized as follows. The Riesz-space distributed-order fractional derivative discretization is presented in Section 2. In Section 3, the time-stepping method is developed, and an implementation algorithm is provided. The convergence theorem of the numerical method is given in Section 4. Numerical experiments are shown in Section 5. Solution profiles and convergence tables, along with CPU times, are also given in the same section. Finally, some concluding remarks are included in Section 6.

2. Distributed-Order Space-Fractional Derivative Approximation

Let $1={\alpha }_0<{\alpha }_1<\cdots <{\alpha }_{N_1}=2$ and $1={\beta }_0<{\beta }_1<\cdots <{\beta }_{N_2}=2$ be uniform discretizations of the interval $[1,2]$. Let $\Delta \alpha =1/N_1$ and $\Delta \beta =1/N_2$. By applying the fourth-order Simpson’s three-eighths rule to the distributed terms, we obtain

$${\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{{\partial \left|x\right|}^{\alpha }} d\alpha =\sum _{i=1}^{N_1}{a}_{i}P\left({\alpha }_i\right)\frac{{\partial }^{{\alpha }_i}u}{{\partial \left|x\right|}^{{\alpha }_i}}+O({(\Delta \alpha )}^4),$$

(3)

$${\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{{\partial \left|x\right|}^{\beta }} d\beta =\sum _{j=1}^{N_2}{b}_{j}Q\left({\beta }_j\right)\frac{{\partial }^{{\beta }_j}u}{{\partial \left|x\right|}^{{\beta }_j}}+O({(\Delta \beta )}^4),$$

(4)

where $a_i$ and $b_j$ are the coefficients of Simpson’s three-eighths rule.

To approximate the Riesz derivatives in the right-hand sides of (3) and (4), we use the fractional centered-difference introduced by Ortigueira [14]. We consider $x_m=a+m{h}_x$, $m=0,1,\dots ,M$ with $h_x=(b-a)/M$ as the spatial mesh points. Suppose $u\left(x\right)$ to be a sufficiently smooth function defined for $-\infty <x<\infty$. Then, for $i=1,2,\dots ,N_1$, we have

$$\frac{d^{{\alpha }_i}}{{d\left|x\right|}^{{\alpha }_i}}u\left(x\right)=-\frac{1}{2cos\frac{\pi {\alpha }_i}{2}} \left[{}_{-\infty }{D}_x^{{\alpha }_i}+{}_x{D}_{\infty }^{{\alpha }_i}\right]u(x,t)=\frac{-1}{h_x^{{\alpha }_i}} {\Delta }_{h_x}^{{\alpha }_i}u\left(x\right)+O\left(h^2\right),$$

(5)

where

$${\Delta }_h^{{\alpha }_i}u\left(x\right)=\sum _{j=-\infty }^{\infty }{g}_j^{\left({\alpha }_i\right)}u(x-j{h}_x),$$

(6)

$$g_j^{\left({\alpha }_i\right)}=\frac{{(-1)}^j \mathsf{\Gamma }(1+{\alpha }_i)}{\mathsf{\Gamma }({\alpha }_i/2-j+1) \mathsf{\Gamma }({\alpha }_i/2+j+1)}, j=0, \pm 1, \pm 2, \dots .$$

If $u\left(x\right)$ vanishes outside the interval $(a,b)$ and $u_m=u\left(x_m\right)$ for $m=1,\dots ,M-1$, then we have

$$\begin{array}{ccc}\hfill {\Delta }_h^{{\alpha }_i}v\left(x_m\right)& =& \left[g_{m-1}^{\left({\alpha }_i\right)}{u}_1+\cdots +g_0^{\left({\alpha }_i\right)}{u}_m+\cdots +g_{M-m-1}^{\left({\alpha }_i\right)}{u}_{M-1}\right].\hfill \end{array}$$

We can write this system of equations as:

$$\frac{{\Delta }_{h_x}^{{\alpha }_i}\mathbf{u}}{h_x^{{\alpha }_i}}=G_x^{\left({\alpha }_i\right)}\mathbf{u},$$

with

$$G_x^{\left({\alpha }_i\right)}=\frac{1}{h_x^{{\alpha }_i}}\left[\begin{array}{ccccccc}\hfill g_0^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_2^{\left({\alpha }_i\right)}& \hfill \cdots & \hfill g_{M-4}^{\left({\alpha }_i\right)}& \hfill g_{M-3}^{\left({\alpha }_i\right)}& \hfill g_{M-2}^{\left({\alpha }_i\right)}\\ \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_0^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill \cdots & \hfill g_{M-5}^{\left({\alpha }_i\right)}& \hfill g_{M-4}^{\left({\alpha }_i\right)}& \hfill g_{M-3}^{\left({\alpha }_i\right)}\\ \hfill g_2^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_0^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_2^{\left({\alpha }_i\right)}& \hfill \cdots & \hfill g_{M-4}^{\left({\alpha }_i\right)}\\ \hfill ⋮& \hfill \ddots & \hfill \ddots & \hfill \ddots & \hfill \ddots & \hfill \ddots & \hfill ⋮\\ \hfill g_{M-4}^{\left({\alpha }_i\right)}& \hfill \cdots & \hfill g_2^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_0^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_2^{\left({\alpha }_i\right)}\\ \hfill g_{M-3}^{\left({\alpha }_i\right)}& \hfill g_{M-4}^{\left({\alpha }_i\right)}& \hfill \cdots & \hfill g_2^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_0^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}\\ \hfill g_{M-2}^{\left({\alpha }_i\right)}& \hfill g_{M-3}^{\left({\alpha }_i\right)}& \hfill g_{M-4}^{\left({\alpha }_i\right)}& \hfill \cdots & \hfill g_2^{\left({\alpha }_i\right)}& \hfill g_1^{\left({\alpha }_i\right)}& \hfill g_0^{\left({\alpha }_i\right)}\end{array}\right], \mathbf{u}=\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ ⋮\\ u_{M-3}\\ u_{M-2}\\ u_{M-1}\end{array}\right].$$

Thus, for each ${\alpha }_i$, we have the space-fractional derivative approximations

$$\frac{d^{{\alpha }_i}}{{d\left|x\right|}^{{\alpha }_i}}\approx -G_x^{{\alpha }_i}.$$

(7)

Similarly, by considering the spatial nodes: $y_n=c+n{h}_y$, $n=0,1,\dots ,N$ with $h_y=(c-d)/N$, we obtain the following approximation:

$$\frac{d^{{\beta }_j}}{{d\left|y\right|}^{{\beta }_j}}\approx -G_y^{{\beta }_j}.$$

(8)

Using the approximations (7) and (8), the distributed-order terms can be approximated as

$${\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }}{{\partial \left|x\right|}^{\alpha }} d\alpha \approx \sum _{i=1}^{N_1}-a_{i}P\left({\alpha }_i\right)G_x^{{\alpha }_i}=G_x^{\alpha },\hspace{1em}{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }}{{\partial \left|y\right|}^{\beta }} d\beta \approx \sum _{j=1}^{N_2}-b_{j}Q\left({\beta }_j\right)G_y^{{\beta }_j}=G_y^{\beta }.$$

(9)

By applying the Riesz derivative approximation to Equation (1), the following semi-discrete system is obtained:

$$\frac{d\mathbf{u}}{dt}+A\mathbf{u}=\mathbf{f}\left(t\right),$$

(10)

where $A=K_x{G}_x^{\alpha }\otimes I+I\otimes K_y{G}_y^{\beta }$ is an $(M-1)(N-1)\times (M-1)(N-1)$ matrix, I is the $(M-1)(N-1)\times (M-1)(N-1)$ identity matrix and $\mathbf{u}$ is the $(M-1)(N-1)\times 1$ vector that consists of columns of the matrix $\left[u_{i,j}\right]$, where $u_{i,j}=u(x_i,y_j)|\hspace{1em}1\le i\le M-1,$ $1\le j\le N-1$. The inhomogeneous term $\mathbf{f}\left(\mathbf{t}\right)={\left[f_1,\dots ,f_{M-1}\right]}^T$ is an $(M-1)(N-1)\times 1$ vector, with $f_j={[f(x_1,y_j,t),f(x_2,y_j,t),\cdots ,f(x_{M-1},y_j,t)]}^T$, $j=1,2,\cdots N-1.$

3. Time-Stepping Method

We consider the following abstract initial value problem:

$$\begin{array}{ccc}\hfill u_t+Au& =& f\left(t\right), t\in \left(0,T\right]=J,\hfill \\ \hfill u\left(0\right)& =& u_0,\hfill \end{array}$$

(11)

to develop the numerical method and to discuss the convergence analysis that works without dependence on the spatial mesh size; see Thomée [15] [Ch. 3, 7–9]. Using Duhamel’s principle [15], the exact solution of (11) is written as:

$$u\left(t\right)=e^{-tA}{u}_0+{\int }_0^t{e}^{-(t-s)A}f\left(s\right)ds,$$

(12)

where the matrix exponential function $e^{-tA}$ is the solution which corresponds to the homogeneous problem having $f\equiv 0$. First, we replace the variable t by the shifted value $t+k$, and then we use the following change in variable $s-t=k\tau$ and write the exact solution (12) as:

$$u(t+k)=e^{-kA}u\left(t\right)+k{\int }_0^1{e}^{-k(1-\tau )A}f(t+k\tau )d\tau ,$$

(13)

and setup the following recurrence formula as

$$u\left(t_{n+1}\right)=e^{-kA}u\left(t_n\right)+k {\int }_0^1{e}^{-kA(1-\tau )}f(t_n+\tau k)d\tau ,$$

(14)

where k, with $0<k\le k_0$ for some $k_0$, is the temporal step size, and temporal mesh points are given by $t_n=nk$ with $0\le n\le \overline{n}=\left[\frac{T}{k}\right]$.

Our fourth-order A-stable method is based on the following method from [15]:

$$v_{n+1}\approx r\left(kA\right)v_n+k\sum _{i=1}^{\tilde{m}}{P}_i\left(kA\right)f(t_n+{\tau }_{i}k), n\ge 0, v_0=v.$$

(15)

where $r\left(z\right)$ and ${\left\{P_i\left(z\right)\right\}}_{i=1}^{\tilde{m}}$ are the rational approximations of $e^{-kA}$ and $e^{-kA(1-{\tau }_i)}$, respectively. These rational approximations are uniformly bounded on the spectrum of $kA$ in k and h, where h represents the spatial discretization step size. The real numbers ${\left\{{\tau }_i\right\}}_{i=1}^{\tilde{m}}$ are the $\tilde{m}$ Gaussian quadrature points in the interval $[0,1]$. Our aim is to obtain a procedure which admits an optimal order-error estimate $\parallel v_n-u\left(t_n\right)\parallel =O(h^{\alpha }+k^q)$, with spatial discretization order $\alpha$. The real number $q>0$ is determined by the properties of the rational functions $r\left(z\right)$ and $P_i\left(z\right)$, for $i=1,2,\dots ,\tilde{m}.$

The time-stepping method (15) is accurate for order q if it satisfies some equivalent conditions given in [15]. The reader may consult chapter 9 of [15] to fill in various details omitted here for brevity. The accuracy of the time-stepping method (15) is defined in the following definition.

Definition 1

([15] (Ch. 9)). The time discretization method (15) is said to be accurate for order q if the solution of (11) satisfies (15) with an error of order $O\left(k^{q+1}\right)$, as $k\to 0$ for any choice of linear operator A and a smooth function f on R.

The following Lemma describes the accuracy of the method (15) and establishes some equivalent relations which are then used in the proof of the main results.

Lemma 1

([15] (Lemma 8.1)). The time discretization method (15) is accurate for order q if and only if

$$r\left(\lambda \right)=e^{-\lambda }+O\left({\lambda }^{q+1}\right), \lambda \to 0,$$

(16)

and for $0\le l\le q,$

$$\sum _{i=1}^{\tilde{m}}{\tau }_i^l{P}_i\left(\lambda \right)=\frac{l!}{{(-\lambda )}^{l+1}}\left(e^{-\lambda }-\sum _{j=0}^l\frac{{(-\lambda )}^j}{j!}\right)+O\left({\lambda }^{q-l}\right), \lambda \to 0,$$

(17)

or equivalently

$$\sum _{i=1}^{\tilde{m}}{\tau }_i^l{P}_i\left(\lambda \right)=\underset{0}{\overset{1}{\int }}{s}^l{e}^{-\lambda (1-s)}ds+O\left({\lambda }^{q-l}\right), \lambda \to 0.$$

(18)

A computationally efficient method can be developed by considering $r\left(\lambda \right)$ and ${\left\{P_i\left(\lambda \right)\right\}}_{i=1}^{\tilde{m}}$ such that they have the same denominator (the same poles). Let

$$r\left(\lambda \right)=\frac{\mathcal{N}\left(\lambda \right)}{\mathcal{D}\left(\lambda \right)}\hspace{1em}\mathrm{and}\hspace{1em}{P}_i\left(\lambda \right)=\frac{{\mathcal{N}}_i\left(\lambda \right)}{\mathcal{D}\left(\lambda \right)},\hspace{1em}i=1,2,\cdots ,\tilde{m}$$

(19)

be bounded on the spectrum of $kA,$ uniformly in h and k. The method (15) is approximated as:

$$v_{n+1}\approx \frac{\mathcal{N}\left(kA\right)}{\mathcal{D}\left(kA\right)}{v}_n+k\sum _{i=1}^{\tilde{m}}\frac{{\mathcal{N}}_i\left(kA\right)}{\mathcal{D}\left(kA\right)}f(t_n+{\tau }_{i}k), n\ge 0, v_0=v.$$

(20)

For the case when $\tilde{m}=q$, we can achieve the conditions of Lemma 1 by choosing a rational function $r\left(\lambda \right)$ which satisfies (16) and by selecting the distinct real numbers as Gaussian quadrature points ${\left\{{\tau }_i\right\}}_{i=1}^{\tilde{m}}$. Then, we solve the system of equations [15]

$$\sum _{i=1}^q{\tau }_i^l{P}_i\left(\lambda \right)=\frac{l!}{{(-\lambda )}^{l+1}}\left(e^{-\lambda }-\sum _{j=0}^l\frac{{(-\lambda )}^j}{j!}\right), l=0,1,\cdots q-1,$$

(21)

to find $P_i\left(\lambda \right)$. The system given in (21) is of Vandermonde type, and its determinant is not zero. The rational functions ${\left\{P_i\left(\lambda \right)\right\}}_{i=1}^q$ are obtained as linear combinations of the terms on the right-hand side of (21). Additionally, if $r\left(\lambda \right)$ is bounded for large $\lambda$, then the right-hand sides of (21) are small for large $\lambda$, and the numerator polynomials of $P_i\left(\lambda \right)$ would be of a smaller degree than their denominator polynomials for each i.

A fourth-order, A-stable method is developed by considering $r\left(\lambda \right)=R_{2,2}\left(\lambda \right)$, where

$$R_{2,2}\left(\lambda \right)=\frac{1-\frac{1}{2}\lambda +\frac{1}{12}{\lambda }^2}{1+\frac{1}{2}\lambda +\frac{1}{12}{\lambda }^2}=1+\frac{-\lambda }{1+\frac{1}{2}\lambda +\frac{1}{12}{\lambda }^2},$$

(22)

is the fourth-order, A-acceptable (2,2)-Padé approximation of $e^{-\lambda }$. By replacing the matrix exponential $e^{-kA}$ by rational (2,2)-Padé approximation $R_{2,2}\left(kA\right)$ and taking the Gaussian quadrature points ${\tau }_1=\frac{3-\sqrt{3}}{6}, {\tau }_2=\frac{3+\sqrt{3}}{6}$, the system (21) can be written as:

$$\begin{array}{ccc}\hfill P_1\left(\lambda \right)+P_2\left(\lambda \right)& =& -\frac{1}{\lambda }\left(R_{2,2}\left(\lambda \right)-1\right),\hfill \\ \hfill {\tau }_1{P}_1\left(\lambda \right)+{\tau }_2{P}_2\left(\lambda \right)& =& \frac{1}{{\lambda }^2}\left(R_{2,2}\left(\lambda \right)-1+\lambda \right),\hfill \end{array}$$

which results in

$$P_1\left(\lambda \right)=\frac{1-\frac{\sqrt{3}}{6}\lambda }{2(1+\frac{1}{2}\lambda +\frac{1}{12}{\lambda }^2)}, P_2\left(\lambda \right)=\frac{1+\frac{\sqrt{3}}{6}\lambda }{2(1+\frac{1}{2}\lambda +\frac{1}{12}{\lambda }^2)}.$$

Using these rational approximations, the method (15) is written as

$$v_{n+1}\approx R_{2,2}\left(kA\right)u_n+k{P}_1\left(kA\right)f\left(t_n+{\tau }_{1}k\right)+k{P}_2\left(kA\right)f\left(t_n+{\tau }_{2}k\right).$$

(23)

The above-mentioned method (23) is of fourth-order accuracy of Lemma 1 [15] (Ch. 9), under the assumption that initial data have sufficient regularity.

3.1. Computationally Efficient Version of the Method

In order to implement the methods, it is required to compute matrix exponential functions, which would be computationally expensive and compromise the computational efficiency of the time-stepping methods. Another challenge is to invert higher-degree matrix polynomials which can cause computational difficulties due to the ill-conditioning of the spatial discretization matrix A. Use of the splitting technique not only resolves this but also results in a highly efficient method; see Khaliq, Twizell, and Voss [17] and references therein. We can write:

$$R_{2,2}\left(\lambda \right)=1+2\Re \left(\frac{w}{\lambda -z}\right)$$

and the corresponding ${\left\{P_i\left(\lambda \right)\right\}}_{i=1}^2$ takes the form:

$$P_i\left(\lambda \right)=2\Re \left(\frac{w_i}{\lambda -z}\right), i=1,2,$$

where c is the non real pole of $R_{2,2}$ and the $P_i$ with corresponding weights w and $w_i$, respectively. All the poles and corresponding weights were computed using MAPLE 11.

3.2. Algorithm

Solve $\left(kA-zI\right)y=w{u}_n+{\displaystyle \sum _{j=1}^2}k{w}_{j}f\left(t_n+{\tau }_{j}k\right)$ for y, and then compute $u_{n+1}=u_n+2\Re \left(y\right),\hspace{1em}n=0,1,\cdots$, where $\Re \left(y\right)=Real\left(y\right)$. The poles and corresponding weights are:

$$\begin{array}{ccc}\hfill z& =& -3.0-1.73205080757 i,\hfill \\ \hfill \omega & =& -6.0+10.3923048454 i,\hfill \\ \hfill {\omega }_1& =& -0.86602540378+3.23205080757 i,\hfill \\ \hfill {\omega }_2& =& 0.86602540378+0.23205080757 i.\hfill \end{array}$$

4. Convergence Analysis

We present convergence in the Hilbert space case assuming A is a self-adjoint operator. We followed the approach of Brenner et al. described in [16], which is also summarized in [15] (Ch. 9]). In this analysis, we used the spaces ${\dot{H}}^s=\mathcal{D}\left(A^{s/2}\right)$, as defined in [15] by the norm

$${\left|u\right|}_s={(A^{s}u,u)}^{1/2}=\parallel A^{s/2}u\parallel ={\left(\sum _{j=1}^N{\lambda }_j^s{(u,{\varphi }_j)}^2\right)}^{1/2},$$

where ${\left\{{\varphi }_j\right\}}_{j=1}^N$ are orthonormal eigenfunctions of A with corresponding positive eigenvalues ${\left\{{\lambda }_j\right\}}_{j=1}^N$. We assume $f\in {\dot{H}}^s$ to have sufficient regularity and also use the concept that the operator $E_k=r\left(kA\right)$ is said to be stable in $\mathcal{H}$ if $\parallel E_k^n\parallel \le C$ for $n\ge 1$, $0<k\le \overline{k}$, $nk\le \overline{t}$; see [15].

Theorem 1.

Let A be a self-adjoint operator defined on the Hilbert space $\mathcal{H}$; the solution operator $E_k=r\left(kA\right)$ is stable in $\mathcal{H}$; and the time discretization method (15) is accurate for order $q=2m$, where m is a positive integer. Suppose $f^{\left(l\right)}\left(t\right)\in {\dot{H}}^{2q-2l}$ for $l<q$, $t\ge 0$. Then, there exists a constant $C=C\left(t\right)$ such that

$$\parallel v_n-u\left(t_n\right)\parallel \le C{k}^q\left(t_n^{-q}\parallel v\parallel +t_n\sum _{l=0}^{q-1}{\mathcal{S}}_l+{\int }_0^{t_n}\parallel f^{\left(q\right)}\parallel ds\right),\hspace{1em}0\le n\le \overline{n},\hspace{1em}0\le k\le \overline{k},$$

(24)

where ${\mathcal{S}}_l=\underset{s\le t_n}{sup}{\left|f^l\left(c\right)\right|}_{2q-2l}.$

Proof .

By letting

$${\mathcal{R}}_{k}f\left(t\right)=\sum _{i=0}^s{P}_i\left(kA\right)f(t_n+k{\tau }_i),$$

we can write method (15) as

$$v_n=r^n\left(kA\right)v+k\sum _{j=0}^{n-1}{r}^{n-1-j}\left(kA\right){\mathcal{R}}_{k}f\left(t_j\right), \mathrm{for} \mathit{n}=1,2,\cdots$$

(25)

By denoting $E\left(t\right)=e^{-tA}$, we write the exact solution, (14), of Equation (11) as:

$$u\left(t_n\right)=E\left(t_n\right)v+k\sum _{j=0}^{n-1}E\left(t_{n-1-j}\right){\mathcal{I}}_{k}f\left(t_j\right),$$

(26)

where

$${\mathcal{I}}_{k}f\left(t_j\right)={\int }_0^{1}E(k-sk)f(t_j+sk)ds.$$

For $n\ge 0$, the error ${\mathcal{E}}^n=v_n-u\left(t_n\right)$ can be written as:

$$\begin{array}{ccc}\hfill {\mathcal{E}}^n& =& r^n\left(kA\right)v-E\left(t_n\right)v+k\sum _{j=0}^{n-1}\left(r_m^{n-1-j}\left(kA\right){\mathcal{R}}_{k}f\left(t_j\right)-E\left(t_{n-1-j}\right){\mathcal{I}}_{k}f\left(t_j\right)\right)\hfill \\ & =& {\mathcal{E}}_0^n+{\mathcal{E}}_m^n,\hfill \end{array}$$

(27)

where the error ${\mathcal{E}}_0^n$ corresponds to the homogeneous equation and ${\mathcal{E}}_m^n$ is the error due to the inhomogeneous part of the method. The error ${\mathcal{E}}_0^n$ is approximated by the established result in [15] (Theorem 7.2) as:

$$\parallel {\mathcal{E}}_0^n\parallel =\parallel \left(r_m^{n-2}\left(kA\right)r_s^2\left(kA\right)-E\left(t_n\right)\right)\parallel \le C{k}^q{t}_n^{-q}\parallel v\parallel .$$

(28)

By adding and subtracting $r_m^{n-1-j}\left(kA\right){\mathcal{I}}_{k}f\left(t_j\right)$ in the error term ${\mathcal{E}}_m^n$ and rearranging the terms, we get

$$\begin{array}{ccc}\hfill {\mathcal{E}}_m^n& =& k\sum _{j=0}^{n-1}\left(r_m^{n-1-j}\left(kA\right)-E\left(t_{n-1-j}\right)\right){\mathcal{I}}_{k}f\left(t_j\right)+k\sum _{j=0}^{n-1}{r}_m^{n-1-j}\left(kA\right)({\mathcal{R}}_k-{\mathcal{I}}_k)f\left(t_j\right)\hfill \\ & =& {\mathcal{E}}_{m1}^n+{\mathcal{E}}_{m2}^n.\hfill \end{array}$$

(29)

Using the change of variable $t_j+sk=t$, we can write

$$\begin{array}{c}\hfill \underset{0}{\overset{1}{\int }}f(t_j+sk)ds=\frac{1}{k}\underset{t_j}{\overset{t_{j+1}}{\int }}f\left(t\right)dt\end{array}$$

and

$$\begin{array}{c}\hfill \sum _{j=0}^{n-1}\underset{0}{\overset{1}{\int }}f(t_j+sk)ds=\frac{1}{k}\underset{0}{\overset{t_n}{\int }}f\left(t\right)dt\end{array}$$

Additionally, using the facts:

$$\begin{array}{c}\hfill \underset{0\le s\le 1}{max}E(k-sk)=\underset{0<s\le 1}{max}{e}^{-(1-s)k}=I,\hspace{1em}\mathrm{at}\mathrm{s}=1,\end{array}$$

(30)

$E(s-sk)$ commutes with $r^n\left(kA\right)-E\left(t_n\right)$ and $r\left(kA\right)$ is a q-th order approximation of $E\left(t\right)=e^{-kA}$. We get the following estimate:

$$\begin{array}{ccc}\hfill \parallel {\mathcal{E}}_{m1}^n\parallel & \le & k\sum _{j=0}^{n-1}\parallel \left(r_m^{n-1-j}\left(kA\right)-E\left(t_{n-1-j}\right)\right){\mathcal{I}}_{k}f\left(t_j\right)\parallel \hfill \\ & \le & k\sum _{j=0}^{n-1}\underset{0}{\overset{1}{\int }}\parallel E(k-sk)\left(r_m^{n-1-j}\left(kA\right)-E\left(t_{n-1-j}\right)\right)f(t_j+sk)\parallel ds\hfill \\ & \le & k^{q+1}\sum _{j=0}^{n-1}\underset{0}{\overset{1}{\int }}|f(t_j+sk){|}_{2q}ds=C{k}^q\underset{0}{\overset{t_n}{\int }}{|f\left(t\right)|}_{2q}dt,\hfill \end{array}$$

(31)

which is bounded by the right-hand side of (24). Using Taylor-series expansions of $f(t_j+sk)$ and $f(t_j+sk)$ and the approach given in [15] (Theorem 8.1), an estimate for ${\mathcal{E}}_{m2}^n$ can be obtained as follows:

$$\begin{array}{ccc}\hfill \parallel {\mathcal{E}}_{m2}^n\parallel & \le & \sum _{j=2}^{n-1}C{k}^{q+1}\sum _{l=0}^{q-1}{|f^{\left(l\right)}\left(t_j\right)|}_{2q-2l}+C{k}^q\sum _{j=2}^{n-1}{\int }_{t_j}^{t_{j+1}}\parallel f^{\left(q\right)}\parallel ds.\hfill \end{array}$$

(32)

Since the right-hand side of (31) is bounded by the right-hand side of (32),

$$\begin{array}{ccc}\hfill \parallel {\mathcal{E}}_m^n\parallel & \le & \sum _{j=0}^{n-1}C{k}^{q+1}\sum _{l=0}^{q-1}{\left|f^{\left(l\right)}\left(t_j\right)\right|}_{2q-2l}+C{k}^q\sum _{j=0}^{n-1}{\int }_{t_j}^{t_{j+1}}\parallel f^{\left(q\right)}\parallel ds\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& \le & C{k}^q{t}_n\sum _{l=0}^{q-1}{\mathcal{S}}_l+C{k}^q{\int }_0^{t_n}\parallel f^{\left(q\right)}\parallel ds\hfill \end{array}$$

(34)

where ${\mathcal{S}}_l=\underset{s\le t_n}{sup}{\left|f^{\left(l\right)}\left(s\right)\right|}_{2q-2l}$, and (28) together with (33), completes the proof. □

5. Numerical Experiments

In this section, we present the solutions of two test problems and discuss the results obtained. The errors between the consecutive solutions were calculated by decreasing the time step size by half. The following formula was used to calculate the rate of convergence:

$$r=ln\frac{Error\left(2k\right)}{Error\left(k\right)},$$

where $Error\left(k\right)$ denotes the error between the consecutive solutions corresponding to the numbers of time steps k and $2k$, respectively. The $error\left(k\right)$ are computed by using the $inf$ norm. The rate of convergence of the method is computed using this approach when an analytical solution of the problem is not available.

5.1. Example 1

First we consider the following problem with $f(x,t)=0$; see [10]:

$$\frac{\partial u}{\partial t}=\underset{1}{\overset{2}{\int }}{K}_{x}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{{\partial \left|x\right|}^{\alpha }}d\alpha ,\hspace{1em}(x,t)\in (0,1)\times [0,T],$$

(35)

with homogeneous Dirichlet boundary condition

$$u(0,t)=0, u(1,t)=0, >0$$

(36)

and initial condition

$$u(x,0)=\delta (\alpha -0.5),\hspace{1em}x\in (0,1),$$

(37)

where $P\left(\alpha \right)=l^{\alpha -2}K[A_1\delta (\alpha -{\delta }_1)+A_2\delta (\alpha -{\delta }_2)]$ with dimensionless constants l and K. Additionally, $0<{\delta }_1<{\delta }_2\le 2$, $A_1>0, A_2>0$.

Figure 1 displays the numerical solution $u(x,t)$ at different times, which decays with time. Figure 2 illustrates the impacts of ${\delta }_1$ and ${\delta }_2$ on the diffusion behavior of $u(x,t)$. As the values of ${\delta }_1$ and ${\delta }_2$ increase, the amplitude decreases and more diffusive behavior appears in the profiles. Figure 3 shows how different values of l affect the numerical solution $u(x,t)$. It is evident that the amplitude of the solution increases as the value of l increases. Figure 4 shows the time evolution graphs of $u(x,t)$ at $t=0.1$ and at $t=1$, respectively. Table 1 shows the error and convergence rate of the time-stepping method. A column of CPU time is also included in this table to show the computational efficiency of the method.

Figure 1. Example 1: Numerical solutions at different values of t using $h=k=1/200$, $l=2$, $K=1$, $A_1=A_2=1$, ${\delta }_1=1.255$, and ${\delta }_2=1.75$.

Figure 2. Example 1: Numerical solutions using for different values of ${\delta }_1$ and ${\delta }_2$ using $h=k=1/200$, $l=2$, $K=1$, and $A_1=A_2=1$.

Figure 3. Example 1: Numerical solutions at $t=1$ using ${\delta }_1=1.255$ and ${\delta }_2=1.755$ with $h=k=1/200$, $K=1$, and $A_1=A_2=1$ for different values of l.

Figure 4. Time evolution graph of Example 1 at $t=0.1$ LEFT and $t=1$ RIGHT, using ${\delta }_1=1.255$ and ${\delta }_2=1.755$ with $h=k=1/200$, $l=2$, $K=1$, and $A_1=A_2=1$.

Table 1. Example 1: Convergence results for the time-stepping method.

$\Delta \mathit{t}$	Error	Order	CPU Time
0.04000			0.0218
0.02000	2.6347 × 10${}^{-9}$		0.0132
0.01000	1.6361 × 10${}^{-10}$	4.009	0.0177
0.00500	1.0219 × 10${}^{-11}$	4.001	0.0337
0.00250	6.4051 × 10${}^{-13}$	3.996	0.1029
0.00125	3.8032 × 10${}^{-14}$	4.074	0.1542

5.2. Example 2

Here we consider the two-dimensional problem on the rectangular domain $\mathsf{\Omega }=(0,1)\times (0,1)$ [1]:

$$\frac{\partial u}{\partial t}=\underset{1}{\overset{2}{\int }}{K}_{x}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{{\partial \left|x\right|}^{\alpha }}d\alpha +\underset{1}{\overset{2}{\int }}{K}_{y}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{{\partial \left|y\right|}^{\beta }}d\beta +f(x,y,t),\hspace{1em}(x,y,t)\in \mathsf{\Omega }\times [0,T],$$

(38)

with the homogeneous Dirichlet boundary condition

$$u(x,y,t)=0,\hspace{1em}(x,y)\in \partial \mathsf{\Omega },$$

(39)

and the initial condition

$$u(x,y,0)=u_0(x,y)=x^2{(1-x)}^2{y}^2{(1-y)}^2,\hspace{1em}(x,y)\in \mathsf{\Omega },$$

(40)

where $P\left(\alpha \right)=Q\left(\alpha \right)=-2\mathsf{\Gamma }(5-\alpha )cos\left(\frac{\alpha \pi }{2}\right)$ are non-negative functions and the inhomogeneous term is

$$\begin{array}{ccc}\hfill f(x,y,t)& =& e^t{x}^2{(1-x)}^2{y}^2{(1-y)}^2\hfill \\ & -& e^t{x}^2{(1-x)}^2[R\left(x\right)+R(1-x)]\hfill \\ & -& e^t{y}^2{(1-y)}^2[R\left(y\right)+R(1-y)]\hfill \end{array}$$

with

$$\begin{array}{ccc}\hfill R\left(r\right)& =& \mathsf{\Gamma }\left(5\right)R_1\left(r\right)-2\mathsf{\Gamma }\left(4\right)R_2\left(r\right)+\mathsf{\Gamma }\left(3\right)R_3\left(r\right),\hfill \\ \hfill R_1\left(r\right)& =& \frac{1}{lnr}(r^3-r^2),\hfill \\ \hfill R_2\left(r\right)& =& \frac{1}{lnr}(3r^2-2r)+\frac{1}{{(lnr)}^2}(r-r^2),\hfill \\ \hfill R_3\left(r\right)& =& \frac{1}{lnr}(6r-2)+\frac{1}{{(lnr)}^2}(3-5r)+\frac{2}{{(lnr)}^3}(r-1).\hfill \end{array}$$

The exact solution of this problem is given as: $u(x,y,t)=e^t{x}^2{(1-x)}^2{y}^2{(1-y)}^2$.

Figure 5 shows the graph’s exact and numerical solution of the problem (38). Convergence results along with CPU times are given in Table 2.

Figure 5. Exact and numerical solutions of Example 2 with $\Delta x=0.04$ and $\Delta y=0.02$.

Table 2. Example 2: Convergence results for the time-stepping method.

$\Delta \mathit{t}$	Error	Order	CPU Time
0.02500	6.1233 × 10${}^{-4}$		0.1087
0.01250	4.1451 × 10${}^{-5}$	3.736	0.1243
0.00625	2.9543 × 10${}^{-6}$	3.811	0.2656
0.00313	2.0695 × 10${}^{-7}$	3.836	0.4343
0.00156	1.2276 × 10${}^{-8}$	4.075	1.2353
0.00078	7.2832 × 10${}^{-10}$	4.075	2.1253

6. Conclusions

By synthesizing diverse ideas, we developed an implementation strategy to numerically solve the Riesz distributed-order, space-fractional, inhomogeneous diffusion equations. A fourth-order A-stable method was developed using a diagonal (2,2)-Padé approximation of a matrix exponential function. Use of the partial fraction splitting makes the method more efficient, stable, and accurate. It can also be noted that we can implement this fourth-order method with the same computational complexity as a first-order method.