Exponential Enclosures for the Verified Simulation of Fractional-Order Differential Equations

Abstract

Fractional-order differential equations are powerful tools for the representation of dynamic systems that exhibit long-term memory effects. The verified simulation of such system models with the help of interval tools allows for the computation of guaranteed enclosures of the domains of reachable pseudo states over a certain finite time horizon. In the previous work of the author, an iteration scheme—derived on the basis of the Picard iteration—was published that makes use of Mittag-Leffler functions to determine guaranteed pseudo-state enclosures. In this paper, the corresponding iteration is generalized toward the use of exponential functions during the evaluation of the iteration scheme. Such exponential functions are well-known from a verified solution of integer-order sets of differential equations. The aim of this work is to demonstrate that the use of exponential functions instead of pure box-type interval enclosures for Mittag-Leffler functions does not only improve the tightness of the computed pseudo-state enclosures but also reduces the required computational effort. These statements are demonstrated with the help of a close-to-life simulation model for the charging/discharging dynamics of Lithium-ion batteries.

1. Introduction

Fractional differential equations have the property of an infinite-horizon memory of the previous evolution of the system dynamics [1,2,3,4]. As opposed to integer-order models, where only initial conditions for the state variables at a certain point of time and the external system inputs after that time instant are necessary for determining a unique solution for the evaluation of the system states, fractional-order models need to be initialized with the complete past behavior as the initialization function [5].

Due to this reason, the system state at a specific point in time is typically referred to as a pseudo state for fractional system models as the complete history of its evolution is required for a unique solution [5]. To solve this difficulty when initializing a simulation at a specific point in time, additive (interval-valued) correction terms of the right-hand sides of explicit fractional-order models have been employed in [6] to account for the past pseudo-state evolution. Simulation methods, which make use of further extensions on the basis of a (pseudo) state observer concept for tightening these additive corrections after the reset of fractional integrators, were developed in [7]. These extensions exploit a formula derived by Podlubny in [1] for shifting the reference point in time, associated with the definition of a fractional differentiation operator.

On the one hand, the infinite-horizon memory property of fractional differential equations allows to efficiently model dynamic systems with long-term memory effects. On the other hand, however, interval-based simulations, allowing for enclosing the domains of reachable (pseudo) states in a guaranteed way, are significantly complicated because classical Taylor series-based simulation approaches, such as those employed in tools such as AWA [8], VNODE-LP [9,10,11], or VSPODE [12], for systems of integer-order ordinary differential equations, can no longer be employed without modifications.

Therefore, the author has developed an iterative pseudo-state enclosure approach in [6,13] which is based on the Picard iteration [14]. Under the assumption that the pseudo state at the point of time $t=0$ corresponds also to the complete previous, temporally constant state evolution for $t<0$, corresponding to Caputo’s definition of fractional derivatives, the iterative solution makes use of Mittag-Leffler functions [15,16,17,18,19] to represent pseudo-state enclosures in a guaranteed manner. This kind of function represents the true pseudo-state trajectories of linear fractional differential equations with the aforementioned Caputo-type initialization [20,21]. For nonlinear models, the iteration procedure developed in [6,13] yields outer bounds for the actually reachable pseudo states.

It has to be noted that this iteration scheme is a natural generalization of a counterpart making use of classical exponential functions in the integer-order case, cf. [6]. However, the drawback is an increased complexity of the numerical evaluation because the typically arising quotients of Mittag-Leffler functions with different arguments cannot be simplified further in an analytic manner to reduce the overestimation that is well-known in the domain of interval methods [22,23]. This issue is further discussed in the current paper and resolved by outer exponential enclosures of Mittag-Leffler functions.

In this paper, Section 2 summarizes the Mittag-Leffler function representation of guaranteed solution enclosures for fractional-order system models as presented in [6,13]. It is extended in Section 3 toward exponential functions for the computation of guaranteed pseudo-state enclosures. The representative simulation results, focusing on the tightness of the resulting pseudo-state enclosures and the required computational effort, are presented in Section 4 for a close-to-life quasi-linear fractional model of the charging/discharging behavior of Lithium-ion batteries before conclusions and an outlook on future work are given in Section 5.

2. Fundamentals of Verified Mittag-Leffler-Type Pseudo-State Enclosures for Fractional Differential Equations

2.1. System Models under Consideration

Throughout this article, we analyze and derive set-valued simulation approaches for commensurate fractional-order differential equations of the form

$${\mathbf{x}}^{\left(\nu \right)}\left(t\right)=\mathbf{f}\left(\mathbf{x}\left(t\right)\right),\mathbf{f}:{\mathbb{R}}^n\mapsto {\mathbb{R}}^n,$$

(1)

with the order $0<\nu \le 1$, where the right-hand side $\mathbf{f}\left(\mathbf{x}\left(t\right)\right)$ is assumed to be given by a continuous function. Moreover, we assume that the system model (1) is initialized by the pseudo state $\mathbf{x}\left(0\right)$ at the time instant $t=0$, where $\mathbf{x}\left(t\right)=\mathbf{x}\left(0\right)$ holds for all $t<0$. This case corresponds to the Caputo definition of fractional derivatives as described, for example, in [1,2].

To account for uncertainty in the pseudo-state initialization, we use the interval representation

$$\mathbf{x}\left(0\right)\in \left[\mathbf{x}\right]\left(0\right):=\left[\underset{¯}{\mathbf{x}}\left(0\right);\overline{\mathbf{x}}\left(0\right)\right],$$

(2)

for which ${\underset{¯}{x}}_i\left(0\right)\le {\overline{x}}_i\left(0\right)$ holds for each vector component $i\in \{1,\dots ,n\}$. Note that the property of temporally constant initializations for $t<0$ is still assumed to hold.

2.2. Linear Scalar System Models

For the special case of scalar fractional differential equations

$$x^{\left(\nu \right)}\left(t\right)=\lambda ·x\left(t\right)\mathrm{with}x\left(0\right)=x_0$$

(3)

which are linear in the pseudo state $x\left(t\right)$ with the parameter $\lambda \in \mathbb{R}$ and which are initialized according to the previous subsection in the Caputo-type sense, it is well-known according to [20,21] that the exact solution is given in the form

$$x\left(t\right)=E_{\nu ,1}\left(\lambda t^{\nu }\right)·x\left(0\right).$$

(4)

In (4), $E_{\nu ,\beta }\left(\zeta \right)$ is the two-parameter Mittag-Leffler function. It is defined by the infinite series

$$E_{\nu ,\beta }\left(\zeta \right)=\sum _{i=0}^{\infty }\frac{{\zeta }^i}{\mathsf{\Gamma }\left(\nu i+\beta \right)}$$

(5)

for the general argument $\zeta \in \mathbb{C}$. In (4), $\mathsf{\Gamma }\left(\nu i+\beta \right)$ denotes the gamma function of the respective argument and $\nu$ is the derivative order as introduced in (1). To obtain the solution in (4), the parameter $\beta$ is set to the value $\beta =1$.

Remark 1.

The classical exponential function $e^{\zeta }$ is obtained as a special case of the Mittag-Leffler function (5) when setting $\nu =1$ and $\beta =1$.

Remark 2.

For an interval extension of the Mittag-Leffler function on the basis of the accurate floating-point Matlab implementation by R. Garrappa [18,24], see [13].

2.3. Mittag-Leffler Functions as Pseudo-State Enclosures for Fractional-Order Differential Equations

For nonlinear scalar and vector-valued system models (1), the Mittag-Leffler functions introduced in the previous subsection can be used to define guaranteed pseudo-state enclosures according to Definition 1.

Definition 1

(Mittag-Leffler-type pseudo-state enclosure). A verified Mittag-Leffler-type pseudo-state enclosure for the system model (1) with (2) is defined by the time-dependent enclosure function

$${\mathbf{x}}^{*}\left(t\right)\in \left[{\mathbf{x}}_e\right]\left(t\right)={\mathbf{E}}_{\nu ,1}\left(\left[\mathsf{\Lambda }\right]·t^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right),\left[{\mathbf{x}}_e\right]\left(0\right)=\left[{\mathbf{x}}_0\right]$$

(6)

with the diagonal parameter matrix $\left[\mathsf{\Lambda }\right]:=\mathrm{diag}\left\{\left[{\lambda }_i\right]\right\}$, $i\in \{1,\dots ,n\}$, if it is determined according to Theorem 1. In (6), the generalization of the scalar Mittag-Leffler function $E_{\nu ,1}$ to the matrix case ${\mathbf{E}}_{\nu ,1}$ is given by the following diagonal matrix

$${\mathbf{E}}_{\nu ,1}\left(\left[\mathsf{\Lambda }\right]·t^{\nu }\right)=\mathrm{diag}\left\{\right[\begin{array}{ccc}{E}_{\nu ,1}\left(\left[{\lambda }_1\right]·t^{\nu }\right)& \dots & E_{\nu ,1}\left(\left[{\lambda }_n\right]·t^{\nu }\right)\end{array}\left]\right\}.$$

(7)

Theorem 1

([6,13,25] Iteration for Mittag-Leffler-type enclosures). All reachable pseudo states ${\mathbf{x}}^{*}\left(T\right)$ are enclosed in accordance with Theorem 1 by the Mittag-Leffler-type pseudo-state enclosure

$${\mathbf{x}}^{*}\left(T\right)\in \left[{\mathbf{x}}_e\right]\left(T\right)={\mathbf{E}}_{\nu ,1}\left(\left[\mathsf{\Lambda }\right]·T^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right)$$

(8)

at the point of time $t=T>0$ if $\left[\mathsf{\Lambda }\right]$ is set to the outcome of the converging iteration

$${\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }:=\frac{f_i\left({\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa \rangle }·{\left[t\right]}^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right)\right)}{E_{\nu ,1}\left({\left[{\lambda }_i\right]}^{\langle \kappa \rangle }·{\left[t\right]}^{\nu }\right)·\left[x_{e,i}\right]\left(0\right)},$$

(9)

$i\in \{1,\dots ,n\}$, with the prediction horizon $\left[t\right]=\left[0;T\right]$. To ensure convergence, the value $x_i^{*}=0$ must not belong to the solution for any vector component $i\in \{1,\dots ,n\}$.

Remark 3.

Typically, the iteration according to Theorem 1 is initialized with intervals centered around the eigenvalues of the Jacobian of the right-hand side of (1), evaluated for the midpoint of the interval vector (2).

As a preparation for the derivation of the exponential enclosure approach presented for the first time in this paper, the following proof of Theorem 1, according to [6,13,25], is summarized.

Proof. 

Formulate a Picard iteration (iteration index $\kappa$) for computing pseudo-state enclosures in the differential form

$${\left[{\mathbf{x}}^{\left(\nu \right)}\right]}^{\langle \kappa \rangle }\left(\left[0;T\right]\right)\supset {\left[{\mathbf{x}}^{\left(\nu \right)}\right]}^{\langle \kappa +1\rangle }\left(\left[0;T\right]\right)=\mathbf{f}\left({\left[{\mathbf{x}}^{\left(\nu \right)}\right]}^{\langle \kappa \rangle }\left(\left[0;T\right]\right)\right),$$

(10)

where ${\left[{\mathbf{x}}^{\left(\nu \right)}\right]}^{\langle \kappa \rangle }\left(\left[0;T\right]\right)$ is an interval extension of the temporal derivative of order $\nu$ of the inclusion function ${\left[\mathbf{x}\right]}^{\langle \kappa \rangle }\left(t\right)$ over the time interval $t\in \left[t\right]=\left[0;T\right]$. Substituting the pseudo-state enclosure given in Definition 1 into (10) yields the expression

$$\begin{array}{cc}\hfill {\mathbf{x}}^{\left(\nu \right)}\left(t\right)& \in \left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa +1\rangle }\right)·{\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa +1\rangle }·t^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right)\hfill \\ \hfill & =\mathbf{f}\left({\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa \rangle }·t^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right)\right)\mathrm{for}\mathrm{all}t\in \left[t\right].\hfill \end{array}$$

(11)

A converging iteration implies the set-valued relation

$${\left[{\mathbf{x}}_e\right]}^{\langle \kappa +1\rangle }\left(\left[t\right]\right)\subset {\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right),$$

(12)

which corresponds to the relation

$${\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }\subset {\left[{\lambda }_i\right]}^{\langle \kappa \rangle }$$

(13)

for the unknown intervals of the solution parameters ${\lambda }_i$.

Overapproximating the interval evaluation of the Mittag-Leffler-type enclosure

$${\left[\mathbf{x}\right]}^{\langle \kappa +1\rangle }\left(t\right)={\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa +1\rangle }·t^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right)$$

(14)

in the iteration step $\kappa +1$ on the first line of (11) by the enclosure ${\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right)$ in the case of convergence, i.e., using the relation

$$\begin{array}{c}\hfill \left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa +1\rangle }\right)·{\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa +1\rangle }·t^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right)\subset \left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa +1\rangle }\right)·{\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa \rangle }·t^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right),\end{array}$$

(15)

leads to the new iteration formula

$$\begin{array}{cc}\hfill & \mathrm{diag}\left\{{\left[{\tilde{\lambda }}_i\right]}^{\langle \kappa +1\rangle }\right\}·{\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right)=\mathbf{f}\left({\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right)\right),\hfill \end{array}$$

(16)

where

$$\mathrm{diag}\left\{{\left[{\tilde{\lambda }}_i\right]}^{\langle \kappa +1\rangle }\right\}\supseteq \mathrm{diag}\left\{{\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }\right\}.$$

(17)

Solving expression (16) for ${\left[{\tilde{\lambda }}_i\right]}^{\langle \kappa +1\rangle }$ with subsequent renaming of this parameter into ${\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }$ completes the proof of Theorem 1. For further details, the reader is referred to the references [6,13,25]. □

Corollary 1.

In the case that the fractional-order differential equations given in Equation (1) with the initial conditions (2) can be rewritten into the quasi-linear form

$${\mathbf{x}}^{\left(\nu \right)}\left(t\right)=\mathcal{A}\left(\mathbf{x}\left(t\right)\right)·\mathbf{x}\left(t\right)\mathrm{with}0<\nu \le 1,$$

(18)

with an equilibrium at $\mathbf{x}=\mathbf{0}$ and the state-dependent matrix $\mathcal{A}\left(\mathbf{x}\left(t\right)\right)$, Theorem 1 simplifies to the iteration scheme

$$\begin{array}{cc}\hfill {\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }:=& a_{ii}\left({\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right)\right)+\sum _{\genfrac{}{}{0pt}{}{j=1}{j\ne i}}^n\left\{a_{ij}\left({\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right)\right)·\frac{E_{\nu ,1}\left({\left[{\lambda }_j\right]}^{\langle \kappa \rangle }·{\left[t\right]}^{\nu }\right)}{E_{\nu ,1}\left({\left[{\lambda }_i\right]}^{\langle \kappa \rangle }·{\left[t\right]}^{\nu }\right)}·\frac{\left[x_{e,j}\right]\left(0\right)}{\left[x_{e,i}\right]\left(0\right)}\right\}.\hfill \end{array}$$

(19)

Remark 4.

In (19), the quotient of two Mittag-Leffler functions can usually only be simplified further for $\nu =1$. In all other cases, where $\nu \ne 1$, overestimation due to the so-called dependency effect [23] (which arises due to multiple dependencies on common interval parameters) can be reduced by exploiting the monotonicity properties of the Mittag-Leffler function that were analyzed in detail in [13].

3. Exponential Enclosures for Fractional-Order System Models

Exponential functions can be introduced in general at two different stages of the solution procedure presented in the previous section. These are:

• The replacement of the solution representation $\left[{\mathbf{x}}_e\right]\left(t\right)$ given so far by Mittag-Leffler functions by exponential functions; or
• The introduction of exponential enclosures for the interval evaluation of the Mittag-Leffler function instead of the currently employed box-type representations.

These two alternative options are further discussed in the current section.

3.1. Exponential Pseudo-State Enclosures

To directly replace the Mittag-Leffler functions by exponential ones in the enclosure technique according to Theorem 1 and Corollary 1, it is necessary to determine the Caputo fractional derivative of order $\nu$ (initialized at $t=0$) of a classical exponential function.

According to [26,27], the derivative of $e^{\lambda t}$ is given by the closed-form representation

$$\frac{{\mathrm{d}}^{\nu }{e}^{\lambda t}}{\mathrm{d}{t}^{\nu }}=\lambda ·\left(t^{1-\nu }·E_{1,2-\nu }\left(\lambda t\right)\right)$$

(20)

with $t\ge 0$ and $\lambda \in \mathbb{R}$. In (20), the right-hand side again depends on the two-parameter Mittag-Leffler function (5). Note that this two-parameter Mittag-Leffler function, if substituted into the first line of Equation (11), leads to the same difficulty already observed in Equation (19) of Corollary 1 that the arising quotients of functions cannot be simplified, even in the case of (quasi-)linear system models in which $a_{ij}\left({\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left(\left[t\right]\right)\right)\ne 0$ holds for at least one $i\ne j$.

Moreover, it has to be pointed out that an interval evaluation of this fractional derivative of the exponential function on the time interval $t\in \left[0;T\right]$ always contains the value 0 at the left end point of this time interval, so that the division of the differential formulation of the Picard iteration according to (11) by the term in parentheses in (20) is undefined. Therefore, solution representations in the form $e^{\lambda t}$ are not useful to generalize the iteration scheme according to Theorem 1.

At least theoretically, one could try to resolve this second problem by changing the solution template from $e^{\lambda t}$ to $e^{\lambda t^{\nu }}$ with a non-integer power of the time variable t. Unfortunately, however, its Caputo derivative of order $\nu$ does not have a closed-form, exponential-type solution in the general case so the problem persists that the solution presented in (19) can still not be simplified further. For this reason, we are switching to the idea of the following subsection in which the interval box enclosures of Mittag-Leffler functions employed in (9) as well as in (19) are replaced by tubes parameterized in terms of exponential functions.

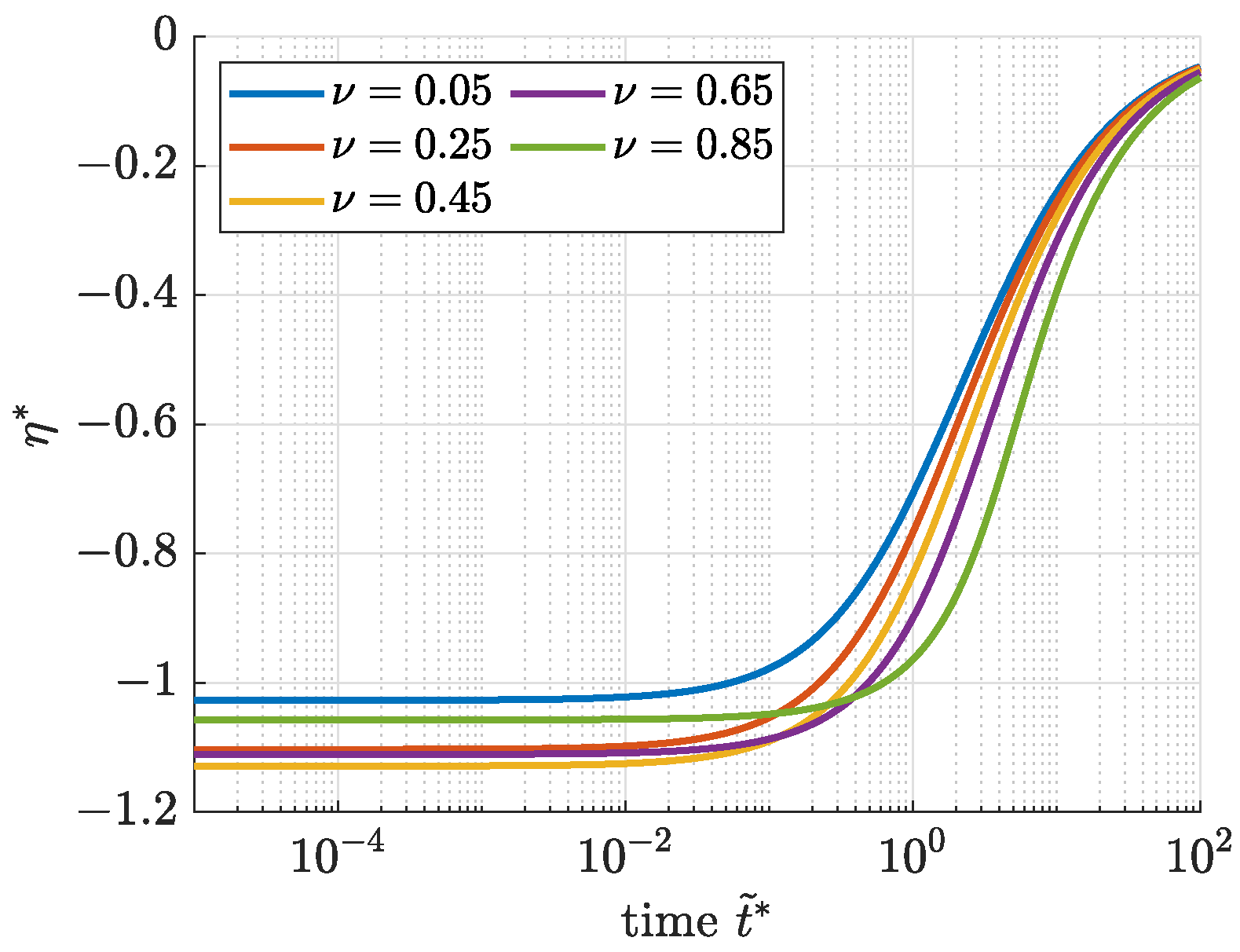
3.2. Exponential Enclosures of the Mittag-Leffler Function

For the computation of exponential tube enclosures of time-dependent Mittag-Leffler functions, the following monotonicity theorem is employed. It is a simplified version of Theorem 4 published in [13], where also the fractional derivative order $\nu$ was considered as a (temporally constant) interval parameter.

Theorem 2

(Box-type interval bounds for the Mittag-Leffler function). The range of function values for the Mittag-Leffler function in (4) with the uncertain real-valued parameter $\lambda \in \left[\underset{¯}{\lambda };\overline{\lambda }\right]$, $\overline{\lambda }<0$ and the non-negative time argument $t\in \left[\underset{¯}{t};\overline{t}\right]$, $\underset{¯}{t}\ge 0$, with $0<\nu \le 1$, is bounded by the box-type interval enclosure

$$E_{\nu ,1}\left(\lambda t^{\nu }\right)\in \left[E_{\nu ,1}^{*}\right]\left(\left[\mathcal{X}\right]\right)=\left[E_{\nu ,1}^{*}\left(inf\left(\left[\mathcal{X}\right]\right)\right);E_{\nu ,1}^{*}\left(sup\left(\left[\mathcal{X}\right]\right)\right)\right]$$

(21)

with $\left[\mathcal{X}\right]:=\left[\lambda \right]·{\left[t\right]}^{\left[\nu \right]}$, where $sup\left(\left[\mathcal{X}\right]\right)\le 0$ holds and $\left[E_{\nu ,1}^{*}\right]$ is obtained by the outward rounded interval extension of a floating-point evaluation of the two-parameter Mittag-Leffler function according to Equation (31) of [13]. Due to $\overline{\lambda }<0$, Equation (21) simplifies to

$$E_{\nu ,1}\left(\lambda t^{\nu }\right)\in \left[E_{\nu ,1}^{*}\left(\underset{¯}{\lambda }·{\overline{t}}^{\nu }\right);E_{\nu ,1}^{*}\left(\overline{\lambda }·{\underset{¯}{t}}^{\nu }\right)\right].$$

(22)

Proof. 

For a detailed proof of this theorem, the reader is referred to the proof of Theorem 4 published in [13]. It is a direct consequence of the fact that the two-parameter Mittag-Leffler function is strictly monotonically decreasing for a growing time argument t with $\lambda <0$. This property is also reflected by the so-called complete monotonicity of the Mittag-Leffler function that is reported, for example, in [16,17].

Furthermore, monotonicity with respect to the parameter $\lambda$ is verified by differentiating $E_{\nu ,1}\left(\lambda t^{\nu }\right)$ with respect to $\lambda$ together with the change of variables $\tau :={\lambda }^{\frac{1}{\nu }}·t<0$. This leads to

$$\frac{\partial E_{\nu ,1}\left(\lambda t^{\nu }\right)}{\partial \lambda }=\frac{\partial E_{\nu ,1}\left({\tau }^{\nu }\right)}{\partial \tau }·\frac{\partial \tau }{\partial \lambda }=\frac{\partial E_{\nu ,1}\left({\tau }^{\nu }\right)}{\partial \tau }·\frac{t·{\lambda }^{\left(\frac{1}{\nu }-1\right)}}{\nu }.$$

(23)

In (23), the first factor is non-positive due to the complete monotonicity of the Mittag-Leffer function as shown in [16,17]; for any $t\ge 0$ and $\lambda \le 0$, the second factor is also non-positive, leading to $\frac{\partial E_{\nu ,1}\left(\lambda t^{\nu }\right)}{\partial \lambda }\ge 0$, which completes the proof. □

Theorem 3

(Exponential enclosures for the Mittag-Leffler function). The range of function values for the Mittag-Leffler function in (4) with the uncertain real-valued parameter $\lambda \in \left[\underset{¯}{\lambda };\overline{\lambda }\right]$, $\overline{\lambda }<0$ and the non-negative time argument $t\in \left[\underset{¯}{t};\overline{t}\right]$, $\underset{¯}{t}\ge 0$, $\overline{t}>\underset{¯}{t}$, with $0<\nu \le 1$, is bounded by the exponential enclosure

$$E_{\nu ,1}\left(\lambda t^{\nu }\right)\in e^{\left[\underset{¯}{\eta };\overline{\eta }\right]·\left[\underset{¯}{t};\overline{t}\right]},$$

(24)

where

$$\underset{¯}{\eta }=\left\{\begin{array}{cc}inf\left({\displaystyle \frac{1}{{\underset{¯}{t}}^{\nu }}}·ln\left(\left[E_{\nu ,1}^{*}\right]\left(\underset{¯}{\lambda }·{\underset{¯}{t}}^{\nu }\right)\right)\right)\hfill & for\underset{¯}{t}>0\hfill \\ {\displaystyle \frac{\underset{¯}{\lambda }}{\Gamma (\nu +1)}}\hfill & for\underset{¯}{t}=0\hfill \end{array}\right.$$

(25)

and

$$\overline{\eta }=sup\left(\frac{1}{{\overline{t}}^{\nu }}·ln\left(\left[E_{\nu ,1}^{*}\right]\left(\overline{\lambda }·{\overline{t}}^{\nu }\right)\right)\right)$$

(26)

with $\left[E_{\nu ,1}^{*}\right]$ being the outward rounded interval extension of a floating-point evaluation of the two-parameter Mittag-Leffler function according to Equation (31) of [13].

Proof. 

Consider the Mittag-Leffler function

$$f\left(\tilde{t}\right)=E_{\nu ,1}(-\tilde{t}).$$

(27)

Its derivative with respect to $\tilde{t}$ satisfies the following properties:

• ${\displaystyle \frac{\mathrm{d}f}{\mathrm{d}\tilde{t}}}\left(0\right)=-{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu +1)}}$;
• $\underset{\tilde{t}\to \infty }{lim}{\displaystyle \frac{\mathrm{d}f}{\mathrm{d}\tilde{t}}}\left(\tilde{t}\right)=0$;
• ${\displaystyle \frac{\mathrm{d}f}{\mathrm{d}\tilde{t}}}\left(\tilde{t}\right)<0$ for $\tilde{t}>0$; and
• ${\displaystyle \frac{{\mathrm{d}}^{2}f}{\mathrm{d}{\tilde{t}}^2}}\left(\tilde{t}\right)>0$ for $\tilde{t}>0$.

Property 1 is a consequence of the series definition (5) of the Mittag-Leffler function, while the properties 2–4 result from its complete monotonicity according to [16,17].

Case 1:

For a fixed positive point $\tilde{t}={\tilde{t}}^{*}>0$, determine the intersection of an exponential function $e^{\eta \tilde{t}}$ and the Mittag-Leffler function $f\left(\tilde{t}\right)$ according to

$$E_{\nu ,1}(-{\tilde{t}}^{*})=e^{{\eta }^{*}·{\tilde{t}}^{*}}>0⟺{\eta }^{*}=\frac{1}{{\tilde{t}}^{*}}·ln\left(E_{\nu ,1}(-{\tilde{t}}^{*})\right)<0,$$

(28)

where $E_{\nu ,1}\left(0\right)=e^0=1$ obviously holds according to (5) and $0<E_{\nu ,1}(-{\tilde{t}}^{*})<1$ due to the property of complete monotonicity.

Case 2:

In the case $\tilde{t}\to 0$, $\tilde{t}\in {\mathbb{R}}_0^{+}$, the limit value

$$\begin{array}{cc}\hfill {\eta }^{*}& =\underset{{\tilde{t}}^{*}\to 0}{lim}\left(\frac{1}{{\tilde{t}}^{*}}·ln\left(E_{\nu ,1}(-{\tilde{t}}^{*})\right)\right)\hfill \\ \hfill & =\underset{{\tilde{t}}^{*}\to 0}{lim}\left(\frac{1}{E_{\nu ,1}(-{\tilde{t}}^{*})}·\frac{\mathrm{d}\left(E_{\nu ,1}(-{\tilde{t}}^{*})\right)}{\mathrm{d}{\tilde{t}}^{*}}\right)=-\frac{1}{\mathsf{\Gamma }(\nu +1)}\hfill \end{array}$$

(29)

is obtained, where the second line results from the application of L’Hôpital’s rule.

Moreover, the property $\eta <\overline{\eta }$, necessary for the interval definition in (24), is obvious due to the fact that ${\eta }^{*}$ in (28) is defined as the quotient of a strictly monotonically decreasing numerator and a strictly monotonically increasing denominator.

Thus, the substitution $\tilde{t}:=-\lambda t^{\nu }$ together with the monotonicity of the Mittag-Leffler function with respect to the parameter $\lambda$, as already also exploited in Theorem 2, cf. (23), concludes the proof. □

The Figure 1a,b give a comparison of the box-type interval enclosures of Mittag-Leffler functions according to Theorem 2 with the exponential enclosures according to Theorem 3. According to the Figure 1c,d, it becomes obvious that for identical subdivisions of the time interval $t\in \left[0;1\right]$, the box-type enclosure is much more pessimistic at the beginning of the time horizon than at its end. Therefore, to obtain an identical degree of overestimation for both types of enclosures, a significantly larger number of subintervals would be required in the box-type case at the beginning of the considered time span. Moreover, the lower bound for the range of the Mittag-Leffler function is exactly represented at the beginning of each temporal subslice by the exponential enclosure, while the lower bound at the endpoint is represented exactly by the box-type enclosure, cf. Figure 1c. For the upper bound of the range, this property is reversed between both representations for the enclosure of the Mittag-Leffler function, cf. Figure 1d.

Furthermore, Figure 2 illustrates the property stated in the proof above that ${\eta }^{*}$ is a strictly monotonically increasing function for increasing values of the time argument ${\tilde{t}}^{*}$. To show that this property holds for all $0<\nu <1$, several values of this fractional differentiation order are depicted. Moreover, the limit case for $\tilde{t}\to 0$ according to (29) is also depicted in this graph by using a logarithmic time scale.

3.3. Iterative Pseudo-State Enclosures for Box-Type and Exponential Representations of Mittag-Leffler Functions

Both box-type and exponential enclosures are used in this subsection to evaluate the iteration Formula (19) of Corollary 1. In this subsection, an interval subdivision scheme with respect to the time interval $\left[t\right]$ is employed to reduce the effect of overestimation.

For that purpose, we assume that $\left[t\right]=\left[0;T\right]$ is subdivided into $\Xi$ not necessarily equally wide subintervals

$$\left[t\right]=\bigcup _{\xi =1}^{\Xi }\left[t_{\xi -1};t_{\xi }\right]=\bigcup _{\xi =1}^{\Xi }{\left[t\right]}_{\xi },$$

(30)

where $t_0:=0$, $t_{\Xi }:=T$, and $t_0<t_1<\dots <t_{\Xi }$.

Then, a subinterval-based evaluation of the iteration Formula (19) of Corollary 1 is given by

$$\begin{array}{cc}\hfill {\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }:=& \underset{\xi =1}{\overset{\Xi }{⨆}}\left(a_{ii}\left({\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left({\left[t\right]}_{\xi }\right)\right)+\phantom{\frac{E_{\nu ,1}\left({\left[{\lambda }_j\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)}{E_{\nu ,1}\left({\left[{\lambda }_i\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)}}\right.\hfill \\ \hfill & \left.\sum _{\genfrac{}{}{0pt}{}{j=1}{j\ne i}}^n\left\{a_{ij}\left({\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left({\left[t\right]}_{\xi }\right)\right)·\frac{E_{\nu ,1}\left({\left[{\lambda }_j\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)}{E_{\nu ,1}\left({\left[{\lambda }_i\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)}·\frac{\left[x_{e,j}\right]\left(0\right)}{\left[x_{e,i}\right]\left(0\right)}\right\}\right),\hfill \end{array}$$

(31)

where the symbol ⨆ denotes the convex interval hull around all arguments of this operator.

Moreover, the expression

$${\left[{\mathbf{x}}_e\right]}^{\langle \kappa \rangle }\left({\left[t\right]}_{\xi }\right)={\mathbf{E}}_{\nu ,1}\left({\left[\mathsf{\Lambda }\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)·\left[{\mathbf{x}}_e\right]\left(0\right),\left[{\mathbf{x}}_e\right]\left(0\right)=\left[{\mathbf{x}}_0\right]$$

(32)

in (31) represents the evaluation of the Mittag-Leffler-type pseudo-state enclosure for each temporal subinterval ${\left[t\right]}_{\xi }$.

To replace the evaluation of the iteration Formula (31) by a counterpart that exploits the novel exponential enclosures of the Mittag-Leffler function for each temporal subinterval, define the enclosure

$$E_{\nu ,1}\left(\lambda ·t^{\nu }\right)\in e^{\left[{\underset{¯}{\eta }}_{i,\xi }^{\langle \kappa \rangle };{\overline{\eta }}_{i,\xi }^{\langle \kappa \rangle }\right]·{\left[t_{\xi -1};t_{\xi }\right]}^{\nu }}$$

(33)

for $\lambda \in {\left[\lambda \right]}_i^{\langle \kappa \rangle }$ and $t\in {\left[t\right]}_{\xi }$. The interval bounds ${\underset{¯}{\eta }}_{i,\xi }^{\langle \kappa \rangle }$ and ${\overline{\eta }}_{i,\xi }^{\langle \kappa \rangle }$ on the right-hand side of (33) are obtained by replacing $\underset{¯}{\lambda }$ with ${\underset{¯}{\lambda }}_i^{\langle \kappa \rangle }$, $\overline{\lambda }$ with ${\overline{\lambda }}_i^{\langle \kappa \rangle }$, $\underset{¯}{t}$ with $t_{\xi -1}$, and $\overline{t}$ with $t_{\xi }$ in the Equations (25) and (26) that are defined in Theorem 3.

Then, the iteration Formula (19) of Corollary 1 is replaced with the expression

$$\begin{array}{cc}\hfill {\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }:=& \underset{\xi =1}{\overset{\Xi }{⨆}}\left(a_{ii}\left({\left[{\mathfrak{x}}_e\right]}^{\langle \kappa \rangle }\left({\left[t\right]}_{\xi }\right)\right)+\phantom{\frac{E_{\nu ,1}\left({\left[{\lambda }_j\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)}{E_{\nu ,1}\left({\left[{\lambda }_i\right]}^{\langle \kappa \rangle }·{\left[t\right]}_{\xi }^{\nu }\right)}}\right.\hfill \\ \hfill & \left.\sum _{\genfrac{}{}{0pt}{}{j=1}{j\ne i}}^n\left\{a_{ij}\left({\left[{\mathfrak{x}}_e\right]}^{\langle \kappa \rangle }\left({\left[t\right]}_{\xi }\right)\right)·e^{\left(\left[{\underset{¯}{\eta }}_{j,\xi }^{\langle \kappa \rangle };{\overline{\eta }}_{j,\xi }^{\langle \kappa \rangle }\right]-\left[{\underset{¯}{\eta }}_{i,\xi }^{\langle \kappa \rangle };{\overline{\eta }}_{i,\xi }^{\langle \kappa \rangle }\right]\right)·{\left[t\right]}_{\xi }^{\nu }}·\frac{\left[x_{e,j}\right]\left(0\right)}{\left[x_{e,i}\right]\left(0\right)}\right\}\right),\hfill \end{array}$$

(34)

where

$${\left[{\mathfrak{x}}_e\right]}^{\langle \kappa \rangle }\left({\left[t\right]}_{\xi }\right)=exp\left(\mathrm{diag}\left\{\left[\begin{array}{ccc}\left[{\underset{¯}{\eta }}_{1,\xi }^{\langle \kappa \rangle };{\overline{\eta }}_{1,\xi }^{\langle \kappa \rangle }\right]& \dots & \left[{\underset{¯}{\eta }}_{1,\xi }^{\langle \kappa \rangle };{\overline{\eta }}_{1,\xi }^{\langle \kappa \rangle }\right]\end{array}\right]\right\}·{\left[t\right]}_{\xi }^{\nu }\right)$$

(35)

is a direct substitute for (32) that was included before in (31).

As a preparation for the evaluation of Formulas (31) and (34) in the following section, the true range as well as both the box-type and exponential enclosures of the quotient

$$\frac{E_{\nu ,1}\left({\lambda }_1{t}^{\nu }\right)}{E_{\nu ,1}\left({\lambda }_2{t}^{\nu }\right)}$$

(36)

are illustrated in Figure 3 for the mutually independent interval parameters ${\lambda }_1\in \left[-2;-1\right]$ and ${\lambda }_2\in \left[-1.9;-1\right]$. It becomes obvious that the box-type enclosure (as already discussed in Figure 1) is much more pessimistic for small points in time than for larger ones. Therefore, it can be expected that an intersection of both enclosure approaches leads to less pessimism during the evaluation of the iteration Formula (34). Note that this comes with practically no additional computational effort because the box-type range bounds form the basis for the application of Theorem 3.

In the following section, both subdivision-based Formulas (31) and (34) are compared for the computation of guaranteed pseudo-state enclosures for a quasi-linear model of the charging/discharging dynamics of a Lithium-ion battery. The comparison is based on a quantification of the tightness of the obtained solution enclosures and a count of the numbers of iterations $\kappa$ for identical numbers $\mathsf{\Xi }$ of temporal subintervals.

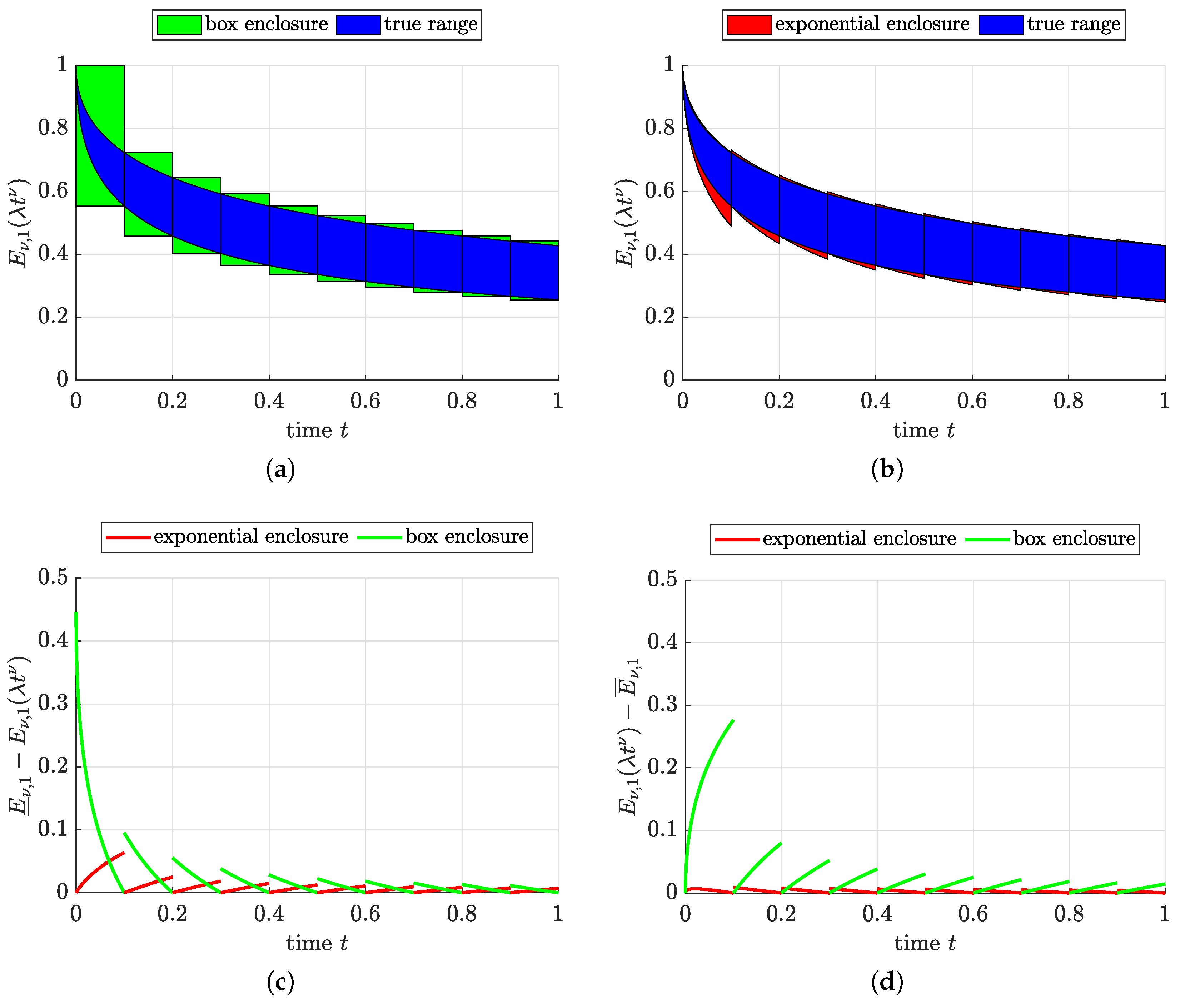
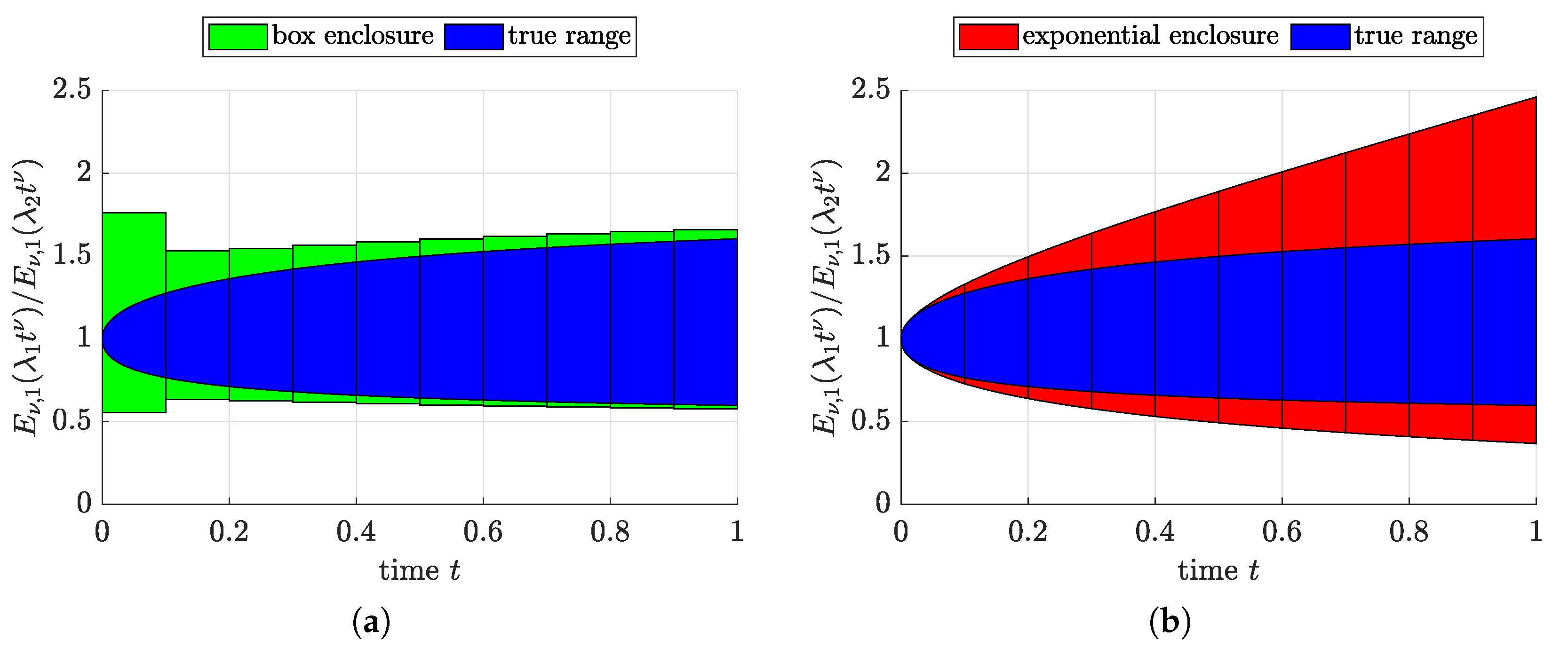
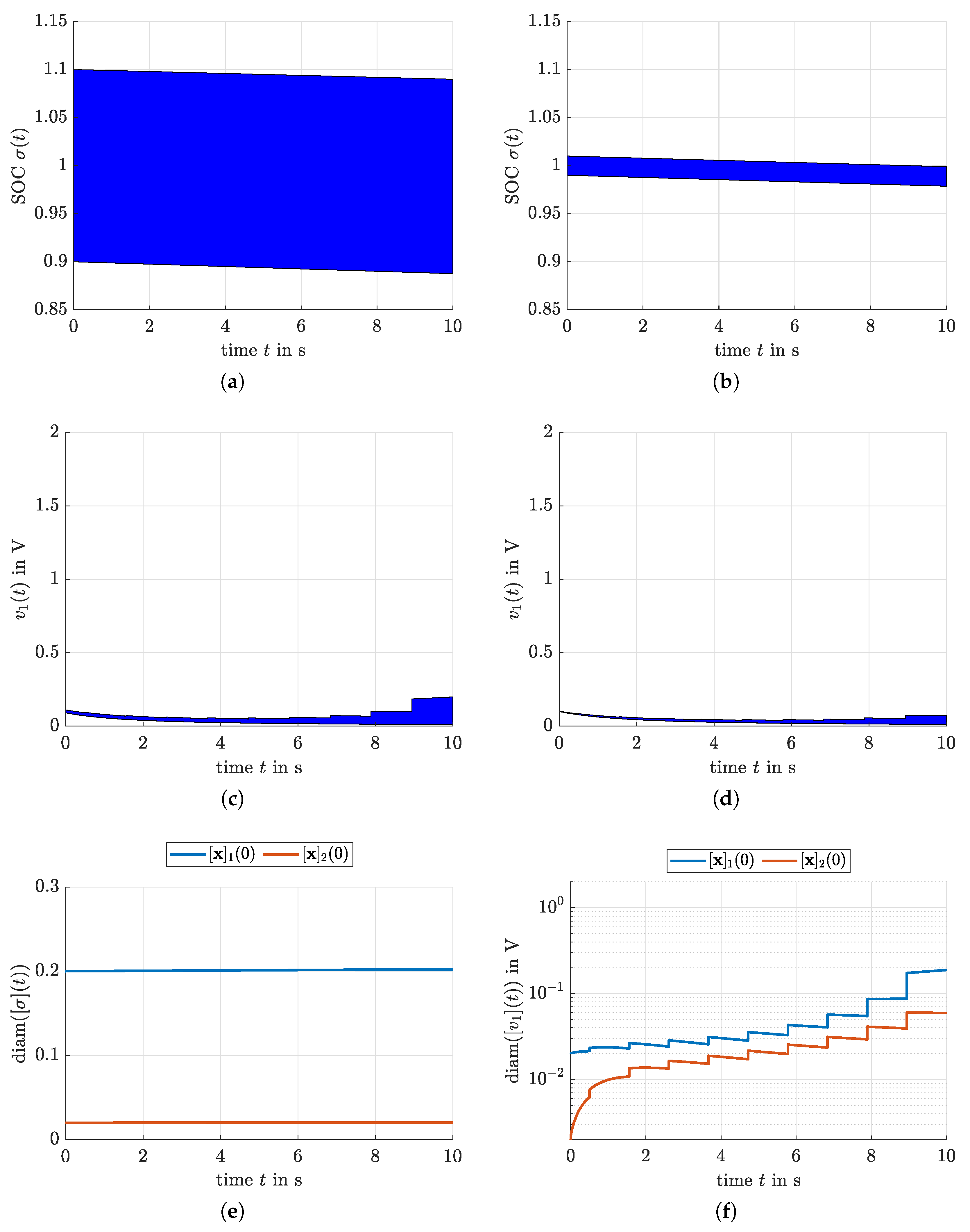
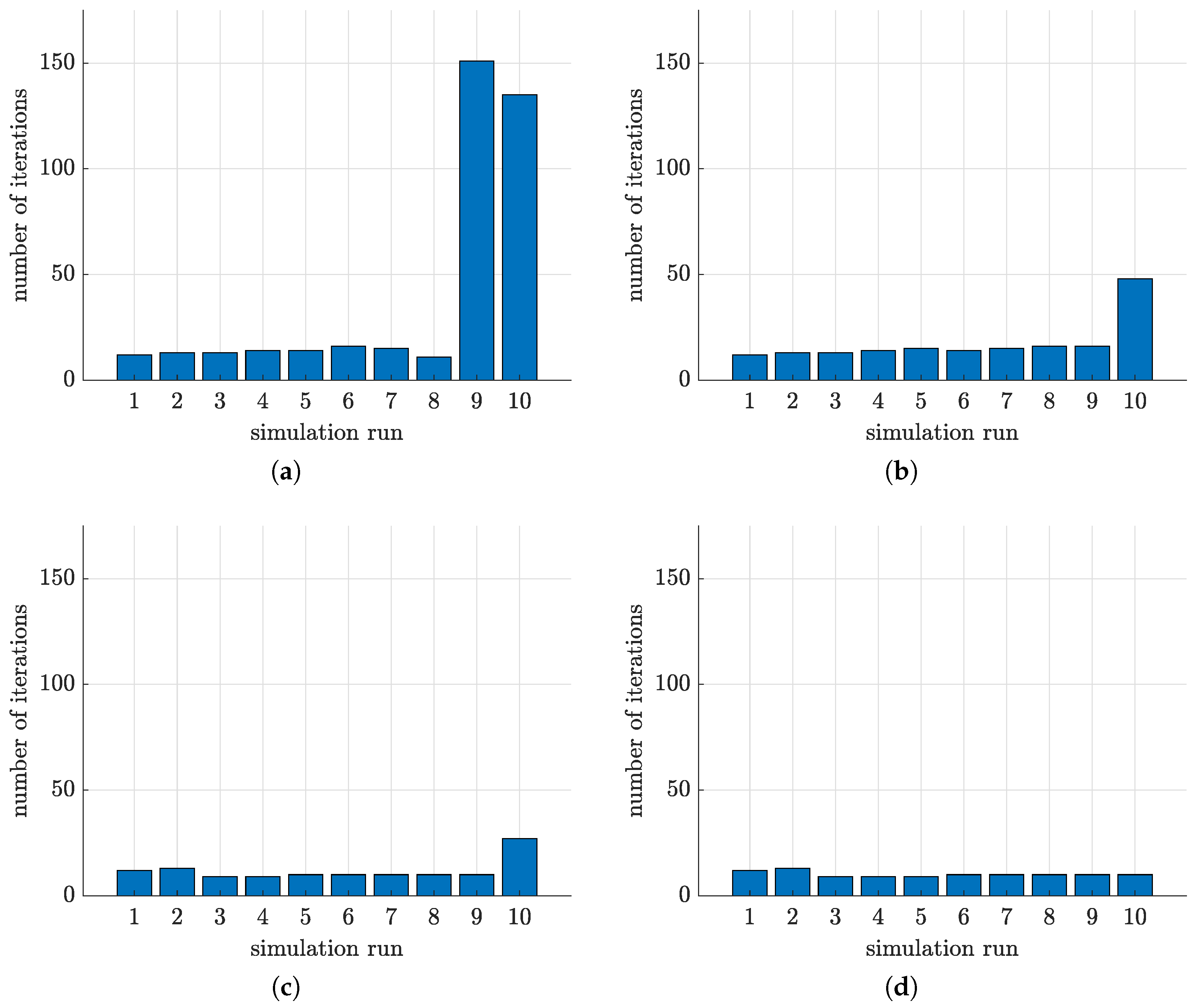
4. Simulation Results

The benchmark application considered in this section for the comparison of both iteration Formulas (31) and (34) is the simplified model of a Lithium-ion battery originally investigated in [25]. For the sake of completeness, this model is summarized in the following subsection before the respective simulation results are presented.

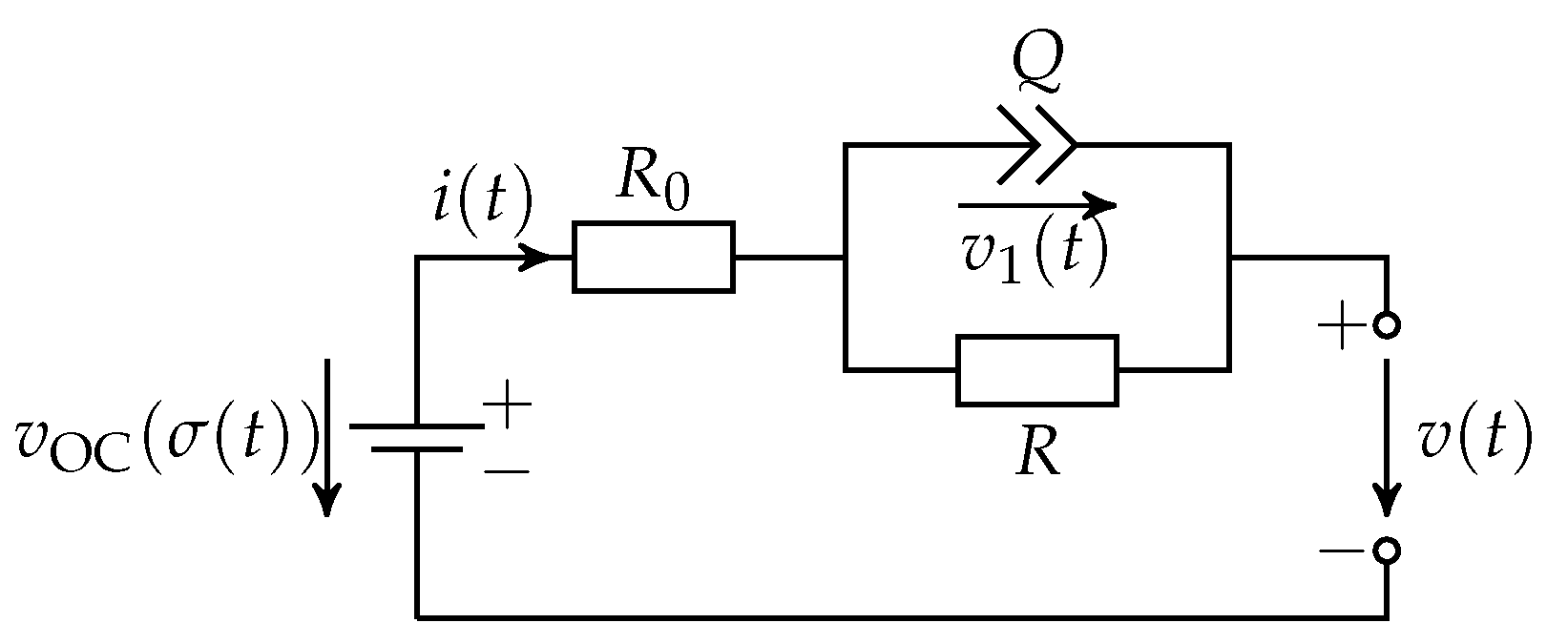
4.1. Simplified Fractional-Order Battery Model

Figure 4 illustrates a fractional-order equivalent circuit model of the charging/discharging behavior of a Lithium-ion battery, where the state of charge $\sigma \left(t\right)$, its fractional derivative ${}_0{\mathcal{D}}_t^{0.5}\sigma \left(t\right)$ of order $\nu =0.5$, and the voltage drop $v_1\left(t\right)$ across the fractional-order constant phase element Q (as a generalization of an ideal capacitor [28,29,30]) are employed as pseudo-state variables.

These pseudo-state variables are summarized in the vector

$$\mathbf{x}\left(t\right)={\left[\begin{array}{ccc}\sigma \left(t\right)& {}_0{\mathcal{D}}_t^{0.5}\sigma \left(t\right)& v_1\left(t\right)\end{array}\right]}^T\in {\mathbb{R}}^3.$$

(37)

Using the modeling steps described in [28] and generalizing the charging/discharging dynamics to

$${}_0{\mathcal{D}}_t^1\sigma \left(t\right)=-\frac{{\eta }_0·i\left(t\right)+{\eta }_1·\sigma \left(t\right)·\mathrm{sign}\left(i\left(t\right)\right)}{3600C_{\mathrm{N}}}$$

(38)

as described in [25] with the terminal current $i\left(t\right)$ as the system input, the commensurate fractional-order quasi-linear state equations

$${}_0{\mathcal{D}}_t^{0.5}\mathbf{x}\left(t\right)=𝓐·\mathbf{x}\left(t\right)+𝓫·i\left(t\right)$$

(39)

with the system and input matrices

$$𝓐=\left[\begin{array}{ccc}0& \phantom{-}1& \phantom{-}0\\ \frac{{\eta }_1·\mathrm{sign}\left(i\left(t\right)\right)}{3600C_{\mathrm{N}}}& \phantom{-}0& \phantom{-}0\\ 0& \phantom{-}0& -\frac{1}{RQ}\end{array}\right]\mathrm{and}𝓫=\left[\begin{array}{c}\phantom{-}0\\ -\frac{{\eta }_0}{3600C_{\mathrm{N}}}\\ \phantom{-}\frac{1}{Q}\end{array}\right]$$

(40)

are obtained.

The simulations discussed in the following two subsections consider the parameters listed in

Table 1. Parameters of the Lithium-ion battery model.

${\mathit{R}}_0\left[\mathbf{\Omega }\right]$	$\mathit{Q}[\mathbf{F}/{\mathbf{s}}^{0.5}]$	$\mathit{R}\left[\mathbf{\Omega }\right]$	${\mathit{\eta }}_0[-]$	${\mathit{\eta }}_1[-]$	${\mathit{C}}_{\mathbf{N}}\left[\mathbf{Ah}\right]$
$+1.7·{10}^{-5}$	$+20.591$	$+0.1005$	$+1.0000$	$+0.1000$	$+3.1000$

which are a subset of those used in [25]. To make the evaluation based on the novel exponential enclosures for the Mittag-Leffler function according to Theorem 3 comparable with the previous work reported in [25], we employ the same linear state feedback controller for the discharging phase ($i\left(t\right)>0$) that was designed in terms of an assignment of the asymptotically stable eigenvalues $\lambda \in \{-0.0001;-0.0002;-0.4832\}$ to the closed-loop dynamics. This leads to the closed-loop dynamic model

$${\mathcal{D}}_t^{0.5}\mathbf{x}\left(t\right)=\left(𝓐-𝓫{𝓴}^T\right)·\mathbf{x}\left(t\right)=:{𝓐}_{\mathrm{C}}·\mathbf{x}\left(t\right),$$

(41)

where the matrix entries ${\mathcal{A}}_{\mathrm{C},2,1}$, ${\mathcal{A}}_{\mathrm{C},2,2}$, ${\mathcal{A}}_{\mathrm{C},2,3}$ are inflated to interval parameters by symmetric bounds of a $1\%$ radius of the respective nominal quantity and ${𝓐}_{\mathrm{C},3,3}$ to $10\%$, respectively.

To investigate the effect of the novel exponential enclosure approach for Mittag-Leffler functions, the following simulations also make use of the intersection of the solution to the system model (41) with an alternative representation resulting from a time-invariant similarity transformation of the system matrix ${𝓐}_{\mathrm{C}}$ into an interval-valued diagonally dominant representation. This transformation, as detailed in [25], employs the matrix of eigenvectors for a matrix containing the elementwise-defined interval midpoints of ${\mathcal{A}}_{\mathrm{C}}$. As discussed in [25], this transformation reduces the overestimation due to the wrapping effect of interval analysis [23,31] when evaluating both iteration Formulas (31) and (34).

For the rest of this paper, consider the two sets of initial pseudo-state vectors

$$\mathbf{x}\left(0\right)\in {\left[\mathbf{x}\right]}_1\left(0\right)=\left[\begin{array}{c}\left[\phantom{-}0.9000;\phantom{-}1.1000\right]\\ \left[-0.0011;-0.0009\right]\\ \left[\phantom{-}0.0900;\phantom{-}0.1100\right]\end{array}\right]$$

(42)

and

$$\mathbf{x}\left(0\right)\in {\left[\mathbf{x}\right]}_2\left(0\right)=\left[\begin{array}{c}\left[\phantom{-}0.99000;\phantom{-}1.01000\right]\\ \left[-0.00101;-0.00099\right]\\ \left[\phantom{-}0.09900;\phantom{-}0.10100\right]\end{array}\right]$$

(43)

in the sense of a Caputo-type initialization of the controlled battery model (41), i.e., with $\mathbf{x}\left(0\right)$ corresponding to $\mathbf{x}\left(t\right)$ for all $t<0$.

In all simulations summarized in the following two subsections, the final points in time T for the evaluation of the iteration Formulas (31) and (34) are chosen as either of the ten values

$$T\in \left\{0.5,0.5+\frac{10-0.5}{9},0.5+2·\frac{10-0.5}{9},\dots ,10\right\}$$

(44)

with $t_{\xi }-t_{\xi -1}=0.005$. Note that this latter choice for the interval subdivision is not identical to the one used in [25], where for all the different values T the considered time ranges were always subdivided into 100 equally spaced slices.

4.2. Simulation with the Help of Box-Type Enclosures

In Figure 5, the iteration Formula (31) has been used to compute guaranteed enclosures for the pseudo states of the controlled Lithium-ion battery for the two differently wide enclosures of initial values.

Due to the fact that the solution parameters ${\lambda }_i$ are determined in such a way that they are valid for the complete time interval $\left[0;T\right]$, longer simulation horizons lead to inflating interval bounds as long as the integrator reset approach derived in [25] and its extended version published in [7] are not employed. The simulations show clearly that the overestimation of the range enclosures for the pseudo states is larger for those variables that change faster. In this scenario, the faster changing variable is the voltage $v_1\left(t\right)$ as compared to the state of charge $\sigma \left(t\right)$. However, it can also be seen that the blow-up of the solution bounds can be reduced by tighter bounds for the pseudo-state initialization which gives rise to the option to repeat the simulations after paving the possible initial pseudo-state domain.

4.3. Simulation with the Help of Exponential Enclosures

Figure 6 shows that the pseudo-state enclosures are significantly tightened by using the intersection of the novel exponential enclosures of Mittag-Leffler functions with the box-type ones that were solely used in Figure 5. This advantage cannot only be observed for the case of the wide initialization $\mathbf{x}\left(0\right)\in {\left[\mathbf{x}\right]}_1\left(0\right)$ but also for the tighter one $\mathbf{x}\left(0\right)\in {\left[\mathbf{x}\right]}_2\left(0\right)$.

The second advantage of this new enclosure approach is illustrated in Figure 7, where the required maximum numbers of evaluations of both (31) and (34) are illustrated for the ten different choices of the simulation horizon T. There, it can be seen clearly that the novel exponential enclosure approach allows to reduce the number of required iterations significantly for longer simulation horizons T. To make this comparison fair, the iterations have been stopped in all cases if the diameters of all ${\left[{\lambda }_i\right]}^{\langle \kappa +1\rangle }$ and ${\left[{\lambda }_i\right]}^{\langle \kappa \rangle }$ deviate from each other by less than the value ${10}^{-4}$.

As a summary, the new enclosure approach does not only allow to significantly reduce the overestimation in the computation of guaranteed bounds for the pseudo states but—at least for the application scenario at hand—also reduces the computational effort by up to $80\%$ due to significantly less required iterations.

5. Conclusions and Outlook on Future Work

In this paper, a novel enclosure approach for the pseudo states of fractional-order differential equations has been presented. It is based on enclosing Mittag-Leffler functions by exponential enclosures instead of box-type enclosures employed so far in previous work. By using a close-to-life model for the charging/discharging dynamics of a Lithium-ion battery, it has been shown that this new enclosure technique leads not only to significantly tighter enclosures, yet preserving the guaranteed enclosure property, but also leads to a noticeable reduction in the computational effort by significantly less iterations required to obtain an identical enclosure quality.

Future work will aim at extending the presented approach to system models with non-commensurate orders. In addition, the approach will be included into the observer-based technique presented in [7] for the quantification of truncation errors which allows for resetting fractional integrators in a guaranteed way. In such a way, it is planned to make the proposed simulation approach applicable to tasks such as the parameter identification of fractional-order differential equations and to the identification of their initialization functions for $t<0$. Moreover, the application to more complex dynamic models from the domains of electrochemical energy storage and energy conversion will be investigated.