An Adaptive Projection Gradient Method for Solving Nonlinear Fractional Programming
Abstract
1. Introduction
- ()
- The function is convex (Fréchet) differentiable, the gradient of which is Lipschitz continuous with a Lipschitz constant and for all .
- ()
- The function is concave (Fréchet) differentiable, the gradient of which is Lipschitz continuous with a Lipschitz constant and there is such that for all .
2. Preliminaries
3. Algorithm and Convergence Results
| Algorithm 1: Adaptive projection gradient method. |
| Initialization: Choose an initial point , two real numbers and
. Set and . Step 1: For a current iterate and a step size (). Set Otherwise, set |
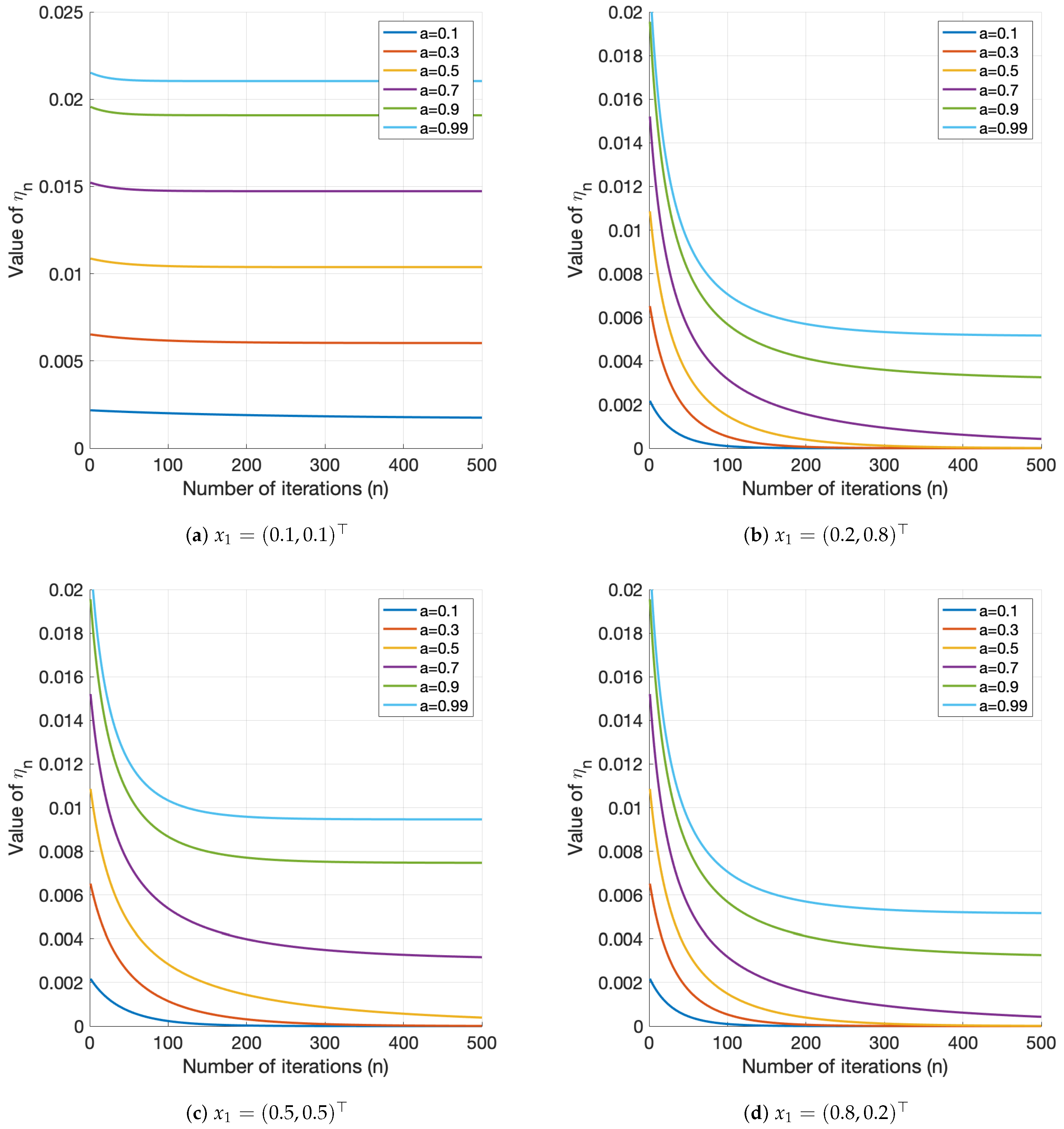
4. Numerical Examples
4.1. Convex–Concave Fractional Programming
4.2. Convex–Concave Fractional Programming with Linear Constraints
4.3. Quadratic Fractional Programming
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bradley, S.P.; Frey, S.C., Jr. Fractional programming with homogeneous functions. Oper. Res. 1974, 22, 350–357. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Konno, H.; Inori, M. Bond portfolio optimization by bilinear fractional programming. J. Oper. Res. Soc. Jpn. 1989, 32, 143–158. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Sandström, M.; Zopounidis, C. On the use of optimization models for portfolio selection: A review and some computational results. Comput. Econ. 1994, 7, 227–244. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. A fast fixed-point algorithm for independent component analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Li, Q.; Shen, L.; Zhang, N.; Zhou, J. A proximal algorithm with backtracked extrapolation for a class of structured fractional programming. Appl. Comput. Harmon. Anal. 2022, 56, 98–122. [Google Scholar] [CrossRef]
- Zhang, N.; Li, Q. First-order algorithms for a class of fractional optimization problems. SIAM J. Optim. 2022, 32, 100–129. [Google Scholar] [CrossRef]
- Shen, K.; Yu, W. Fractional programming for communication systems-part I: Power control and beamforming. IEEE Trans. Signal Process. 2018, 66, 2616–2630. [Google Scholar] [CrossRef]
- Zappone, A.; Björnson, E.; Sanguinetti, L.; Jorswieck, E. Globally optimal energy-efficient power control and receiver design in wireless networks. IEEE Trans. Signal Process. 2017, 65, 2844–2859. [Google Scholar] [CrossRef]
- Zappone, A.; Sanguinetti, L.; Debbah, M. Energy-delay efficient power control in wireless networks. IEEE Trans. Commun. 2017, 66, 418–431. [Google Scholar] [CrossRef]
- Chen, L.; He, S.; Zhang, S.Z. When all risk-adjusted performance measures are the same: In praise of the Sharpe ratio. Quant. Financ. 2011, 11, 1439–1447. [Google Scholar] [CrossRef]
- Archetti, C.; Desaulniers, G.; Speranza, M.G. Minimizing the logistic ratio in the inventory routing problem. EURO J. Transp. Logist. 2017, 6, 289–306. [Google Scholar] [CrossRef]
- Chen, F.; Huang, G.H.; Fan, Y.R.; Liao, R.F. A nonlinear fractional programming approach for environmental-economic power dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 463–469. [Google Scholar] [CrossRef]
- Rahimi, Y.; Wang, C.; Dong, H.; Lou, Y. A scale-invariant approach for sparse signal recovery. SIAM J. Sci. Comput. 2019, 41, 3649–3672. [Google Scholar] [CrossRef]
- Boţ, R.I.; Dao, M.N.; Li, G. Inertial proximal block coordinate method for a class of nonsmooth sum-of-ratios optimization problems. SIAM J. Optim. 2022; accepted. [Google Scholar]
- Stancu-Minasian, I.M. Fractional Programming: Theory, Methods, and Applications; Kluwer Academic Publishers: Boston, MA, USA, 1997. [Google Scholar]
- Stancu-Minasian, I.M. A ninth bibliography of fractional programming. Optimization 2019, 68, 2125–2169. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1976, 13, 492–498. [Google Scholar] [CrossRef]
- Crouzeix, J.P.; Ferland, J.A.; Schaible, S. An algorithm for generalized fractional programs. J. Optim. Theory Appl. 1985, 47, 35–49. [Google Scholar] [CrossRef]
- Ibaraki, T. Parametric approaches to fractional programs. Math. Program. 1983, 26, 45–362. [Google Scholar] [CrossRef]
- Schaible, S. Fractional programming. II, on Dinkelbach’s algorithm. Manag. Sci. 1976, 22, 868–873. [Google Scholar] [CrossRef]
- Jagannathan, R. On some properties of programming problems in parametric form pertaining to fractional programming. Manag. Sci. 1966, 12, 609–615. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; CMS Books in Mathematics; Springer: New York, NY, USA, 2017. [Google Scholar]
- Boţ, R.I.; Dao, M.N.; Li, G. Extrapolated proximal sub-gradient algorithms for nonconvex and nonsmooth fractional programs. Math. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Aragón Artacho, F.J.; Campoy, R.; Tam, M.K. Strengthened splitting methods for computing resolvents. Comput. Optim. Appl. 2021, 80, 549–585. [Google Scholar] [CrossRef]
- Cegielski, A. Iterative Methods for Fixed Point Problems in Hilbert Spaces; Lecture Notes in Mathematics 2057; Springer: Berlin, Germany, 2012. [Google Scholar]
- Polyak, B.T. Introduction to Optimization; Optimization Software: New York, NY, USA, 1987. [Google Scholar]
- Malitsky, Y.; Mishchenko, K. Adaptive gradient descent without descent. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; Volume 119 of Proceedings of Machine Learning Research. pp. 6702–6712. [Google Scholar]
- Boţ, R.I.; Csetnek, E.R. Proximal-gradient algorithms for fractional programming. Optimization 2017, 66, 1383–1396. [Google Scholar] [CrossRef] [PubMed]
- Boţ, R.I.; Csetnek, E.R.; Vuong, P.T. The forward-backward-forward method from continuous and discrete perspective for pseudo-monotone variational inequalities in Hilbert spaces. Eur. J. Oper. Res. 2020, 287, 49–60. [Google Scholar] [CrossRef]
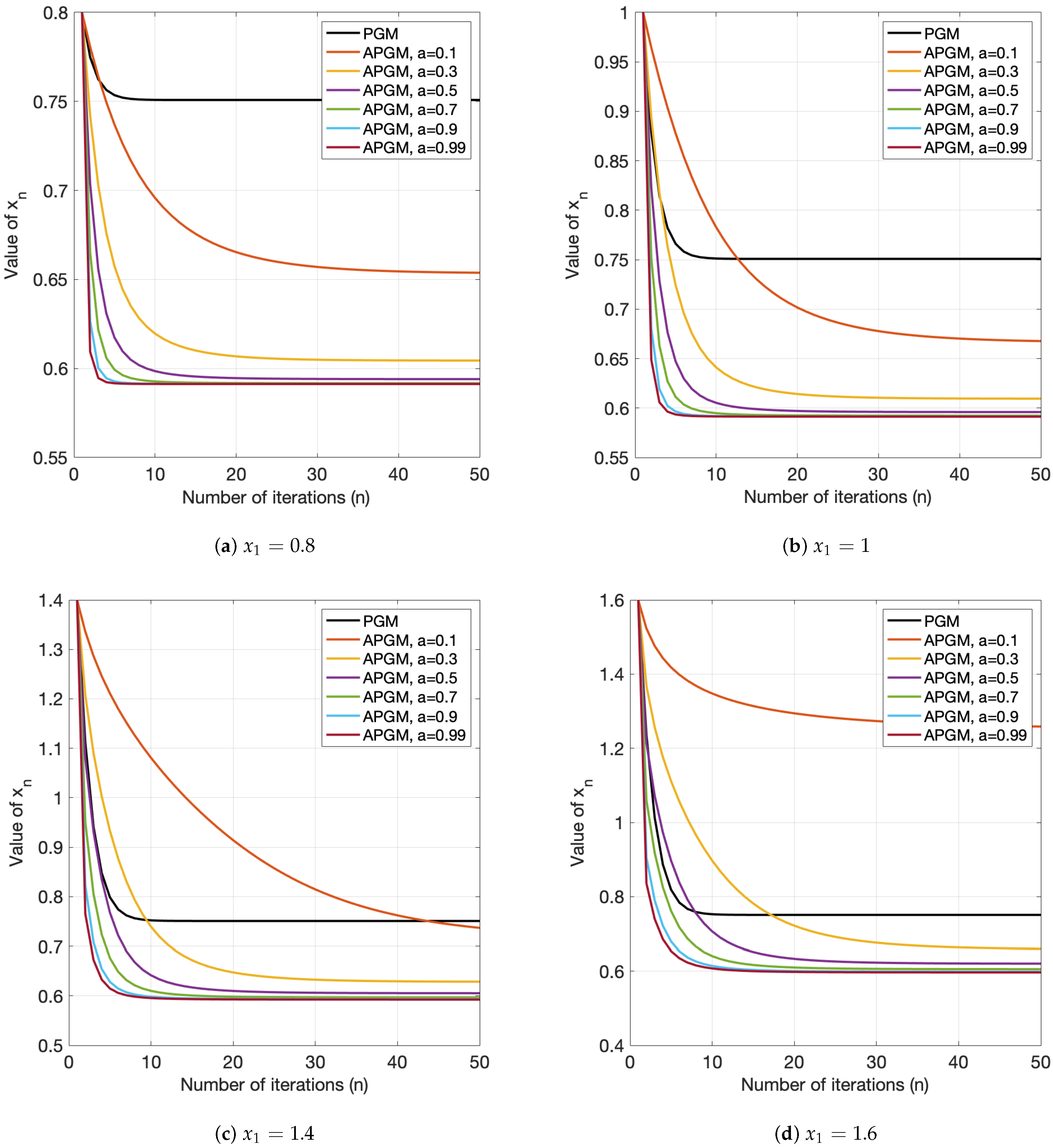
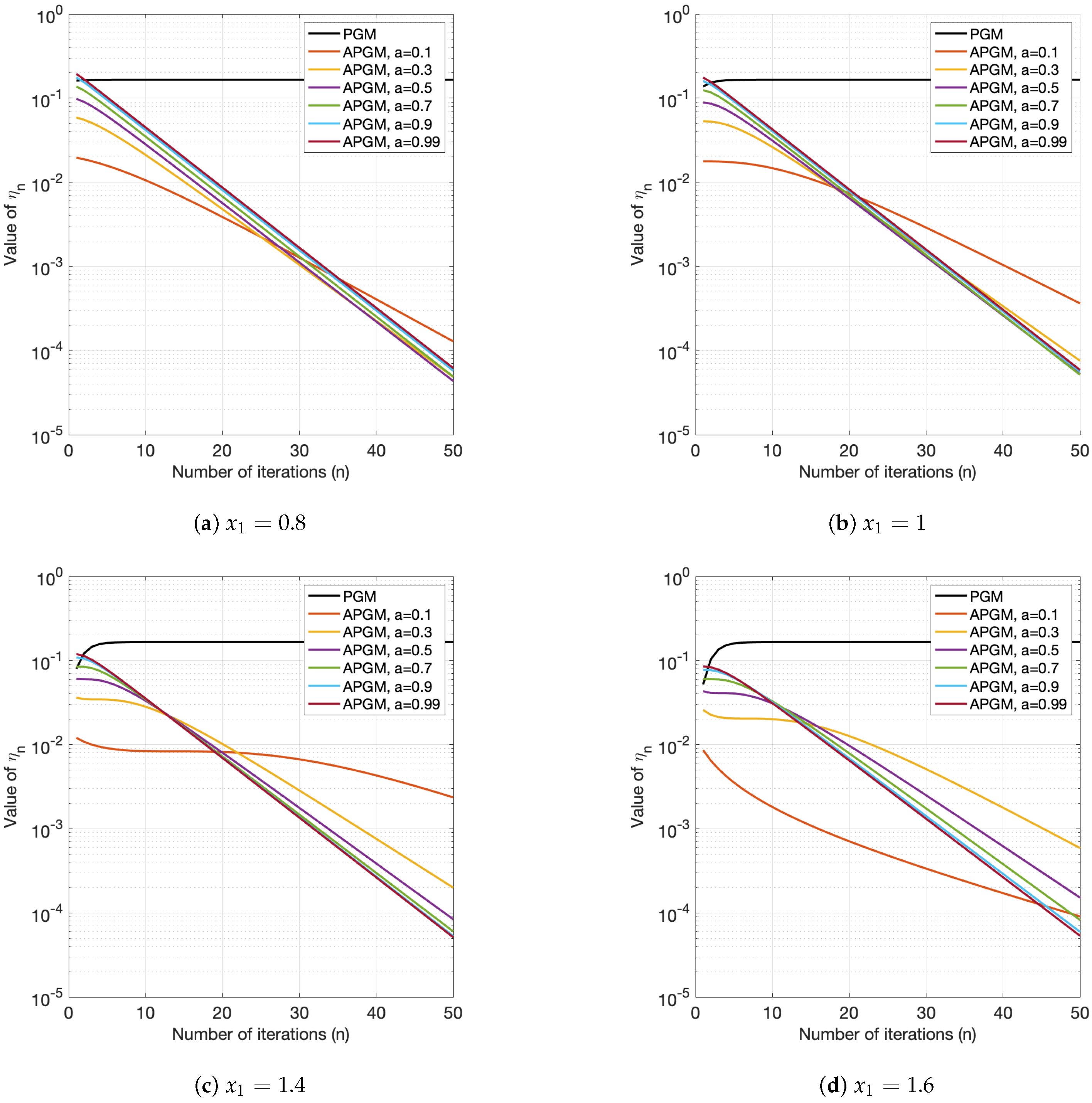
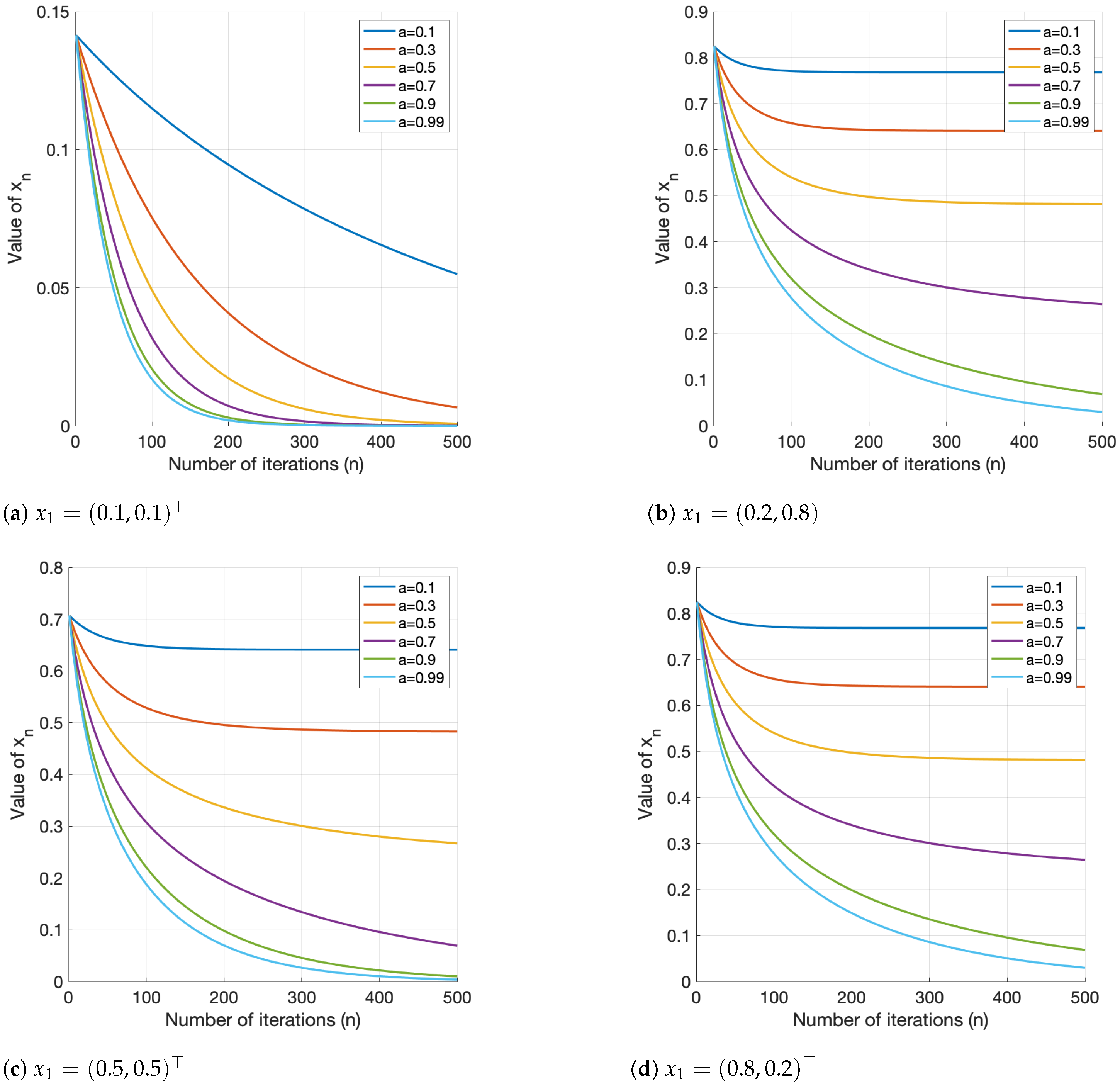
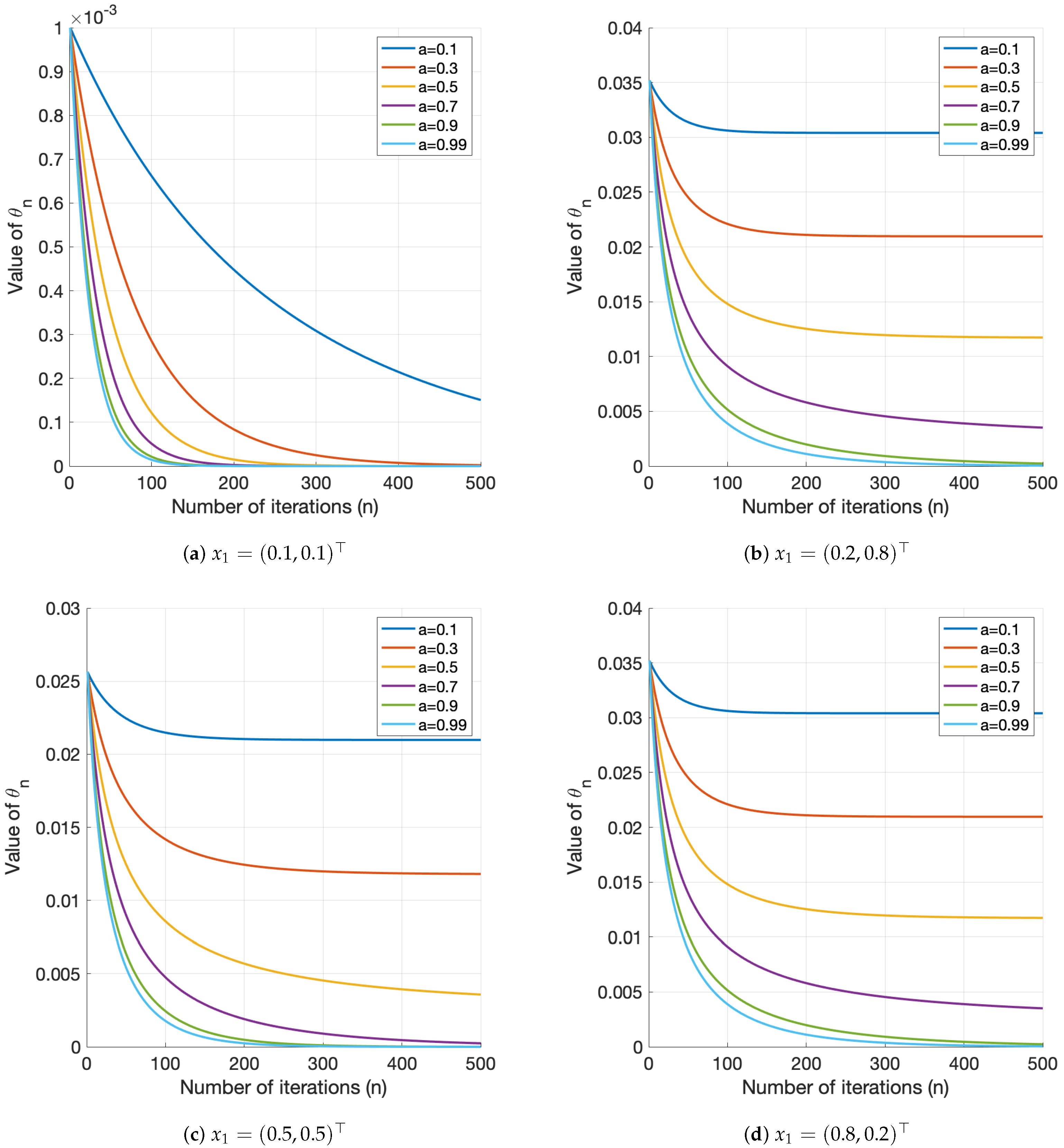
| a | n | APGM | PGSA ([8], Algorithm 1) | ||
|---|---|---|---|---|---|
| 1 | 6.6630 | 6.6630 | |||
| 2 | 2.4070 | 2.4070 | |||
| 3 | 1.6641 | 1.6375 | |||
| 4 | 1.6190 | 1.6190 | |||
| 1 | 6.6630 | 6.6630 | |||
| 2 | 2.1025 | 2.1025 | |||
| 3 | 1.6190 | 1.6190 | |||
| 1 | 6.6630 | 6.6630 | |||
| 2 | 1.7443 | 1.7443 | |||
| 3 | 1.6190 | 1.6190 | |||
| 1 | 6.6630 | 6.6630 | |||
| 2 | 1.6190 | 1.6190 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prangprakhon, M.; Feesantia, T.; Nimana, N. An Adaptive Projection Gradient Method for Solving Nonlinear Fractional Programming. Fractal Fract. 2022, 6, 566. https://doi.org/10.3390/fractalfract6100566
Prangprakhon M, Feesantia T, Nimana N. An Adaptive Projection Gradient Method for Solving Nonlinear Fractional Programming. Fractal and Fractional. 2022; 6(10):566. https://doi.org/10.3390/fractalfract6100566
Chicago/Turabian StylePrangprakhon, Mootta, Thipagon Feesantia, and Nimit Nimana. 2022. "An Adaptive Projection Gradient Method for Solving Nonlinear Fractional Programming" Fractal and Fractional 6, no. 10: 566. https://doi.org/10.3390/fractalfract6100566
APA StylePrangprakhon, M., Feesantia, T., & Nimana, N. (2022). An Adaptive Projection Gradient Method for Solving Nonlinear Fractional Programming. Fractal and Fractional, 6(10), 566. https://doi.org/10.3390/fractalfract6100566






