Characterization of Ceramic Thermal Shock Cracks Based on the Multifractal Spectrum
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermal Shock Test
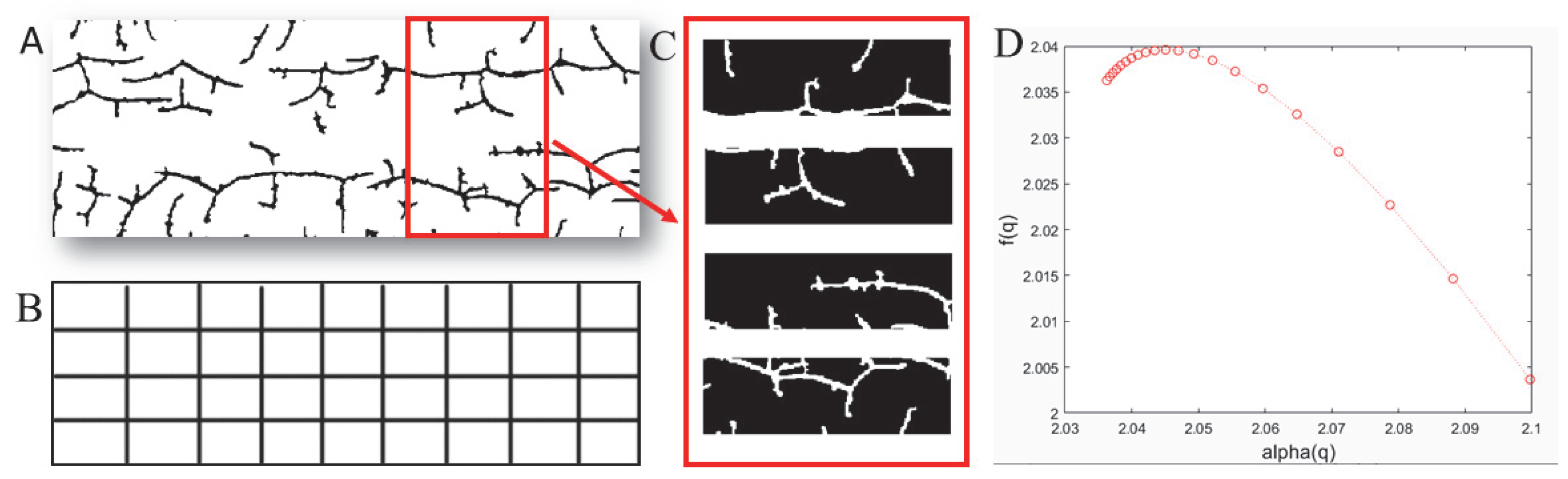
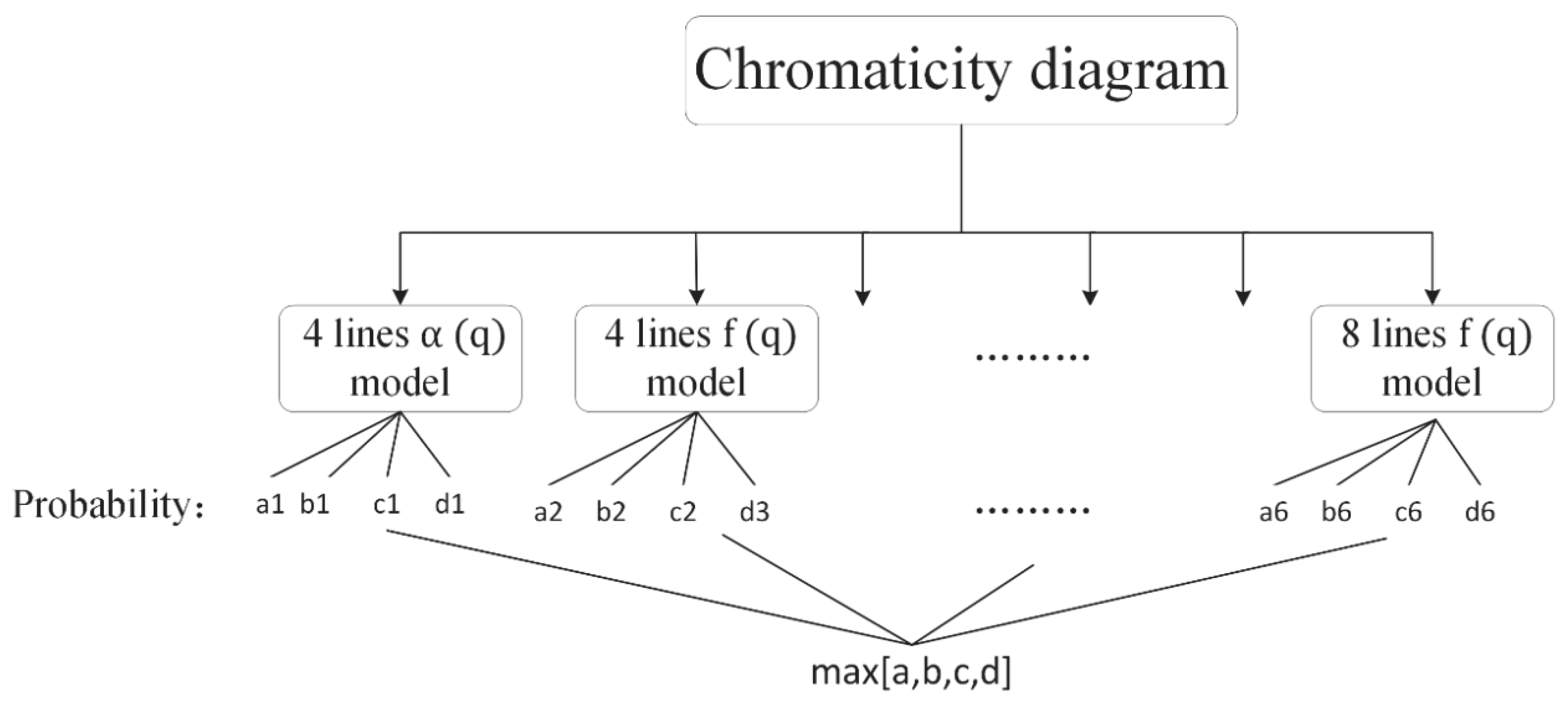
2.2. Multifractal Spectrum Calculation
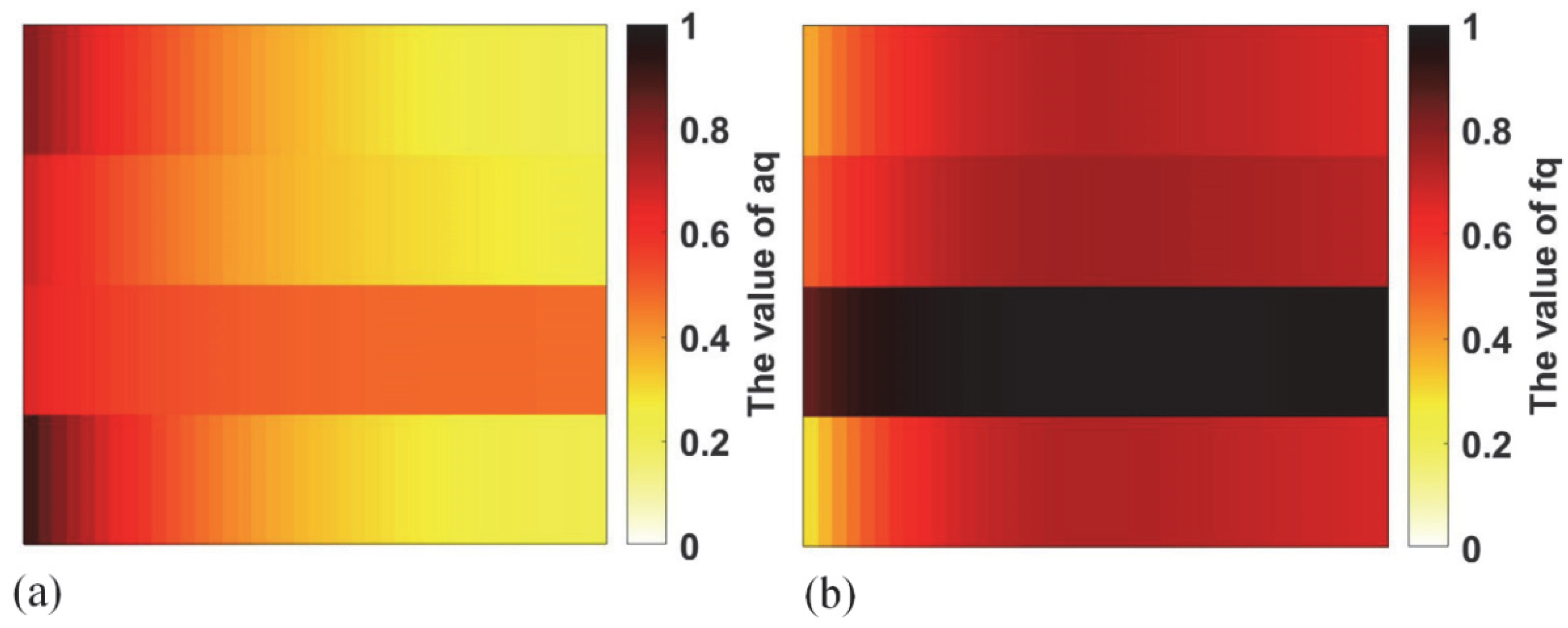
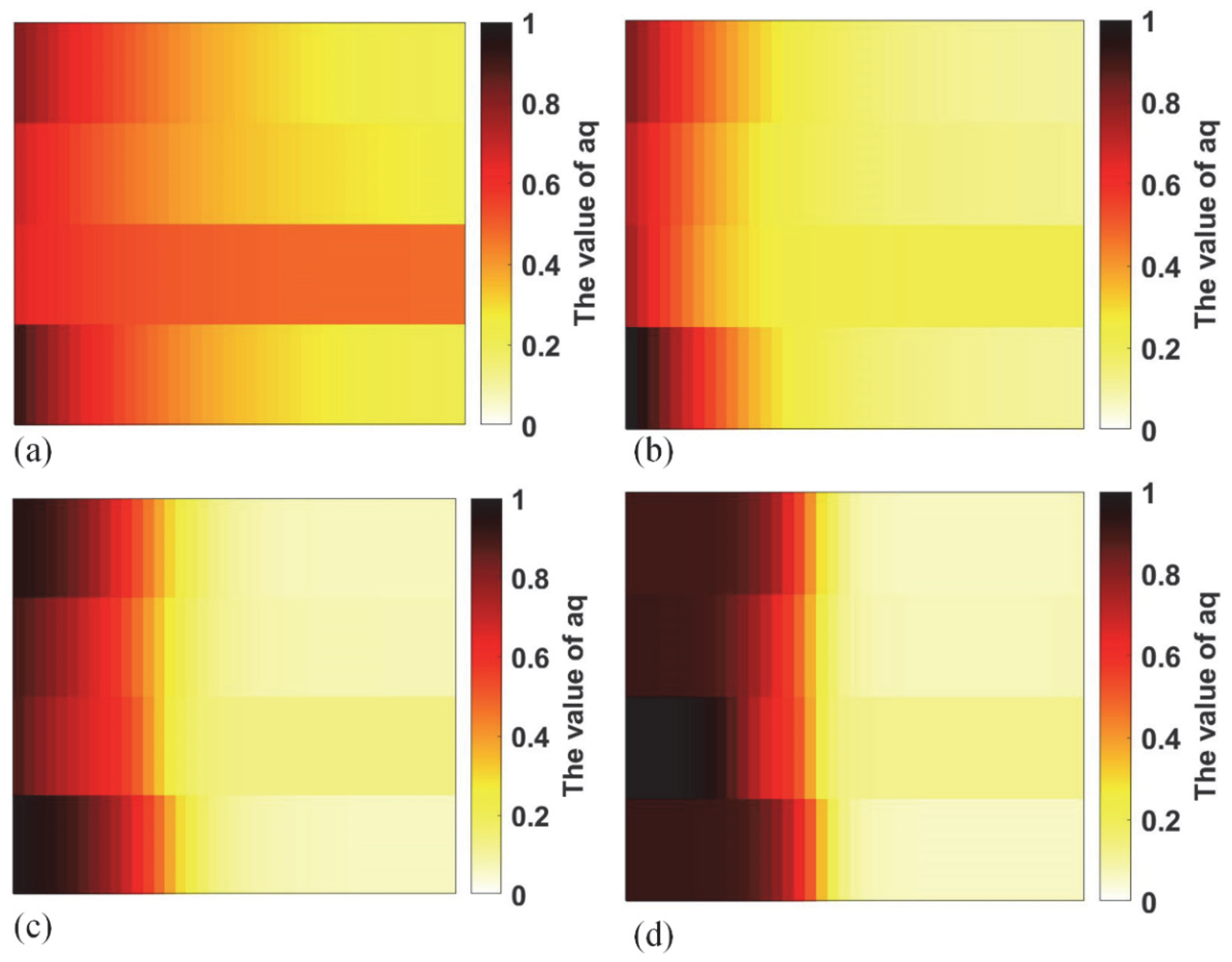
2.3. Construction of Deep Learning Model
3. Results
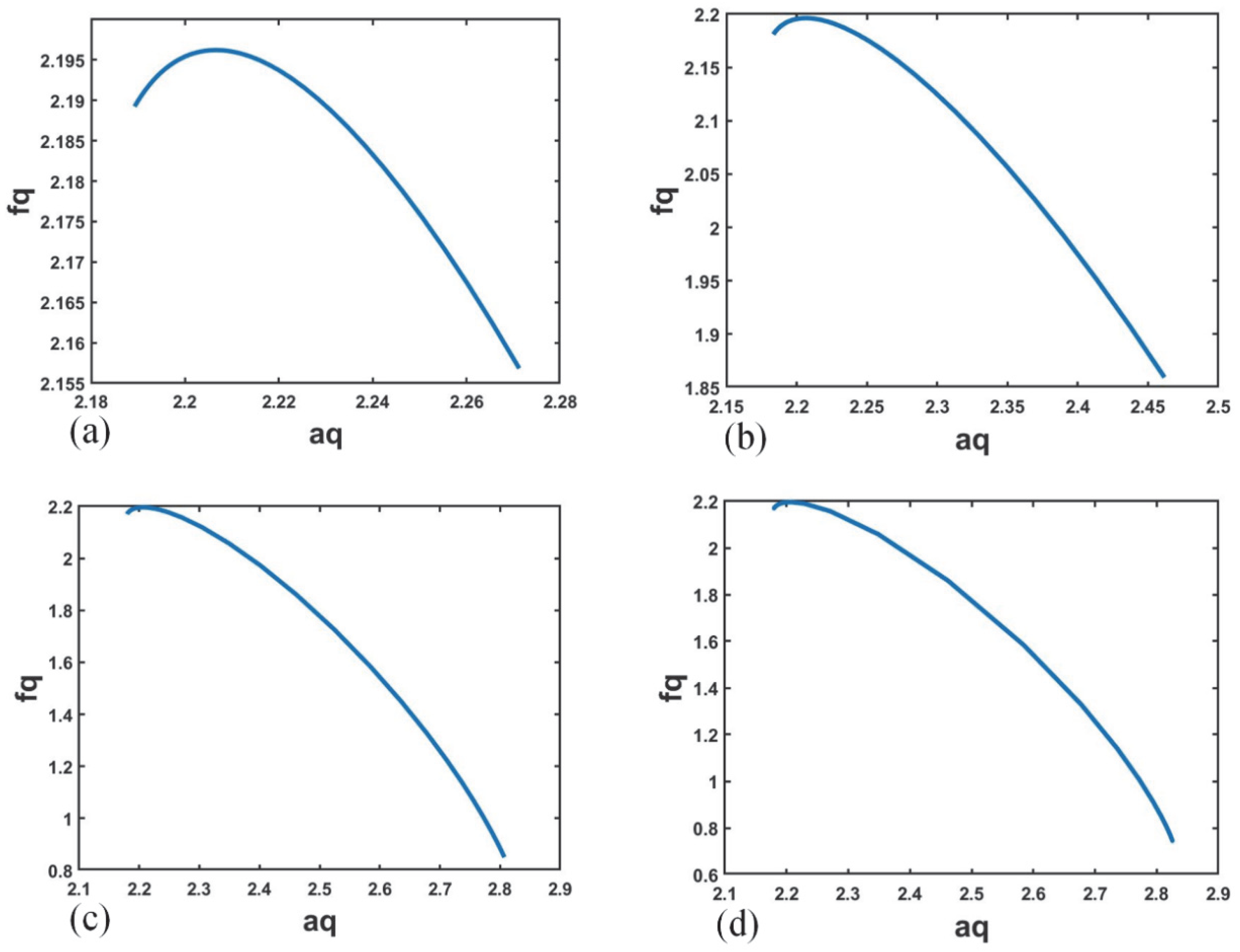
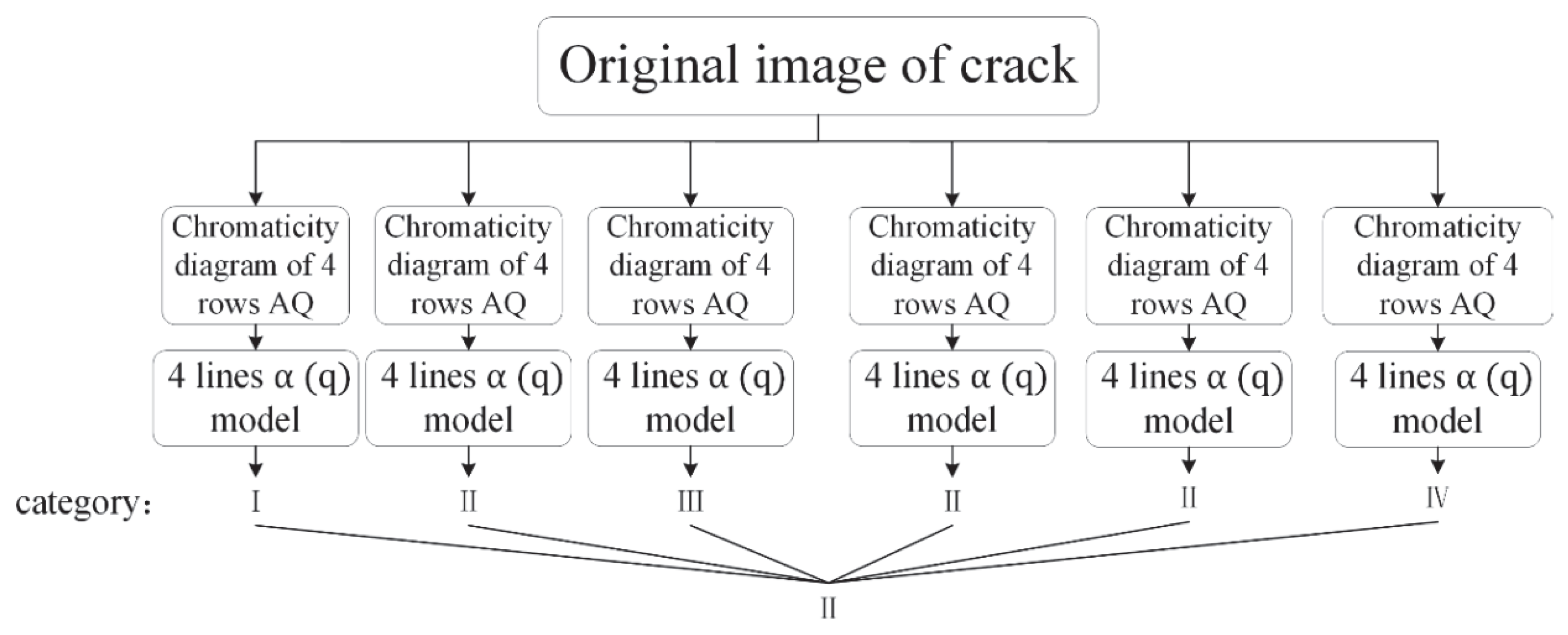
3.1. Calculation Results of Multifractal Spectrum of Crack Image
3.2. Recognition Results of Deep Learning Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, Y.L.; Wang, W.M. Progress of Investigation on Thermal Shock Resistance of Ceramic Materials. Adv. Ceram. 2004, 1, 37–41. [Google Scholar] [CrossRef]
- Li, W.J.; Zhang, Y.; Zhang, X.H.; Hong, C.Q.; Han, W.B. Thermal Shock Behavior of ZrB2-SiC Ultra-high Temperature Ceramics with Addition of Zirconia. J. Alloys Compd. 2009, 478, 386–391. [Google Scholar] [CrossRef]
- Griffith, A.A. The Phenomena of Rupture and Flow in Solids. Philos. Trans. R. Soc. Lond. 1921, 221, 163–198. [Google Scholar]
- Duan, W.J.; Jia, D.C.; Cai, D.L.; Niu, B.; Yang, H.L.; Yang, Z.H.; Zhou, Y. Thermal shock damage assessment of a BNW/SiO2 ceramic: Insight from temperature-dependent material properties. Ceram. Int. 2021, 47, 19737–19742. [Google Scholar] [CrossRef]
- Luo, J.T.; Wang, H.T.; Xi, C.Y.; Zhai, H.; Gu, Y.F.; Zhang, C.X. Indentation size effect–crack propagation model and finite element simulation verification for microhardness test of ceramic materials. Ceram. Int. 2021, 47, 4914–4924. [Google Scholar] [CrossRef]
- Li, Y.Q.; Liu, B.Y.; Wang, X.H.; Shao, Y.F.; Li, L.; Wei, J.C.; Song, F. The effect of a prefabricated crack on the crack growth in ceramics during quenching. Ceram. Int. 2021, 47, 3643–3648. [Google Scholar] [CrossRef]
- Qi, F.; Meng, S.H.; Song, F.; Guo, H.; Xu, X.H.; Shao, Y.F.; Chen, Y. Fractal characterization of ceramic crack patterns after thermal shocks. J. Am. Ceram. Soc. 2019, 102, 3641–3652. [Google Scholar] [CrossRef]
- Ricco, P.; Ramos, N.C.; Campos, T.M.B.; Soares, V.O.; Boas, M.O.C.V.; Melo, R.M. The roles of microstructure and surface energy on subcritical crack growth in glass-ceramics. Ceram. Int. 2021, 47, 6827–6833. [Google Scholar] [CrossRef]
- Quan, H.; Alderliesten, R.C. The energy dissipation during fatigue crack growth in metallic materials. Eng. Fract. Mech. 2022, 269, 108567. [Google Scholar] [CrossRef]
- Quan, H.; Alderliesten, R.C. The energy dissipation during fatigue crack growth in adhesive joints under Mode-I loading. Theor. Appl. Fract. Mech. 2022, 120, 103418. [Google Scholar] [CrossRef]
- Zhu, W.W.; Lei, G.; He, X.P.; Patzek, T.W.; Wang, M. Fractal and multifractal characterization of stochastic fracture networks and real outcrops. J. Struct. Geol. 2022, 155, 104508. [Google Scholar] [CrossRef]
- Ji, Z.H.; Zhang, S.; Ma, X.; Ding, K.Y.; Chen, T.T. Phase Structure Characterization and High-speed Scraping Behavior Analysis of Abrasable Coatings Based on Multifractal. Surf. Technol. 2020, 49, 165–171. [Google Scholar] [CrossRef]
- Pan, L.X.; Carrillo, J.L.; Cao, M.; Sha, G. Multifractal-spectrum shape parameters for characterizing distribution and evolution of multiple cracks in concrete structures. Eng. Fract. Mech. 2022, 264, 108329. [Google Scholar] [CrossRef]
- Butenko, P.N.; Hilarov, V.L.B.A. Crystallization of Ni50Ti50 metallic glass ribbon in the concept of multifractal formalism. Phase Transit. 2022, 95, 537–550. [Google Scholar] [CrossRef]
- Martsepp, M.; Laas, T.; Laas, K.; Priimets, J.; Mikli, V.; Antonov, M. Multifractal analysis of high-temperature plasma irradiated tungsten surfaces. Surf. Topogr. Metrol. Prop. 2021, 9, 035030. [Google Scholar] [CrossRef]
- Feng, J.J.; Wang, E.Y.; Huang, Q.S.; Ding, H.C.; Dang, L. Time-varying Multifractal Analysis of Crack Propagation and Internal Fracture Process of Coal under Dynamic Loading. Fractals 2021, 29, 2150089. [Google Scholar] [CrossRef]
- Jouini, M.S.; Bouchaala, F.; Riahi, M.K.; Sassi, M.; Abderrahmane, H.; Hjouj, F. Multifractal Analysis of Reservoir Rock Samples Using 3D X-Ray Micro Computed Tomography Images. IEEE Access 2022, 10, 67898–67909. [Google Scholar] [CrossRef]
- Astinchap, B.; Ghanbaripour, H.; Amuzgar, R. Multifractal analysis of chest CT images of patients with the 2019 novel coronavirus disease (COVID-19). Chaos Solitons Fractals 2022, 156, 111820. [Google Scholar] [CrossRef]
- Tsvetkov, V.P.; Mikheev, S.A.; Tsvetkov, I.V.; Derbov, V.L.; Gusev, A.A.; Vinitsky, S.I. Modeling the multifractal dynamics of COVID-19 pandemic. Chaos Solitons Fractals 2022, 161, 112301. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Xiong, X. Vibration discrimination based upon multifractal spectrum and improved probabilistic neural network in the dual Mach–Zehnder interferometric perimeter system. Opt. Rev. 2022, 29, 13–24. [Google Scholar] [CrossRef]
- Xu, S.H.; Xia, M. Fractal Dimension and Multifractal Spectrum of Surface Morphology of Corroded Steel. Mater. Rep. 2020, 34, 16140–16143. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Shi, Z.W.; Liu, T.; Wu, G.Y. An Effective and Efficient Algorithm for Text Categorization. Comput. Eng. Appl. 2005, 29, 180–183. [Google Scholar]



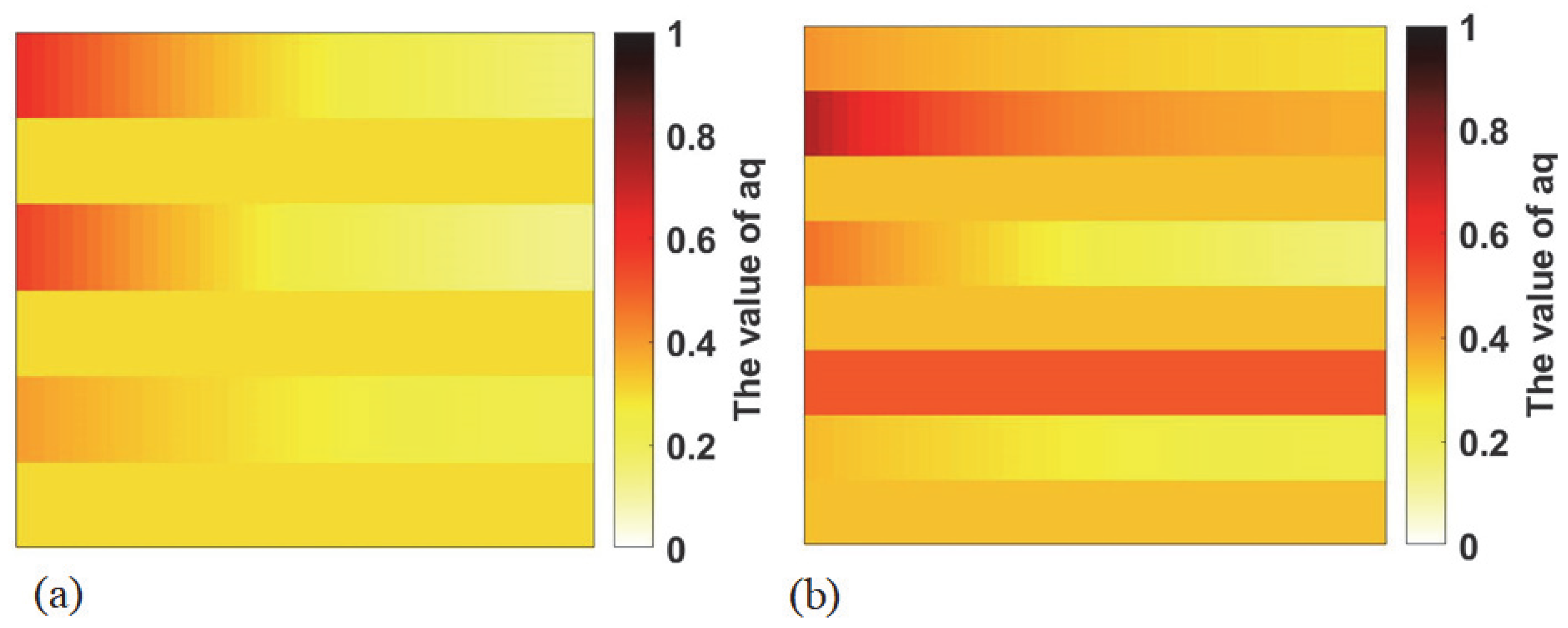

| Learning Rate/Training Rounds | 0.05/80 | 0.01/80 | 0.005/50 | 0.001/100 |
|---|---|---|---|---|
| Chromaticity Diagram of | 60.28% | 60.57% | 60.23% | 54.46% |
| Chromaticity Diagram of | 64.13% | 68.20% | 67.27% | 65.48% |
| Model | ||||||
|---|---|---|---|---|---|---|
| Recognition Rate | 61.39% | 70.26% | 75.20% | 52.38% | 73.82% | 80.33% |
| Model | ||||||
|---|---|---|---|---|---|---|
| Recognition Rate | 62.50% | 70.80% | 79.16% | 58.33% | 75.00% | 83.30% |
| The Sample is Actually Positive | The Sample is Actually Negative | |
|---|---|---|
| The Sample Prediction is Positive | TP | FP |
| The Sample Prediction is Negative | FN | TN |
| Precision | Recall | F1-Measure | |
|---|---|---|---|
| Mac | 0.8875 | 0.8750 | 0.8812 |
| Mic | 0.8750 | 0.8750 | 0.8750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, C.; Guo, H.; Meng, S.; Shao, Y.; Wang, S.; Xie, S.; Qi, F. Characterization of Ceramic Thermal Shock Cracks Based on the Multifractal Spectrum. Fractal Fract. 2022, 6, 539. https://doi.org/10.3390/fractalfract6100539
Shao C, Guo H, Meng S, Shao Y, Wang S, Xie S, Qi F. Characterization of Ceramic Thermal Shock Cracks Based on the Multifractal Spectrum. Fractal and Fractional. 2022; 6(10):539. https://doi.org/10.3390/fractalfract6100539
Chicago/Turabian StyleShao, Changxu, Hao Guo, Songhe Meng, Yingfeng Shao, Shanxiang Wang, Shangjian Xie, and Fei Qi. 2022. "Characterization of Ceramic Thermal Shock Cracks Based on the Multifractal Spectrum" Fractal and Fractional 6, no. 10: 539. https://doi.org/10.3390/fractalfract6100539
APA StyleShao, C., Guo, H., Meng, S., Shao, Y., Wang, S., Xie, S., & Qi, F. (2022). Characterization of Ceramic Thermal Shock Cracks Based on the Multifractal Spectrum. Fractal and Fractional, 6(10), 539. https://doi.org/10.3390/fractalfract6100539







