Fractal Nature Bridge between Neural Networks and Graph Theory Approach within Material Structure Characterization

Abstract

Many recently published research papers examine the representation of nanostructures and biomimetic materials, especially using mathematical methods. For this purpose, it is important that the mathematical method is simple and powerful. Theory of fractals, artificial neural networks and graph theory are most commonly used in such papers. These methods are useful tools for applying mathematics in nanostructures, especially given the diversity of the methods, as well as their compatibility and complementarity. The purpose of this paper is to provide an overview of existing results in the field of electrochemical and magnetic nanostructures parameter modeling by applying the three methods that are “easy to use”: theory of fractals, artificial neural networks and graph theory. We also give some new conclusions about applicability, advantages and disadvantages in various different circumstances.

1. Introduction

The development of new and advanced technologies for micro-electronic complex devices, as well as their further miniaturization and integrations, becomes more and more interesting every day for industry as well as for scientific research teams. To achieve this goal, defining and predicting electrophysical parameters of the ceramic material is important. The application of fractal nature analysis on electro-ceramic materials’ micro-structure characterization opens a variety of new frontiers for higher-level microelectronic devices and integrations, especially if the approach is scientific and inspired by self-similarities that exist in nature. The shape, size and structure of grains and pores, or other aspects of a ceramic material’s micro-structure morphology, influence its intergranular physical properties, such as dielectric, ferroelectric and magnetic properties. This is important for the design of electro-ceramic materials with desired features. To enhance this research, especially regarding the determination and prediction of dielectric properties at the nano level by applying fractal nature analysis, we introduced two other practical and useful methods: artificial neural networks and graph theory.

The use of artificial neural networks is a kind of biomimetic approach, inspired by biological neural networks. In this research, they are used for calculating ceramics’ microelectronic parameters between grains, based on the measurements on the bulk samples, consolidated under different sintering conditions and with different modifying agents. The idea of this mathematical method is mapping input–output data, with an error appearing at the network’s output, which is propagated backwards and replaced by an examined parameter. In order to improve the understanding and presentation of the obtained results, graph theory is implemented as an intuitive and applicable mathematical tool. Fractal analysis supported by neural networks and graph theory presents the expanding field in current materials science research, especially regarding the significance of the design of advanced ceramic materials.

Aiming to establish a relationship between pore surface, grain size and a particle’s Brownian motions with measured dielectric properties, we modified BaTiO₃. The self-similarity of nature of the biosystems brought us to the idea to use fractal analysis. The recognized geometry structure controls chaotic structures, so we have disorder controlled towards order. For the reconstruction of the bacterial or virus motions, we used a fractal interpolation curve. Artificial neural networks constitute the second approach used to calculate the properties of grain boundaries, based on the measurements of bulk samples. The usage of simple operations for solving complex mathematical problems is possible due to their biomimetic ability. The graph theory is applied as a third method, and we developed 1D, 2D and 3D cases.

This paper is organized as follows. After the introductory part, we present possibilities for applications of fractals and fractal analysis (Section 2), artificial neural networks (Section 3) and graph theory (Section 4). Then, we compare methods (Section 5), and we give some conclusions regarding the efficiency of the methods. At the end of this paper, a list of references is provided.

2. Fractals and Fractal Analysis

We can find fractal nature within structures of physical systems and within surfaces of contacts, from micro-structures up to the global bulk shapes and down to the nano-scale level (Figure 1). Fractals are scalable to any size in nature. This includes macro, micro and nano space [1]. Fractal nature characterization can be applied on large or small elements, on microelectronic ceramic materials and on biophysical systems. Here, we consider fractal nature within the whole universe as one general phenomenon. There are many examples in nature (Figure 1). There are examples in the morphological and in the functional sphere: telecommunication noise, a statistical performance of a spoken language, different plants’ biomasses and animal species variations.

The common property of these objects is that their structure is replicated. Such objects are called fractals, and they possess the self-similarity characteristic—each part of an object is similar to the whole.

The term fractal is derived from the Latin adjective fractus, and it means fragmented or irregular. All those objects and properties were finally systematized by Benoit Mandelbrot in the 1980s [2], and this gave a new way of thinking about the order of things in nature. The idea of fractal analysis development was inspired by self-similarity in biosystems in nature. The recognized geometry structures establish control of the chaotic structures (Figure 2).

The Euclidean classical geometry objects idealize abstractions from real life and use them in modeling. As their structure is much more complex, it could not always be adequate, leading to unfavorable results. Fractal objects cannot be successfully described without involving infinity because of their complexity.

The crystal growth, chaotic motion, turbulence, etc., cannot be properly described by Euclidean geometry because of their high irregularity. Thus, these objects became subjects of fractal geometry (Figure 3).

Intuitive dimensions of Euclidean geometry objects are described with a topological dimension (TD): TD = 1 is curves, TD = 2 is surfaces and TD = 3 is solids. In order to recognize fractals, we use Hausdorff (fractal) dimension FD, a natural extension of topological dimension. The Hausdorff dimension is not a unique descriptor. Many other descriptors of fractal properties exist.

Fractal nature analysis offers a specific approach in this field (see Refs. [3,4]), and today, it is one of the most expansive research fields (see Refs. [5,6,7]) and there are various possible applications (see Refs. [8,9]).

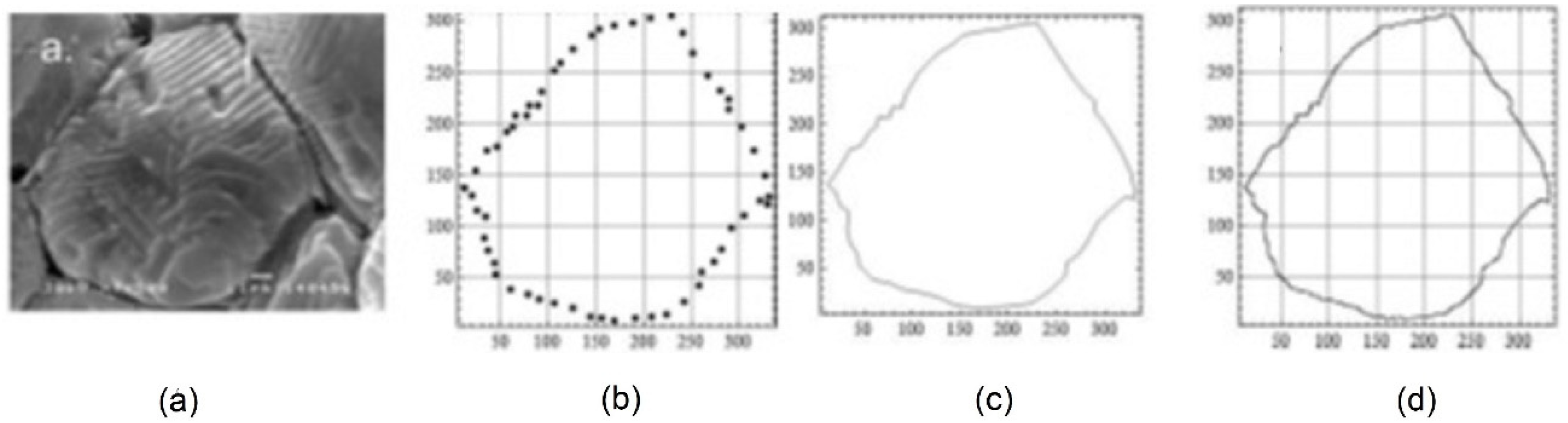
The new procedure in the characterization of materials’ micro-structure is illustrated in Figure 4. This is a fractal method of structural material reconstruction, aiming to make an advanced prognosis of microstructural property possible [10] (Figure 4). Electronic microscopy methods enable obtaining micro-graphs, regardless of resolution and magnification. This can be applied to any material, but was applied here on BaTiO₃, refractory, silicate and other ceramics.

The contribution of fractal corrections has already been explored, observed and explained in previously published works, such as on the Heywang intergranular capacity model, the Curie–Weiss law, the Schottky barrier and the Clausius-Mossotti relation [11,12]. The relation with other dielectric and ferroelectric material parameters is successfully explained by introducing the complex fractal correction factor α (grain and pore surface influence and Brownian particle motion) [4]. There are certain interesting parameters [10]: normalized surface fractality (0 < α_S < 1), fractal parameter that transforms fractality of porosity (0 < α_P < 1) and dynamic correction factor (0 < α_M < 1):

$${\alpha }_S=1-\left[D{H}_f\left(S_S\right)-D_T\left(S_S\right)\right]$$

$${\alpha }_P=1-\left[D{H}_f\left(S_P\right)-D_T\left(S_P\right)\right]$$

$${\alpha }_M=1-\left[D{H}_f\left(L_M\right)-D_T\left(L_M\right)\right].$$

Parameter α, the fractal corrective factor (0 < α < 1), was established to correct the measured BaTiO₃ ceramic sintering temperature T and to obtain the real temperature due to the fact that T is influenced by fractality.

$$T_f=\alpha T.$$

If we consider the Curie–Weiss law,

$${\epsilon }_r(T)=\frac{C_c}{T-T_S}$$

the dielectric constant is:

$${\epsilon }_r(T_f,\alpha )=\frac{C_c}{T-T_C}=\frac{C_c}{\left(T_f/\alpha \right)-T_C}=\frac{\alpha }{T_f}\frac{C_c}{1-\alpha \left(\frac{T_C}{T_f}\right)}$$

If u = v = w = 1/3, then:

$${\epsilon }_r(T_f,\alpha )={\epsilon }_r(T_f,{\alpha }_S,{\alpha }_P,{\alpha }_M)=\frac{C_C}{\left(\frac{3T_f}{{\alpha }_S+{\alpha }_P+\dim {\displaystyle \sum _{i=0}^{n}X\left(t_i\right)Bi\left(t\right)-1}}\right)-T_C}$$

This is an important equation, because it shows that the dielectric constant is the function of fractal parameters, which defines the relation between electronic and microstructure properties. The ceramic material changes morphology during sintering, and this leads to a change in intergranular physical properties. In our case, these are dielectric and ferroelectric properties. Modification of the ceramic also alters these properties, and it is often employed to enhance these properties.

The application of this type of fractal analysis for the determination of dielectric properties at the grain boundary level for samples obtained with different sintering conditions and modifying agents will enable researchers to build more efficient materials for higher-level microelectronic devices and integrations.

3. Artificial Neural Networks

The next part of this research considers the application of artificial neural networks as one biomimetic approach for a material’s thorough characterization at the microstructure level. They offer a possibility for using a simple mathematical apparatus for solving complex problems due to their ability to mimic biological neural cells. During the learning process of back propagation neural networks, an error that occurs in the output is spread backwards throughout the whole network. This enables electrophysical properties to be processed in the same manner [13,14].

Neural networks are used for the determination of dielectric properties at the nano/grain boundary scale. Considering the material structure as a neural network, any signal measured on the sample surface could be spread through the network. This enables the calculation of measured signal components. In this manner, we can perform calculation of intergranular physical values.

Neural networks constitute an interesting and expansive research field (see Refs. [15,16]) with a multitude of applications (see Refs. [17,18,19,20,21,22]).

Artificial neural networks are the original method and tool used for mapping data, and can be applied on parameters of microelectronic ceramics. This is due to biomimetic similarity. The inspiration for the artificial neural networks came from the biological nervous system, functionally organized on the neural network principle.

The neuron, as the fundamental unit of the nervous system, has the main role in this process, transferring neural impulses as a change in electric potential. These signals are processed through artificial neurons. They use a simple function for processing input signals, and sensitivity to inputs is represented as an adjustable parameter. The integrated network output is practically the sum of outputs of the large number of inner neurons.

Neurons that receive inputs of the whole network compose the input layer while neurons that generate the network output compose the output layer. All other neurons, if any, are in the hidden layers (Figure 5).

Neural network training is a process of adjusting the neural network parameters. It could be supervised or unsupervised. Supervised learning implies that desired neural network input–output mapping is known in advance. Neural networks generate some output for some input signal. The value of this output depends on input values, as well as on the values of the weight coefficient. All weight coefficients must have correct values in order to perform correct mapping and to obtain appropriate input. Starting with random values of weight coefficients, through adjusting, known as network training, we reduce unpredictable error and improve accuracy by adjusting the weight coefficients. This network property to spread error signals could be widened, allowing any signal of interest, such as a material’s electrophysical properties, to be processed.

In Refs. [10,16], we showed an application of neural networks on sintering and calculation of various parameters within different sintering temperature intervals, especially the density of sintered material, measured on a surface. The result of this research is the study of a functional relation definition between voltage (U), sintering temperature and relative capacitance change, from the bulk sample surface down to the coating thin films around the grains during consolidation. Therefore, ANNs represent a novel tool and method for the prediction of microelectronic parameters around the grains in the thin ceramic films based on the bulk surface measurements, opening new perspectives in microelectronic miniaturization. The network structure is identified here with grains of sintered material.

4. Graph Theory

Graph theory is suitable for describing and modeling different problems in technology, computer science, mathematics, engineering and nature. It is one of the simplest and most applicable mathematical fields. Graph theory has one special advantage—a mathematical approach, which enables visualization of the problems and easy application of graph algorithms to some new problems [23], even if they are not closely related to graphs. Graph theory is widely used in various fields: computer science [24,25,26], energy, chemistry [27,28,29,30,31,32], traffic [33,34,35], medicine [36,37], social networks [38,39,40], etc.

If we graph any problem or process from the materials science field, then it is possible to realize more efficient simulation of these processes. Moreover, we can use various algorithms for graph operations and calculations on a large data set. Such calculations are typical for models with high grain numbers. Matrices are suitable for presenting and describing graph properties, and the most used matrices are the adjacency matrix and the incidence matrix.

Developing methods for the design of ceramic materials and processes is important. We assume that a ceramic structure is a coating of multiple thin layers around the grains that are mutually interconnected. The design of such a structure using a graph has already been demonstrated [41,42]. Basic elements of ceramic structures are grains and pores, and they are represented by vertices in graphs and interconnecting lines between them.

There is another type of connection between artificial neural networks and graphs. The novel approach entails a graph theory application for electronic parameters distributing and networking between the grains, to compare them with the values measured on the sample. Different numbers of neighboring grains and different voltages have shown that capacitance change can be successfully calculated on the layers between grains using graph theory.

An original application of the graph theory is developed. It is a specific tool with which we can obtain and control intergranular parameter changes distributed from the global values measured on each bulk sample. Thus, we practically use a graph network as, e.g., an electrical–electronic network of parameter values based on measured values, such as distribution per grain and every few connected grains.

We developed the application of the graph ceramic structures with adequate mathematical calculations with 1D and 2D examples and equations. By introducing graph theory, capacitance change can be determined locally between two grains. In the area of miniaturization and micro-packaging, these have given us a new perspective, because we now have the method to obtain the values of electrical–electronic–dielectric parameters on a micro level, but not only as a statistically variable global measured result distribution (example in Figure 6).

5. General Approach

The main idea of this general approach draws from Refs. [10,13,41]. It is possible to show it on example of modified barium–titanate thin film synthesis under various conditions and with a combination of Yttrium-based inorganic and organometallic modifying agents, with the expected core–shell structure (Figure 7).

After the experimental fractal nature microstructure analysis (Figure 8), we use the results for the next step in synthesis with the adopted improvements based on predictions from fractal data analysis.

The next step in synthesis is the characterization of the microstructure (FESEM, STEM, EDX, etc.), including the ferroelectric, dielectric and ferromagnetic properties of obtained barium–titanate nanoparticles, especially on the nanoscale between coated ceramic grains. After the experimental fractal nature microstructure analysis (Figure 8), we use the results (

Table 1. Dielectric constant and tangent loss at 1 kHz of BaTiO₃ doped by different types of Y.

Sample	KZM100-Y2O3	BT02-Y2O3
Dk	394	561
Df	0.029	0.045

and

Table 2. KZM100-Y₂O₃ capacitance change with DC bias.

Capacitance change, %	100	100.12	108.78	111.67	114.00	114.27	114.00	56.23
V, DC bias	0	1	2	3	4	5	6	7

) for the next step.

Next, we apply fractal analysis (Figure 9) for the correction of different models and physical equations to determine the influence of grain and pore size and shape, along with the Brownian motions, on the changes in dielectric properties. We implement artificial neural networks to calculate and define the values of electrophysical parameters between barium–titanate grains, based on appropriate measurements on the bulk samples (Figure 10). Within the application of the artificial neural network, we use graph theory to better understand and present electrophysical parameters.

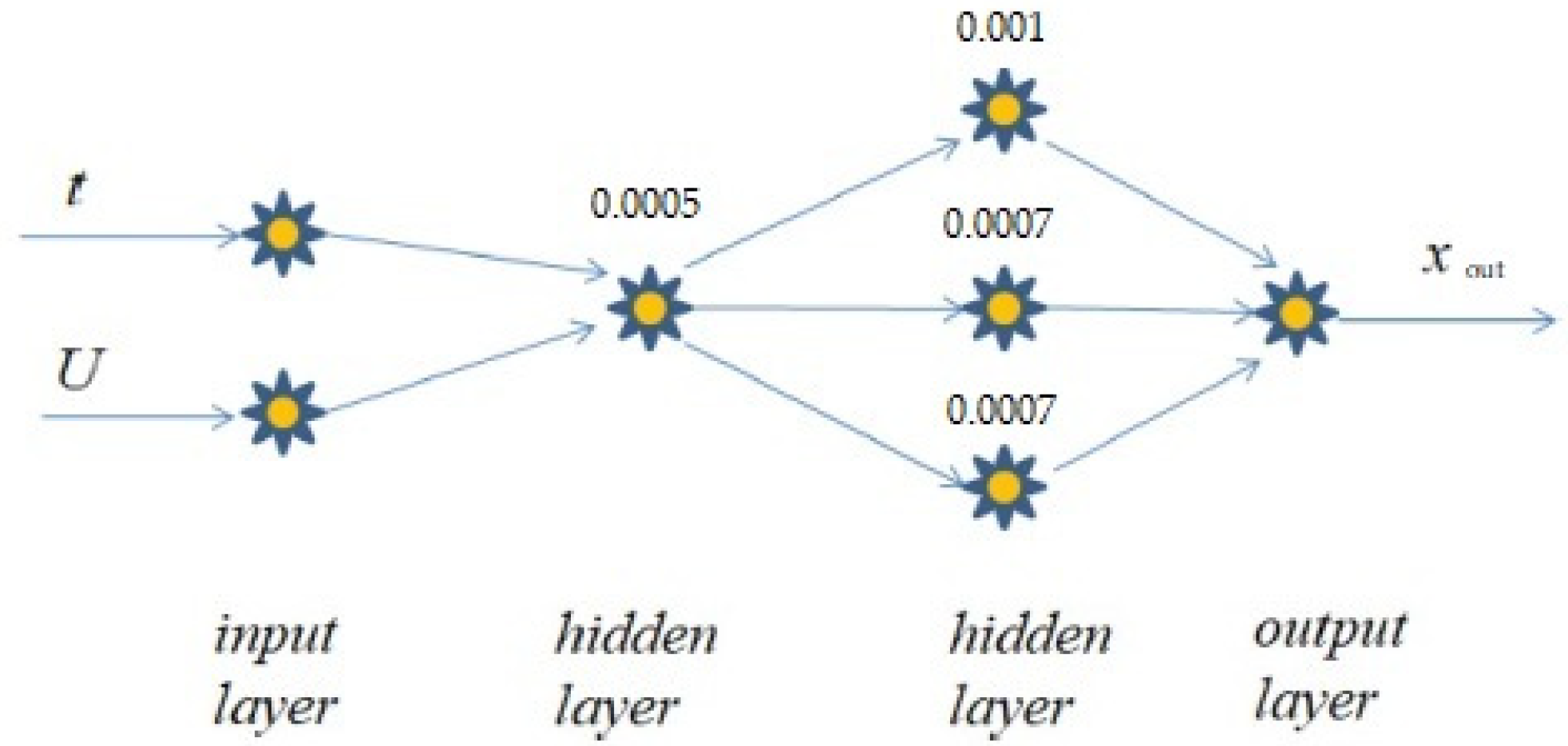
By this successful experience, it is possible to apply the results and approach to some other electro-physical characteristics, such as resistivity or inductivity. It is also possible to design a neural network application, not only for sintering temperature, but for sintering pressure or sintering time. The increase in the number of neurons and hidden layers will increase the micro-capacity calculation accuracy.

An example of a neural network with two hidden layers with one neuron in the first and three neurons in the second hidden layer with calculated relative capacitance values in hidden layers is depicted in Figure 11. The value of the calculated error is shown in

Table 3. Network error.

Neuron	First Hidden Layer	Second Hidden Layer
1	−0.08029	−0.18172
2	-	−0.12159
3	-	−0.11799

(see Refs. [22,23]).

We can also use graph theory for the same or similar purpose. A graph model of grain structure for n = 8 vertices (grains) and m = 13 edges is shown in Figure 12 as an example. Suppose that we can divide overall capacitance change into a local measure that characterizes the relationship between two grains (two vertices in graph). For example, for a DC bias of 25 V, we have an overall capacity change of 68.73 [41].

After the presentation and explanation of the three methods, and after their comparison, we can draw some conclusions regarding the possibility and efficiency of their use.

Conclusion 1:

Instead of the most commonly used approximative methods, numerical methods or some statistical approaches in the application of mathematics in ceramic structure analysis, the use of fractal theory, artificial neural networks and graph theory is “one step ahead”. These methods offer better precision and simplify mathematics, and there is an obvious improvement and a new quality in mathematics applications in this scientific field.

Conclusion 2:

Fractal theory, as a mathematical tool in ceramic structure analysis, has a special advantage in applications when we cannot obtain precise enough results using classical Euclidian geometry. The use of the Hausdorff dimension and fractal correction brings us to better results with improved precision.

Conclusion 3:

Artificial neural networks, when compared with other mathematical tools, have one key advantage—a network training process. Having this in mind, their use can primarily contribute to situations where time consumption is not crucial, but where precision in ceramic structure analysis is essential. Additionally, when adding more neurons in hidden layers, the increased number of neurons leads to improved precision.

Conclusion 4:

Graph theory, as a simple and visual mathematical field, can be useful in situations where graphical representation (one-dimensional, two-dimensional or three-dimensional) of ceramic structure is important and can contribute to easier modeling and simulation processes. The simplicity of mathematical tools while using graph theory, mostly consisting of addition and multiplication of matrices, is an additional advantage of this mathematical tool for ceramic structure analysis.

Conclusion 5:

Each of the three methods has its own specifics, but all of them are complementary, so they cover almost all aspects and needs for mathematical tools in the analysis of ceramic structure. This makes them powerful research tools to reach new results and widen frontiers in material structure analysis.

6. Conclusions

Fractal theory, artificial neural networks and graph theory offer new ways of conducting analysis of ceramic structures. This is especially obvious while describing and modeling the shapes of grains and establishing the relations between electrophysical properties and morphology. This research, which deals with all three methods, has significance from the point of view of all aspects of ceramic microstructure consolidation prognosis. It also has significance regarding the possibility of having better insight into some internal properties.

Using fractal correction and fractal dimension during analysis, it is possible to obtain more precise results. Through this method and results, we are opening new fractal microstructure scale frontiers and technological processes. Using artificial neural networks is especially important because of the possibility to obtain better precision and to reduce error through the process of back propagation. Graph theory simplifies applications where we can transform whole problems into visual models and then into matrix form. Many matrix algorithms and graph algorithms are available for easy use in ceramic structure analysis.

With this successful experience, we can apply this advanced knowledge to other electro-physical characteristics such as resistivity, inductivity, etc. In future research, we plan to develop new applications of the three approaches. Regarding fractals, we will extend the obtained method regarding capacity parameters between two pores, which are important as influences on a sample’s total bulk capacity. Regarding artificial neural networks, we will continue to increase the number of neurons and hidden layers, which improves the micro-capacity calculation accuracy.

The idea of joint examination and linking of living and nonliving systems as a biomimetic approach could be of great importance for further microelectronic miniaturization and integration, and also for developing new advanced technologies for complex biodevices. We plan to apply all three methods in this field.