Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative
Abstract
1. Introduction
2. Fractional Calculus Operators
3. Constructive Equations
4. Solutions Procedures
4.1. Temperature Distribution
4.2. Velocity Distribution
5. Results and Discussions
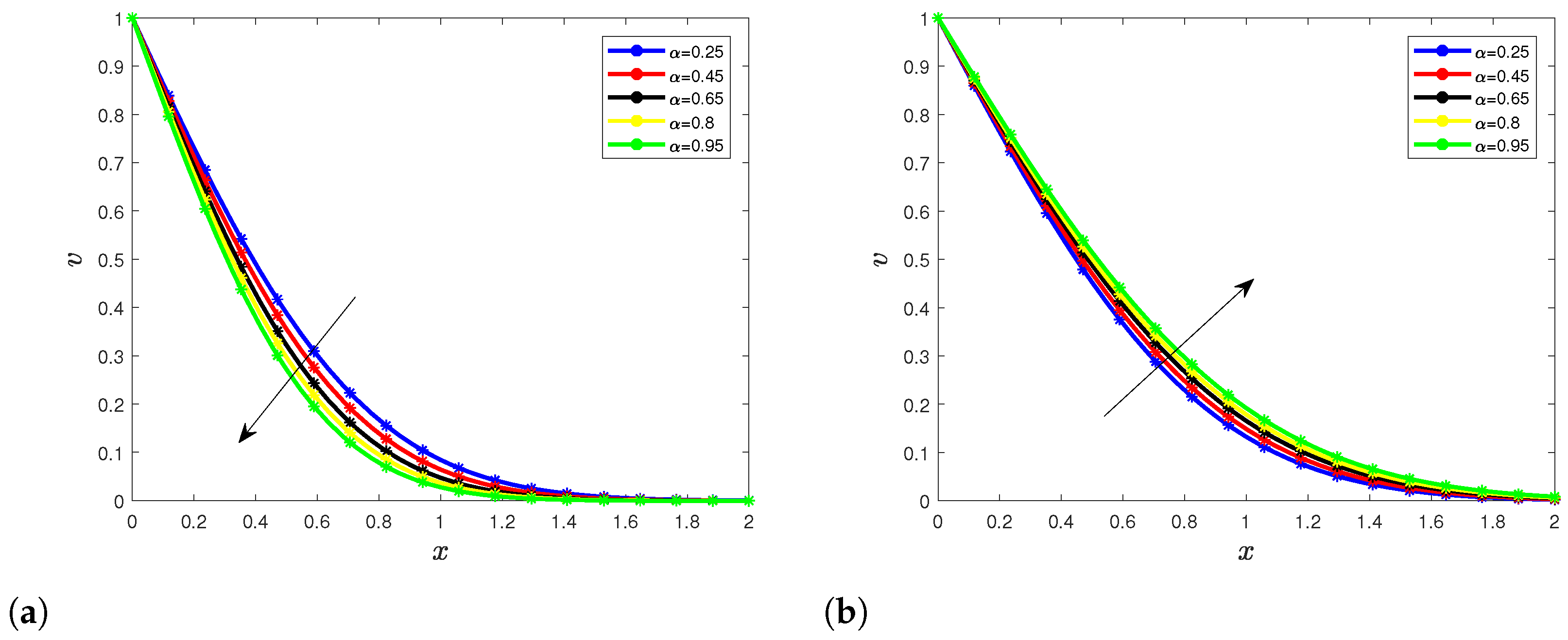
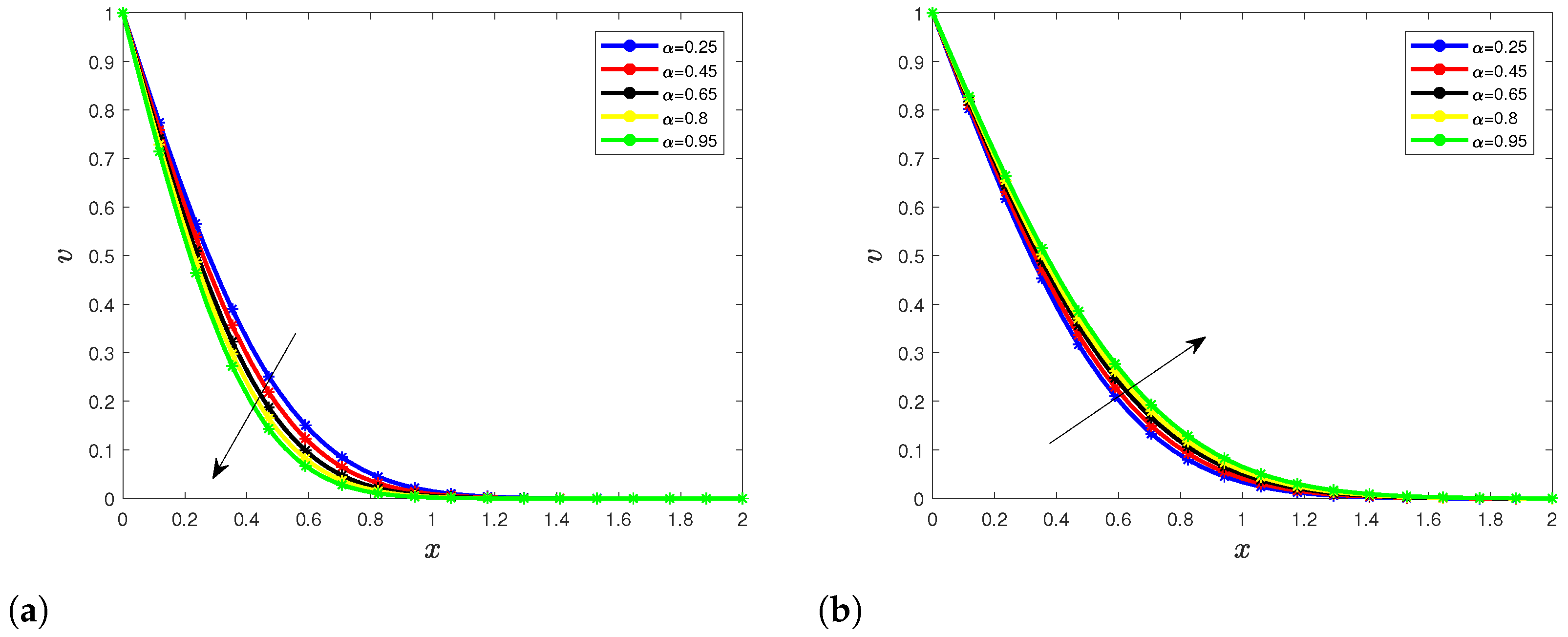
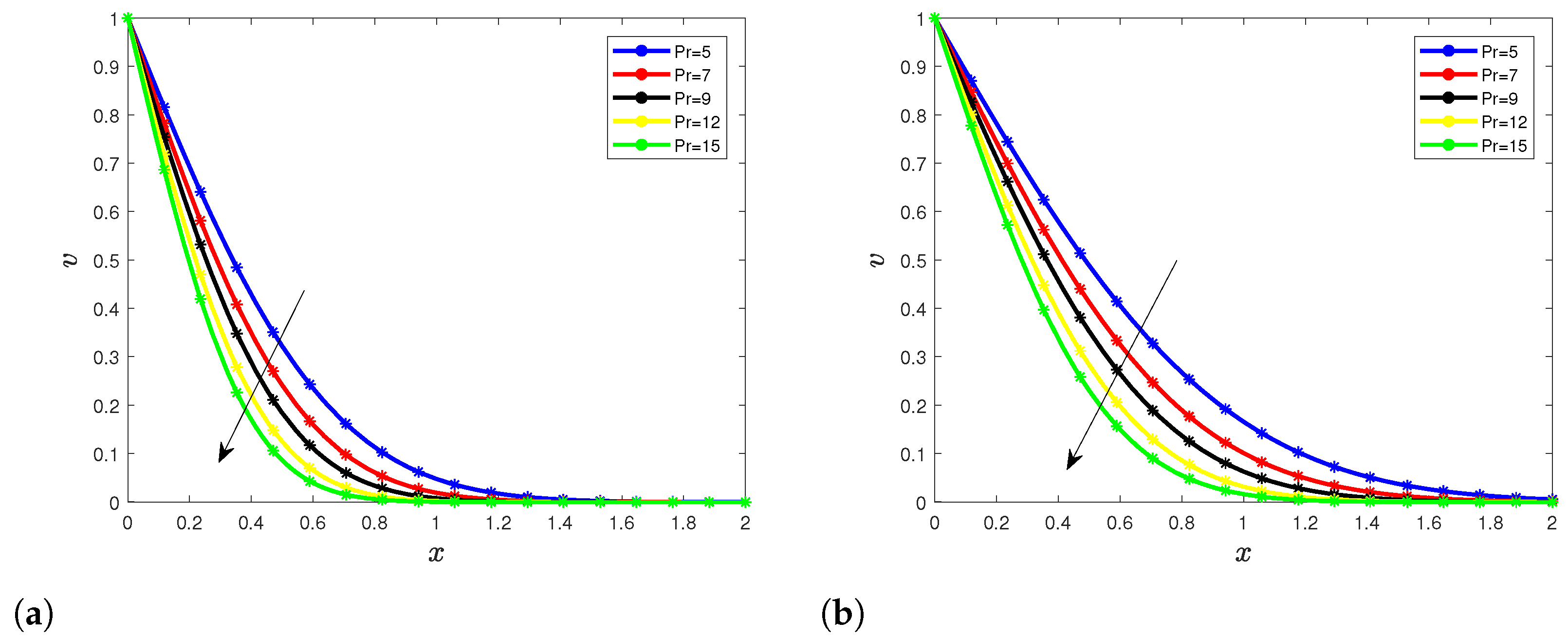
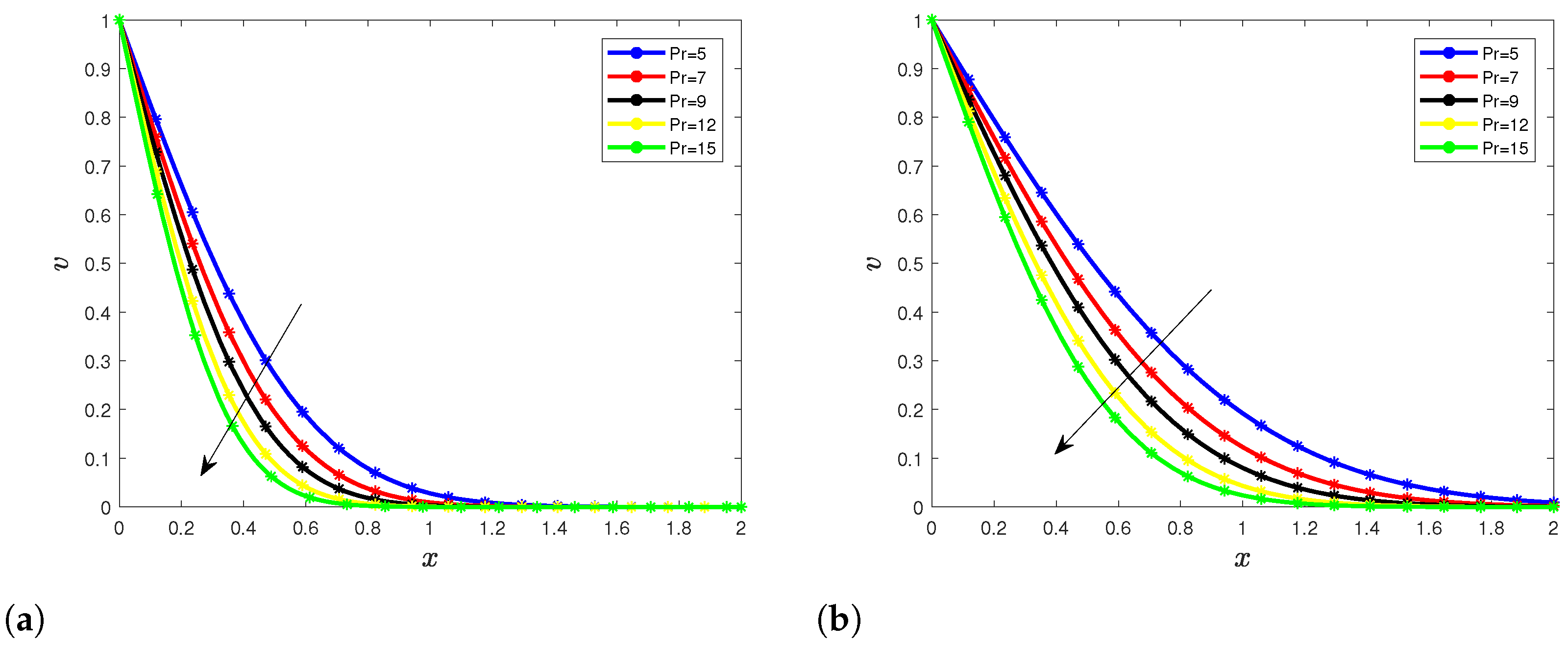
5.1. Temperature Profile
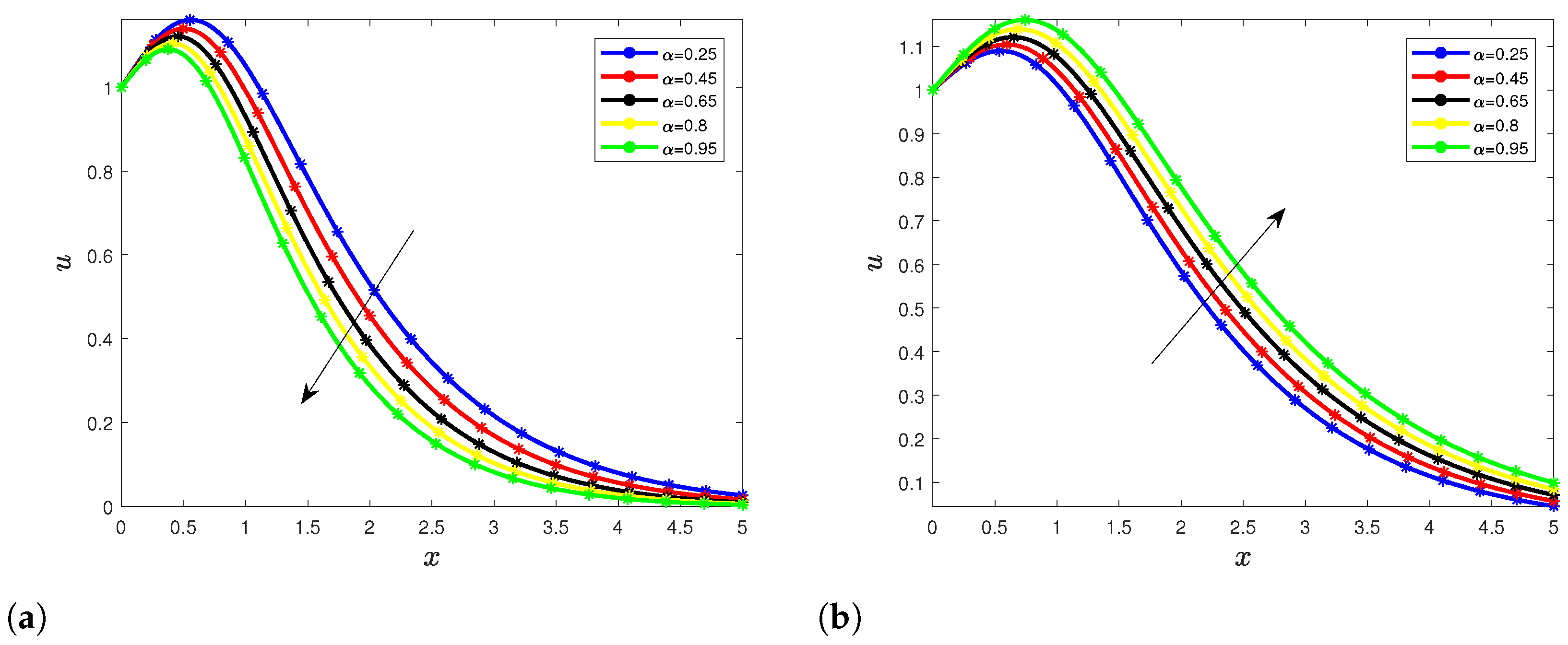
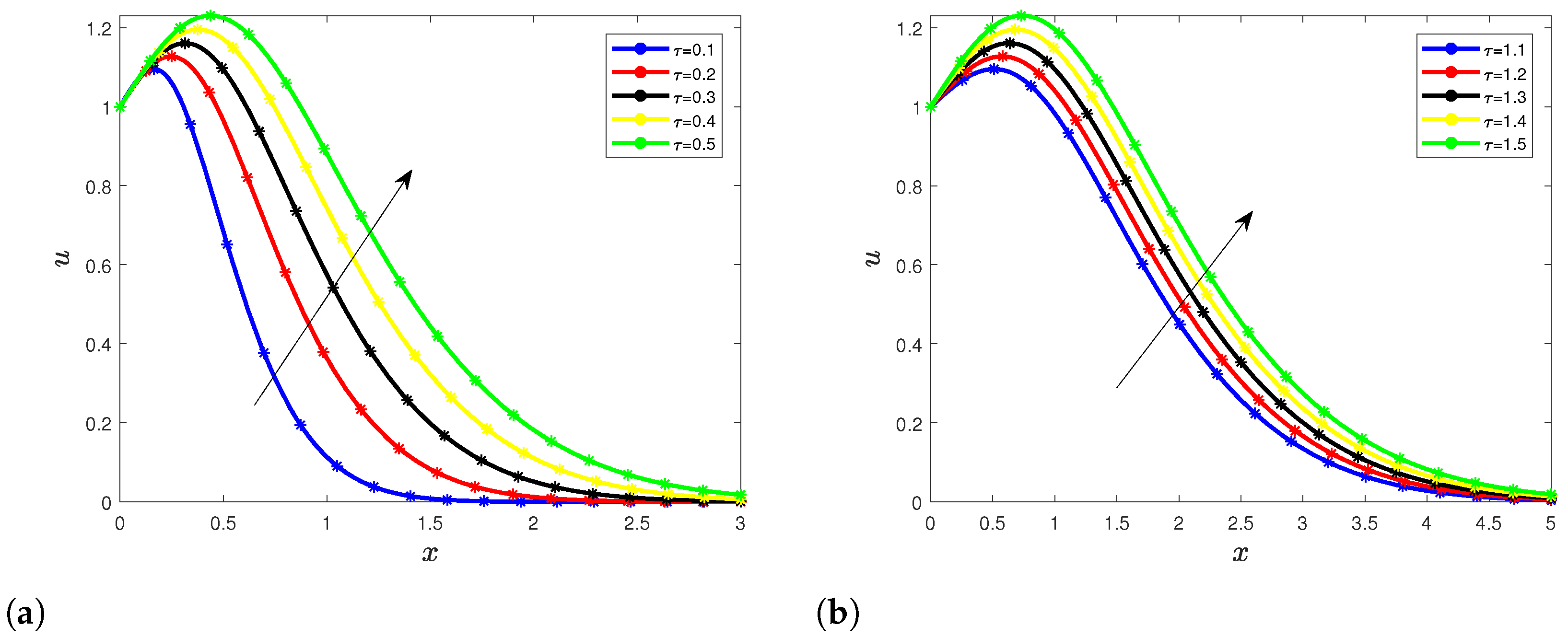
5.2. Velocity Profile
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atangana, A.; Araz, S.I. Extension of Atangana-Seda numerical method to partial differential equations with integer and non-integer order. Alex. Eng. J. 2020, 59, 2355–2370. [Google Scholar] [CrossRef]
- Qurashi, M.M.A.; Korpinar, Z.; Baleanu, D.; Inc, M. A new iterative algorithm on the time-fractional Fisher equation: Residual power series method. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Avci, D.; Yavuz, M.; Ozdemir, N. Fundamental Solutions to the Cauchy and Dirichlet Problems for a Heat Conduction Equation Equipped with the Caputo–Fabrizio Differentiation; Nova Science Publishers: Hauppauge, NY, USA, 2019; pp. 95–107. [Google Scholar]
- Lohana, B.; Abro, K.A.; Shaikh, A.W. Thermodynamical analysis of heat transfer of gravity-driven fluid flow via fractional treatment: An analytical study. J. Therm. Anal. Calorim. 2021, 144, 155–165. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Birajdar, G.A. An Implicit Numerical Method for Semilinear Space-Time Fractional Diffusion Equation. Dyn. Contin. Discret. Impuls. Syst. Ser. A Math. Anal. 2020, 27, 209–217. [Google Scholar]
- Birajdar, G.A. A New Approach for Non-linear Fractional Heat Transfer Model by Adomian Decomposition Method. In Mathematical Analysis and Computing. ICMAC 2019; Mohapatra, R.N., Yugesh, S., Kalpana, G., Kalaivani, C., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Berlin/Heidelberg, Germany, 2021; Volume 344. [Google Scholar]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; p. 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999; p. 198. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Fahd, J.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 2017, 10, 2607–2619. [Google Scholar]
- Fahd, J.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discret. Contin. Dyn. Syst.-S 2019, 13, 709–722. [Google Scholar]
- Wang, X.; Wang, Z. Dynamic Analysis of a Delayed Fractional-Order SIR Model with Saturated Incidence and Treatment Function. Int. J. Bifurc. Chaos 2018, 28, 1850180. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. On the formulation of Adams-Bashforth scheme with Atangana-Baleanu-Caputo fractional derivative to model chaotic problems. Chaos 2019, 29, 023111. [Google Scholar] [CrossRef]
- Hahn, D.W.; Özişik, M.N. Heat Conduction, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Imran, M.A.; Shah, N.A.; Khan, I.; Aleem, M. Applications of non-integer Caputo time fractional derivatives to natural convection flow subject to arbitrary velocity and Newtonian heating. Neural Comput. Appl. 2018, 30, 1589–1599. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef]
- Khan, A.; Abro, K.A.; Tassaddiq, A.; Khan, I. Atangana-Baleanu and Caputo Fabrizio analysis of fractional derivatives for heat and mass transfer of second grade fluids over a vertical plate: A comparative study. Entropy 2017, 19, 279. [Google Scholar] [CrossRef]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef]
- Abro, K.A. A Fractional and Analytic Investigation of Thermo-Diffusion Process on Free Convection Flow: An Application to Surface Modification Technology. Eur. Phys. J. Plus 2019, 135, 31–45. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid model with Caputo-Liouville generalized fractional derivative. Chaos Solitons Fractals 2020, 133, 109631. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A. A comparative study of Atangana-Baleanu and Caputo–Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid. Eur. Phys. J. Plus 2017, 132, 54. [Google Scholar] [CrossRef]
- Abro, K.A.; Atangana, A. A comparative study of convective fluid motion in rotating cavity via Atangana–Baleanu and Caputo–Fabrizio fractal–fractional differentiations. Eur. Phys. J. Plus 2020, 135, 226. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo–Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Sene, N. Integral Balance Methods for Stokes’ First Equation Described by the Left Generalized Fractional Derivative. Physics 2019, 1, 154–166. [Google Scholar] [CrossRef]
- Khan, I.; Shah, N.A.; Vieru, D. Unsteady flow of generalized Casson fluid with fractional derivative due to an infinite plate. Eur. Phys. J. Plus 2016, 131, 181. [Google Scholar] [CrossRef]
- Shen, F.; Tan, W.; Zhao, Y.; Masuoka, T. The Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model. Nonlinear Anal. Real World Appl. 2006, 7, 1072–1080. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–15. [Google Scholar]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Sene, N. A Numerical Algorithm Applied to Free Convection Flows of the Casson Fluid along with Heat and Mass Transfer Described by the Caputo Derivative. Adv. Math. Phys. 2021, 2021, 5225019. [Google Scholar] [CrossRef]
- Sene, N. Stokes’ first problem for heated flat plate with Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Sene, N. Analysis of the fractional diffusion equations described by Atangana-Baleanu-Caputo fractional derivative. Chaos Solitons Fractals 2019, 127, 158–164. [Google Scholar] [CrossRef]
- Sene, N. Analytical solutions and numerical schemes of certain generalized fractional diffusion models. Eur. Phys. J. Plus 2019, 134, 199. [Google Scholar] [CrossRef]
- Fazzino, S.; Caponetto, R.; Patane, C. A new model of Hopfield network with fractional-order neurons for parameter estimation. Nonlinear Dyn. Vol. 2021, 104, 2671–2685. [Google Scholar] [CrossRef]
- Mashayekhi, S.; Miles, P.; Hussainia, M.Y.; Oates, W.S. Fractional viscoelasticity in fractal and non-fractal media: Theory, experimental validation, and uncertainty analysis. J. Mech. Phys. Solids 2018, 111, 134–156. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Mishra, T.N.; Rai, K.N. Fractional single-phase-lagging heat conduction model for describing anomalous diffusion. Propuls. Power Res. 2016, 5, 45–54. [Google Scholar] [CrossRef][Green Version]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Solutions with Wright Function for Time Fractional Free Convection Flow of Casson Fluid. Arab. J. Sci. Eng. 2017, 42, 2565–2572. [Google Scholar] [CrossRef]


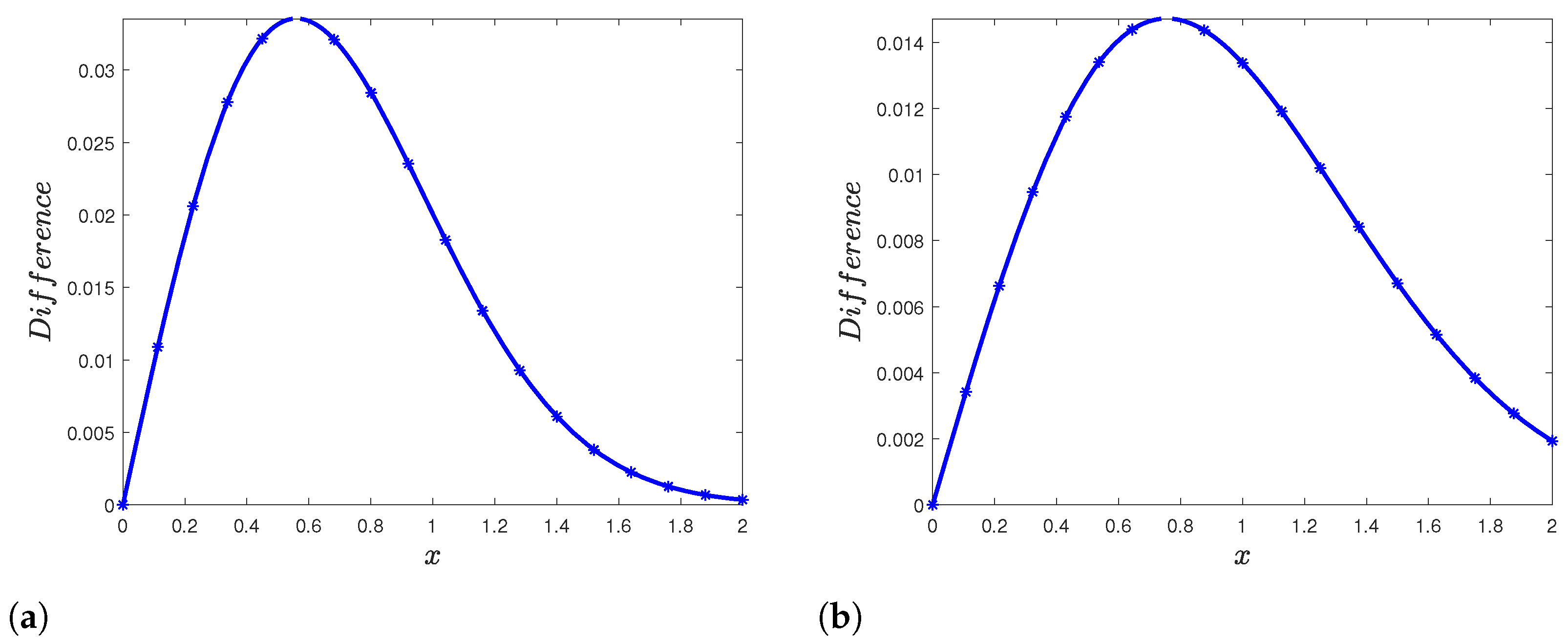
| x | at and | at and | Difference ( |
|---|---|---|---|
| 0.0 | 1.0 | 1.0 | 0 |
| 0.1176 | 0.8392 | 0.8278 | 0.0114 |
| 0.2353 | 0.6848 | 0.6635 | 0.0213 |
| 0.3529 | 0.5426 | 0.514 | 0.0286 |
| 0.4706 | 0.4168 | 0.3842 | 0.03826 |
| 0.5892 | 0.3094 | 0.2759 | 0.0335 |
| 0.7059 | 0.2232 | 0.1917 | 0.0315 |
| 0.8235 | 0.1552 | 0.1276 | 0.0276 |
| 0.9412 | 0.1042 | 0.08152 | 0.02268 |
| 1.059 | 0.06743 | 0.0499 | 0.01753 |
| 1.529 | 0.0007859 | 0.004203 | 0.0034171 |
| x | at and | at and | Difference ( |
|---|---|---|---|
| 0.0 | 1.0 | 1.0 | 0 |
| 0.1176 | 0.8743 | 0.878 | 0.0037 |
| 0.2353 | 0.7516 | 0.7588 | 0.0072 |
| 0.3529 | 0.635 | 0.6451 | 0.0101 |
| 0.4706 | 0.5267 | 0.5392 | 0.0125 |
| 0.5892 | 0.428 | 0.442 | 0.014 |
| 0.7059 | 0.3423 | 0.3569 | 0.0146 |
| 0.8235 | 0.2679 | 0.2825 | 0.0146 |
| 0.9412 | 0.2053 | 0.2193 | 0.014 |
| 1.059 | 0.1542 | 0.1669 | 0.0127 |
| 1.529 | 0.03928 | 0.04561 | 0.00633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sene, N. Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative. Fractal Fract. 2022, 6, 35. https://doi.org/10.3390/fractalfract6010035
Sene N. Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative. Fractal and Fractional. 2022; 6(1):35. https://doi.org/10.3390/fractalfract6010035
Chicago/Turabian StyleSene, Ndolane. 2022. "Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative" Fractal and Fractional 6, no. 1: 35. https://doi.org/10.3390/fractalfract6010035
APA StyleSene, N. (2022). Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative. Fractal and Fractional, 6(1), 35. https://doi.org/10.3390/fractalfract6010035