Improved Results on Finite-Time Passivity and Synchronization Problem for Fractional-Order Memristor-Based Competitive Neural Networks: Interval Matrix Approach
Abstract
:1. Introduction
2. System Description and Preliminaries
2.1. Preliminaries
2.2. Model Description
3. Finite-Time Passivity
- 1.
- When measured output , FOMBCNN (9) is finite-time bounded with respect to .
- 2.
- Under the zero initial values, there exists a constant such that
4. Finite-Time Synchronization
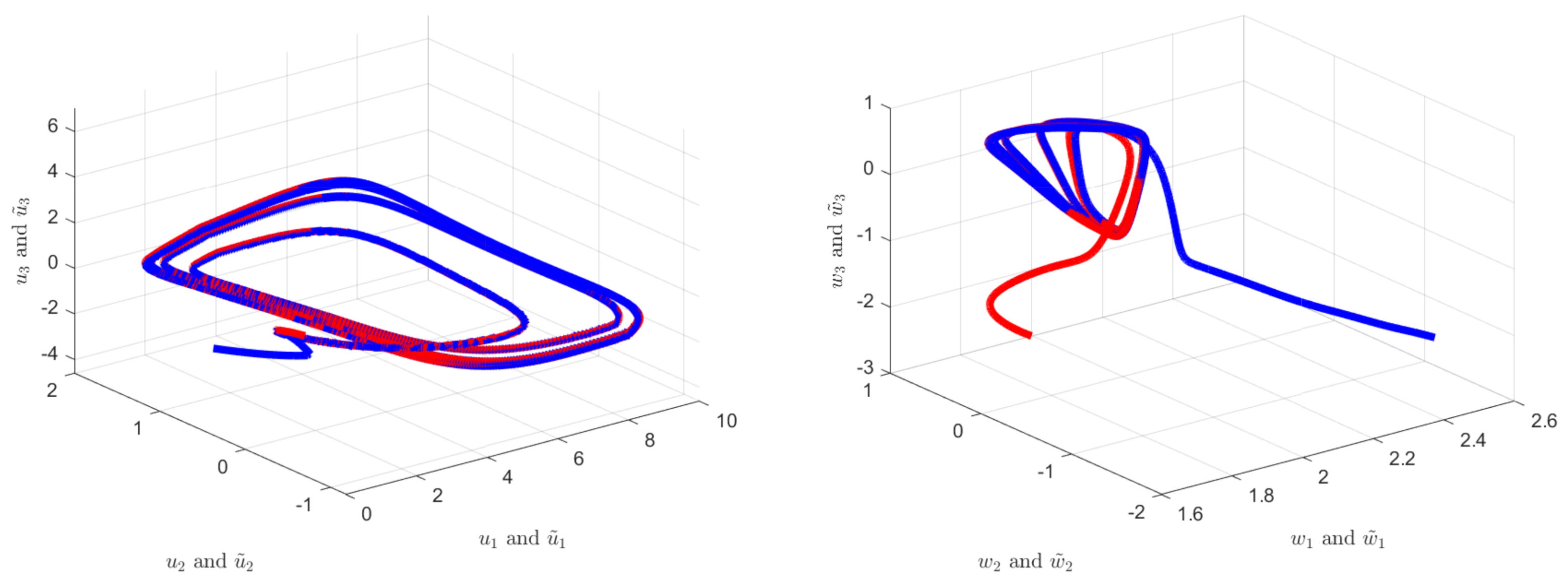
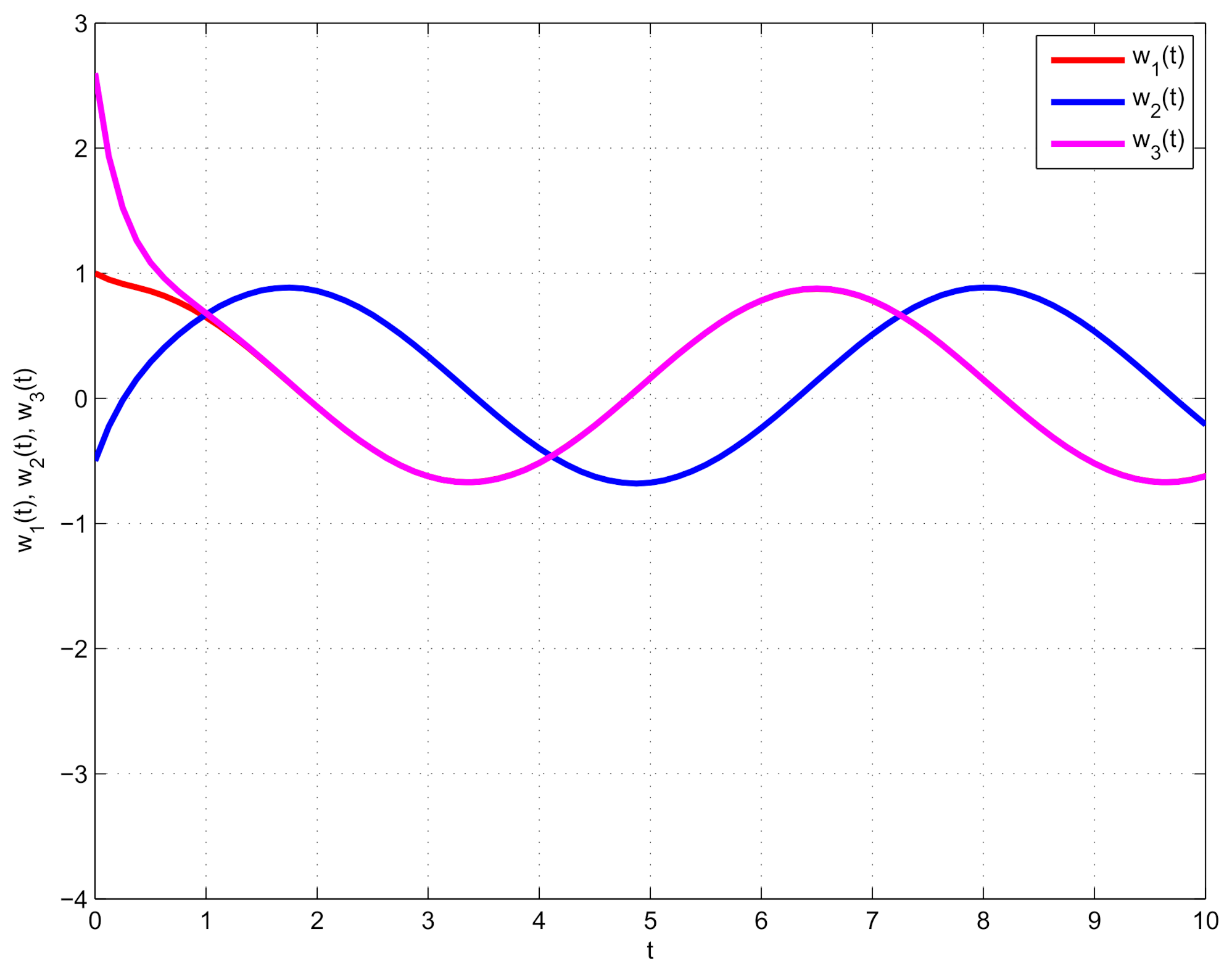
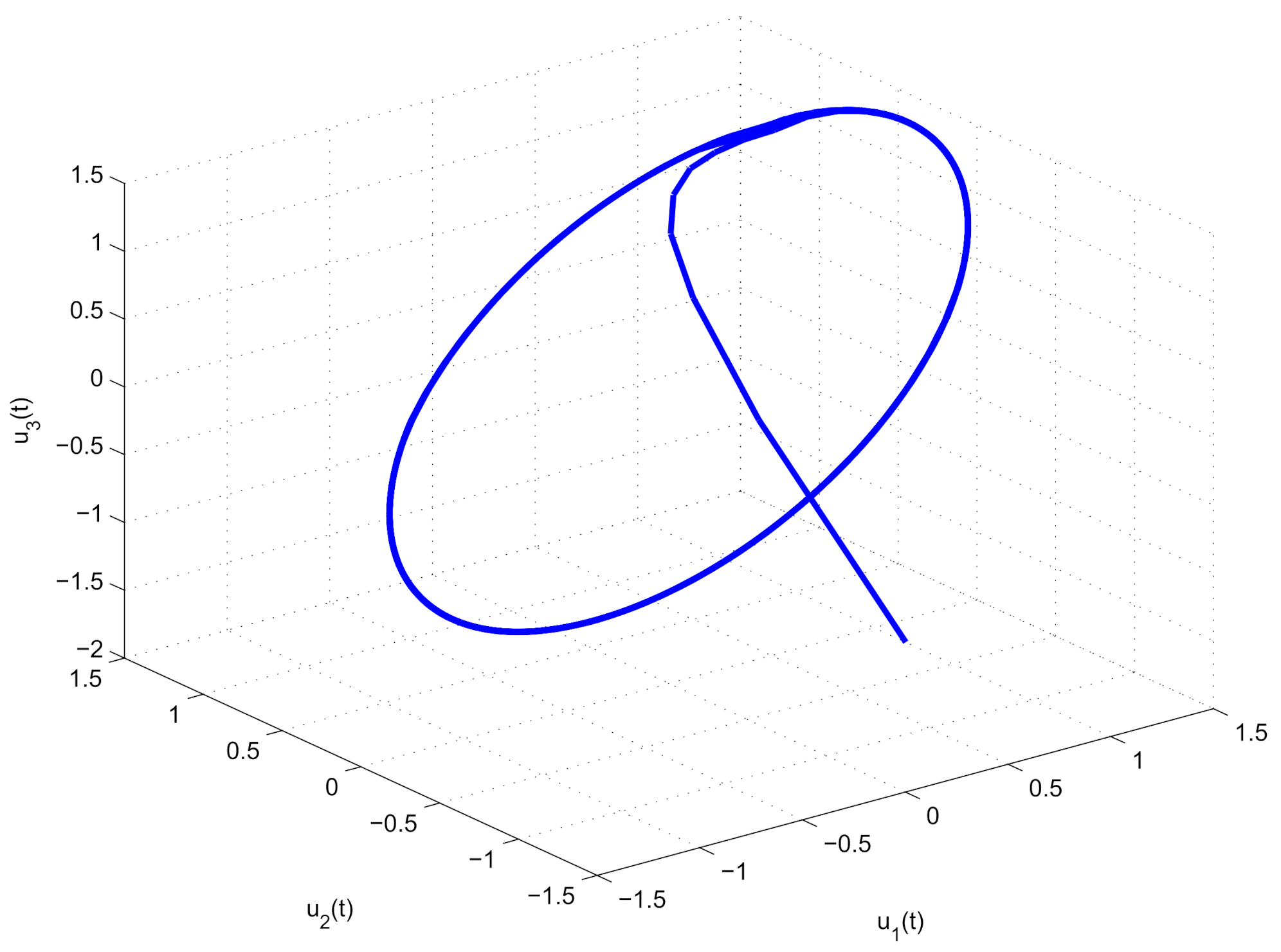
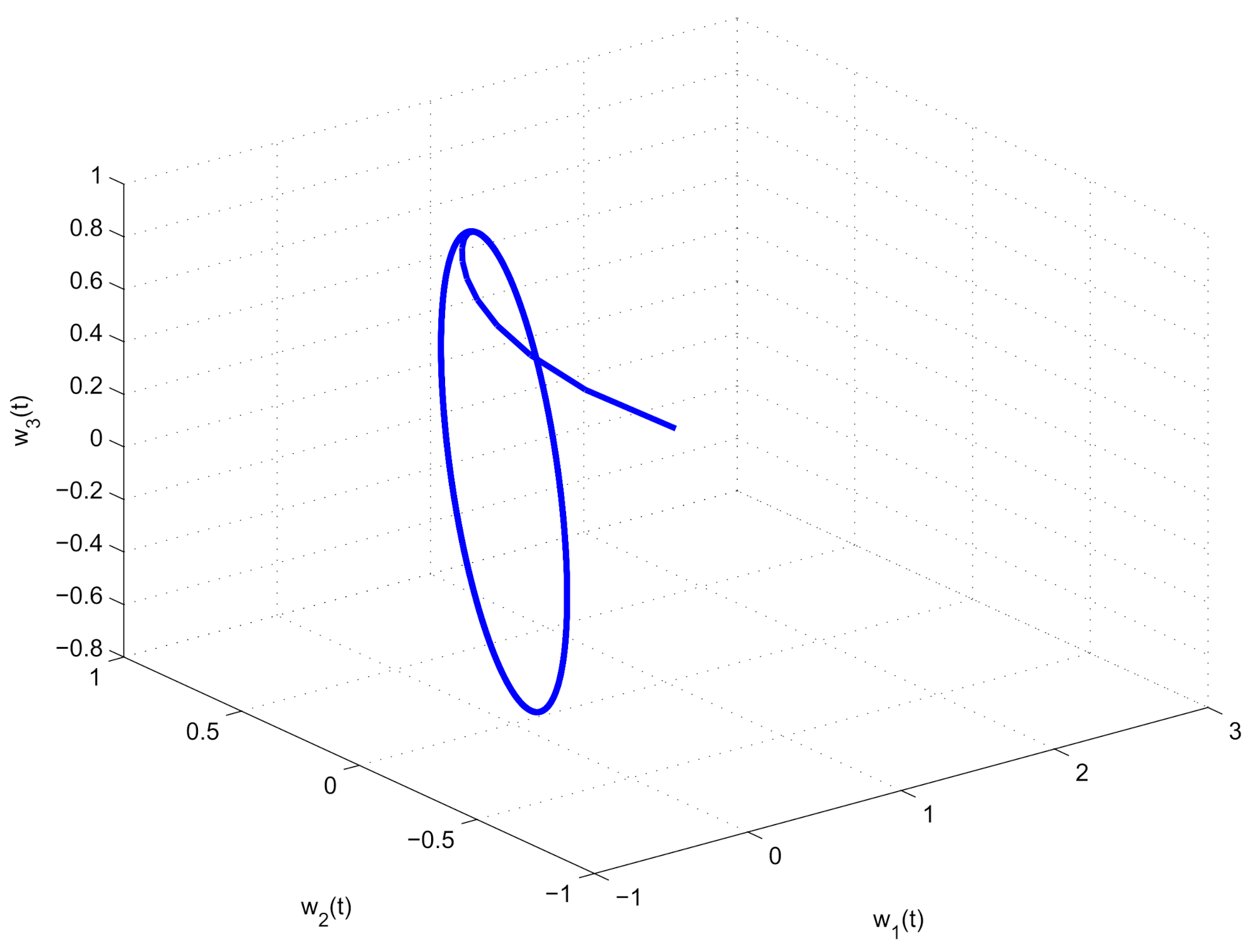
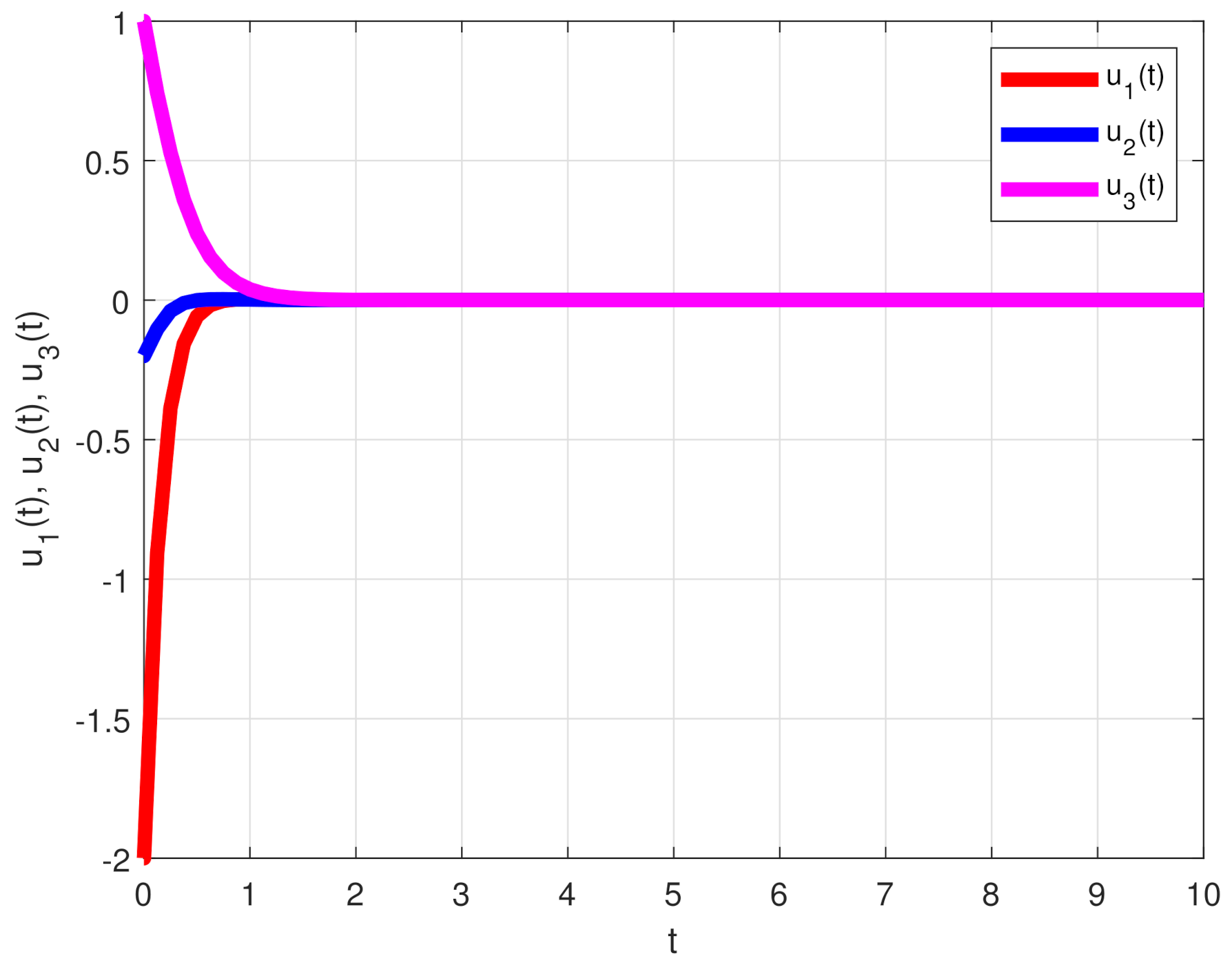
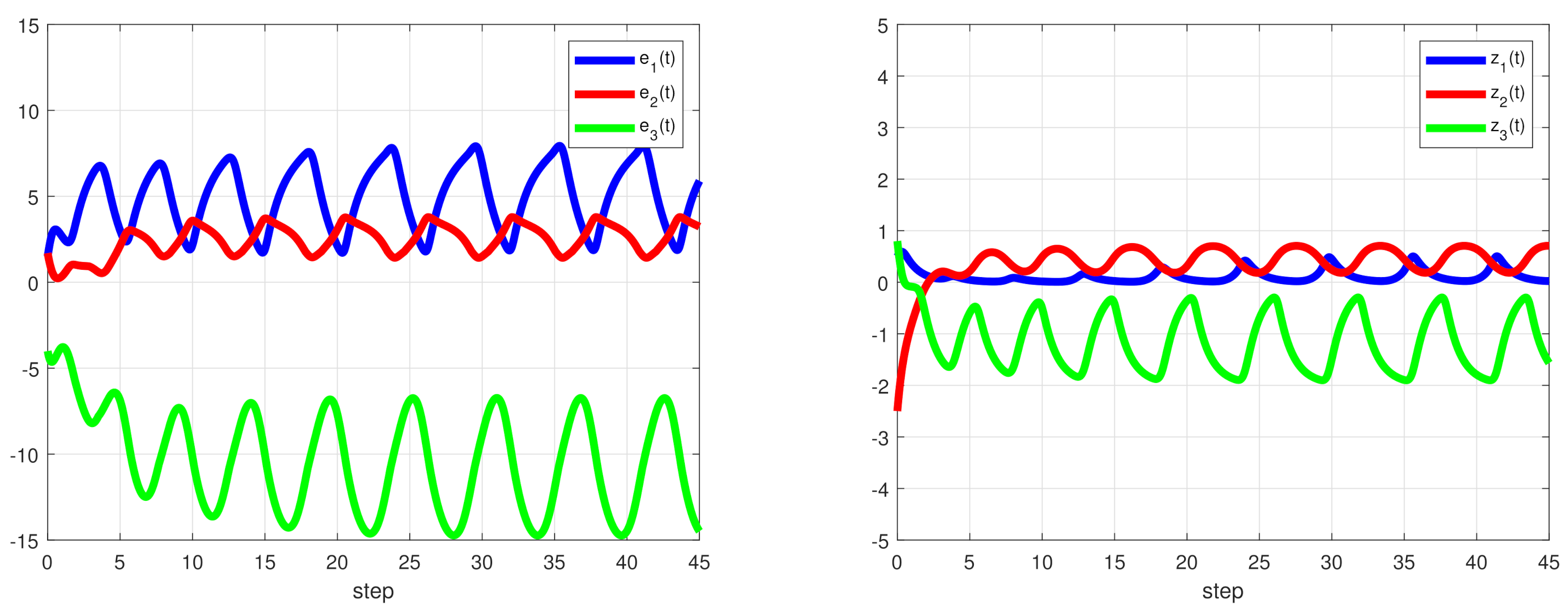
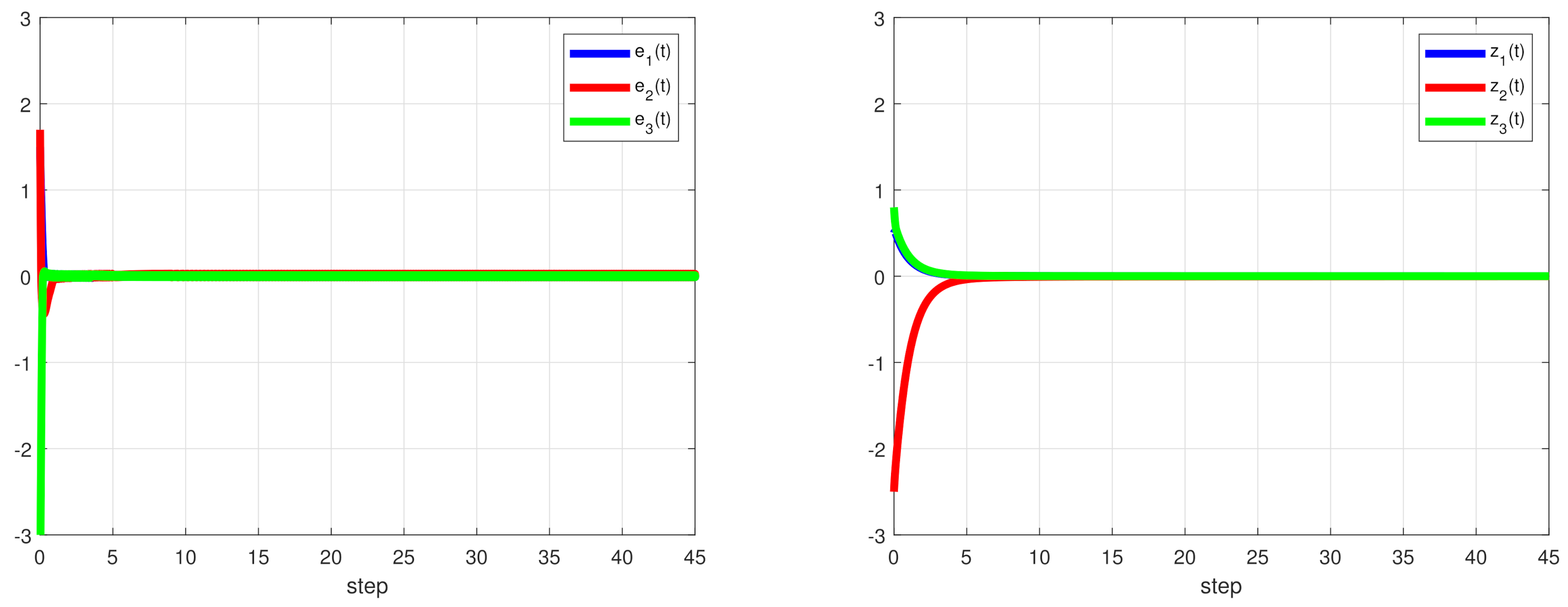
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, Q.; Yu, Q.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Boundedness and global robust stability analysis of delayed complex-valued neural networks with interval parameter uncertainties. Neural Netw. 2018, 103, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Yan, H.; Zhao, Z.; Liu, Y. Global exponential stability of impulsive complex-valued neural networks with both asynchronous time-varying and continuously distributed delays. Neural Netw. 2016, 81, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Wang, Z. Dynamical behaviors of fuzzy reaction-diffusion periodic cellular neural networks with variable coefficients and delays. Appl. Math. Model. 2009, 33, 3533–3545. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Z.; Li, Y. Global exponential stability of BAM neural networks with distributed delays and reaction-diffusion terms. Phys. Lett. A 2005, 335, 213–225. [Google Scholar] [CrossRef]
- Arbi, A.; Cao, J. Pseudo-almost periodic solution on time-space scales for a novel class of competitive neutral-type neural networks with mixed time-varying delays and leakage delays. Neural Process. Lett. 2017, 46, 719–745. [Google Scholar] [CrossRef]
- Duan, L.; Huang, L. Global dynamics of equilibrium point for delayed competitive neural networks with different time scales and discontinuous activations. Neurocomputing 2016, 123, 318–327. [Google Scholar] [CrossRef]
- Yang, X.; Cao, J.; Long, Y.; Rui, W. Adaptive lag synchronization for competitive neural networks with mixed delays and uncertain hybrid perturbations. IEEE Trans. Neural Netw. 2010, 21, 1656–1667. [Google Scholar] [CrossRef] [PubMed]
- Yingchun, L.; Yang, X.; Shi, L. Finite-time synchronization for competitive neural networks with mixed delays and non-identical perturbations. Neurocomputing 2016, 185, 242–253. [Google Scholar]
- Liu, P.; Nie, X.; Liang, J.; Cao, J. Multiple Mittag–Leffler stability of fractional-order competitive neural networks with Gaussian activation functions. Neural Netw. 2018, 108, 452–465. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Fardoun, H.M. Stability and synchronization criteria for fractional order competitive neural networks with time delays: An asymptotic expansion of Mittag Leffler function. J. Frankl. Inst. 2019, 356, 2212–2239. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Alsaadi, F.E. Further synchronization in finite time analysis for time-varying delayed fractional order memristive competitive neural networks with leakage delay. Neurocomputing 2018, 317, 110–126. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Agarwal, R.P.; Cao, J. Stability analysis and robust synchronization of fractional-order competitive neural networks with different time scales and impulsive perturbations. Int. J. Adapt. Control Signal Process. 2019, 33, 1635–1660. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, M.; Cao, J.; Alsaedi, A. Synchronization control of Riemann–Liouville fractional competitive network systems with time-varying delay and different time scales. Int. J. Control Autom. Syst. 2018, 16, 1404–1414. [Google Scholar] [CrossRef]
- Chua, L.Q. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Mathiyalagan, K.; Anbuvithya, R.; Sakthivel, R.; Park, J.H.; Prakash, P. Non-fragile H∞ synchronization of memristor-based neural networks using passivity theory. Neural Netw. 2016, 74, 85–100. [Google Scholar] [CrossRef]
- Qin, X.; Wang, C.; Li, L.; Peng, H.; Yang, Y.; Ye, L. Finite-time modified projective synchronization of memristor-based neural network with multi-links and leakage delay. Chaos Solitons Fractals 2018, 116, 302–315. [Google Scholar] [CrossRef]
- Yang, Z.; Biao, L.; Derong, L.; Yueheng, L. Pinning synchronization of memristor-based neural networks with time-varying delays. Neural Netw. 2017, 93, 143–151. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Zhou, D.; Lin, C.; Chen, J.; Wang, H. Finite-time stabilizability and instabilizability for complex-valued memristive neural networks with time delays. IEEE Trans. Syst. Man Cybern Syst. 2018, 48, 2371–2382. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, J.; Yan, Z. Attractivity analysis of memristor-based cellular neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 704–717. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kim, T.; Pinkham, J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 2000, 27, 115–198. [Google Scholar]
- Lundstrom, B.; Higgs, M.; Spain, W. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335–1342. [Google Scholar] [CrossRef]
- Alzabut, J.; Mohammadaliee, B.; Samei, M.E. Solutions of two fractional q–integro–differential equations under sum and integral boundary value conditions on a time scale. Adv. Differ. Equ. 2020, 2020, 304. [Google Scholar] [CrossRef]
- Alzabut, J.; Viji, J.; Muthulakshmi, V.; Sudsutad, W. Oscillatory behavior of a type of generalized proportional fractional differential equations with forcing and damping terms. Mathematics 2020, 8, 1037. [Google Scholar] [CrossRef]
- Alzabut, J.; Selvam, A.; Dhineshbabu, R.; Kaabar, M.K.A. The Existence, Uniqueness, and stability analysis of the discrete fractional three-point boundary value problem for the elastic beam equation. Symmetry 2021, 13, 789. [Google Scholar] [CrossRef]
- Aadhithiyan, S.; Raja, R.; Zhu, Q.; Alzabut, J.; Niezabitowski, M.; Lim, C.P. Modified projective synchronization of distributive fractional order complex dynamic networks with model uncertainty via adaptive control. Chaos Solitons Fractals 2021, 147, 110853. [Google Scholar] [CrossRef]
- Stephen, A.; Raja, R.; Alzabut, J.; Zhu, Q.; Niezabitowski, M.; Lim, C.P. A Lyapunov–Krasovskii functional approach to stability and linear feedback synchronization control for nonlinear multi-agent systems with mixed time delays. Math. Probl. Eng. 2021, 1–20. [Google Scholar] [CrossRef]
- Wang, F.; Yang, T.Q.; Hu, M.F. Asymptotic stability of delayed fractional-order neural networks with impulsive effects. Neurocomputing 2015, 154, 239–244. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Y.; Xu, X.; Li, L. Global asymptotic stability of impulsive fractional-order BAM neural networks with time delay. Neural Comput. Appl. 2017, 28, 345–352. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Xue, S.; Wang, L.; Wang, Y. LMI conditions to global Mittag–Leffler stability of fractional-order neural networks with impulses. Neurocomputing 2016, 193, 148–154. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Yu, J. LMI conditions for global stability of fractional-order neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2423–2433. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Jiang, M.; Yan, M. Stability analysis of memristor-based time-delay fractional-order neural networks. Neurocomputing 2019, 323, 117–127. [Google Scholar] [CrossRef]
- Zheng, M.; Li, L.; Peng, H.; Xiao, J.; Yang, Y.; Zhang, Y.; Zhao, H. Finite-time stability and synchronization of memristor-based fractional-order fuzzy cellular neural networks. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 272–291. [Google Scholar] [CrossRef]
- Ailong, A.; Zhigang, Z. Global Mittag–Leffler stabilization of fractional-order memristive neural networks. IEEE Tranctions Neural Netw. Learn. Syst. 2016, 28, 2016–2027. [Google Scholar]
- Wenting, C.; Song, Z.; Jinyu, L.; Kaili, S. Global Mittag–Leffler stabilization of fractional-order complex-valued memristive neural networks. Appl. Math. Comput. 2018, 338, 346–362. [Google Scholar]
- Bao, H.; Cao, J.; Kurths, J. State estimation of fractional-order delayed memristive neural networks. Nonlinear Dyn. 2014, 94, 1215–1225. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.H.; Cao, J. Non-fragile state estimation for fractional-order delayed memristive BAM neural networks. Neural Netw. 2019, 119, 190–199. [Google Scholar] [CrossRef]
- Mathiyalagan, K.; Park, J.H.; Sakthivel, R. Novel results on robust finite-time passivity for discrete-time delayed neural networks. Neurocomputing 2016, 177, 585–593. [Google Scholar] [CrossRef]
- Qi, W.; Gao, X.; Wang, J. Finite-time passivity and passification for stochastic time-delayed Markovian switching systems with partly known transition rates. Circuits Syst. Signal Process. 2016, 35, 3913–3934. [Google Scholar] [CrossRef]
- Rajavel, S.; Samidurai, R.; Cao, J.; Alsaedi, A.; Ahmad, B. Finite-time non-fragile passivity control for neural networks with time-varying delay. Appl. Math. Comput. 2017, 297, 145–158. [Google Scholar] [CrossRef]
- Song, Q.; Liang, J.; Wang, Z. Passivity analysis of discrete-time stochastic neural networks with time-varying delays. Neurocomputing 2009, 72, 1782–1788. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Z.; Yang, J. Passivity and passification for stochastic Takagi-Sugeno fuzzy systems with mixed time-varying delays. Neurocomputing 2013, 122, 330–337. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Z. Global dissipativity of neural networks with both variable and unbounded delays. Chaos Solitons Fractals 2005, 25, 393–401. [Google Scholar] [CrossRef]
- Wen, S.; Zeng, Z.; Huang, T.; Chen, Y. Passivity analysis of memristor-based recurrent neural networks with time-varying delays. J. Frankl. Inst. 2013, 350, 2354–2370. [Google Scholar] [CrossRef]
- Zhixia, D.; Zeng, Z.; Zhang, H.; Wang, L.; Liheng, W. New results on passivity of fractional-order uncertain neural networks. Neurocomputing 2019, 351, 51–59. [Google Scholar]
- Yang, X.; Li, C.; Huang, T.; Song, Q.; Chen, X. Quasi-uniform synchronization of fractional-order memristor-based neural networks with delay. Neurocomputing 2017, 234, 205–215. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y. Different impulsive effects on synchronization of fractional-order memristive BAM neural networks. Nonlinear Dyn. 2018, 93, 233–250. [Google Scholar] [CrossRef]
- Liu, X.; Ho, D.W.C.; Cao, J.; Xu, W. Discontinuous observers design for finite-time consensus of multiagent systems with external disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2826–2830. [Google Scholar] [CrossRef]
- Liu, X.; Ho, D.W.C.; Song, Q.; Xu, W. Finite/Fixed-time pinning synchronization of complex networks with stochastic disturbances. IEEE Trans. Cybern. 2019, 49, 2398–2403. [Google Scholar] [CrossRef]
- Liu, X.; Ho, D.W.C.; Xie, C. Prespecified-time cluster synchronization of complex networks via a smooth control approach. IEEE Trans. Cybern. 2020, 50, 1771–1775. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R.; Cao, J. Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 2016, 73, 36–46. [Google Scholar] [CrossRef]
- Xiao, J.; Zhong, S.; Li, Y.; Xu, F. Finite-time Mittag–Leffler synchronization of fractional-order memristive BAM neural networks with time delays. Neurocomputing 2017, 219, 431–439. [Google Scholar] [CrossRef]
- Thuan, M.V.; Huong, D.C.; Hong, D.T. New results on robust finite-time passivity for fractional-order neural networks with uncertainties. Neural Process. Lett. 2019, 50, 1065–1078. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Right-Hand Sides; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Aubin, J.P.; Cellina, A. Differential Inclusions; Springer: Berlin, Germany, 1984. [Google Scholar]
- Kuang, J. Applied Inequalities; Shandong Science and Technology Press: Jinan, China, 2004. [Google Scholar]
- Singh, V. New global robust stability results for delayed cellular neural networks based on norm-bounded uncertainties. Chaos Solitons Fractals 2016, 30, 1165–1171. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; Xiao, H.Q. Improved conditions for passivity of neural networks with a time-varying delay. IEEE Trans. Cybern. 2014, 44, 785–792. [Google Scholar] [CrossRef]
- Rajchakit, G.; Chanthorn, P.; Niezabitowski, M.; Raja, R.; Baleanu, D.; Pratap, A. Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks. Neurocomputing 2020, 417, 290–301. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X.; Yang, S.; Alsaedi, A. Finite-time and fixed-time bipartite synchronization of complex networks with signed graphs. Math. Comput. Simul. 2021, 188, 319–329. [Google Scholar] [CrossRef]
- Zhou, Y.; Wan, X.; Huang, C.; Yang, X. Finite-time stochastic synchronization of dynamic networks with nonlinear coupling strength via quantized intermittent control. Appl. Math. Comput. 2020, 376, 125157. [Google Scholar] [CrossRef]
- Yang, X.; Ho, D.W.C. Synchronization of delayed memristive neural networks: Robust analysis approach. IEEE Trans. Cybern. 2016, 46, 3377–3387. [Google Scholar] [CrossRef]
- Yang, X.; Cao, J.; Liang, J. Exponential synchronization of memristive neural networks with delays: Interval matrix method. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1878–1888. [Google Scholar] [CrossRef]
- Stephen, A.; Raja, R.; Alzabut, J.; Zhu, Q.; Niezabitowski, M.; Bagdasar, O. Mixed time-delayed nonlinear multi-agent dynamic systems for asymptotic stability and non-fragile synchronization criteria. Neural Process. Lett. 2021, 1–32. [Google Scholar] [CrossRef]
- Yang, X.; Cao, J.; Qiu, J. pth moment exponential stochastic synchronization of coupled memristor-based neural networks with mixed delays via delayed impulsive control. Neural Netw. 2016, 65, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Su, H.; Tang, R.; Yang, X. Finite-time bipartite synchronization of switched competitive neural networks with time delay via quantized control. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Yang, X.; Song, Q.; Cao, J. Synchronization of memristive neural networks with mixed delays via quantized intermittent control. Appl. Math. Comput. 2018, 339, 874–887. [Google Scholar] [CrossRef]




| Methods | [60] | Corollary 1 | Improvement |
|---|---|---|---|
| 60.0412 | 56.5105 | 5.8804% | |
| The number of decision variables | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anbalagan, P.; Ramachandran, R.; Alzabut, J.; Hincal, E.; Niezabitowski, M. Improved Results on Finite-Time Passivity and Synchronization Problem for Fractional-Order Memristor-Based Competitive Neural Networks: Interval Matrix Approach. Fractal Fract. 2022, 6, 36. https://doi.org/10.3390/fractalfract6010036
Anbalagan P, Ramachandran R, Alzabut J, Hincal E, Niezabitowski M. Improved Results on Finite-Time Passivity and Synchronization Problem for Fractional-Order Memristor-Based Competitive Neural Networks: Interval Matrix Approach. Fractal and Fractional. 2022; 6(1):36. https://doi.org/10.3390/fractalfract6010036
Chicago/Turabian StyleAnbalagan, Pratap, Raja Ramachandran, Jehad Alzabut, Evren Hincal, and Michal Niezabitowski. 2022. "Improved Results on Finite-Time Passivity and Synchronization Problem for Fractional-Order Memristor-Based Competitive Neural Networks: Interval Matrix Approach" Fractal and Fractional 6, no. 1: 36. https://doi.org/10.3390/fractalfract6010036
APA StyleAnbalagan, P., Ramachandran, R., Alzabut, J., Hincal, E., & Niezabitowski, M. (2022). Improved Results on Finite-Time Passivity and Synchronization Problem for Fractional-Order Memristor-Based Competitive Neural Networks: Interval Matrix Approach. Fractal and Fractional, 6(1), 36. https://doi.org/10.3390/fractalfract6010036