An Implicit Numerical Approach for 2D Rayleigh Stokes Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative
Abstract
1. Introduction
- (i)
- (ii)
- (iii)
- There exist a positive constant. Such that
- (iv)
2. Methodology of the Proposed Scheme
2.1. Stability
2.2. Convergence
3. Numerical Experiment
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| RSP-HGSGF | Rayleigh–Stokes problem for heated generalized second-grade fluid |
| 2D | Two-dimensional |
| FEM | Finite element method |
| RBF-FD | Radial basis function finite difference |
| INF | Implicit numerical approximation scheme |
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.B.; Spanier, J. Fractional Calculus; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach Science: Philadelphia, PA, USA, 1993. [Google Scholar]
- Ma, L.; Liu, D. An implicit difference approximation for fractional cable equation in high-dimensional case. J. Liaoning Tech. Univ. 2014, 4, 24. [Google Scholar]
- Liu, J.; Li, H.; Liu, Y. A new fully discrete finite difference/element approximation for fractional cable equation. J. Appl. Math. Comput. 2016, 52, 345–361. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Turner, L.; Anh, V. Galerkin finite element method and error analysis for the fractional cable equation. Numer. Algor. 2016, 72, 447–466. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Assiri, T.A. non-standard Crank-Nicholson method for solving the variable order fractional cable equation, Appl. Math. Inf. Sci. 2015, 9, 943–951. [Google Scholar]
- Cavlak, E.; Bayram, M. An approximate solution of fractional cable equation by homotopy analysis method. Boun. Valu. Prob. 2014, 58, 10. [Google Scholar]
- Hu, Z.; Zhang, L. Implicit compact difference schemes the fractional cable equation. Appl. Math Model. 2012, 36, 4027–4043. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Q.; Turner, I. Two new implicit numerical methods for the fractional cable equation. J. Comput. Nonlinear Dyn. 2014, 6, 7. [Google Scholar] [CrossRef]
- Yu, B.; Jiang, X.; Qi, H. An inverse problem to estimate an unknown order of a Riemann-Liouville fractional derivative for a fractional Stocks’ first problem for a heated generalized second grade fluid. Acta Mech. Sin. 2015, 31, 153–161. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Anh, V.; Turner, I. Numerical methods for solving a two-dimensional variable-order anomalous subdiffusion equation. Math. Comput. 2011, 277, 345–366. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turne, I. New solution and analytical tech- niques of the implicit numerical methods for the anomalous sub-diffusion equation. SIAM J. Numer. Anal. 2008, 46, 10791095. [Google Scholar] [CrossRef]
- Yang, Q. Novel Analytical and Numerical Methods for Solving Fractional Dynamical Systems. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2010. [Google Scholar]
- Cui, M. Compact Alternating direction implicit method for two-dimensional time fractional diffusion equation. J. Comput. Phys. 2012, 231, 2621–2633. [Google Scholar] [CrossRef]
- Zhai, S.; Feng, X.; He, Y. An unconditionally stable compact ADI method for 3D time-fractional convection-diffusion equation. J. Comp. Phys. 2014, 269, 138–155. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Burrage, K.; Chen, Y. Numerical method of the variable-order Rayleigh-Stocks’ problem for a heated generalized second grade fluid with fractional derivative. IMA J. Appl. Math. 2005, 78, 1–21. [Google Scholar]
- Chunhong, W. Numerical solution for Stocks’ first problem for a heated generalized second grade fluid with fractional derivative. Appl. Num. Math. 2009, 59, 2571–2583. [Google Scholar]
- Chen, C.M.; Liu, F.; Turner, I.; Anh, V. Numerical schemes and multivariate extrapolation of a two-dimensional anomalous sub-diffusion equation. Numer. Algor. 2010, 54, 1–21. [Google Scholar] [CrossRef][Green Version]
- Chen, C.M.; Liu, F.; Turner, I.; Anh, V. Numerical methods with fourth-order spatial accuracy for variable-order nonlinear Stocks’ first problem for a heated generalized second grade fluid. Comput. Math. Appl. 2011, 62, 971–986. [Google Scholar] [CrossRef]
- Mohebbi, A.; Abbaszadeh, M.; Dehghan, M. Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh-Stocks prob- lem for a heated generalized second grade fluid with fractional derivatives. Comput. Mathods Appl. Mech. Eng. 2013, 624, 163–177. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, W. Numerical method for Stockes’ first problem for a heated generalized second grade fluid with fractional derivatives. Numer. Methods Partial. Differ. Equ. 2011, 27, 1599–1609. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. Numerical study of the nonlinear anomalous reaction–subdiffusion process arising in the electroanalytical chemistry. J. Comput. Sci. 2021, 53, 101394. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. A local stabilized approach for approximating the modified time-fractional diffusion problem arising in heat and mass transfer. J. Adv. Res. 2021, 32, 45–60. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z. An improved localized radial basis-pseudospectral method for solving fractional reaction–subdiffusion problem. Results Phys. 2021, 23, 104048. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. Numerical investigation of fractional nonlinear sine-Gordon and Klein-Gordon models arising in relativistic quantum mechanics. Eng. Anal. Bound. Elem. 2020, 120, 223–237. [Google Scholar] [CrossRef]
- Khater, M.; Ali, U.; Khan, M.A.; Mousa, A.A.; Attia, R.A.M. A New Numerical Approach for Solving 1D Fractional Diffusion-Wave Equation. J. Funct. Spaces 2021, 2021, 6638597. [Google Scholar] [CrossRef]
- Salama, F.M.; Hamid, N.N.A.; Ali, N.H.M.; Ali, U. An efficient modified hybrid explicit group iterative method for the time-fractional diffusion equation in two space dimensions. AIMS Math. 2022, 7, 2370–2392. [Google Scholar] [CrossRef]
- Ali, A.; Ali, N.H.M. On skewed grid point iterative method for solving 2D hyperbolic telegraph fractional differential equation. Adv. Differ. Equ. 2019, 2019, 1–29. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. A generalized fractional-order elastodynamic theory for non-local attenuating media. Proc. R. Soc. A 2020, 476, 20200200. [Google Scholar] [CrossRef] [PubMed]
- Patnaik, S.; Jokar, M.; Semperlotti, F. Variable-order approach to nonlocal elasticity: Theoretical formulation, order identification via deep learning, and applications. Comput. Mech. 2021. Available online: https://link.springer.com/article/10.1007/s00466-021-02093-3 (accessed on 28 October 2021). [CrossRef]
- Sumelka, W. Fractional viscoplasticity. Mech. Res. Commun. 2014, 56, 31–36. [Google Scholar] [CrossRef]
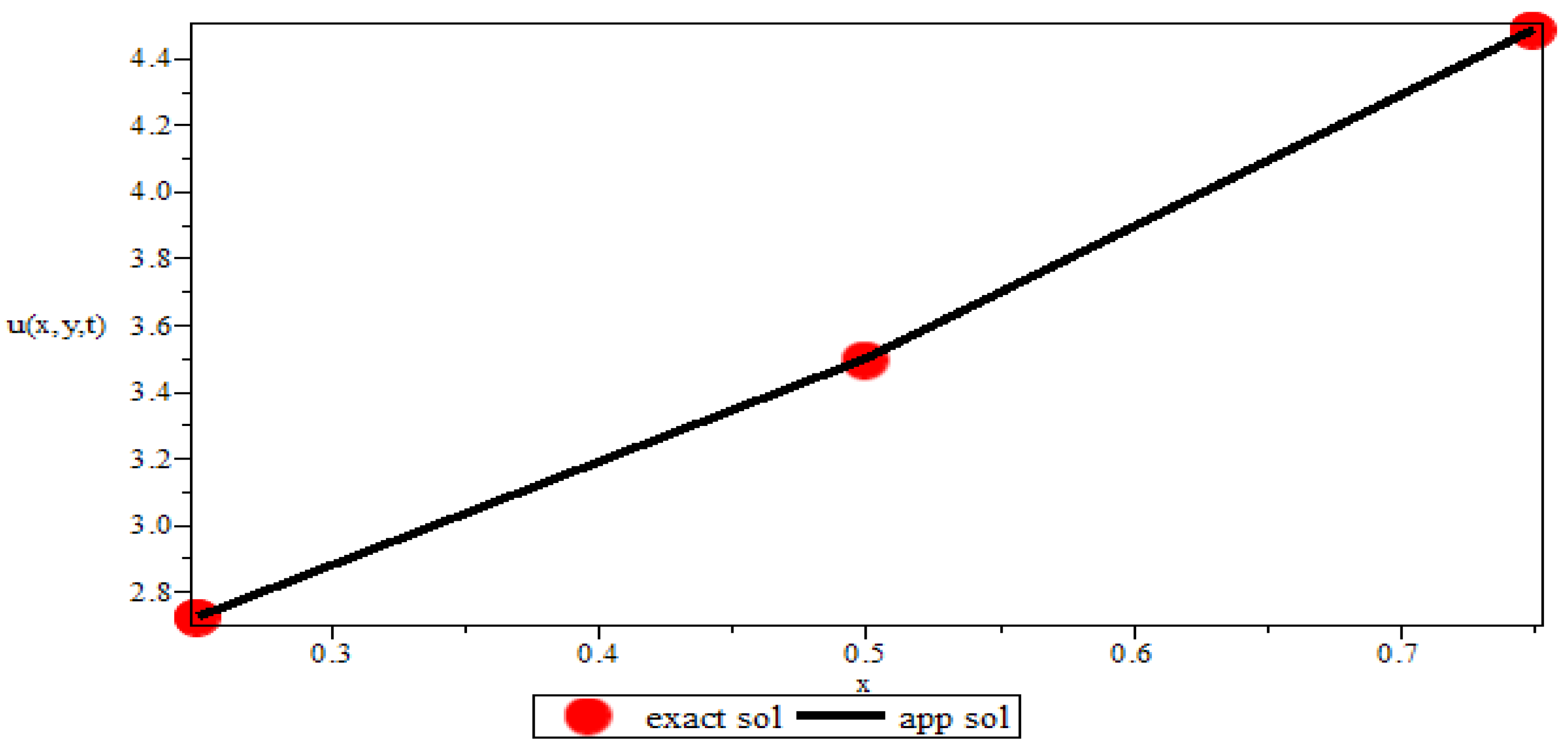
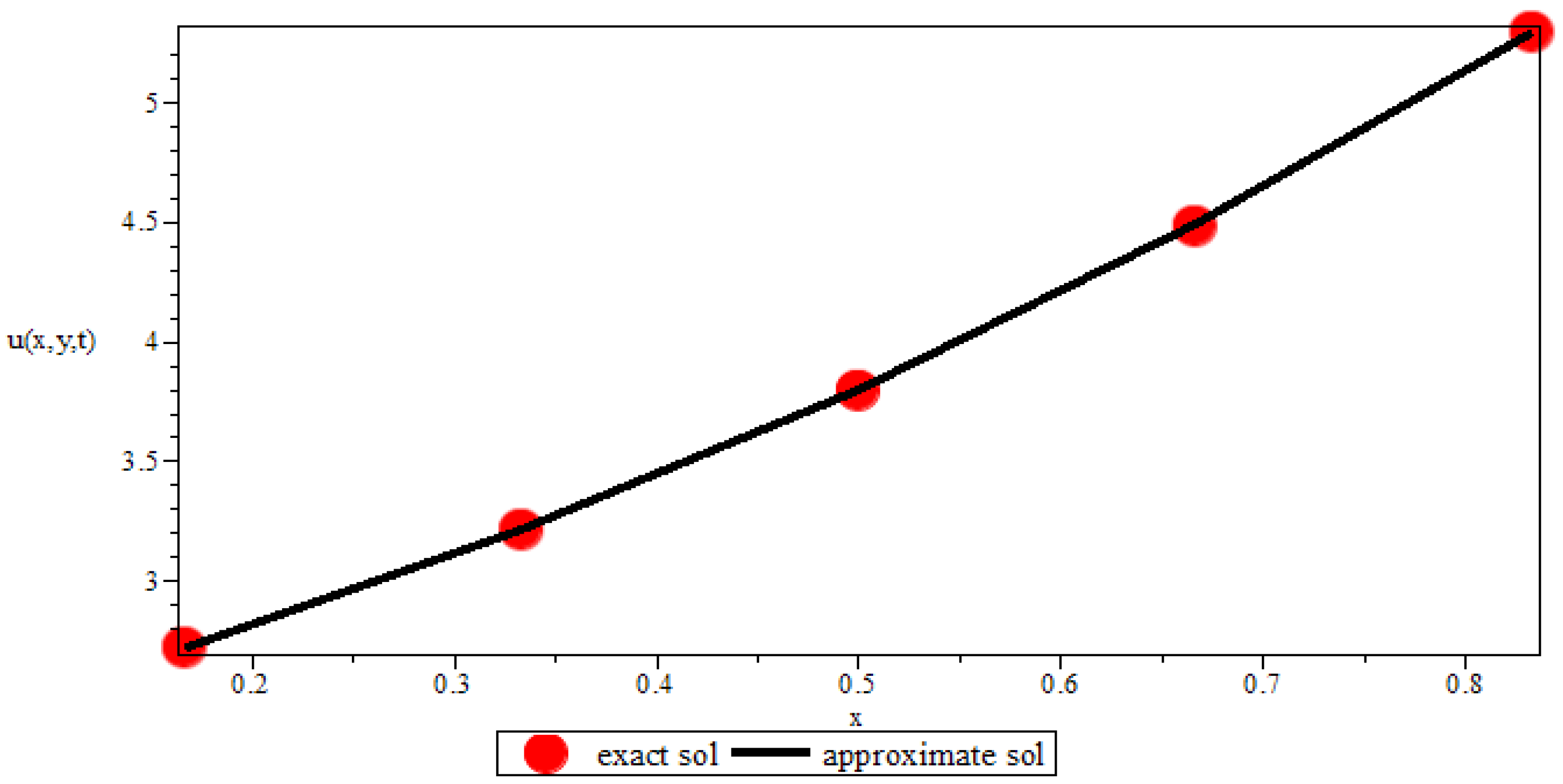
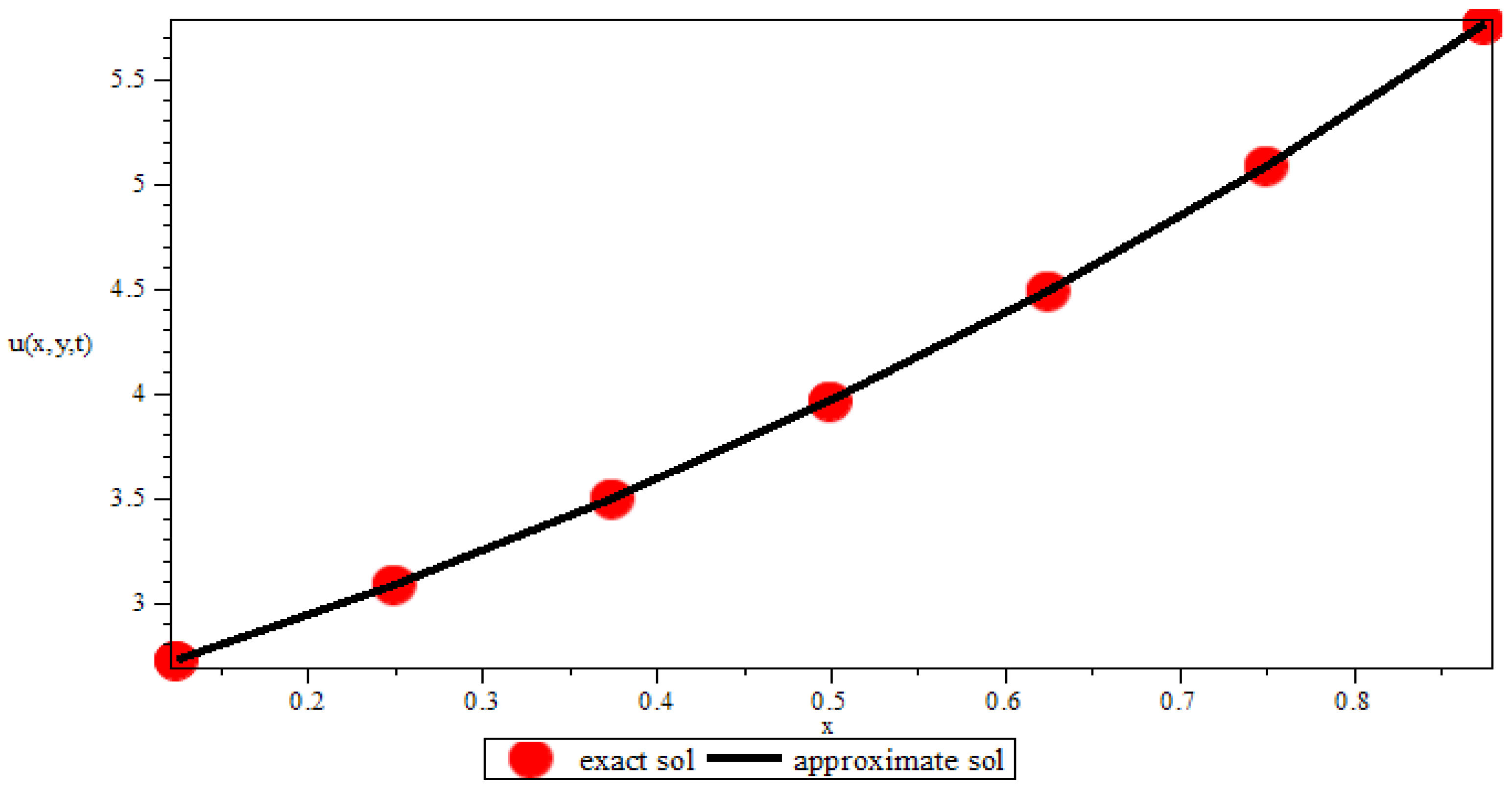
| 1/2 | 0.013169 | 0.016017 | 0.018890 | 0.021807 | 0.024819 | |
| 1/2 | |||
| 1/4 | |||
| 20 | ||||
| 40 | ||||
| 60 |
| CPU-Time (s) | |||
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naz, A.; Ali, U.; Elfasakhany, A.; Ismail, K.A.; Al-Sehemi, A.G.; Al-Ghamdi, A.A. An Implicit Numerical Approach for 2D Rayleigh Stokes Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative. Fractal Fract. 2021, 5, 283. https://doi.org/10.3390/fractalfract5040283
Naz A, Ali U, Elfasakhany A, Ismail KA, Al-Sehemi AG, Al-Ghamdi AA. An Implicit Numerical Approach for 2D Rayleigh Stokes Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative. Fractal and Fractional. 2021; 5(4):283. https://doi.org/10.3390/fractalfract5040283
Chicago/Turabian StyleNaz, Anam, Umair Ali, Ashraf Elfasakhany, Khadiga Ahmed Ismail, Abdullah G. Al-Sehemi, and Ahmed A. Al-Ghamdi. 2021. "An Implicit Numerical Approach for 2D Rayleigh Stokes Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative" Fractal and Fractional 5, no. 4: 283. https://doi.org/10.3390/fractalfract5040283
APA StyleNaz, A., Ali, U., Elfasakhany, A., Ismail, K. A., Al-Sehemi, A. G., & Al-Ghamdi, A. A. (2021). An Implicit Numerical Approach for 2D Rayleigh Stokes Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative. Fractal and Fractional, 5(4), 283. https://doi.org/10.3390/fractalfract5040283







