Dynamics of Fractional Model of Biological Pest Control in Tea Plants with Beddington–DeAngelis Functional Response
Abstract
:1. Introduction
- (i)
- The natural enemies bring about a long-term positive result in controlling the pests;
- (ii)
- In biological control methods, the risk of resistance development becomes lower in insects. Pesticides kill all the varieties of pests that may be useful or harmful species. The use of natural enemies is a successful and effective way to control the pests because the natural enemies attack and kill only the target organisms hence it is useful for controlling particular pests [17].
2. Some Essential Theorems
- (i.)
- If , then is a non-decreasing function for each ,
- (ii.)
- If , then is a non-increasing function for each
3. Model Formulation
4. Existence of the Solutions
- 1.
- Using system (10), the recursive form can now be written as follows:The prerequisites are: By applying the norm to the first Equation (14), we getUsing Lipchitz condition Equation (12), we obtain:Similarly,As a result, we can write:As a result, the existence and continuity are established.
- 2.
- To illustrate that the relation Equation (19) formulated the solution for Equation (8), we assume the following:In order to achieve the desired outcomes, we setThis yieldsContinuing the same procedure recursively, we getAt , we haveFrom Equation (22), it results that, as n tends to ∞, tends to 0 provided Similarly, it may be demonstrated that tends to 0.
- 3.
- We will now demonstrate the uniqueness for the solution of the system (8). Suppose that there is a different set of solutions of the system (8), namely Then, from the first equation of Equation (10) we write:Using the norm, the equation above becomes:By applying the Lipschitz condition, we getAt some this results yields,Since , we must have This implies
5. Non-Negativity and Boundedness
6. Existence of Points of Equilibrium and Their Stability
- 1.
- Axial equilibrium point is and it always exists.
- 2.
- Biological enemy free equilibrium point is
- 3.
- The coexistence equilibrium point is where and are the solutions of the system:It can be shown that:Substituting the above values in Equation (36), we get:whereLetUsing Descartes’ rule of signs, we may state that the fourth degree equation has one and only one positive root if any one of the following inequalities holds:Hence, the equilibrium point exists and is unique if any one of the inequalities in Equation (42) holds.
7. Global Stability
8. Numerical Method
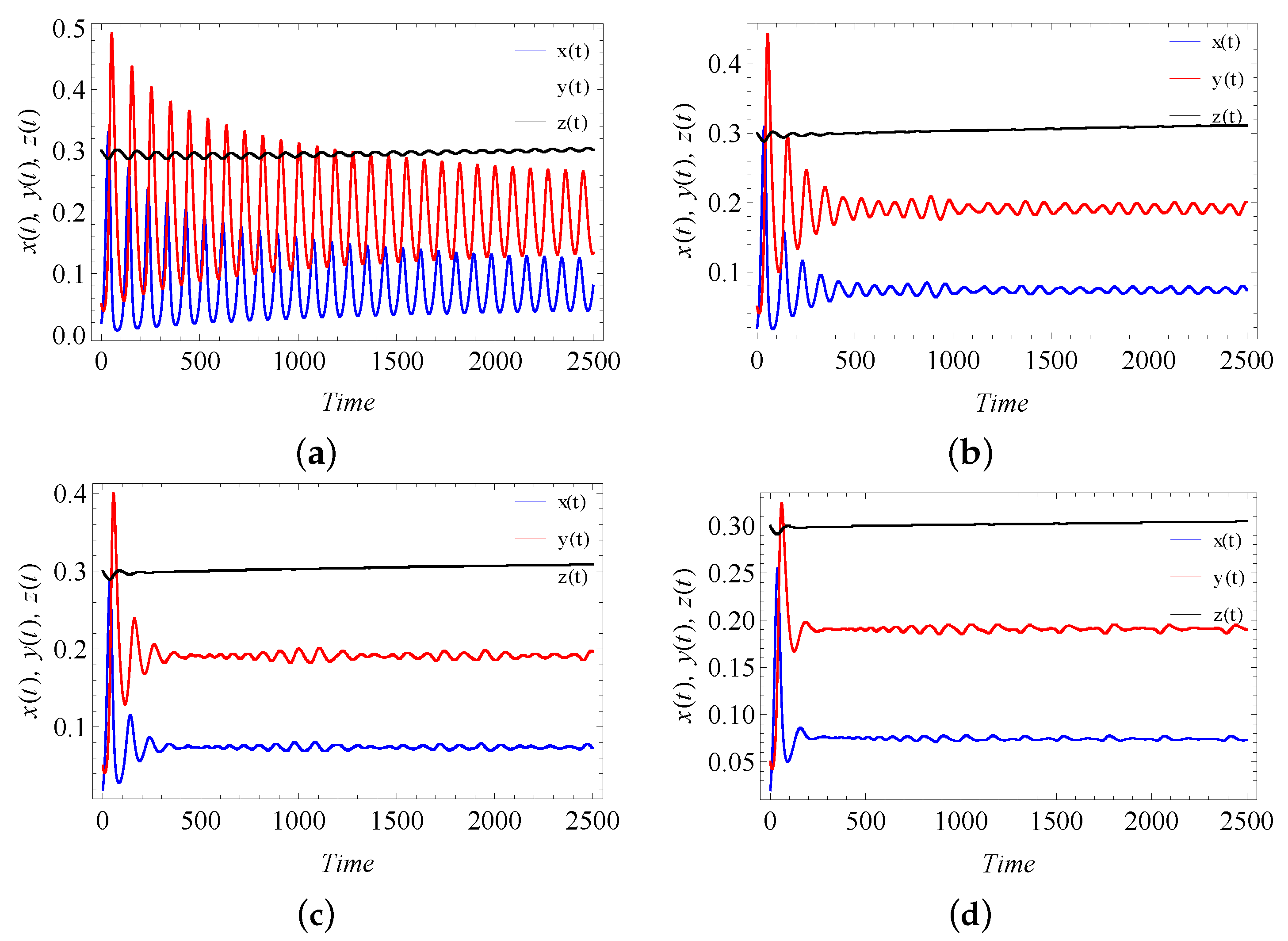
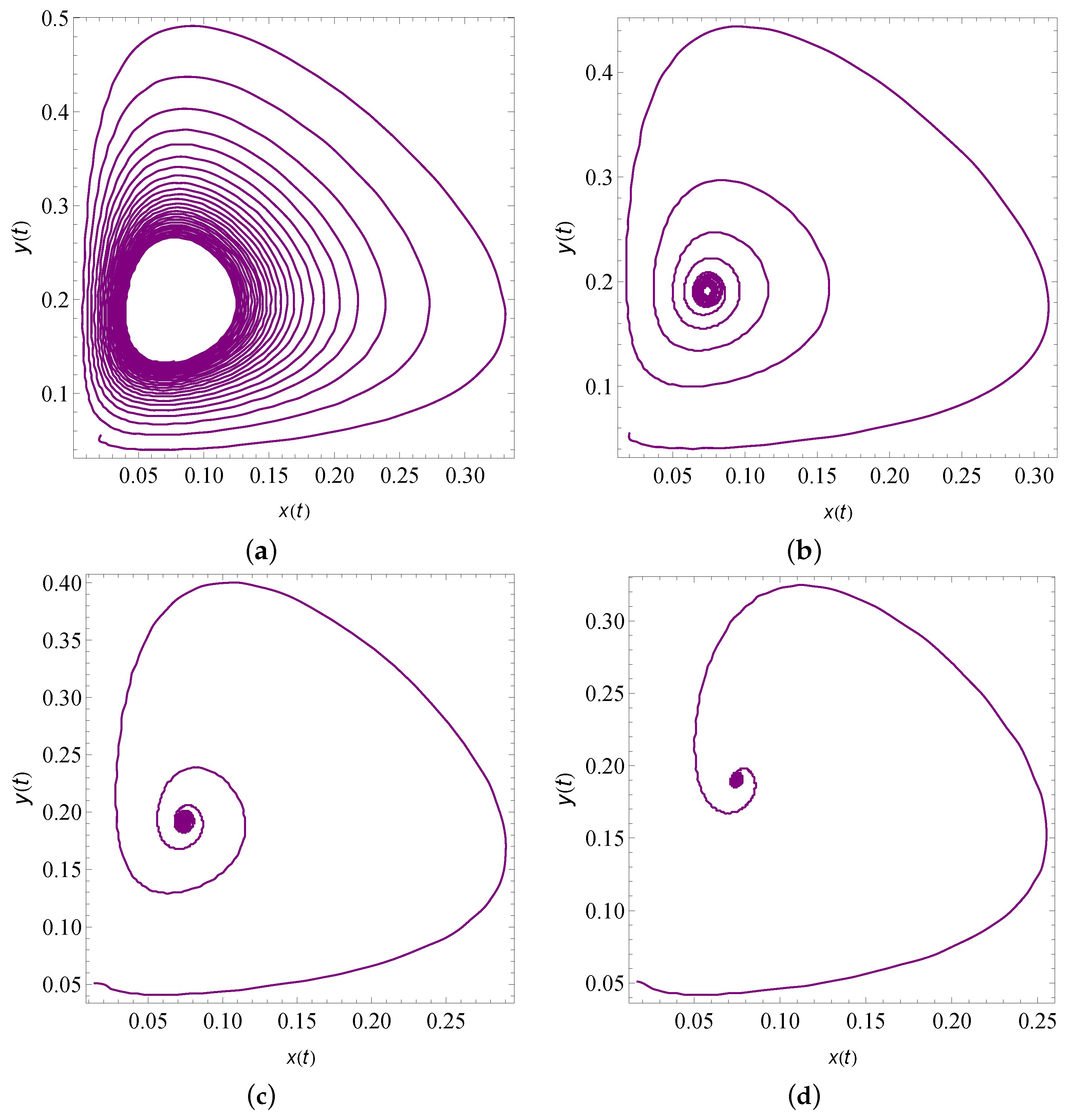
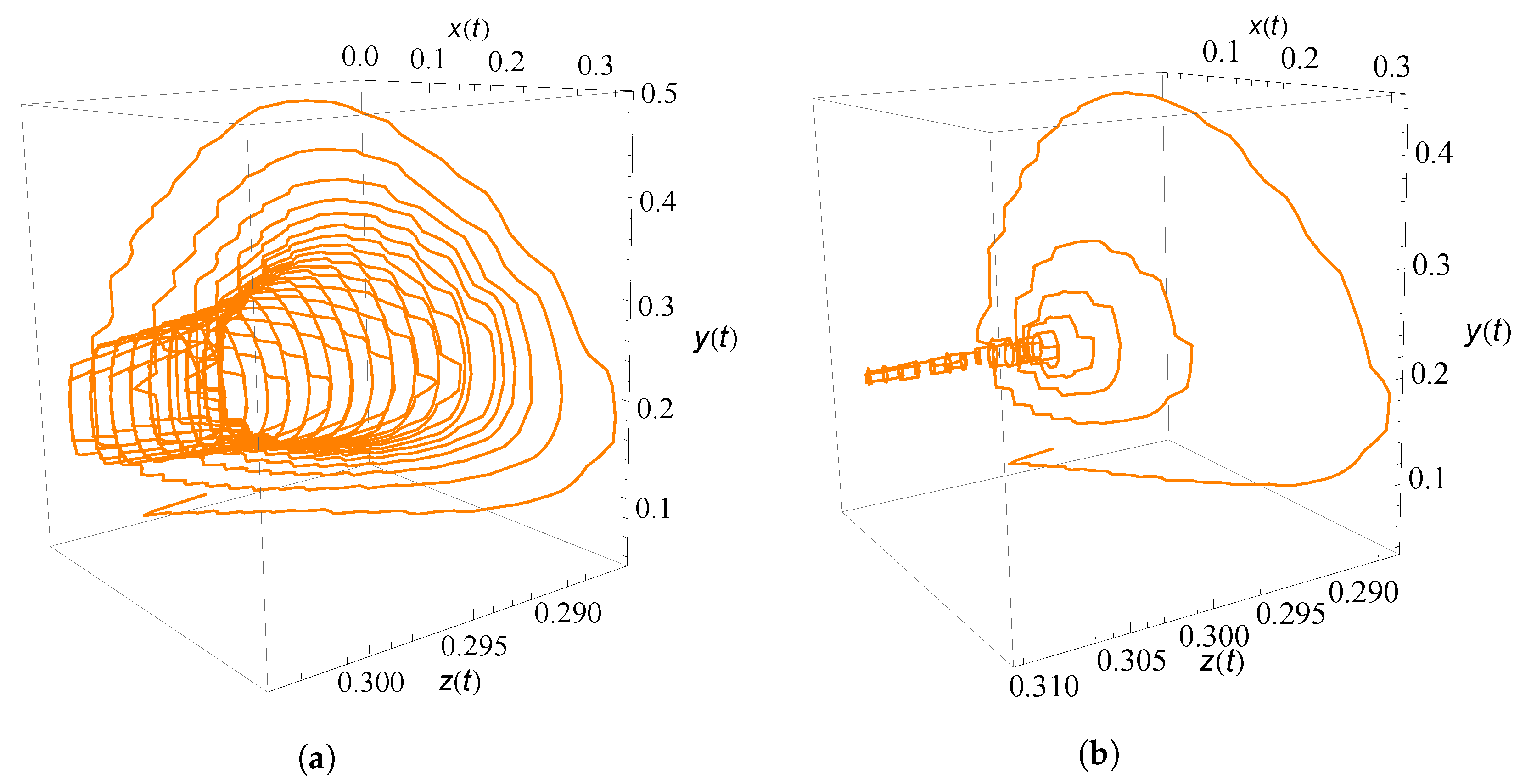
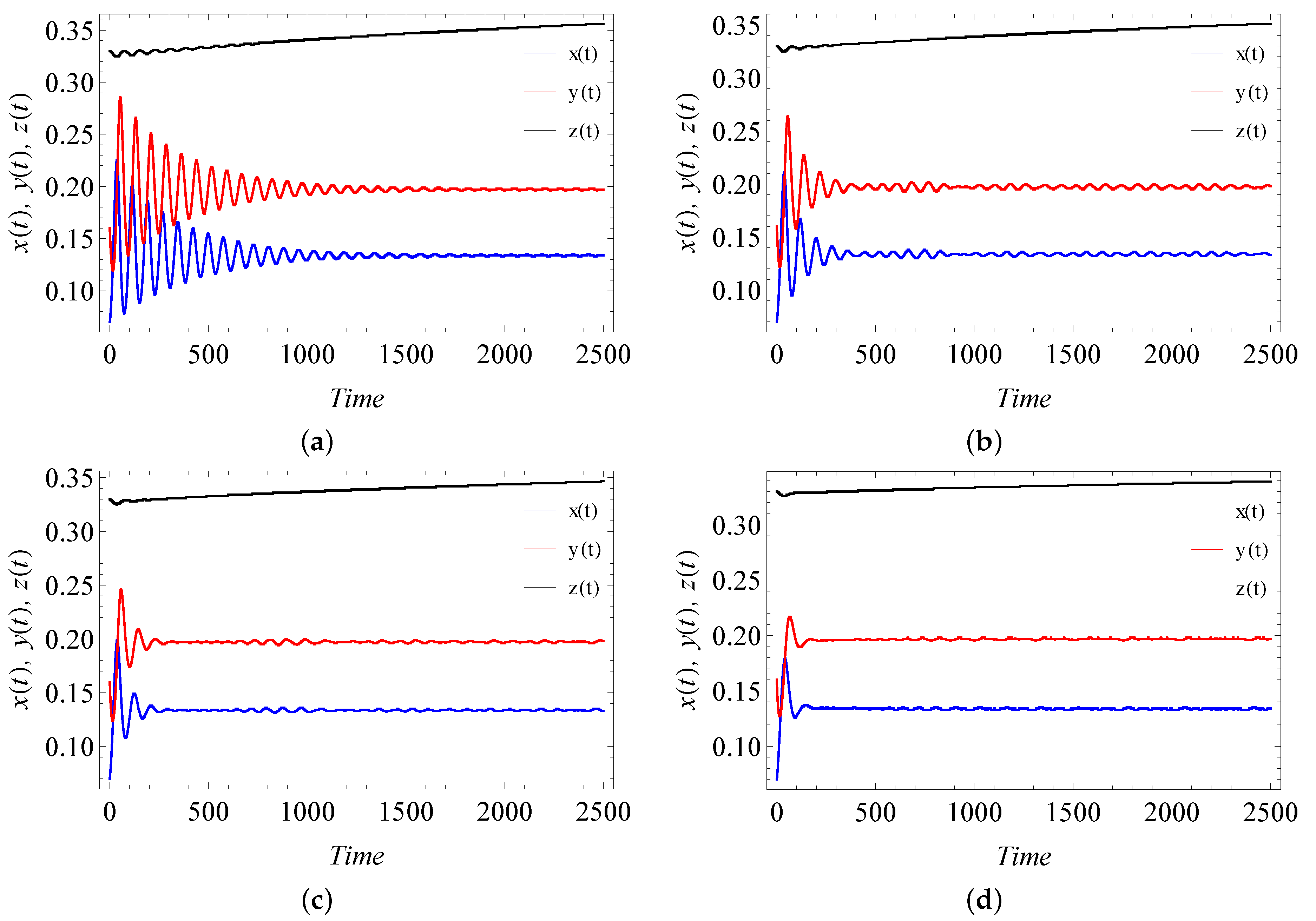
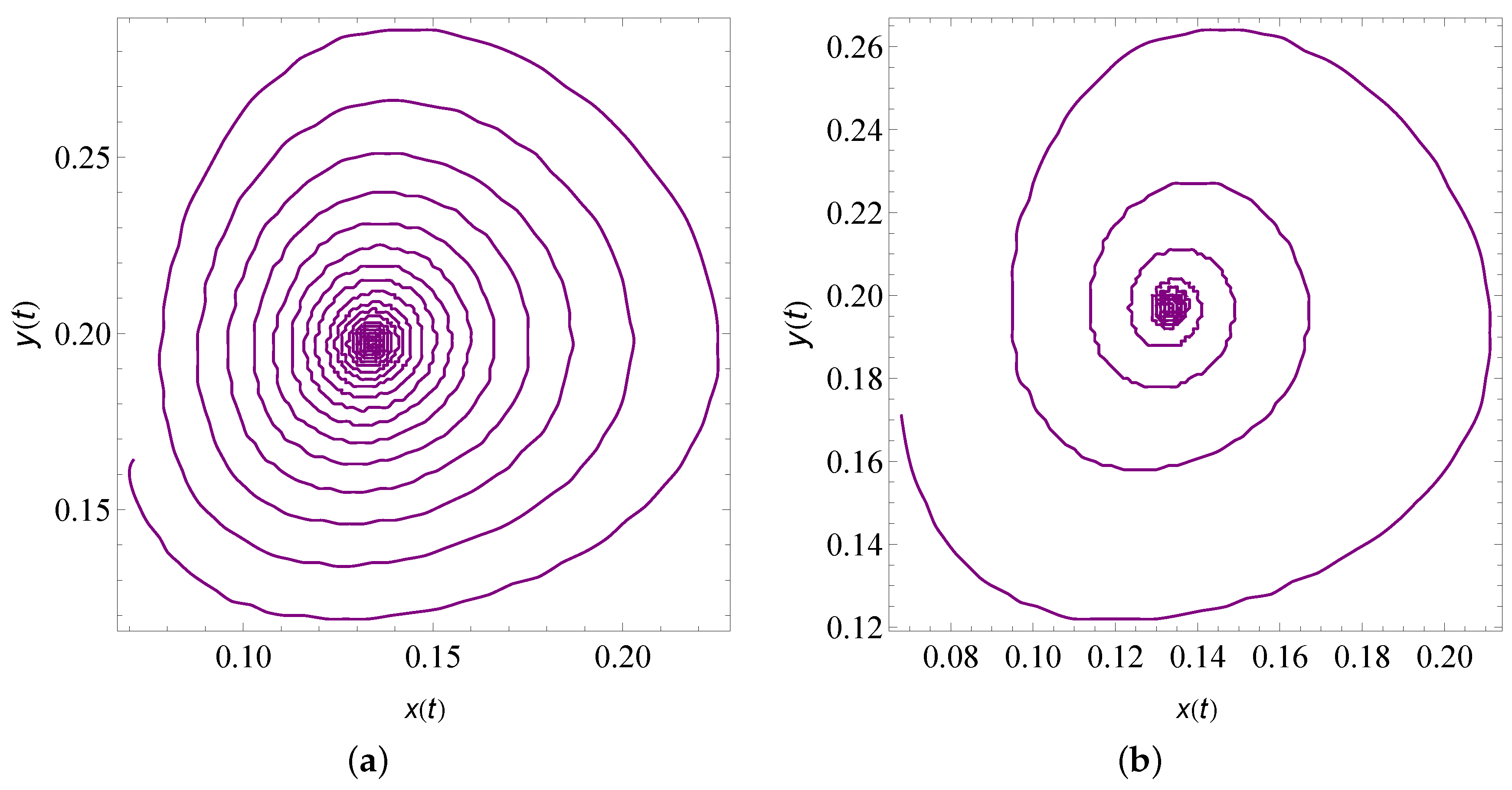
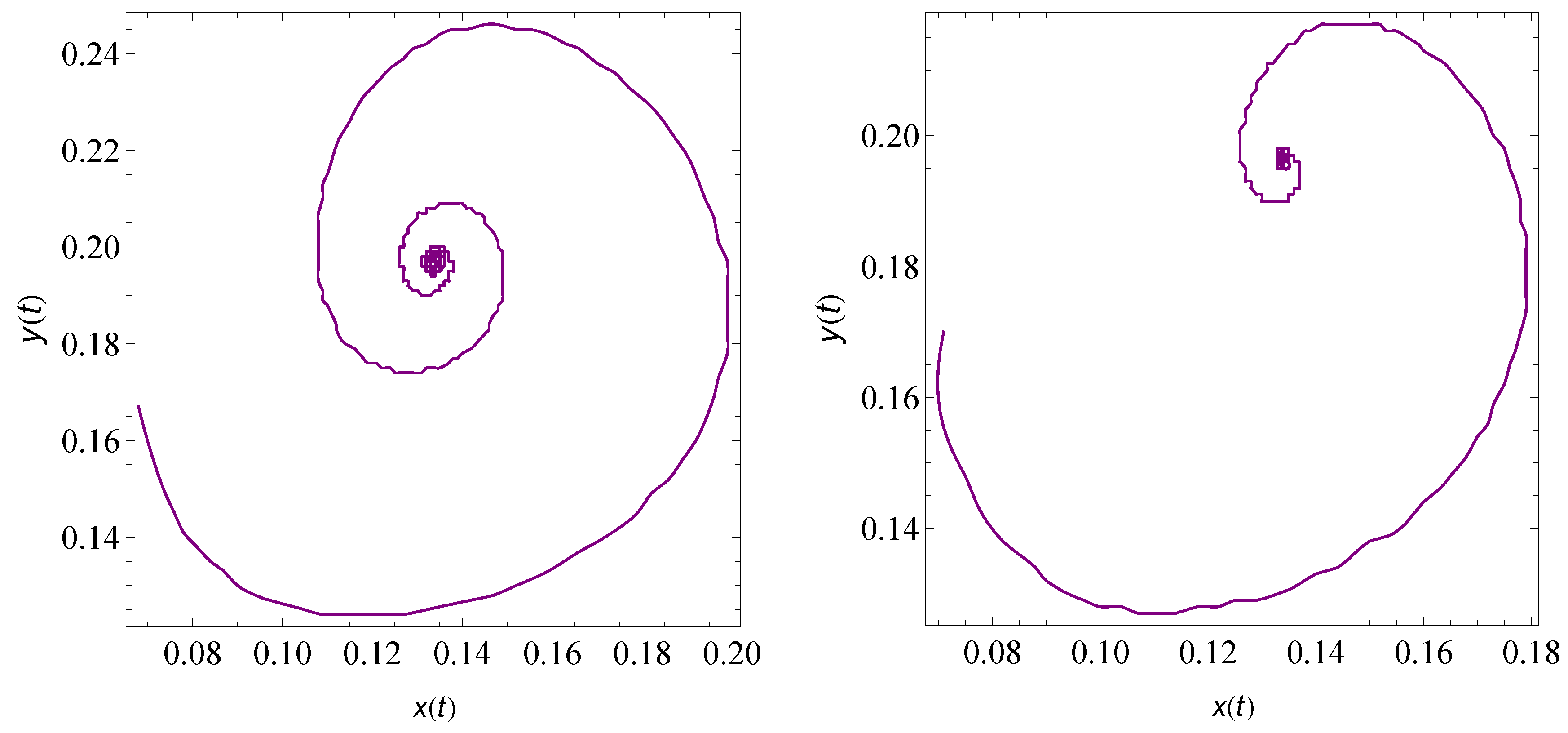
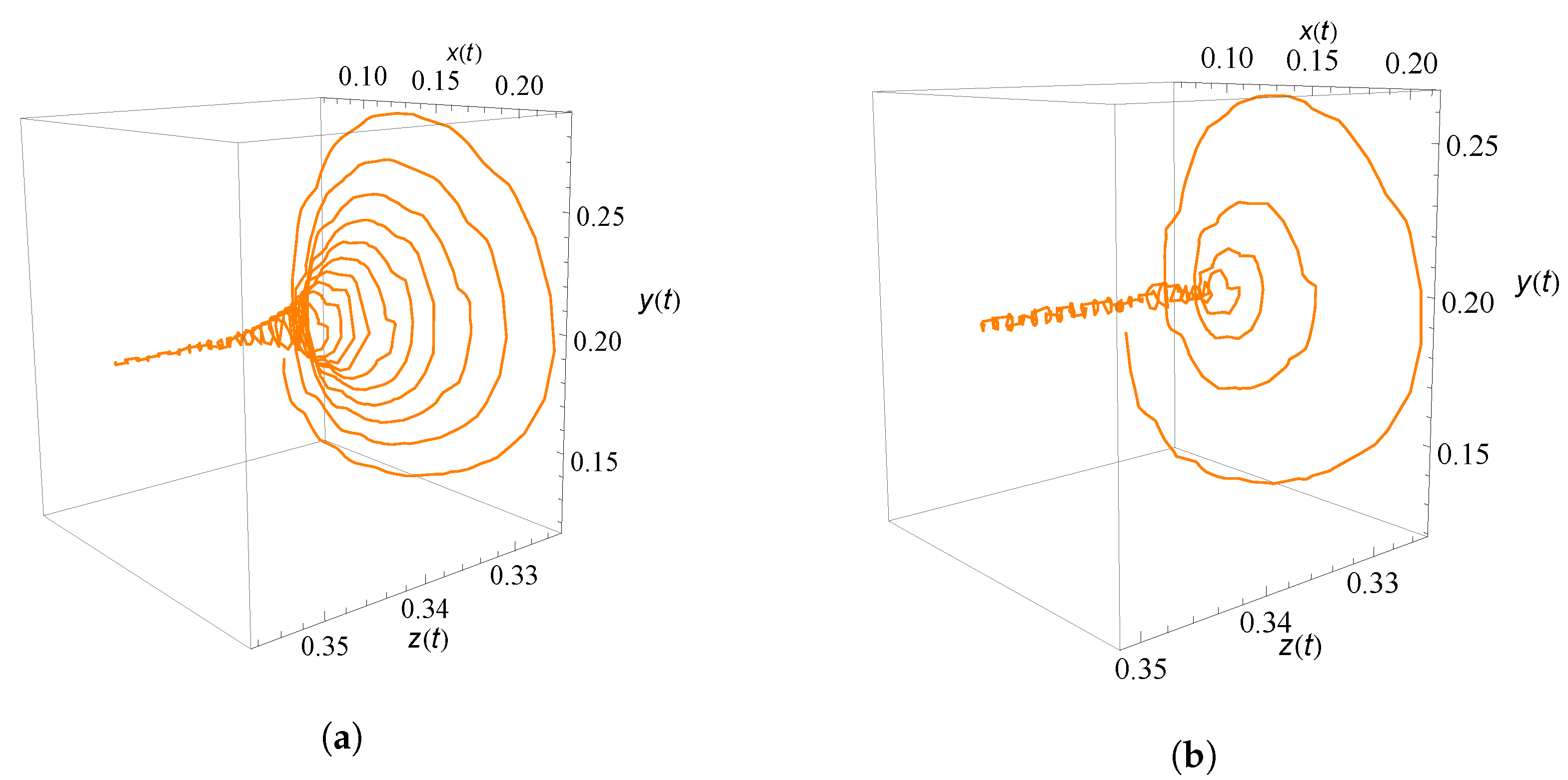
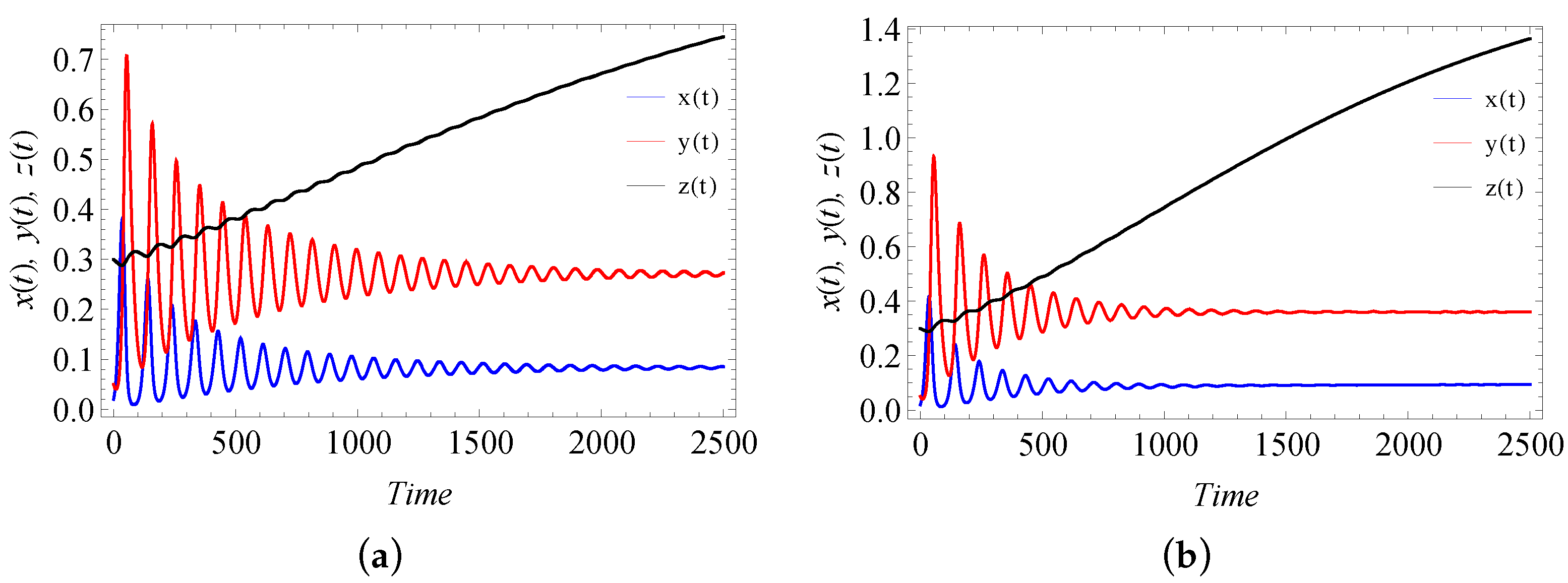
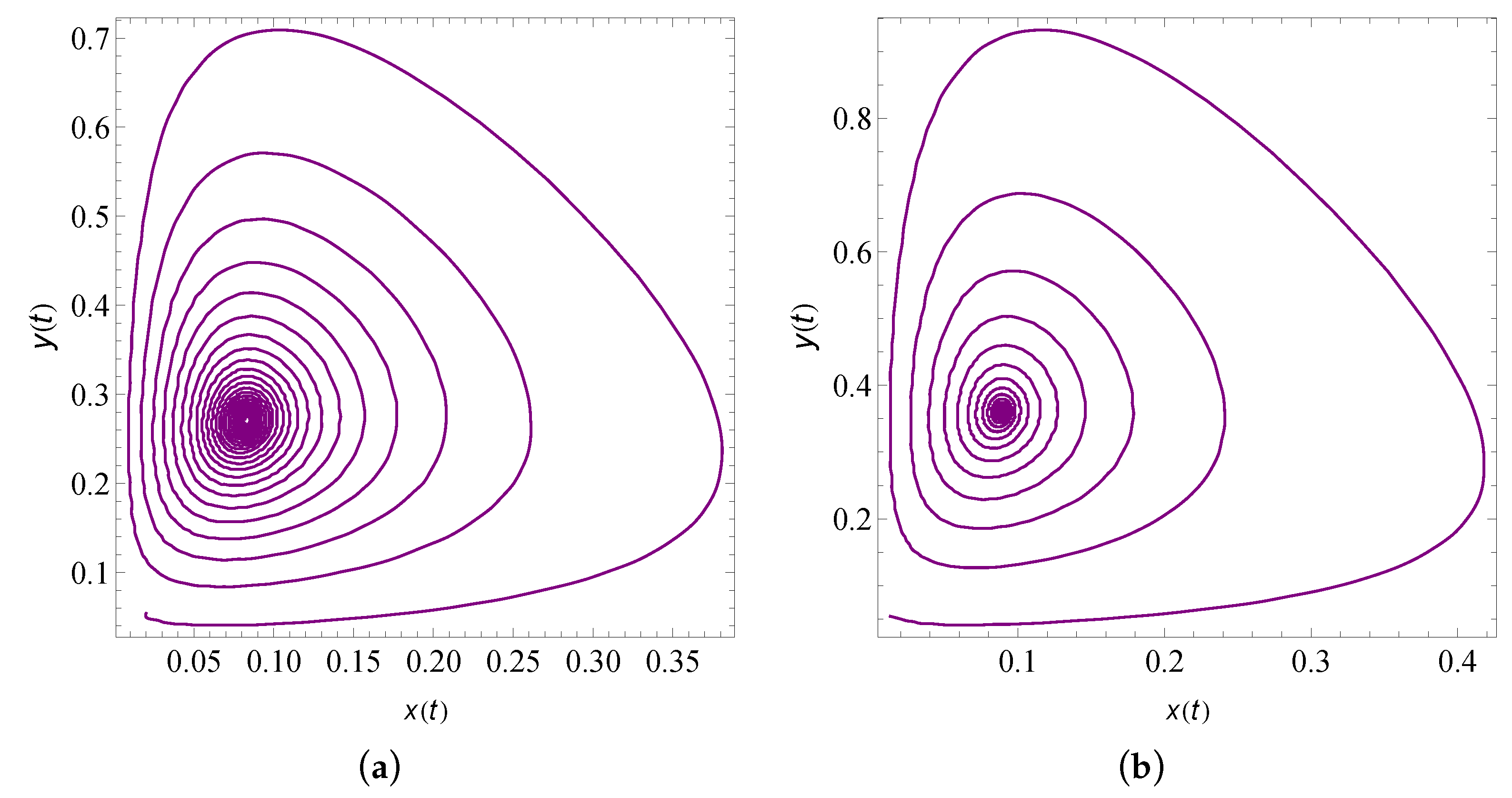
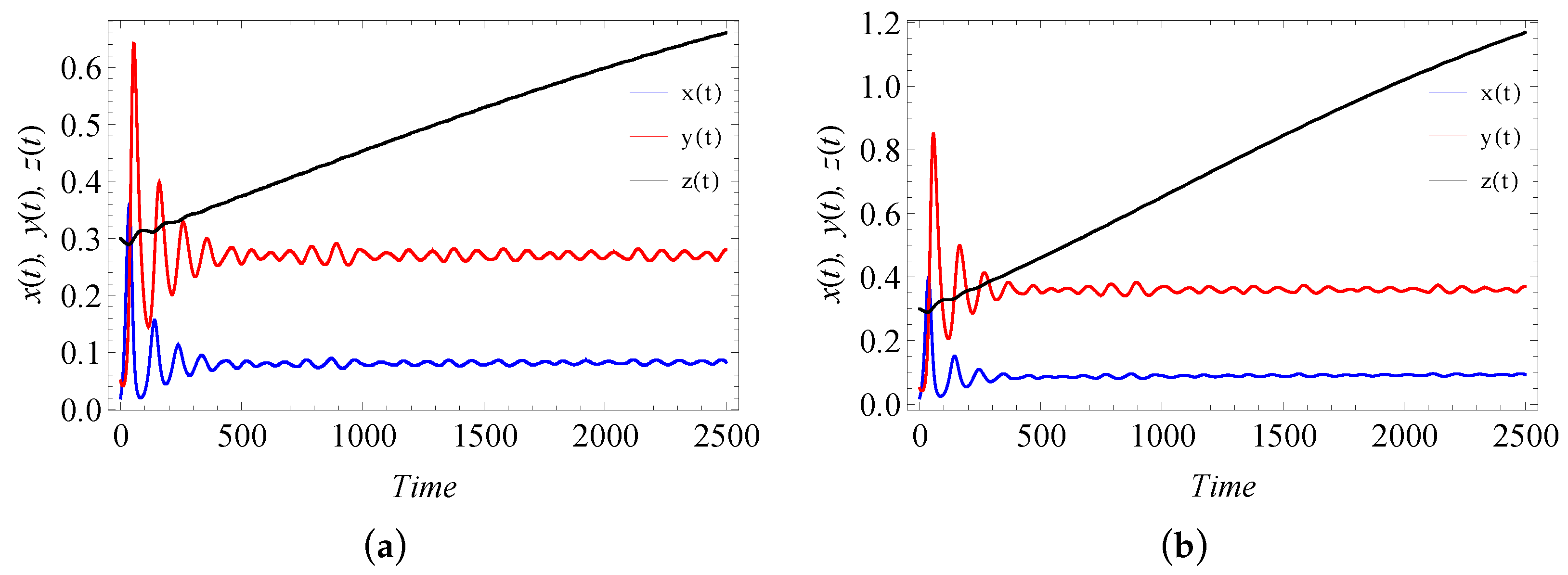
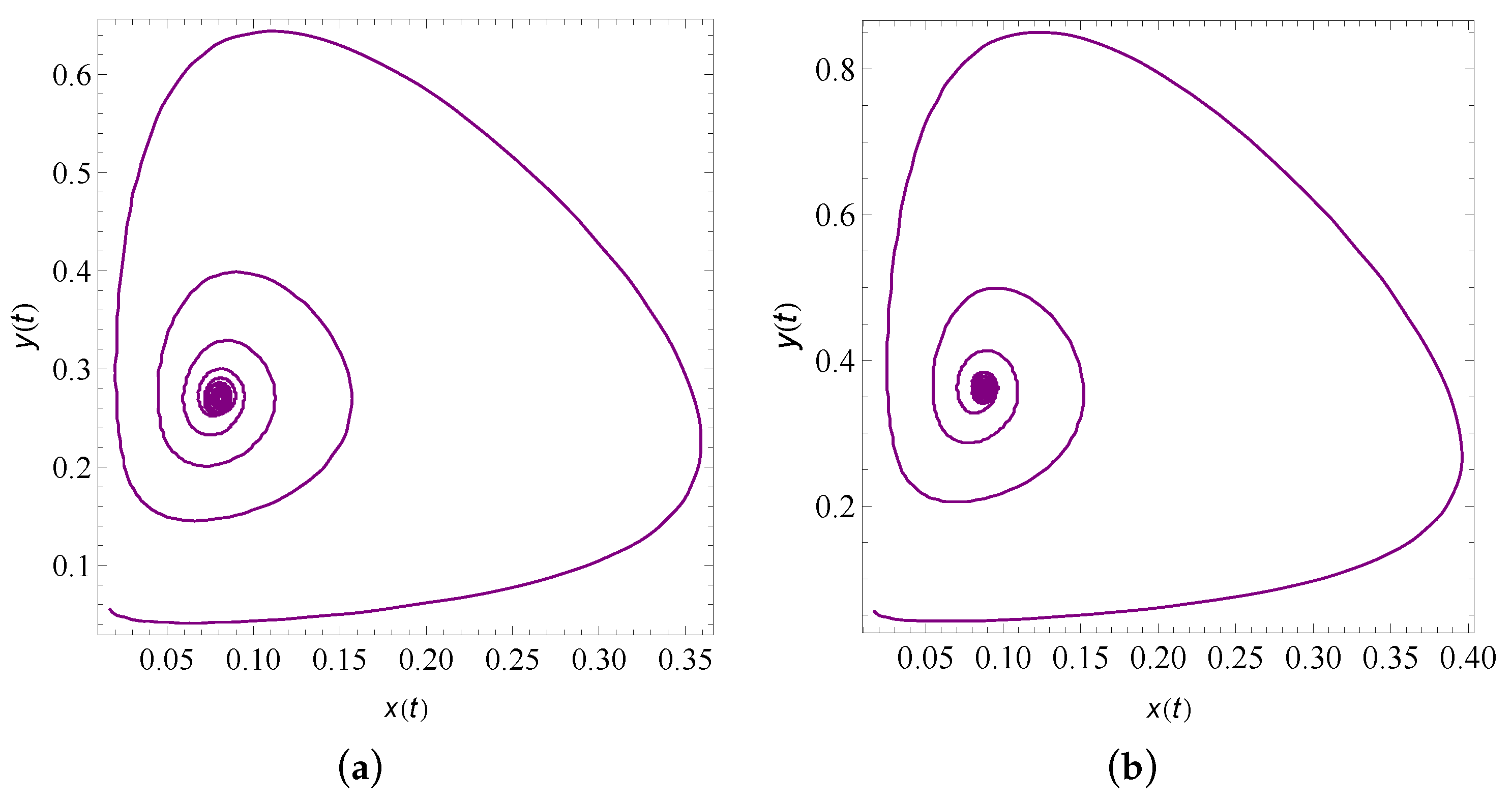
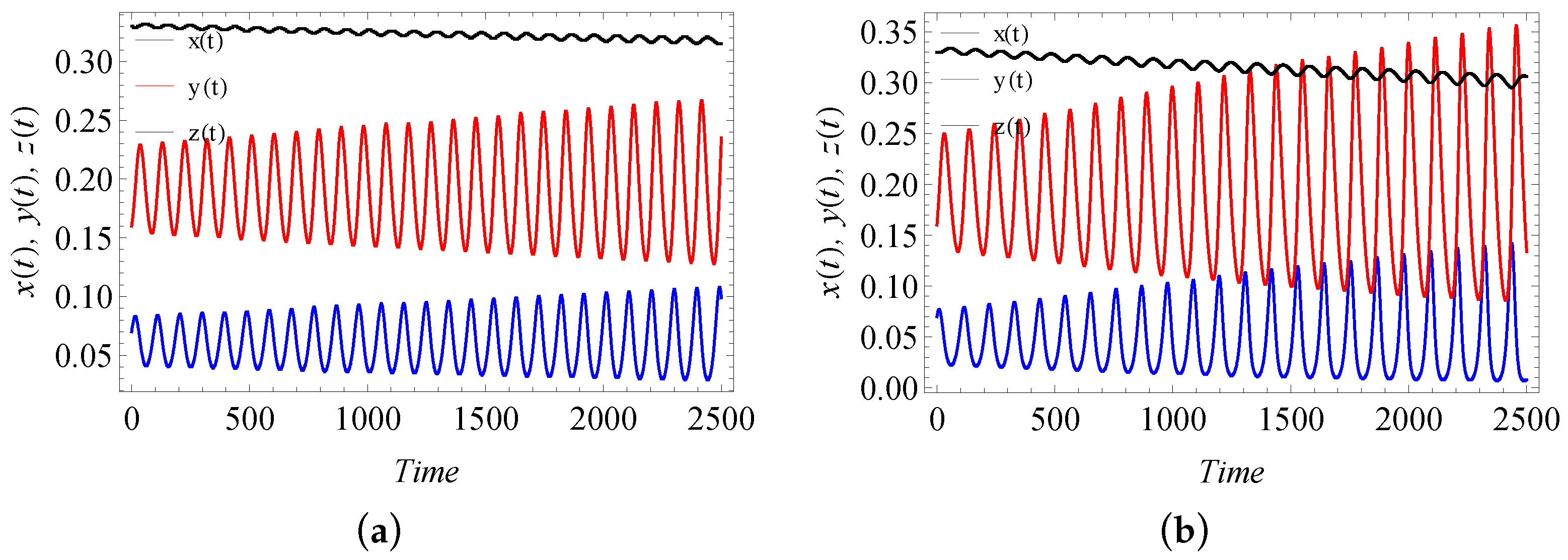
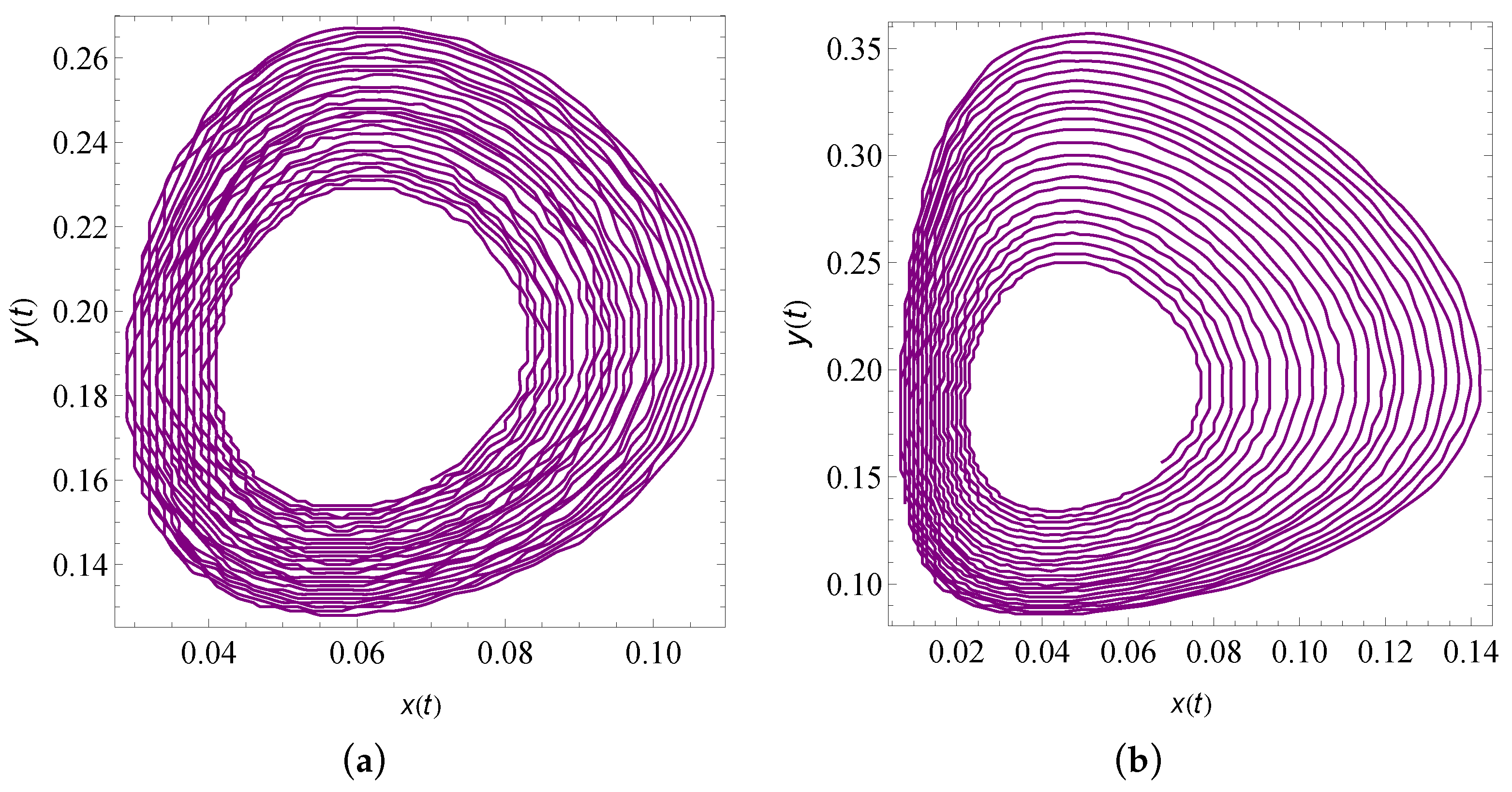
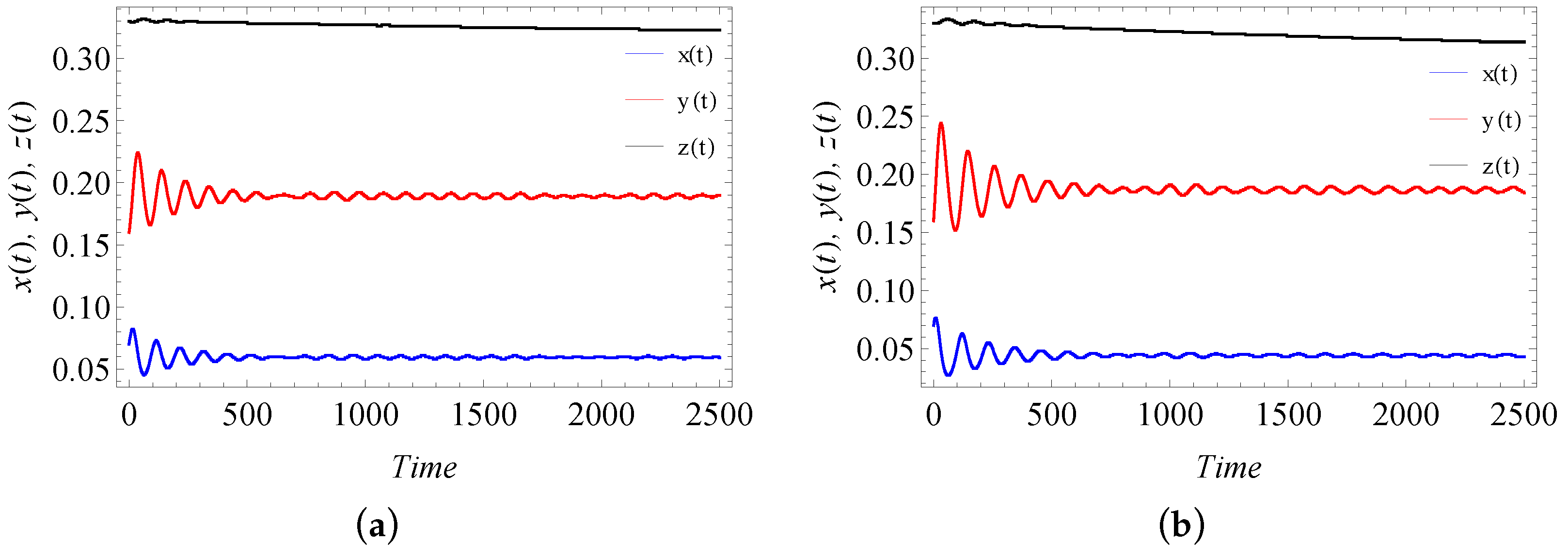
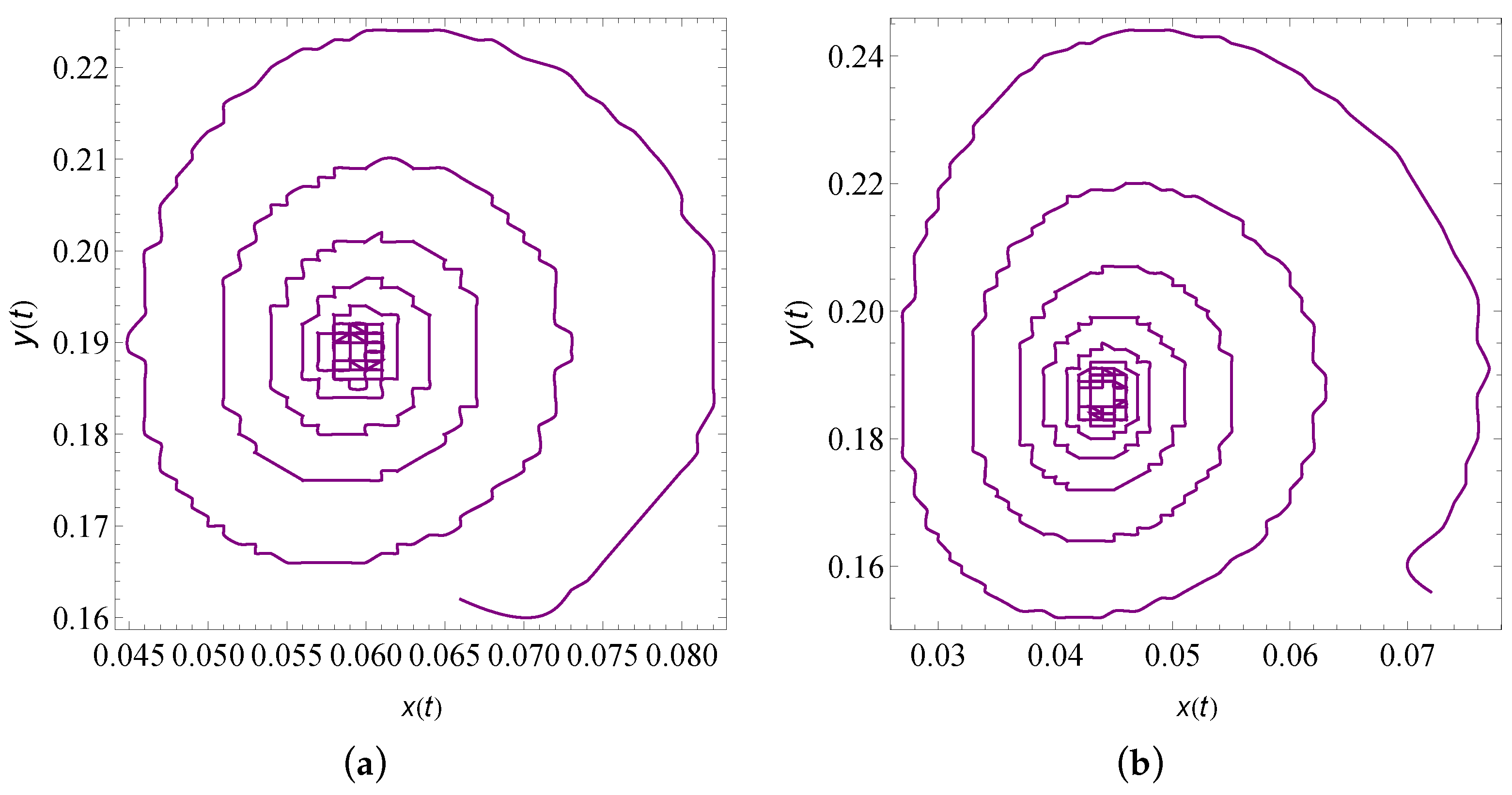
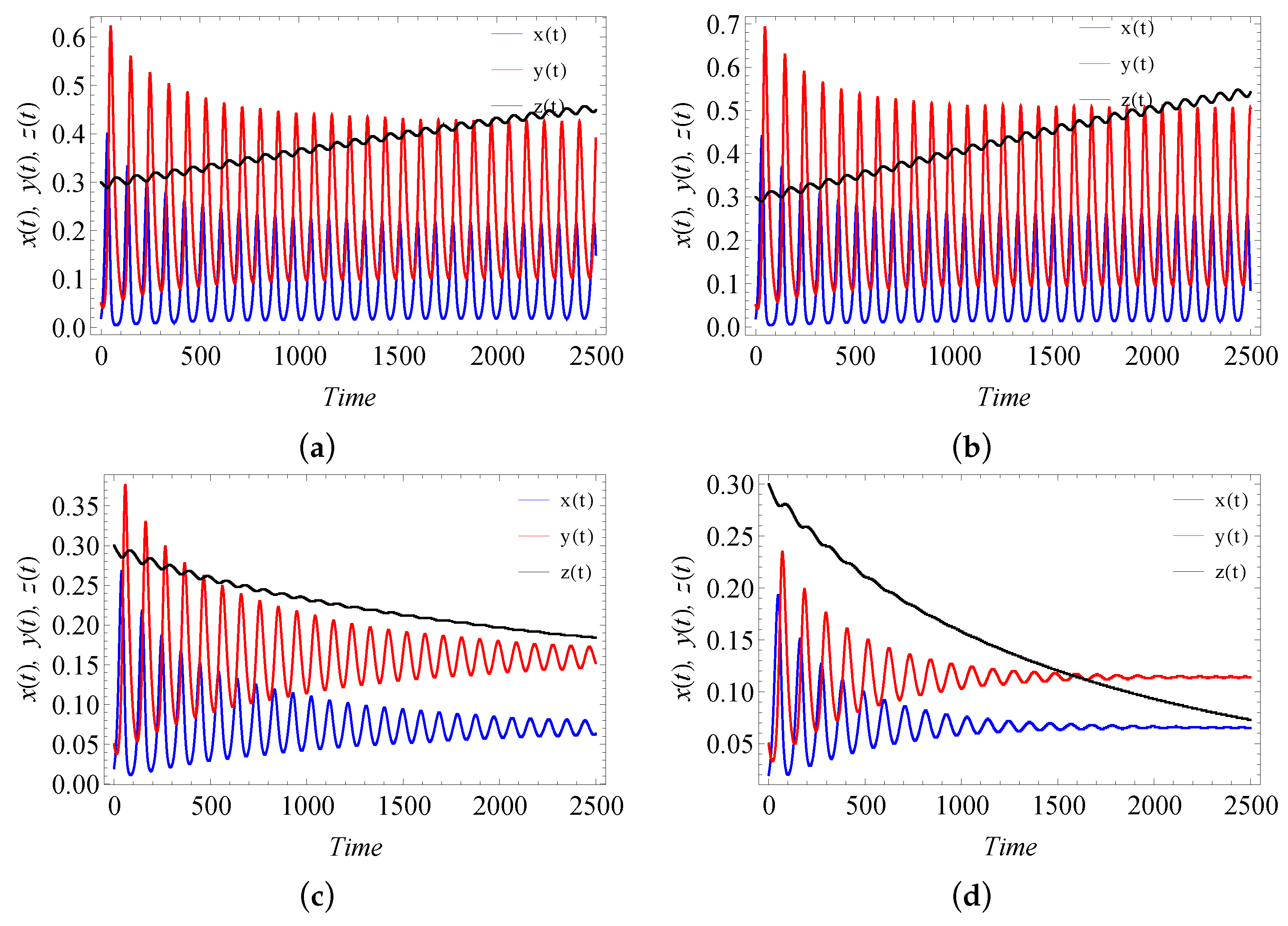
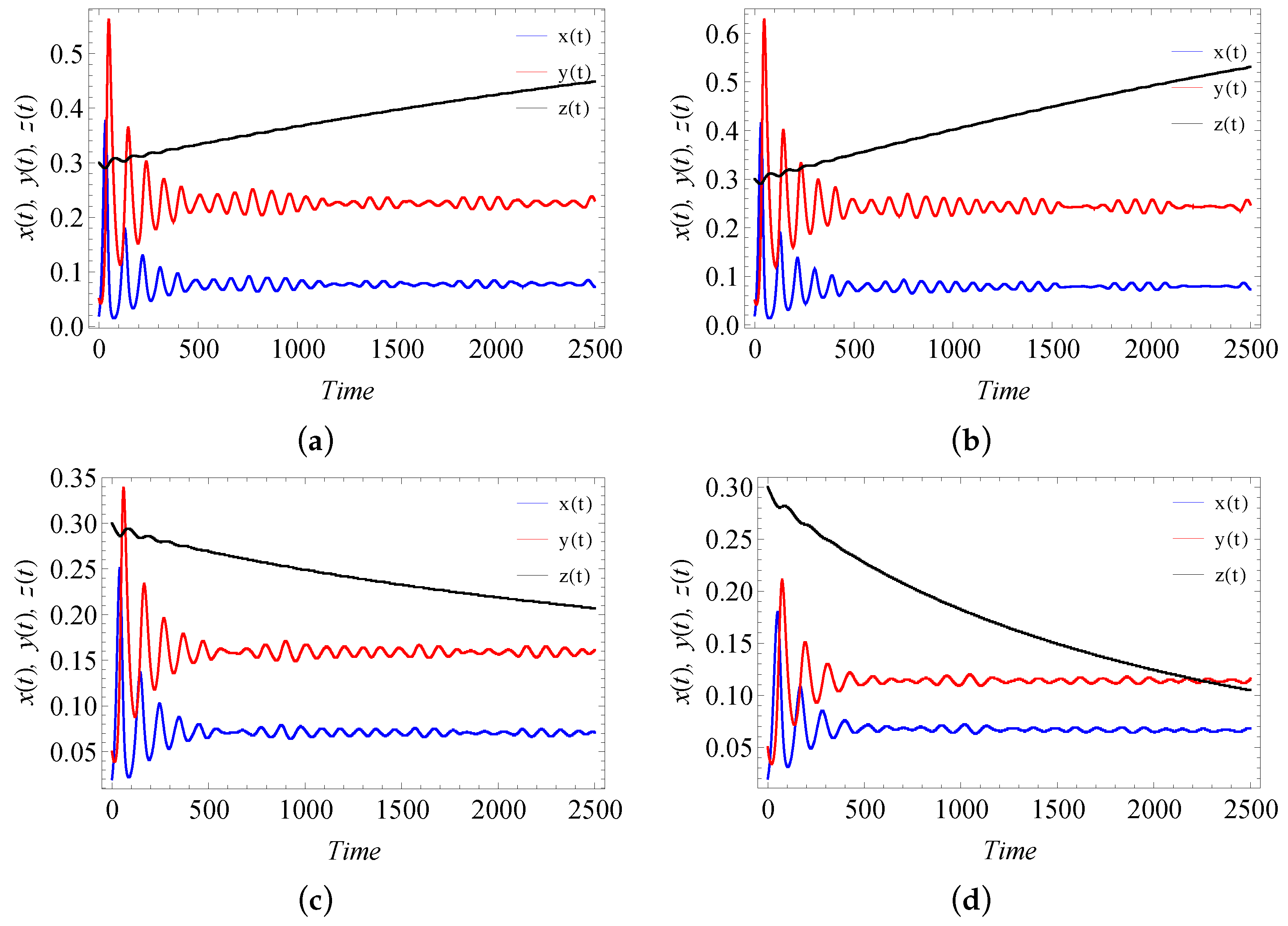
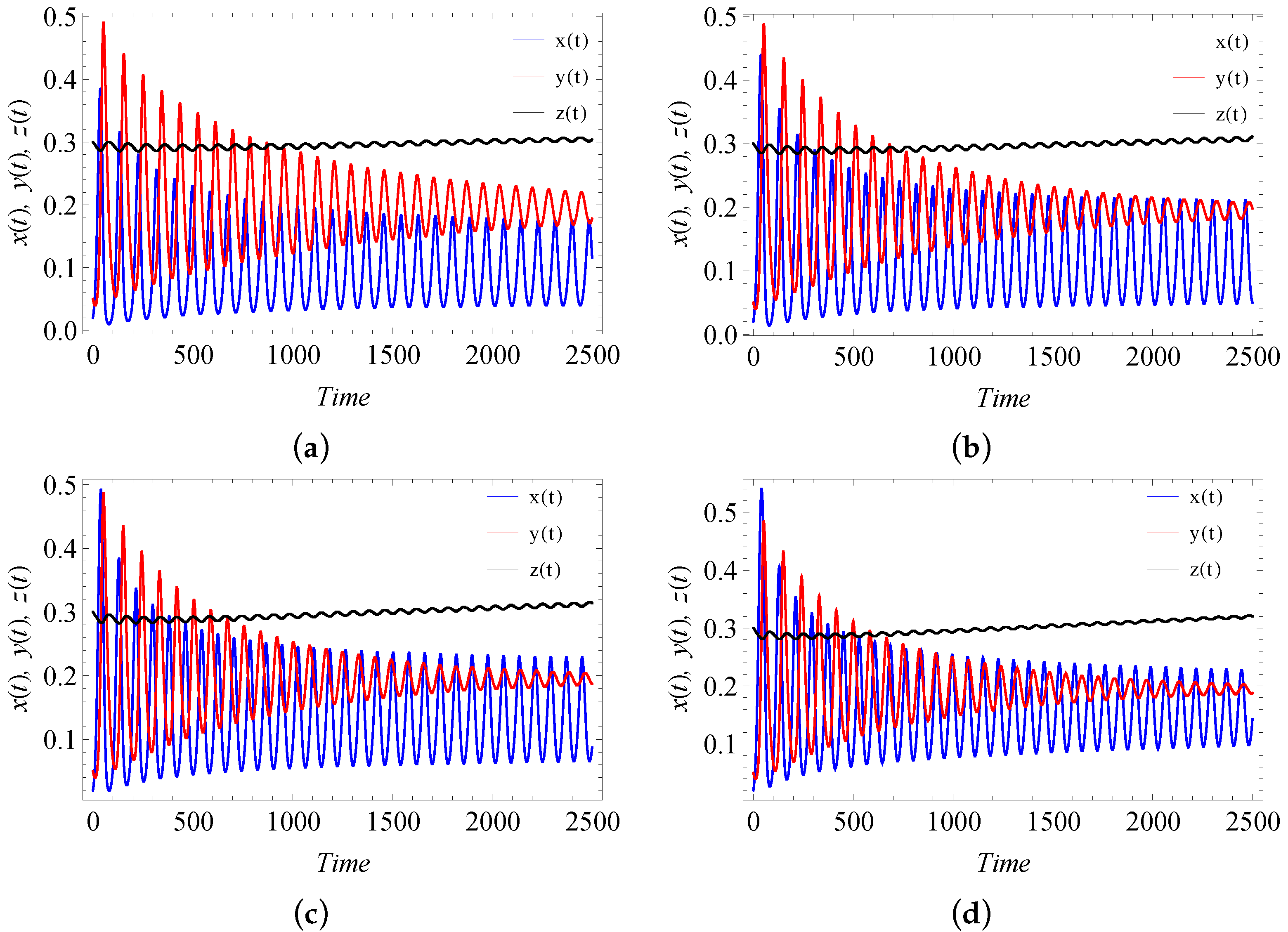
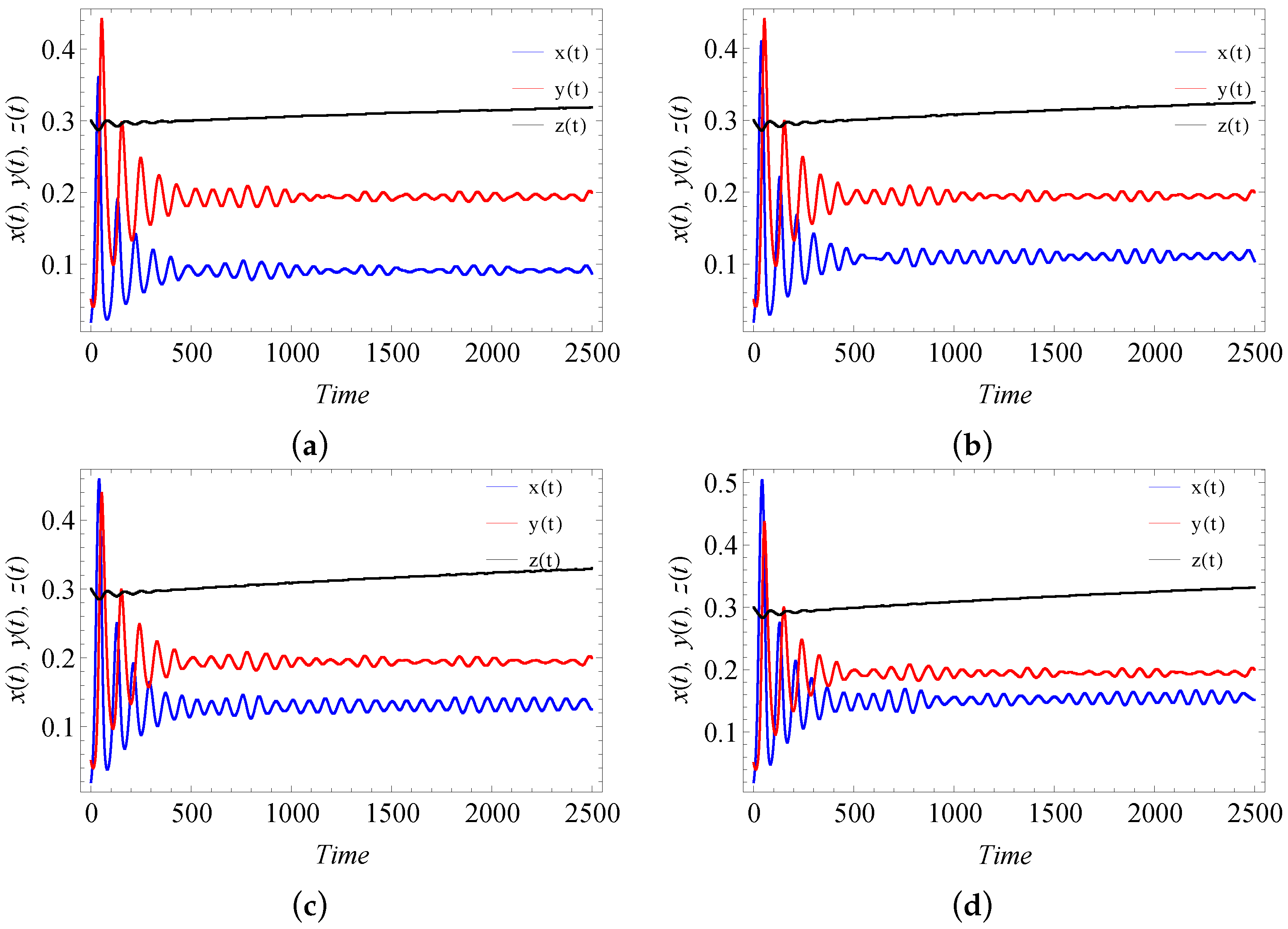
9. Numerical Simulation
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biological Control: An Eco-Friendly Way of Pest Management in Tea. 2018. Available online: https://gmsciencein.com/2018/04/23/biological-control-pest-management-tea (accessed on 13 September 2021).
- Basu Majumder, A.; Bera, B.; Rajan, A. Tea statistics: Global scenario. Inc. J. Tea Sci. 2010, 8, 121–124. [Google Scholar]
- Cranham, J.E. Tea pests and their control. Annu. Rev. Entomol. 1966, 11, 491–514. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Shah, Z.; Ali, N.; Alzahrani, E.O.; Shutaywi, M. Mathematical and stability Analysis of Fractional Order Model for Spread of Pests in Tea Plants. Fractals 2021, 29, 2150008. [Google Scholar] [CrossRef]
- Hazarika, L.K.; Bhuyan, M.; Hazarika, B.N. Insect pests of tea and their management. Annu. Rev. Entomol. 2009, 54, 267–284. [Google Scholar] [CrossRef] [Green Version]
- Hazarika, L.K.; Puzari, K.C.; Wahab, S. Biological control of tea pests. In Biocontrol Potential and Its Exploitation in Sustainable Agriculture; Springer: Boston, MA, USA, 2001; pp. 159–180. [Google Scholar]
- Maiti, A.; Patra, B.; Samanta, G.P. Sterile insect release method as a control measure of insect pests: A mathematical model. J. Appl. Math. Comput. 2006, 22, 71–86. [Google Scholar] [CrossRef]
- Pathak, S.; Maiti, A. Microbial pest control: A mathematical model. J. Biol. Syst. 2010, 18, 455–478. [Google Scholar] [CrossRef]
- Mamun, M.S.A.; Ahmed, M.; Paul, S.K. Integrated approaches in tea pest management for sustainable tea production. In Proceedings of the Workshop on Tea Production Technology Updated, Dhaka, Bangladesh, 24 December 2014; Bangladesh Tea Research Institute, Srimangal, Moulvibazar and Krishi Gobeshona Foundation, BARC Campus: Dhaka, Bangladesh, 2014; Volume 24, pp. 18–32. [Google Scholar]
- Muraleedharan, N. Pest control in Asia. In Tea; Springer: Dordrecht, The Netherlands, 1992; pp. 375–412. [Google Scholar]
- Liu, S.S.; Rao, A.; Vinson, S.B. Biological control in china: Past, present and future—An introduction to this special issue. Biol. Control 2014, 68, 1–5. [Google Scholar] [CrossRef]
- Landis, D.A.; Orr, D.B. Biological Control: Approaches and Applications. 1996. Available online: https://ipmworld.umn.edu/landis (accessed on 13 September 2021).
- The Advantages and Disadvantages of Pesticides. Available online: https://www.chefsbest.com/advantages-disadvantages-pesticides/ (accessed on 13 September 2021).
- Aktar, M.W.; Sengupta, D.; Chowdhury, A. Impact of pesticides use in agriculture: Their benefits and hazards. Interdiscip. Toxicol. 2009, 2, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Wahab, S. Tea pests and their management with bio-pesticides. Int. J. Tea Sci. 2004, 3, 1–10. [Google Scholar]
- Nakai, M. Biological control of tortricidae in tea fields in Japan using insect viruses and parasitoids. Virol. Sin. 2009, 24, 323–332. [Google Scholar] [CrossRef]
- Stoner, K. Approaches to the Biological Control of Insect Pests. Available online: https://portal.ct.gov/CAES/Fact-Sheets/Entomology/Approaches-to-the-Biological-Control-of-Insect-Pests (accessed on 14 September 2021).
- Hastings, A.; Powell, T. Chaos in a three-species food chain. Ecology 1991, 72, 896–903. [Google Scholar] [CrossRef]
- Panja, P.; Mondal, S.K.; Jana, D.K. Effects of toxicants on Phytoplankton-Zooplankton-Fish dynamics and harvesting. Chaos Solitons Fractals 2017, 104, 389–399. [Google Scholar] [CrossRef]
- Panja, P. Stability and dynamics of a fractional-order three-species predator–prey model. Theory Biosci. 2019, 138, 251–259. [Google Scholar] [CrossRef]
- Baishya, C.; Veeresha, P. Laguerre polynomial-based operational matrix of integration for solving fractional differential equations with non-singular kernel. Proc. R. Soc. A 2021, 477, 20210438. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Baishya, C. An operational matrix based on the Independence polynomial of a complete bipartite graph for the Caputo fractional derivative. SeMA J. 2021. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S. Exact and approximate solutions of time-fractional models arising from physics via Shehu transform. Math. Methods Appl. Sci. 2020, 43, 7442–7464. [Google Scholar] [CrossRef]
- Baishya, C.; Achar, S.J.; Veeresha, P.; Prakasha, D.G. Dynamics of a fractional epidemiological model with disease infection in both the populations. Chaos 2021, 31, 043130. [Google Scholar] [CrossRef]
- Owusu-Mensah, I.; Akinyemi, L.; Oduro, B.; Iyiola, O.S. A fractional order approach to modeling and simulations of the novel COVID-19. Adv. Differ. Equs. 2020, 2020, 683. [Google Scholar] [CrossRef]
- Veeresha, P.; Baleanu, D. A unifying computational framework for fractional Gross-Pitaevskii equations. Phys. Scr. 2021, 96, 125010. [Google Scholar]
- Iyiola, O.; Oduro, B.; Akinyemi, L. Analysis and solutions of generalized Chagas vectors re-infestation model of fractional order type. Chaos Solitons Fractals 2021, 145, 110797. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Veeresha, P.; Akinyemi, L.; Oluwasegun, K.; Şenol, M.; Oduro, B. Numerical surfaces of fractional Zika virus model with diffusion effect of mosquito-borne and sexually transmitted disease. In Mathematical Methods in the Applied Sciences; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [Green Version]
- Kepten, E.; Weron, A.; Sikora, G.; Burnecki, K.; Garini, Y. Guidelines for the fitting of anomalous diffusion mean square displacement graphs from single particle tracking experiments. PLoS ONE 2015, 10, e0117722. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
- Huang, C.; Li, H.; Cao, J. A novel strategy of bifurcation control for a delayed fractional predator-prey model. Appl. Math. Comput. 2019, 347, 808–838. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, D. Numerical solution of predator-prey model with Beddington-DeAngelis functional response and fractional derivatives with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 063103. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Kumar, A.; Jleli, M. A numerical analysis for fractional model of the spread of pests in tea plants. In Numerical Methods for Partial Differential Equations; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Lopes, A.M.; Machado, J.T. Fractional order models of leaves. J. Vib. Control 2014, 20, 998–1008. [Google Scholar] [CrossRef] [Green Version]
- El-Shahed, M.; Ahmed, A.M.; Abdelstar, I.M. A fractional-order Model for the spread of Pests in tea plants. Adv. Anal. 2016, 1, 68–79. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Wang, B.; Chen, L.Q. Asymptotic stability analysis with numerical confirmation of an axially accelerating beam constituted by the standard linear solid model. J. Sound Vib. 2009, 328, 456–466. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Agarwal, M.; Pathak, R. Harvesting, Hopf bifurcation and chaos in three species food chain model with Beddington-DeAngelis type functional response. J. Glob. Res. Math. Arch. 2013, 1, 49–62. [Google Scholar]
- Diethelm, K. An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal. 1997, 5, 1–6. [Google Scholar]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef] [Green Version]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]

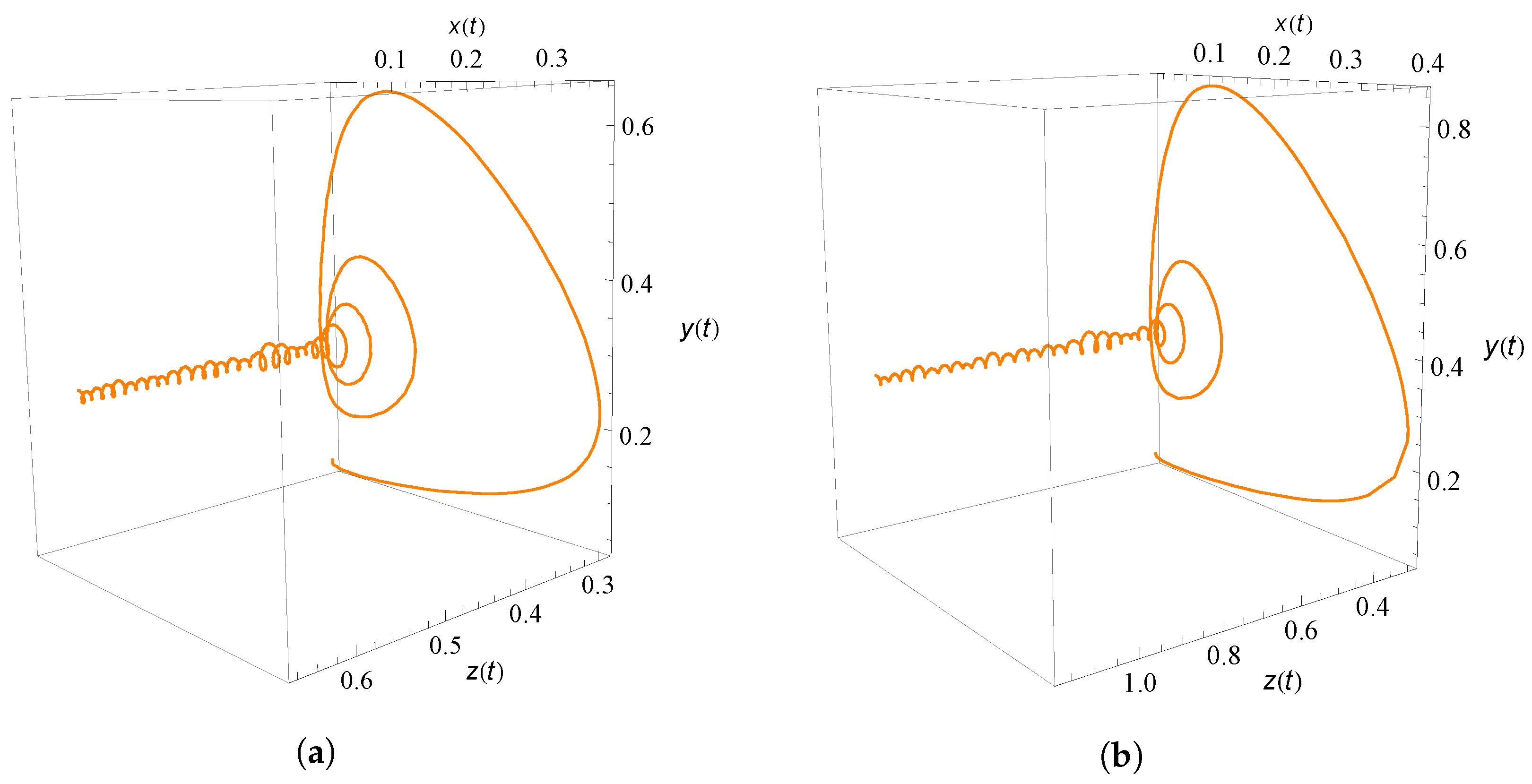

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achar, S.J.; Baishya, C.; Veeresha, P.; Akinyemi, L. Dynamics of Fractional Model of Biological Pest Control in Tea Plants with Beddington–DeAngelis Functional Response. Fractal Fract. 2022, 6, 1. https://doi.org/10.3390/fractalfract6010001
Achar SJ, Baishya C, Veeresha P, Akinyemi L. Dynamics of Fractional Model of Biological Pest Control in Tea Plants with Beddington–DeAngelis Functional Response. Fractal and Fractional. 2022; 6(1):1. https://doi.org/10.3390/fractalfract6010001
Chicago/Turabian StyleAchar, Sindhu J., Chandrali Baishya, Pundikala Veeresha, and Lanre Akinyemi. 2022. "Dynamics of Fractional Model of Biological Pest Control in Tea Plants with Beddington–DeAngelis Functional Response" Fractal and Fractional 6, no. 1: 1. https://doi.org/10.3390/fractalfract6010001
APA StyleAchar, S. J., Baishya, C., Veeresha, P., & Akinyemi, L. (2022). Dynamics of Fractional Model of Biological Pest Control in Tea Plants with Beddington–DeAngelis Functional Response. Fractal and Fractional, 6(1), 1. https://doi.org/10.3390/fractalfract6010001









