Lyapunov Approach for Almost Periodicity in Impulsive Gene Regulatory Networks of Fractional Order with Time-Varying Delays

Abstract

This paper investigates a class of fractional-order delayed impulsive gene regulatory networks (GRNs). The proposed model is an extension of some existing integer-order GRNs using fractional derivatives of Caputo type. The existence and uniqueness of an almost periodic state of the model are investigated and new criteria are established by the Lyapunov functions approach. The effects of time-varying delays and impulsive perturbations at fixed times on the almost periodicity are considered. In addition, sufficient conditions for the global Mittag–Leffler stability of the almost periodic solutions are proposed. To justify our findings a numerical example is also presented.

1. Introduction

The regulation of the genes’ expression in the process of operating of organisms on the molecular level is mainly realized via genetic regulatory systems organised as networks of connections between DNA, RNA, proteins, and small molecules. A very good literature review of the different formalisms that have been employed to describe genetic regulatory systems has been proposed in [1]. Ordinary differential equations are among the proposed formalisms, that are intensively applied by numerous researchers in modelling of GRNs [2,3,4].

Investigating the effects of time delays is very important in the models of GRNs in order to understand the transcriptional process of genetic gene and analyze the limited speed of gene transcription. That is why, GRNs with fixed delays, time-varying delays, random delays are extensively studied and many important qualitative results have been proposed. See, for example, refs. [5,6,7] for some very good achievements on delayed GRNs. The recently published book [8] is also a very good source of research and provides an essential introduction to the latest advances in delayed GRNs.

Using the formalism of delayed differential equations, a model of a delayed GRN proposed in [6] can be represented as follows

$$\left\{\begin{array}{c}{\displaystyle {\dot{m}}_i\left(t\right)=-a_i{m}_i\left(t\right)+\sum _{j=1}^n{w}_{ij}{f}_j\left(p_j(t-\sigma \left(t\right))\right)+B_i}\hfill \\ {\displaystyle {\dot{p}}_i\left(t\right)=-c_i{p}_i\left(t\right)+d_i{m}_i(t-\tau \left(t\right)),}\hfill \end{array}\right.$$

(1)

where $i=1,2,\cdots ,n$, $m_i\left(t\right)$ and $p_i\left(t\right)$ denote the i-th mRNA molecule’s concentration and i-th protein’s concentration at time t, respectively, the real constants $a_i$ and $c_i$ denote the degradation rates in the i-th mRNA molecule’s concentration and i-th protein’s concentration, respectively, the positive constants $d_i$ are the translation rates, the regulatory function $f_j$ for any $j=1,2,\cdots ,n$ is of the following Hill form

$${\displaystyle f_j\left(x\right)=\frac{{(x/{\beta }_j)}^{H_j}}{1+{(x/{\beta }_j)}^{H_j}}}$$

where the constants ${\beta }_j>0$ and the constants $H_j$ are known as Hill coefficients, the constants $w_{ij}$ are the connecting parameters, $B_i$ is the basal rate of the repressor of gene i, $\sigma \left(t\right)$ and $\tau \left(t\right)$ represent the time-varying delays.

Additionally, impulsive effects are common in modelling gene regulation processes since the physical environments or external forces may abruptly change the GRNs states. As a result, impulses have been introduced into the GRNs models, and several classes of GRNs have been modelled by impulsive equations [9,10,11]. In fact, impulsive differential equations is an increasingly important area of non-linear analysis. Such equations are capable of describing many phenomena that occur in nature [12,13,14]. In addition, among the control approaches, the impulsive control is a powerful technique to control the qualitative properties of a system under short-term disturbances [15,16,17,18,19]. Impulsive control strategies are also applied to GRNs [20].

On the other side, fractional calculus perspective has been pointed out as very promising in modelling a number of processes in science, biology, and medicine [21,22,23]. Due to the advantages of the fractional-order modelling, fractional-order networks have become an active area of research in the biological and biomedical sciences and have received great attention over the last few years [24,25,26,27]. Very recently, fractional-order approach has been also applied to GRNs. In the [28] the authors applied the Razumikhin strategy to establish criteria for stability and synchronization of the states in fractional order time delayed GRNs. The paper [29] studied a class of fractional-order GRNs and proposed some Mittag–Leffler stability and generalized Mittag–Leffler stability criteria using the fractional Lyapunov method. A type of fractional-order GRNs has been introduced in [30] to synchronize at finite-time point by designing feedback controls. A global stability analysis of fractional-order GRNs with time delay has been conducted in [31]. The paper [32] is devoted to the global uniform asymptotical stability of fractional GRNs with time-varying delays and structured uncertainties.

The investigations on fractional GRNs under impulsive perturbations are still very seldom. Some criteria for stability and synchronization of fractional delayed GRNs under impulsive control have been proposed in [33]. Mittag–Leffler stability criteria for fractional GRNs under impulsive effects are established in [34].

However, all mentioned above studies on fractional GRN’s offered only stability and synchronization results and no results on other qualitative properties are reported in the existing literature. Except stability, there are some main qualitative properties of neural network systems that are very important from the applied point of view. One of these properties is the almost periodicity of the states. On the importance of studying of almost periodic properties and processes we will direct readers to [35,36,37,38,39]. This is the main reason of the existing of numerous results on almost periodicity of different classes of applied problems [40,41,42], including fractional neural networks [43,44,45]. In fact, the non-existence of pure periodic solutions for systems of fractional order has been proved in [46].

Recently, almost periodicity is investigated only for integer-order GRNs in few papers [47,48]. To the best of the authors knowledge, there are not results on the almost periodic properties of fractional-order GRNs and this is the main goal of our study.

In this paper, we will apply the fractional Lyapunov strategy to investigate the existence and stability of almost periodic states for a class of fractional-order GRNs. Indeed, the Lyapunov method is a very powerful technique that is applied intensively by many researches in the investigations of the qualitative properties of fractional-order problems and impulsive control problems [14,16,17,18,23,26,27,49,50,51], including fractional-order GRNs [28,29,30,31,32,33,34].

The main novelty of the paper is in the following five points:

(1)

An impulsive control strategy is considered for a class of fractional-order GRNs with time-varying delays;

(2)

The almost periodicity notion is introduced to the model under consideration which initiates the development of the almost periodicity theory for impulsive fractional GRNs;

(3)

New existence and uniqueness results for the almost periodic states are established;

(4)

New criteria for global Mittag–Leffler stability of an almost periodic state of the impulsive model under consideration are also proved;

(5)

We apply an extended Lyapunov function approach which allows representing the obtained results in terms of the model’s parameters, and leads to a better exploration of the impulsive effect.

Since GRNs are still very popular in science and, studying their qualitative behavior would have diverse applications. Hence, the proposed almost periodicity qualitative results will be of a great importance not only for researchers in applied mathematics and mathematical biology, but also for a wide audience of professionals all over the world.

More precisely, in Section 2 we introduce the model of fractional delayed impulsive GRNs and state some notations, definitions and lemmas. The almost periodicity concept is also introduced to the formulated model. Section 3 is dedicated to the main existence and uniqueness criteria for the almost periodic states. Results on the global Mittag–Leffler stability of the almost periodic solutions are also presented. In Section 4, we demonstrate the presented results by a numerical example. Some conclusion observations are commented in Section 5.

2. The Fractional-Order Impulsive Delayed GRN Model. Preliminaries

Let ${\mathbb{R}}^n$ denotes the n-dimensional Euclidean space and the norm of $U={(U_1,U_2,\cdots ,U_n)}^T$$\in {\mathbb{R}}^n$ is given by ${\displaystyle \left|\right|U\left|\right|=\sqrt{\sum _{i=1}^n{U}_i^2}}$. Let ${\mathbb{R}}_{+}=[0,\infty )$.

First, we will recall some basic fractional calculus definitions and properties.

Definition 1.

Ref. [22] Let $\alpha >0$ and $t\ge t_0$, $t_0\in \mathbb{R}$. An integral of fractional order α for a function u is defined as

$$I_{t_0}^{\alpha }u\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_{t_0}^t\frac{u\left(\lambda \right)}{{(t-\lambda )}^{1-\alpha }}d\lambda ,$$

where Γ is the Gamma function defined by

$$\mathrm{\Gamma }\left(\alpha \right)={\int }_0^{\infty }{e}^{-t}{t}^{\alpha -1}dt.$$

When $t_0=0$, we will denote by

$$I^{\alpha }u\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{u\left(\lambda \right)}{{(t-\lambda )}^{1-\alpha }}d\lambda ,$$

Definition 2.

Let n be an integer, $n>0$ let $n-1<\alpha <n$. The fractional derivative of order α of Caputo type with a lower limit $t_0$ for a function $u\in C^{n+1}[[t_0,\infty ),\mathbb{R}]$ is given by

$${{}_{t_0}^{C}D}_t^{\alpha }u\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_{t_0}^t\frac{u^{\left(n\right)}\left(\lambda \right)}{{(t-\lambda )}^{\alpha -n+1}}d\lambda .$$

For $\alpha \in (0,1)$ and $t_0=0$, we have

$${{}_0^{C}D}_t^{\alpha }u\left(t\right)={{}^{C}D}_t^{\alpha }u\left(t\right)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_{t_0}^t\frac{u^{\prime }\left(\lambda \right)}{{(t-\lambda )}^{\alpha }}d\lambda .$$

We will use the following properties in the proofs of our main almost periodicity results for $t\ge t_0$ and $\alpha \in (0,1)$ [21,22,23]:

P1.

$I_{t_0}^{\alpha }\left({{}_{t_0}^{C}D}_t^{\alpha }u\left(t\right)\right)=u\left(t\right)-u\left(t_0\right).$

P2.

${{}_{t_0}^{C}D}_t^{\alpha }(c_1{u}_1\left(t\right)+c_2{u}_2\left(t\right))=c_1{{}_{t_0}^{C}D}_t^{\alpha }{u}_1\left(t\right)+c_2{{}_{t_0}^{C}D}_t^{\alpha }{u}_2\left(t\right)$.

P3.

Ref. [51] ${{}_{t_0}^{C}D}_t^{\alpha }{u}^2\left(t\right)\le 2u\left(t\right){{}_{t_0}^{C}D}_t^{\alpha }u\left(t\right).$

Additionally, the classes of Mittag–Leffler functions defined by the next definitions will be applied [22].

Definition 3.

For $\alpha >0$, the Mittag–Leffler function is given as

$$E_{\alpha }\left(\vartheta \right)=\sum _{\kappa =0}^{\infty }\frac{{\vartheta }^{\kappa }}{\mathrm{\Gamma }(\alpha \kappa +1)},$$

where ϑ is a complex variable.

Definition 4.

For $\alpha >0$ and $\beta >0$, the Mittag–Leffler function in two parameters, is defined by

$$E_{\alpha ,\beta }\left(\vartheta \right)=\sum _{\kappa =0}^{\infty }\frac{{\vartheta }^{\kappa }}{\mathrm{\Gamma }(\alpha \kappa +\beta )}.$$

In the particular case, when $\alpha >0$ and $\beta =1$, $E_{\alpha }\left(\vartheta \right)=E_{\alpha ,1}\left(\vartheta \right)$. Additionally, for $\alpha =\beta =1$, $E_{1,1}\left(\vartheta \right)=e^{\vartheta }$.

Next, we will define the impulsive GRN model of fractional order with time-varying delays as follows:

$$\left\{\begin{array}{c}{\displaystyle {{}^{C}D}_t^{\alpha }{m}_i\left(t\right)=-a_i{m}_i\left(t\right)+\sum _{j=1}^n{w}_{ij}\left(t\right)f_j\left(p_j(t-{\sigma }_j\left(t\right))\right)+B_i\left(t\right),t\ne t_k,}\hfill \\ {\displaystyle {{}^{C}D}_t^{\alpha }{p}_i\left(t\right)=-c_i{p}_i\left(t\right)+d_i\left(t\right)m_i(t-{\tau }_i\left(t\right)),t\ne t_k,}\hfill \\ \\ m_i\left(t_k^{+}\right)=m_i\left(t_k\right)+P_{ik}\left(m_i\left(t_k\right)\right),p_i\left(t_k^{+}\right)=p_i\left(t_k\right)+Q_{ik}\left(p_i\left(t_k\right)\right),\hfill \end{array}\right.$$

(2)

where:

• $\alpha \in (0,1)$, $t\in \mathbb{R}$, $i=1,2,\cdots ,n$;
• The parameters $a_i,c_i>0$ are the same as in (1);
• The functions of regulation $f_j$, $j=1,2,\cdots ,n$ are the same as in (1) and satisfy

  $$0\le \frac{f_j\left(u\right)-f_j\left(v\right)}{u-v}\le l_j,$$

  (3)

  for some constants $l_j$ and all $u,v\in \mathbb{R}$, $u\ne v$;
• The translation rates $d_i$ and basal rates $B_i$ are extended to functions $d_i\left(t\right)$ and $B_i\left(t\right)$, respectively, $i=1,2,\cdots ,n$, $B_i\left(t\right)={\sum }_{j\in I_i}{b}_{ij}\left(t\right)$, where $I_i$ is the set of all the j which are repressors of the gene i;
• The functions $w_{ij}\left(t\right)$ are represented as:

  $$w_{ij}\left(t\right)=\left\{\begin{array}{c}{\displaystyle b_{ij}\left(t\right),\mathrm{if}j\mathrm{is}\mathrm{an}\mathrm{activator}\mathrm{of}\mathrm{gene}i}\hfill \\ {\displaystyle -b_{ij}\left(t\right),\mathrm{if}j\mathrm{is}\mathrm{a}\mathrm{repressor}\mathrm{of}\mathrm{gene}i}\hfill \\ {\displaystyle 0,\mathrm{if}\mathrm{there}\mathrm{is}\mathrm{no}\mathrm{connection}\mathrm{between}\mathrm{the}\mathrm{node}j\mathrm{and}\mathrm{the}\mathrm{gene}i;}\hfill \end{array}\right.$$
• The time-varying delays ${\sigma }_i\left(t\right)\in C[\mathbb{R},\mathbb{R}]$ and ${\sigma }_i\left(t\right)\in C[\mathbb{R},\mathbb{R}]$ are different for different mRNA and protein molecules, respectively, and satisfy $t>{\sigma }_j,t>{\tau }_i$ and $0\le {\sigma }_j\left(t\right)\le \sigma$ ($\sigma$ = const), $0\le {\tau }_i\left(t\right)\le \tau$, ($\tau$ = const), $i=1,2,\cdots ,n,j=1,2,\cdots ,n$;
• $t_k$ are the impulsive moments (impulsive control instants) and $t_k\in \mathcal{T}$, where $\mathcal{T}$ is the set of all sequences of the type

  $$\left\{t_k\right\}:t_k\in (-\infty ,\infty ),t_k<t_{k+1},t_k\ne 0,k=\pm 1,\pm 2,\cdots ,\underset{k\to \pm \infty }{lim}{t}_k=\pm \infty$$

  with a distance denoted as $\rho \left(\left\{t_k^{\left(1\right)}\right\},\left\{t_k^{\left(2\right)}\right\}\right)$;
• $m_i\left(t_k\right)=m_i\left(t_k^{-}\right)$ and $p_i\left(t_k\right)=p_i\left(t_k^{-}\right)$ denote the i-th mRNA concentration and i-th protein concentration at time $t_k$, respectively, and $m_i\left(t_k^{+}\right)$ and $p_i\left(t_k^{+}\right)$ denote the level of the i-th mRNA concentration and i-th protein concentration, respectively, at $t_k^{+}$, i.e., after an impulsive short-term effect on them at $t_k$;
• The impulsive functions $P_{ik}$ and $Q_{ik}$ denote the amounts of the abrupt variation in $m_i\left(t\right)$ and $p_i\left(t\right)$, respectively, at the impulsive instants $t_k$, i.e., $\Delta m_i\left(t_k\right)=m_i\left(t_k^{+}\right)-m_i\left(t_k\right)=P_{ik}\left(m_i\left(t_k\right)\right)$ and $\Delta p_i\left(t_k\right)=p_i\left(t_k^{+}\right)-p_i\left(t_k\right)=Q_{ik}\left(p_i\left(t_k\right)\right)$, $i=1,2,\cdots ,n$, $k=\pm 1,\pm 2,\cdots$.

To specify the initial conditions associated with the model (2), we will use functions $\chi :\mathbb{R}\to {\mathbb{R}}^n:\chi \left(t\right)$ are piecewise continuous on $\mathbb{R}$ with points of jump discontinuities $t_k\in \mathcal{T}$ at which $\chi \left(t_k^{-}\right)=\chi \left(t_k\right)$. The class of all such functions will be denoted by $PC[\mathbb{R},{\mathbb{R}}^n]$. We will also use initial functions from the classes of bounded and piecewise continuous functions $\varphi \in PC[[-\tau ,0],{\mathbb{R}}^n]$ and $\phi \in PC[[-\sigma ,0],{\mathbb{R}}^n]$ with finite number of points of discontinuities, denoted by $\mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$ and $\mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$, respectively, with norms:

$${\left|\right|\varphi \left|\right|}_{\tau }=\underset{\xi \in [-\tau ,0]}{sup}{\left|\right|\varphi \left(\xi \right)\left|\right|,\left|\right|\phi \left|\right|}_{\sigma }=\underset{\xi \in [-\sigma ,0]}{sup}\left|\right|\phi \left(\xi \right)\left|\right|.$$

Let $\varphi \in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n],$$\varphi ={({\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_n)}^T$ and $\phi \in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$, $\phi ={({\phi }_1,{\phi }_2,\cdots ,{\phi }_n)}^T$. Denote by ${(m\left(t\right),p\left(t\right))}^T={(m(t;0,\varphi ),p(t;0,\phi ))}^T\in {\mathbb{R}}^{2n}$,

$${(m(t;0,\varphi ),p(t;0,\phi ))}^T={(m_1(t;0,\varphi ),\cdots ,m_n(t;0,\varphi ),p_1(t;0,\phi ),\cdots ,p_n(t;0,\phi ))}^T$$

the solution of the model (2) associated with the following initial conditions

$$\left\{\begin{array}{c}{m}_i(\xi ;0,\varphi )={\varphi }_i\left(\xi \right),-\tau \le \xi \le 0,\hfill \\ p_i(\xi ;0,\phi )={\phi }_j\left(\xi \right),-\sigma \le \xi \le 0,\hfill \\ m_i(0^{+},0,\varphi )={\varphi }_i\left(0\right),p_i(0^{+},0,\phi )={\phi }_i\left(0\right),\hfill \end{array}\right.$$

(4)

$i=1,2,\cdots ,n.$

Remark 1.

The model (2) is an extension of the GRN models proposed in [5,6] and some others, considering different time-varying delays, fractional-order derivatives, and impulsive effects.

For the study of the almost periodic properties of the states of the fractional impulsive model (2), we will next apply the almost periodicity concepts from [38,39].

Let the function $\chi \in PC[\mathbb{R},{\mathbb{R}}^n]$ and $\mathrm{X}=(\chi \left(t\right),T)\in PC[\mathbb{R},{\mathbb{R}}^n]\times \mathcal{T}$. Consider the sets ${\theta }_{s_q}\mathrm{X}=\{\chi (t+s_q),T-s_q\}\subset PC[\mathbb{R},{\mathbb{R}}^n]\times \mathcal{T}$, where ${\left\{s_q\right\}}_{q=1}^{\infty }$, $s_q\in \mathbb{R}$, is an arbitrary infinite sequence of real entries and $T-s_q=\{t_k-s_q\}$, $k=\pm 1,\pm 2,\cdots ,$$q=1,2,\cdots$.

Definition 5.

If from any sequence of real numbers $\left\{s{{}^{\prime }}_m\right\}$ it is possible to select a subsequence $\left\{s_q\right\},s_q=s_{m_q}^{\prime }$, such that ${\theta }_{s_q}\mathrm{X}$ to be compact in $PC[\mathbb{R},{\mathbb{R}}^m]\times \mathcal{T}$, then the function $\chi \in PC[\mathbb{R},{\mathbb{R}}^n]$, $\chi =\chi \left(t\right)$, is called almost periodic piecewise continuous function on $\mathbb{R}$.

Definition 6.

A sequence $\left\{{\mathrm{X}}_{\mathrm{q}}\right\}$, ${\mathrm{X}}_{\mathrm{q}}=({\chi }_q\left(t\right),T_q)\in PC[\mathbb{R},{\mathbb{R}}^n]\times \mathcal{T}$, converges uniformly with respect to $t\in \mathbb{R}$ to $\mathrm{X}$, if from the existence of an $\epsilon >0$ there follows the existence of a $q_0>0$, such that the estimates

$$\rho (T,T_q)<\epsilon ,\left|\right|{\chi }_q\left(t\right)-\chi \left(t\right)\left|\right|<\epsilon$$

are satisfied uniformly for any $q\ge q_0$, $t\in \mathbb{R}\setminus \cap \left\{{\theta }_{\epsilon }\left(s(T_q\cup T)\right)\right\},$ where $s(T_q\cup T)$ is a strictly increasing sequence, $s(T_q\cup T):\mathcal{T}\to \mathcal{T}$, and ${\theta }_{\epsilon }\left(s(T_q\cup T)\right)=\{t+\epsilon ,t\in s(T_q\cup T)\}$.

Definition 7.

The set of all sequences of the type $\left\{t_k^l\right\}$, $t_k^l=t_{k+l}-t_k$, $k=\pm 1,\pm 2,\cdots$, $l=\pm 1,\pm 2,\cdots$ is called uniformly almost periodic (UAP), if from each infinite sequence of shifts $\{t_k-s_q\},k=\pm 1,\pm 2,\cdots$, $q=1,2,\cdots$, $s_q\in \mathbb{R}$ it is possible to select a convergent subsequence in $\mathcal{T}$.

Remark 2.

The almost periodicity concepts defined in Definitions 5–7 are adopted from [38,39]. Similar notions are applied in [35,40,41,42,43,44,45]. We will refer the reader to [49,50] for more details and definitions of almost periodic sequences and functions. The case of piecewise continuous almost periodic functions is mainly investigated in [38,39]. The almost periodicity notions are introduced for GRNs in [47], where impulsive effects and fractional derivatives are not considered. For impulsive GRNs the concept is applied in [48] for the integer-order case.

We will consider the introduced fractional impulsive GRNs under the following assumptions:

A1.

The model parameters $d_i\left(t\right)$, $w_{ij}\left(t\right)$, $B_i\left(t\right)$ are almost periodic in the sense of Bohr [38,39] on $\mathbb{R}$ and there exist $w>0$ and $d>0$, such that

$$\left|w_{ij}\left(t\right)\right|\le w,\left|d_i\left(t\right)\right|\le d$$

for every $i,j=1,2,\cdots ,n$ and $t\in \mathbb{R}$;

A2.

The sequences of functions $\left\{P_{ik}\left(m_i\right)\right\}$ and $\left\{Q_{ik}\left(p_i\right)\right\}$, $k=\pm 1,\pm 2,\cdots$, $i=1,2,\cdots ,n$ are almost periodic in the sense of Bohr;

A3.

The initial functions $\varphi \in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$ and $\phi \in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$ are almost periodic;

A4.

The set of sequences $\left\{t_k^l\right\}$, $k=\pm 1,\pm 2,\cdots$, $l=\pm 1,\pm 2,\cdots$ is UAP.

Remark 3.

The reasonableness of the assumptions A1–A4 lies in the theory of almost periodic functions and almost periodic sequences. In fact, the assumptions for almost periodicity for the models’ functional parameters and initial data are essential in the study of the almost periodic behavior of the states of model (2). See [38,39].

Let $\left\{s_l^{\prime }\right\}$ be an arbitrary infinite sequence of real numbers. Then, refs. [38,39,43] the assumptions A1–A4 guarantee that it is possible to select a subsequence $\left\{s_q\right\},s_q=s_{l_q}^{\prime }$ which generates transitions of the GRN (2) to a system of the type

$$\left\{\begin{array}{c}{\displaystyle {{}^{C}D}_t^{\alpha }{m}_i\left(t\right)=-a_i{m}_i\left(t\right)+\sum _{j=1}^n{w}_{ij}^s\left(t\right)f_j\left(p_j(t-{\sigma }_j\left(t\right))\right)+B_i^s\left(t\right),t\ne t_k^s,}\hfill \\ {\displaystyle {{}^{C}D}_t^{\alpha }{p}_i\left(t\right)=-c_i{p}_i\left(t\right)+d_i^s\left(t\right)m_i(t-{\tau }_i\left(t\right)),t\ne t_k^s,}\hfill \\ \\ m_i\left(t_k^{s+}\right)=m_i\left(t_k^s\right)+P_{ik}\left(m_i\left(t_k^s\right)\right),p_i\left(t_k^{s+}\right)=p_i\left(t_k^s\right)+Q_{ik}\left(p_i\left(t_k^s\right)\right).\hfill \end{array}\right.$$

(5)

The set of limiting systems of type (5) which reflect the almost periodicity concept [36] applied to differential systems [52] is known as a hull of the system (2) and will be denoted by $\mathcal{H}\left(2\right)$.

If ${(m\left(t\right),p\left(t\right))}^T$ is a solution of the model (2), then by $\mathcal{H}\left({(m\left(t\right),p\left(t\right))}^T\right)$ we will denote the hull of ${(m\left(t\right),p\left(t\right))}^T$.

In our almost periodicity analysis we will apply the Lyapunov function approach. Define the sets:

$${\mathcal{G}}_k=\{(t,U,V):t\in (t_{k-1},t_k),U,V\in {\mathbb{R}}^n\},k=\pm 1,\pm 2,\cdots ,$$

the set $\mathcal{G}={\bigcup }_{k=\pm 1,\pm 2,...}{\mathcal{G}}_k$ and the class $W_0$ of piecewise continuous Lyapunov functions $W:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}_{+}$, that are continuous in $\mathcal{G}$, locally Lipschitz continuous with respect to $(U,V)$ on every set ${\mathcal{G}}_k$, $k=\pm 1,\pm 2,\cdots$, $W(t,0,0)=0$, $t\in \mathbb{R}$, the limits $W(t_k^{-},U,V)={lim}_{\genfrac{}{}{0pt}{}{t\to t_k}{t<t_k}}W(t,U,V)$, $W(t_k^{+},U,V)={lim}_{\genfrac{}{}{0pt}{}{t\to t_k}{t>t_k}}W(t,U,V)$ exist and are finite, $W(t_k^{-},U,V)=W(t_k,U,V)$, $k=\pm 1,\pm 2,\cdots$, $U,V\in {\mathbb{R}}^n$.

Let $t\ne t_k$, $k=\pm 1,\pm 2,\cdots$, $\mathrm{\Phi }\in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$ and $\mathrm{\Psi }\in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$. The fractional derivative of order $\alpha$, $0<\alpha <1$ for a function $W\in W_0$ will be defined by the next definition [23].

Definition 8.

The function

$${\displaystyle {}^c{D}^{\alpha }W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right))=\underset{h\to 0^{+}}{lim}sup\frac{1}{h^{\alpha }}[W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right))}$$

$$-W(t-h,\mathrm{\Phi }\left(0\right)-h^{\alpha }{F}_1(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }),\mathrm{\Psi }\left(0\right)-h^{\alpha }{F}_2(t,\mathrm{\Phi },\mathrm{\Psi }\left(0\right))]$$

is said to be a Caputo-type fractional derivative of W of order α, $0<\alpha <1$ with respect to a system

$${\displaystyle {{}^{C}D}_t^{\alpha }U\left(t\right)=F_1(t,U,V_t),t\ne t_k,}$$

$${\displaystyle {{}^{C}D}_t^{\alpha }V\left(t\right)=F_2(t,U_t,V),t\ne t_k,}$$

$$U\left(t_k^{+}\right)=U\left(t_k\right)+J_k\left(U\left(t_k\right)\right),V\left(t_k^{+}\right)=V\left(t_k\right)+{\tilde{J}}_k\left(V\left(t_k\right)\right),t=t_k,$$

where $t>0$, $U_t\left(\xi \right)=U(t+\xi )$, $\xi \in [-\tau ,0]$, $V_t\left(\xi \right)=V(t+\xi )$, $\xi \in [-\sigma ,0]$, the continuous vector-functions $F_1:\mathbb{R}\times {\mathbb{R}}^n\times \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]\to {\mathbb{R}}^n$, $F_2:\mathbb{R}\times \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, are locally Lipschitz in their second and third variables, $J_k,{\tilde{J}}_k:{\mathbb{R}}^n\to {\mathbb{R}}^n,k=\pm 1,\pm 2,\cdots$.

From Lemma 1.6 in [23], we obtain the following result.

Lemma 1.

Assume that for the Lyapunov-type function $W\in W_0$ and for $\mathrm{\Phi }\in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$, $\mathrm{\Psi }\in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$ the following conditions hold for $t\ge 0$:

(i)

$W(t^{+},\mathrm{\Phi }\left(0\right)+J_k\left(\mathrm{\Phi }\right),\mathrm{\Psi }\left(0\right)+{\tilde{J}}_k\left(\mathrm{\Psi }\right))\le W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right)),t=t_k,k=\pm 1,\pm 2,\cdots$;

(ii)

The inequality

$${}^c{D}^{\alpha }W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right))\le -\mu W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right))+\nu ,\mu ,\nu \in \mathbb{R},t\ne t_k$$

is valid whenever

$$W(t+\xi ,\mathrm{\Phi }(\xi ),\mathrm{\Psi }(\xi \left)\right)\le W(t,\mathrm{\Phi }(0),\mathrm{\Psi }(0\left)\right),-max[\tau ,\sigma ]\le \xi \le 0.$$

Then

$$W(t,U(t;0,\mathrm{\Phi }),V(t;0,\mathrm{\Psi }\left)\right)$$

$${\displaystyle \le \underset{-max[\tau ,\sigma ]\le \xi \le 0}{sup}W(0,\mathrm{\Phi }\left(\xi \right),\mathrm{\Psi }\left(\xi \right))E_{\alpha }(-\mu t^{\alpha })+\nu t^{\alpha }{E}_{\alpha ,\alpha +1}(-\mu t^{\alpha }),t\ge 0.}$$

Remark 4.

Lemma 1 complements the result in Corollary 1.5 from [23] adding a $\nu \ne 0$. This result also extends Lemma 9 in [53] to the impulsive case. Similar comparison results for impulsive fractional-order systems can be found in [54,55]. Note that, in general, almost periodic problems are considered for $t\in \mathbb{R}$. However, the Lyapunov function approach is applied for $t\ge t_0=0$ [56].

3. Fractional Order Almost Periodicity Theorems

In this section, we will apply the fractional Lyapunov functions approach to determine the existence, uniqueness and stability of almost periodic states of the model (2).

First, we will state the existence and uniqueness almost periodicity result.

Theorem 1.

Assume that assumptions A1–A4 hold and:

(i) 

There exists a real number

$$\mu =2\left(c_{min}-max\left(w\sum _{i=1}^n{l}_i,d\right)\right)>0,$$

where ${\displaystyle c_{min}=min\left(\underset{1\le i\le n}{min}{a}_i,\underset{1\le i\le n}{min}{c}_i\right)}$;

(ii) 

The functions $P_{ik}\left(m_i\right)={\mathrm{P}}_{\mathrm{i}}{m}_i+{\mathrm{A}}_{\mathrm{i}}$, $Q_{ik}\left(p_i\right)={\mathrm{Q}}_{\mathrm{i}}{p}_i+{\mathrm{B}}_{\mathrm{i}}$, $k=\pm 1,\pm 2,\cdots$, where ${\mathrm{A}}_{\mathrm{i}}$, and ${\mathrm{B}}_{\mathrm{i}}$ are positive constants and the constants $\left\{{\mathrm{P}}_{\mathrm{i}}\right\}$, $\left\{{\mathrm{Q}}_{\mathrm{i}}\right\}$, are such that

$$-1\le {\mathrm{P}}_{\mathrm{i}}\le 0,-1\le {\mathrm{Q}}_{\mathrm{i}}\le 0,\mathrm{i}=1,2,\cdots ,\mathrm{n};$$

(iii) 

A solution ${(m\left(t\right),p\left(t\right))}^T$ of the model (2) exists such that

$$\left|\right|m\left(t\right)\left|\right|+\left|\right|p\left(t\right)\left|\right|<\tilde{C},\tilde{C}>0$$

for $t\ge 0$.

Then, the impulsive fractional-order GRN model (2) has a unique almost periodic solution ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$, such that:

(a) 

$\left|\right|\tilde{m}\left(t\right)\left|\right|+\left|\right|\tilde{p}\left(t\right)\left|\right|\le {\tilde{C}}_1,{\tilde{C}}_1<\tilde{C}$;

(b) 

$\mathcal{H}\left({(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T\right)\subset \mathcal{H}\left(2\right)$, where $\mathcal{H}\left({(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T\right)$ is the hull of the almost periodic solution ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$.

Proof. 

Let $\left\{s_q\right\}$ be an infinite sequence of real numbers that generates movements of the fractional-order impulsive model (2) to a system (5) from the set $\mathcal{H}\left(2\right)$, and $s_q\to \infty$ as $q\to \infty$.

Let

$${(m\left(t\right),p\left(t\right))}^T={(m(t;0,\varphi ),p(t;0,\phi ))}^T={(m_1(t;0,\varphi ),\cdots ,m_n(t;0,\varphi ),p_1(t;0,\phi ),\cdots ,p_n(t;0,\phi ))}^T$$

be the solution of the model (2) for $\varphi \in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n],$$\phi \in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n],$ that satisfies condition (iii) of Theorem 1.

Let b be a real number that corresponds to the smallest value of q denoted by $q_0=q_0\left(b\right)$, such that $s_{q_0}+b\ge 0$. From (iii) it follows that there exists ${\tilde{C}}_1$, $0<{\tilde{C}}_1<\tilde{C}$, such that $\left|\right|m\left(t\right)\left|\right|+\left|\right|p\left(t\right)\left|\right|\le {\tilde{C}}_1$ for all $t\ge 0$. Hence, $\left|\right|m(t+s_q)\left|\right|+\left|\right|p(t+s_q)\left|\right|\le {\tilde{C}}_1$ for $t\ge b$, $q\ge q_0$.

Let $\mathrm{\Omega },\mathrm{\Omega }\subset (b,\infty )$ be compact. For $U,V\in {\mathbb{R}}^n$, we construct the following Lyapunov-type function

$$W(t,U\left(t\right),V\left(t\right))=\frac{1}{2}\sum _{i=1}^n{U}_i^2\left(t\right)+\frac{1}{2}\sum _{i=1}^n{V}_i^2\left(t\right),t\in \mathrm{\Omega }.$$

(6)

From the compactness of $\mathrm{\Omega }$ it follows that for any $\epsilon >0$ there exists an integer number $n_0(\epsilon ,b)\ge q_0\left(b\right)$, such that for $l\ge q\ge n_0(\epsilon ,b)$ and $t\in \mathrm{\Omega }$, we have

$$\underset{-\tau \le \xi \le 0}{sup}\sum _{i=1}^n{U}_i^2\left(\varphi \left(\xi \right)\right)+\underset{-\sigma \le \xi \le 0}{sup}\sum _{i=1}^n{V}_i^2\left(\phi \left(\xi \right)\right)<\epsilon E_{\alpha }\left(\mu t^{\alpha }\right).$$

(7)

By condition (ii) of Theorem 1 and A4, for $t=t_k$, $k=\pm 1,\pm 2,\cdots$, we obtain

$$\frac{1}{2}\sum _{i=1}^n{(m_i(t_k^{+}+s_q)-m_i(t_k^{+}+s_l))}^2+\frac{1}{2}\sum _{i=1}^n{(p_i(t_k^{+}+s_q)-p_i(t_k^{+}+s_l))}^2$$

$${\displaystyle =\frac{1}{2}\sum _{i=1}^n{\left[m_i(t_k+s_q)+{\mathrm{P}}_i{m}_i(t_k+s_q)+{\mathrm{A}}_i-m_i(t_k+s_l)-{\mathrm{P}}_i{m}_i(t_k+s_l)-{\mathrm{A}}_i\right]}^2}$$

$${\displaystyle +\frac{1}{2}\sum _{i=1}^n{\left[p_i(t_k+s_q)+{\mathrm{Q}}_i{p}_i(t_k+s_q)+{\mathrm{B}}_i-p_i(t_k+s_l)-{\mathrm{Q}}_i{p}_i(t_k+s_l)-{\mathrm{B}}_i\right]}^2}$$

$${\displaystyle =\frac{1}{2}\sum _{i=1}^n{\left[\left(1+{\mathrm{P}}_i\right)\left(m_i(t_k+s_q)-m_i(t_k+s_l)\right)\right]}^2}$$

$${\displaystyle +\frac{1}{2}\sum _{i=1}^n{\left[\left(1+{\mathrm{Q}}_i\right)\left(p_i(t_k+s_q)-p_i(t_k+s_l)\right)\right]}^2}$$

and, hence

$$W(t_k^{+},m(t_k^{+}+s_q)-m(t_k^{+}+s_l),p(t_k^{+}+s_q)-p(t_k^{+}+s_l))$$

$$\le W(t_k,m(t_k+s_q)-m(t_k+s_l),p(t_k+s_q)-p(t_k+s_l)),k=\pm 1,\pm 2,\cdots .$$

(8)

Next, we will examine the fractional derivative order $\alpha$, $0<\alpha <1$,

$${{}^{C}D}_t^{\alpha }W(t,U\left(t\right),V\left(t\right))$$

of the function (6) for $t\ne t_k,k=\pm 1,\pm 2,\cdots$.

According to P2, we have

$${{}^{C}D}_t^{\alpha }W(t,U\left(t\right),V\left(t\right))={{}^{C}D}_t^{\alpha }\left[\frac{1}{2}\sum _{i=1}^n{U}_i^2\left(t\right)+\frac{1}{2}\sum _{i=1}^n{V}_i^2\left(t\right)\right]=\frac{1}{2}\sum _{i=1}^n{{}^{C}D}_t^{\alpha }{U}_i^2\left(t\right)+\frac{1}{2}\sum _{i=1}^n{{}^{C}D}_t^{\alpha }{V}_i^2\left(t\right)$$

and then, by P3, we obtain

$${{}^{C}D}_t^{\alpha }W(t,U\left(t\right),V\left(t\right))\le \sum _{i=1}^n{U}_i\left(t\right){{}^{C}D}_t^{\alpha }{U}_i\left(t\right)+\sum _{i=1}^n{V}_i\left(t\right){{}^{C}D}_t^{\alpha }{V}_i\left(t\right),t\ne t_k,k=\pm 1,\pm 2,\cdots .$$

(9)

From (9), for the derivative ${{}^{C}D}_t^{\alpha }W(t,m(t+s_q)-m(t+s_l),p(t+s_q)-p(t+s_l))$ with respect to the model (2) for $t\ge 0$ and $t\in [t_{k-1},t_k)$, we have

$${{}^{C}D}_t^{\alpha }W(t,m(t+s_q)-m(t+s_l),p(t+s_q)-p(t+s_l))$$

$$\le \sum _{i=1}^n(m_i(t+s_q)-m_i(t+s_l)){{}^{C}D}_t^{\alpha }((m_i(t+s_q)-m_i(t+s_l))$$

$$+\sum _{i=1}^n(p_i(t+s_q)-p_i(t+s_l)){{}^{C}D}_t^{\alpha }(p_i(t+s_q)-p_i(t+s_l))$$

$$\le \sum _{i=1}^n(m_i(t+s_q)-m_i(t+s_l))\left[{{}^{C}D}_t^{\alpha }{m}_i(t+s_q)-{{}^{C}D}_t^{\alpha }{m}_i(t+s_l)\right]$$

$$+\sum _{i=1}^n(p_i(t+s_q)-p_i(t+s_l))\left[{{}^{C}D}_t^{\alpha }{p}_i(t+s_q)-{{}^{C}D}_t^{\alpha }{p}_i(t+s_l)\right]$$

$$\le \sum _{i=1}^n\left(m_i(t+s_q)-m_i(t+s_l)\right)[-a_i\left(m_i(t+s_q)-m_i(t+s_l)\right)$$

$$+\sum _{j=1}^n{w}_{ij}(t+s_q)f_j\left(p_j(t+s_q-{\sigma }_j(t+s_q))\right)$$

$$-\sum _{j=1}^n{w}_{ij}(t+s_l)f_j\left(p_j(t+s_l-{\sigma }_j(t+s_l))\right)+B_i(t+s_q)-B_i(t+s_l)]$$

$$+\sum _{i=1}^n\left(p_i(t+s_q)-p_i(t+s_l)\right)[-c_i\left(p_i(t+s_q)-p_i(t+s_l)\right)$$

$$+d_i(t+s_q)m_i(t+s_p-{\tau }_i(t+s_q))-d_i(t+s_l)m_i(t+s_l-{\tau }_i(t+s_l))].$$

(10)

We apply the inequality $2ab\le a^2+b^2$ in (10), and get

$${{}^{C}D}_t^{\alpha }W(t,m(t+s_q)-m(t+s_l),p(t+s_q)-p(t+s_l))$$

$$\le -c_{min}\left[\sum _{i=1}^n{(m_i(t+s_q)-m_i(t+s_l))}^2+\sum _{i=1}^n{(p_i(t+s_q)-p_i(t+s_l))}^2\right]$$

$$+\sum _{i=1}^n\left(m_i(t+s_p)-m_i(t+s_l)\right)[\sum _{j=1}^n|w_{ij}(t+s_q)-w_{ij}(t+s_l)\left|\right|f_j\left(p_j(t+s_q-{\sigma }_j(t+s_q))\right|$$

$$+\sum _{j=1}^n|w_{ij}(t+s_l\left|\right|f_j(p_j(t+s_q-{\sigma }_j(t+s_q))-f_j(p_j(t+s_l-{\sigma }_j(t+s_l))|$$

$$+|B_i(t+s_q)-B_i(t+s_l)\left|\right]$$

$$+\sum _{i=1}^n\left(p_i(t+s_q)-p_i(t+s_l)\right)[|d_i(t+s_q)-d_i(t+s_l)|\left|m_i(t+s_q-{\tau }_{i-n}(t+s_q))\right|$$

$$+|d_i(t+s_l)|\left(m_i(t+s_q-{\tau }_i(t+s_q))-m_i(t+s_l-{\tau }_i(t+s_l))\right)]$$

$$\le -c_{min}\left[\sum _{i=1}^n{(m_i(t+s_q)-m_i(t+s_l))}^2+\sum _{i=1}^n{(p_i(t+s_q)-p_i(t+s_l))}^2\right]$$

$$+\sum _{i=1}^n\left(m_i(t+s_q)-m_i(t+s_l)\right)\left[(n+1)\epsilon +w\sum _{j=1}^n{l}_j|p_j(t+s_q-{\sigma }_j(t+s_q)-p_j(t+s_l-{\sigma }_j(t+s_l)|\right]$$

$$+\sum _{i=1}^n\left(p_i(t+s_q)-p_i(t+s_l)\right)\left[\epsilon {\tilde{C}}_1+d|m_i(t+s_q-{\tau }_i(t+s_q))-m_i(t+s_l-{\tau }_i(t+s_l))|\right].$$

(11)

From the above estimate, for $\mathrm{\Phi }\in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$, $\mathrm{\Psi }\in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$, we obtain that the inequality

$${}^c{D}^{\alpha }W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right))\le -\mu W(t,\mathrm{\Phi }\left(0\right),\mathrm{\Psi }\left(0\right))+\nu ,t\ne t_k$$

(12)

is satisfied whenever

$$W(t+\xi ,\mathrm{\Phi }(\xi ),\mathrm{\Psi }(\xi \left)\right)\le W(t,\mathrm{\Phi }(0),\mathrm{\Psi }(0\left)\right),-max[\tau ,\sigma ]\le \xi \le 0,$$

where $\mu$ is determined in condition (i) of Theorem 1 and $\nu =\epsilon 2n\sqrt{2}max({\tilde{C}}_1,n+1).$

We get, by (8), (12), and Lemma 1, that

$$W(t,m(t+s_q)-m(t+s_l),p(t+s_q)-p(t+s_l))<\mathrm{\Lambda }{\epsilon }^2,t\in \mathrm{\Omega },$$

where $\mathrm{\Lambda }$ is a positive constant.

From the choice of the function (6) and from the last inequality, we obtain that for any $t\in \mathrm{\Omega }$

$$\left|\right|m(t+s_q)-m(t+s_l)\left|\right|+\left|\right|p(t+s_q)-p(t+s_l)\left|\right|<{\mathrm{\Lambda }}_1{\epsilon }^2,$$

where ${\mathrm{\Lambda }}_1$ is a positive constant. Hence, there exists ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ such that $(m(t+s_q)$, $p(t+s_q){)}^T\to {(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ as $q\to \infty$ and since b is arbitrary, ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ is uniformly defined on $\mathbb{R}$.

Applying similar arguments, we can prove that the limits

$${\displaystyle \underset{q\to \infty }{lim}{{}^{C}D}_t^{\alpha }m(t+s_q),\underset{q\to \infty }{lim}{{}^{C}D}_t^{\alpha }p(t+s_q)}$$

exist uniformly on all compact subsets of $\mathbb{R}.$

From ${\displaystyle \underset{q\to \infty }{lim}{{}^{C}D}_t^{\alpha }m(t+s_q)={{}^{C}D}_t^{\alpha }\tilde{m}\left(t\right)}$ and ${\displaystyle \underset{q\to \infty }{lim}{{}^{C}D}_t^{\alpha }p(t+s_q)={{}^{C}D}_t^{\alpha }\tilde{p}\left(t\right)}$, we get

$${{}^{C}D}_t^{\alpha }\tilde{m}\left(t\right)=\underset{q\to \infty }{lim}\left(F_1^s(t+s_q,m(t+s_q),p_{t+s_q})-F_1^s(t+s_q,\tilde{m}\left(t\right),{\tilde{p}}_t)+F_1^s(t+s_q,\tilde{m}\left(t\right),{\tilde{p}}_t)\right)$$

$$=F_1(t,\tilde{m}\left(t\right),{\tilde{p}}_t),t\ne t_k^s.$$

(13)

$${{}^{C}D}_t^{\alpha }\tilde{p}\left(t\right)=\underset{q\to \infty }{lim}\left(F_2^s(t+s_q,m_{t+s_q},p(t+s_q))-F_2^s(t+s_q,{\tilde{m}}_t,\tilde{p}\left(t\right))+F_2^s(t+s_q,{\tilde{m}}_t,\tilde{p}\left(t\right))\right)$$

$$=F_2(t,{\tilde{m}}_t,\tilde{p}\left(t\right)),t\ne t_k^s,$$

(14)

where ${\displaystyle t_k^s=\underset{q\to \infty }{lim}(t_k+s_q)}$, $m_t\left(\xi \right)=m(t+\xi )$, $\xi \in [-\tau ,0]$, $p_t\left(\xi \right)=p(t+\xi )$, $\xi \in [-\sigma ,0]$, the continuous vector-functions $F_1:\mathbb{R}\times {\mathbb{R}}^n\times \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]\to {\mathbb{R}}^n$, $F_2:\mathbb{R}\times \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$$\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, denoted the right-hand sides of the model (5) in the matrix form.

Additionally,

$$\tilde{m}\left(t^{+}\right)-\tilde{m}\left(t^{-}\right)=\underset{q\to \infty }{lim}(m(t+s_q+0)-m(t+s_q-0))$$

$$=\underset{q\to \infty }{lim}{J}_k^s\left(m(t+s_q)\right)=J_k\left(\tilde{m}\left(t\right)\right),t=t_k^s,k=\pm 1,\pm 2,\cdots ,$$

(15)

$$\tilde{p}\left(t^{+}\right)-\tilde{p}\left(t^{-}\right)=\underset{q\to \infty }{lim}(p(t+s_q+0)-p(t+s_q-0))$$

$$=\underset{q\to \infty }{lim}{\tilde{J}}_k^s\left(p(t+s_q)\right)={\tilde{J}}_k\left(\tilde{p}\left(t\right)\right),t=t_k^s,k=\pm 1,\pm 2,\cdots ,$$

(16)

where $J_k,{\tilde{J}}_k:{\mathbb{R}}^n\to {\mathbb{R}}^n,k=\pm 1,\pm 2,\cdots$ are the diagonal matrices of impulsive functions in (5).

From (13)–(16), we conclude that ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ is a solution of an impulsive fractional-order system of the type (5).

The proof of the fact that ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ is almost periodic follows from estimates, similar to (7), (8), and (12) for the function

$$W(t,\tilde{m}\left(t\right)-\tilde{m}(t+s_q-s_l),\tilde{p}\left(t\right)-\tilde{p}(t+s_q-s_l))$$

$$=\frac{1}{2}\sum _{i=1}^n{\left({\tilde{m}}_i\left(t\right)-{\tilde{m}}_i(t+s_q-s_l)\right)}^2+\frac{1}{2}\sum _{i=1}^n{\left({\tilde{p}}_i\left(t\right)-{\tilde{p}}_i(t+s_q-s_l)\right)}^2,t\in \mathrm{\Omega }.$$

Hence, operating similarly as above, we can prove the following estimate

$$\left|\right|m(t+s_q)-m(t+s_l)\left|\right|+\left|\right|p(t+s_q)-p(t+s_l)\left|\right|<{\mathrm{\Lambda }}_1{\epsilon }^2,$$

(17)

for $l\ge q\ge n_0\left(\epsilon \right)$.

Additionally, the estimate

$$\rho (t_k+s_q,t_k+s_l)<\epsilon ,l\ge q\ge n_0\left(\epsilon \right)$$

(18)

follows directly from the definition of the sequence $\left\{s_q\right\}$.

The last estimate and (17) imply that ${(\tilde{m}(t+s_q),\tilde{p}(t+s_q))}^T$ converges uniformly to ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$.

Therefore, points (a) and (b) of Theorem 1 are both satisfied, which completes the proof of the Theorem. □

Remark 5.

Recently, there exists just very few results on the almost periodic properties of integer-order GRNs [47,48]. Theorem 1 is an extension of the existent results to the fractional-order case. The result can be applied by the researchers that used the advantages of fractional-order modelling in their qualitative analysis.

Remark 6.

Theorem 1 also is an extension of the results in [47] considering impulsive effects that can be applied as controllers. In addition, it complements the almost periodicity results in [48] obtained by the Cauchy matrix estimations and the theory of contracting operators in Banach spaces, using the Lyapunov function approach. In fact, the advantages of the Lyapunov method are used in the qualitative investigation of numerous problems [14,16,17,18,23,26,27,49,50,51], including fractional-order GRNs [28,29,30,31,32,33,34].

In the last result in this section, we will establish criteria for global Mittag–Leffler stability of the almost periodic state ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ of the model (2).

Definition 9.

The solution ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ of (2) with initial functions $\tilde{\varphi }\in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n],$$\tilde{\phi }\in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n]$ is globally Mittag–Leffler stable, if for any $\varphi \in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n]$, $\phi \in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n],$ such that $\left|\right|\tilde{\varphi }-{\varphi \left|\right|}_{\tau }+\left|\right|\tilde{\phi }-\phi {\left|\right|}_{\sigma }<\overline{\lambda }$, ($\overline{\lambda }>0$) constants $\mu >0$ and $\gamma >0$ exist such that we have

$$\left|\right|\tilde{m}\left(t\right)-m\left(t\right)\left|\right|+\left|\right|\tilde{p}\left(t\right)-p\left(t\right)\left|\right|\le {\left\{\mathcal{M}(\tilde{\varphi }-\varphi ,\tilde{\phi }-\phi )E_{\alpha }(-\mu t^{\alpha })\right\}}^{\gamma },t\ge 0,$$

where ${(m\left(t\right),p\left(t\right))}^T$ is the solution of the model (2) corresponding to initial functions $\varphi ,$$\phi ,$$\mathcal{M}\ge 0$, $\mathcal{M}(0,0)=0$, and $\mathcal{M}$ is Lipschitz continuous with respect to its both variables.

Theorem 2.

Assume that all conditions of Theorem 1 hold. Then the almost periodic solution ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ of the model (2) is globally Mittag–Leffler stable.

Proof. 

Let ${(m\left(t\right),p\left(t\right))}^T$ be the solution of the model (2) for $\varphi \in \mathcal{PCB}[[-\tau ,0],{\mathbb{R}}^n],$$\phi \in \mathcal{PCB}[[-\sigma ,0],{\mathbb{R}}^n].$

Denote by

$${(\widehat{m}\left(t\right),\widehat{p}\left(t\right))}^T={(m\left(t\right)-\tilde{m}\left(t\right),p\left(t\right)-\tilde{p}\left(t\right))}^T$$

and consider the vector functions

$$F_1^s(t,\widehat{m}\left(t\right),{\widehat{p}}_t)=F_1^s(t,\widehat{m}\left(t\right)+\tilde{m}\left(t\right),{\widehat{p}}_t+{\tilde{p}}_t)-F_1^s(t,\tilde{m}\left(t\right),{\tilde{p}}_t),$$

$$F_2^s(t,{\widehat{m}}_t,\widehat{p}\left(t\right))=F_2^s(t,{\widehat{m}}_t+{\tilde{m}}_t,\widehat{p}\left(t\right)+\tilde{p}\left(t\right))-F_2^s(t,{\tilde{m}}_t,\tilde{p}\left(t\right))$$

that generate the system

$$\left\{\begin{array}{c}{\displaystyle {{}^{C}D}_t^{\alpha }\widehat{m}\left(t\right)=F_1^s(t,\widehat{m}\left(t\right),{\widehat{p}}_t),t\ne t_k^s,}\hfill \\ {\displaystyle {{}^{C}D}_t^{\alpha }\widehat{p}\left(t\right)=F_2^s(t,{\widehat{m}}_t,\widehat{p}\left(t\right)),t\ne t_k^s,}\hfill \\ \widehat{m}\left(t^{+}\right)=\widehat{m}\left(t\right)+J_k\left(\widehat{m}\left(t\right)\right),t=t_k^s,k=\pm 1,\pm 2,\cdots ,\hfill \\ \widehat{p}\left(t^{+}\right)=\widehat{p}\left(t\right)+{\tilde{J}}_k\left(\widehat{p}\left(t\right)\right),t=t_k^s,k=\pm 1,\pm 2,\cdots .\hfill \end{array}\right.$$

(19)

Using the Lyapunov-type function $\widehat{W}(t,\widehat{m}\left(t\right),\widehat{p}\left(t\right))=W(t,\tilde{m}\left(t\right)-(\tilde{m}\left(t\right)+\widehat{m}\left(t\right))$, $\tilde{p}\left(t\right)-(\tilde{p}\left(t\right)+\widehat{p}\left(t\right)))$, by Lemma 1 we obtain that the zero solution ${(\widehat{m}\left(t\right),\widehat{p}\left(t\right))}^T={(0,0)}^T$ of the problem (19) is globally Mittag–Leffler stable. Hence, the almost periodic solution ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ of the model (2) is globally Mittag–Leffler stable. This proves Theorem 2. □

Remark 7.

For fractional-order impulsive GRNs, there are some initial findings regarding stability criteria for their steady states [34], including fractional-order impulsive GRNs with delays [33]. The stability properties of almost periodic states for such models are not yet studied in the existing literature. Therefore, our results are new and initiate the development of the stability theory of almost periodic states for impulsive fractional-order GRNs.

4. A Numerical Example

To demonstrate the proposed almost periodicity results we consider the following fractional impulsive GRNs with time-varying delays

$$\left\{\begin{array}{c}{\displaystyle {{}^{C}D}_t^{\alpha }{m}_i\left(t\right)=-a_i{m}_i\left(t\right)+\sum _{j=1}^n{w}_{ij}\left(t\right)f_j\left(p_j(t-{\sigma }_j\left(t\right))\right)+B_i\left(t\right),t\ne t_k,}\hfill \\ {\displaystyle {{}^{C}D}_t^{\alpha }{p}_i\left(t\right)=-c_i{p}_i\left(t\right)+d_i\left(t\right)m_i(t-{\tau }_i\left(t\right)),t\ne t_k,}\hfill \\ \\ m_i\left(t_k^{+}\right)=\frac{i}{i+1}{m}_i\left(t_k\right)+{\mathrm{A}}_{\mathrm{i}},p_i\left(t_k^{+}\right)=\frac{i}{i+1}{p}_i\left(t_k\right)+{\mathrm{B}}_{\mathrm{i}},\hfill \end{array}\right.$$

(20)

where $\alpha =0.89$, $i=1,2,3$, $m\left(t\right)={(m_1\left(t\right),m_2\left(t\right),m_3\left(t\right))}^T$, $p\left(t\right)={(p_1\left(t\right),p_2\left(t\right),p_3\left(t\right))}^T$, $t_k\in \mathcal{T}$, $0\le {\sigma }_j\left(t\right)\le 1$, $0\le {\tau }_i\left(t\right)\le 1$, $a_1=a_2=a_3=5$, $c_1=c_2=c_3=6$, $B_1\left(t\right)=B_2\left(t\right)=B_3\left(t\right)=0.01cos\sqrt{3}t$, $d_1\left(t\right)=1.3+1.1cos\sqrt{3}t$, $d_2\left(t\right)=1.2-0.5sin\sqrt{3}t$, $d_3\left(t\right)=1.5-0.3cos\sqrt{3}t$, $f_j\left(p_j\right)=\frac{p_j^2}{1+p_j^2}$, $j=1,2,$

$$w_{ij}=\left(\begin{array}{ccc}{w}_{11}\hfill & w_{12}& \hfill w_{13}\\ w_{21}\hfill & w_{22}& \hfill w_{23}\\ w_{31}\hfill & w_{32}& \hfill w_{33}\end{array}\right)=\left(\begin{array}{ccc}0\hfill & -0.5& \hfill 0.8\\ 0.7\hfill & 0& \hfill -0.5\\ -0.5\hfill & 0.6& \hfill 0\end{array}\right),$$

${\mathrm{A}}_{\mathrm{i}}={\mathrm{B}}_{\mathrm{i}}=0.2$, $i=1,2,3$.

We have that

$$5=c_{min}>max\left(w\sum _{i=1}^n{l}_i,d\right)=2.4$$

and, hence, condition (i) of Theorem 1 is satisfied.

Additionally, the functions

$${\mathrm{P}}_{\mathrm{i}}={\mathrm{Q}}_{\mathrm{i}}=\frac{-1}{i+1},i=1,2,3$$

satisfy condition (ii) of Theorem 1.

Thus, by Theorem 1 we can conclude that there exists a unique almost periodic state ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T={({\tilde{m}}_1\left(t\right),{\tilde{m}}_2\left(t\right),{\tilde{m}}_3\left(t\right),{\tilde{p}}_1\left(t\right),{\tilde{p}}_2\left(t\right),{\tilde{p}}_3\left(t\right))}^T$ of the fractional impulsive GRN model (20).

Additionally, Theorem 2 guarantees that the almost periodic solution ${(\tilde{m}\left(t\right),\tilde{p}\left(t\right))}^T$ of the impulsive fractional GRNs (20) is globally Mittag–Leffler stable. The almost periodic trajectories of the state variables ${\tilde{m}}_1\left(t\right)$, ${\tilde{m}}_2\left(t\right)$${\tilde{m}}_3\left(t\right)$ for $t_k=17k+sin\sqrt{2}k$ are shown on Figure 1 and the almost periodic trajectories of the state variables ${\tilde{p}}_1\left(t\right)$, ${\tilde{p}}_2\left(t\right)$${\tilde{p}}_3\left(t\right)$ for $t_k=17k+sin\sqrt{2}k$ are shown on Figure 2.

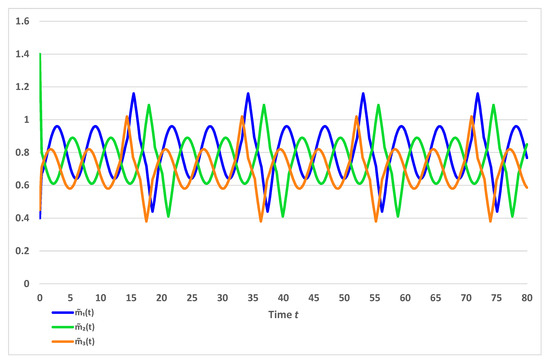
Figure 1. The trajectories of the almost periodic variables ${\tilde{m}}_1\left(t\right)$, ${\tilde{m}}_2\left(t\right)$ ${\tilde{m}}_3\left(t\right)$ of the model (20) for $t_k=17k+sin\sqrt{2}k$.

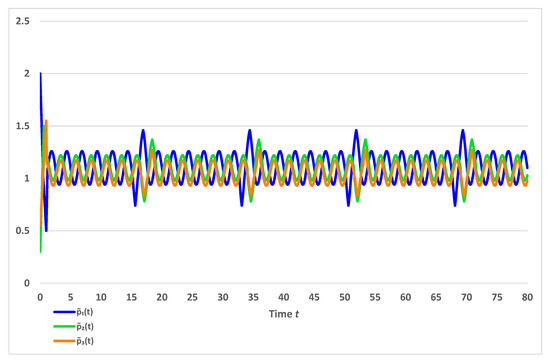
Figure 2. The trajectories of the almost periodic variables ${\tilde{p}}_1\left(t\right)$, ${\tilde{p}}_2\left(t\right)$ ${\tilde{p}}_3\left(t\right)$ of the model (20) for $t_k=17k+sin\sqrt{2}k$.

Remark 8.

The presented example demonstrates the efficiency of the proposed results. The practical meaning of our conclusions is that when the translation rates, basal rates, and the connecting parameters in the considered fractional impulsive GRN are variable (not constants) but bounded, and the magnitudes of the impulsive perturbations satisfy conditions of Theorem 2, then the model is capable to generate a unique globally Mittag–Leffler stable almost periodic process. Indeed, the concept of almost periodicity has deep historical roots [36] and has important applications in applied mathematical models [35,39,40,41,42,47,48]. Indeed, it is an unrealistic assumption that the behavior of the states in the GRNs are not affected by periodical environmental factors. The effects of such factors lead to the existence of pure periodic and almost periodic solutions. For integer-order cases, the problem of exact periodicity of the solutions has limited applicability and, hence the investigation of almost periodic behavior is considered to be more accordant with reality. For fractional-order models [23,43,47,48], the pure periodicity option does not exists. Therefore, studying almost periodic behavior is very necessary and important.

Remark 9.

The presented example also illustrates the ability to impulsively control the almost periodic and stability behavior of the states of the GRN model by satisfying conditions A2, A4, and condition (ii) of Theorem 1. Thus, our results offer an insight on the effects of impulsive control strategy on the interactions of genes. If the impulsive functions do not satisfy condition (ii) of Theorem 1, then due to the impulsive jumps the stable almost periodic neuronal behavior can be changed momentarily. Since the impulses can contribute to chaotic behavior and instability of the states their control power is crucial. Hence, our results can be used to design an impulsive control law under which to stabilize the almost periodic behaviour of different types of impulsive fractional-order models of diverse interest.

5. Conclusions

In this paper, we study the almost periodic properties of an impulsive fractional-order delayed GRN model. By the application of the Lyapunov functions approach, sufficient conditions for the existence and uniqueness of almost periodic states of the proposed model are proved. Moreover, the global Mittag–Leffler stability of the almost periodic solution is also investigated. The proposed results extend some theorems on the almost periodic properties of integer order GRNs to the fractional-order case considering impulsive effects and time-varying delays. They also complement some existing steady states stability results for fractional-order GRNs to the almost periodic case which has numerous applications to applied fractional-order models.