Abstract
This paper deals with the study and analysis of several rational approximations to approach the behavior of arbitrary-order differentiators and integrators in the frequency domain. From the Riemann–Liouville, Grünwald–Letnikov and Caputo basic definitions of arbitrary-order calculus until the reviewed approximation methods, each of them is coded in a Maple 18 environment and their behaviors are compared. For each approximation method, an application example is explained in detail. The advantages and disadvantages of each approximation method are discussed. Afterwards, two model order reduction methods are applied to each rational approximation and assist a posteriori during the synthesis process using analog electronic design or reconfigurable hardware. Examples for each reduction method are discussed, showing the drawbacks and benefits. To wrap up, this survey is very useful for beginners to get started quickly and learn arbitrary-order calculus and then to select and tune the best approximation method for a specific application in the frequency domain. Once the approximation method is selected and the rational transfer function is generated, the order can be reduced by applying a model order reduction method, with the target of facilitating the electronic synthesis.
Keywords:
arbitrary-order calculus; Oustaloup’s approximation; refined Oustaloup’s approximation; Matsuda’s approximation; continued fraction expansion approximation; Charef’s approximation; Carlson’s approximation; curve fitting approximation; modified stability boundary locus approximation; model order reduction 1. Introduction
Arbitrary-order calculus is an important issue that has attracted the attention of research institutes, academic associations, industrial areas and foundry companies. It has shown a better way of modeling and controlling many financial, biological, chemical, physical, electrical and control phenomena [1,2,3]. Capacitors and inductors are dissipative two-terminal passive elements widely used to describe integer-order differentiators, integrators and state-space systems. However, to date, there is no robust passive element with arbitrary characteristics so that it can be used to describe the behavior of a system of arbitrary-order differential equations that models natural phenomena or human-made systems more realistically. In response to this problem, integer-order rational approximations in the frequency domain were developed to approximate the arbitrary order with low level of error and wide bandwidth, such as Oustaloup’s [4], refined Oustaloup’s [5], Charef’s [6], Carlson’s [7,8], Matsuda’s [9], etc. Examples of its use in several applications can be found in the literature. For instance, a synthesis methodology of arbitrary-order chaotic systems was discussed in [10]. The analysis and analog design of arbitrary-order charge/flux controlled memristor emulators of incremental/decremental type was described in [11]. In [3,12,13] the analog design of arbitrary-order proportional-integral-derivative controllers was reported. The arbitrary-order lead/lag compensator was investigated in [14,15]. The design of double exponent arbitrary-order filters and power law filters were investigated in [16,17], respectively, and so on. Note that in each application, a different arbitrary-order approximation method was used; once the rational approximation is deduced, this can be synthesized using analog or digital platforms. Therefore, this survey not only describes and analyzes the main approximation methods reported to date, but two model order reduction methods are also reviewed in order to obtain rational transfer functions of reduced order and with the target of simplifying the electronic synthesis process. Unlike [18,19] and to help beginners get started quickly and learn arbitrary-order calculus, the corresponding Maple 18 code of each approximation method is herein reported.
The paper is organized as follows. Section 2 deals with the three main basic definitions on arbitrary-order calculus. The Maple code for each of them is also introduced in this section. Section 3 describes nine rational approximation methods in the frequency domain. Further, the Maple 18 code for each approximation method is not only presented, but an example of application by each method is also developed. The advantages and disadvantages of each method are also discussed. Section 4 deals with the analysis of two model order reduction methods. Examples for each method are also discussed in this section, showing the drawbacks and benefits. Finally, the results and conclusions are given in Section 5.
2. Basic Definitions
2.1. Arbitrary-Order Integral and Derivative of Riemann–Liouville
The arbitrary-order integral in the sense of Riemann–Liouville is defined as [1,3]
where a and t are the lower and upper limits of integration, is the gamma function, is the arbitrary order and describes a causal function of time. This first basic definition can easily be code in Maple 18 environment, as described in Table 1.

Table 1.
Maple 18 code of (1).
Let us consider an example on the use of Table 1. Defining and we compute the arbitrary-order integral as
making a variable change and defining we have
the last equation in (3) is the first-order integral of the original function described above and was found by applying (1) twice. Despite the ease of application, the main disadvantage of this basic definition is that the analytical solution of complex functions cannot be found easily and the solution is often a function of other nested functions. Moreover, the inverse process of (1), i.e., the arbitrary-order derivative, is defined as
where p is a positive integer such that . Based on the previous programming code, (4) is coded in Table 2.

Table 2.
Maple 18 code of (4).
Let us consider an example on the use of Table 2. Defining , and we get
making, again, a variable change and updating , we have
the last equation in (6) is the first-order derivative of mentioned before and going back to the original function used in the first example. Note that (4) was also applied twice. Aside from the aforementioned disadvantage of limiting to simple functions, another disadvantage of (4) is that the initial conditions of the test function cannot be considered. This is a serious problem from a practical engineering standpoint.
2.2. Arbitrary-Order Integral and Derivative of Grünwald–Letnikov
The arbitrary-order integral in the sense of Grünwald–Letnikov is defined as [1,3]
where h is the integration step. This third basic definition is coded in Maple 18 environment as illustrated in Table 3. Defining , h = 0.01, tf = 3, a = 0 and , we got the numerical behavior of arbitrary-order integral of the function as
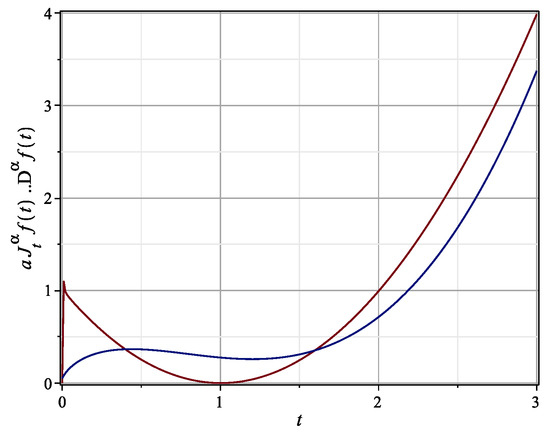
the second line of (8) defines a variable change in f. Because (7) is a discrete function, the time-domain response of complex functions can numerically be computed. However, a level of error is glimpsed compared with its continuous part. This error can be reduced, making , but the CPU time increases. Therefore, there is a trade-off between accuracy and speed. Another disadvantage is related with the memory length since (7) is an iterative procedure and the sum in its scheme becomes longer and longer. Note that whereas the analytical solution is given at the second line of (2), its numerical response is shown in Figure 1 (blue-line).

Table 3.
Maple 18 code of (7).
Moreover, the arbitrary-order derivative is defined as
By virtue of the form of (9) and according to Table 3, the Maple 18 code is given in Table 4. Defining , h = 0.01, tf = 3, a = 0 and , we obtain the numerical behavior of arbitrary-order derivative of the function as

Table 4.
Maple 18 code of (9).
2.3. Arbitrary-Order Derivative of Caputo
The arbitrary-order derivative in the sense of Caputo is defined as [1,3]
This last basic definition is easily coded in the Maple 18 environment, as given in Table 5.

Table 5.
Maple 18 code of (11).
Let us consider an example on the use of Table 5. Defining , and we compute the arbitrary-order derivative as
making, again, a variable change and updating , we have
The last equation of (13) is the first-order derivative of mentioned before, where (11) was also applied twice. A main advantage of this basic definition is that the initial conditions of the test function can be considered, i.e., , ,…,. However, the analytical solution of complex functions cannot be easily computed, and the solution is again a function of other nested functions.
Moreover, natural phenomena are often modeled by state-space representation, which is a system of integer- or arbitrary-order differential equations [2]. Once the physical phenomena are modeled, the following task is to find their solution. From an engineering point of view, there are two ways to solve the state-space system: frequency-domain methods [18] and time-domain methods [20]. Note that the main basic definitions of arbitrary-order calculus are of the second type. Other reported methods in the time domain are the Adomian decomposition method [21], predictor–corrector approach based on one-step Adams–Bashforth–Moulton method [22,23,24,25] and Chebyshev collocation method [26,27]. However, the main disadvantage of all these methods is that numerical simulations can only be performed, and some of them are not robust enough to be encoded on reconfigurable hardware. In this context, frequency-domain methods are based on the approximation of the transition function through pole-zero pairs. Although this type of approximation has two main drawbacks—(1) the approximations of is valid only for few values of and (2) the difference between the original behavior and approximate is still unknown—its major advantage is that integer-order rational polynomials can be synthesized with discrete analog circuits or encoded in reconfigurable hardware and, as a consequence, experimental results can be observed.
3. Rational Approximations in the Frequency Domain
In the analog domain, the expression , where is a constant called fractance device. Several frequency-domain approximation methods have been reported in the literature that can be used to compute the integer-order rational approximations of the fractance, as described below.
3.1. Oustaloup’s Approximation
This approximation method is based on a recursive distribution of zeros and poles into a frequency interval (), where and are the low and high transitional frequencies expressed in rad/s [4]. Thus, the target is to approximate the function of the form
by an integer-order rational approximation
The zeros are computed as
and the poles are computed as
where N is the approximation order. Equations (15)–(17) are coded in Maple 18 as given in Table 6.

Table 6.
Oustaloup’s approximation coded in Maple 18 environment.
Let us consider an example on the use of Table 6. Defining = 0.5, = 0.01, = 100 and N = 4, the rational approximation is computed as
the third line of (18) expresses the rational approximation as a product of poles and zeros, and the fifth line as a quotient of fourth-order rational polynomials. Note that here was approximated by (18), that is, the arbitrary-order derivative. To obtain , i.e., the arbitrary-order integral, the numerator and denominator of (18) must be interchanged. In this sense, whereas the magnitude and phase responses of the arbitrary-order integral approximation along with the ideal behavior (black line) are shown in Figure 2a,c, the errors for each case are depicted in Figure 2b,d, respectively. All magnitude and phase waveforms along with their errors are colored with a blue line. Advantages of this approximation method are that (1) it allows to obtain rational polynomials in a wide range of frequencies and (2) for the same iteration number, the rational approximation has a lower order compared with other approximation methods. However, its major disadvantage is that the phase error does not decrease in the frequency interval despite increasing the number of iterations. As a consequence, high-order rational approximations are generated and later, this becomes a more complex and tedious task when the rational polynomial is synthesized with discrete analog circuits or encoded with reconfigurable hardware.
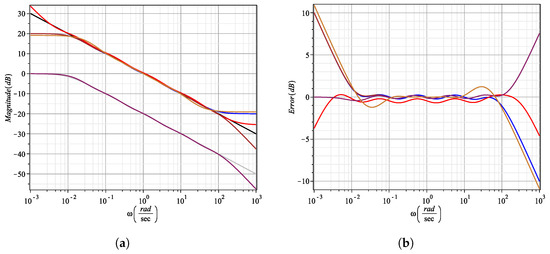
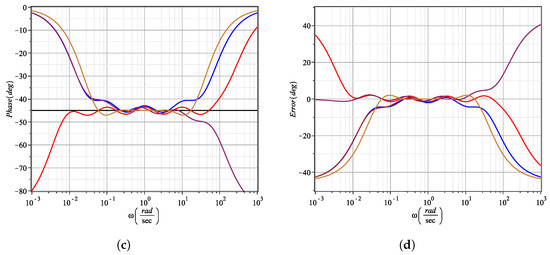
Figure 2.
Ideal behavior (black line), Oustaloup’s (blue line), refined Oustaloup’s (red line), Charef’s V1 (brown line), ideal behavior (gray line) of (26), Charef’s V2 (maroon line) and Carlson’s (gold line) approximation for . (a) Magnitude response. (b) Magnitude error. (c) Phase response. (d) Phase error.
3.2. Refined Oustaloup’s Approximation
This approximation method is defined as [5]
where b = 10 and d = 9 are adjustment parameters and their values were found by experimentation. The zeros and poles are computed by using (16) and (17). Note that in [5], a slight modification was reported compared with (19), where the bottom index of the product starts from -N instead of 1, as in the original Outstaloup’s notation. Nevertheless, both approximations, reported by Equation (23) in [5] and (19) are equivalent. According to Table 6, (19) is easily coded in the Maple 18 environment as shown in Table 7.

Table 7.
Refined Oustaloup’s approximation coded in Maple 18 environment.
Using = 0.5, = 0.01, = 100 and N = 4, the rational approximation is computed as
The magnitude and phase responses of the arbitrary-order integral approximation are illustrated in Figure 2a,c while their errors are shown in Figure 2b,d. All waveforms are colored with a red line. Advantages of this approximation method are that (1) it has a better fitting quality around the frequency band boundaries in both magnitude and phase responses, as can be seen in Figure 2 (red line) and (2) for the same number of iterations, the error decreases compared with the Oustaloup’s method. The main disadvantage found is that the order of the rational approximation increases, as one can see in (20), generating all the drawbacks mentioned above.
3.3. Charef’s Approximation Version 1
The Charef’s approximation method was reported in [6] to approximate the transfer function as a function of singularities of poles an zeros into a frequency bandwidth (), which depends on an approximation error (dB) previously defined. Thus, the objective is to approximate the function
where the coefficients are computed for obtaining a maximum deviation according to . Thus
therefore, the distribution of the poles and zeros becomes
and the total number of singularities is determined as
Here, integer indicates the integer part of the mathematical operation. Equations (21)–(24) are coded in Maple 18 as shown in Table 8.

Table 8.
Code in Maple 18 environment of (21).
Using = 0.5, = 0.01, = 100 and = 2.36, we obtain N = 4 and the rational approximation is computed as
The magnitude and phase responses of (25) are again illustrated in Figure 2a,b, and their errors are also shown in Figure 2b,d. All frequency responses are colored with a brown line. Advantages of Charef’s Version 1 approximation method are that (1) for the upper frequency limit , the magnitude error decreases, whereas for , the magnitude behavior is similar to Oustaloup’s approximation, and (2) the number of iterations depends on . Hence, the error increases or decreases in terms of -dB. Disadvantages of the approximation method are that (1) in the frequency band boundaries, the phase error increases, as one can be seen in Figure 2d (brown line). In fact, the phase response at the lower frequency limit has a similar behavior to Oustaloup’s method. (2) Additionally, for the same number of iterations, the order of the rational approximation is slightly higher than Oustaloup’s method, but slightly lower than the refined Oustaloup’s method.
3.4. Charef’s Approximation Version 2
For this method [6], the goal is to approximate the function
Unlike (21), an arbitrary pole is here included to model the frequency behavior of the transfer function. Note that in general, systems usually exhibits finite magnitude at very low frequency. To compute the zeros and poles, (22)–(24) are also used. Therefore, based on Table 8, (26) is coded in Maple 18 as depicted in Table 9.

Table 9.
Code in Maple 18 environment of (26).
Using = 0.5, = 0.01, = 100 and = 2.36, we obtain N = 4 and the rational approximation is computed as
According to Figure 2 (maroon line), one can observe that for the frequency behavior of the magnitude and phase error responses is equal to Charef’s Version 1 approximation, whereas for , the magnitude and phase errors have better behavior in comparison with Charef’s Version 1 method. Another advantage of this method is that the number of iterations depends on and, as a consequence, the error is controlled in terms of -dB. The disadvantages of the approximation method are the same as those described in Charef’s Version 1 approximation method. Comparing (25) and (27), it can seen that the only difference is the gain of the transfer functions.
3.5. Carlson’s Approximation
The method proposed in [7] was derived from a regular Newton process used for iterative approximation of the -th root. The starting point of the method is defined as
Defining the initial value as = 1, the approximated rational function is obtained as
where G(s) = s defines the derivative and G(s) = defines the integral. The code in Maple 18 environment of (29) is written in Table 10.

Table 10.
Code in Maple 18 environment of (29).
For this case, we use = , G(s) = and N = 2. The rational approximation is obtained as
the fourth line in (30) gets the zeros, poles and gain of the function described in the third line and hence, the approximated function is built in terms of poles and zeros, as described in the fifth line. The magnitude and phase responses of the arbitrary-order integral approximation are depicted in Figure 2a,c and the error for each case is shown in Figure 2b,d. Here, a gold color line is used to plot the waveform at each case. The main advantage of this approximation method is that the magnitude and phase errors are almost zero within a narrow bandwidth. However, if one wants to enlarge the bandwidth, it is necessary to increase N. However, if N = 3, the order of the generated polynomials is 13 and for N = 4 the order increases to 40, which is infeasible from the point of view of electronic synthesis. Other disadvantages found are that (1) there is no control over the frequency interval of interest (), and (2) for some values of 0 < 1 with one or two digits, the method generates terms of s raised to a rational exponent. For instance, for = one obtains
which becomes a difficult or impossible task during the electronic synthesis process. One possible solution is to compute several rational transfer functions with different [8]. Thus, we can generate = , obtaining
(3) If 0, then the order of the generated polynomials increases exponentially, as one can verify in the second term of (32).
3.6. Matsuda’s Approximation
This approximation method was suggested in [9], which fits the original function in a set of logarithmically spaced frequencies given by w = and = and by using the following functions
getting a superior triangular matrix as
where each element of the main diagonal of D is used to recursively approximate the desired function as a continued fraction
All equations mentioned before are coded in Maple 18 as given in Table 11.

Table 11.
Matsuda’s method coded in Maple 18 environment.
The second line of Table 11 defines the logspace function. As an example on the use of Table 11, we define = −0.5, = 0.01, = 100, N = 8 and gain k = 1. Therefore, the rational approximation is computed as
The magnitude and phase responses of the approximation are depicted in Figure 3a,c, and the error for each of them is also shown in Figure 3b,d. All frequency responses are colored with a blue line. The main advantage of this approximation method is that the magnitude and phase errors are low within the desired bandwidth and still can be minimized by increasing the number of iterations N. In fact, the order of the rational transfer function is always N/2. For this reason, N must be even. Otherwise, improper transfer functions are generated. After several numerical simulations, we recommend using, as a starting point, N = 8 in order to obtain magnitude and phase errors within ±2 dB and ±6, respectively. On the other hand, the main disadvantages found are that (1) if N is very large, then high-order rational transfer functions are generated. This fact becomes a tedious task during the electronic synthesis process. (2) Additionally, for the parameters used, we note that from N = 16, some positive poles are generated, hence conditioning the stability of the rational approximation.
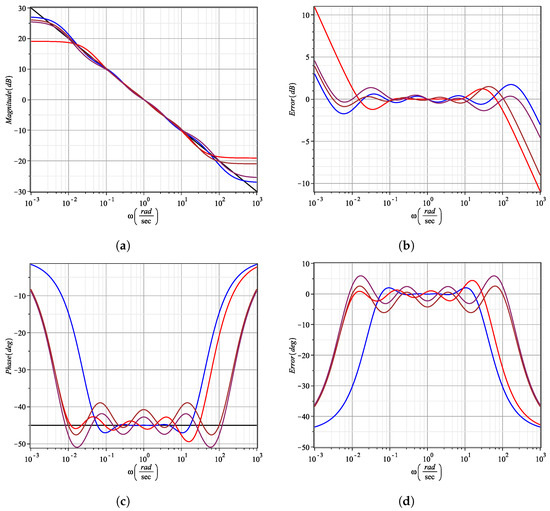
Figure 3.
Ideal behavior (black line), Matsuda’s (blue line), continued fraction expansion (red line), curve fitting (brown line) and MSBL (maroon line) approximation for . (a) Magnitude response. (b) Magnitude error. (c) Phase response. (d) Phase error.
3.7. Continued Fraction Expansion Approximation
This method is widely used for evaluation of functions since it converges faster than power series expansions within a larger domain in the complex plane [28]. Continued fraction expansion is defined as
Replacing , we can approximate . To obtain the arbitrary-order integral, i.e., , the numerical value of must be negative. Table 12 shows the code in Maple 8 of (37).

Table 12.
Code in Maple 18 environment of (37).
Now, by defining = −0.5 and N = 8, the rational transfer function is computed as
Note that for these parameters, (38) is equal to (30), but this is not always the case. The magnitude and phase responses in the frequency domain of the rational transfer function are depicted in Figure 3a,c and the error for each case is shown in Figure 3b,d, respectively. In this case, a red line is used to plot all waveforms. After several numerical simulations, one concluded that the main advantages of this approximation method are that (1) the magnitude and phase errors are almost zero within a narrow bandwidth and (2) the order = N/2 of the transfer function holds, where N is always even. In order to extend the bandwidth, N must be increased. Similarly to Matsuda’s method, we also recommend use, as starting point, N = 8 and hence, the magnitude and phase errors are ±1.5 and ±5, approximately. Moreover, the disadvantages found are that (1) there is no control in the frequency range of interest (), (2) if N is odd, then improper transfer functions are generated, and (3) high-order rational polynomials are generated when N becomes very large and consequently affects the electronic synthesis process.
3.8. Curve-Fitting Approximation
This approximation method was reported in [29,30], which is based on obtaining the frequency response data of into a set of logarithmically spaced frequencies given as w = ∈ (). Next, by iteratively applying the Sanathanan–Koerner least-squares method [31], the integer-order transfer function is approximated from the frequencies response data and defined as
where P, Q, and are defined as
The target is to obtain each coefficient of P and Q into the desired frequency range w. To do, Levy’s linearized cost function along with the Sanathanan–Koerner least-squares iteration are used to minimize the difference between data samples = and (39) as
where is the iteration step and ⊤ is the number of iterations. The curve fitting is achieved when approaches to , and for obtaining a minimal realization of (39), equivalent poles and zeros must be canceled. The last step is to convert the obtained state-space representation to a transfer function. Unfortunately, this method is complex to code in Maple 18, but easy to implement in the Matlab environment, due to the use of frd and fitfrd functions. However, it is possible to link Maple 18 with Matlab. The first block of Table 13 shows the Maple 18 code to link and call the Matlab script shown in the second block.

Table 13.
Code in Maple 18 environment to call the m-file and Matlab script.
We now define = −0.5, = 0.01, = 100 and N = 4. The rational approximation is computed as
The magnitude and phase responses are depicted in Figure 3a,c, and the errors are shown in Figure 3b,d. All the curves are colored with a brown line. The main advantages of this approximation method are that (1) if N is low, for instance N = 4, the magnitude error is low into the desired frequency range, ±2 dB approximately, and the ripples can be minimized by increasing N. (2) If N is large, the phase error becomes very low into the frequency interval. The disadvantages found are that (1) if N is low, for instance N = 4, then close to the upper limit, the ripple of the phase error is high, −25 approximately. (2) Additionally, when N increases, the magnitude error at is slightly higher than the error at . Note that if N becomes very large, then the electronic synthesis process could be a tedious and complex task.
3.9. Modified Stability Boundary Locus (MSBL) Fitting Approximation
This approximation method was reported in [19,32], which is an improved version of the stability boundaries locus fitting approximation method [33]. According to [19], the method uses a set of logarithmically spaced frequency sampling points = ∈ (), for approximating the behavior of . A closed-loop control system composed by the plant, i.e., , and a proportional–integral controller is assumed. Following the analysis of [19,33], the equations of the method are
and the unknown coefficients of the approximate model are computed as
and the approximated integer-order rational transfer function is given by

Table 14.
Maple 18 code of MSBL method.
By using = −0.5, = 0.01, = 100 and N = 4, the rational approximation is computed as
The magnitude and phase responses are illustrated in Figure 3a,c and the errors are depicted in Figure 3b,d, respectively. For this last method, all curves are colored with a maroon line. The main advantages of this approximation method are that (1) the magnitude and phase responses are improving when N increases and for the parameters described before, the magnitude error is ±1.5 dB and for the phase error is ±7, approximately, and (2) the method can not only be used to approximate arbitrary-order operators, but can also be used to approximate transfer functions. The main disadvantage found is that should be set close to zero since if drifts toward higher frequencies, then the method fails.
It is worth mentioning that other approximation methods of rational transfer functions can be found in the literature, such as the Fourier series and inverse Fourier transform method [20], vector fitting method [34], Abdelbaki’s method [35], Maione’s approximation [36], Thiele’s approximation [37], El-Khazali’s method [38], AbdelAty’s method [39]. However, the accuracy of each method is almost the same or less with some method described above. For this reason, these approximation methods are not discussed herein.
4. Model Order Reduction
From the point of view of electronic design, low-order accurate transfer functions are widely required. This is because they are easier to synthesize with analog circuits or be encoded with reconfigurable hardware. In this context, two model order reduction methods are described below.
4.1. Pade’s Approximation
The Pade’s method approximates a continuous function by a rational function of [m/n] order [40]. Given a function with two integers and , Pade’s approximation is defined as
and have as many of their derivatives as possible equal to .
Note that for , the obtained approximation is the Maclaurin expansion for . In the Maple 18 environment, Pade’s approximation can be computed as given in Table 15.

Table 15.
Maple 18 code of Pade’s method.
Applying the algorithm of Table 15 to each rational transfer function associated with each approximation method, we obtain
As one can observe, from each original rational transfer function, Pade’s method is applied to reduce only an order in each polynomial. According to Figure 4a,b, the magnitude bandwidth is not only reduced, but for some approximation methods, the magnitude error is increased drastically in the desired frequency range . This same behavior is observed in the phase responses, as illustrated in Figure 4c,d. Of all of them, the Oustaloup’s, refined Oustaloup’s and Charef’s V2 methods have the least errors one decade down. Therefore, we conclude that Pade’s method fails because there is no approximation control in the frequency interval.
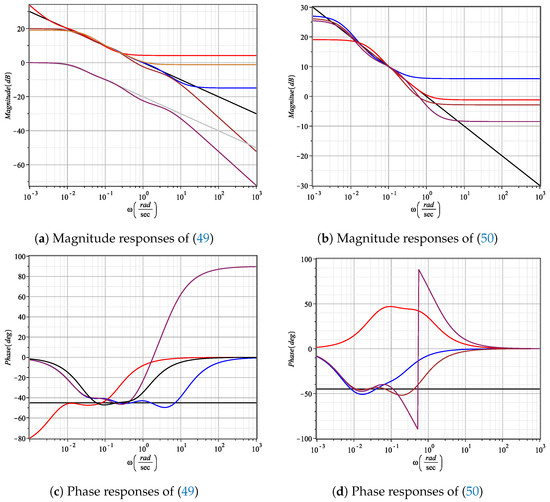
Figure 4.
Magnitude and phase responses of reduced order transfer functions by applying Pade’s approximation. (a) Ideal behavior (black line) of , Oustaloup’s (blue line), refined Oustaloup’s (red line), Charef’s V1 (brown line), ideal behavior (gray line) of , Charef’s V2 (maroon line) and Carlson’s (gold line), (b) ideal behavior (black line) of , Matsuda’s (blue line), continued fraction expansion (red line), curve fitting (brown line) and MSBL (maroon line), (c) phase responses of (a,d), phase responses of (b).
4.2. Stochastic Balancing Method
The balred function of Matlab defines the stochastic balancing related model reduction method [41,42]. Applying this function to each rational transfer function associated with each approximation method as
where is the original transfer function, is the reduced order transfer function and R is the order, we obtain
Similarly as before, the stochastic balancing method is applied to reduce an order in each numerator and denominator of the original transfer function. Thus, whereas the magnitude responses of (52) are depicted in Figure 5a, those of (53) are illustrated in Figure 5b. At this stage, one can observe that for Oustaloup’s and refined Oustloup’s methods, the bandwidth is slightly kept in the desired frequency range. However, for phase responses, the bandwidth of all approximation methods is reduced, as shown in Figure 5c,d.
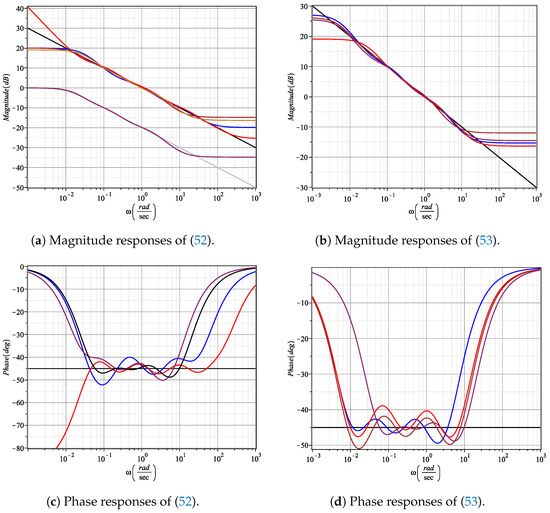
Figure 5.
Magnitude and phase diagrams of reduced order transfer functions by applying stochastic balancing method. (a) Ideal behavior (black line) of , Oustaloup’s (blue line), refined Oustaloup’s (red line), Charef’s V1 (brown line), ideal behavior (gray line) of , Charef’s V2 (maroon line) and Carlson’s (gold line), (b) ideal behavior (black line) of , Matsuda’s (blue line), continued fraction expansion (red line), curve fitting (brown line) and MSBL (maroon line), (c) phase responses of (a,d), phase responses of (b).
5. Results and Conclusions
Three basic definitions of arbitrary-order calculus were revised, and the Maple 18 code for each of them along with an application example were shown. Afterwards, the frequency-domain approximation methods were introduced. For each approximation method, not only the Maple 18 code was presented, but an application example was also explained, where the closed form transfer functions were derived for = 1/2. The advantages and disadvantages of each approximation method were also discussed. From the frequency response waveforms, it is evident that curve fitting and MSBL methods are better suited to the ideal behavior. On the one hand, if the required bandwidth for a specific application is narrow, then continued fraction expansion or Matsuda’s method can be used. On the other hand, if the application needs to control the approximation error, then Charef’s V1 and V2 methods should be used. Furthermore, we also note that in general, the accuracy of the approximation methods depends on N ( for Charef’s V1 and V2) and the desired frequency interval. Therefore, for a large bandwidth, N should be increased to obtain the desired accuracy, but if the bandwidth is narrow, then N can be reduced. For all approximation methods, the rational transfer function as a product of poles and zeros was also derived. This is important because each pole–zero pair can be synthesized in the analog domain by using first-order shelving equalizers, and for the case of a pole with gain, a low-pass filter topology can be used. Finally, we showed two model order reduction methods and according to the numerical results, the stochastic balancing method achieves the best reduced-order transfer functions, despite all its disadvantages. As a consequence, the electronic synthesis process will be accelerated.
Author Contributions
Conceptualization, J.D.C.-C. and C.S.-L.; methodology, J.D.C.-C., C.S.-L., R.O.-M., D.T.-M. and C.M.H.-M.; software, J.D.C.-C., C.S.-L. and L.A.S.-G.; validation, L.A.S.-G., H.G.G.-H. and C.S.-L.; formal analysis, J.D.C.-C., C.S.-L., R.O.-M., D.T.-M., C.M.H.-M., L.A.S.-G. and H.G.G.-H.; investigation, J.D.C.-C., C.S.-L., R.O.-M., D.T.-M., C.M.H.-M., L.A.S.-G. and H.G.G.-H.; writing—original draft preparation, C.S.-L., L.A.S.-G. and H.G.G.-H.; writing—review and editing, C.S.-L., R.O.-M. and D.T.-M.; supervision, C.S.-L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order, 1st ed.; Dover Publications: Mineola, NY, USA, 2006. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–223. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems, Modeling, Analysis and Simulation, 1st ed.; Springer: London, UK; New York, NY, USA, 2011. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency band complex noninteger differentiator: Characterization and synthesis. Trans. Circuits Syst. I 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Xue, D.; Zhao, C.; Chen, Y. A Modified Approximation Method of Fractional Order System. In Proceedings of the International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1043–1048. [Google Scholar]
- Charef, A.; Sun, H.H.; Tsao, Y.Y.; Onaral, B. Fractal system as represented by singularity function. Trans. Autom. Control 1992, 37, 1465–1470. [Google Scholar] [CrossRef]
- Carlson, G.E.; Halijak, C.A. Approximation of a fractional capacitors (1/s) by a regular Newton process. Trans. Circuits Theory CT-11 1964, 2, 210–213. [Google Scholar] [CrossRef]
- Shrivastava, N.; Varshney, P. Rational Approximation of Fractional Order Systems Using Carlson Method. In Proceedings of the International Conference on Soft Computing Techniques and Implementation, Faridabad, India, 8–10 October 2015; pp. 76–80. [Google Scholar]
- Matsuda, K.; Fujii, H. H∞ optimized wave-absorbing control: Analytical and experimental results. J. Guid. Control Dyn. 1993, 16, 1146–1153. [Google Scholar] [CrossRef]
- Sánchez-López, C. An experimental synthesis methodology of fractional-order chaotic attractors. Nonlinear Dyn. 2020, 100, 3907–3923. [Google Scholar] [CrossRef]
- Sánchez-López, C.; Carbajal-Gómez, V.H.; Carrasco-Aguilar, M.A.; Carro-Pérez, I. Fractional-Order Memristor Emulator Circuits. Complexity 2018, 2018, 2806976. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; García-Jiménez, L.V.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. New alternatives for analog implementation of fractional-order integrators, differentiators and PID controllers based on integer-order integrators. Nonlinear Dyn. 2017, 90, 241–256. [Google Scholar] [CrossRef]
- Raynaud, H.F.; Zergaïnoh, A. State-space representation for fractional order controllers. Automatica 2000, 36, 1017–1021. [Google Scholar] [CrossRef]
- Monje, C.A.; Vinagre, B.M.; Calderon, A.J.; Feliu, V.; Chen, Y.Q. Auto-tuning of fractional lead-lag compensators. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 4–8 July 2005; pp. 319–324. [Google Scholar]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Double exponent fractional-order filters: Approximation methods and realization. Circuits Syst. Signal Process. 2021, 40, 993–1004. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator. AEU-Int. J. Electron. Commun. 2021, 129, 153537. [Google Scholar] [CrossRef]
- Krishna, B.T. Studies on fractional order differentiators and integrators: A survey. Signal Process. 2011, 91, 386–426. [Google Scholar] [CrossRef]
- Nur-Deniz, F.; Baykant-Alagoz, B.; Tan, N.; Koseoglu, M. Revisiting four approximation methods for fractional order transfer function implementations: Stability preservation, time and frequency response matching analyses. Annu. Rev. Control 2020, 49, 239–257. [Google Scholar] [CrossRef]
- Atherton, D.P.; Tan, N.; Yüce, A. Methods for computing the time response of fractional-order systems. IET Control Theory Appl. 2015, 9, 817–830. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Fractional-order Chua’s circuit: Time-domain analysis, bifurcation, chaotic behaviour and test for chaos. Int. J. Bifur. Chaos. 2008, 18, 261–267. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Deng, W. Numerical algorithm for the time fractional Fokker-Planck equation. J. Comput. Phy. 2007, 227, 1510–1522. [Google Scholar] [CrossRef]
- Li, C.; Xiong, J.; Li, W.; Tong, Y.; Zeng, Y. Robust synchronization for a class of fractional-order dynamical system via linear state variable. Indian J. Phys. 2013, 87, 673–678. [Google Scholar] [CrossRef]
- Parsa-Moghaddam, B.; Yaghoobi, S.; Tenreiro-Machado, J.A. An extended predictor-corrector algorithm for variable-order fractional delay differential equations. J. Compu. Nonlinear Dyn. 2016, 11. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E.A. Stable fractional Chebyshev differentiation matrix for the numerical solution of multi-order fractional differential equations. Nonlinear Dyn. 2017, 90, 185–201. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E.A. Numerical solution of multi-order fractional differential equations with multiple delays via spectral collocation methods. Appl. Math. Model. 2018, 56, 424–448. [Google Scholar] [CrossRef]
- Khovanskii, A.N. The Application of Continued Fractions and Their Generalizations to Problems in Approximation Theory; Noordhoff, Ltd.: Groningen, The Netherlands, 1963; pp. 100–110. [Google Scholar]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassam, S.M.; Harindran, V.R. Frequency response based curve fitting approximation of fractional-order PID controllers. Int. J. Appl. Math. Comput. Sci. 2019, 29, 311–326. [Google Scholar] [CrossRef] [Green Version]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassam, S.M.; Harindran, V.R. Fractional-Order Systems and PID Controllers; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Sanathanan, C.; Koerner, J. Transfer function synthesis as a ratio of two complex polynomials. IEEE Trans. Autom. Control 1963, 8, 56–58. [Google Scholar] [CrossRef]
- Koseoglu, M.; Nur-Deniz, F.; Baykant-Alagoz, B.; Alisoy, H. An effective analog circuit design of approximate fractional-order derivative models of M-SBL fitting method. Int. J. Eng. Sci. Technol. 2021, 1, 1–15. [Google Scholar] [CrossRef]
- Nur-Deniz, F.; Baykant-Alagoz, B.; Tan, N.; Atherton, D.P. An integer order approximation method based on stability boundary locus for fractional order derivative/integrator operators. ISA Trans. 2016, 62, 154–163. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Djouambi, A.; Charef, A.; Besancon, A.V. Optimal approximation, simulation and analog realization of the fundamental fractional order transfer function. Int. J. Appl. Math. Comput. Sci. 2007, 17, 455–462. [Google Scholar] [CrossRef] [Green Version]
- Maione, G. Continued fractions approximation of the impulse response of fractional order dynamic systems. IET Control Theory Appl. 2008, 2, 564–572. [Google Scholar] [CrossRef]
- Maione, G. Closed-Form Rational Approximations of Fractional, Analog and Digital Differentiators/Integrators. J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- El-Khazali, R. Discretization of fractional-order Laplacian operators. In Proceedings of the 19th IFAC Congress, Cape Town, South Africa, 24–29 August 2014; pp. 2016–2021. [Google Scholar]
- AbdelAty, A.M.; Elwakil, A.S.; Radwan, A.G.; Psychalinos, C.; Maundy, B.J. Approximation of the fractional-order Laplacian sα as a weighted sum of first-order high-pass filters. IEEE Trans. Circuit. Sys. II Express Briefs 2018, 65, 1114–1118. [Google Scholar]
- Baker George, A. Essentials of Padé Approximants, 1st ed.; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Green, M. A Relative Error Bound for Balanced Stochastic Truncation. Trans. Autom. Control 1998, 62, 961–965. [Google Scholar] [CrossRef]
- Varga, A. On stochastic balancing related model reduction. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 12–15 December 2000; pp. 2385–2390. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).