Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential Equation with Weakly Singular Kernel
Abstract
1. Introduction
2. Mathematical Preliminaries
2.1. Basic Tools
2.2. The Shifted Jacobi Polynomials
2.3. Fractional-Order Shifted Jacobi Polynomials
3. Algorithm for Solving VO-FIDE-WSK
4. Algorithm for Solving VO-FIDE-WSK with Nonlocal Boundary Conditions
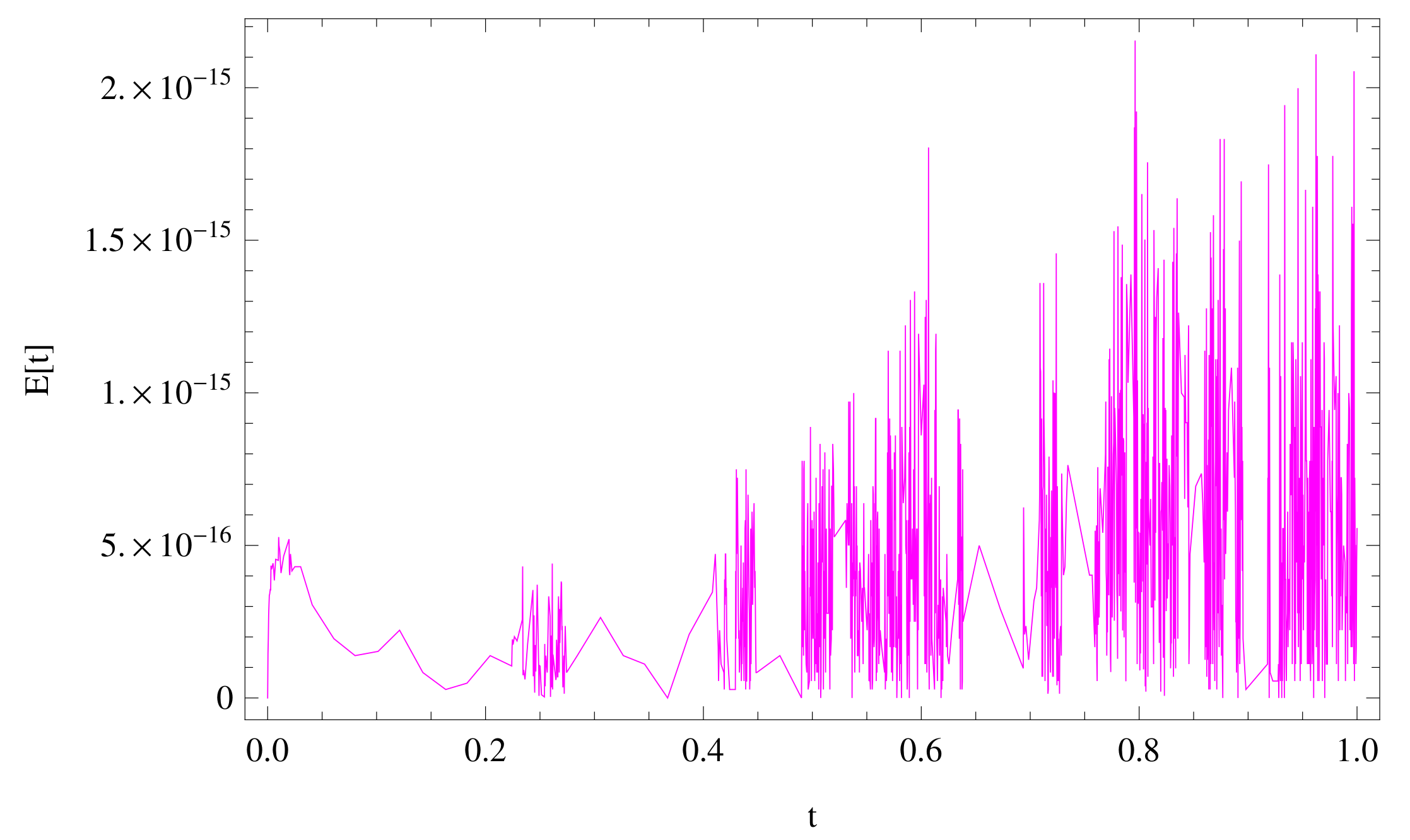
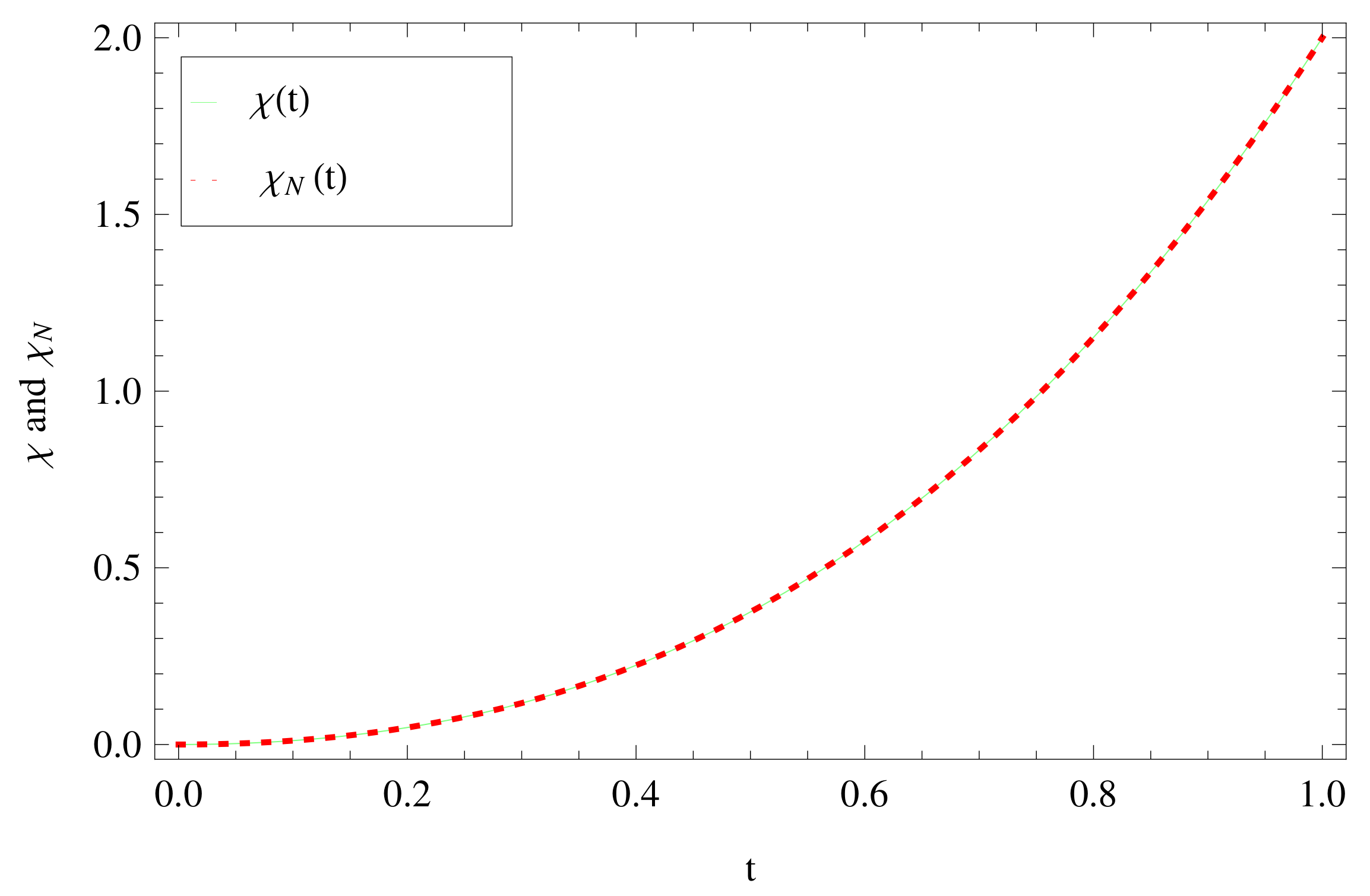
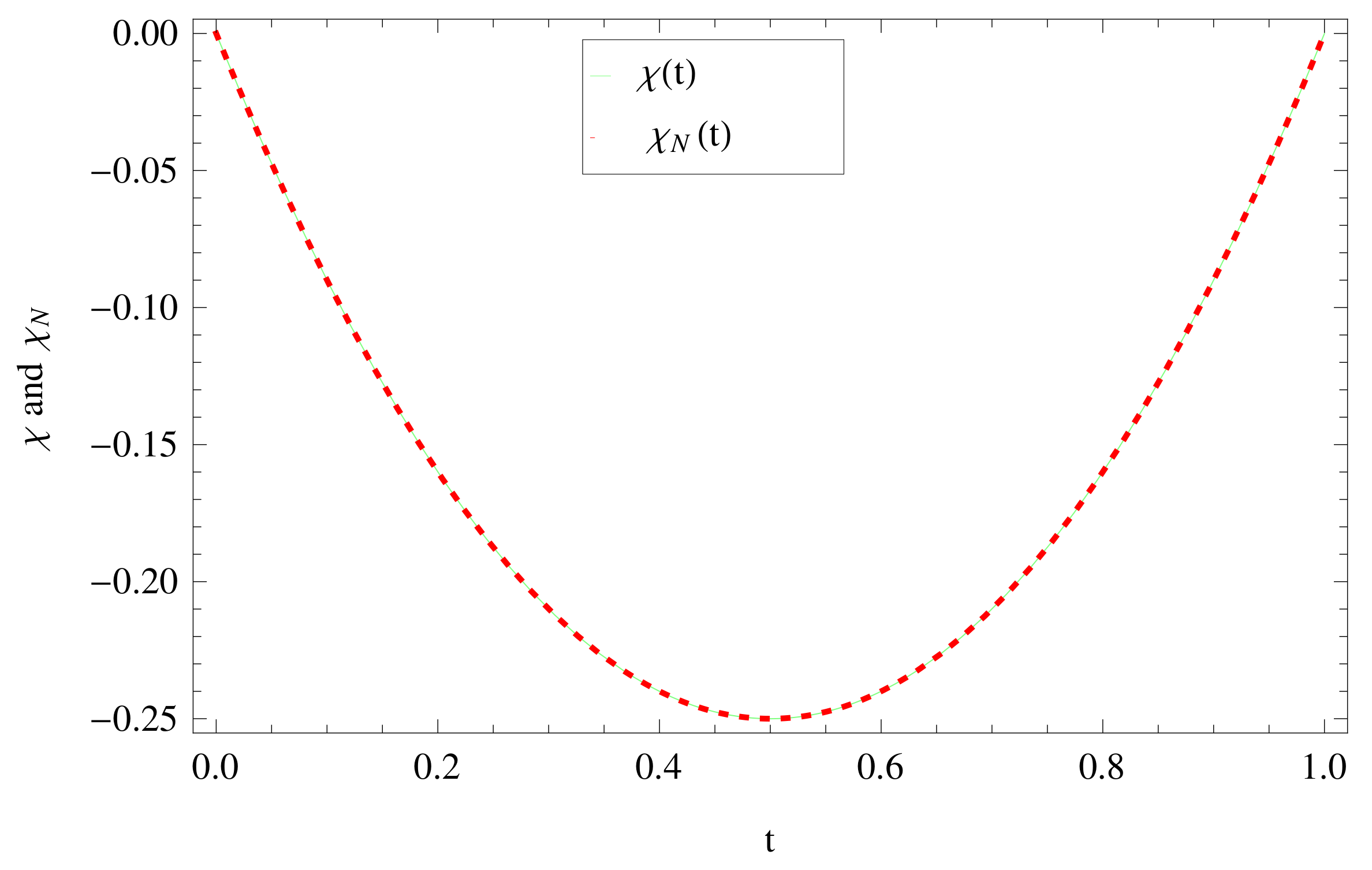
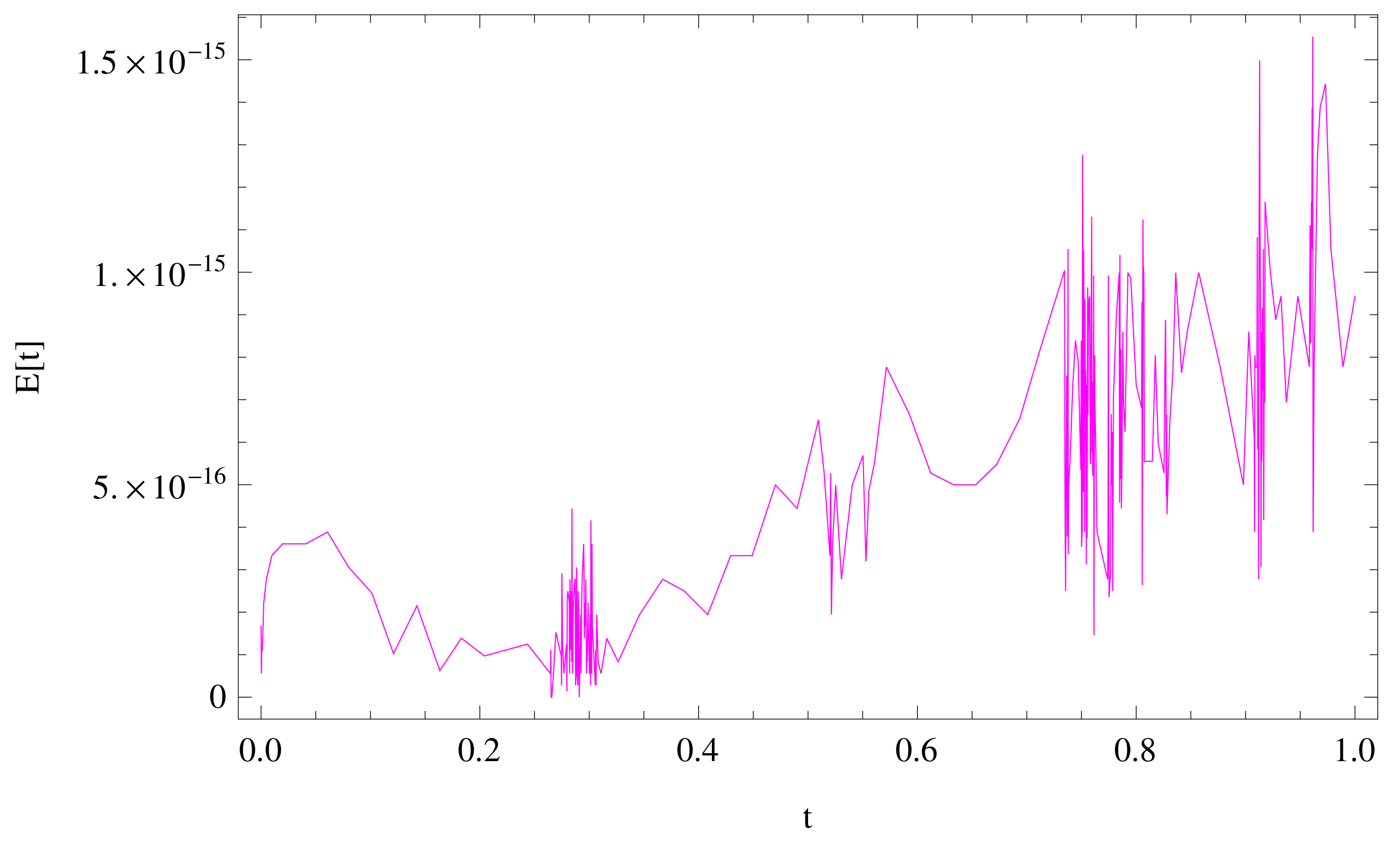
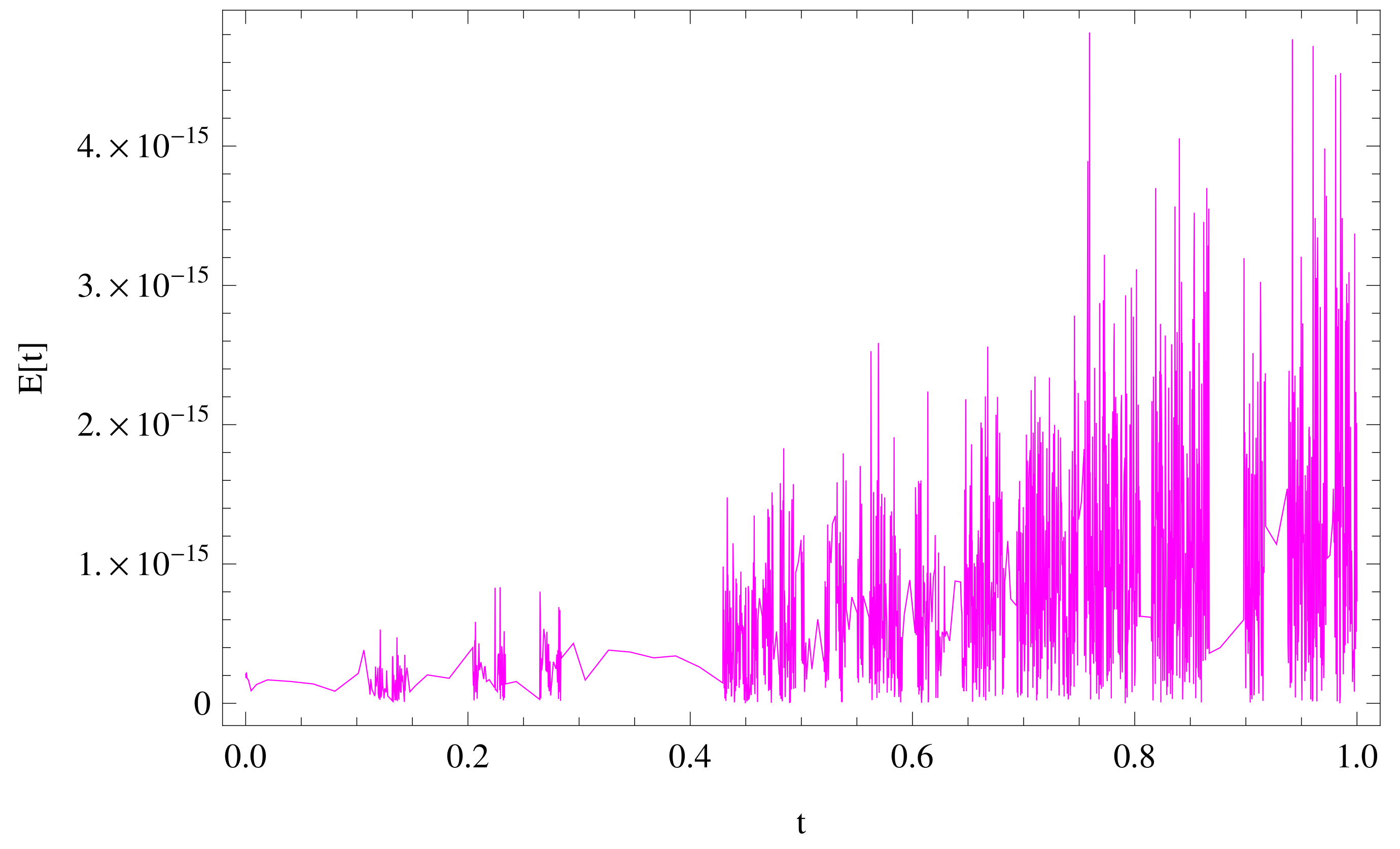
5. Illustrative Examples
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdelkawy, M.A.; Ezz-Eldien, S.S.; Amin, A.Z. A Jacobi spectral collocation scheme for solving Abel’s integral equations. Prog. Fract. Differ. Appl. 2015, 1, 1–14. [Google Scholar]
- Eslahchi, M.; Dehghan, M.; Parvizi, M. Application of the collocation method for solving nonlinear fractional integro-differential equations. J. Comput. Appl. Math. 2014, 257, 105–128. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Bhrawy, A.H.; Abdelkawy, M.A. A fully spectral collocation approximation for multi-dimensional fractional Schrödinger equations. J. Comput. Phys. 2015, 294, 462–483. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Exponentially accurate spectral and spectral element methods for fractional ODEs. J. Comput. Phys. 2014, 257, 460–480. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Machado, J.T.; Baleanu, D. A new fractional derivative involving the normalized sinc function without singular kernel. Eur. Phys. J. Spec. Top. 2017, 226, 3567–3575. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.; Nieto, J.J. A new family of the local fractional PDEs. Fundam. Informaticae 2017, 151, 63–75. [Google Scholar] [CrossRef]
- Yang, X.J.; Abdel-Aty, M.; Cattani, C. A new general fractional-order derivataive with Rabotnov fractional-exponential kernel applied to model the anomalous heat transfer. Therm. Sci. 2019, 23, 1677–1681. [Google Scholar] [CrossRef]
- Chen, L.; Pan, W.; Wu, R.; Tenreiro Machado, J.; Lopes, A.M. Design and implementation of grid multi-scroll fractional-order chaotic attractors. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 084303. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Modeling vegetable fractals by means of fractional-order equations. J. Vib. Control 2016, 22, 2100–2108. [Google Scholar] [CrossRef]
- Momani, S.; Noor, M.A. Numerical methods for fourth-order fractional integro-differential equations. Appl. Math. Comput. 2006, 182, 754–760. [Google Scholar] [CrossRef]
- Nemati, S.; Sedaghat, S.; Mohammadi, I. A fast numerical algorithm based on the second kind Chebyshev polynomials for fractional integro-differential equations with weakly singular kernels. J. Comput. Appl. Math. 2016, 308, 231–242. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L. SCW method for solving the fractional integro-differential equations with a weakly singular kernel. Appl. Math. Comput. 2016, 275, 72–80. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, J.; Ford, N.J. Collocation methods for fractional integro-differential equations with weakly singular kernels. Numer. Algorithms 2014, 65, 723–743. [Google Scholar] [CrossRef]
- Mokhtary, P. Numerical analysis of an operational Jacobi Tau method for fractional weakly singular integro-differential equations. Appl. Numer. Math. 2017, 121, 52–67. [Google Scholar] [CrossRef]
- Yi, M.; Wang, L.; Huang, J. Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel. Appl. Math. Model. 2016, 40, 3422–3437. [Google Scholar] [CrossRef]
- Pedas, A.; Tamme, E.; Vikerpuur, M. Spline collocation for fractional weakly singular integro-differential equations. Appl. Numer. Math. 2016, 110, 204–214. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A.; Baleanu, D.; Amin, A.Z. A spectral technique for solving two-dimensional fractional integral equations with weakly singular kernel. Hacet. J. Math. Stat. 2018, 47, 553–566. [Google Scholar] [CrossRef]
- Yi, M.; Huang, J. CAS wavelet method for solving the fractional integro-differential equation with a weakly singular kernel. Int. J. Comput. Math. 2015, 92, 1715–1728. [Google Scholar] [CrossRef]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.; Lopes, A.M. Shifted Jacobi–Gauss-collocation with convergence analysis for fractional integro-differential equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 342–359. [Google Scholar] [CrossRef]
- Xu, Y.; Suat, E.V. A finite difference technique for solving variable-order fractional integro-differential equations. Bull. Iran. Math. Soc. 2014, 40, 699–712. [Google Scholar]
- Chen, Y.M.; Wei, Y.Q.; Liu, D.Y.; Yu, H. Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl. Math. Lett. 2015, 46, 83–88. [Google Scholar] [CrossRef]
- Sun, K.; Zhu, M. Numerical algorithm to solve a class of variable order fractional integral-differential equation based on Chebyshev polynomials. Math. Probl. Eng. 2015, 2015, 902161. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Li, B.; Sun, Y. Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl. Math. Comput. 2014, 238, 329–341. [Google Scholar] [CrossRef]
- Bhrawy, A.; Zaky, M. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2015, 80, 101–116. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 2016, 35, 69–87. [Google Scholar] [CrossRef]
- Atangana, A. On the stability and convergence of the time-fractional variable order telegraph equation. J. Comput. Phys. 2015, 293, 104–114. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Zhuang, P.; Turner, I.; Anh, V. Numerical analysis of a new space–time variable fractional order advection–dispersion equation. Appl. Math. Comput. 2014, 242, 541–550. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Fractional spectral collocation methods for linear and nonlinear variable order FPDEs. J. Comput. Phys. 2015, 293, 312–338. [Google Scholar] [CrossRef]
- Abd-Elkawy, M.A.; Alqahtani, R.T. Space-time spectral collocation algorithm for the variable-order Galilei invariant advection diffusion equations with a nonlinear source term. Math. Model. Anal. 2017, 22, 1–20. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z.; Karniadakis, G.E. Second-order approximations for variable order fractional derivatives: Algorithms and applications. J. Comput. Phys. 2015, 293, 184–200. [Google Scholar] [CrossRef]
- Chen, S.; Liu, F.; Burrage, K. Numerical simulation of a new two-dimensional variable-order fractional percolation equation in non-homogeneous porous media. Comput. Math. Appl. 2014, 68, 2133–2141. [Google Scholar] [CrossRef]
- Alikhanov, A.A. Numerical methods of solutions of boundary value problems for the multi-term variable-distributed order diffusion equation. Appl. Math. Comput. 2015, 268, 12–22. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Assiri, T.A.R. Numerical simulations for the space-time variable order nonlinear fractional wave equation. J. Appl. Math. 2013, 2013, 586870. [Google Scholar] [CrossRef][Green Version]
- Razminia, A.; Dizaji, A.F.; Majd, V.J. Solution existence for non-autonomous variable-order fractional differential equations. Math. Comput. Model. 2012, 55, 1106–1117. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wu, L. An operational matrix technique for solving variable order fractional differential-integral equation based on the second kind of Chebyshev polynomials. Adv. Math. Phys. 2016, 2016, 6345978. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Burrage, K. Numerical analysis for a variable-order nonlinear cable equation. J. Comput. Appl. Math. 2011, 236, 209–224. [Google Scholar] [CrossRef]
- Lin, R.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl. Math. Comput. 2009, 212, 435–445. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Alofi, A.S. A Jacobi–Gauss collocation method for solving nonlinear Lane–Emden type equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 62–70. [Google Scholar] [CrossRef]
- Bhrawy, A.; Abdelkawy, M.; Machado, J.T.; Amin, A. Legendre–Gauss–Lobatto collocation method for solving multi-dimensional Fredholm integral equations. Comput. Math. Appl. 2016, 4, 1–13. [Google Scholar] [CrossRef]
- Bhrawy, A.H. A Jacobi–Gauss–Lobatto collocation method for solving generalized Fitzhugh–Nagumo equation with time-dependent coefficients. Appl. Math. Comput. 2013, 222, 255–264. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Amin, A.Z.; Bhrawy, A.H.; Machado, J.A.T.; Lopes, A.M. Jacobi collocation approximation for solving multi-dimensional Volterra integral equations. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 411–425. [Google Scholar] [CrossRef]
- Doha, E.; Bhrawy, A.; Baleanu, D.; Hafez, R. A new Jacobi rational–Gauss collocation method for numerical solution of generalized pantograph equations. Appl. Numer. Math. 2014, 77, 43–54. [Google Scholar] [CrossRef]
- Ghoreishi, F.; Yazdani, S. An extension of the spectral Tau method for numerical solution of multi-order fractional differential equations with convergence analysis. Comput. Math. Appl. 2011, 61, 30–43. [Google Scholar] [CrossRef]
- Mokhtary, P.; Ghoreishi, F. The L2-convergence of the Legendre spectral Tau matrix formulation for nonlinear fractional integro differential equations. Numer. Algorithms 2011, 58, 475–496. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Doha, E.H.; Baleanu, D.; Ezz-Eldien, S.S. A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 2015, 293, 142–156. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H. An efficient direct solver for multidimensional elliptic Robin boundary value problems using a Legendre spectral-Galerkin method. Comput. Math. Appl. 2012, 64, 558–571. [Google Scholar] [CrossRef]
- Chen, F.; Shen, J. Efficient spectral-Galerkin methods for systems of coupled second-order equations and their applications. J. Comput. Phys. 2012, 231, 5016–5028. [Google Scholar] [CrossRef]
- Shen, J. A new dual-Petrov-Galerkin method for third and higher odd-order differential equations: Application to the KDV equation. SIAM J. Numer. Anal. 2003, 41, 1595–1619. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Hafez, R. A Jacobi–Jacobi dual-Petrov–Galerkin method for third-and fifth-order differential equations. Math. Comput. Model. 2011, 53, 1820–1832. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Y. An approximation of semiconductor device by mixed finite element method and characteristics-mixed finite element method. Appl. Math. Comput. 2013, 225, 407–424. [Google Scholar]
- Wen, J.; He, Y. Convergence analysis of a new multiscale finite element method for the stationary Navier–Stokes problem. Comput. Math. Appl. 2014, 67, 1–25. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Okuzono, T.; Otsuru, T.; Tomiku, R.; Okamoto, N. A finite-element method using dispersion reduced spline elements for room acoustics simulation. Appl. Acoust. 2014, 79, 1–8. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations. Comput. Math. Appl. 2017, 73, 1100–1117. [Google Scholar] [CrossRef]
- Zaky, M. Correction to: Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2018, 94, 757. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Lopes, A.M.; Babatin, M.M. Shifted fractional Jacobi collocation method for solving fractional functional differential equations of variable order. Chaos Solitons Fractals 2020, 134, 109721. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Babatin, M.M.; Lopes, A.M. Highly accurate technique for solving distributed-order time-fractional-sub-diffusion equations of fourth order. Comput. Appl. Math. 2020, 39, 1–22. [Google Scholar] [CrossRef]



| New Method at | ||
|---|---|---|
| 0 | ||
| New Method at | ||
|---|---|---|
| 0 | 0 | 0 |
| Operational Matrix [12] | Operational Tau Method [15] | New Method | ||
|---|---|---|---|---|
| N | ||||
| 2 | ||||
| 4 | ||||
| 6 | ||||
| 8 | ||||
| 16 | − | |||
| 18 | − | |||
| 20 | − |
| N | ||
|---|---|---|
| 2 | ||
| 4 | ||
| 6 | ||
| 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M.; Hashim, I.; Babatin, M.M. Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential Equation with Weakly Singular Kernel. Fractal Fract. 2022, 6, 19. https://doi.org/10.3390/fractalfract6010019
Abdelkawy MA, Amin AZM, Lopes AM, Hashim I, Babatin MM. Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential Equation with Weakly Singular Kernel. Fractal and Fractional. 2022; 6(1):19. https://doi.org/10.3390/fractalfract6010019
Chicago/Turabian StyleAbdelkawy, Mohamed A., Ahmed Z. M. Amin, António M. Lopes, Ishak Hashim, and Mohammed M. Babatin. 2022. "Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential Equation with Weakly Singular Kernel" Fractal and Fractional 6, no. 1: 19. https://doi.org/10.3390/fractalfract6010019
APA StyleAbdelkawy, M. A., Amin, A. Z. M., Lopes, A. M., Hashim, I., & Babatin, M. M. (2022). Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential Equation with Weakly Singular Kernel. Fractal and Fractional, 6(1), 19. https://doi.org/10.3390/fractalfract6010019








