Dual Penta-Compound Combination Anti-Synchronization with Analysis and Application to a Novel Fractional Chaotic System
Abstract
:1. Introduction
2. Preliminaries
3. New Fractional Chaotic System
4. Dynamics of the Novel System
4.1. Symmetry, Dissipativity, and Stagnation Points
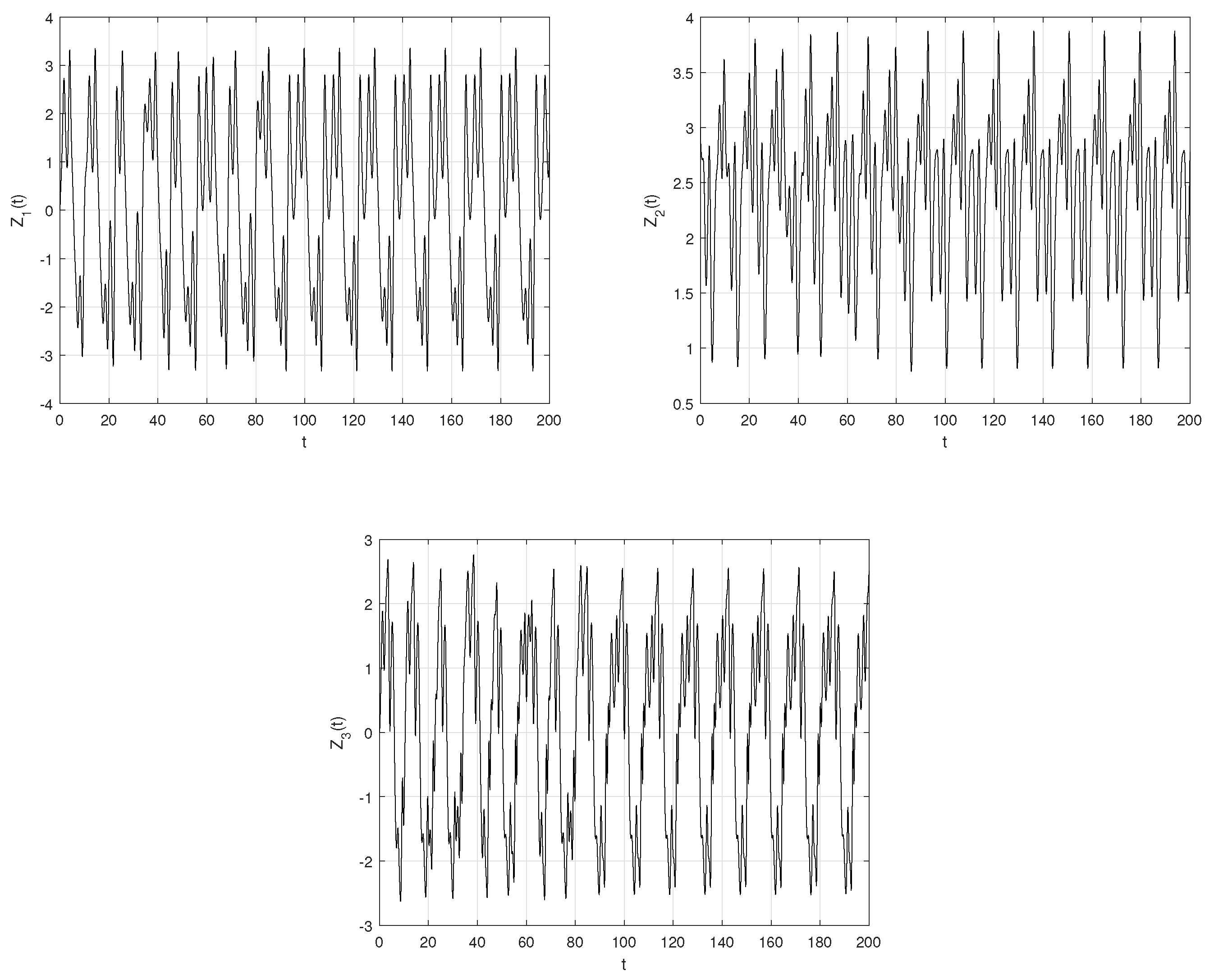
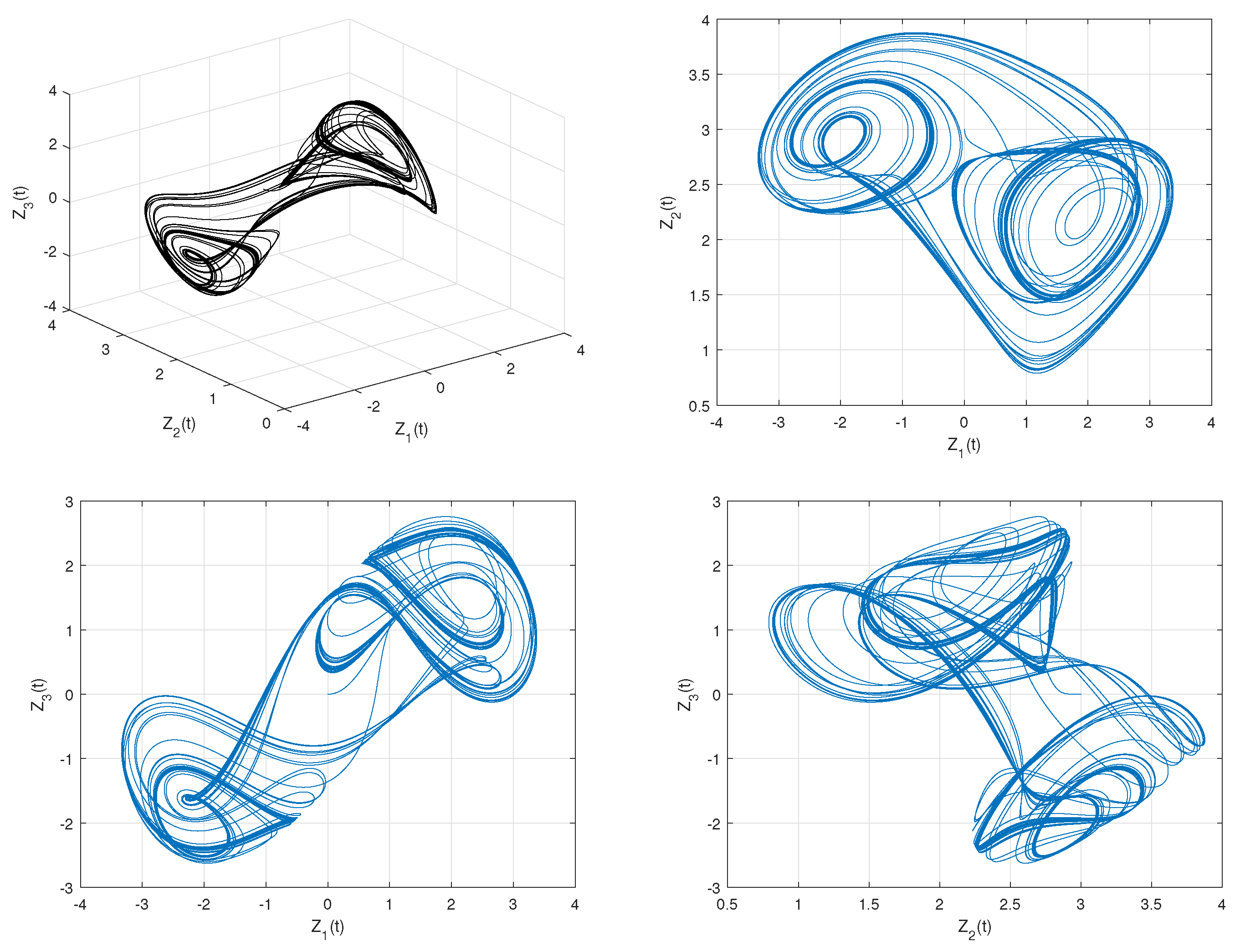
4.2. Solution of the Novel Fractional-Order Chaotic System
4.3. Lyapunov Dynamics and Bifurcation Analysis
4.4. Stability of the Trivial Equilibrium Point
5. Dual Penta-Compound Combination Anti-Synchronization
5.1. Via Non-Linear Control
5.2. Via Adaptive Sliding Mode Control
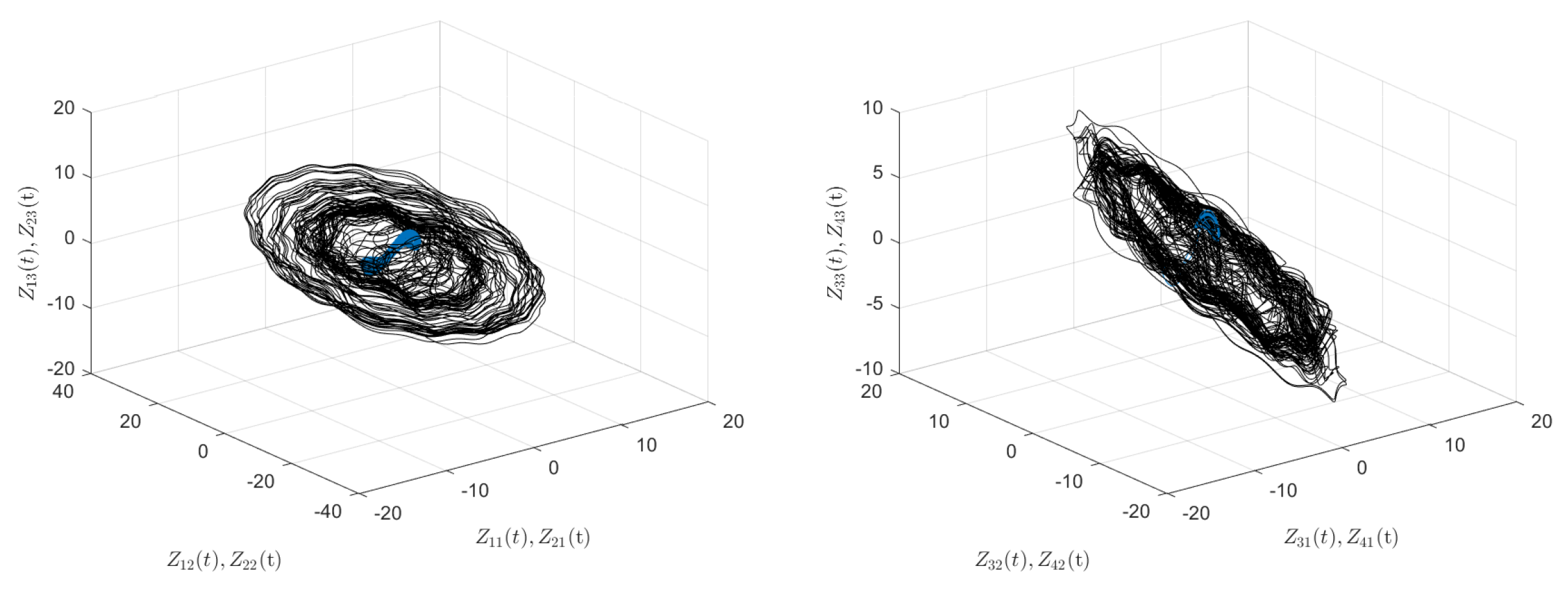
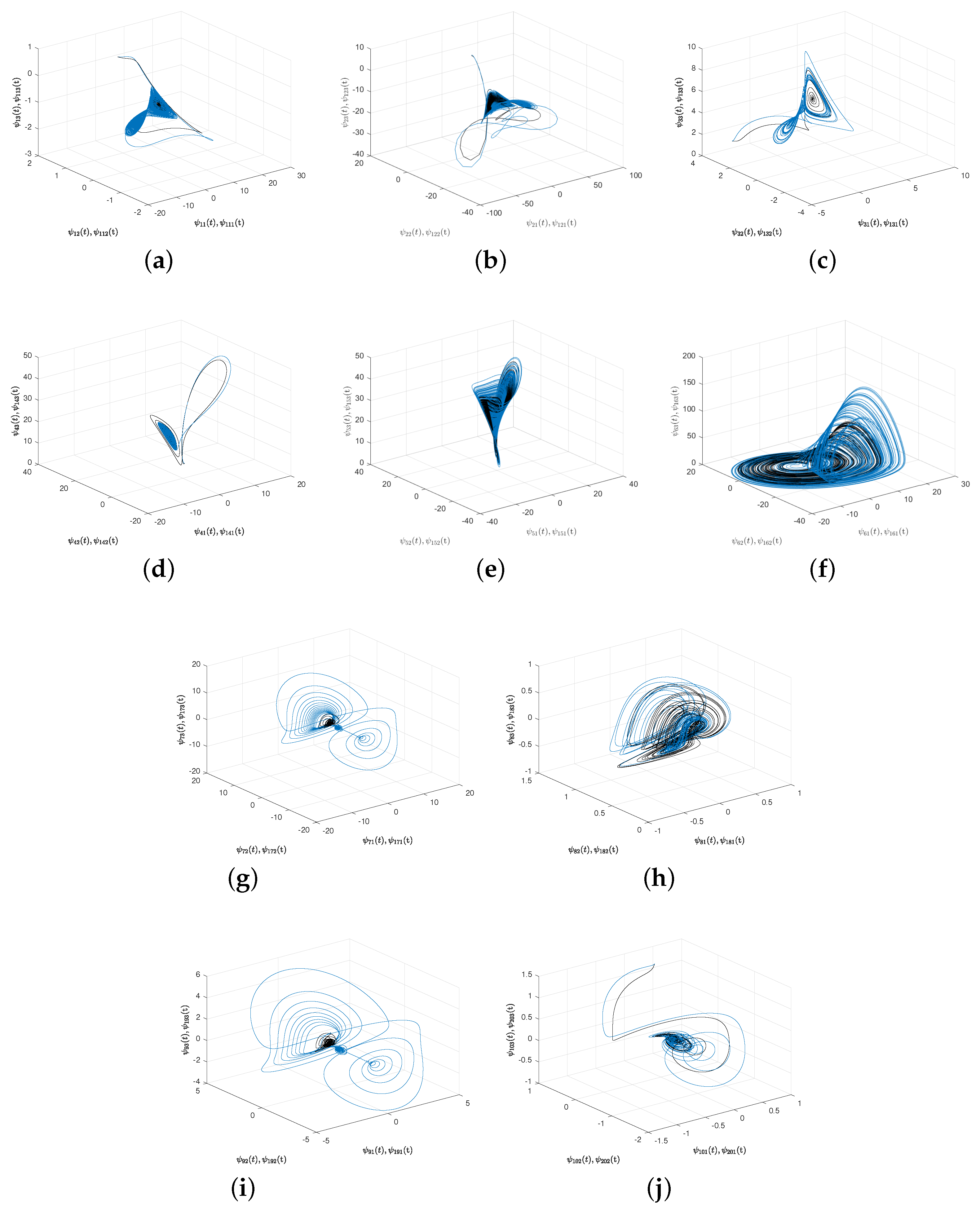
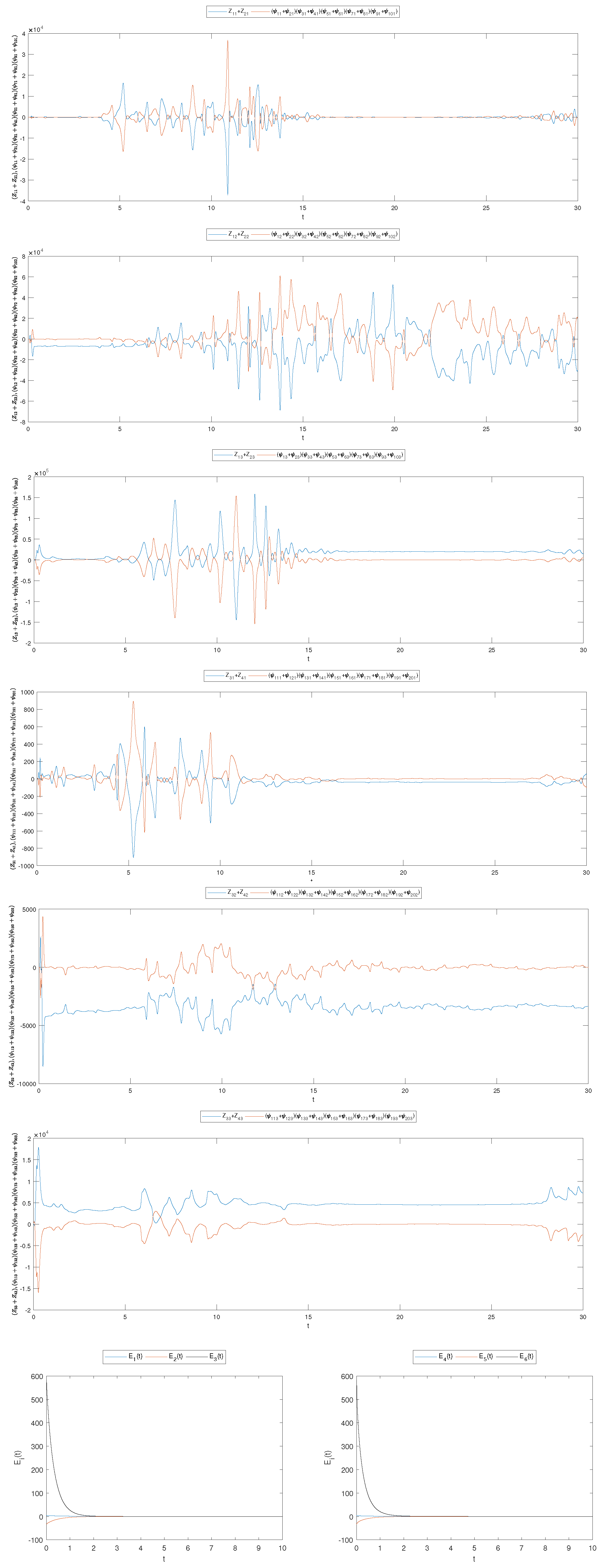
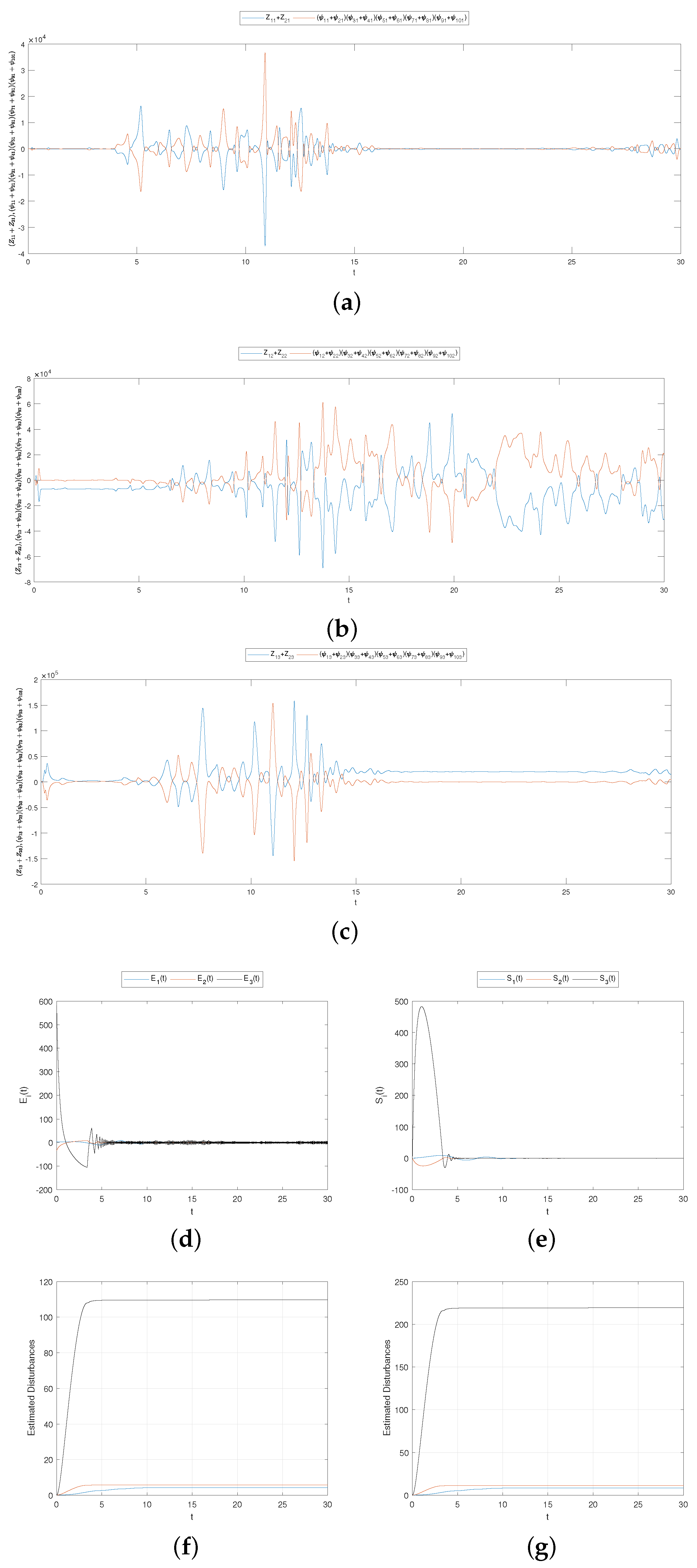
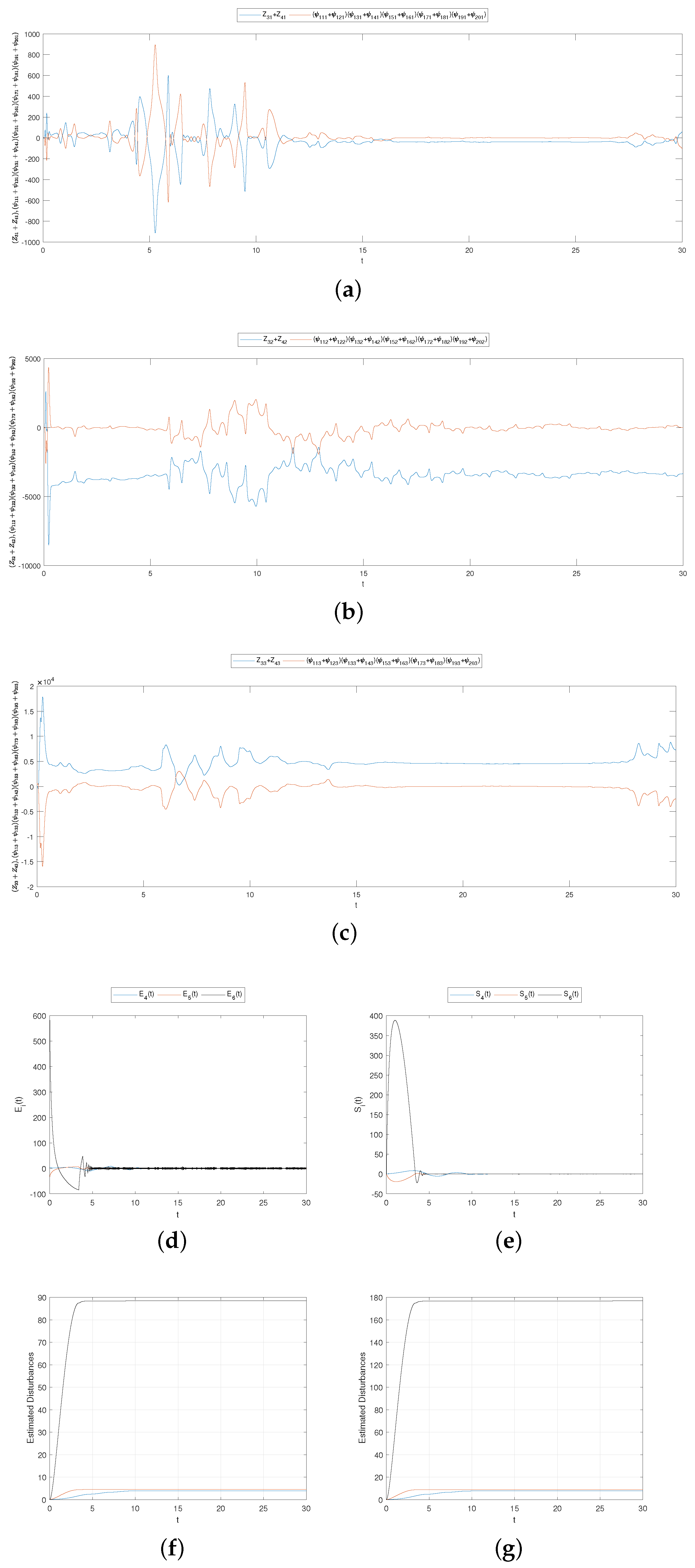
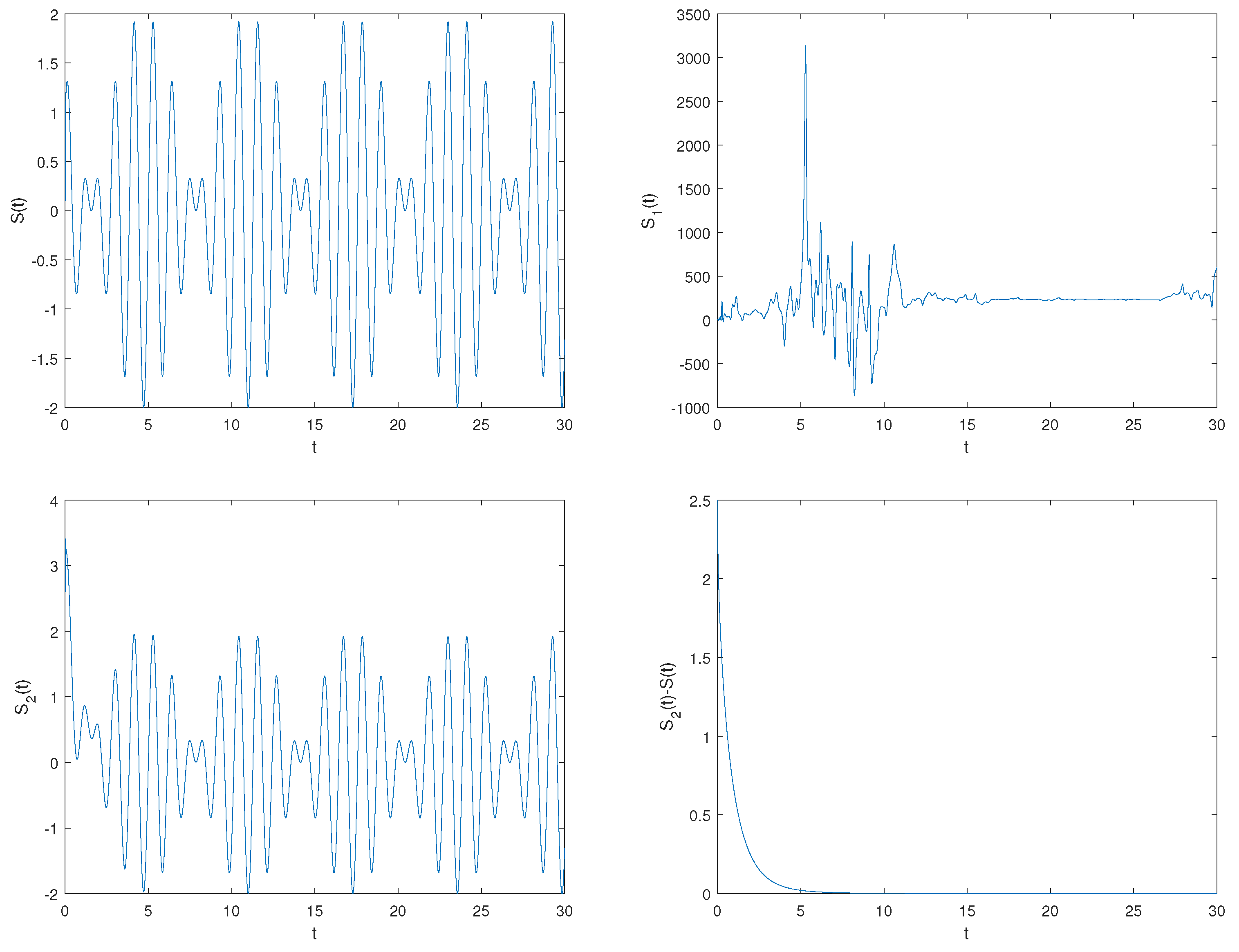
5.3. Simulations and Proposed Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Javidi, M.; Nyamoradi, N. Dynamic analysis of a fractional order prey-predator interaction with harvesting. Appl. Math. Model. 2013, 37, 28946–28956. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Sajjadi, S.S.; Asad, J.H. The fractional features of a harmonic oscillator with position-dependent mass. In Communications in Theoretical Physics; IOP Publishing: Philadelphia, PA, USA, 2020; Volume 72. [Google Scholar]
- Baleanu, D.; Etemad, S.; Rezapour, S. A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020, 64, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Trikha, P. Study of earths changing polarity using compound difference synchronization. GEM Int. J. Geomath. 2020, 11, 7. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Trikha, P.; Lone, S.J. Secure Communication: Using synchronization on a novel fractional-order chaotic system. In Proceedings of the ICPECA, New Delhi, India, 16–17 November 2019. [Google Scholar]
- Sun, S. A novel hyperchaotic image encryption scheme based on dna encoding, pixel-level scrambling and bit-level scrambling. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Trikha, P.; Jahanzaib, L.S. Dynamical analysis of a novel 5-d hyper-chaotic system with no equilibrium point and its application in secure communication. Differ. Geom. Dyn. Syst. 2020, 22, 269–288. [Google Scholar]
- Zhang, S.; Zeng, Y.; Li, Z. One to four-wing chaotic attractors coined from a novel 3d fractional-order chaotic system with complex dynamics. Chin. J. Phys. 2018, 56, 793–806. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Cang, S. A 3-D Spherical Attractor. Acta Phys. Polonica Ser. B 2011, B42, 235–247. [Google Scholar] [CrossRef]
- Yu, S.; Lu, J.; Chen, G. Multifolded torus chaotic attractors: Design and implementation. Chaos: Interdiscip. J. Nonlinear Sci. 2007, 17, 013118. [Google Scholar] [CrossRef] [Green Version]
- Chua, L.; Komuro, M.; Matsumoto, T. The double scroll family. IEEE Trans. Circuits Syst. 1986, 33, 1072–1118. [Google Scholar] [CrossRef] [Green Version]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Trikha, P.; Jahanzaib, L.S. Secure Communication: Using Double Compound-Combination Hybrid Synchronization. In Proceedings of the International Conference on Artificial Intelligence and Applications; Springer: Singapore, 2021; pp. 81–91. [Google Scholar]
- Khan, A.; Trikha, P. Compound difference anti-synchronization between chaotic systems of integer and fractional order. SN Appl. Sci. 2019, 1, 757. [Google Scholar] [CrossRef] [Green Version]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. From phase to lag synchronization in coupled chaotic oscillators. Phys. Rev. E 1997, 78, 4193. [Google Scholar] [CrossRef]
- Runzi, L.; Yinglan, W.; Shucheng, D. Combination synchronization of three classic chaotic systems using active backstepping design. Chaos: Interdiscip. J. Nonlinear Sci. 2011, 21, 043114. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S.; Trikha, P. Secure Communication: Using Parallel Synchronization Technique On Novel Fractional Order Chaotic System. IFAC-PapersOnLine 2020, 53, 307–312. [Google Scholar] [CrossRef]
- Khan, A.; Trikha, P.; Jahanzaib, L.S. Dislocated hybrid synchronization via. tracking control & parameter estimation methods with application. Int. J. Model. Simul. 2020, 41, 415–425. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S.; Trikha, P. Fractional Inverse Matrix Projective Combination Synchronization with Application in Secure Communication. In Proceedings of the International Conference on Artificial Intelligence and Applications; Springer: Singapore, 2021; pp. 93–101. [Google Scholar]
- Mahmoud, E.E.; Jahanzaib, L.S.; Trikha, P.; Alkinani, M.H. Anti-synchronized quad-compound combination among parallel systems of fractional chaotic system with application. Alex. Eng. J. 2020, 59, 4183–4200. [Google Scholar] [CrossRef]
- Sun, J.; Li, N.; Fang, J. Combination-combination projective synchronization of multiple chaotic systems using sliding mode control. Adv. Math. Phys. 2018, 2018, 2031942. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Shen, Y.; Yin, Q.; Xu, C. Compound synchronization of four memristor chaotic oscillator systems and secure communication. Chaos: Interdiscip. J. Nonlinear Sci. 2013, 23, 140. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Cui, G.; Shen, Y. Compound-combination synchronization of five chaotic systems via nonlinear control. Int. J. Light Electron. Opt. 2016, 127, 4136–4143. [Google Scholar] [CrossRef]
- Khan, A.; Lone, S.J.; Trikha, P. Analysis of a Novel 3-D Fractional Order Chaotic System. In Proceedings of the ICPECA, New Delhi, India, 16–17 November 2019. [Google Scholar]
- Geist, K.; Parlitz, U.; Lauterborn, W. Comparison of different methods for computing lyapunov exponents. Prog. Theor. Phys. 1990, 83, 875–893. [Google Scholar] [CrossRef]
- Tavassoli, M.H.; Tavassoli, A.; Rahimi, M.R.O. The geometric and physical interpretation of fractional-order derivatives of polynomial functions. Differ. Geom. Dyn. Syst. 2013, 15, 93–104. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Computational Engineering in Systems Applications; IMACS; IEEE-SMC: Lille, France, 1996; Volume 2, pp. 963–968. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002; Volume 42. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jahanzaib, L.S.; Trikha, P.; Matoog, R.T.; Muhammad, S.; Al-Ghamdi, A.; Higazy, M. Dual Penta-Compound Combination Anti-Synchronization with Analysis and Application to a Novel Fractional Chaotic System. Fractal Fract. 2021, 5, 264. https://doi.org/10.3390/fractalfract5040264
Jahanzaib LS, Trikha P, Matoog RT, Muhammad S, Al-Ghamdi A, Higazy M. Dual Penta-Compound Combination Anti-Synchronization with Analysis and Application to a Novel Fractional Chaotic System. Fractal and Fractional. 2021; 5(4):264. https://doi.org/10.3390/fractalfract5040264
Chicago/Turabian StyleJahanzaib, Lone Seth, Pushali Trikha, Rajaa T. Matoog, Shabbir Muhammad, Ahmed Al-Ghamdi, and Mahmoud Higazy. 2021. "Dual Penta-Compound Combination Anti-Synchronization with Analysis and Application to a Novel Fractional Chaotic System" Fractal and Fractional 5, no. 4: 264. https://doi.org/10.3390/fractalfract5040264
APA StyleJahanzaib, L. S., Trikha, P., Matoog, R. T., Muhammad, S., Al-Ghamdi, A., & Higazy, M. (2021). Dual Penta-Compound Combination Anti-Synchronization with Analysis and Application to a Novel Fractional Chaotic System. Fractal and Fractional, 5(4), 264. https://doi.org/10.3390/fractalfract5040264






