Abstract
Cement-based materials, including cement and concrete, are the most widely used construction materials in the world. In recent years, the investigation and application of fractal theory in cement-based materials have attracted a large amount of attention worldwide. The microstructures of cement-based materials, such as the pore structures, the mesostructures, such as air voids, and the morphological features of powders, as well as the fracture surfaces and cracks, commonly present extremely complex and irregular characteristics that are difficult to describe in terms of geometry but that can be studied by fractal theory. This paper summarizes the latest progress in the investigation and application of fractal theory in cement-based materials. Firstly, this paper summarizes the principles and classification of the seven fractal dimensions commonly used in cement-based materials. These fractal dimensions have different physical meanings since they are obtained from various testing techniques and fractal models. Then, the testing techniques and fractal models for testing and calculating these fractal dimensions are introduced and analyzed individually, such as the mercury intrusion porosimeter (MIP), nitrogen adsorption/desorption (NAD), and Zhang’s model, Neimark’s model, etc. Finally, the applications of these fractal dimensions in investigating the macroproperties of cement-based materials are summarized and discussed. These properties mainly include the mechanical properties, volumetric stability, durability (e.g., permeability, frost and corrosion resistance), fracture mechanics, as well as the evaluation of the pozzolanic reactivity of the mineral materials and the dispersion state of the powders.
1. Introduction
As the most widely used construction materials, cement-based materials, including cement paste, mortar, and concrete, play an indispensable role in the construction of infrastructure and building engineering, such as houses, bridges, tunnels, ports, dams, roadways, etc. [1,2,3,4,5,6,7] Cement-based materials always show highly heterogeneous compositions and complex spatial distributions, from the nano- to the macroscales [8,9,10]. The development of advanced and effective testing techniques during the last decades has demonstrated that the macrolevel properties of cement-based materials, e.g., the mechanical properties, volumetric stability, permeability, and durability, are intrinsically related to their material structure at the micro- and mesoscales [11,12,13,14,15,16,17,18], and resolving their structure–property relationships is essential to the novel design and usage of cement-based materials in practice [9,19,20,21,22,23].
Fractal geometry is a new branch of mathematics, proposed and fundamentally established by French mathematician, Mandelbrot, in 1977, focusing on the irregularities, as well as the haphazard phenomena and behaviors, in nature [24,25]. Since then, fractal theory has been rapidly applied in many research fields, such as civil engineering, materials science, information science, and computer science [26,27]. In 1985, by using the X-ray scattering technique, Winslow [28] first proposed that the internal pore structure of cement paste was essentially fractal and proved that the fractal theory can quantitatively characterize the complexity and self-similarity of the pore network in cement paste. More recently, fractal theory has been used more and more for investigating the multiscale structures of porous materials, including cement-based materials [29]. The microstructures of cement-based materials, including the pore structures and mesostructures, such as the air voids as well as the morphological features of powders and the fracture surfaces, commonly present extremely complex and irregular features, which are difficult to describe in terms of geometry but that can be studied by fractal theory [12,14,30,31]. The fractal dimension, which is determined by various testing techniques and various fractal models, is one of the core contents of fractal theory and can be used to characterize the complexity and irregularity of the microstructures and mesostructures of cement-based materials effectively and quantitatively [4,9,12,31,32,33,34,35,36]. Moreover, many researchers [33,37] have demonstrated that fractal theory links the structures at the micro- and mesoscales with the macroperformance of cement-based materials well, and vice versa. The fractal dimensions of cement-based materials have proven again and again to be closely related to the macroperformance, such as the mechanical strength, permeability, frost resistance, etc. [14,15,30,38]. Since the fractal theory provides a brand-new and effective method for characterizing the microstructures and mesostructures of cement-based materials, as well as the correlations with the macroproperties, fractal theory is of great importance in the study of cement-based materials.
This paper presents a comprehensive review of the application of fractal theory in the research field of cement-based materials in recent years. Herein, the review includes the following parts: (1) A summary of the principles and classification of the commonly used fractal dimensions applied in the research field of cement-based materials; (2) A summary and analysis of the testing techniques and fractal models determining and calculating these fractal dimensions; (3) An introduction and discussion on the application of fractal theory for studying the macroproperties of cement-based materials, including the mechanical properties, volumetric stability, durability (e.g., permeability, frost and corrosion resistance), the fracture mechanism and fracture mechanics, the flexural performance and fracture energy, as well as the pozzolanic reactivity of the mineral materials and the dispersion state of the powders. It is expected that the present review work may help to inspire new ideas and provide a basic guide for researchers who want to study cement-based materials in terms of fractal theory. The aim of this work is also to promote a deeper and more comprehensive investigation and application of fractal theory in cement-based material research.
2. Fractal Dimensions
Many kinds of fractal dimensions have been developed and applied in the research field of cement-based materials, including the fractal dimensions of the pore surface, pore volume, tortuosity, air void, fracture surface, cracks, as well as the particle size distribution, etc. [9,31,32,35,36]. These fractal dimensions have quite different physical meanings since they are obtained from various testing techniques and fractal models, which can be applied to study different material properties. Some commonly used fractal dimensions in cement-based materials are summarized in Table 1. This Section describes the definition and principle of each fractal dimension listed in Table 1.

Table 1.
Some commonly used fractal dimensions in cement-based materials.
2.1. Fractal Dimension of Pore Structure
The pores in cement-based materials are extremely complex and irregular. On the basis of the classification method proposed by Mindess et al. [76], pores from 2.5 to 10 nm, from 10 to 50 nm, and from 50 nm to 10 μm are defined as small capillary (or gel) pores, medium capillary pores, and large capillary pores, respectively. Most of the macroproperties of cement-based materials, such as the mechanical properties, volume stability, frost resistance, and permeability are related to the pore structure [11,12,13,14,15,77,78]. The existing pore structure parameters mainly include the porosity, pore size distribution, pore surface area, pore volume, pore tortuosity, etc., which cannot quantitatively characterize the complexity and inhomogeneity of the pore structures [49,79]. The fractal theory can therefore be adopted to characterize the pore structures. Three main fractal dimensions of the pore structure have been proposed and developed, namely, the fractal dimension of the pore surface (Ds), the fractal dimension of the pore volume (Dv), and the fractal dimension of the pore tortuosity (Dt) [50,53,54]. These fractal dimensions can describe the structural characteristics of the pores in different dimensions [15]. It should be noted that cement-based materials also include many interlayer pores at the subnanometer scale, for example, the size of the interlayer space between the C-S-H layers is around 0.1–1 nm [80]. These pores are of great significance for C-S-H, a primary binding phase of cement-based materials [81]. However, so far, there are no fractal studies on these subnanometric pores. This is a subject needing further investigation, which is beyond the scope of this paper.
2.1.1. Fractal Dimension of Pore Surface (Ds)
Neimark was the first researcher to express the fractal dimension through the pore surface and the pore diameter relation [41]. According to Pfeifer and Avnir [42], the fractal dimension of the pore surface (Ds) reflects the roughness and irregularities of the internal pore surface of porous materials. Theoretically, all of the test methods that are able to probe the pore surfaces can be adopted to calculate the Ds by using some proper fractal models. It is generally accepted that all the fractal dimensions of pore surface (Ds) determined by various methods have the same physical meaning; they have a typical range of 2 ≤ Ds < 3. When the Ds of a porous object is equal to 2, it indicates that the measured object has a perfectly smooth plane. The pore structure becomes rougher and more complex when the Ds value approaches 3 [39,43].
2.1.2. Fractal Dimension of Pore Volume (Dv)
Many researchers have used different techniques and developed different fractal models to calculate the Dv. Overall, the Dv is an index used to describe the pore volume distribution or the complexity of the pore structures in porous materials [33,47,48]. Theoretically, all the techniques that can measure the pore volume, such as the mercury intrusion porosimeter (MIP), 1H low-field nuclear magnetic resonance (1H LF NMR), small-angle neutron scattering (SANS), the small-angle scattering of X-rays (SAXS), low-temperature differential scanning calorimetry (LT-DSC), etc., can be used to determine the Dv by adopting certain fractal models.
However, contrary to the Ds, there is no precise definition for the Dv so far. It can be found from the extensive literature with regard to this that the Dv values determined by different testing techniques and fractal models with different fundamentals are quite different. For example, according to the studies of Li et al. [48], and Zarnaghi et al. [33], the Dv of cement-based materials calculated by the MIP results and the Menger sponge model has a typical range of 2.0~3.0. They concluded that the rougher and more complex the pore structure in cement-based materials, or the broader the pore size distribution, the higher the Dv value will be. On the basis of the MIP results and the space-filling model, it is predicted that the Dv of hardened cement pastes is between 0 and 3 [47]. While, in the study by Tang et al., the Dv values of the cement pastes obtained by the LT-DSC technique are between 1 and 5 [30].
The test methods and fractal models determining the Dv, as well as their basic principles, will be revealed in Section 3.1.2.
2.1.3. Fractal Dimension of Pore Tortuosity (Dt)
Many studies have pointed out that the permeability of cement-based materials is significantly determined by the tortuosity of the pores [77]. The tortuosity of the pore structure (τ) can be calculated by Equation (1) [14,54]:
where Lt(λ) is the actual tortuous length along the flow direction; L0 is the straight length along the gradient; and λ is the diameter of a capillary tube in the object.
The fractal dimension of pore tortuosity (Dt) is an index used to describe the extent of the tortuosity of a porous object. According to Yu et al. [50], a porous object with various internal pore sizes can be considered a bundle of tortuous capillary tubes with variable cross-sectional areas. On the basis of the fractal scaling/tortuosity relationship, first revealed by Wheatcraft and Tyler [53], Yu et al. [50] propose that the relationship between the tube diameter and the length of the capillary tubes exhibits a fractal scaling law, which is shown in Equation (2):
where Dt is the fractal dimension of the pore tortuosity, which refers to the extent of the convolutedness of the capillary pathways for fluid flow through an object. It has a range of , and a Dt value of 1 implies a straight capillary path when Lt is equal to , while a larger Dt value implies a more tortuous capillary. A Dt value of 2 represents a highly tortuous line that fills a plane; λ is the diameter of a capillary tube in the object; Lt(λ) is the actual tortuous length along the flow direction; and is the straight length along the gradient. For a straight capillary, is equal to , while, for a porous object with many inner tortuous capillary tubes, is much larger than .
2.2. Fractal Dimension of Air Void (Da)
Cement-based materials in cold regions usually suffer from serious frost damage due to the frequent freeze–thaw cycles. It is well-known that a proper air-void system is needed in normal concrete to prevent frost damage during freeze–thaw cycles, since many closed, small, and evenly distributed air voids in concrete can ease the volumetric expansion and cut off potential water channels to improve the frost resistance of concrete [49,82,83]. According to the classification proposed by Mindess et al. [76], pores in cement-based materials sized over 10 μm are defined as air voids. The air-void parameters, such as the air content (A), the total number of air voids (N), the average air-void diameter (D), and the spacing factor (), etc., are known to significantly affect the frost resistance of concrete [15,49,83]. In addition, it is reported that the pore size distribution of air voids in concrete also plays an important role in determining the frost resistance of concrete [15].
Currently, it is difficult to characterize the air-void distribution through traditional approaches owing to the complexity of air voids in concrete. The fractal dimension of an air void (Da), which was first proposed and deduced by Hu [84], who used a fractal model based on air-void data, is a parameter reflecting the size distribution of the air voids. In order to better assess frost resistance in terms of the air voids in concrete, an improved and more reliable fractal model was proposed by Jin et al. [15] to determine the fractal dimension of the air void (Da), which will be described specifically in Section 3.2.
2.3. Fractal Dimension of Fracture Surface (Dfs)
Cement-based materials are quasi-brittle, and the nature of their fracture surfaces continues to be the subject of intensive research [58,63]. The fracture surfaces are caused not only by the fracture process itself, but also by the inner material texture and the microstructure rearrangement [63]. The main objectives of the studies on the fracture surfaces were to reveal the micromechanism of the fractures, and to evaluate the fracture mechanical properties of cement-based materials [61]. In the last two decades, many attempts have been made to establish the relationship between the fracture surface texture and the mechanical behavior of cement-based materials [62,85]. Moreover, the quantitative description of rough surfaces and interfaces has been an important task and challenge for many years [86].
Fractal analysis is a simple and powerful tool for quantifying the roughness and irregularities of fractured surfaces [86] since rough surfaces can be described quite well in terms of fractal geometry [24,25]. The fractal dimension of fracture surfaces (Dfs) was proposed by Mandelbrot et al. [87], who tried to link this fractal dimension with the fracture toughness of metal materials. According to Pfeifer and Avnir [42], the Dfs reflects the intrinsic surface irregularities: The higher the Dfs, the more irregular the fracture surfaces. Nowadays, more and more attention has been paid to the relationship between the Dfs and the fracture mechanics parameters, which will be introduced in detail in Section 3.3.
2.4. Fractal Dimension of Crack (Dc)
The cracks occurring in the volume and on the surface are considered to be the most common types of damage of cement-based materials, which can weaken the material structure [69]. The deterioration of the material properties of cement-based materials caused by cracks includes a reduction in the mechanical property, reduced watertightness, weakened impermeability to ion ingress, etc. [67]. Therefore, the study of cracks and cracking patterns is one of the key areas in the research field of cement-based materials.
The formation and evolution process of cracks are too complex to be accurately and quantitatively described by traditional mechanical analysis methods [68]. The concept of fractal dimension is typically used in fractal theory to quantify the effectiveness of space occupied by fractal shapes and paths [88]. The larger the fractal dimension, the more complex the fractal shape. In recent years, fractal geometry has been widely used to describe some irregular phenomena in the fracture behavior of materials [71]. Some typical applications of fractal theory are to quantitatively describe the development and evolution process of cracks in cement-based materials, and to establish a relationship between the cracks and their fractal characteristics [68].
According to the fractal theory, the cracking patterns, crack distribution, and crack morphology on the surface of cement-based materials exhibit fractal characteristics [65,67,69]. Thus, it is possible to characterize the cracking degree [67], the geometric complexity of the cracking pattern [26,67,70], the crack distribution [65,68,69] as well as the crack morphology [70] by the fractal theory. In recent years, using the fractal dimension of cracks (Dc) to describe the cracks of cement-based materials, and to probe the relationship between the fractal dimension of cracks and the material properties, have become research hot spots [68].
2.5. Fractal Dimension of Particle Distribution (Dp)
Cement-based materials, such as cement and fly ash, are powder materials. The properties of powder materials are closely related to the composition and structure of the powders. The particle size distribution of the powders and their fineness are the most important physical properties of powder materials, which often determine the physical and chemical properties of the cement-based materials [89].
It has been shown [73,90,91,92] that the particle size distribution and fineness of ordinary silicate cement particles, as well as the mineral admixtures, such as fly ash, can be described by fractal geometry. The fractal dimension of the particle size distribution (Dp) reflects the particle size distribution (gradation) and the fineness of the powder particles, which is a more intuitive parameter for describing the gradation and fineness of powders than traditional parameters [89,93]. Fractal dimensions of this kind can be used to evaluate the particle size distribution (gradation) and the fineness of powders [73,90]. Moreover, many studies have tried to correlate the Dp of mineral material, such as fly ash and silica fume, with their pozzolanic reactivities [93,94].
In addition, fresh cement paste is generally considered to be a suspension system, which is typically featured by typical particle agglomeration and dispersion. These parameters can be reflected by the fractal dimension of the particle spatial distribution (Dp) [74,75]. The Dp can be used to evaluate the dispersion state of cement particles affected by the inclusion of superplasticizers [74,75].
3. Investigation of the Test Methods and Fractal Models of Cement-Based Materials
3.1. Fractal Dimension of Pore Structure
It is important to determine the pore parameters accurately, which is fundamental to the establishment of fractal models. At present, the pore characteristics can be tested by MIP, NMR, SANS, LT-DSC, nitrogen adsorption/desorption isotherm (NAD), scanning electron microscopy (SEM), the noncontact impedance measurement (NCIM), etc. Notably, each of the existing techniques above can only probe pores with a certain scale, which will be discussed later.
In this section, the testing methods and fractal models calculating the main fractal dimensions of the pore structure, namely, the Ds, Dv, and Dt have been described individually.
3.1.1. Fractal Dimension of Pore Surface (Ds)
Ds by MIP, Zhang’s Model, and Neimark’s Model
The MIP is one of the most commonly used pore-testing techniques for analyzing the pore structures of cement-based materials because a MIP can detect a relatively wide pore size, ranging from about ~+2 nm to 100 μm [41]. It should be noted that the accuracy of MIP results is usually compromised by the “ink bottle” effect. This intrinsic drawback sometimes mistakes the large ink-bottle-shaped pores for small pores, thus mistakenly increasing the proportion of small pores [32,47]. Moreover, excessive mercury intrusion pressure may damage the pore structure of materials, especially loose cement-based materials [48]. However, the MIP is the only method available that can evaluate almost all the pore sizes in cement-based materials and, therefore, it has been widely used worldwide [33,47,52,95]. The principle of the MIP method is that cement-based materials cannot be wetted by liquid mercury and, therefore, the pore diameter of concrete can be measured by changing the pressure applied to the liquid mercury [3,96]. During MIP tests, mercury enters the large pores first, and then continuously occupies the small pores by increasing the mercury injection pressure [96]. The pore size can be calculated using the famous Washburn equation [97]. This equation, as shown in Equation (3), which assumes the pores have a cylindrical shape, transforms the pressure, P, of the mercury filling the pore with a radius of r.
where r is the pore radius, m; P is the mercury injection pressure, Pa; is the surface tension of the mercury, which is 0.485 N/m; and is the contact angle between the mercury and the pore surface, in the cases of cement-based materials where θ is equal to 130°.
Additionally, fractal models based on MIP results mainly include the thermodynamic fractal model (e.g., Zhang’s model [39,40] and Neimark’s model [41]), as well as other types of model, such as the space-filling model [47], and the Menger sponge model [42,48]. The principle of the thermodynamic fractal models is that the increase in the mercury surface energy is equal to the work done by the external force to the mercury during the MIP test [98]. Therefore, thermodynamic fractal models are commonly used to calculate the fractal dimension of the pore surface (Ds). The latter two fractal models are usually used to calculate the fractal dimension of the pore volume (Dv), which will be described in later subsections.
According to Neimark’s [41] model, there exists an energy equilibrium between the nonwetting internal surface extension and the external work of the mercury penetrating during the MIP test. Therefore, the internal pore surface (S) can be estimated by Equation (4), based on the MIP results [41]:
According to Pfeifer and Avnir [42], the internal pore surface can exhibit fractal property only if Equation (5) is satisfied:
where stands for the pore radius; and Ds refers to the fractal dimension of pore surface.
Putting Equations (3) and (5) together into Equation (4) produces a logarithmic relationship between the pore internal surface and the intrusion pressure, as exhibited in Equation (6):
Zhang et al. [39,40] provide another different thermodynamic fractal model for calculating the Ds. From Zhang’s fractal model [39,40], there exists a thermodynamic relationship that is, during the MIP test, the accumulated injection work () on the mercury and the total volume mercury intruded into the pores () following a logarithmic law, as presented in Equation (7):
where is the pore radius at the n-th mercury injection; Ds is the fractal dimension of the pore surface; C is a regression constant; n refers to the n-th mercury injection during the MIP test, which is the number between 1 and the total number of mercury injections.
can be determined by Equation (8):
where i refers to the i-th mercury injection, which is the number between 1 and n; is the pressure at the i-th mercury injection; Pa; is the volume of the mercury injected at the i-th mercury injection, m3; and n is the number of mercury injections during the MIP test.
The values of , , , and can be calculated on the basis of the MIP test results and Equation (8). After obtaining these values, the fitting line in Equation (7) can be plotted, and the slope of this line is the target Ds. The correlation coefficient (R2) of the fitting line was also recorded to evaluate the accuracy of the Ds. The closer the R2 value approaches to 1, the better the correlations between and , and a more accurate Ds is calculated.
Moreover, some studies proved Zhang’s model to be more realistic than Neimark’s model in terms of geometry [13,31].
Ds by NAD and FHH Isotherm Equation
NAD is also widely used to evaluate the fractal characteristics of cement-based materials, since NAD is able to provide a great deal of information about the pore surface area and the pore size [30,96]. Unlike the MIP, the NAD method only covers a pore size range between 1 nm and 100 nm [30,32,95,96].
The fundamental of NAD is that the internal surface of pores can adsorb a certain quantity of gas (nitrogen) molecules, and the volume of the gas (nitrogen) in the pores is assumed to be the actual volume of the pores in cement-based materials [96]. During the test, NAD records the nitrogen gas pressure and the adsorbed nitrogen quantity and provides an adsorption isotherm at the same time. When the gas pressure is relatively low, the surface adsorption dominates. With the increase in the gas pressure, nitrogen condensation happens in small pores [95,96]. The relationship between the relative pressure, , and pore size, d, can be expressed by Equation (9), which was deduced from the Kelvin equation [95,99]:
where is the surface tension of the liquid nitrogen (8.85 × 10−3 N/m); V is the molar volume of the liquid nitrogen (3.467 × 10−5 m3/mol); R is the gas constant (8.314 J/K/mol); T is the temperature of the liquid nitrogen (77.3 K); P and P0 are the experimental and saturation pressures of the nitrogen, respectively.
As for the fractal models based on the NAD method, several isotherm equations have been derived for various models of the physical adsorption on fractal surfaces, such as the Frenkel–Halsey–Hill (FHH) equation [43,45] and Neimark’s thermodynamic method [44]. These equations contain the fractal dimension, Ds, as a dominate parameter and describe the surface coverage as a function of the equilibrium pressure [43].
The FHH equation can be expressed as a logarithmic formula, as seen in Equation (10) [32,43,45]:
where V is the amount of nitrogen adsorbed at the relative pressure,; C is a constant, which is the intercept of the straight line shown in Equation (10); is the slope of the same straight line; and is the relative pressure during the NAD test.
Pfeifer et al. [46] and Jaroniec [43] further studied the FHH exponent and its relation with the Ds. They found that, at the beginning of the NAD test, when the relative pressure is low, van der Waals attraction forces are dominating (that is, the liquid/gas surface tension forces are negligible), and then the slope can be estimated by Equation (11). In this case, the van der Waals forces at the gas/solid interface tended to form the adsorbed film, which replicated the surface roughness [43]:
However, with the increase in the relative pressure, the absorbent surface is completely formed, and then the interface is controlled by the liquid/gas surface tension (capillary condensation), due to the greater thickness of the surface film. In this case, the slope,, can be estimated by Equation (12) [43]:
By using the FHH equation and the NAD method, Tang and Li [100] found that the surfaces of cement-based materials exhibited obvious fractal characteristics, and the Ds was in a range between 2.369 and 2.580. Moreover, the addition of mineral admixtures, such as silica fume and slag, could reduce the Ds values.
Ds by NAD and Neimark’s Thermodynamic Method
In addition to the (FHH) equation, Neimark and Unger [44] proposed a thermodynamic method for calculating the Ds based on the NAD results. It should be noted that Neimark’s thermodynamic method is only valid for capillary condensation on a fractal surface. The theoretical basis for this method is a simple relationship between the surface area of the adsorbed liquid film (S) and the average pore radius (r), as shown in Equation (13). The slope of this plot is related to the Ds:
where Ds is the fractal dimension of the pore surface; A is a constant and is the intercept of the line, versus ; r is the average radius of the curvature of this interface, which is the half of the pore size, d, calculated from Equation (9); S is the surface area of the liquid-gas interface at a given value of relative pressure, , which can be calculated on the basis of the NAD test results and the Kiselev equation, as shown in Equation (14) [44]:
where Nmax is the maximum adsorption volume; N is the equilibrium adsorption volume; is the surface tension of the liquid nitrogen (8.85 × 10−3 N/m); R is the gas constant (8.314 J/K/mol); T is the temperature of the liquid nitrogen (77.3 K); P and P0 are the experimental and saturation pressures of the nitrogen, respectively.
Putting Equations (9) and (14) into Equation (13) produces the Ds value.
3.1.2. Fractal Dimension of Pore Volume (Dv)
Dv by the MIP, the Space-Filling Model, and the Menger Sponge Model
It has been reported that the Dv can be calculated on the basis of the MIP results by using the Menger sponge model [33,42,48] and the space-filling model [47], respectively.
In 1983, Pfeifer and Avnir [42] first used the Menger sponge model to build the porous body. They proposed that the Dv can be calculated by using the logarithmic relationship between the intrusion volume, V, and the radius, r, obtained via the MIP tests. Recently, Li et al. [48] and Zarnaghi et al. [33] have specifically described how to use the Menger sponge fractal model to simulate the pore structure of cement-based materials and calculate the Dv values. The typical steps for constructing the Menger sponge model include: (1) Taking an initial cube, with a side length, R, and dividing it equally into m3-small cubes, with side lengths, R/m; (2) Taking out n cubes randomly and the number of remaining small cubes is ; (3) After executing Steps (1) and (2) for k times, then the side length and the amount of the remaining small cubes are and , respectively. According to the principle of fractal geometry, the Dv can be calculated by Equation (15):
As for the space-filling model, Ji et al. [47] constructed a space-filling model for simulating the space-filling process of cement hydration products in cement paste in 1997. The construction process and the theory of this space-fractal model are as follows: Imagine that there is a cube of a unit volume. At first, divide the cube into m3 equal small cubes, with a side length of l/m. The hydration of cement produces many hydration products that can fill in n small cubes (n < m3), resulting in (m3 − n) blank small cubes (pores). This process is called the "generator" of the fractal space-filling process of the solid phases of cement paste. Then, divide every one of the remaining blank (m3 − n) small cubes into m3 smaller cubes, each with a side length of l/m2. With the prolongation of the hydration age, the n smaller subcubes in each of the remaining blank (m3 − n) small cubes are filled with hydration products. By conducting such division and filling processes iteratively, the space-fractal model is established for simulating the space-filling process of cement hydration products in cement paste, due to the continuous cement hydration. According to this model, no matter how completely the cement grains hydrate, there remains some blank space (pores) that cannot be occupied completely by the hydration products. The Dv in the space-filling model can be calculated by Equation (16):
A careful comparison between the Menger sponge model and the space-filling model above demonstrates that their fundamental basis and model construction steps, and even the calculation equations, are almost the same, indicating that these two models are the same, but with different designations. Nevertheless, by using the MIP results and these models, there exists different subsequent equations for calculating the final Dv.
The typical method for calculating the Dv on the basis of MIP data and the Menger sponge model is introduced as follows: Commonly, the cumulative pore volume, V, can be calculated by accumulating the incremental pore volume in the order of greatest pore diameter to smallest pore diameter [49]. Ji et al. [47] propose a new cumulative pore volume, V*, which is defined by accumulating the incremental pore volume in the reversed order, that is, from smallest pore to greatest pore. The number of pores, dM, in the pore radius range from ρ toρ + dρ, calculated by Equation (17):
The total number of air molecules, Na, that the whole network of pores can accept is Equation (18):
where c is a constant, and r is the radius of the air molecules used as a yardstick. Only the pores with the radii, , can accept the air molecules of the radius, . The total number of air molecules, Na, that can be accepted by the pore with the radius, , is determined by Equation (19):
where ρmax is the maximum pore radius in the hardened cement paste that can be measured by the MIP technique.
Combining Equation (18) and Equation (19) yields Equation (20):
Differentiating Equation (20) with respect to r leads to Equation (21):
Assuming that the minimum pore radius in hardened cement paste is 0, then integrate in Equation (21) with respect to from 0 to , giving Equation (22):
By taking the logarithm of Equation (22), Equation (23) can be obtained:
where ; and d is the diameter of the pore, .
If the slope of the straight line of Equation (23) in the double logarithmic coordinate system is k, then:
On the basis of the MIP results and Equation (24), the Dv can be computed.
Moreover, it is interesting to note that there is another method for calculating the Dv on the basis of MIP data and the Menger sponge model, proposed by Li et al. [48]. They pointed out that the structural volume is shown in Equation (25):
When , , , and the pore volume is , then the following Equation (26) can be obtained:
Obviously, the value of the Dv depends on the pore volume, as determined by the MIP. During the MIP tests, the r of the pore is directly related to the intrusion mercury pressure, P, as shown in Equation (3). Let l equal r, putting Equation (26) into Equation (3), and then Equation (27) can be deduced as:
Subsequently, the Dv can be determined by 4 plus the slope of the straight line, versus in Equation (27). In the research, the Dv of cement pastes is in the range between 2.0 and 3.0, and it increases with an increasing curing temperature. Under the impact of the high temperature, the spatial structure of the pores tends to be more complex, thus leading to larger Dv values [48].
Dv by LT-DSC and the Menger Sponge Model
Yu and Cheng [50] indicate that, in a unit cell, the cumulative number, N, of pores with size λ greater than a particular r follows the fractal scaling law, as shown in Equation (28):
Liang et al. [51] further propose that the total number of pores from the minimum radius, rmin, to the maximum radius, rmax, can be defined as Equation (29):
On the basis of the equations above, Tang et al. [30] used a modified equation to calculate the Dv on the basis of the sponge model and the LT-DSC results, which is shown in Equation (30):
where is the pore volume fractal dimension; refers to the total number of volumes larger than ; and are the maximum pore volume and the minimum pore volume, respectively, which are the upper limits and the lower limits of what the LT-DSC techniques can probe.
The LT-DSC technique is a reliable technique for evaluating the porosity and pore volume in cement-based materials at a low scale by quantifying the water enclosed in the small pores [101]. According to [30], the data of the LT-DSC tests are selected on the basis of several criterions: (1) Continuous dataset segments are selected; (2) Temperature is less than 273.15 K; (3) A heat flow <0 for the melting process, and a heat flow >0 for the freezing process; and (4) A pore size in the range of 2–200 nm. Moreover, when the nonfreezable water layer on the pore surface is considered, the modified Gibbs–Thompson equation, associated with the test temperature (Tm) and the pore radius (r), is used, as shown in Equation (31):
where r has the unit of the nanometer;
is 273.15 K; and δ is an empirical parameter, which is 1.2 nm for cement-based materials. With respect to the LT-DSC test, the maximal pore volume, Vmax, is derived by summing up all of the incremental pore volumes (dV), as shown in Equation (32) [52]:
where dt is the time difference of the two adjacent temperatures, Tm1 and Tm2; P1 and P2 are the heat powers at the two temperatures; m is the mass of the investigated cementitious material; ∆Hm1(Tm1) and ∆Hm1(Tm2) are the change in the molar heat of the ice–water transition; ρ(Tm1) and ρ(Tm2) are the densities of the water as a function temperature. The derivations of ∆Hm1(Tm1)), ∆Hm1(Tm2), ρ(Tm1), and ρ(Tm2) can be seen in [52].
Finally, the Dv can be determined by putting Equation (33) into Equation (30) [30] and using the LT-DSC results together.
As described above, it has been found that the Vmax values are difficult to accurately test. In fact, it is not necessary to determine the detailed Vmax values in some studies. For example, Zeng et al. [4] modified Equation (28) as Equation (33) and stated that one can alternatively estimate the Dv by gathering the slope of the lg(N)–λ plot, i.e., Dv∝−lg(N(λ))/lg(λ).
In the work of Zeng et al. [4], the values of lg(N) and λ were calculated by the box-counting method and the SEM images. Then, the lg(N)–lg(λ) relationship can be plotted and the Dv can be estimated, which was close to 1.448.
Dv by 1H Low-Field NMR
The technique, 1H LF NMR, was first used by Halperin et al. [102] to probe the pore structures of cement paste. Since then, it has been widely used, especially in recent years, to effectively monitor the early hydration processes and characterize the microstructures of cement-based materials [103]. Fundamental to the technique is that 1H LF NMR is able to measure the relaxation behavior of the hydrogen protons in water molecules. By collecting the relaxation time and the relaxation signal intensity under nondestructive conditions, 1H LF NMR is able to detect the cement hydration, hydration kinetics, pore size distribution, etc. [104] The primary advantage of the 1H LF NMR technique is that it is a nondestructive method that can probe both the open and closed pores. Moreover, it can be performed at room temperature. Nevertheless, it should be noted that the iron phase, which is common in cementitious material, could greatly affect the precision of the NMR results [32,105,106,107].
The basis of 1H LF NMR, according to Pop et al. [108], is that the transverse relaxation time (T2) correlates with S/V, which is related to the size of the pores. Accordingly, the transverse relaxation time (T2) can be defined by the following Equation (34) [104,108]:
where is the relaxation time of the surface; is the ratio of the pore surface area to the pore volume; is a constant related to the thickness of the surface hydrate water; and r is the pore radius.
Since T2 is proportional to the pore size when the pores are assumed to be spherical and evenly distributed in cement-based materials, a logarithmic formula [32], as shown in Equation (35), has been developed to reveal the relationship between the accumulated volume fraction () and each pore category (T2,i), which is less than T2,max during the 1H LF NMR test.
Finally, the Dv can be calculated according to Equation (35) and the 1H LF NMR test results.
Dv by SANS or SAXS and a Simple Logarithmic Equation
The fractal characteristics of the pores in cement paste can be assessed by using SAXS or SANS since both the SAXS and SANS techniques are powerful tools for investigating the pores, sized from several nm to tens of nm, or even 100–150 nm, in cement-based materials [13,32].
During the SAXS and SANS experiments, an incident wave of X-rays, or neutrons with a wavelength of λ, will be scattered and/or absorbed by the material. The geometric angle (2θ) of the scattering between the incident wave and the scattered beams is transformed into a scattering vector, of magnitude (Q), as shown in Equation (36):
where λ is the neutron or X-ray wavelength. In general, the scattering from the fine microstructure system leads to the large values of the scattering angles or Q, and vice versa. More detailed descriptions of the SAXS and SANS techniques and their testing procedures can be found in [80].
It is noted that the scattering cross-section is a material property. The Dv of cement-based materials can be obtained from the slope of the log–log plotting of the scattering cross-section versus Q [32].
3.1.3. Fractal Dimension of Pore Tortuosity (Dt)
Dt by Image Analysis and the Box-Counting Method
Yu et al. [50] assumed that there is a similarity in the tortuosity of flow pathways among clusters, or particles within clusters. As described in Section 2.1.3, the tortuosity of flow paths between clusters is very similar to the streamtubes, which exhibit a fractal scaling law [53]. Yu et al. [50] propose that the Dt can be determined by the box-counting method. This method is based on the image analysis of a unit cell, or a sufficiently large cross-section of a sample along a plane normal to the flow direction. The image analysis for the box-counting method can be conducted by optical microscope [50], SEM [9], or the BSE technique [4].
In a study by Yu et al. [50], the calculation of the Dt by image analysis and the box-counting method was described as follows: In their optical microscope images of the polished porous sample, with a porosity of 0.52, the black and white regions are the pores and the clusters formed by the agglomeration of copper particles, respectively. The software, Photoshop 5.0 and Visual C++5.0, were used to record the cumulative number and pore sizes, r, of the macropores. Then, the cross-section of the sample is discretized using square boxes with a size of λ, and the number of boxes, (λ), required to completely cover the tortuous pathways is recorded. Subsequently, the logarithmic plots of the cumulative number of macropores, N(λ ≥ r), versus the pore size, r, are drawn. Finally, the Dt can be determined, which is the slope of a linear line, (λ), versus λ. Figure 1 gives a typical calculation of the Dt based on the box-counting method in the study of Yu et al. [50]. Figure 1a–e present five random flow pathways between the clusters in the porous sample. On the basis of the calculation, the (λ) versus λ line can be drawn in Figure 1f, in which the slope (Dt) can be determined as 1.12. Similarly, the values of the Dt of the other four pathways (Figure 1a–d) can be calculated as 1.07, 1.08, 1.09, and 1.13, respectively.
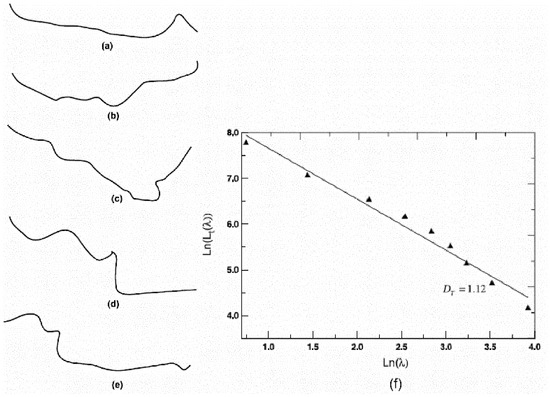
Figure 1.
The typical calculation of the Dt based on the box-counting method: (a–e) five random flow pathways between clusters in the porous sample; and (f) the calculation of the Dt for the e-th path [50].
Dt by the Backscattered Electron (BSE) Imaging Model
Zeng et al. [4] considered that the actual pores were distributed in the cement matrix in complex three-dimensional (3D) patterns, and provided another method for calculating the Dt based on the backscattered electron (BSE) imaging model. According to Zeng et al. [4], a typical element volume (REV) of porous cement-based materials, shown in Figure 2, where the pores for diffusion are tortuous in the z direction and their x−y cross-sectional sizes obey a fractal distribution. If porous cement-based materials are macroscopically isotropic, one can assume that Lx = Ly = Lz in Figure 2. For an individual tortuous pore (or streamtube), the pore tortuosity, τ, can be obtained by combing Equations (1) and (2), as exhibited in Equation (37):
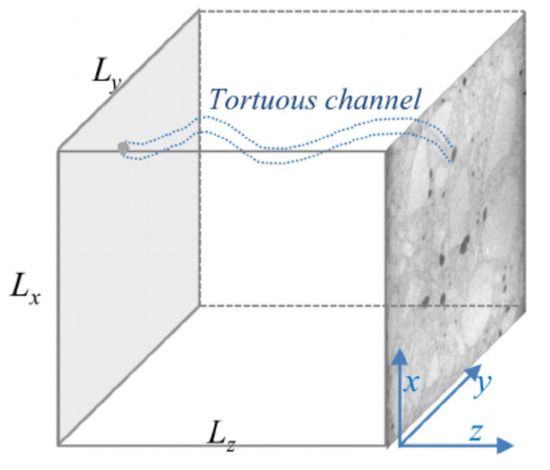
Figure 2.
A representative element volume (REV) of porous cementitious material with tortuous channels or pores for mass diffusion [4].
Here, the tortuosity fractal dimension, Dt, can be calculated from the series of equations (Equations (38)–(40)) below, proposed by Yu et al. [50,54].
where is the average pore tortuosity; and is the average pore diameter (m).
For a material in a granular compactness, the average pore tortuosity may be given by Equation (39) [50]:
The term can be estimated by Equation (40) [109]:
where θ is a pore parameter identical to λmin/λmax; is porosity and can be approximately determined by the BSE. For the fractal structure of the capillary pores in cement paste determined by the BSE, the pixel ratio of λmin/λmax is around 0.01 [4]. It should be noted that Dt may vary in different models since the equations for determining and are different.
Dt by NCIM Method and Two-Phase Fractal Model
The noncontact impedance measurement (NCIM) is a nondestructive method for studying the hydration, pore structure, ion transportation, and permeability of cement pastes [55,56,57]. The principle of the NCIM is shown in Figure 3 [57]. During the NCIM test, the sine wave, with a frequency ranging from 1 kHz to 100 kHz, is applied on the primary coil of the transformer via the signal generator. The ring-shaped cement paste specimen, with a volume of 1.4 L, can be identified as the secondary coil of the transformer in Figure 3. The current going through the specimen is measured and recorded by the leakage current meter continuously. All the impedance data collected within the first three days of hydration is utilized to analyze the pore structure evolution of the cement paste.
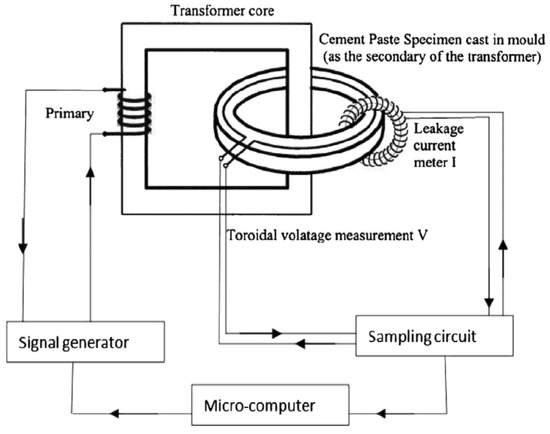
Figure 3.
Illustration of the noncontact impedance measurement (NCIM) [57].
In a study by Tang et al. [56], a novel fractal permeability model based on NCIM results was proposed to compute the Dt. In this model, the Dt is also determined using Equation (37) above, while the and can be calculated using Equations (41)–(43) below:
where is the average pore tortuosity; is the average pore diameter (m); is the porosity and can be determined by the NCIM technique; Df is the fractal dimension of the pore space. Thus far, the Df has been solely reported by Tang et al. [55,56,57] and Yu et al. [50]. The Df is the slope of the logarithmic plot of the cumulative pore number () versus [50]. It should be noted that, since the Df is not a commonly used fractal dimension, with no clear physical meaning and definition, it is not discussed and described in detail in this paper.
For the porous cement paste, the maximal pore diameter () in Equation (42) can be expressed as Equation (43):
where is the mean diameter of the cement particles, which is measured as 15–20 μm. The minimal pore diameter () in Equation (42), determined by the NCIM, is predicted as 6.2 nm [56].
3.2. Fractal Dimension of Air Void (Da) by Air-Void Analyzer and Box-Counting Method
The air-void parameters mainly include the air content (A), the total number of air voids (N), the average air-void diameter (D), and the spacing factor (L). These parameters are usually determined by the air-void analyzer and the linear traverse method [49,82]. The test apparatus, as well as the testing procedure, are schematically illustrated in Figure 4. More detailed information of this test can be seen in ASTM C 457 [110] and the Chinese standard DL/T 5150 [111].
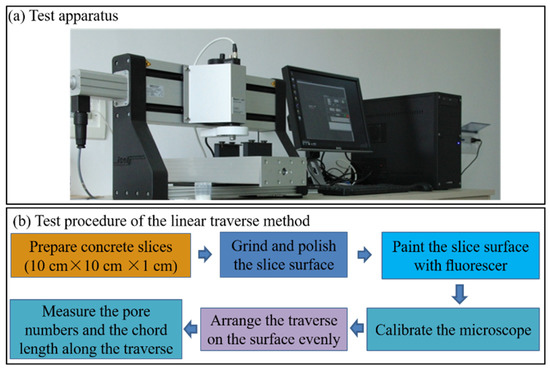
Figure 4.
The air-void test: (a) air-void analyzer; and (b) testing procedure of linear traverse method [82].
Jin et al. [15] report that the fractal dimension of an air void (Da) can be determined by using the air-void analyzer and the box-counting method together. According to this method, the boxes used to cover the air voids in concrete were chosen as circles in the fractal model. The diameter of the air voids, d, was defined as the box-size diameter. Air voids in n groups with different diameters, di (i = 1, 2, ..., n), were used to construct the fractal model. The smallest number of the boxes required to cover all the air voids can be calculated as the equivalent number of air voids, Nei (i = 1, 2, ..., n). On the basis of series sets of the diameters and the equivalent numbers of the air voids, [d1, Ne1], [d2, Ne2]... [dn, Nen], the relationship between di and Nei, as shown in Equation (44), can be revealed by the following linear equation (Equation (44)). The minus of the slope of Equation (44) is defined as Da:
where is the equivalent number of air voids; Da is the fractal dimension of the air-void size distribution; d is the diameter of the air voids; and C is a constant.
Figure 5 gives an example how to use this box-counting method to calculate the Da of concrete. In Figure 5, the logarithmic diagram of d and Ne is plotted. The slope of the line in Figure 5, which is also the Da, is 2.0345 for this concrete specimen.
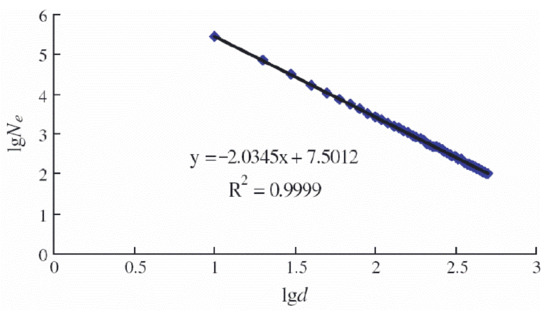
Figure 5.
Fractal analysis based on the fractal model proposed in [15] *. Note *: For different studies that have used the box-counting method, the number of boxes have different designations, such as Nei in this subsection, N in Section 3.1.2.2 and Section 3.3.5, (λ) in Section 3.1.3.1, and in Section 3.4. However, all these designations have the same meaning in terms of the box-counting method.
3.3. Fractal Dimension of Fracture Surface (Dfs)
The accurate measurement of the fracture surfaces is the key to developing fractal models of fracture surfaces, and for calculating the fractal dimension of the fracture surface (Dfs). Many effective techniques and fractal models have been utilized together to characterize the Dfs, including stereoscopic scanning electron microscopy (SEM) combined with Friel’s method [60], 3D laser scanning technology combined with the projective covering method [61], the image analysis technique combined with the 2D fast Fourier transform function [58,59], a laser profilometer combined with the chord method [62], as well as the confocal microscope/SEM technique together with box-counting method [63,85].
3.3.1. Dfs by Stereoscopic SEM and Friel’s Method
A fractal study on the fracture surfaces of cement pastes and mortars using the stereoscopic SEM method was conducted by Wang et al. [60]. The fundamental basis of this method is that if the heights of all points on the fracture surface above a base reference plane can be established, its true surface area can be measured. According to this method, a grid of points is placed on the rough fracture surface, from which the surface is “profiled” by subdividing it into an array of triangular cells tilted at various angles to each other. The measured or “profiled” surface areas (adjusted for the raster scan area) were plotted against the measurement scales on a log–log plot. Then, the Dfs can be calculated from the slope of the plot. The equation used for the final calculation, as proposed by Friel and Pande [112], is shown in Equation (45):
where S is the profiled surface area; is a constant; Dfs is the fractal dimension of fracture surface; and is the characteristic measurement scale area.
3.3.2. Dfs by 3D Laser Scanning Technology and the Projective Covering Method
In a study by Yan et al. [61], 3D laser scanning technology based on the triangulation method was used to measure the 3D profile of the fracture surfaces of concrete. First, the surface topographies of all the fracture surfaces were measured using this technique. Then, the digitized fracture surfaces were analyzed directly by using the projective covering method, which is similar to the box-counting method. The Dfs is evaluated from the rate of the divergence of the apparent area, A, as the size of the elements, r, decreases. Then, the projective covering method was established to determine the fractal characteristics of the fracture surface, as shown in Equation (46):
where A is the total area of the fracture surface with the grid size, r.
3.3.3. Dfs by Image Analyzer Method and 2D Fast Fourier Transform Function
The image analyzer method [58] is described as follows. The fracture surface is placed in dyed water. A photo is taken from the top and analyzed by an image analyzer. At each threshold level (intensity of light) increment, new islands appear, and their perimeter and area are measured. Then Equations (47) and (48) are used to compute the Dfs:
where D′ is determined from the power function of the relationship between the area, A, and the perimeter, P, of the islands.
Subsequently, a 2D fast Fourier transform function is used to calculate the Dfs of an image. Within the Fourier domain, the spectral density has a power law dependence on the wave number. The Dfs is related to the slope of the log–log plot of the 2D spectral density versus the wave number, as given in Equation (49) and reported by [113]:
According to this method, the wave numbers of the image, and their corresponding spectral energy densities, are computed. After that, these data are plotted in a log–log diagraph, and its slope can be determined using a linear least squares regression technique. At last, the Dfs can be calculated using Equation (49).
3.3.4. Dfs by Laser Profilometer and the Chord Method
In Janusz and Prokopski’s research [62], the shape of the profile lines of the cracks was obtained using a laser profilometer designed for the fast contactless measurement of 3D surface topography. Then, the obtained data were entered into a software program, named Fractal Dimension2D, and the final computations were made.
The Dfs was calculated by the chord method [62]. According to the chord method, the measurement of the profile line length is taken at varying measurement steps by counting their number and calculating the total profile line length. There is a certain exponential relationship between the value of the measurement step () and a geometric quantity determined using the measurement step, such as the curve length. Then, the logarithmic function revealing the relationship among the Dfs, the curve length, and the measurement step can be expressed as Equation (50):
where is the curve length, as measured by the i-th step, , and is the curve slope in the logarithmic graph in Equation (50).
An example of the Dfs calculation in Janusz and Prokopski’s study [62] is given in Figure 6. The values of the si are laid on x-axis, while the values of the logarithms of the length of the curve, L(si), obtained for that step, si, are laid on the y-axis. Then, the Dfs value can be graphically obtained as the slope of the straight line in Figure 6. In the case of Figure 6, the Dfs is determined to be 1.0254.
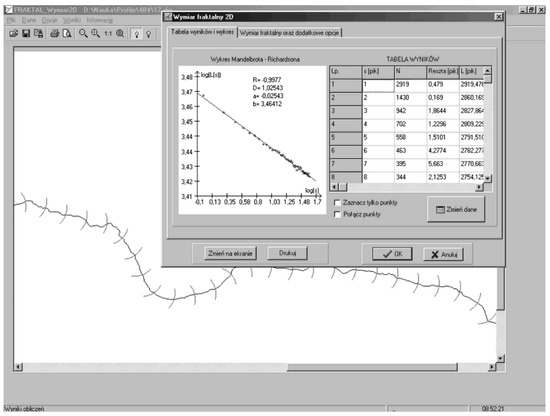
Figure 6.
An example of the Dfs calculation: A visible concrete fracture surface profile line with the measurement step marked, and the graph of the log(L(si))–log(si) line [62].
3.3.5. Dfs by Confocal Microscope/SEM and the Box-Counting Method
The confocal microscope technique can be applied to study the contours of concrete fracture surfaces [63,85]. During the confocal microscopic test, laser light reflected from a dichroic mirror into a scanning device moves in a raster scan in an x–y plane. A point source is imaged in the object plane. By coupling a step motor to the focusing unit, whole series of sectional images can be produced by changing the focal plane. This information is used to rebuild a 3D image of an object by overlaying the images of a section series.
From the optical measurement data, the Dfs can be determined by using the box-counting method [63,85]. Figure 7 exhibits an example of the Dfs calculation by confocal microscope and the box-counting method [85]. Figure 7a gives a typical contour of the fracture concrete surface built by the confocal microscope technique. Cubes with the number of s2 are generated to cover the 3D contour data (Figure 7b). The number of cubes, N, that intersect the fracture surface, divided by the s2 cubes necessary to cover the projection surface, is plotted against the inverse of the cube size, l, on a ln–ln scale. If a linear relationship is found, then the Dfs can be determined by adding the fractal increment, dCC (which corresponds to the slope of the linear line), to the dimension of a plane= 2 (Figure 7c). In this study, 512 × 512 mesh data have been used for each monitored spot with a size of 0.64 mm × 0.64 mm.
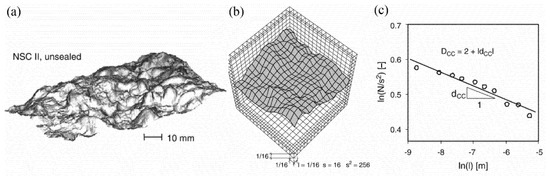
Figure 7.
An example of the Dfs calculation by confocal microscope and the box-counting method: (a) Typical contour of fracture concrete surface; (b) Coverage of the fracture surface by 3D boxes (l = 1/16); (c) Plot of ln(N/s2)–ln(l) line [85].
Furthermore, some researchers [9] have reported another effective method for determining the Dfs. According to their method, massive SEM pictures of the fracture surfaces were used to calculate the Dfs by the box-counting algorithm, which was programmed on the MATLAB platform. An image with continually distributed grey values, which is in M × M pixels, was first read in the modeling system, then the box-counting method was conducted to analyze the image. Finally, the Dfs can be determined as the slope of the line ln (N) versus the ln (l). A more detailed description of the box-counting method can be found in [9].
3.4. Fractal Dimension of Crack (Dc) by Various Testing Techniques and Box-Counting Method
The proper measurement of cracks is of significance for correctly estimating the fractal characteristics of cracks. Various methods have been adopted to measure the crack paths, including visual observation [68,70], tracing drawing technology of plastic sheets [69], X-ray computed tomography (X-ray CT) [26,65,66], the photoelastic coating set-up [71], a digital camera equipped with image software [64], an optical scanner (or digital camera) combined with machine learning algorithms [67,72].
In Zheng’s research [70], the geometric shapes of cracks and their distribution in concrete beams under flexural load were visually observed. The geometrical morphology of cracks in the research of Zhuang et al. [69] was mapped by tracing them onto a plastic sheet. In Jun et al.’s research [71], the photoclastic coating set-up is applied in order to observe the crack paths in the splitting-tensile tests. Owing to the ability of the X-rays to pass through thick and opaque objects, three-dimensional images of the internal micro-cracks in concrete samples can be obtained by using an X-ray CT [26,65,66]. The captured images can be digitized and converted into binary images to reveal the crack paths by using the computer image analysis software [64]. Furthermore, the cracks in cement pastes can be analyzed an optical scanner (or digital camera) combined with machine learning algorithms. The principle of this method is to implement machine learning algorithms with defined parameters of the desired pattern to produce pixel-based segmentations [67,72].
Overall, the crack paths of concrete specimens can be obtained by many different methods. After obtaining the crack information, the fractal dimension of the cracks (Dc) can be evaluated by using the box-counting method.
The calculation steps of the Dc conforming to the box-counting method are as follows [26,64,65,67,68,69,70,71,72]: The surface crack area of the specimen is covered by multiple square grids of different lengths, and the density of these grids can be changed by adjusting the square length. The total number of grids covering the crack area is counted. For each square length (r), if Equations (51) and (52) are satisfied, the Dc can be determined accordingly [68,114].
where is the total number of the grids covering the crack area; and is the square length.
3.5. Fractal Dimension of Particle Distribution (Dp)
The fractal dimension of the particle distribution can be calculated based on the particle size distribution information of the powders. The laser granulometry can precisely detect the particle size distribution powders with a size range of 20 nm–2000 μm. There are also other testing techniques that can analyze the particle size distribution, such as an optical microscope and the image analysis system [75].
3.5.1. Dp by Laser Granulometry and Yu’s Method
On the basis of the laser granulometry results, the fractal dimension of the particle size distribution (Dp) can be computed by the following fractal equations, proposed by Yu et al. [73] and Wang et al. [74]:
where denotes the ratio of the number of cement particles with sizes less than to the number of particles, and the Dp is the fractal dimension of the cement particle size distribution.
Assuming that the density of each particle in the powder is homogenized at this point, the mass of particles, , with particle sizes ranging between and can be expressed as:
where W is the total mass of particles in the powder; denotes the ratio of the number of cement particles with sizes less than to the number of particles. The particle size distribution of the powder should satisfy the following equation:
It should be noted that the existence of a straight-line segment in the double logarithmic coordinates, ~, indicates that the particle size distribution of the powder has a fractal structure, and the slope was calculated to obtain the fractal dimension of the particle size distribution:
The particle mass cumulative distribution curve obtained by the laser particle size analyzer is described in the double logarithmic coordinate (~), and the particle distribution data is subjected to linear regression analysis under this coordinate system. The slope of the regression line is b = 3 . Then can be estimated as .
3.5.2. Dp by Image Analysis System
The fractal dimension of the particle spatial distribution (Dp) can be determined on the basis of analyzing a large number of particle images captured by an image analysis system. In the research of Zhang et al. [75], a high-resolution image analytical instrument, Morphologi G3, was employed to characterize the morphological properties of the cement grains in a cement suspension sample. During the test, a high-quality image of each cement particle in the tested sample was captured by the instrument. Meanwhile, a 2D projection of the 3D cement grain was performed on these captured images using software inside the instrument. On the basis of the two-dimensional projections of the hundreds of thousands of particles in the cement suspension sample, the Dp can be determined by Equation (58), which was derived from the statistical analysis theory on the mesh simplification on 2D projections of particle images [75]:
where is the side length of the mesh; is the amount of meshes on all 2D projection images during the test. Generally, a larger Dp implies a higher dispersive degree of cement grains in the cement suspension sample, and vice versa.
4. Application of Fractal Theory on Performance of Cement-Based Materials
There are some basic and fundamental macroproperties of cement-based materials, including mainly the mechanical properties, volume stability, permeability, frost resistance, corrosion resistance, fracture behavior, etc. The application of fractal theory on these properties of cement-based materials will be described and discussed individually in this section.
4.1. Mechanical Properties
It is well-known that the pore structure strongly affects the mechanical properties of cement-based materials. Many studies have attempted to reveal the relationship between the fractal dimensions associated with the pore structure and the macroproperties of cement-based materials. Such findings are summarized in Table 2. Table 2 clearly shows that the mechanical properties of cement-based materials are closely related to the fractal dimensions of the pore structure, such as Ds and Dv.

Table 2.
Application of fractal theory on mechanical property of cement-based materials.
As for the Ds, it can be seen from Table 2 that the compressive strength of cement-based materials generally increase as the Ds increases; that is, there is a positive correlation between the Ds and the mechanical property. For example, Jin et al. [31] conducted tests on the strength and pore structure of thirteen cement mortar mixtures, and determined their Ds by a MIP and Zhang’s fractal model. Their results reveal that the relationship between the compressive strength of the mortars and the Ds presents a power function with the correlation coefficient, R2 of 0.7214, and the compressive strength increases with the increase in the Ds. Wang et al. [34] conducted a pore structural and fractal analysis on the influence of 20 wt.% fly ash and 5 wt.% silica fumes on the mechanical property of concrete. They calculated the Ds by using an MIP and Zhang’s fractal model and revealed the compressive strengths of concrete are positively correlated with the Ds, with a R2 value of 0.878. The mechanism beneath is that both the fly ash and silica powder can reduce the porosity of the concrete but can make the pore structure more complex at the same time, thereby increasing the Ds values. It is commonly accepted that the mechanical property of concrete is negatively corelated with the porosity [49,115]; hence, the concrete containing the fly ash and silica that exhibits the lowest porosity and the largest Ds value presents the best mechanical property among all the concretes analyzed in this study. This mechanism is demonstrated again in another study by Wang et al. [37], in which they studied the pore structure and the Ds of silica fume (SF) modified low-heat Portland cement-based materials. In this study, they reported that, with the increase in the SF dosage from 4 wt.% to 12 wt.%, the porosity of the concrete decreases, while the Ds increases since the presence of SF could fill up the pores while making the pore structure more complex. They also report that the compressive strength presents a positive correlation with the Ds, with a high R2 value of 0.924. Hence, they concluded that the effect of SF on the compressive strength of LHP cement concrete can be understood from the perspective of the Ds.
Nevertheless, there also exists a negative correlation between the mechanical property of cementitious material and the Ds. Kim et al. [88] found that the compressive strength of GGBFS-based cement pastes is negatively related to the Ds, which was determined by an MIP and Zhang’s fractal model, with a relatively weak R2 value of 0.493; however, this is only valid for the Ds of pores larger than 100 nm. In fact, among the five different pore size ranges in this study, namely, mesopores (6–10 nm, 10–25 nm, 25–50 nm), middle capillary pores (50–100 nm), and larger capillary pores (>100 nm), only the pores larger than 100 nm, and the mesopores in ranges of 6–10 nm and 10–25 nm, exhibited fractal characteristics. What is more, the Ds of the pores in the range of 6–10 nm and 10–25 nm did not show any correlation with the compressive strength at all. It is also interesting to note that the Ds of all of the ranges of pores in this study is 3.15, which is beyond the range of 2 ≤ Ds < 3 and, hence, the authors themselves considered this result not in accordance with the fundamental assumptions of fractal theory.
As for the Dv, there are also reverse conclusions on the relationships between the mechanical property of cementitious material, and Dv. Naderi et al. reported [33] a positive linear correlation, in which the compressive strength of lightweight self-compacting concrete increases with the increase in the Dv, as determined by an MIP and the Menger sponge model. They explained that, because of the continuous cement hydration, large pores in the concrete were divided into smaller ones, generating more small pores and making the pore structure more dispersed, which, in turn, increased the Dv value. At the same time, smaller porosity and a more condensed pore structure will strengthen the concrete. As a result, the relationship between the compressive strength and the Dv presents a positive linear function, with an acceptable R2 value of 0.8036. On the contrary, Li et al. [48] report that the compressive, flexural, and splitting tensile strengths of high-temperature-treated cement pastes (up to 900 °C) are negatively correlated with the Dv, which was also determined by an MIP and the Menger sponge model. The reason for this negative relation is that the high temperature (especially higher than 700 °C) could coarsen and complicate the pore structures of the cement paste, increasing the Dv values from about 2.2 to 3.0. However, the nano- and macromechanical properties of the cement paste degenerat significantly when the temperature exceeds 700 °C because of the decomposition of the hydration products. As a result, negative correlations between the mechanical strengths of the cement pastes and the Dv in this high-temperature case can be found.
In addition to the pore structure, which is supposed to be closely related to the mechanical properties of cement-based materials, many researchers confirm that the fracture surface texture is related to the mechanical behavior of cement-based materials [62,85]. Accordingly, the fractal dimension of the fracture surface (Dfs) has been verified to be relevant to the mechanical properties of cementitious material by some researchers [9,63]. For instance, Lu et al. [9] showed that the compressive strength of concrete declines linearly with the increase in the Dfs. They assessed the compressive strength and microstructure (the micromorphology and pore structure) of concrete, blended with 0–16% SF by weight of binder, and calculated the Dfs by the box-counting method based on SEM images. In their study, increasing the SF dosage from 0 to 16 wt.% improves the compressive strength by about 40%. Meanwhile, the increased SF dosage changes the concrete matrix from heterogeneous, rough, and porous to homogeneous, flat, and dense, respectively. Since the Dfs reflects the intrinsic surface irregularities [42], the homogenizing effect of SF depresses the irregularity of the fractured surfaces, thereby lowering the Dfs from about 2.8 to 2.5. As a result, the compressive strength presents a negative relationship with the Dfs. However, T. Ficker [63] points out that there is a positive exponential relationship between the compressive strength of cement pastes and the Dfs, which ranged from 2.07 to 2.18, as determined by the box-counting method and a confocal microscope.
Overall, it can be seen that there are no uniform relationships or functions between the mechanical properties of cement-based materials and the various fractal dimensions (Ds, Dv and Dfs), which can be explained by the following possible reasons: (1) The fractal dimensions in these studies are mainly determined by different fractal models and have different physical implications and, thus, they present different correlations with the mechanical properties of concrete. For instance, the addition of SF into concrete can reduce surface irregularities and the Dfs but elevate the complexity of the pore structure and increase the Ds at the same time, thus the complete reverse correlations of the Dfs and the Ds with compressive strength can be observed; (2) Any fractal dimension of the pore structure can only reflect some aspects of one single pore structure parameter, and the pore structure is not the only factor determining the mechanical properties of cement-based materials. After all, the mechanical properties can be affected by many other factors, such as the mixture proportions, compositions, curing time, temperature, etc. As a result, even the same fractal dimension as the Ds exhibits completely different, and even reverse, correlations with the compressive strength; (3) Similarly, although the facture can affect the mechanical properties of cement-based materials significantly, it is still not the only dominant parameter. Thus, the Dfs characterizing the facture features of cement-based materials does not exhibit a uniform relationship with the mechanical properties; (4) Another important factor that cannot be ignored, which is to say that the fractal study on cement-based materials is still in its initial stages, is that there may exist some deviations in the understanding of the physical meanings and the fractal model parameters of the same fractal dimension. Thus, contrary results may be achieved from various studies, even on the same fractal dimension. This phenomenon is more prominent in the fractal study on pore structures. In summary, the specific relationship between the mechanical properties and the fractal dimension of pores or fracture surfaces should be analyzed on a case-by-case basis.
4.2. Volume Stability
It is widely reported that the shrinkage behavior of concrete is governed by the pore structure [37,116,117,118,119]. Autogenous shrinkage and drying shrinkage are the two main types of concrete volume deformation [37,115,120]. To evaluate the shrinkage behavior of cement-based materials in terms of fractal geometry, the relationships between shrinkage (including the autogenous shrinkage and drying shrinkage) and the Ds of concrete are revealed.
In a study by Wang et al. [37], the pore structure and fractal characteristics of reference concrete (C0), and concrete containing 0 wt.% silica fume (designated as LC0), 4 wt.% silica fume (LC4), 8 wt.% silica fume (LC8) and 12 wt.% silica fume (LC12) were studied. The Ds values were calculated using MIP results and Zhang’s fractal model. They found that the autogenous shrinkage and drying shrinkage, as well as the Ds values of the concrete, increased with the SF dosage. They also report that both the autogenous shrinkage and the drying shrinkage exhibit a positively linear relationship with the Ds, and the R2 are 0.878 and 0.912, respectively, as shown in Figure 8. On this basis, they concluded that the Ds can serve as a new pore structure parameter for evaluating concrete shrinkage behavior. Their conclusion is supported by the following points: (1) It is well-known that the drying shrinkage is caused by the capillary tension arising from the evaporation of water from the capillary pores in concrete in a drying environment, while the autogenous shrinkage is attributed to the capillary tension brought about by the self-desiccation in the pores resulting from the cement hydration [37,116,117]. Many researchers [121,122] further report that the pores with sizes less than 50 nm critically affected both the drying shrinkage and the autogenous shrinkage, since the capillary tension increased rapidly within the pores in this range; (2) The presence of SF could raise the proportions of pores with sizes less than 50 nm significantly and, consequently, the autogenous shrinkage and drying shrinkage of the concrete would increase with the SF dosage; (3) Meanwhile, as the factions of the gel pores (<10 nm) and the medium capillary pores (10–50 nm) increase, the pore structures become more complex and exhibit large pore surface areas, leading to higher Ds values. Thus, the shrinkage exhibits a positive relationship with the Ds values. It is worth noting that this is the first time the parameter fractal dimension has been linked with the shrinkage behavior of cement-based materials.
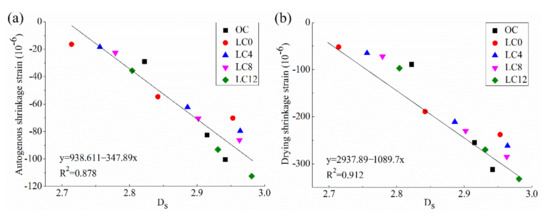
Figure 8.
Relationship between shrinkage behavior and the Ds of concrete: (a) Autogenous shrinkage strain; (b) Drying shrinkage strain [37].
4.3. Durability
4.3.1. Transport Properties
Mass transport properties (e.g., water/ion/gas diffusion), which are of great significance to the durability of cement-based materials, are believed to be significantly affected by the pore parameters (porosity, tortuosity, pore size, etc.) [32,49,123,124,125,126]. For instance, it has been demonstrated that a higher porosity and a larger pore size facilitated the generation of channels for water/ion/gas penetration and transportation [49,123,124]. Moreover, increasing the tortuosity of the transport path would lower the pore channels, thus inhibiting the corrosion of the materials caused by water/ion/gas diffusion [127,128]. Obviously, improved impermeability is beneficial for the improvement of the durability of cement-based materials. This is true for frost resistance, chloride- and sulfate-penetration resistance, anti-carbonation resistance, and so on. Through experimental and theoretical verifications, many researchers [9,33,50,56,123,129] report that the transport properties of cement-based materials are related to the fractal dimensions of the pore structure, such as the Dt, the Ds , and the Dv. The application of fractal theory on the transport properties of cement-based materials in recent years is summarized in Table 3.

Table 3.
Application of fractal theory on transport properties of cement-based materials.
Regarding the relationship between the Dt and transport properties, Yu and Cheng [50] propose a fractal permeability model for bi-dispersed porous media based on the box-counting method. Using Darcy’s law, they obtained a formula to calculate the permeability (K) of a porous medium, as shown in Equation (59):
where is the hydraulic pressure gradient; is the viscosity of the fluid; A and were the cross-section area and representative length of the materials, respectively; Q is the total flow rate; Df is the fractal dimension of the pore space, as described in Section 3.1.3.3; the Dt is the fractal dimension of the pore tortuosity; and is the maximum pore radius.
Their study showed that the permeability (K) decreases with the increase in the Dt, as can be seen in Figure 9. This is because when the Dt increases, the flow pathways are more tortuous, resulting in a better resistance to the fluid flow and a lowered permeability value.
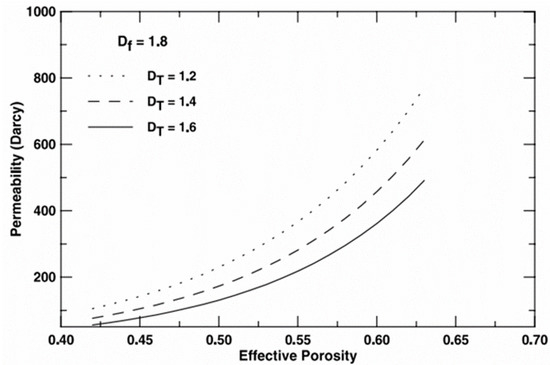
Figure 9.
Effects of on permeability of porous materials [50].
Later, they proposed a modified equation to calculate the permeability (K) of cement-based materials based on Equation (59), as exhibited in Equation (60) [129]:
where ∅; is the porosity.
By using Equations (43) and (60), as well as NCIM test results, Tang et al. [56] simulated the permeability values (K) of fresh cement pastes by a two-phase fractal model. Their results showed that the K values of the cement pastes with porosities ranging from 15% to 70% increased from 8.87 × 10−23 m2/s to 2.11 × 10−19 m2/s. Their simulated results of K agreed well with those obtained from NCIM experiments in the same study.
Regarding the relationship between the Ds and transport properties, Wang et al. [123] reported that the chloride diffusion coefficients (DRCM) of concrete containing phosphorus slag (PHS) with different dosages (0, 20 and 40 wt.%), and fineness (302 and 505 m2/kg), were negatively correlated with the Ds, with a high R2 value of 0.962, as shown in Figure 10. The Ds in this study was determined by Zhang’s fractal model and MIP results. They reported that the effect of the PHS, with different content and fineness, on the DRCM, can be understood by the Ds. Specifically, the Ds decreased with an increasing PHS content or decreasing PHS fineness at early ages. Therefore, the concrete with the low fineness of 302 m2/kg, and a high PHS dosage of 40 wt.% (labelled as PLC40), has the lowest Ds value at 3 days and shows the weakest chlorine permeability resistance, i.e., the largest DRCM values. On the contrary, the concrete with a high fineness of 505 m2/kg and a low dosage of 20 wt.% PHS (denoted as PHC20) shows the highest Ds value and renders the best chloride permeability resistance among all the concrete samples in this work.
Figure 10.
The relationship between chloride diffusion coefficient (DRCM) and Ds [123].
Concerning the relationship between the Dt and transport properties, Zarnaghi et al. [33] reveal that there was a good correlation between the water penetration depth of concrete and the Dv, with a R2 of 0.7063. They found that the penetration depth increased with an increasing Dv. They explained that the higher penetration depth was aroused by the increase in the hydration age and cement hydration. However, this is a controversial phenomenon since, theoretically, the progress of cement hydration would densify the pore structure and make the concrete less permeable, that is, it would decrease the water penetration depth rather than increase it. This seemingly controversial phenomenon in this study needs more verification.
Apart from the pore-structure-related fractal dimensions, such as Dt, Ds, and Dv, the fractal dimension of the fracture surface (Dfs) has been reported to be associated with the transport properties of cement-based materials. Lü et al. [9] evaluated the Dfs values of concrete mixed with different dosages of silica fume (0 wt.%, 3 wt.%, 6 wt.%, 9 wt.%, 12 wt.%, and 16 wt.%) by SEM and the box-counting method. They found that the permeability increases with the increase in the Dfs, and this lg(K) − Dfs relationship follows an exponential growth function. They also reported that the presence of SF could densify and homogenize the concrete matrices, which, in turn, diminishes the water permeation paths, leading to a decrease in the permeability and the Dfs, simultaneously. Nevertheless, the correlation between Dfs and permeation needs more verification since the authors themselves attribute the permeability promotion in this work to the increase of pore tortuosity. In fact, no more literature can be found about the relationship between the fracture surface texture and the transport property. After all, as stated by Katz and Thompson [130], the transport property is one kind of bulk property that is more likely to be determined by the threshold paths for water permeation (pore tortuosity) rather than by the material surface irregularity.
4.3.2. Frost Resistance
The freezing and thawing damage is one of the major reasons for the deterioration of concrete in highway pavements, airport pavements, bridge decks, and other concrete structures in cold weather environments [15,131]. The weight loss and the relative dynamic elastic modulus are the two indexes used to evaluate the frost resistance of concrete [111,132]. As described above, the frost durability of concrete is closely related to its air-void parameters. Moreover, the pore structure is also considered to be closely related to the frost resistance of concrete [78,82,133]. For example, Powers and Brownyard [133] demonstrated that the freezing point of water declined as the pore size decreased. An et al. [78] proved that the ice first grew in large capillary pores in concrete, and then formed into finer capillary pores with decreasing temperature. Wang et al. [82] reported a close relationship between the frost resistance of concrete and the pore structure parameters, specifically, frost resistance enhanced with the decrease in both the porosity and the average pore diameter. Therefore, the differences in the frost resistances of various cement-based materials are often analyzed in terms of the air-void and pore structures. Correspondingly, the fractal dimension of air void (Da) and the fractal dimension of the pore surface (Ds), which reflect the size distributions of the air voids and the fine pores, respectively, have been used to assess the frost resistance of concrete in recent years.
As for the relationship between the Da and frost resistance, Jin et al. [15] revealed a strong positive exponential function between the Da and the durability factor, with a high R2 of 0.9195, as shown in Figure 11. In this study, the index durability factor reflects the frost resistance of the concrete, and a higher durability factor implies a smaller loss, both in weight and the relative dynamic elastic modulus; that is, better frost resistance. In addition, the Da values and the air-void parameters in this work were obtained by an air-void analyzer and the box-counting method conducted on eight kinds of concrete, including five groups of non-air-entrained and three groups of air-entrained concrete. The results indicate that the size-distribution of the air voids in the concrete had significant effects on the frost resistance.
Figure 11.
Relationship between fractal dimension of air void (Da) and durability factor [15].
With regard to the correlation between Ds and frost resistance, Wang et al. [82] reported that the Ds is positively correlated with the relative dynamic elastic modulus of concrete with an R2 of 0.972 and is negatively correlated with the mass loss with a R2 of 0.940, as can be seen in Figure 12. In other words, there is a linear relationship between the frost resistance and the Ds. This conclusion was obtained from an analysis of the MIP results and Zhang’s model conducted on five groups of concrete, namely, reference concrete (labelled as C0), concrete with 20 wt.% fly ash (C1), concrete with 0.8 kg/m3 PVA fiber (C2), concrete with 20 wt.% fly ash (C3), concrete with 0.8 kg/m3 PVA fiber (C4), as well as concrete added with 6 wt.% MgO and 1.0 wt.% shrinkage-reducing admixtures (SRA) together (C5). They reported that the synergy effect of the PVA fiber and the fly ash can refine and optimize the pore structure, thus increasing the Ds and improving frost resistance. On the contrary, MgO and SRA are less effective in refining the pores than PVA fiber and fly ash, so a relatively smaller Ds and weaker frost resistance are produced. As a result, a positive correlation between Ds and frost resistance is exhibited.
Figure 12.
Relationship between Ds and (a) relative dynamic elastic modulus, and (b) mass loss [82].
4.3.3. Corrosion Resistance
Recently, the resistance of concrete to chloride erosion, sulfuric acid attack, or other corrosions has been analyzed in terms of the fractal dimension [64,134,135,136,137].
Erdem. S [64] conducted a fractal analysis on chloride erosion—induced cracking in normal self-compacting concrete (SCC) and self-compacting lightweight concrete (SCLC). The results reveal that the fractal dimension of the cracks (Dc), as determined by a digital camera and the box-counting method, is positively correlated with the complexity of the corrosion morphology of the concrete. To be specific, Dc and fracture energy of SCC are much higher than those of SCLC. In addition, Dc increases with the increase in the complexity of the corrosion morphology. These phenomena can be explained by the change in the fracture plane. In the case of SCC, the combined effects of high particle stiffness and less impedance mismatches between the matrix and the aggregate particles could lead to the generation of secondary crack branches and crack deflections, resulting in a more tortuous crack profile and a higher Dc. Different from SCC, the higher porosity and higher content of fly ash in SCLC than SCC favor the accommodation of corrosion products and, therefore, eased the stress created by the dissolved Fe2+ from the steel. As a result, SCLC exhibits less corrosion-induced cracks and, hence, a smaller Dc value than SCC, as shown in Figure 13. It is worth noting that, after a comprehensive examination of the related references in recent decades, this was the first time that fractal analysis has been carried out to study the corrosion-induced damage of concrete at the macroscale.
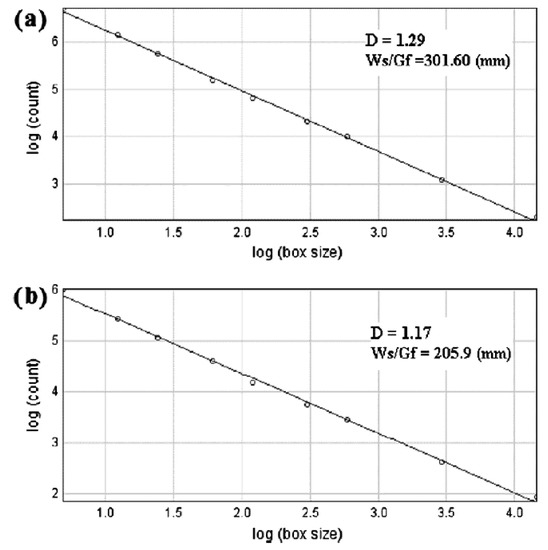
Figure 13.
Fractal dimension of cracks (Dc) in concrete after corrosion: (a) SCC concrete; and (b) SCLC concrete [64].
Similarly, Zhuang et al. [69] report that the Dc, as determined by the tracing drawing technology of plastic sheets and the box-counting method, increased with the extent of corrosion. In this study, the cracking behavior of carbon-fiber-reinforced polymer (CFRP) concrete piles, caused by reinforcement corrosion in harsh marine environments, was investigated. Their results reveal that the CFRP-strengthening technique resulted in less corrosion damage to the concrete, as indicated by a smaller crack width and smaller Dc. Additionally, it was found that the Dc increased linearly with the maximum load of piles after corrosion. Therefore, they considered the Dc to be a reliable index evaluating the strength loss and corrosion extent of the concrete piles.
Moreover, Xiao et al. [134,135,136,137] calculated the fractal dimension of a concrete surface by using 3D laser scanning technology and the covering method, and found that there was a nonlinear relationship between the fractal dimension of the concrete surface and the interface friction angle. The interface friction angle between the concrete pipe surface and the surrounding corrosive sand plays a dominant role in the shear strength: the larger the interface friction angle, the stronger the shear strength. Their results show that, as the sulfuric acid corrosion time increased, the concrete surface became rougher, and the fractal dimensions, the sand-corroded concrete interface friction angle, as well as the shear displacement became larger. Hence, they concluded that this fractal dimension can be used to evaluate the surface characteristics of concrete subjected to sulfuric acid.
4.4. Fracture Mechanism and Fracture Mechanics
The fracture surface is determined mainly by the composition of the cement-based materials and the loading conditions [61]. It is commonly accepted that the roughness of the fracture surface of concrete varies, depending on the mix design. To better understand the mechanical fracture behavior and the fracture mechanism of concrete, many researchers have investigated the effects of material composition on the fracture surface roughness.
Yan et al. [61] used 3D laser scanning technology to evaluate the influence of the concrete composition on the fracture surface of concrete. They found that the material composition of concrete, including the water-to-binder (W/B) ratio, the aggregate size, and the aggregate type, apparently affected the fractal dimension of the fracture surface (Dfs). With the increase in the W/B ratio, the Dfs increases. For the same W/B ratio, the Dfs increases with the increase in the aggregate size. Moreover, they found that the Dfs of crushed gravel concrete is the highest, while that of light-weighted gravel concrete is the lowest. Similar findings were reported by Issa and Hammad [138], who studied the effects of three maximum aggregate sizes (namely, 4.7, 18.8, and 37.5 mm) on the Dfs and found that the roughness and the Dfs increase monotonically with the increasing maximum aggregate size.
By using the stereoscopic SEM method, Wang et al. [60] found that the presence of silica fume appears not to influence the fractal characteristics of the fracture surfaces of cement pastes and mortars.
Winslow [28] systematically studied the effects of W/B ratios on the Dfs of cement paste specimens. It was observed that different W/B ratios led to various rough surfaces, and that higher W/B ratios usually produce fewer irregular surfaces and a lower Dfs.
In addition to revealing the micromechanism of the fracture of cement-based materials, in terms of material composition, the fracture mechanical properties of cement-based materials can be well-illustrated by the Dfs.
In Mechtcherine’s study [85] regarding the fracture mechanical behavior of concrete, the fracture surfaces of the tested concrete specimens were investigated in detail and quantified using the fractal geometry. Their experimental results display strong correlations between the shape of the stress–crack opening relation of concrete, and the values of the roughness as well as the Dfs. Specifically, with increasing temperature and decreasing concrete strength, or with continuous drying at an early age, the heterogeneity of concrete increases, thus exhibiting higher values of roughness and Dfs. Meantime, a higher degree of concrete heterogeneity and a larger Dfs result in a more developed crack system, i.e., more pronounced crack branching and bridging, as well as subsequently rougher crack profiles.
Janusz and Prokopski [62] proved that the fracture toughness of metakaolinite-modified concretes is higher than that of nonmodified concretes. By using a laser profilometer and fractal geometry together, they obtained the morphology and the Dfs of concrete. They concluded that the concrete fracture surface morphology and the Dfs were closely related to the fracture toughness, as expressed by the critical stress intensity factor.
Similar trends have been reported by Lange et al. [59] and Cai et al. [139]. Lange et al. [59] used an image analysis technique to compute the roughness parameter and the Dfs of cement and mortar specimens. They found that the Dfs increased as the roughness number increased and demonstrated that there was a good correlation between the fracture surface roughness and the fracture toughness. In the research of Cai et al. [139], the fractal characteristics of the fracture surfaces of alkali-slag concrete under freeze–thaw cycles were studied. Their results show that the Dfs and fracture toughness had a good linear relationship.
4.5. Evaluation of the Crack Irregularity, Concrete Flexural Performance, and Fracture Energy
In recent years, the investigation of fractal theory in the cracks of cement-based materials has mainly focused on the following three aspects: (1) To geometrically describe the irregularity of cracks, such as the crack pattern and crack distribution; (2) To evaluate the bearing capacity and the flexural performance, and (3) To evaluate the fracture energy.
As for the fractal analysis of the irregularity of cracks, Shang et al. [26] used the CT technique and fractal geometry to quantitatively characterize the mesocracks and the mesocrack propagation of recycled aggregate concrete. Their results reveal that the fractal dimensions in the 2D images and the 3D mesocracks of cracks decrease with an increasing recycled aggregate replacement rate. In other words, a higher recycled aggregate content results in a lower fractal dimension of the interior mesocracks (Dc) for recycled aggregate concrete, with fewer tortuous cracks. They concluded that this trend means that the number of main and branch cracks in the local area decreases and that the complexity of the cracks weakens with the increasing recycled aggregate replacement rate.
Szelag [67] applied machine learning algorithms and fractal geometry to analyze the total crack area and the crack density, as well as the fractal dimension of the cracking patterns (Dc). They indicated that the Dc increases with the increase in both the total crack area and the crack density. As well, they showed that a strong correlation exists among the tensile strength, the Dc, and the crack density.
By using the CT technique and the fractal theory together, Zheng et al. [65] studied the evolution of the internal microcracks of concrete and their fractal characteristics. Their results show that, with fiber dosage increases, the Dc first increases, then decreases, and then increases once again. The first increase in the Dc indicates that the characteristics of the concrete cracks are complex. This situation can be improved by adding a moderate amount of fiber, which would make the microcracks develop steadily and, therefore, reduce the Dc. However, excess fiber addition could cause new defects in the concrete because of the fiber agglomeration effect, leading to an increased Dc.
Zhuang et al. [69] studied the cracking behavior of reinforced concrete piles in a marine environment using the fractal theory. The experimental results showed that crack patterns at different states of corrosion exhibited a well-defined fractal character. Thus, fractal analysis could be exploited to assess the corrosion damage of piles when mechanical testing is not available.
Ebrahimkhanlou et al. [140] investigated the fractal characteristics of the crack patterns of prestressed concrete members under load. They demonstrated that the fractal theory could effectively quantify the cracking degree of the prestressed concrete members and reveal their cracking mechanisms [20].
In addition, as for the fractal analysis of the bearing capacity and the flexural performance of cement-based materials, Zheng et al. [70] investigated the influence of carbon-fiber-reinforced polymer (CFRP) anchors on the bearing capacity and fatigue behavior of reinforced concrete beams. They proposed a novel damage index based on the good correlation between the residual bearing capacity and the fractal dimension of the surface cracks (Dc) of the beams. Their results showed that Dc can be used as a parameter, not only to identify the cracking patterns of specimens, but also to warn of the failure of the CFRP anchorage system. In addition, they summarized that the novel damage index derived from the Dc was consistent with the loss rate of the ultimate load and, thus, can be used to estimate the damage degree attributable to the fatigue of the concrete beams.
Zhu et al. [68] investigated the flexural properties (the load-carrying capacity and flexural toughness) of polypropylene-fiber-reinforced cement-based composites (ECC). Flexural toughness is often used to evaluate the flexural performance of cement-based materials. Toughness refers to the energy absorption capacity of cement-based materials before the cracks occur under load [115]. In Zhu et al.’s [68] research, they verified that the distribution of the surface cracks of specimens under flexural load exhibit fractal characteristics. As well, they explored the inherent relationship between the mechanical properties of the specimens in a bending test and the Dc, then pointed out that the Dc can be used to characterize the flexural properties of the ECC.
Moreover, with regard to the fractal analysis for evaluating the fracture energy, Peng et al. [71] analyzed the fracture behavior of concrete by fractal geometry and explained qualitatively the effects of the fracture energy on the Dc based on experimental and analytical analyses, which included the dynamics of the microcrack coalescence. They demonstrated that the mechanism of the fracture surface formation in concrete is closely related to the dynamic processes of the cascade coalescence of the microcracks. Moreover, a unimodal relation between the Dc and the coalescence threshold can qualitatively explain the relationship between the Dc and the fracture energy.
4.6. Evaluation of Pozzolanic Reactivity and Dispersion State of Powders
The investigation of the fractal theory to characterize the particle distribution of cement-based materials has attracted great attention. The focus in this regard mainly includes the following issues: (1) To characterize the particle size distribution and fineness of powder particles; (2) To evaluate the pozzolanic reactivity of mineral materials; and (3) To characterize the dispersion state of cement particles in a suspension system.
As for the characterization of the particle size features, Moskovits [90] first proposed that the fractal dimension could describe the particle size distribution of cement. Some researchers et al. [73,90,91,92] have confirmed that the fractal dimension of the particle size distribution (Dp) could better evaluate the cement particle gradation distribution and the particle shape characteristics than traditional parameters, such as the residue on the sieve and the specific surface area. Yu and Zheng [73] reported that, under the same particle size distribution of cement particles, the larger the Dp, the finer its fineness and the more uneven the particle size distribution. They also demonstrated that the Dp is related to the grinding efficiency, and the large Dp usually corresponds to a low grinding efficiency. Guo et al. [91] reported that the Dp values of various cements ranged between 2.21 and 2.37, and increased with the increase in the specific surface area of the cement. A similar conclusion was obtained by Tang and Ba [93], who conducted a fractal study on fly ash particles with various fineness. Zhu et al. [92] demonstrated that the hydration rate and the compressive strength of cement pastes are closely related to the Dp of cement particles.
Regarding the evaluation of the pozzolanic reactivity of the mineral materials in terms of the fractal dimension, Tang et al. [93,94] determined the fractal dimension of the particle size distribution (Dp) of fly ash and slag by using laser granulometry and fractal theory. They found that the pozzolanic reactivity of the powders increases linearly with their Dp.
With regard to the characterization of the dispersion state of cement particles in a suspension system, Wang et al. [74] analyzed the effects of different superplasticizers on the dispersion state of cement particles via the fractal method combined with laser granulometry. They found that the fractal dimension of particle spatial distribution (Dp) would vary significantly if the superplasticizer dosage exceeds a certain value. They further pointed out that this critical superplasticizer dosage is the optimal dosage for dispersing cement grains in cement pastes. On this basis, they established a new fractal dimension-related method to determine the optimal superplasticizer dosage.
Zhang et al. [75] also reported that the fractal dimension of the particle spatial distribution (Dp) can quantitatively characterize the dispersion state of cement particles in fresh cement paste at a mesoscopic scale by using a high-resolution analytical morphology method. They showed that the Dp of cement particles increased from 1.68 to 1.94 after adding superplasticizer, indicating a superior dispersion state of cement particles achieved in the presence of superplasticizer. Finally, they established a relationship between the mesostructure and the rheological behavior of fresh cement paste. Specifically, higher fluidity corresponds to larger Dp values.
The surface texture and aspect ratio of the particles also have some effects on the materials properties. However, there is no fractal study on these topics so far. Further studies are encouraged to cover such interesting topics.
5. Conclusions and Outlook
Fractal theory is a new tool for revealing the complex nature of cement-based materials at the micro-, meso-, and macrolevels. On the basis of the above review work and analysis, the following conclusions can be drawn:
(1) There are many kinds of fractal dimensions nowadays. The paper summarizes in detail the principles and classification of seven commonly used fractal dimensions applied in the research field of cement-based materials, including the fractal dimensions of the pore surface (Ds), pore volume (Dv), pore tortuosity (Dt), air void (Da), fracture surface (Dfs), cracks (Dc) as well as the particle size distribution or particle spatial distribution (Dp);
(2) The testing techniques and fractal models used to determine these fractal dimensions are described individually in this work. The testing techniques are utilized to characterize the physical parameters of cement-based materials such as pore structure, air-void structure, fracture surface roughness, etc., while the fractal models are adopted to calculate the fractal dimensions based on the testing results;
(3) Many macroproperties of cement-based materials (e.g., mechanical properties, volume stability, durability performance, including the transport properties, frost and corrosion resistance, fracture mechanics and energy, crack irregularity, pozzolanic reactivity, and the dispersion state of powders) are found to be closely related to fractal dimensions. Fractal theory provides a novel and effective means to characterize, and even predict, the macroproperties of cement-based materials.
Although lots of meaningful and significant results have been obtained regarding the investigation and application of fractal theory in the research field of cement-based materials, the following drawbacks and aspects need to be considered and carried out further:
(1) Fractal dimensions are commonly obtained from testing techniques and fractal models conducted on different physical parameters; thus, these fractal dimensions have different physical meanings and present different correlations with the macroproperties of cement-based materials. There are no uniform relationships or functions between any macroproperties with fractal dimensions, and the results from different fractal models are not comparable;
(2) Even for the same fractal dimension obtained from the same test technique and fractal model, some different, or even reverse, conclusions on the relationship between fractal dimensions and macroproperties have been proposed. One main reason may be that each fractal dimension solely reflects only some aspects of any one single physical parameter of cement-based materials, while the bulk macroproperty is often affected by many factors and physical parameters. The other possible reason is that the fractal study on cement-based materials is still in its initial stages, and there may exist some deviations in the understanding of the physical meanings and fractal model parameters of the same fractal dimension. This phenomenon is more prominent in the fractal study of pore structures;
(3) Although some simple functional relationships between fractal dimensions and the basic macroproperties have been proposed, there are still very few studies with regard to this. Much more profound and comprehensive fractal studies should be conducted on the mechanical properties, shrinkage behavior, fracture mechanics, and durability performance to establish much closer quantitative relationships between them and the micro- and macrostructure property models to better understand the nature of cementitious material properties.
Author Contributions
Conceptualization, writing—original draft, supervision, project administration funding acquisition, L.W.; writing—original draft, writing—review and editing, X.Z.; investigation, H.Y., X.L., F.G. and Y.S.; investigation, formal analysis, A.H. All authors have read and agreed to the published version of the manuscript.
Funding
The authors appreciate the financial support provided by the Opening Funds of the Belt and Road Special Foundation of the State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering (2020492311), the State Key Laboratory of Building Safety and Built Environment, the National Engineering Research Center of Building Technology (BSBE2020-2), the Opening Project of the State Key Laboratory of Green Building Materials (2020GBM07), the open funding of the National Dam Safety Research Center (CX2019B12), the Natural Science Research Project of the Shaanxi Provincial Department of Education (20JK0722), and the National Natural Science Foundation of China (U2040222, 52109147 and 51409016).
Acknowledgments
The authors would like to thank all the anonymous referees for their constructive comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, L.; Li, G.; Li, X.; Guo, F.; Tang, S.; Lu, X.; Haniff, A. Influence of reactivity and dosage of MgO expansive agent on shrinkage and crack resistance of face slab concrete. Cem. Concr. Compos. 2021, 125, 104333. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, K.; Wang, J.; Guo, J.; Ling, Y. Macroscopic and microscopic analyses on mechanical performance of metakaolin/fly ash based geopolymer mortar. J. Clean. Prod. 2021, 294, 126193. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, K.; Yuan, Q. Limited fractal behavior in cement paste upon mercury intrusion porosimetry test: Analysis and models. Constr. Build. Mater. 2021, 276, 122231. [Google Scholar] [CrossRef]
- Zeng, Q.; Jike, N.; Liu, J.; Wang, Z.; Wang, J. Fractal analysis of stress-dependent diffusivity of porous cementitious materials. Fractals 2020, 28, 2050117. [Google Scholar] [CrossRef]
- Wang, X.; Yu, R.; Shui, Z.; Song, Q.; Zhang, Z. Mix design and characteristics evaluation of an eco-friendly Ultra-High Performance Concrete incorporating recycled coral based materials. J. Clean. Prod. 2017, 165, 70–80. [Google Scholar] [CrossRef]
- Lv, X.; Shen, W.; Wang, L.; Dong, Y.; Zhang, J.; Xie, Z. A comparative study on the practical utilization of iron tailings as a complete replacement of normal aggregates in dam concrete with different gradation. J. Clean. Prod. 2019, 211, 704–715. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, K.; Wang, J.; Guo, J.; Hu, S.; Ling, Y. Mechanical properties and prediction of fracture parameters of geopolymer/alkali-activated mortar modified with PVA fiber and nano-SiO2. Ceram. Int. 2020, 46, 20027–20037. [Google Scholar] [CrossRef]
- Wang, L.; Tang, S. Editorial: An introduction to fractals in construction materials. Fractals 2021, 29, 2102001. [Google Scholar] [CrossRef]
- Lü, Q.; Qiu, Q.; Zheng, J.; Wang, J.; Zeng, Q. Fractal dimension of concrete incorporating silica fume and its correlations to pore structure, strength and permeability. Constr. Build. Mater. 2019, 228, 116986. [Google Scholar] [CrossRef]
- Wang, L.; Chen, E.; Ruan, S.; Tang, S. Editorial: New Technologies for Investigating Microstructures and Enhancing Performance of Cementitious Materials. Front. Mater. 2021, 8, 669862. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, J. Fractal characteristics of pore structure of hardened cement paste prepared by pressurized compact molding. Constr. Build. Mater. 2020, 259, 119856. [Google Scholar] [CrossRef]
- Zeng, Q.; Luo, M.; Pang, X.; Li, L.; Li, K. Surface fractal dimension: An indicator to characterize the microstructure of cement-based porous materials. Appl. Surf. Sci. 2013, 282, 302–307. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-Chong, T.; Dangla, P. Surface fractal analysis of pore structure of high-volume fly-ash cement pastes. Appl. Surf. Sci. 2010, 257, 762–768. [Google Scholar] [CrossRef]
- Yu, P.; Duan, Y.; Chen, E.; Tang, S.; Wang, X.R. Microstructure-based fractal models for heat and mass transport properties of cement paste. Int. J. Heat Mass Transf. 2018, 126, 432–447. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, J.; Huang, B. Fractal analysis of effect of air void on freeze–thaw resistance of concrete. Constr. Build. Mater. 2013, 47, 126–130. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y.; Geng, Z.; Xu, X.; Yu, W.; Chen, J. Structure, Fractality, Mechanics and Durability of Calcium Silicate Hydrates. Fractal Fract. 2021, 5, 47. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, Z.; Wang, J.; Wang, K. Numerical modeling of rebar-matrix bond behaviors of nano-SiO2 and PVA fiber reinforced geopolymer composites. Ceram. Int. 2021, 47, 11727–11737. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, L.; Zhu, Z.; Fu, Z.; Lv, X. Simulation of the temperature field for massive concrete structures using an interval finite element method. Eng. Comput. 2020, 37, 45. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, S.; Shi, Y.; Tang, S.; Chen, E. Effect of silica fume and PVA fiber on the abrasion resistance and volume stability of concrete. Compos. Part B: Eng. 2017, 130, 28–37. [Google Scholar] [CrossRef]
- Erdem, S.; Dawson, A.; Thom, N.H. Influence of the micro- and nanoscale local mechanical properties of the interfacial transition zone on impact behavior of concrete made with different aggregates. Cem. Concr. Res. 2012, 42, 447–458. [Google Scholar] [CrossRef]
- Peled, A.; Castro, J.; Weiss, W. Atomic force and lateral force microscopy (AFM and LFM) examinations of cement and cement hydration products. Cem. Concr. Compos. 2013, 36, 48–55. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, P.; Guo, J.; Wang, K. Bonding behavior of concrete matrix and alkali-activated mortar incorporating nano-SiO2 and polyvinyl alcohol fiber: Theoretical analysis and prediction model. Ceram. Int. 2021, 47, 31638–31649. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Zhou, S.; Tang, S.; Lu, X. Investigation of microstructure of C-S-H and micro-mechanics of cement pastes under NH4NO3 dissolution by 29Si MAS NMR and microhardness. Measurement 2021, 185, 110019. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal GEOMETRY of Nature; W.H. Freeman and Company: San Francisco, CA, USA, 1983. [Google Scholar]
- Shang, X.; Yang, J.; Wang, S.; Zhang, M. Fractal analysis of 2D and 3D mesocracks in recycled aggregate concrete using X-ray computed tomography images. J. Clean. Prod. 2021, 304, 127083. [Google Scholar] [CrossRef]
- Yin, Y.; Ren, Q.; Shen, L. Study on the effect of aggregate distribution on mechanical properties and damage cracks of concrete based on multifractal theory. Constr. Build. Mater. 2020, 262, 120086. [Google Scholar] [CrossRef]
- Winslow, D.N. The fractal nature of the surface of cement paste. Cem. Concr. Res. 1985, 15, 817–824. [Google Scholar] [CrossRef]
- Gao, Y.; Gu, Y.; Mu, S.; Jiang, J.; Liu, J. The multifractal property of heterogeneous microstructure in cement paste. Fractals 2021, 29, 2140006. [Google Scholar] [CrossRef]
- Tang, S.; He, Z.; Cai, X.; Cai, R.; Zhou, W.; Li, Z.; Shao, H.; Wu, T.; Chen, E. Volume and surface fractal dimensions of pore structure by NAD and LT-DSC in calcium sulfoaluminate cement pastes. Constr. Build. Mater. 2017, 143, 395–418. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, J.; Han, S. Fractal analysis of relation between strength and pore structure of hardened mortar. Constr. Build. Mater. 2017, 135, 1–7. [Google Scholar] [CrossRef]
- Tang, S.; Huang, J.; Duan, L.; Yu, P.; Chen, E. A review on fractal footprint of cement-based materials. Powder Technol. 2020, 370, 237–250. [Google Scholar] [CrossRef]
- Zarnaghi, V.N.; Fouroghi-Asl, A.; Nourani, V.; Ma, H. On the pore structures of lightweight self-compacting concrete containing silica fume. Constr. Build. Mater. 2018, 193, 557–564. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.M.; Guo, F.X.; Wang, Y.; Tang, S.W. Pore Structural and Fractal Analysis of the Influence of FLY ASH and Silica Fume on the Mechanical Property and Abrasion Resistance of Concrete. Fractals 2021, 29, 2140003. [Google Scholar] [CrossRef]
- Liu, P.; Chen, Y.; Sha, F.; Yu, Z.; Shao, G. Study on micro structure and composition distribution of concrete surface zone based on fractal theory and XCT technology. Constr. Build. Mater. 2020, 263, 120209. [Google Scholar] [CrossRef]
- Rolph, S. Fractal geometry: Mathematical foundations and applications. Math. Gaz. 1990, 74, 288–317. [Google Scholar]
- Wang, L.; Jin, M.; Wu, Y.; Zhou, Y.; Tang, S. Hydration, shrinkage, pore structure and fractal dimension of silica fume modified low heat Portland cement-based materials. Constr. Build. Mater. 2021, 272, 121952. [Google Scholar] [CrossRef]
- Huang, J.; Li, W.; Huang, D.; Wang, L.; Chen, E.; Wu, C.; Wang, B.; Deng, H.; Tang, S.; Shi, Y.; et al. Fractal Analysis on Pore Structure and Hydration of Magnesium Oxysulfate Cements by First Principle, Thermodynamic and Microstructure-Based Methods. Fractal Fract. 2021, 5, 164. [Google Scholar] [CrossRef]
- Zhang, B.; Li, S. Determination of the Surface Fractal Dimension for Porous Media by Mercury Porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, W.; Liu, X. Scale-dependent nature of the surface fractal dimension for bi- and multi-disperse porous solids by mercury porosimetry. Appl. Surf. Sci. 2006, 253, 1349–1355. [Google Scholar] [CrossRef]
- Neimark, A. A new approach to the determination of the surface fractal dimension of porous solids. Phys. A: Stat. Mech. its Appl. 1992, 191, 258–262. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three. I. Fractal theory of heterogeneous surfaces. J. Chem. Phys. 1983, 79, 3558–3565. [Google Scholar] [CrossRef]
- Jaroniec, M. Evaluation of the fractal dimension from a single adsorption isotherm. Langmuir 1995, 11, 2316–2317. [Google Scholar] [CrossRef]
- Neimark, A.V.; Unger, K.K. Method of Discrimination of Surface Fractality. J. Colloid Interface Sci. 1993, 158, 412–419. [Google Scholar] [CrossRef]
- Avnir, D.; Jaroniec, M. An isotherm equation for adsorption on fractal surfaces of heterogeneous porous materials. Langmuir 1989, 5, 1431–1433. [Google Scholar] [CrossRef]
- Pfeifer, P.; Cole, M.W.; Krim, J. Pfeifer, Cole, and Krim reply. Phys. Rev. Lett. 1990, 65, 663. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Chan, S.; Feng, N. Fractal model for simulating the space-filling process of cement hydrates and fractal dimensions of pore structure of cement-based materials. Cem. Concr. Res. 1997, 27, 1691–1699. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Cao, M.; Tang, Y.; Zhang, Z. Nanoindentation and porosity fractal dimension of calcium carbonate whisker reinforced cement paste after elevated temperatures (up to 900 °C). Fractals 2021, 29, 2140001. [Google Scholar] [CrossRef]
- Wang, L.; He, T.; Zhou, Y.; Tang, S.; Tan, J.; Liu, Z.; Su, J. The influence of fiber type and length on the cracking resistance, durability and pore structure of face slab concrete. Constr. Build. Mater. 2021, 282, 122706. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Liang, M.; Yang, S.; Miao, T.; Yu, B. Analysis of electroosmotic characters in fractal porous media. Chem. Eng. Sci. 2015, 127, 202–209. [Google Scholar] [CrossRef]
- Tang, S.; Cai, X.; Zhou, W.; Shao, H.; He, Z.; Li, Z.; Ji, W.; Chen, E. In-situ and continuous monitoring of pore evolution of calcium sulfoaluminate cement at early age by electrical impedance measurement. Constr. Build. Mater. 2016, 117, 8–19. [Google Scholar] [CrossRef]
- Wheatcraft, S.W.; Tyler, S.W. An explanation of scale-dependent dispersivity in heterogeneous aquifers using concepts of fractal geometry. Water Resour. Res. 1988, 24, 566–578. [Google Scholar] [CrossRef]
- Yu, B. Analysis of Flow in Fractal Porous Media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Tang, S.; Chen, E.; Shao, H.; Li, Z. A fractal approach to determine thermal conductivity in cement pastes. Constr. Build. Mater. 2015, 74, 73–82. [Google Scholar] [CrossRef]
- Tang, S.; Li, Z.; Zhu, H.; Shao, H.; Chen, E. Permeability interpretation for young cement paste based on impedance measurement. Constr. Build. Mater. 2014, 59, 120–128. [Google Scholar] [CrossRef]
- Tang, S.W.; Li, Z.J.; Chen, E.; Shao, H.Y. Impedance measurement to characterize the pore structure in Portland cement paste. Constr. Build. Mater. 2014, 51, 106–112. [Google Scholar] [CrossRef]
- Issa, M.A.; Issa, M.A.; Islam, M.S.; Chudnovsky, A. Fractal dimension—A measure of fracture roughness and toughness of concrete. Eng. Fract. Mech. 2003, 70, 125–137. [Google Scholar] [CrossRef]
- Lange, D.; Jennings, H.M.; Shah, S.P. Relationship between Fracture Surface Roughness and Fracture Behavior of Cement Paste and Mortar. J. Am. Ceram. Soc. 1993, 76, 589–597. [Google Scholar] [CrossRef]
- Wang, Y.; Diamond, S. A fractal study of the fracture surfaces of cement pastes and mortars using a stereoscopic SEM method. Cem. Concr. Res. 2001, 31, 1385–1392. [Google Scholar] [CrossRef]
- Yan, A.; Wu, K.-R.; Zhang, N.; Yao, W. Influence of concrete composition on the characterization of fracture surface. Cem. Concr. Compos. 2003, 25, 153–157. [Google Scholar] [CrossRef]
- Konkol, J.; Prokopski, G. Fracture toughness and fracture surfaces morphology of metakaolinite-modified concrete. Constr. Build. Mater. 2016, 123, 638–648. [Google Scholar] [CrossRef]
- Ficker, T. Fractal strength of cement gels and universal dimension of fracture surfaces. Theor. Appl. Fract. Mech. 2008, 50, 167–171. [Google Scholar] [CrossRef]
- Erdem, S. X-ray computed tomography and fractal analysis for the evaluation of segregation resistance, strength response and accelerated corrosion behaviour of self-compacting lightweight concrete. Constr. Build. Mater. 2014, 61, 10–17. [Google Scholar] [CrossRef]
- Zheng, D.; Song, W.; Fu, J.; Xue, G.; Li, J.; Cao, S. Research on mechanical characteristics, fractal dimension and internal structure of fiber reinforced concrete under uniaxial compression. Constr. Build. Mater. 2020, 258, 120351. [Google Scholar] [CrossRef]
- Ringot, E.; Bascoul, A. About the analysis of microcracking in concrete. Cem. Concr. Compos. 2001, 23, 261–266. [Google Scholar] [CrossRef]
- Szeląg, M. Fractal characterization of thermal cracking patterns and fracture zone in low-alkali cement matrix modified with microsilica. Cem. Concr. Compos. 2020, 114, 103732. [Google Scholar] [CrossRef]
- Zhu, D.; Tang, A.; Wan, C.; Zeng, Y.; Wang, Z. Investigation on the flexural toughness evaluation method and surface cracks fractal characteristics of polypropylene fiber reinforced cement-based composites. J. Build. Eng. 2021, 43, 103045. [Google Scholar] [CrossRef]
- Zhuang, N.; Dong, H.; Zhou, Y.; Chen, D. Cracking behavior of reinforced concrete piles externally bonded with carbon fiber reinforced polymer in a marine environment. Constr. Build. Mater. 2018, 190, 1154–1162. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, Y.; Zhou, Y.; Pan, T.; Zhang, Q.; Liu, D. Cracking behavior of reinforced concrete beams strengthened with CFRP anchorage system under cyclic and monotonic loading. Eng. Struct. 2020, 207, 110222. [Google Scholar] [CrossRef]
- Peng, J.; Wu, Z.; Zhao, G. Fractal analysis of fracture in concrete. Theor. Appl. Fract. Mech. 1997, 27, 135–140. [Google Scholar] [CrossRef]
- Li, L.; Sun, H.-X.; Zhang, Y.; Yu, B. Surface Cracking and Fractal Characteristics of Bending Fractured Polypropylene Fiber-Reinforced Geopolymer Mortar. Fractal Fract. 2021, 5, 142. [Google Scholar] [CrossRef]
- Yu, K.; Zheng, Z.S. Fractal study on granularity distribution of powder. Mat. Sci. Eng. 1995, 13, 30–34. [Google Scholar] [CrossRef]
- Wang, L.J.; Huang, F.Y.; Ma, X.C. Experimental research on the saturation point of superplasticizers in cement based on frac-tal dimension. J. Wuhan Univ. Technol. 2008, 30, 36–39. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, X.; Gao, L.; Bai, Y. Characterization of the mesostructural organization of cement particles in fresh cement paste. Constr. Build. Mater. 2016, 124, 1038–1050. [Google Scholar] [CrossRef]
- Mindess, S.; Young, J.F.; Darwin, D. Concrete, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Duan, P.; Shui, Z.; Chen, W.; Shen, C. Effects of metakaolin, silica fume and slag on pore structure, interfacial transition zone and compressive strength of concrete. Constr. Build. Mater. 2013, 44, 1–6. [Google Scholar] [CrossRef]
- An, M.; Wang, Y.; Yu, Z. Damage mechanisms of ultra-high-performance concrete under freeze–thaw cycling in salt solution considering the effect of rehydration. Constr. Build. Mater. 2019, 198, 546–552. [Google Scholar] [CrossRef]
- Jin, S.; Zheng, G.; Yu, J. A micro freeze-thaw damage model of concrete with fractal dimension. Constr. Build. Mater. 2020, 257, 119434. [Google Scholar] [CrossRef]
- Aili, A.; Maruyama, I. Review of Several Experimental Methods for Characterization of Micro- and Nano-Scale Pores in Cement-Based Material. Int. J. Concr. Struct. Mater. 2020, 14, 14. [Google Scholar] [CrossRef]
- Honorio, T.; Bary, B.; Benboudjema, F. Thermal properties of cement-based materials: Multiscale estimations at early-age. Cem. Concr. Compos. 2018, 87, 205–219. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.X.; Yang, H.M.; Wang, Y.; Tang, S.W. Comparison of FLY ASH, PVA Fiber, MgO and Shrinkage-reducing Admixture on the Frost Resistance of Face Slab Concrete via Pore Structural and Fractal Analysis. Fractals 2021, 29, 2140002. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, G.; Pang, C.; Yan, X.; Qin, H. Influence of pore structures on the frost resistance of concrete. Mag. Concr. Res. 2017, 69, 271–279. [Google Scholar] [CrossRef]
- Hu, W. Modeling the Influence of Composition and Pore Structure on Mechanical Properties of Autoclaved Cellular Concrete. Ph.D. Dissertation, University of Pittsburgh, Pittsburgh, PA, USA, 1997. [Google Scholar]
- Mechtcherine, V. Fracture mechanical behavior of concrete and the condition of its fracture surface. Cem. Concr. Res. 2009, 39, 620–628. [Google Scholar] [CrossRef]
- Erdem, S.; Blankson, M.A. Fractal–fracture analysis and characterization of impact-fractured surfaces in different types of concrete using digital image analysis and 3D nanomap laser profilometery. Constr. Build. Mater. 2013, 40, 70–76. [Google Scholar] [CrossRef]
- Matsuoka, S. Fractal Character of Fracture Surfaces on Metals. Zairyo 1991, 40, 498–505. [Google Scholar] [CrossRef][Green Version]
- Kim, J.; Choi, Y.C.; Choi, S. Fractal Characteristics of Pore Structures in GGBFS-based Cement Pastes. Appl. Surf. Sci. 2018, 428, 304–314. [Google Scholar] [CrossRef]
- Guo, W.; Qin, H.G.; Chen, H.S.; Sun, W. Fractal theory and its applications in the study of concrete materials. J. Chin. Silic. Soc. 2010, 38, 1362–1368. [Google Scholar] [CrossRef]
- Moskovits, M. The fractal nature of particle size distributions of grounds clinker. Cem. Concr. Res. 1990, 20, 499–505. [Google Scholar] [CrossRef]
- Guo, W.; Qin, H.; Ji, X.; Shui, Z. Fractal study on properties of general Portland cement. China Concr. Cem. Prod. 2018, 4, 22–25. (In Chinese) [Google Scholar]
- Zhu, M.; Hu, S.; He, Z. Research on the physiochemical properties of Portland cement and its fractal theory. J. Wuhan Univ. Technol. 2008, 30, 28–31. [Google Scholar] [CrossRef]
- Tang, M.; Ba, H. Study on fractal characteristics and activity of superfine fly ash. Mater. Sci. Technol. 2002, 10, 89–92. (In Chinese) [Google Scholar] [CrossRef]
- Tang, M.; Yang, F.; Chen, Z. Chaos and fractal characteristics and durablity of cement- based materials. Concrete 2010, 6, 1–6. (In Chinese) [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-Chong, T.; Dangla, P. Pore structure of cement pastes through NAD and MIP analysis. Adv. Cem. Res. 2016, 28, 23–32. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-Chong, T.; Dangla, P. Pore structure characterization of cement pastes blended with high-volume fly-ash. Cem. Concr. Res. 2012, 42, 194–204. [Google Scholar] [CrossRef]
- Washburn, E.W. Note on a Method of Determining the Distribution of Pore Sizes in a Porous Material. Proc. Natl. Acad. Sci. USA 1921, 7, 115–116. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Cui, S.; Li, Z.; Xu, X.; Guo, C. Influence of surrounding rock temperature on mechanical property and pore structure of concrete for shotcrete use in a hot-dry environment of high-temperature geothermal tunnel. Constr. Build. Mater. 2019, 207, 329–337. [Google Scholar] [CrossRef]
- Aligizaki, K.K. Pore Structure of Cement-Based Materials: Testing, Interpretation and Requirements; CRC Press: Boca Raton, FL, USA, 2005; pp. 1349–1355. [Google Scholar]
- Tang, M.; Li, J.Q. Research on Fractal Characteristics of Cement-Based Materials by Nitrogen Adsorption Method. Adv. Mater. Res. 2011, 415–417, 1545–1552. [Google Scholar] [CrossRef]
- Ridi, F.; Fratini, E.; Baglioni, P. Fractal Structure Evolution during Cement Hydration by Differential Scanning Calorimetry: Effect of Organic Additives. J. Phys. Chem. C 2013, 117, 25478–25487. [Google Scholar] [CrossRef]
- Halperin, W.P.; Jehng, J.-Y.; Song, Y.-Q. Application of spin-spin relaxation to measurement of surface area and pore size distributions in a hydrating cement paste. Magn. Reson. Imaging 1994, 12, 169–173. [Google Scholar] [CrossRef]
- She, A.; Ma, K.; Liao, G.; Yao, W.; Zuo, J. Investigation of hydration and setting process in nanosilica-cement blended pastes: In situ characterization using low field nuclear magnetic resonance. Constr. Build. Mater. 2021, 304, 124631. [Google Scholar] [CrossRef]
- Ji, Y.; Sun, Z.; Yang, X.; Li, C.; Tang, X. Assessment and mechanism study of bleeding process in cement paste by 1H low-field NMR. Constr. Build. Mater. 2015, 100, 255–261. [Google Scholar] [CrossRef]
- Wang, L.; He, Z.; Cai, X. Characterization of pozzolanic reaction and its effect on the C-S-H Gel in fly Ash-cement paste. J. Wuhan Univ. Technol. Sci. Ed. 2011, 26, 319–324. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H.; Zhou, S.; Chen, E.; Tang, S. Hydration, mechanical property and C-S-H structure of early-strength low-heat cement-based materials. Mater. Lett. 2018, 217, 151–154. [Google Scholar] [CrossRef]
- He, Z.; Liang, W.; Wang, L.; Wang, J. Synthesis of C3S by sol-gel technique and its features. J. Wuhan Univ. Technol. Sci. Ed. 2010, 25, 138–141. [Google Scholar] [CrossRef]
- Pop, A.; Badea, C.; Ardelean, I. The Effects of Different Superplasticizers and Water-to-Cement Ratios on the Hydration of Gray Cement Using T2-NMR. Appl. Magn. Reson. 2013, 44, 1223–1234. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B.; Zou, M.; Luo, L. Fractal characterization of spontaneous co-current imbibition in porous media. Energy Fuels 2010, 24, 1860–1867. [Google Scholar] [CrossRef]
- ASTM International. ASTM C457/457M-16. In Standard Test Method for Microscopical Determination of Parameters of the Air-Void System in Hardened Concrete; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- China Electricity Council. DL/T 5150-2017. In Test Code for Hydraulic Concrete; China Electric Power Press: Beijing, China, 2017. [Google Scholar]
- Friel, J.; Pande, C. A direct determination of fractal dimension of fracture surfaces using scanning electron microscopy and stereoscopy. J. Mater. Res. 1993, 8, 100–104. [Google Scholar] [CrossRef]
- Goff, T. Comment on “Fractal mapping of digitized images: Application to the topography of Arizona and comparison with synthetic images” by J. Huang and DL Turcotte. J. Geophys. Res.-Sol. Ea. 1990, 95, 5159. [Google Scholar] [CrossRef]
- Cao, T.; Wang, W.; Tighe, S.; Wang, S. Crack image detection based on fractional differential and fractal dimension. IET Comput. Vis. 2019, 13, 79–85. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H.; Zhou, S.; Chen, E.; Tang, S. Mechanical properties, long-term hydration heat, shinkage behavior and crack resistance of dam concrete designed with low heat Portland (LHP) cement and fly ash. Constr. Build. Mater. 2018, 187, 1073–1091. [Google Scholar] [CrossRef]
- Yang, X.; Li, L.; Dai, H.; Jia, M. Effect of fractal dimension in concrete meso-structure on its axial mechanical behavior: A numerical case study. Fractals 2021, 29, 2140011. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H.; Dong, Y.; Chen, E.; Tang, S. Environmental evaluation, hydration, pore structure, volume deformation and abrasion resistance of low heat Portland (LHP) cement-based materials. J. Clean. Prod. 2018, 203, 540–558. [Google Scholar] [CrossRef]
- Shi, Y.; Dong, Y.; Wang, L.; Chen, X.; Li, X. Different Chemical Composition of Aggregate Impact on Hydraulic Concrete Interfacial Transition Zone. Asian J. Chem. 2014, 26, 1267–1270. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.; Lin, Y.; Yang, H.; Tang, S. Comparison between the effects of phosphorous slag and fly ash on the C-S-H structure, long-term hydration heat and volume deformation of cement-based materials. Constr. Build. Mater. 2020, 250, 118807. [Google Scholar] [CrossRef]
- Wang, L.; Dong, Y.; Zhou, S.; Chen, E.; Tang, S. Energy saving benefit, mechanical performance, volume stabilities, hydration properties and products of low heat cement-based materials. Energy Build. 2018, 170, 157–169. [Google Scholar] [CrossRef]
- Li, Y.; Bao, J.; Guo, Y. The relationship between autogenous shrinkage and pore structure of cement paste with mineral admixtures. Constr. Build. Mater. 2010, 24, 1855–1860. [Google Scholar] [CrossRef]
- Ma, Y.; Ye, G. The shrinkage of alkali activated fly ash. Cem. Concr. Res. 2015, 68, 75–82. [Google Scholar] [CrossRef]
- Wang, L.; Luo, R.Y.; Zhang, W.; Jin, M.M.; Tang, S.W. Effects of Fineness and Content of Phosphorus Slag on Cement Hydration, Permeability, Pore Structure and Fractal Dimension of Concrete. Fractals 2021, 29, 2140004. [Google Scholar] [CrossRef]
- Zheng, J.-J.; Wong, H.; Buenfeld, N.R. Assessing the influence of ITZ on the steady-state chloride diffusivity of concrete using a numerical model. Cem. Concr. Res. 2009, 39, 805–813. [Google Scholar] [CrossRef]
- Lv, X.; Dong, Y.; Wang, R.; Lu, C.; Wang, X. Resistance improvement of cement mortar containing silica fume to external sulfate attacks at normal temperature. Constr. Build. Mater. 2020, 258, 119630. [Google Scholar] [CrossRef]
- Dong, Y. Effects of mineral admixture on the carbonic acid leaching resistance of cement-based materials. Ceram.-Silik. 2017, 61, 276–284. [Google Scholar] [CrossRef][Green Version]
- Awoyera, P.; Akinmusuru, J.; Dawson, A.; Ndambuki, J.; Thom, N. Microstructural characteristics, porosity and strength development in ceramic-laterized concrete. Cem. Concr. Compos. 2018, 86, 224–237. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Crumbie, A.K.; Laugesen, P. The Interfacial Transition Zone (ITZ) Between Cement Paste and Aggregate in Concrete. Interface Sci. 2004, 12, 411–421. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Quantitative prediction of permeability in porous rock. Phys. Rev. B 1986, 34, 8179–8181. [Google Scholar] [CrossRef] [PubMed]
- Şahmaran, M.; Özbay, E.; Yücel, H.E.; Lachemi, M.; Li, V. Frost resistance and microstructure of Engineered Cementitious Composites: Influence of fly ash and micro polyvinyl alcohol fiber. Cem. Concr. Compos. 2012, 34, 156–165. [Google Scholar] [CrossRef]
- ASTM International. ASTM C666/666M-15. In Standard Test Method for Resistance of Concrete to Rapid freezing and Thawing; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Powers, T.C.; Brownyard, T.L. Studies of the physical properties of hardened Portland cement paste—Part 8. The freezing of water in hardened Portland cement paste. J. Am. Concr. Inst. 1947, 18, 933–969. [Google Scholar]
- Xiao, J.; Qu, W.; Jiang, H.; Li, L.; Huang, J.; Chen, L. Fractal characterization and mechanical behavior of pile-soil interface Subjected to sulfuric acid. Fractals 2021, 29, 2140010. [Google Scholar] [CrossRef]
- Xiao, J.; Long, X.; Qu, W.; Li, L.; Jiang, H.; Zhong, Z. Influence of sulfuric acid corrosion on concrete stress-strain relationship under uniaxial compression. Measurement 2021, 185, 110318. [Google Scholar] [CrossRef]
- Xiao, J.; Long, X.; Li, L.; Jiang, H.; Zhang, Y.; Qu, W. Study on the Influence of Three Factors on Mass Loss and Surface Fractal Dimension of Concrete in Sulfuric Acid Environments. Fractal Fract. 2021, 5, 146. [Google Scholar] [CrossRef]
- Xiao, J.; Qu, W.; Jiang, H.; Dong, W. Three-Dimensional Fractal Characterization of Concrete Surface Subjected to Sulfuric Acid Attacks. J. Nondestruct. Eval. 2020, 39, 57. [Google Scholar] [CrossRef]
- Issa, M.; Hammad, A. Assessment and evaluation of fractal dimension of concrete fracture surface digitized images. Cem. Concr. Res. 1994, 24, 325–334. [Google Scholar] [CrossRef]
- Cai, W.; Cen, G.; Wang, H. Fracture Surface Fractal Characteristics of Alkali-Slag Concrete under Freeze-Thaw Cycles. Adv. Mater. Sci. Eng. 2017, 2017, 168913. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Athanasiou, A.; Hrynyk, T.; Bayrak, O.; Salamone, S. Fractal and Multifractal Analysis of Crack Patterns in Prestressed Concrete Girders. J. Bridg. Eng. 2019, 24, 04019059. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).