Fractal Analysis on Pore Structure and Hydration of Magnesium Oxysulfate Cements by First Principle, Thermodynamic and Microstructure-Based Methods

Abstract

Magnesium oxysulfate (MOS) cement is a typical eco-friendly cementitious material, which presents excellent performances. In this work, a novel multiscale modeling strategy is proposed to simulate the hydration and pore structure of MOS cement system. This work collected and evaluated the Gibbs free energy of formation for main hydrates and equilibrium constant of main reactions in MOS cement system based on a first principle calculation using Material Studio. Followingly, the equilibrium phase compositions of MOS cement system were simulated through PHREEQC to investigate the molar ratio dependence of equilibrium phase compositions. Results showed that large M (MgO/MgSO₄) was beneficial for the formation of 5Mg(OH)₂·MgSO₄·7H₂O (Phase 517) and large H (H₂O/MgSO₄) tended to decompose MOS cement paste and cause leaching. The microstructure-based method visualized the hydration status of MOS cement systems at initial and ultimate stages via MATLAB and the results showed that large M was significant to reduce porosity, and similar results for the case of small H. Fractal analysis confirms that fractal dimension of pore structure (D_f) was significantly decreased after the hydration of MOS and was positively correlated to the porosity of the paste. In addition, it can be referred that large M and small H were beneficial for modifying the microstructure of MOS paste by decreasing the value of D_f.

1. Introduction

In recent decades, the explosive development of MgO-based cements has lied in an environmental consideration. Compared to the manufacture temperature of ordinary Portland cement, the lower temperature is required to produce MgO. Therefore, the energy saving associated with this decreased temperature makes MgO-based cements the core of eco-friendly cement production in the future. Magnesium oxysulfate cement (MOS) is a typical eco-friendly non-hydraulic material, first proposed by a Belgian scholar in 1957, similar to the magnesium oxychloride cement (MOC) [1,2]. MOS paste is prepared through the chemical reaction of active MgO powder and magnesium sulfate solution. MOS-based materials have attracted much attention due to their excellent performances, such as good fire resistance, good steel protection, low density and thermal conductivity, etc. [3,4]. MOS paste is similar in concept to MOC paste, except that MgSO₄ solution is used instead of MgCl₂ solution to form cementitious binder. Typically, the main chemical reactions in MOS cement system are shown as below:

$$5\mathsf{M}\mathsf{g}\mathsf{O}+\mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4+12{\mathsf{H}}_2\mathsf{O}\to 5\mathsf{M}\mathsf{g}{(\mathsf{O}\mathsf{H})}_2\cdot \mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4\cdot 7{\mathsf{H}}_2\mathsf{O}$$

(1)

$$3\mathsf{M}\mathsf{g}\mathsf{O}+\mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4+11{\mathsf{H}}_2\mathsf{O}\to 3\mathsf{M}\mathsf{g}{(\mathsf{O}\mathsf{H})}_2\cdot \mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4\cdot 8{\mathsf{H}}_2\mathsf{O}$$

(2)

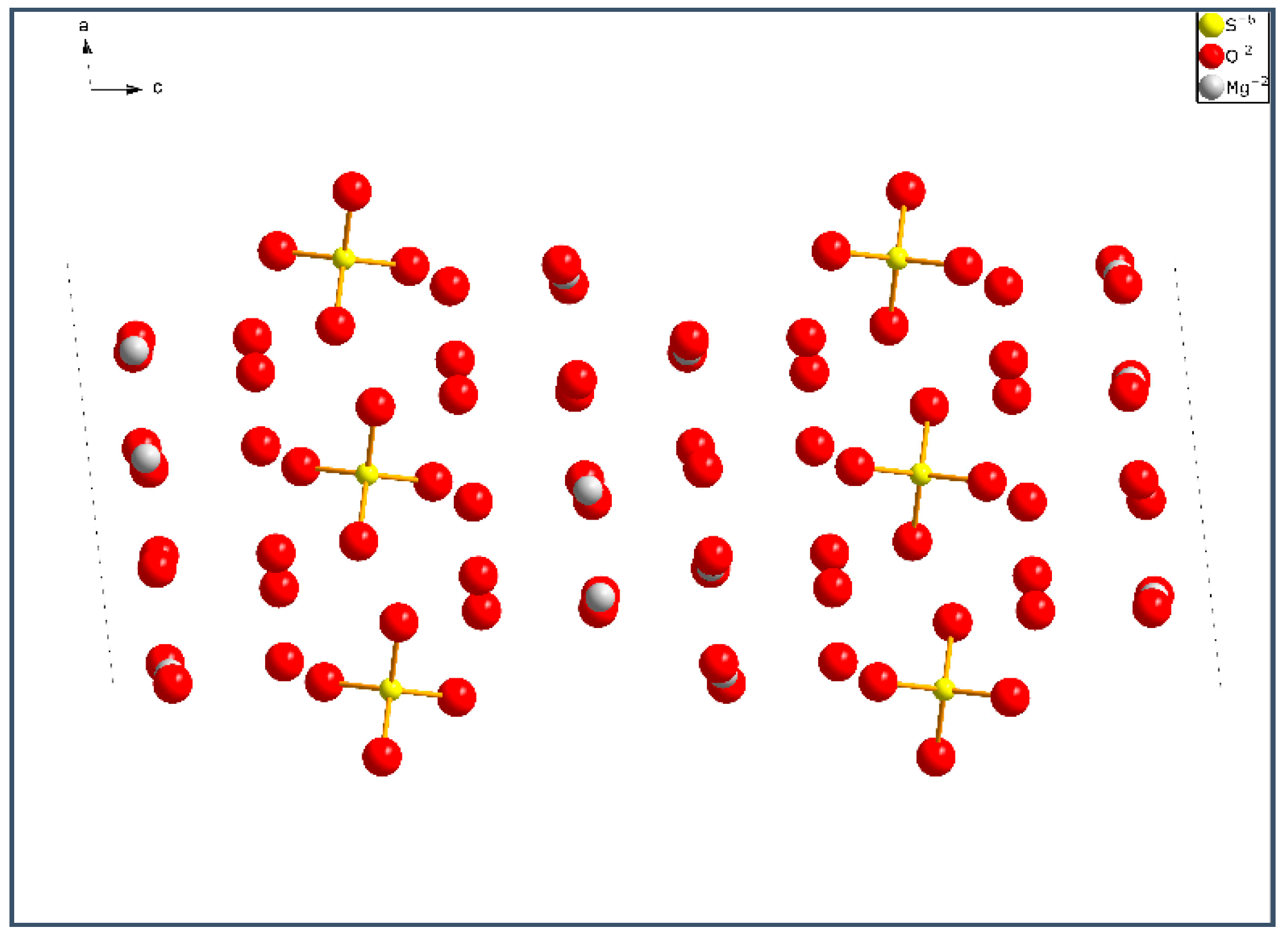
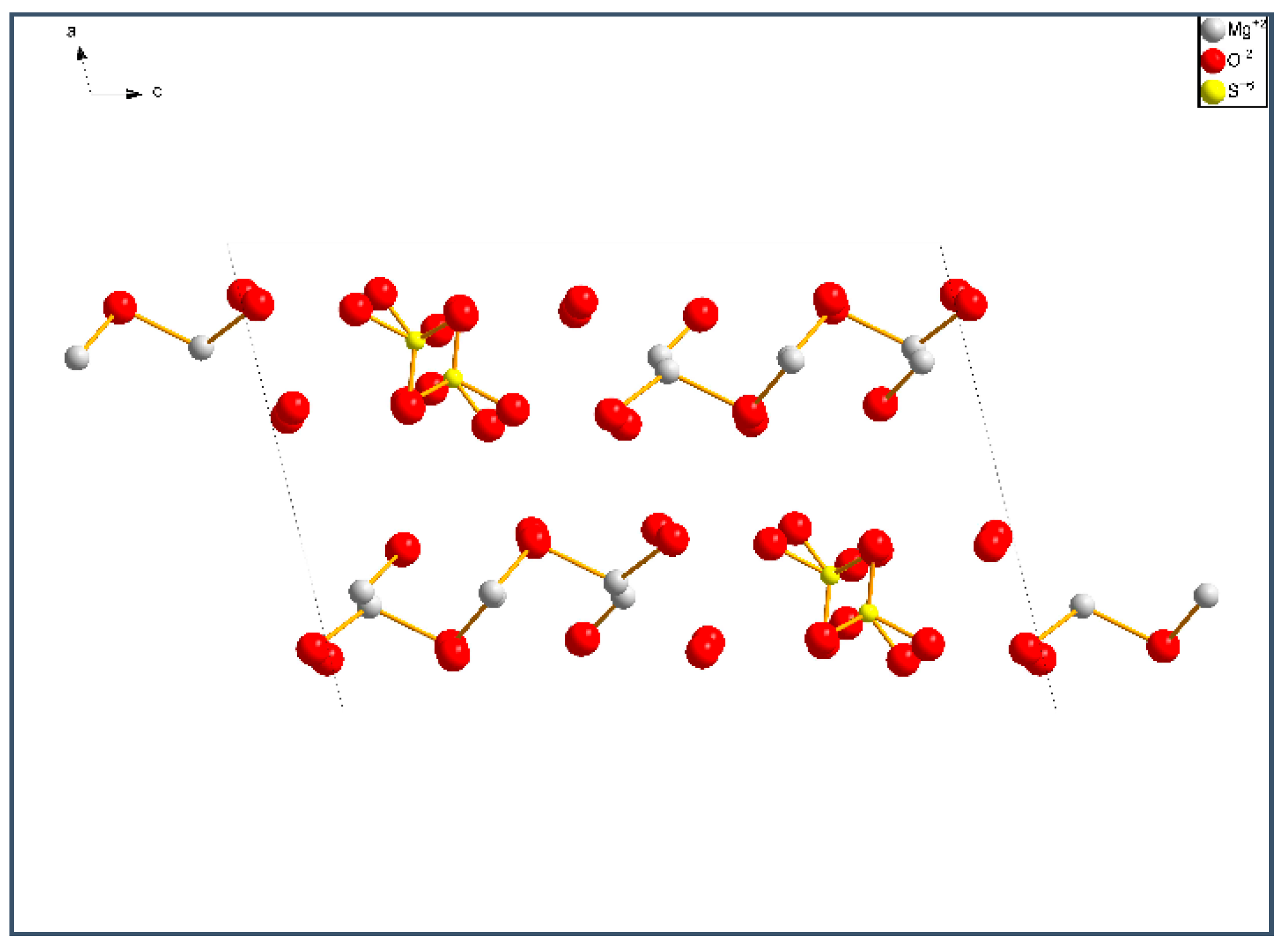
As early as in 1957, Demediuk and Cole [1] analyzed the hydrated products in the MOS paste under the temperature range of 30–120 °C. They identified four magnesium oxysulfate phases (Phase 318, Phase 513, Phase 115 and Phase 123). Phases 512, 517, 131, 122, 251 and 514 were reported in other literatures [5]. These phases observed in MOS pastes are shown in

Table 1. Phases observed in MOS pastes.

Phase Notation	Chemical Formula	References
318	3Mg(OH)2·MgSO4·8H2O	Dinnebier et al. [5]
513 (or 512)	5Mg(OH)2·MgSO4·3H2O (5Mg(OH)2·MgSO4·2H2O)	Demediuk and Cole [1]
115	Mg(OH)2·MgSO4·5H2O	Demediuk and Cole [1]
123	Mg(OH)2·2MgSO4·3H2O	Demediuk and Cole [1]
122	Mg(OH)2·2MgSO4·2H2O	Demediuk and Cole [1]
251	2Mg(OH)2·5MgSO4·H2O	Demediuk and Cole [1]
517	5Mg(OH)2·MgSO4·7H2O	Runčevski et al. [6]
131	Mg(OH)2·3MgSO4·H2O	Keefer et al. [7]
514	5Mg(OH)2·MgSO4·4H2O	Hamada et al. [8]

.

The phase transformation and stability of hydrated phases in MOS paste, are expected to be primarily associated with two molar ratios, i.e., MgO/MgSO₄ (M) and H₂O/MgSO₄ (H). 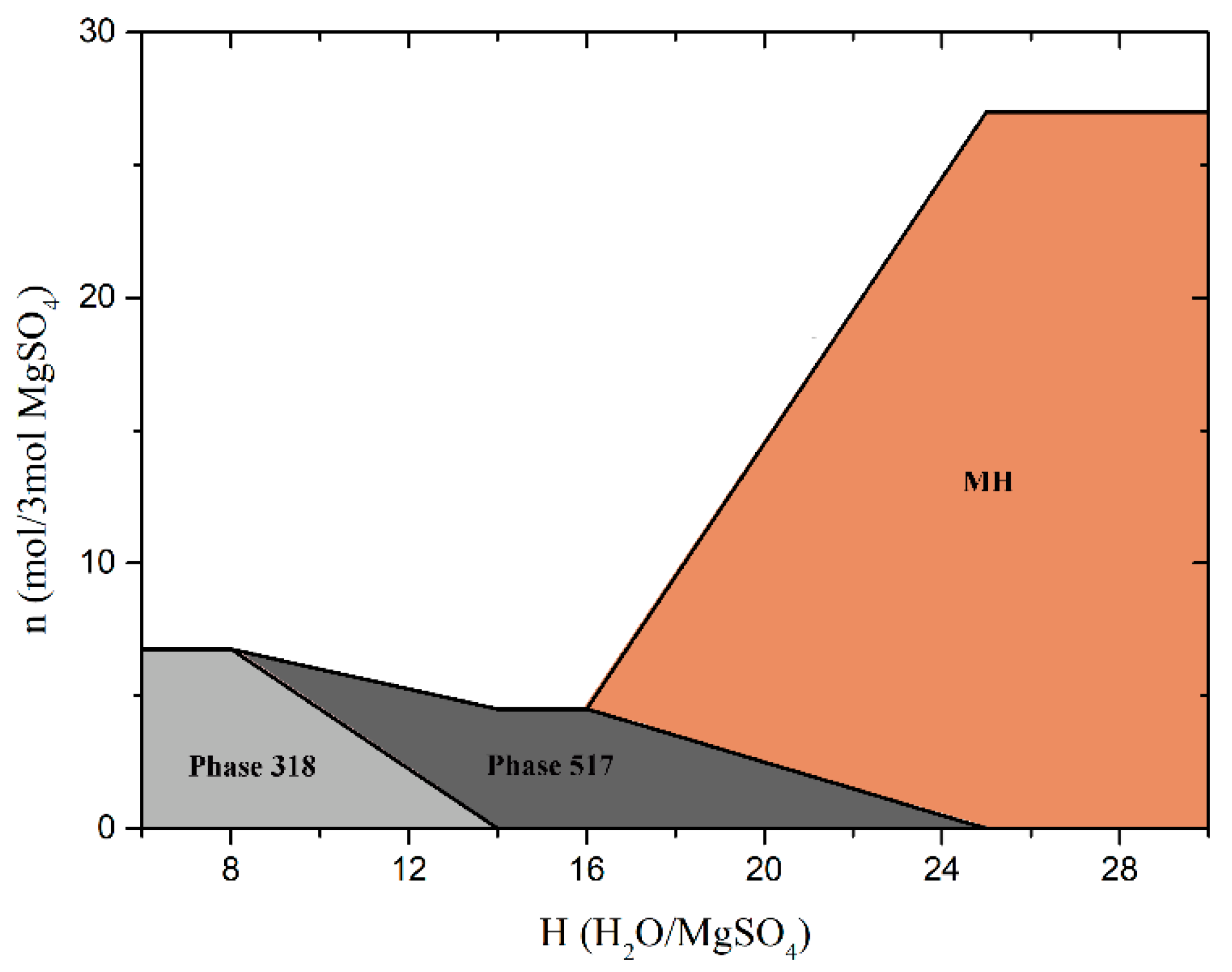Generally, the following six main phases are generated within the temperature range from 30 °C to 120 °C [9]: Phase 517 (5Mg(OH)₂·MgSO₄·7H₂O), Phase 318 (3Mg(OH)₂·MgSO₄·8H₂O), Phase 513 (5Mg(OH)₂·MgSO₄·3H₂O), Phase 115 (Mg(OH)₂·MgSO₄·5H₂O), Phase 123 (Mg(OH)₂·2MgSO₄·3H₂O) and magnesium hydroxide (MH). When M increases from 3 to 9, the main hydrated products are found to be Phase 318, Phase 517, and MH [10,11]. It is believed that Phase 517 has the high strength and good water resistance [9]. However, it is noted that the low strength and chemical instability of eco-friendly MOS-based materials primarily hinder their large-scale applications to some extent.

Thermodynamics is an indispensable tool for understanding and studying chemical reactions [12]. It is generally accepted that the thermodynamic simulation can be applied to characterize the composition of hydrated products of cement pastes. Lothenbach et al. developed a model to simulate the composition of pore solution and the hydrated products in the hydration process of ordinary Portland cement based on the Parrot-Killoh hydration rate equation [13] where the influences of sulfate attacks [14], temperature [15] and additives [16] were considered. Similarly, Möschner et al. [17] explored the effect of citric acid on the composition of solid and liquid phases in the hydrating cement pastes based on thermodynamic calculations. The citric acid was found to significantly change the composition of hydrated products but had little influence on the composition of the pore solution. Recently, Zhou et al. [18] utilized a thermodynamic approach to study the formation conditions of two major hydrated products (Mg₃(OH)₅Cl·4H₂O and Mg₂(OH)₃Cl·4H₂O) of MOC pastes under room temperature. The results showed that the formation of hydrated products was controlled by the concentration of MgCl₂, activity of H₂O and pH values of the paste. The equilibrium of solid phase diagram and the solubility of different hydrated phases were consistent with those results obtained from experimental studies. Li et al. [19] developed a temperature-dependent thermodynamic model for Mg(OH)₂ + MgSO₄ + H₂O system based on CALPHAD approach. Thermodynamic properties of several magnesium hydroxide sulfate hydrates were determined as functions of temperature. In summary, the present thermodynamic simulations have primarily been applied to simulate Portland cements and sulphoaluminate cements. The relevant thermodynamics database is only applicable for Portland cement and sulphoaluminate cements, and there is lack of report on the thermodynamic database dedicated to the MOS cement system. First principle calculation, as one powerful research tool inquiring the properties of materials from the atomic and molecular levels, has been successfully applied to investigate the thermodynamic properties of materials [20,21]. The most widely-used software based on the first principle calculation are WIEN [22], Gaussian 98 [23] and Material Studio [24]. A comparison among them is listed in

Table 2. A Comparison of different software based on the first principle calculation.

Software	Advantage(s)	Disadvantage(s)	References
WIEN	Base on Linux operating system; a concise user interface; Compiled using FORTRAN language	Not available in WINDOWS	[22]
Gaussian 98	Different calculation methods; Suitable for organic macromolecular material	Not suitable for heavy metals	[23]
Material Studio	Establish model easily	Time-consuming	[24]

. Therefore, it is very meaningful to establish a thermodynamic database that is applicable for the hydrating MOS-based materials through the first principle calculation.

Customarily, cement-based materials are considered as porous composite materials, perhaps consisting of a binding matrix and/or fragment of aggregates [25,26]. The pore structure affects the physical and chemical properties, and controls the durability of material [27,28,29]. During past few years, several microstructure-based models, such as the durability models of concrete model (DuCOM) by Chaube et al. [30], HYMOSTRUC by Van Breugel [31], and μic by Bishnoi and Scrivener [32], have been proposed to simulate the pore structure of cement paste at the micro level. Recently, a status-oriented computer model [33] has been proposed to simulate the microstructure of OPC pastes. It is assumed that four phases (unhydrated cement grains, large capillary pores, inner and outer hydrated product layers) are contained in the hydrated cement paste. The microstructure of cement paste can be simulated as a function of cement particle distribution, water to cement ratio, and degree of hydration. Compared to early developed models, HYMOSTRUC and μic only focus on the early hydration stage of cement-based materials and DuCOM is inapplicable to the poly-size particle system. Therefore, the status-oriented computer model is adopted in this work. A comparison among these microstructure-based models is illustrated in

Table 3. A comparison among these microstructure-based models.

	HYMOSTRUC [31]	μic [32]	DuCOM [30]	Proposed Model [33]
Modeling strategy	Discrete element	Vector based	Discrete element	Discrete element
Particle size distribution	Poly-size	Poly-size	Mono-size	Poly-size
Particle kinetics	No	Yes	No	Yes
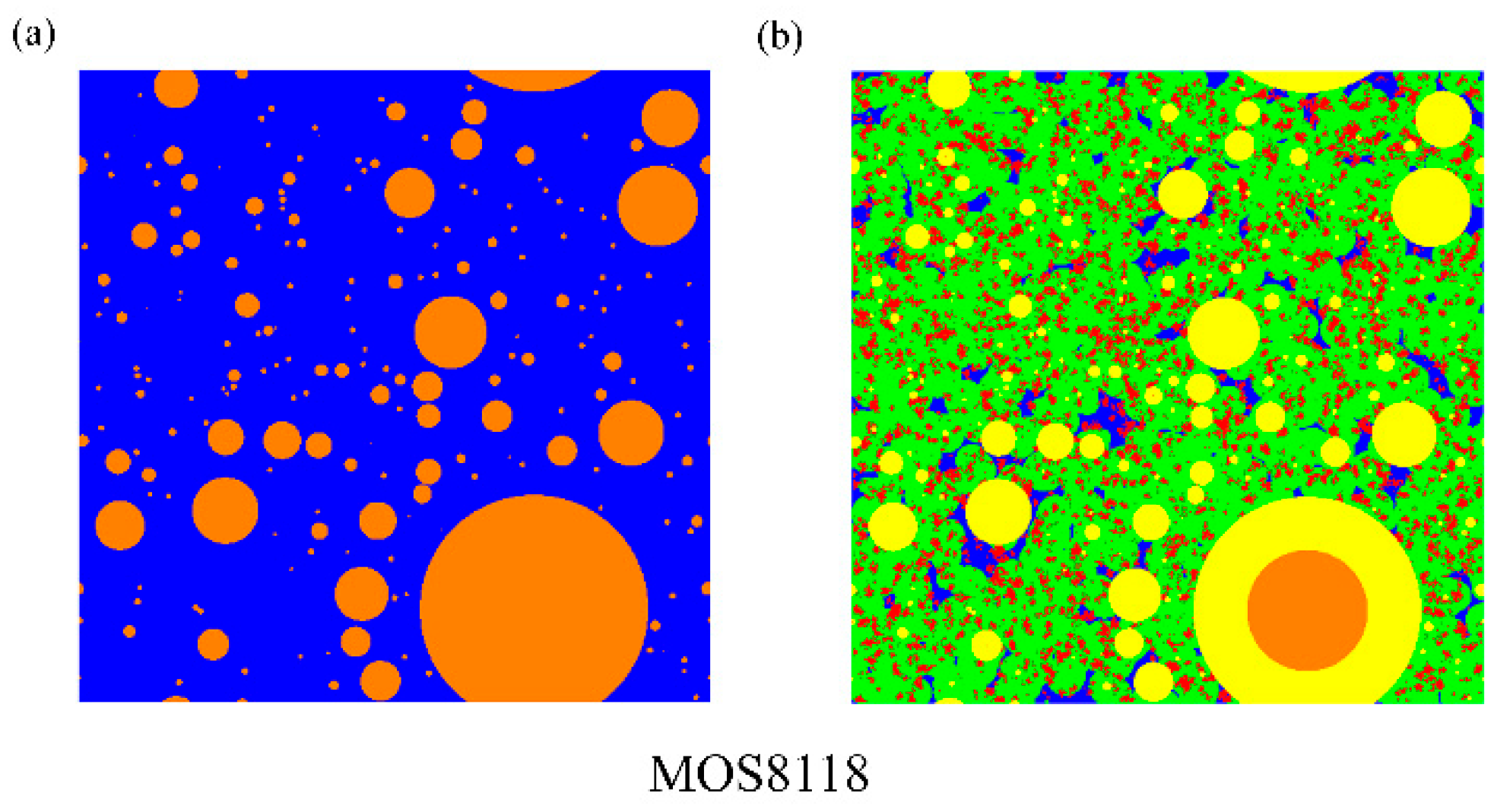
Prediction age	Early term	Early term	Long term	Long term

. The pores in cement-based materials are usually irregular and disordered, which show evident fractal features. The study on the fractal properties of cement-based materials is of great meaning as fractal theories enable to provide novel and effective ways to characterize of the microstructure of cement-based materials.

To address application scenarios of hydration and pore structure modeling on MOS cement paste, a preliminary research is carried out as follows: (1) the thermodynamic database relevant to MOS paste at 25 °C are collected and evaluated by the first principle calculation. (2) By using the established thermodynamic database and the geochemical speciation code PHREEQC, the influence of molar ratios on the equilibrium hydrated products assemblage is investigated. In addition, the basic relationship between the composition of hydrated products at equilibrium state and initial molar ratio is established. (3) Based on the obtained composition of equilibrium product, the visualization of microstructure is carried out based on the proposed models. A comparison among the porosities of MOS pastes with different molar ratios is given and a fractal analysis on the pore structure of MOS paste is conducted. In this work, a first principle calculation is originally adopted to evaluate the thermodynamic properties of phases in MOS cement system considering very little research on the evaluation of thermodynamic data among studies concerning MOS. The calculated thermodynamic data set the basis for the following thermodynamic analysis on the hydration products of MOS system, and thus facilitate the simulation and fractal analysis of pore structure of MOS paste.

2. Methods and Algorithms

2.1. Thermodynamic Modeling

In this work, the thermodynamic modeling is carried out using the geochemical speciation code PHREEQC since it can be used for free, and the database is open to users. In this work, the molar ratios of MgO/MgSO₄/H₂O in MOS cement pastes are set as 6:1:20, 8:1:18, 8:1:20, 8:1:22 and 10:1:20. The corresponding notations of pastes are taken as “MOS6120”, “MOS8118”, “MOS8120”, “MOS8122” and “MOS10120”. The implemented thermodynamic algorithm is appropriate for the MOS paste under temperature between 0 °C and 100 °C, and pressure 0.1 MPa [18]. In the thermodynamic algorithm, there is 3 mol MgSO₄ dissolved in 0.972, 1.08, and 1.188 kg water respectively, and then 30 mol MgO is added into the solution in 1000 steps. The reactions and hydrated products of pastes are recorded until the equilibrium status of MOS paste reaches. Since Phase 115 and Phase 123 are metastable under room temperature and Phase 513 (512) can be stable only under steam-curing conditions [34], it is suggested that Phase 318, Phase 517 and MH should be main products considered in this work. By means of this algorithm, the evolution of Phase 318, Phase 517 and MH with different M and H under temperature 25 °C is investigated in this work [35,36,37,38].

2.2. First Principle Calculation

The thermodynamic data (such as thermodynamic equilibrium constant, K) of MH has been reported. Further, $\mathsf{log}{\mathsf{K}}_{\mathsf{M}\mathsf{g}{(\mathsf{O}\mathsf{H})}_2}=17.11$ is accepted by most literature so that it will be adopted in this work [36,39,40]. Unfortunately, the thermodynamic data of Phase 318 and Phase 517 are not available since the detailed structural information associated with these two phases is not clear and little literature focuses on the investigation of the thermodynamic properties of these two phases. In this work, Material Studio is adopted to carry out a first principle calculation to obtain the thermodynamic data of these two phases.

The crystal structures of Phase 318 (collection code: 425732) and Phase 517 (collection code: 425847) are available in the Inorganic Crystal Structure Database. Figure 1 and Figure 2 show crystal structures of Phase 318 and Phase 517 reconstructed using Diamond software, in which hydrogen atoms are omitted for clarity. First principle calculations are performed using CASTEP based on the density functional theory. There are two types of pseudo-potentials adopted in the CASTEP, i.e., Vanderbilt-type ultrasoft and norm pseudo-potentials. To evaluate the accuracy of two pseudo-potentials, the equilibrium constant of MH is calculated using these two pseudo-potentials to make a comparison as shown in

Table 4. Comparison of two pseudo-potentials by calculating equilibrium constant of MH.

	Experimental Value	Simulation Value	Accuracy (%)
Ultrasoft pseudo-potentials	17.11	17.38	98.4
Norm pseudo-potentials	17.11	17.54	97.5

. Although both pseudo-potentials highly evaluate the equilibrium constant of MH, ultrasoft-pseudo potential presents a better accuracy and performance. Therefore, Vanderbilt-type ultrasoft pseudo-potentials [41] and electron-ion interactions are adopted to evaluate the thermodynamic properties of Phase 318 and Phase 517.

The exchange correlation potential of Ceperley and Alder [42] parameterized by Perdew and Zunger [43] in the local density approximation is used. The self-consistent convergence of the total energy is 2 × 10⁻⁵ eV/atom and the maximal force on the atom is found to be 0.05 eV/Å. For the determination of phonon density of states, the dynamical matrix elements are calculated on the 2 × 2 × 1 grid of k-points using the finite displacement approach. The linear responses to ionic displacements and electric field are measured within the density functional perturbation theory as implemented in CASTEP code.

2.3. Hydration Algorithm

With respect to the hydration of MOS paste, the physical parameters of starting materials and hydrated phases are listed in

Table 5. Physical parameters of starting materials and hydrated phases.

Material	Molar Mass (g/mol)	Density (g/cm3)	Molar Density (cm3/mol)
MgO	40	3.59	11.14
Phase 517	536	1.88	285.11
Phase 318	438	1.875	233.60
MH	58	2.36	24.58

. The computer simulation is performed based on the assumption of the growing of spheres [44,45]. The initial unhydrated MgO particles are considered to be spheres by randomly distributed in a cubic representative elementary volume (REV) with the size of 100 × 100 × 100 μm³ and periodic boundary condition. It is reported that the determination of size of REV is based on the particle size distribution (PSD) of reactive MgO, water to cement ratio and hydration degree [46,47,48,49,50]. The PSD of MgO is accessed from the data of Ref. [51], while those particles whose sizes are smaller than 0.5 μm or larger than 45 μm are not considered in this work for the purpose of reducing the burden of computational simulation. Then the specific PSD is given in REV that is discretized into 500 × 500 × 500 cubic voxels with a length resolution of 0.2 μm. The detailed information of hydration algorithm is consulted in Ref. [45].

The algorithm of calculating porosity is called as “Disk Filling Method” that is based on the ultimate hydration stage of MOS pastes. In this algorithm, a disk with an initial radius is applied to fill the pore in the paste. The radius of the disk will be constantly increased until the pores are fully filled. Therefore, the corresponding pore volume is considered to be equal to the volume of these disks. Therefore, the cumulative porosities of MOS pastes are obtained when the volume of REV is known.

2.4. Fractal Dimensions for Pore Structure

In recent years, fractal theory has been widely used in the study of cementitious materials [52,53,54,55]. According to the fractal theory, the number of pores (N(d)) whose diameters are larger than d and the probability density function of pore size distribution (f(d)) can be expressed as:

$$\mathsf{N}(\mathsf{d})={({\mathsf{d}}_{\mathsf{m}\mathsf{a}\mathsf{x}}/\mathsf{d})}^{{\mathsf{D}}_{\mathsf{f}}}$$

(3)

$$\mathsf{f}(\mathsf{d})={\mathsf{D}}_{\mathsf{f}}\cdot {\mathsf{d}}_{\mathsf{min}}^{{\mathsf{D}}_{\mathsf{f}}}\cdot {\mathsf{d}}^{-{\mathsf{D}}_{\mathsf{f}}-1}$$

(4)

where d, d_max, and d_min are the specific, maximum, minimum pore size, D_f denotes the fractal dimension for pore size and varies in the range of 1–2 in 2D space.

Based on the simulated microstructure, D_f can be efficiently calculated using the box-counting method [44]. This method is based on the image analysis of cross-section of a sample within a plane. In this work, the box-counting method is performed on ten representative slices of REV. At each slice, the D_f is taken as the opposite number of the slope derived from the logarithmic fitting plot (Figure 3) in which N(d ≥ γ) is the cumulative account of pores and γ is the size of box. In addition, following this, ten values are averaged to obtain the final D_f of MOS paste.

3. Results and Analysis

3.1. Results from First Principle Calculation

In this section, the thermodynamic data for different phases from the first principle calculation is presented. The Gibbs free energy (G) of different phases and atoms calculated based on the first principle is shown in

Table 6. The Gibbs free energy of different phases and atoms calculated based on the first principle.

Phases/Atoms	$\mathbf{G}$ (eV)
Phase 318	−14,846.324
Phase 517	−19,252.431
Mg	−973.951
O2	−856.874
H2	−27.348
S	−277.965

.

To further analyze the thermodynamic properties of Phase 318 and Phase 517, the Gibbs free energy of formation (${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$) of these two phases is studied according to the following equation:

$${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}=\frac{1}{\mathsf{a}+\mathsf{b}+\mathsf{c}+\mathsf{d}}({\mathsf{G}}_{\mathsf{t}\mathsf{o}\mathsf{t}\mathsf{a}\mathsf{l}}-\mathsf{a}{\mathsf{G}}_{\mathsf{M}\mathsf{g}}-\frac{\mathsf{b}}{2}{\mathsf{G}}_{{\mathsf{O}}_2}-\frac{\mathsf{c}}{2}{\mathsf{G}}_{{\mathsf{H}}_2}-\mathsf{d}{\mathsf{G}}_{\mathsf{S}})$$

(5)

where ${\mathsf{G}}_{\mathsf{t}\mathsf{o}\mathsf{t}\mathsf{a}\mathsf{l}}$ is the total Gibbs free energy of Phase 318 or Phase 517, ${\mathsf{G}}_{\mathsf{M}\mathsf{g}}$, ${\mathsf{G}}_{{\mathsf{O}}_2}$, ${\mathsf{G}}_{{\mathsf{H}}_2}$, and ${\mathsf{G}}_{\mathsf{S}}$ are Gibbs free energy of Mg, O₂, H₂ and S, which can be consulted in Table 6, a, b, c, d are numbers of corresponding atoms in the phase. ${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$ of Phase 318 and Phase 517 is listed in

Table 7. ${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$ of Phase 318 and Phase 517.

Phases	$\mathbf{Gibbs} \mathbf{Free} \mathbf{Energy} \mathbf{of} \mathbf{Formation}, {\mathbf{\Delta }}_{\mathbf{f}}\mathbf{G} (\mathbf{eV}/\mathbf{atom})$
Phase 318	−58.33
Phase 517	−73.18

. The calculated results are comparable to the results reported from Ref. [19], in which ${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$ of Phase 318 and Phase 517 are −58.06 eV and −72.82 eV.

Once ${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$ is obtained, the Gibbs free energy change (${\mathsf{\Delta }}_{\mathsf{r}}{\mathsf{G}}_{\mathsf{m}}$) of different ionic reactions in the solution is deduced based on the equation below:

$${\mathsf{\Delta }}_{\mathsf{r}}{\mathsf{G}}_{\mathsf{m}}={({\displaystyle \sum _{\mathsf{i}}{\mathsf{\nu }}_{\mathsf{i}}{\mathsf{\Delta }}_{\mathsf{f}}{\mathsf{G}}_{\mathsf{i}}})}_{\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{d}\mathsf{u}\mathsf{c}\mathsf{t}}-{({\displaystyle \sum _{\mathsf{i}}{\mathsf{\nu }}_{\mathsf{i}}{\mathsf{\Delta }}_{\mathsf{f}}{\mathsf{G}}_{\mathsf{i}}})}_{\mathsf{r}\mathsf{e}\mathsf{a}\mathsf{c}\mathsf{t}\mathsf{a}\mathsf{n}\mathsf{t}}$$

(6)

where ${\mathsf{\nu }}_{\mathsf{i}}$ is the stoichiometric number of different species i involved in the reaction. Equation (6) shows a difference of summation of ${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$ between products and reactants. c of different ions is shown in

Table 8. The Gibbs free energy of formation (${\mathsf{\Delta }}_{\mathsf{f}}\mathsf{G}$) of different ions in the paste.

Types of Ions	${\mathbf{\Delta }}_{\mathbf{f}}\mathbf{G} (\mathbf{kJ}/\mathbf{mol})$
Mg2+	−454.8
H+	0
H2O	−237.1
SO42-	−744.5

. Therefore, the relation between ${\mathsf{\Delta }}_{\mathsf{r}}{\mathsf{G}}_{\mathsf{m}}$ and K is established as:

$${\mathsf{\Delta }}_{\mathsf{r}}{\mathsf{G}}_{\mathsf{m}}=-\mathsf{R}\mathsf{T}\mathsf{ln}\mathsf{K}$$

(7)

where R is the gas constant (8.314 J·mol⁻¹·K⁻¹) and T is thermodynamic temperature. The main chemical reactions and corresponding thermodynamic equilibrium constants involved in MOS paste are listed in

Table 9. Main chemical reactions and corresponding thermodynamic equilibrium constants involved in MOS paste.

Equations	Log K	References
${\mathsf{H}}_2\mathsf{O}={\mathsf{H}}^{+}+\mathsf{O}{\mathsf{H}}^{-}$	−13.99	[36]
$\mathsf{M}\mathrm{g}\mathsf{O}+2{\mathsf{H}}^{+}=\mathsf{M}{\mathsf{g}}^{2+}+{\mathsf{H}}_2\mathsf{O}$	21.58	[37]
$\mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4\cdot 7{\mathsf{H}}_2\mathsf{O}=\mathsf{M}{\mathsf{g}}^{2+}+{\mathsf{S}{\mathsf{O}}_4}^{2-}+7{\mathsf{H}}_2\mathsf{O}$	−1.88	[38]
$3\mathsf{M}\mathsf{g}{(\mathsf{O}\mathsf{H})}_2\cdot \mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4\cdot 8{\mathsf{H}}_2\mathsf{O}+6{\mathsf{H}}^{+}=4\mathsf{M}{\mathsf{g}}^{2+}+{\mathsf{S}{\mathsf{O}}_4}^{2-}+14{\mathsf{H}}_2\mathsf{O}$	44.70	This work
$5\mathsf{M}\mathsf{g}{(\mathsf{O}\mathsf{H})}_2\cdot \mathsf{M}\mathsf{g}\mathsf{S}{\mathsf{O}}_4\cdot 7{\mathsf{H}}_2\mathsf{O}+10{\mathsf{H}}^{+}=6\mathsf{M}{\mathsf{g}}^{2+}+{\mathsf{S}{\mathsf{O}}_4}^{2-}+17{\mathsf{H}}_2\mathsf{O}$	77.65	This work

.

3.2. Formation Conditions for Phase 318 and Phase 517

Equations (1) and (2) describe the formation of Phase 318 and Phase 517 in MOS pastes. Apparently exhibited by the chemical formations, reaction products, Phase 318 and Phase 517, are closely related to activity of Mg²⁺, SO₄²⁻, H₂O and pH. According to the law of mass action, the formations of Phase 318 and Phase 517 in MgO-MgSO₄-H₂O cement system must meet the following inequalities, respectively:

$$\mathsf{log}{\mathsf{K}}_{(318)}<4\mathsf{log}{\mathsf{a}}_{\mathsf{M}{\mathsf{g}}^{2+}}+\mathsf{log}{\mathsf{a}}_{{\mathsf{S}{\mathsf{O}}_4}^{2-}}+6\mathsf{log}{\mathsf{a}}_{\mathsf{O}{\mathsf{H}}^{-}}+8\mathsf{log}{\mathsf{a}}_{{\mathsf{H}}_2\mathsf{O}}$$

(8)

$$\mathsf{log}{\mathsf{K}}_{(517)}<6\mathsf{log}{\mathsf{a}}_{\mathsf{M}{\mathsf{g}}^{2+}}+\mathsf{log}{\mathsf{a}}_{{\mathsf{S}{\mathsf{O}}_4}^{2-}}+10\mathsf{log}{\mathsf{a}}_{\mathsf{O}{\mathsf{H}}^{-}}+7\mathsf{log}{\mathsf{a}}_{{\mathsf{H}}_2\mathsf{O}}$$

(9)

where a represents the activity of ions. The subscripts of a represent different ions and water molecular. ${\mathsf{K}}_{(318)}$ and ${\mathsf{K}}_{(517)}$ are thermodynamic equilibrium constants of Phase 318 and Phase 517.

3.3. Influence of Molar Ratios on Hydrated Products

The equilibrium phase diagram in the cement system of MgO-MgSO₄-H₂O when H is equal to 18, is shown in Figure 4. “n” marked in the vertical axis represents the mole of hydrated product assemblage.

It can be observed that large M makes for the formation of Phase 517 and MH in Figure 4. When M is equal to 3, Phase 517 begins to appear in the MOS paste. As M is smaller than 3, the hydrated products are mainly Phase 318. With the increase of M, Phase 517 is gradually produced and coexists with Phase 318. It has been suggested by [3] that the compressive strength of MOS cement paste is primarily dependent on the contents of Phase 318 and Phase 517. As similarly reported by [10], the experimental results reveal that the compressive strength of MOS cement paste increases as M increases from 3 to 5, which can be attributed to the accumulation of Phase 318 and Phase 517. When M exceeds about 5, accompanying with the disappearance of Phase 318, Phase 517 turns to be the dominant product, indicating that the formation of Phase 517 is preferred with high MgO content. Further increase of M value to 5 can give birth to MH as there is not enough MgSO₄ solution to be reacted and the amount of MgO is excessive. It is also revealed in [10] that the compressive strength of MOS cement decreases when M continuously increases from 5 to 13, giving birth to more MH, which is consistent with simulation results in this work. It is suggested that large M should not be recommended since the total volume of MH increases with the increment of M, which is unfavorable to the strength development of MOS cement pastes.

The influence of H on the phase composition is demonstrated in Figure 5 with a fixed value of M = 8. It can be observed that there is only Phase 318 in the paste when H is small. As H is equal to around 8, Phase 517 starts to appear in the system and Phase 318 gradually decomposes. MH does not emerge until H comes to 16 when Phase 517 starts to decompose. When H approaches 25, Phase 517 is totally disappeared, indicating that the initial formation of loose paste structure. Further increase of H gives accumulation of MH and gradually results in the collapse of paste structure, demonstrating the low water-resistance of MOS cement paste. Similar experimental results have been reported in [56], in which XRD results exhibits stronger peak intensity of Phase 517 and weaker peak intensity of MH when H = 20 than H = 28, indicating the decomposition of Phase 517 and generation of more MH. It is suggested that when H is around 14–16, the only equilibrium phase is Phase 517, which is favorable to the strength development for MOS cement paste. Therefore, in practical application of MOS cement, the appropriate value of H should be taken around 14 to 16 to form MOS cement paste with higher mechanical strength and better water resistance.

The phase compositions of MOS pastes obtained from this work are compared with the ones from other literature [3,9,57], as shown in

Table 10. Comparison of phase composition among simulated and literature results.

Molar Ratio	Phase 517 (%)	MH (%)	Other Phases (%)	References
M = 10, H = 18	51.18	48.82	-	This work
M = 8, H = 20	65.82	34.18	-	This work
M = 8, H = 11	48.69	12.67	38.64	[57]
M = 8, H = 11	44.93	-	56.07	This work
M = 8, H = 20	60.24	24.13	15.63	[3]
M = 7	51.05	31.46	17.49	[9]

. Accordingly, when M = 8, the mass fractions of Phase 517 predicted in this work are 65.82 and 44.93 for H = 20 and H = 11, respectively, while the ones are 60.24 and 48.69 obtained from the previous experimental works. Although there is slight difference among the simulated and experimental results, the consistency is clear. The mass fractions of Phase 517 are relatively consistent in Table 10 while the ones of other phases are uncertain since different minerals in experimental MgO powders and possible additives may be incorporated. Besides, the carbonation of MH and other hydrated phases are not taken into consideration in this work [3], which may lead to some discrepancies of results in Table 10.

3.4. Initial and Ultimate Hydration Stages

Slices of REV with size of 100 × 100 × 100 μm³ in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 exhibit the initial and ultimate hydration stages of MOS pastes. Different colors in these figures stand for different phases in paste. Orange, red, blue, yellow and green represent the unhydrated MgO particle, MH crystal, pore, inner and outer hydrated products. In this work, the ultimate hydration stage corresponds to 80% hydration degree and is referred to as such stage in which the diffusion behavior is dominated in the paste. From these figures, it is expected that small MgO particles are totally hydrated due to the rapid reaction, while the hydration of large ones is partially controlled by the water diffusion in deposited hydrates covered onto the surface of MgO particles. Therefore, the interior unhydrated MgO part has the potential to hydrate again once the outer hydrates decompose and MgO particles are exposed to water. Additionally, the original pores of MOS pastes at the initial hydration stage are gradually filled by hydrated products during the hydration process. The solid skeleton of pastes is gradually formed, which contributes to the strength gain of pastes. It is noteworthy that large M is beneficial for the refinement of pore structure of MOS pastes but large H has an opposite effect, which is verified by the porosity analysis in the next section.

3.5. Pore Structure of MOS Pastes

One of the most commonly used indicators to describe the pore structure is porosity [58]. In this work, the porosities of MOS pastes with different M and H are calculated by MATLAB. The comparison of cumulative porosities in different MOS pastes is presented in Figure 11. It can be obviously seen that porosity of MOS cement paste decreases from 22.58% to 4.30% with the increase of M when H is fixed at 20. This may be attributed to the fact that increased content of MgO reacts with excessive water and the products fill in the pores, and thus, a small porosity is obtained [59]. On the contrary, large H is beneficial for the formation of MH with loose structure and leads to a large porosity when M is fixed [60].

With respect to MOS paste for the given molar ratios (M = 8 and H = 20) in the ultimate hydration stage, the total porosity in terms of the pores whose diameter is from 5 nm to 330 μm, determined by the mercury intrusion porosimetry test is claimed to be 25.07% in the work by Wu et al. [3], while the one derived from this work is approximately 13.07%. Since the pore size range considered in the calculation of porosity is from 0.2 μm to 10 μm in this work, the presented result is smaller than that of literature [3]. Besides, it is reported that porosity from the porosimetric characterization is sometimes overestimated because the cracks caused by mercury intrusion are erroneously identified as “Pores” [61]. To some extent, the simulated results are consistent with experimental ones. Other experimental results with different M and H [60,62,63] are collected in the

Table 11. Comparison of porosities among simulated and experimental results.

	Molar Ratio	Porosity (%)	References
Simulation	MOS6120	22.58
	MOS8118	5.54
	MOS8120	13.07	This work
	MOS8122	19.61
	MOS10120	4.30
Experiments	MOS8120	25.07	[3]
	MOS14112	12.74	[62]
	MOS8111	18.53	[57]
	MOS7120	17.97	[9]
	MOS10117	16.78	[63]
	MOS8118	6.69	[60]
	MOS8120	10.46	[60]
	MOS8122	13.71	[60]

. It should be emphasized that the exact hydration age obtained from our simulation is a bit ambiguous because the simulation is status-oriented. Sometimes, the comparison in terms of hydration age may not be achieved easily. Besides, the size of the REV is pivotal when the porosity of cement paste is examined based on microstructure methods. Herein, four different sizes of REV are adopted to evaluate the porosity of MOS cement paste and the results are presented in

Table 12. Comparison of porosities with different REV sizes.

Size of REV (μm3)	Porosity (%)
	MOS6120	MOS8118	MOS8120	MOS8122	MOS10120
50 × 50 × 50	20.54 ± 0.85	5.47 ± 0.09	12.85 ± 0.36	19.14 ± 0.76	4.12 ± 0.05
100 × 100 × 100	22.58 ± 0.93	5.54 ± 0.15	13.07 ± 0.52	19.61 ± 0.84	4.30 ± 0.04
200 × 200 × 200	24.65 ± 1.04	6.34 ± 0.14	14.22 ± 0.57	19.87 ± 0.88	4.95 ± 0.02
300 × 300 × 300	27.32 ± 1.24	7.88 ± 0.11	16.41± 0.48	21.38 ± 0.74	6.09 ± 0.07

and Figure 12, respectively. It can be easily observed that the porosity of MOS cement paste increases with the increase of the REV size. It is attributed to the factor that small REV may not cover all large particles, and thus, large pores are neglected, resulting in a relatively small porosity [48]. Based on affordable computational efficiency and resolution, appropriate REV contains almost all the MgO particles is massively considered when the porosity is examined.

3.6. Analysis of Fractal Features of MOS Pastes

Based on Equations (3) and (4), D_f of different MOS pastes at initial and ultimate stage of hydration can be derived and the results are presented in

Table 13. D_f and porosity of different MOS pastes at initial and ultimate stage of hydration.

Designation	Initial Stage		Ultimate Stage
	Porosity (%)	Df	Porosity (%)	Df
MOS6120	91.54	1.964	22.58	1.657
MOS8118	89.25	1.950	5.54	1.461
MOS8120	88.64	1.955	13.07	1.579
MOS8122	87.56	1.954	19.61	1.640
MOS10120	85.27	1.946	4.30	1.415

and Figure 13. Figure 12 illustrates that D_f obtained from simulation results varies from 1–2, which is consistent with the range reported in Ref. [64]. Meanwhile, it can be noticed that D_f increases with the increase of porosity, which is similar to the trend discovered by Yu et al. [65]. This also confirms the reliability of pore structure obtained from the present simulation. From Table 13, it can be also observed that D_f approaches to its possible maximum value two when the porosity is around one at the initial stage. The decrease in the D_f from initial stage to ultimate stage of hydration can be attributed to the evolution of microstructure of MOS paste. As MOS hydrates, the pores of cement pastes are gradually filled with hydration products, leading to a large porosity and D_f.

Besides, it is noteworthy that D_f obtained from this work is not only related to the porosity of cement paste but also to the value of M and H. The MOS paste with high M shows small D_f while large H gives birth to high D_f. This phenomenon may be explained as the complexity of pore size distribution in cement paste. With respect to different M and H, differences in pore size distribution may generate in simulations, leading to different fractal features. The MOS paste with high M has a relatively large initial pore space so that a large portion of hydration products generates with gel and small capillary pore embedded in, resulting in a small D_f. While for large H, a large portion of space is occupied by water, leading to large pores and D_f.

4. Conclusions and Prospects

In this work, a novel multiscale modeling strategy is proposed to evaluate the pore structure and fractals in MOS cement system. A first principle calculation is initially performed to obtain the thermodynamic data for main phases and aqueous geochemical calculations are followed to evaluate the phase composition. Finally, the hydration status is visualized using microstructure-based method and porosity and pore fractals are analyzed. Based on the findings, several conclusions can be drawn:

(1) Based on the common molar ratios of magnesium oxysulfate cement, the basic thermodynamic data of MOS cement system under the temperature of 25 °C is obtained through literature and first principle calculation. The consistency in the phase composition between simulation results using PHREEQC and experimental results demonstrates that the thermodynamic simulation is applicable to the MOS cement system.

(2) Using the established thermodynamic database of MOS cement system, the hydration of MOS cement system and the stability of hydrated products under normal temperature and pressure are well studied. Results show that the composition of hydrated products in MOS cement system is sensitive to M and H. Phase 517 is precipitated with the increase of M and Phase 318 disappears gradually. When MgO is excessive, only MH will generate. Phase 318 solely exists when H is low, and Phase 517 appears gradually with increase of H. When H is large enough, MH comes to the only products, which corresponds to the low strength and water resistance of MOS pastes. It provides a certain benefit for mixture design: it is recommended that when H is equal to 18, M = 5 is beneficial to the strength and water resistance development of MOS cement pastes, meanwhile, when M is equal to 8, H = 14–16 is appropriate for mixture design.

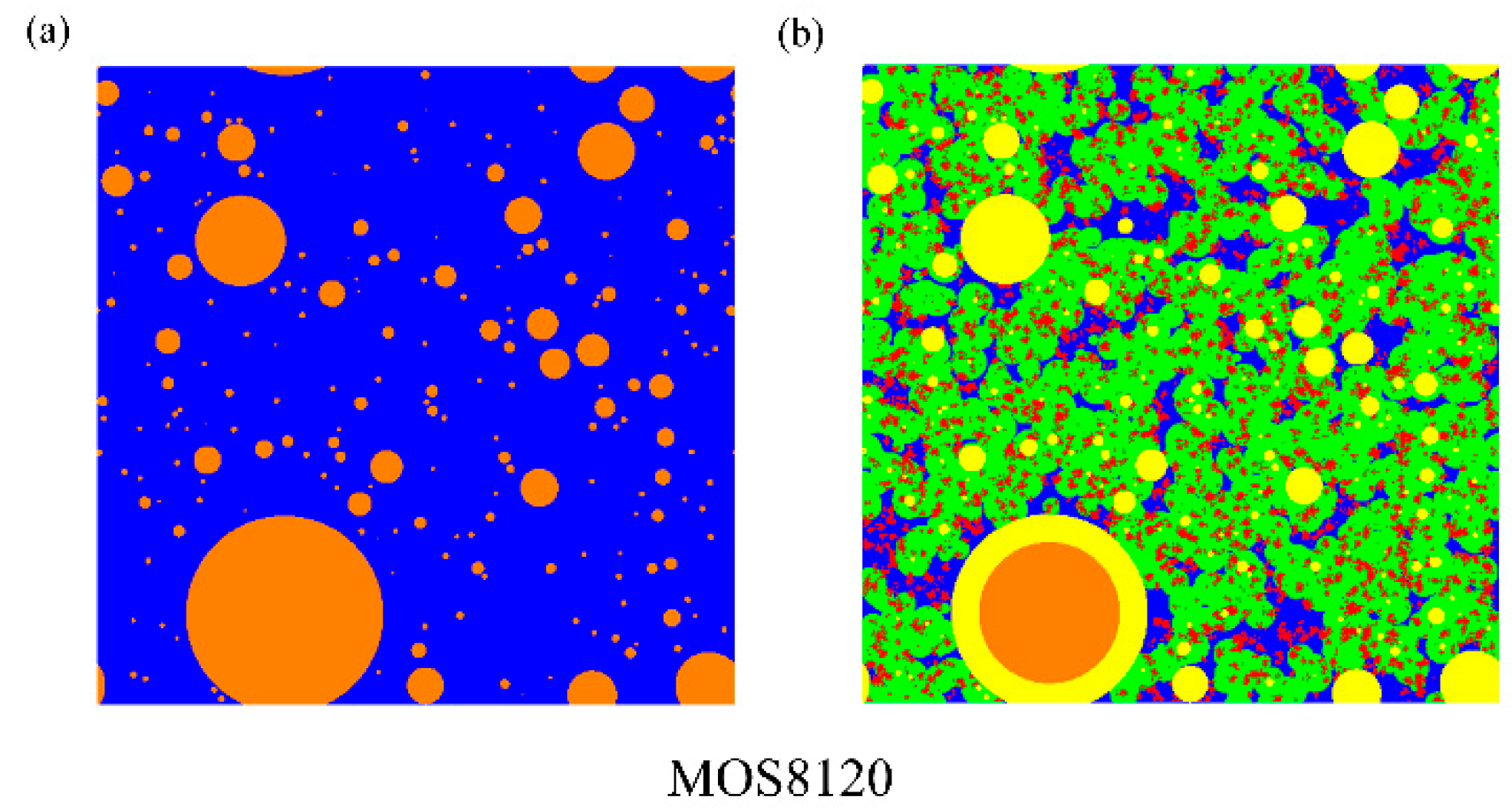
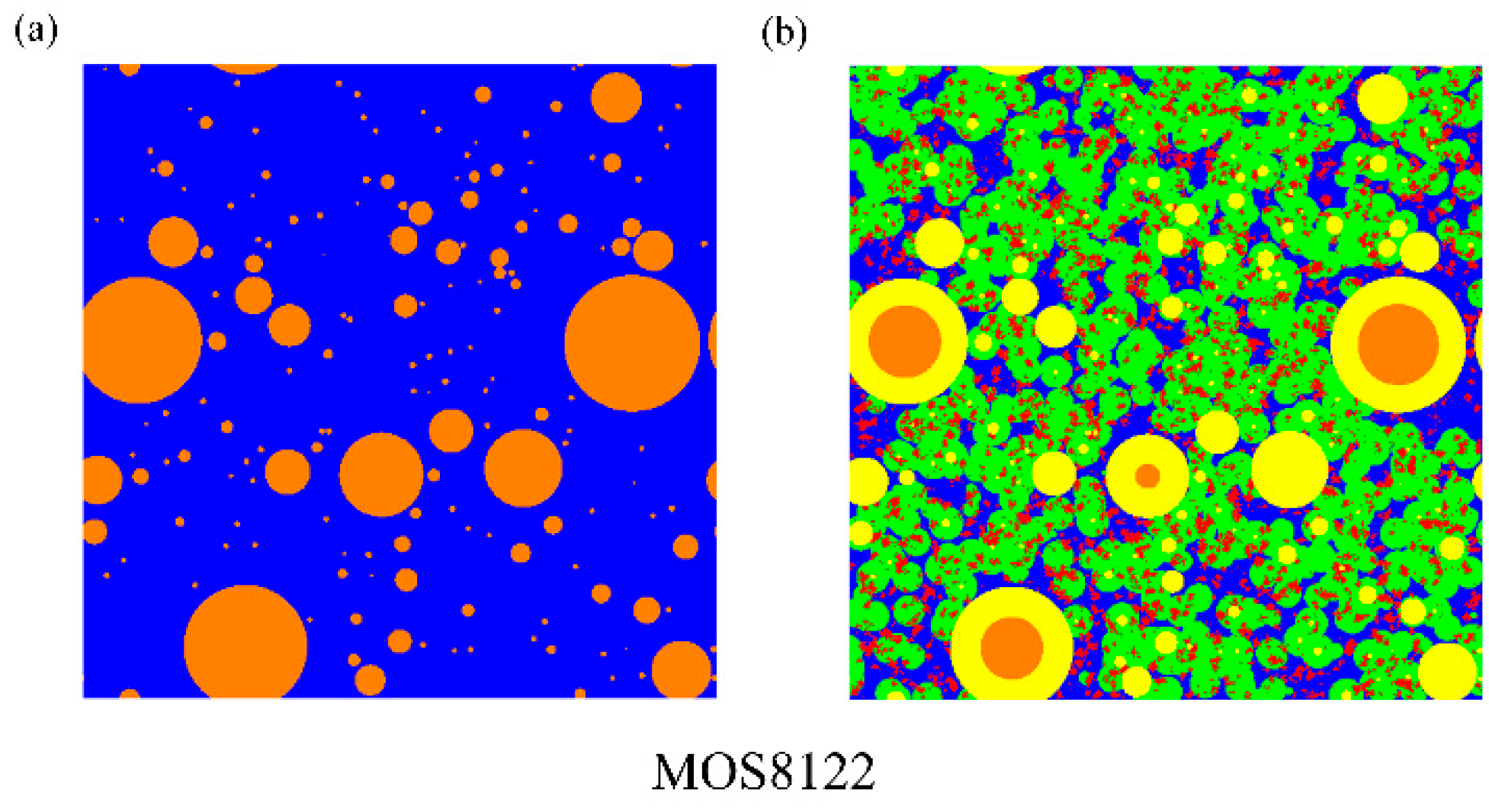
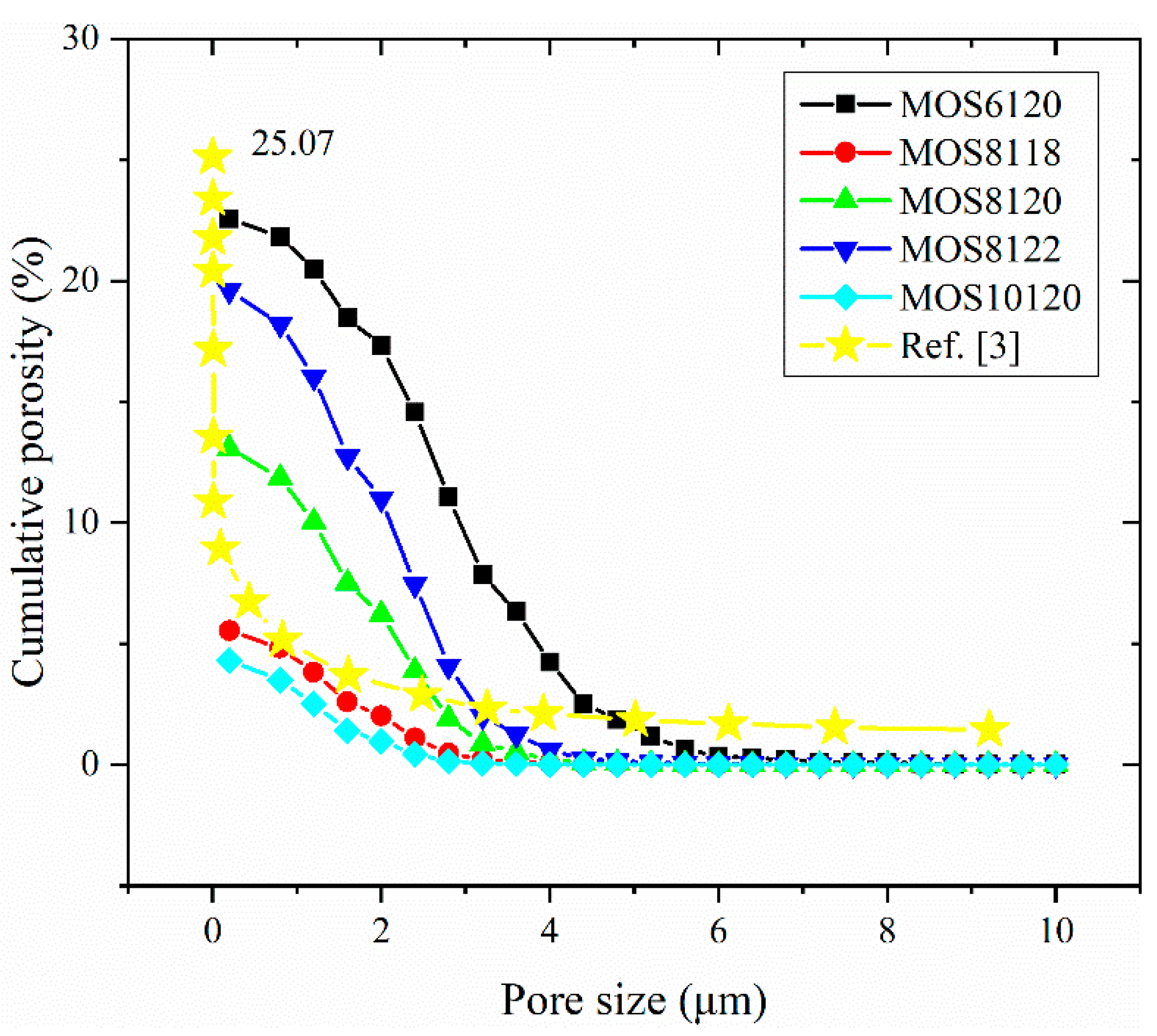
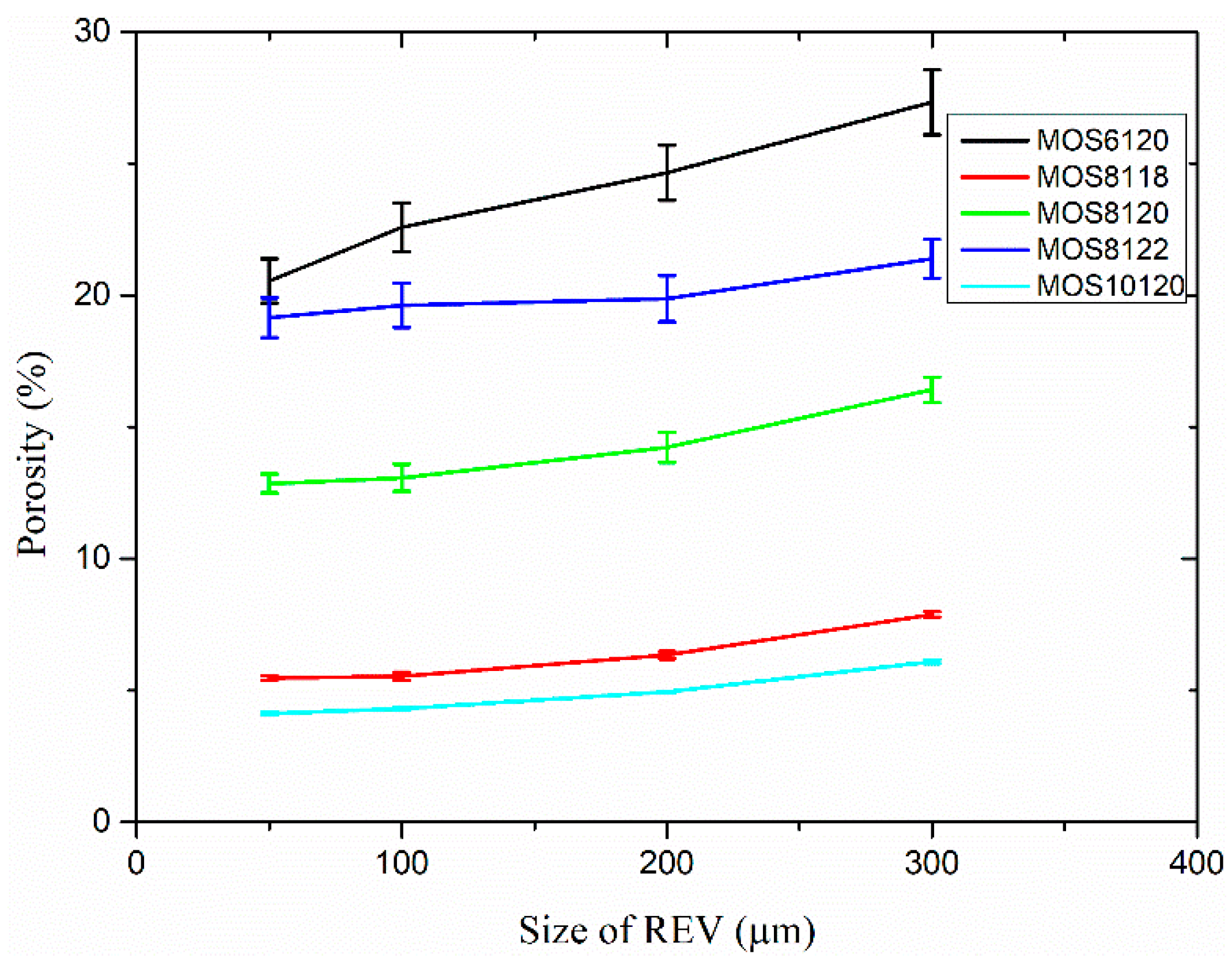
(3) The microstructure in initial and ultimate hydration stages of MOS pastes are visualized by means of MATLAB. Based on the hydration status, the evaluation of porosity and analysis of fractal feature of pore structure are conducted. The comparison of cumulative porosities in MOS pastes with different molar ratios shows that a large M is beneficial to reducing porosity and similar trend for the case of small H. Besides, fractal analysis reveals that D_f of MOS paste is positively proportional to the porosity and large M, as well as small H is beneficial for the modification of microstructure of MOS paste by reducing the D_f.

This work provides a novel modeling strategy for MOS cement system integrating different scales and methods. In the future, more attributes will be taken into consideration when simulating the hydration behavior of MOS cement, such as the influence of temperature, additives, etc. Besides, other important properties of MOS cement will be investigated including leaching, thermal conductivity, durability and other long-term performance of such material. In addition, the dynamic process of hydration of MOS cement system based on thermodynamics and kinetics will also be of great significance to understand the toughening mechanism for this eco-friendly construction materials.