FPAA-Based Realization of Filters with Fractional Laplace Operators of Different Orders
Abstract
:1. Introduction
- (a)
- Employment of fractional-order capacitors, which substitute the conventional (i.e., integer-order) capacitors in the topologies of integer-order standard filters. Due to the absence of commercial availability of such elements, they are approximated by RC schemes, such as the Foster and Cauer networks. The price paid for the offered quick design procedure is the absence of on-the-fly tuning of the filter’s characteristics, making it suitable only for cases of filters with pre-defined type and frequency characteristics [3,4,5].
- (b)
- Approximation of the fractional-order Laplace operators in (1) using appropriate tools, such as Continued Fraction Expansion, Oustaloup, Matsuda and Carlson [6], and then substitution of the resulting rational function approximations of these operators. The derived filter function is an integer-order polynomial ratio that can be implemented utilizing classical filter design techniques, such as cascade connection of elementary filter stages and multi-feedback structures. This design procedure is more complicated than the previous one, but it offers the advantage of electronic tuning capability of the derived filter structures, considering that active elements with electronically controlled characteristics (e.g., transconductance) are utilized [2,7,8,9,10,11]. However, this approach is efficient only for approximations of filter functions with a single fractional order. In the case of functions, such as the one in (1), the order of the derived rational function will be at least double the applied order of approximation [2].
- (a)
- Instead of individually approximating the fractional-order Laplace operators, the magnitude and phase frequency responses of the whole filter function in (1) are fitted by a suitable integer-order transfer function derived through the employment of specialized Symbolic Math Toolbox™ built-in functions.
- (b)
- The order of the derived rational function is always equal to the order of the employed approximation, and thus, this approach offers the advantage of minimizing the circuit complexity, compared to the aforementioned conventional approach.The paper is organized as follows: an investigation of the problem regarding the approximation of the general filter function following the conventional and the proposed procedures is discussed in Section 2, and a design example for comparison purposes is given in Section 3. The validity of the suggested procedure was experimentally evaluated using a field-programmable analog array (FPAA) device [12] and the results are presented in Section 4.
2. Proposed Design Procedure
- step #1:
- Extraction of the frequency response data of (1) within a specific frequency range of interest, a process that is performed using the frd built-in function.
- step #2:
- Approximation of the obtained data, based on the fitfrd built-in function, which forms the state-space model of the data for a given order of approximation .
- step #3:
- Conversion of the model to an integer-order transfer function of the form in (3) using the ss2tf built-in function.
3. Design Example and Comparative Results
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AP | All pass |
| BP | Band pass |
| BS | Band stop |
| CAB | Configurable analogue block |
| FO | Fractional order |
| FBD | Functional block diagram |
| FLF | Follow the leader feedback |
| FPAA | Field-programmable analog array |
| HP | High pass |
| IAE | Integral absolute of error |
| LP | Low pass |
References
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A. Design of CMOS Analog Integrated Fractional-Order Circuits: Applications in Medicine and Biology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A.S. Fractional-order electronically controlled generalized filters. Int. J. Circuit Theory Appl. 2017, 45, 595–612. [Google Scholar] [CrossRef]
- Sladok, O.; Koton, J.; Kubanek, D.; Dvorak, J.; Psychalinos, C. Pseudo-differential (2 + α)-order Butterworth frequency filter. IEEE Access 2021, 1. [Google Scholar] [CrossRef]
- Biswal, K.; Tripathy, M.C.; Kar, S. Performance analysis of fractional order low-pass filter. In Advances in Intelligent Computing and Communication; Springer: Berlin/Heidelberg, Germany, 2020; pp. 224–231. [Google Scholar]
- Mijat, N.; Jurisic, D.; Moschytz, G.S. Analog Modeling of Fractional-Order Elements: A Classical Circuit Theory Approach. IEEE Access 2021, 9, 110309–110331. [Google Scholar] [CrossRef]
- Hamed, E.M.; AbdelAty, A.M.; Said, L.A.; Radwan, A.G. Effect of different approximation techniques on fractional-order KHN filter design. Circuits Syst. Signal Process. 2018, 37, 5222–5252. [Google Scholar] [CrossRef]
- Langhammer, L.; Dvorak, J.; Sotner, R.; Jerabek, J.; Bertsias, P. Reconnection–less reconfigurable low–pass filtering topology suitable for higher–order fractional–order design. J. Adv. Res. 2020, 25, 257–274. [Google Scholar] [CrossRef] [PubMed]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Double exponent fractional-order filters: Approximation methods and realization. Circuits Syst. Signal Process. 2021, 40, 993–1004. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator. AEU-Int. J. Electron. Commun. 2021, 129, 153537. [Google Scholar] [CrossRef]
- Jerabek, J.; Sotner, R.; Dvorak, J.; Polak, J.; Kubanek, D.; Herencsar, N.; Koton, J. Reconfigurable fractional-order filter with electronically controllable slope of attenuation, pole frequency and type of approximation. J. Circuits Syst. Comput. 2017, 26, 1750157. [Google Scholar] [CrossRef] [Green Version]
- Mahata, S.; Herencsar, N.; Kubanek, D. Optimal Approximation of Fractional-Order Butterworth Filter Based on Weighted Sum of Classical Butterworth Filters. IEEE Access 2021, 9, 81097–81114. [Google Scholar] [CrossRef]
- Hasler, J.; Shah, S. An SoC FPAA based programmable, ladder-filter based, linear-phase analog filter. IEEE Trans. Circuits Syst. Regul. Pap. 2020, 68, 592–602. [Google Scholar] [CrossRef]
- Xue, D. Fractional-Order Control Systems; de Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Anadigm. AN231E04 dpASP: The AN231E04 dpASP Dynamically Reconfigurable Analog Signal Processor. Available online: https://anadigm.com/an231e04.asp (accessed on 5 November 2021).
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Field programmable analogue array implementation of fractional step filters. IET Circuits Devices Syst. 2010, 4, 514–524. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B. Incorporating FPAAs into laboratory exercises for analogue filter design. Int. J. Electr. Eng. Educ. 2013, 50, 188–200. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; García-Jiménez, L.V.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. New alternatives for analog implementation of fractional-order integrators, differentiators and PID controllers based on integer-order integrators. Nonlinear Dyn. 2017, 90, 241–256. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Lino, P.; Maione, G.; Stasi, S.; Padula, F.; Visioli, A. Synthesis of fractional-order PI controllers and fractional-order filters for industrial electrical drives. IEEE/CAA J. Autom. Sin. 2017, 4, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Azar, A.T.; Radwan, A.G.; Vaidyanathan, S. Fractional Order Systems: Optimization, Control, Circuit Realizations and Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mohsen, M.; Said, L.A.; Madian, A.H.; Radwan, A.G.; Elwakil, A.S. Fractional-Order Bio-Impedance Modeling for Interdisciplinary Applications: A Review. IEEE Access 2021, 9, 33158–33168. [Google Scholar] [CrossRef]
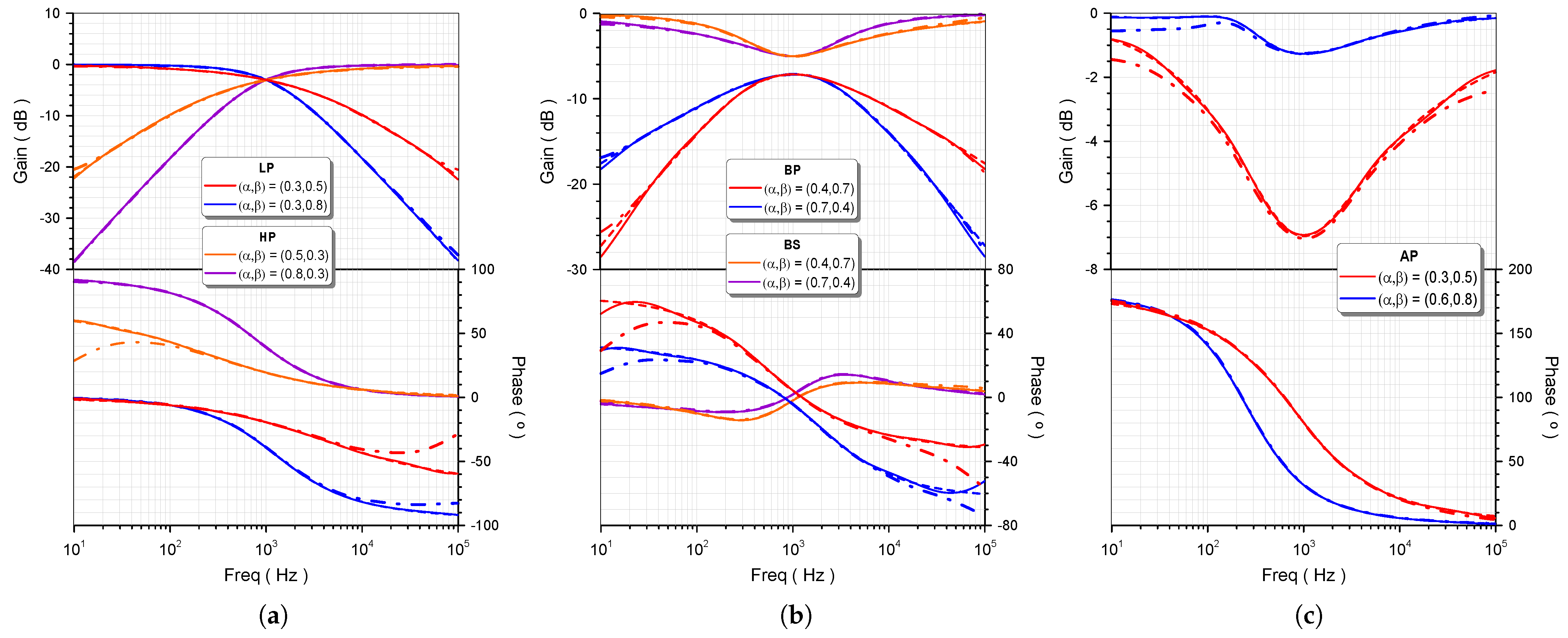

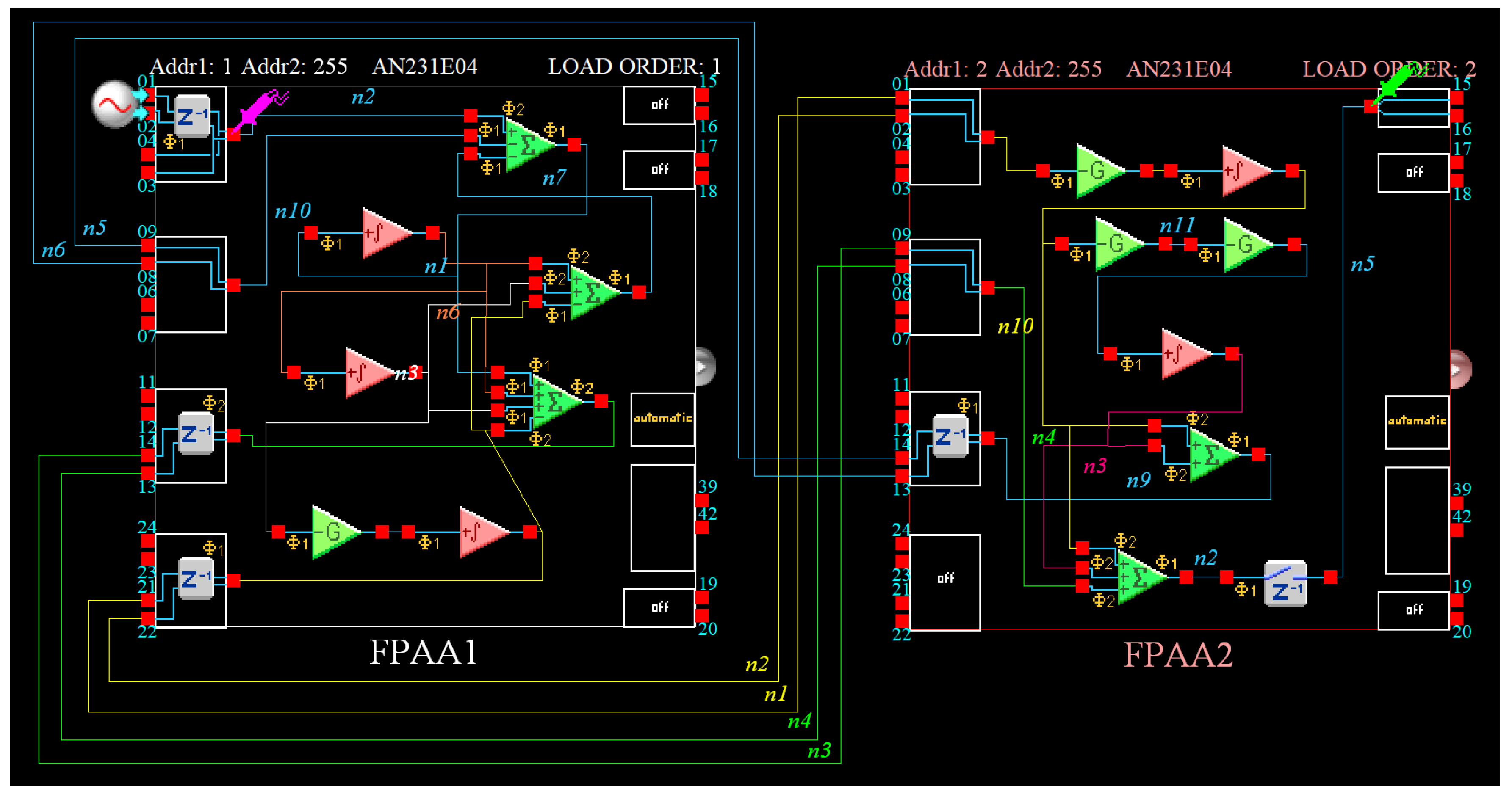


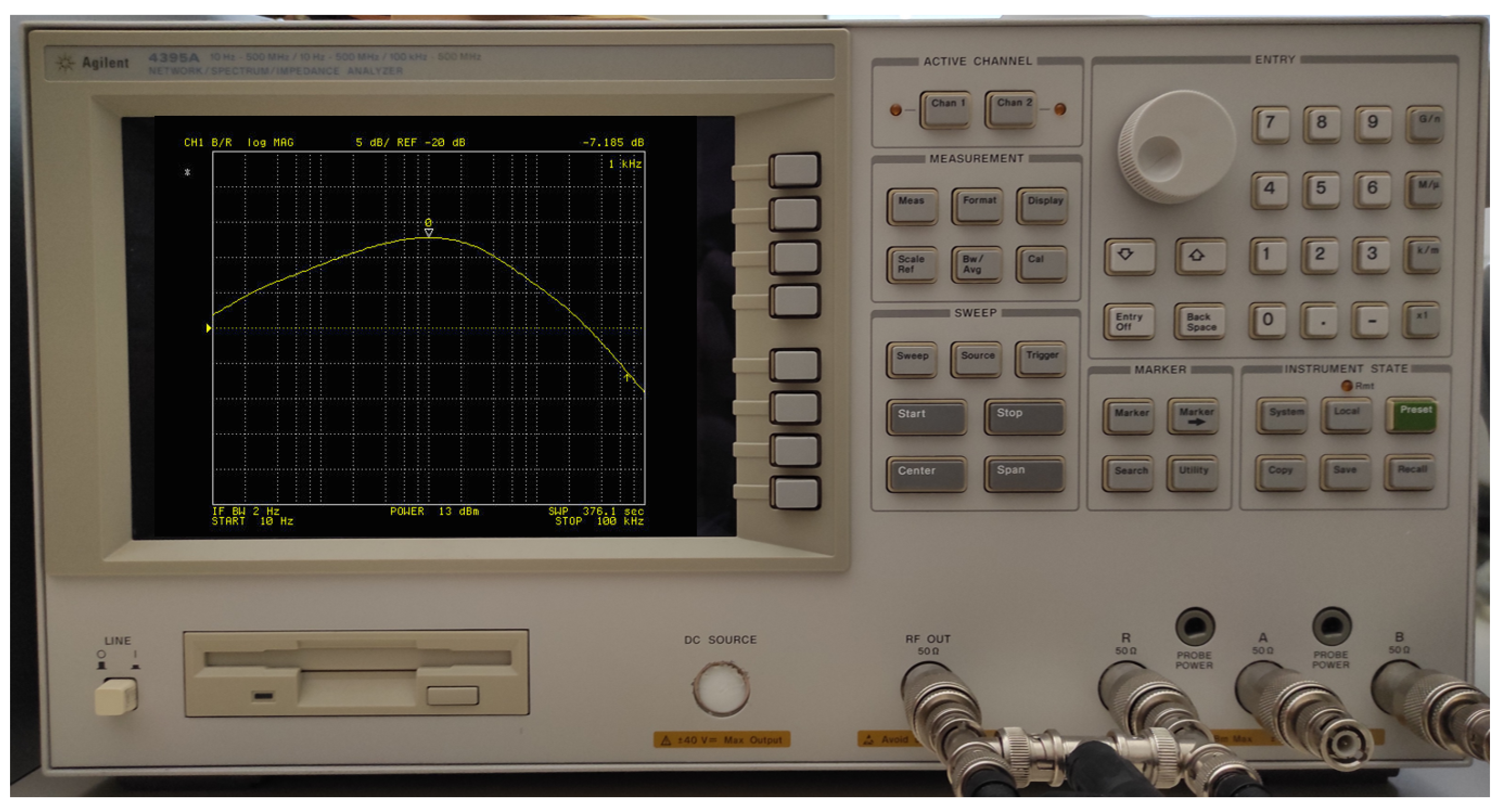
| Filter | Order | |
|---|---|---|
| LP | ||
| HP | ||
| BP | ||
| BS | ||
| AP | ||
| Filter | Parameter | ||
|---|---|---|---|
| LP | |||
| HP | |||
| BP | |||
| BS | |||
| AP | |||
| Coefficient | Filter | |||||
|---|---|---|---|---|---|---|
| LP | HP | BP | BS | AP | ||
| Coefficient | Filter | |||||
|---|---|---|---|---|---|---|
| LP | P | BP | BS | AP | ||
| 3.18 (s) | 13.32 (s) | 7.31 (s) | 6.79 (s) | 3.95 (s) | 6.546 (s) | |
| 19.05 (s) | 87.5 (s) | 49.7 (s) | 45.71 (s) | 32.63 (s) | 49.81 (s) | |
| 83.92 (s) | 390.5 (s) | 327 (s) | 304.2 (s) | 166.8 (s) | 246.6 (s) | |
| 387.9 (s) | 1.69 (ms) | 1.53 (ms) | 1.78 (ms) | 789.25 (s) | 634.1 (s) | |
| 2.71 (ms) | 10 (ms) | 9.75 (ms) | 9.85 (ms) | 5.31 (ms) | 1.68 (ms) | |
| Frequency | Filter | ||||
|---|---|---|---|---|---|
| LP | HP | BP | BS | AP | |
| (kHz) | 1 (1) | 1 (1) | 1 (1) | 1 (1) | 1 (1) |
| (Hz) | – | – | 142.5 (140.7) | 173.8 (174.1) | – |
| (kHz) | – | – | 4.36 (4.32) | 3.48 (3.37) | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. FPAA-Based Realization of Filters with Fractional Laplace Operators of Different Orders. Fractal Fract. 2021, 5, 218. https://doi.org/10.3390/fractalfract5040218
Kapoulea S, Psychalinos C, Elwakil AS. FPAA-Based Realization of Filters with Fractional Laplace Operators of Different Orders. Fractal and Fractional. 2021; 5(4):218. https://doi.org/10.3390/fractalfract5040218
Chicago/Turabian StyleKapoulea, Stavroula, Costas Psychalinos, and Ahmed S. Elwakil. 2021. "FPAA-Based Realization of Filters with Fractional Laplace Operators of Different Orders" Fractal and Fractional 5, no. 4: 218. https://doi.org/10.3390/fractalfract5040218
APA StyleKapoulea, S., Psychalinos, C., & Elwakil, A. S. (2021). FPAA-Based Realization of Filters with Fractional Laplace Operators of Different Orders. Fractal and Fractional, 5(4), 218. https://doi.org/10.3390/fractalfract5040218








