Numerical Solution of Variable-Order Fractional Differential Equations Using Bernoulli Polynomials
Abstract
:1. Introduction
2. Preliminaries
2.1. Some Preliminaries of Variable-Order Fractional Calculus
2.2. Bernoulli Polynomials
3. Operational Matrix of Variable-Order Fractional Integration
4. Numerical Method
5. Error Estimate
6. Illustrative Examples
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almeida, R.; Tavares, D.; Torres, D.F.M. The Variable-Order Fractional Calculus of Variations; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef] [Green Version]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Translated from the 1987 Russian Original; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar] [CrossRef]
- Tuan, N.H.; Ganji, R.M.; Jafari, H. A numerical study of fractional rheological models and fractional Newell-Whitehead-Segel equation with nonlocal and nonsingular kernel. Chin. J. Phys. 2020, 68, 308–320. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integr. Transf. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Odzijewicz, T.; Malinowska, A.B.; Torres, D.F.M. Noether’s theorem for fractional variational problems of variable order. Cent. Eur. J. Phys. 2013, 11, 691–701. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, F.; Burrage, K. Numerical simulation of a new two-dimensional variable-order fractional percolation equation in non-homogeneous porous media. Comput. Math. Appl. 2014, 67, 1673–1681. [Google Scholar] [CrossRef]
- Coimbra, C.F.M.; Soon, C.M.; Kobayashi, M.H. The variable viscoelasticity operator. Ann. Phys. 2005, 14, 378–389. [Google Scholar] [CrossRef]
- Odzijewicz, T.; Malinowska, A.B.; Torres, D.F.M. Fractional Variational Calculus of Variable Order. In Advances in Harmonic Analysis and Operator Theory. Operator Theory: Advances and Applications; Almeida, A., Castro, L., Speck, F.O., Eds.; Birkhäuser: Basel, Switzerland, 2013; Volume 229, pp. 291–301. [Google Scholar] [CrossRef] [Green Version]
- Ostalczyk, P.W.; Duch, P.; Brzeziński, D.W.; Sankowski, D. Order functions selection in the variable fractional-order PID controller. Advances in Modelling and Control of Non-integer-Order Systems. Lect. Notes Electr. Eng. 2015, 320, 159–170. [Google Scholar] [CrossRef]
- Rapaić, M.R.; Pisano, A. Variable-order fractional operators for adaptive order and parameter estimation. IEEE Trans. Autom. Contr. 2014, 59, 798–803. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Variable-order particle dynamics: Formulation and application to the simulation of edge dislocations. Philos. Trans. R. Soc. A 2020, 378, 20190290. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Bekus, K.; Szajek, K.; Sumelka, W. Approximation and application of the Riesz-Caputo fractional derivative of variable order with fixed memory. Meccanica 2021, in press. [Google Scholar] [CrossRef]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. A novel approach to nonlinear variable-order fractional viscoelasticity. Philos. Trans. R. Soc. A 2020, 378, 20190296. [Google Scholar] [CrossRef]
- Burlon, A.; Alotta, G.; Di Paola, M.; Failla, G. An original perspective on variable-order fractional operators for viscoelastic materials. Meccanica 2021, 56, 769–784. [Google Scholar] [CrossRef]
- Patnaik, S.; Jokar, M.; Semperlotti, F. Variable-order approach to nonlocal elasticity: Theoretical formulation, order identification via deep learning, and applications. Comput. Mech. 2021, in press. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Agarwal, P. Numerical solution of multiterm variable-order fractional differential equations via shifted Legendre polynomials. Math. Meth. Appl. Sci. 2019, 42, 3978–3991. [Google Scholar] [CrossRef]
- Wang, L.F.; Ma, Y.P.; Yang, Y.Q. Legendre polynomials method for solving a class of variable order fractional differential equation. CMES-Comp. Model. Eng. 2014, 101, 97–111. [Google Scholar] [CrossRef]
- Chen, Y.M.; Wei, Y.Q.; Liu, D.Y.; Yu, H. Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl. Math. Lett. 2015, 46, 83–88. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wu, L. An operational matrix of fractional differentiation of the second kind of Chebyshev polynomial for solving multiterm variable order fractional differential equation. Math. Probl. Eng. 2016, 2016, 7126080. [Google Scholar] [CrossRef] [Green Version]
- Nagy, A.M.; Sweilam, N.H.; El-Sayed, A.A. New operational matrix for solving multiterm variable order fractional differential equations. J. Comput. Nonlinear Dyn. 2018, 13, 11001–11007. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, L.Q.; Li, B.F.; Sun, Y. Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl. Math. Comput. 2014, 238, 329–341. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F.M. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. 2016, 35, 69–87. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Liu, F.; Chen, J.; Turner, I.; Anh, V. Numerical techniques for the variable order time fractional diffusion equation. Appl. Math. Comput. 2012, 218, 10861–10870. [Google Scholar] [CrossRef] [Green Version]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Ganji, R.M.; Jafari, H.; Baleanu, D. A new approach for solving multi variable orders differential equations with Mittag-Leffler kernel. Chaos Solitons Fractals 2020, 130, 109405. [Google Scholar] [CrossRef]
- Eghbali, A.; Johansson, H.; Saramäki, T. A method for the design of Farrow-structure based variable fractional-delay FIR filters. Signal Process. 2013, 93, 1341–1348. [Google Scholar] [CrossRef]
- Yu, C.; Teo, K.L.; Dam, H.H. Design of all pass variable fractional delay filter with signed powers-of-two coefficients. Signal Process. 2014, 95, 32–42. [Google Scholar] [CrossRef]
- Cooper, G.R.J.; Cowan, D.R. Filtering using variable order vertical derivatives. Comput. Geosci. 2004, 30, 455–459. [Google Scholar] [CrossRef]
- Tseng, C.-C. Design of variable and adaptive fractional order FIR differentiators. Signal Process. 2006, 86, 2554–2566. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Tohidi, E.; Soleymani, F. A new Bernoulli matrix method for solving high-order linear and nonlinear Fredholm integro-differential equations with piecewise intervals. Appl. Math. Comput. 2012, 219, 482–497. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Toutounian, F.; Tohidi, E. A new Bernoulli matrix method for solving second order linear partial differential equations with the convergence analysis. Appl. Math. Comput. 2013, 223, 298–310. [Google Scholar] [CrossRef]
- Bazm, S. Bernoulli polynomials for the numerical solution of some classes of linear and nonlinear integral equations. J. Comput. Appl. Math. 2015, 275, 44–60. [Google Scholar] [CrossRef]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. A numerical solution for fractional optimal control problems via Bernoulli polynomials. J. Vib. Control 2016, 22, 3889–3903. [Google Scholar] [CrossRef]
- Costabile, F.; Dellaccio, F.; Gualtieri, M.I. A new approach to Bernoulli polynomials. Rend. Mat. Ser. VII 2006, 26, 1–12. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed.; Academic Press: San Diego, CA, USA, 1985. [Google Scholar]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; CRC Press LLC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hassani, H.; Dahaghin, M.S.; Heydari, H. A new optimized method for solving variable-order fractional differential equations. J. Math. Ext. 2017, 11, 85–98. [Google Scholar]
- Li, X.; Li, H.; Wu, B. A new numerical method for variable order fractional functional differential equations. Appl. Math. Lett. 2017, 68, 80–86. [Google Scholar] [CrossRef]
- Nemati, S.; Lima, P.; Sedaghat, S. An effective numerical method for solving fractional pantograph differential equations using modification of hat functions. Appl. Numer. Math. 2018, 131, 174–189. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer. Algorithms 2017, 74, 223–245. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, Y.; Lima, P.M. A novel Lagrange operational matrix and Tau-collocation method for solving variable-order fractional differential equations. Iran J. Sci. Technol. Trans. Sci. 2020, 44, 127–135. [Google Scholar] [CrossRef]
- Nikan, O.; Jafari, H.; Golbabai, A. Numerical analysis of the fractional evolution model for heat flow in materials with memory. Alex. Eng. J. 2020, 59, 2627–2637. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
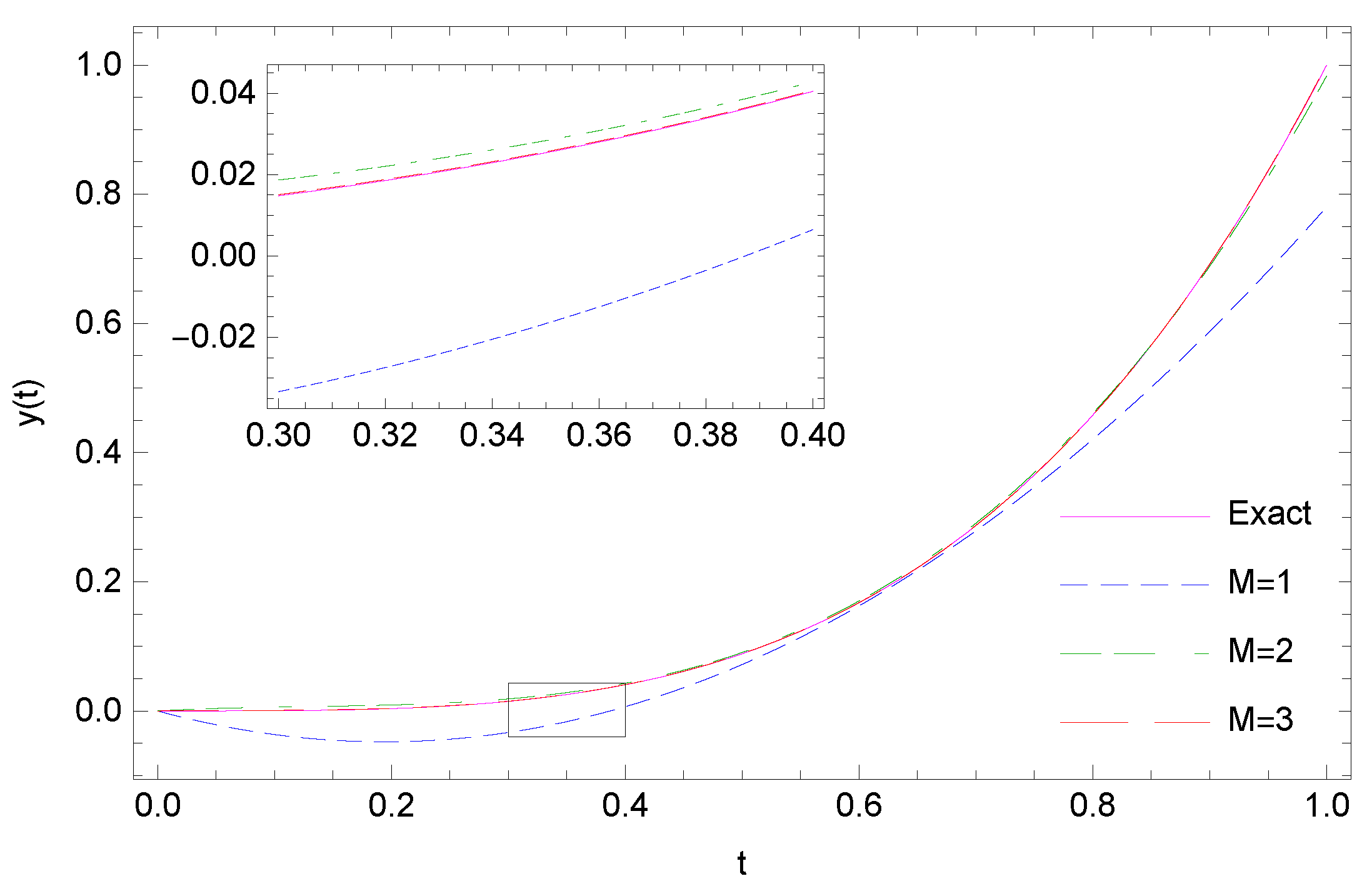

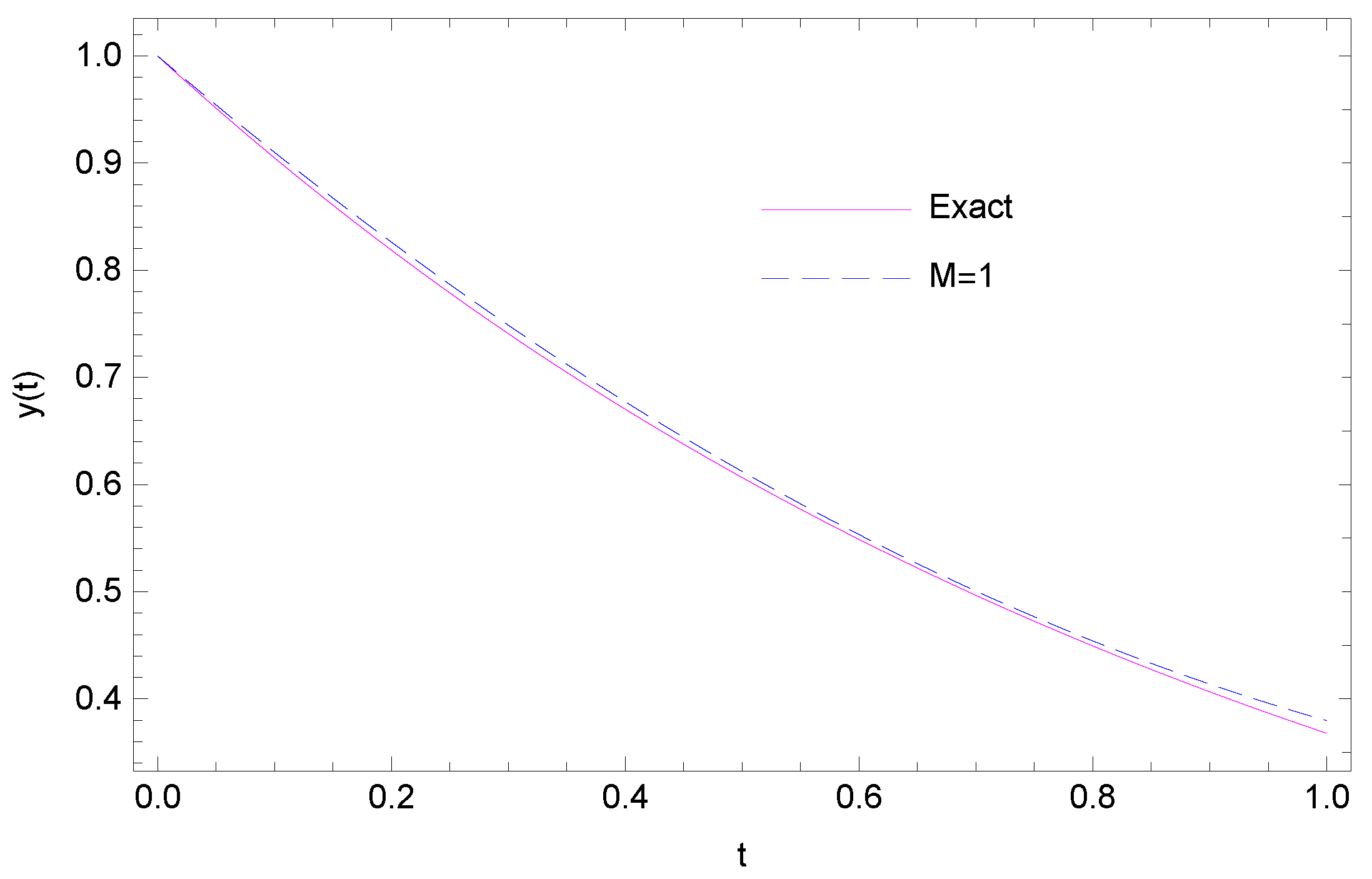
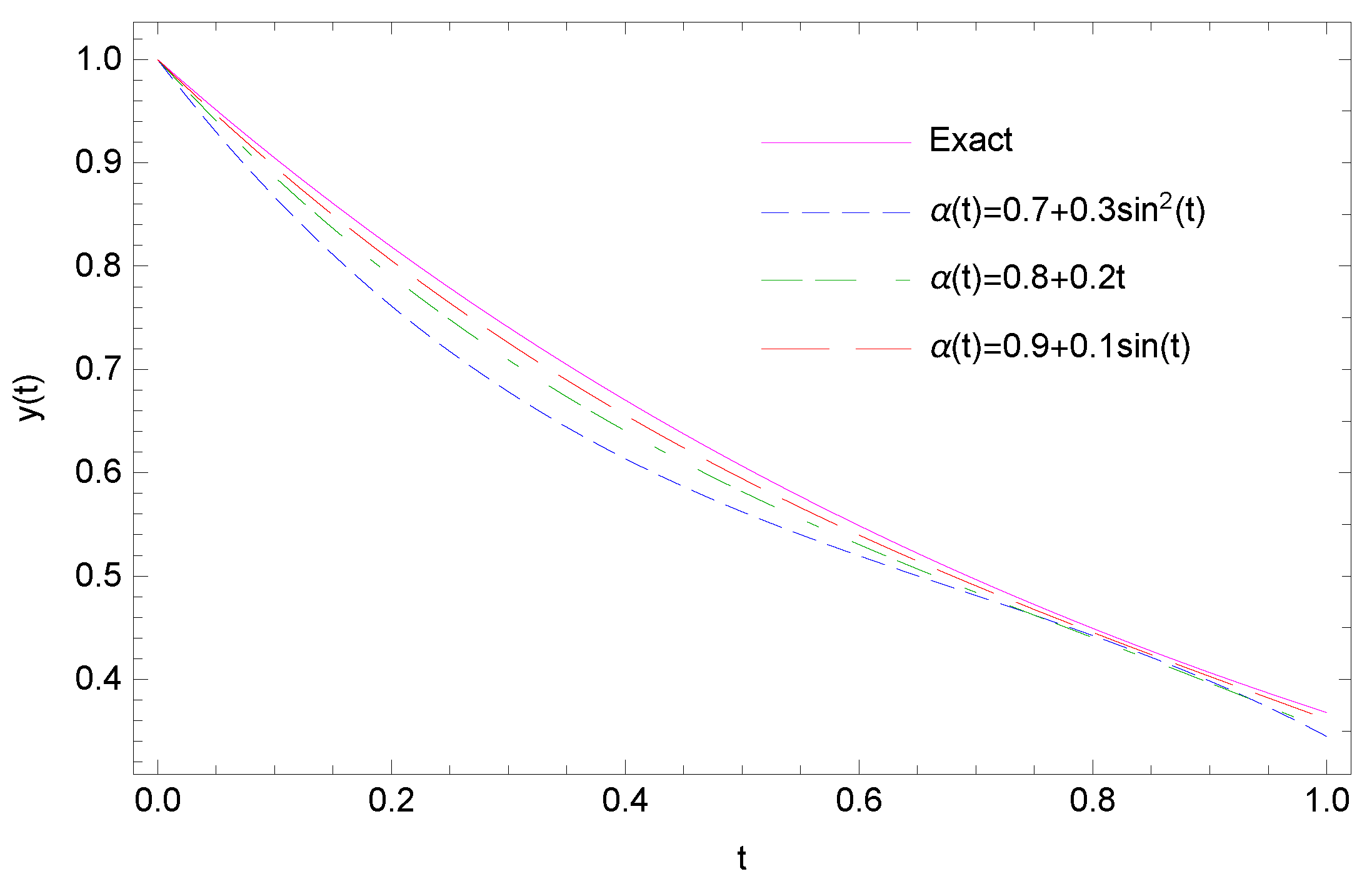
| t | |||
|---|---|---|---|
| Method of [43] | Method of [44] | Present Method | |||
|---|---|---|---|---|---|
| Method of [45] | Present Method | ||||
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemati, S.; Lima, P.M.; Torres, D.F.M. Numerical Solution of Variable-Order Fractional Differential Equations Using Bernoulli Polynomials. Fractal Fract. 2021, 5, 219. https://doi.org/10.3390/fractalfract5040219
Nemati S, Lima PM, Torres DFM. Numerical Solution of Variable-Order Fractional Differential Equations Using Bernoulli Polynomials. Fractal and Fractional. 2021; 5(4):219. https://doi.org/10.3390/fractalfract5040219
Chicago/Turabian StyleNemati, Somayeh, Pedro M. Lima, and Delfim F. M. Torres. 2021. "Numerical Solution of Variable-Order Fractional Differential Equations Using Bernoulli Polynomials" Fractal and Fractional 5, no. 4: 219. https://doi.org/10.3390/fractalfract5040219
APA StyleNemati, S., Lima, P. M., & Torres, D. F. M. (2021). Numerical Solution of Variable-Order Fractional Differential Equations Using Bernoulli Polynomials. Fractal and Fractional, 5(4), 219. https://doi.org/10.3390/fractalfract5040219







