CMOS OTA-Based Filters for Designing Fractional-Order Chaotic Oscillators
Abstract
:1. Introduction
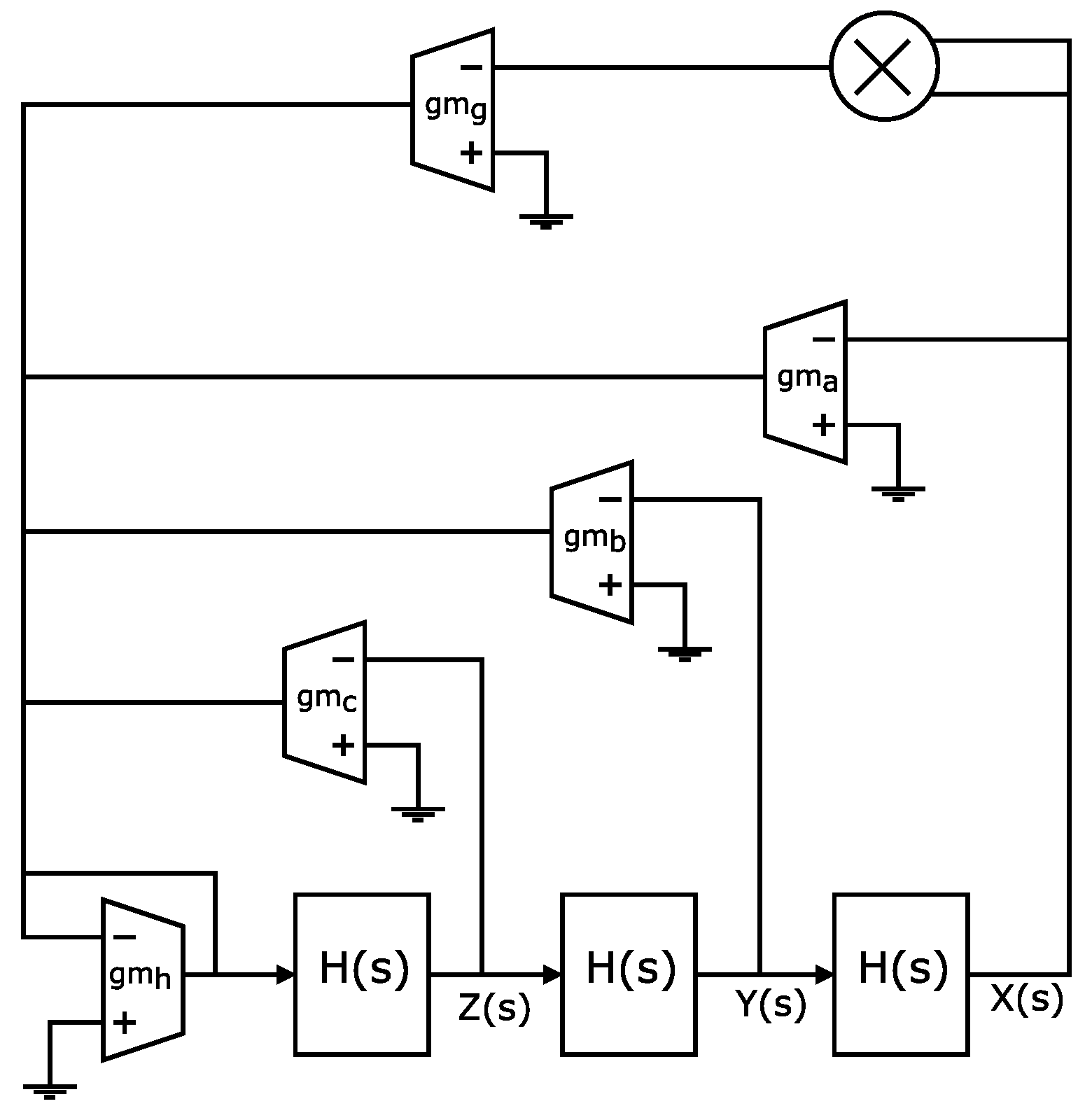
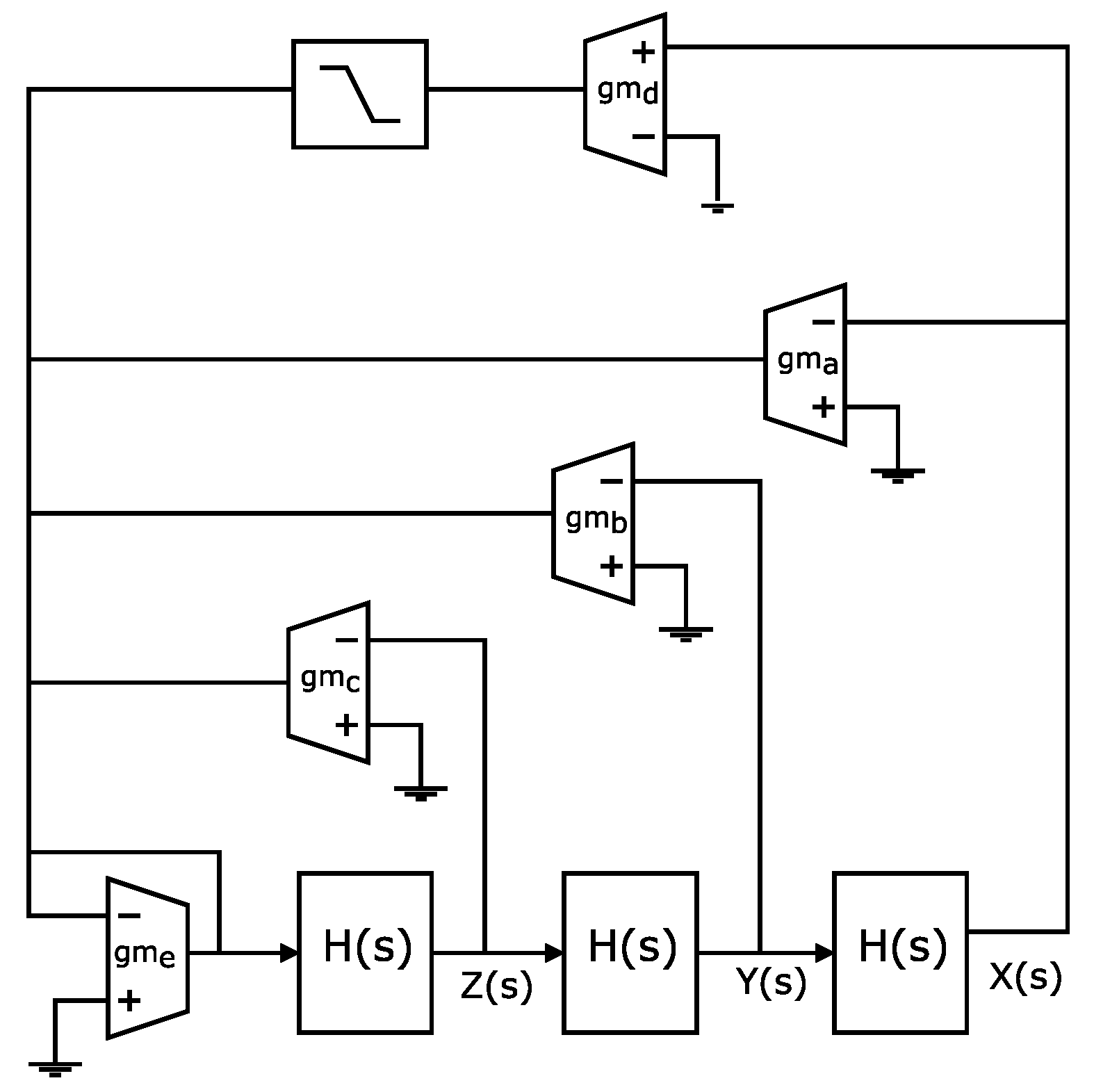
2. Fractional-Order Chaotic Oscillators
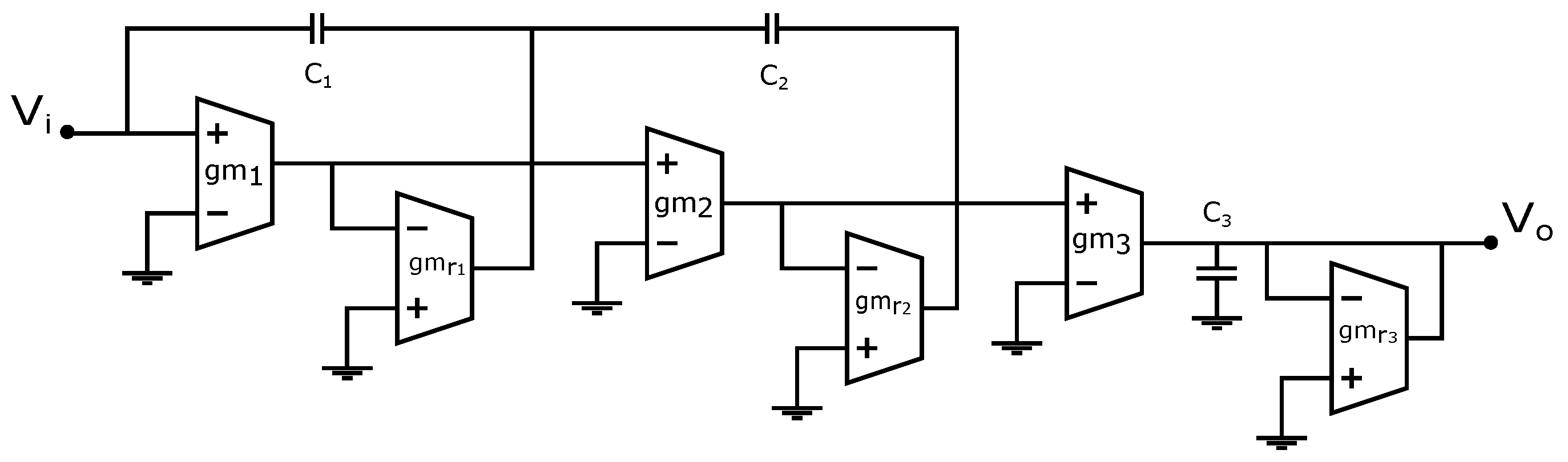
3. Approximation of the Fractional-Order Integrator by OTA Filters
4. CMOS Design of the OTAs, Multiplier, Nonlinear Function and Fractional-Order Integrator
4.1. CMOS Operational Transconductance Amplifier (OTA)
4.2. CMOS Multiplier Design
4.3. Saturated Nonlinear Function (SNLF) Design
4.4. Proposed CMOS Fractional-Order Integrator
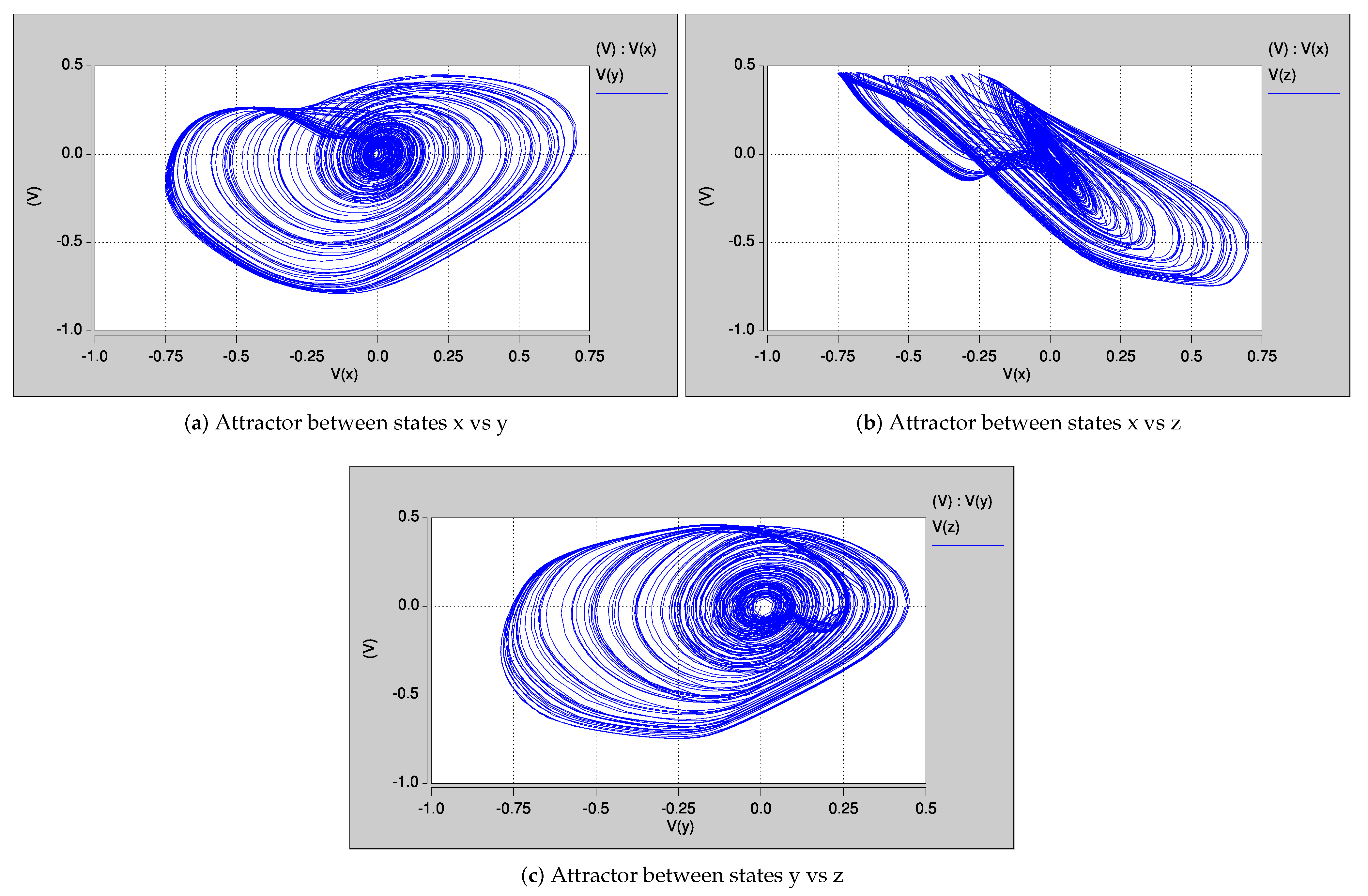
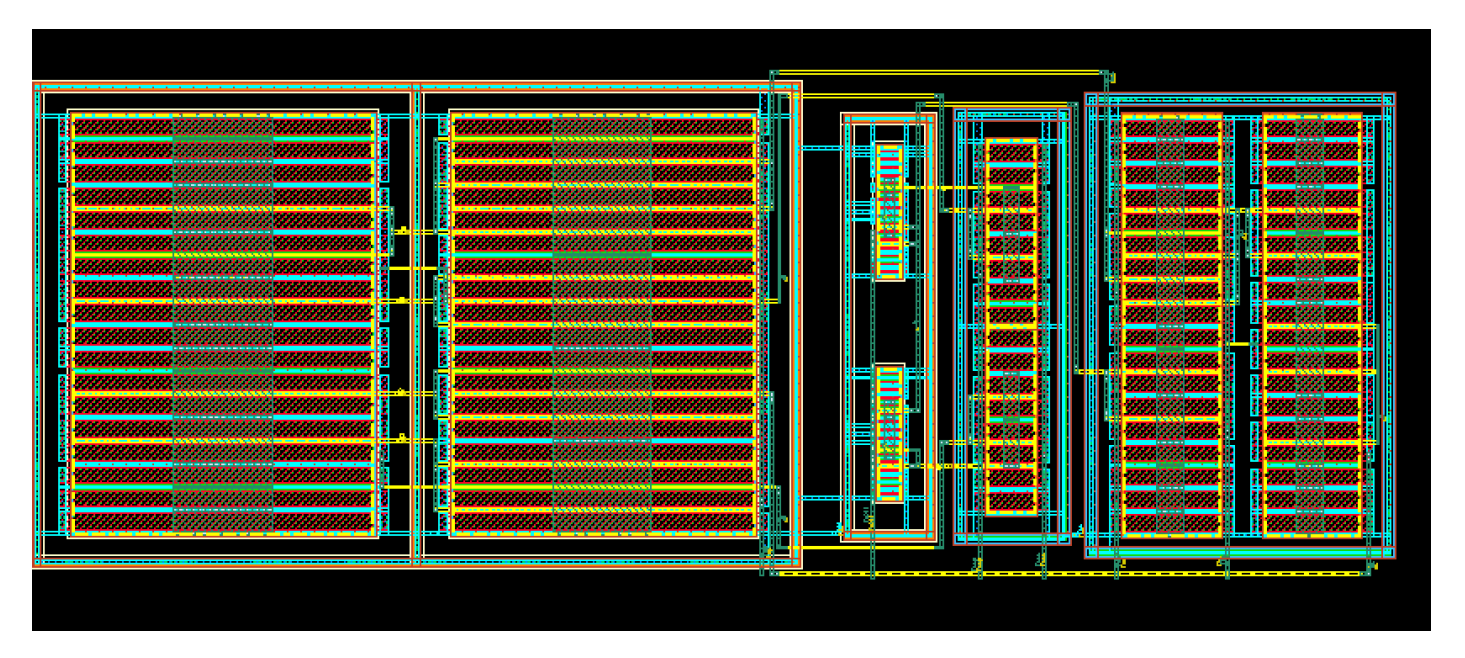
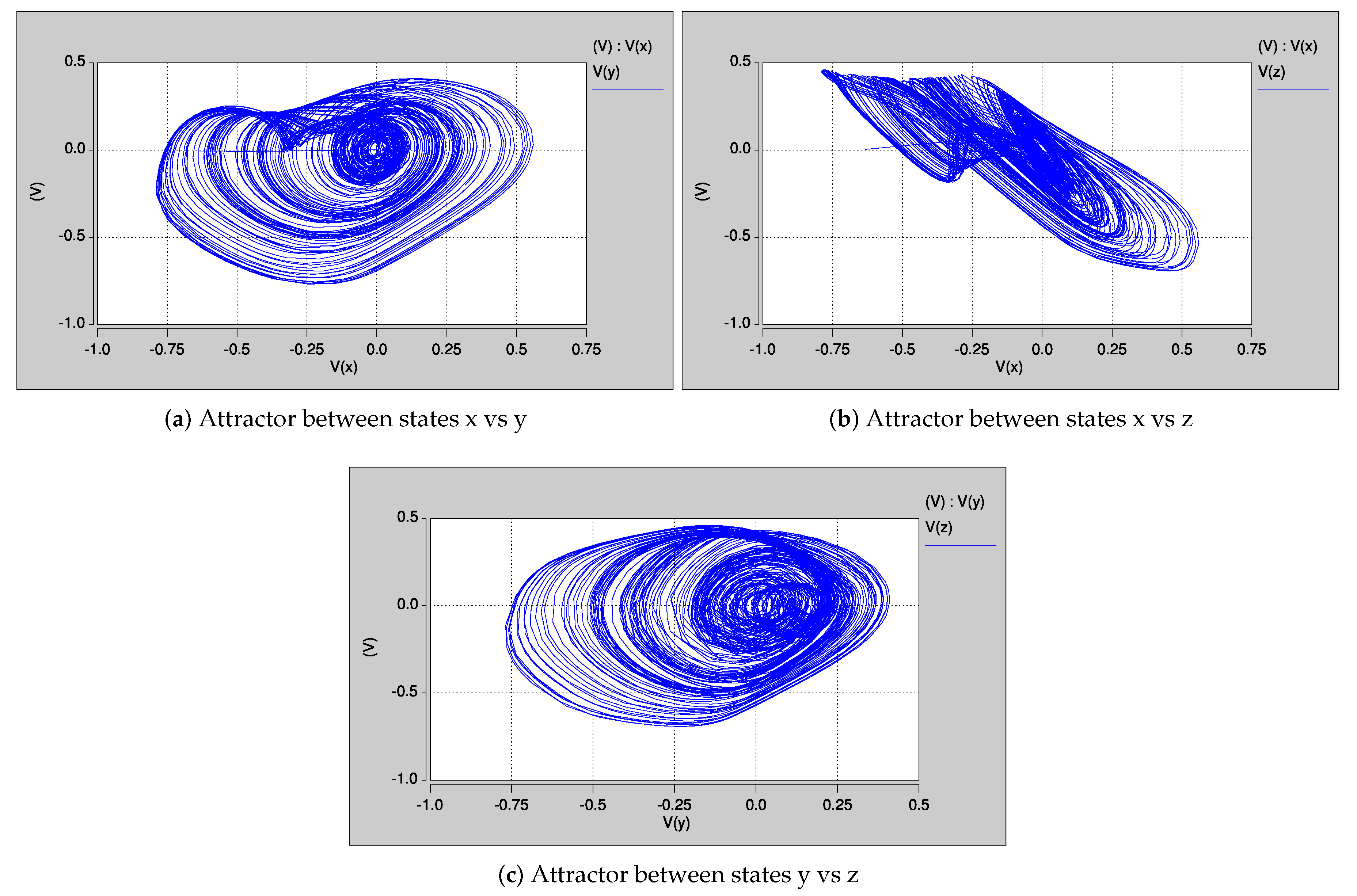
5. Layout Design and Post-Layout Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Vázquez, A.; Delgado-Restituto, M. CMOS design of chaotic oscillators using state variables: A monolithic Chua’s circuit. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 596–613. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Ma, C.; Mou, J.; Li, P.; Yang, F.; Liu, T. Multistability Analysis and Digital Circuit Implementation of a New Conformable Fractional-Order Chaotic System. Mob. Netw. Appl. 2020, 1–10. [Google Scholar] [CrossRef]
- Cui, L.; Lu, M.; Ou, Q.; Duan, H.; Luo, W. Analysis and Circuit Implementation of Fractional Order Multi-wing Hidden Attractors. Chaos Solitons Fractals 2020, 138, 109894. [Google Scholar] [CrossRef]
- Yao, J.; Wang, K.; Huang, P.; Chen, L.; Machado, J.A.T. Analysis and implementation of fractional-order chaotic system with standard components. J. Adv. Res. 2020, 25, 97–109. [Google Scholar] [CrossRef]
- Buscarino, A.; Caponetto, R.; Graziani, S.; Murgano, E. Realization of fractional order circuits by a Constant Phase Element. Eur. J. Control. 2020, 54, 64–72. [Google Scholar] [CrossRef]
- Khan, N.A.; Qureshi, M.A.; Hameed, T.; Akbar, S.; Ullah, S. Behavioral effects of a four-wing attractor with circuit realization: A cryptographic perspective on immersion. Commun. Theor. Phys. 2020, 72, 125004. [Google Scholar] [CrossRef]
- Elwakil, A.S. Fractional-order circuits and systems: An emerging interdisciplinary research area. IEEE Circuits Syst. Mag. 2010, 10, 40–50. [Google Scholar] [CrossRef]
- Bertsias, P.; Psychalinos, C.; Maundy, B.J.; Elwakil, A.S.; Radwan, A.G. Partial fraction expansion–based realizations of fractional-order differentiators and integrators using active filters. Int. J. Circuit Theory Appl. 2019, 47, 513–531. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator. AEU-Int. J. Electron. Commun. 2021, 129, 153537. [Google Scholar] [CrossRef]
- Silva-Juarez, A.; Tlelo-Cuautle, E.; de la Fraga, L.G.; Li, R. FPAA-based implementation of fractional-order chaotic oscillators using first-order active filter blocks. J. Adv. Res. 2020, 25, 77–85. [Google Scholar] [CrossRef]
- Joshi, M.; Ranjan, A. Investigation of dynamical properties in hysteresis-based a simple chaotic waveform generator with two stable equilibrium. Chaos Solitons Fractals 2020, 134, 109693. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Wen, Z. One-to-four-wing hyperchaotic fractional-order system and its circuit realization. Circuit World 2020, 46, 107–115. [Google Scholar] [CrossRef]
- Echenausia-Monroy, J.L.; Gilardi-Velazquez, H.E.; Jaimes-Reategui, R.; Aboites, V.; Huerta-Cuellar, G. A physical interpretation of fractional-order-derivatives in a jerk system: Electronic approach. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105413. [Google Scholar] [CrossRef]
- Trejo-Guerra, R.; Tlelo-Cuautle, E.; Carbajal-Gómez, V.H.; Rodriguez-Gomez, G. A survey on the integrated design of chaotic oscillators. Appl. Math. Comput. 2013, 219, 5113–5122. [Google Scholar] [CrossRef]
- Choubey, C.K.; Paul, S.K. Implementation of chaotic oscillator by designing a simple Chua’s diode using a single VDTA. Aeu-Int. J. Electron. Commun. 2020, 124, 153360. [Google Scholar] [CrossRef]
- Marquez-Cabrera, A.; Sanchez-Lopez, C. A nonlinear macromodel for current backward transconductance amplifier. Aeu-Int. J. Electron. Commun. 2020, 123, 153286. [Google Scholar] [CrossRef]
- Joshi, M.; Ranjan, A. An autonomous chaotic and hyperchaotic oscillator using OTRA. Analog. Integr. Circuits Signal Process. 2019, 101, 401–413. [Google Scholar] [CrossRef]
- Khalil, N.A.; Said, L.A.; Radwan, A.G.; Soliman, A.M. Emulation circuits of fractional-order memelements with multiple pinched points and their applications. Chaos Solitons Fractals 2020, 138, 109882. [Google Scholar] [CrossRef]
- Yildirim, M. DNA encoding for RGB image encryption with memristor based neuron model and chaos phenomenon. Microelectron. J. 2020, 104, 104878. [Google Scholar] [CrossRef]
- Dar, M.R.; Kant, N.A.; Khanday, F.A. Realization of Integrable Incommensurate-Fractional-Order-Rossler-System Design Using Operational Transconductance Amplifiers (OTAs) and Its Experimental Verification. Int. J. Bifurc. Chaos 2017, 27, 1750077. [Google Scholar] [CrossRef]
- Dar, M.R.; Kant, N.A.; Khanday, F.A. Electronic Implementation of Fractional-Order Newton-Leipnik Chaotic System With Application to Communication. J. Comput. Nonlinear Dyn. 2017, 12, 054502. [Google Scholar] [CrossRef]
- Khanday, F.A.; Dar, M.R.; Kant, N.A.; Rossello, J.L.; Psychalinos, C. 0.65V integrable electronic realisation of integer- and fractional-order Hindmarsh-Rose neuron model using companding technique. IET Circuits Devices Syst. 2018, 12, 696–706. [Google Scholar] [CrossRef]
- Kant, N.A.; Dar, M.R.; Khanday, F.A.; Psychalinos, C. Ultra-low-Voltage Integrable Electronic Realization of Integer- and Fractional-Order Liao’s Chaotic Delayed Neuron Model. Circuits Syst. Signal Process. 2017, 36, 4844–4868. [Google Scholar] [CrossRef]
- Duman, M.E.; Suvak, O. Uncertainty Quantification of CMOS Active Filter Circuits: A Non-Intrusive Computational Approach Based on Generalized Polynomial Chaos. IEEE Access 2020, 8, 189246–189261. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, L.; Zhong, Z.; Lou, Y.; Zhang, S. Detection and defense of active attacks for generating secret key from wireless channels in static environment. ISA Trans. 2020, 99, 231–239. [Google Scholar] [CrossRef]
- Babazadeh, M. Edge analytics for anomaly detection in water networks by an Arduino101-LoRa based WSN. ISA Trans. 2019, 92, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Tavazoei, M.S.; Tavakoli-Kakhki, M.; Bizzarri, F. Nonlinear Fractional-Order Circuits and Systems: Motivation, a Brief Overview, and Some Future Directions. IEEE Open J. Circuits Syst. 2020. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus. In Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 1997; pp. 223–276. [Google Scholar]
- Pandey, A.; Baghel, R.; Singh, R. Analysis and circuit realization of a new autonomous chaotic system. Int. J. Electron. Commun. Eng. 2012, 5, 487–495. [Google Scholar]
- Lu, J.; Chen, G.; Yu, X.; Leung, H. Design and analysis of multiscroll chaotic attractors from saturated function series. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 2476–2490. [Google Scholar] [CrossRef] [Green Version]
- Geiger, R.L.; Sanchez-Sinencio, E. Active filter design using operational transconductance amplifiers: A tutorial. IEEE Circuits Devices Mag. 1985, 1, 20–32. [Google Scholar] [CrossRef]
- De la Fraga, L.G.; Tlelo-Cuautle, E. Linearizing the Transconductance of an OTA Through the Optimal Sizing by Applying NSGA-II. In Proceedings of the 2018 15th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Prague, Czech Republic, 2–5 July 2018; pp. 1–9. [Google Scholar]
- Tlelo-Cuautle, E.; Valencia-Ponce, M.A.; de la Fraga, L.G. Sizing CMOS Amplifiers by PSO and MOL to Improve DC Operating Point Conditions. Electronics 2020, 9, 1027. [Google Scholar] [CrossRef]
- Carbajal-Gomez, V.H.; Tlelo-Cuautle, E.; Muñoz-Pacheco, J.M.; de la Fraga, L.G.; Sanchez-Lopez, C.; Fernandez-Fernandez, F.V. Optimization and CMOS design of chaotic oscillators robust to PVT variations. Integration 2019, 65, 32–42. [Google Scholar] [CrossRef]
- Carvajal, R.G.; Ramírez-Angulo, J.; López-Martín, A.J.; Torralba, A.; Galán, J.A.G.; Carlosena, A.; Chavero, F.M. The flipped voltage follower: A useful cell for low-voltage low-power circuit design. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1276–1291. [Google Scholar] [CrossRef]
- Nandini, A.; Madhavan, S.; Sharma, C. Design and implementation of analog multiplier with improved linearity. Int. J. VLSI Des. Commun. Syst. 2012, 3, 93. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Muñoz-Pacheco, J.M.; Martínez-Carballido, J. Frequency scaling simulation of Chua’s circuit by automatic determination and control of step-size. Appl. Math. Comput. 2007, 194, 486–491. [Google Scholar] [CrossRef]
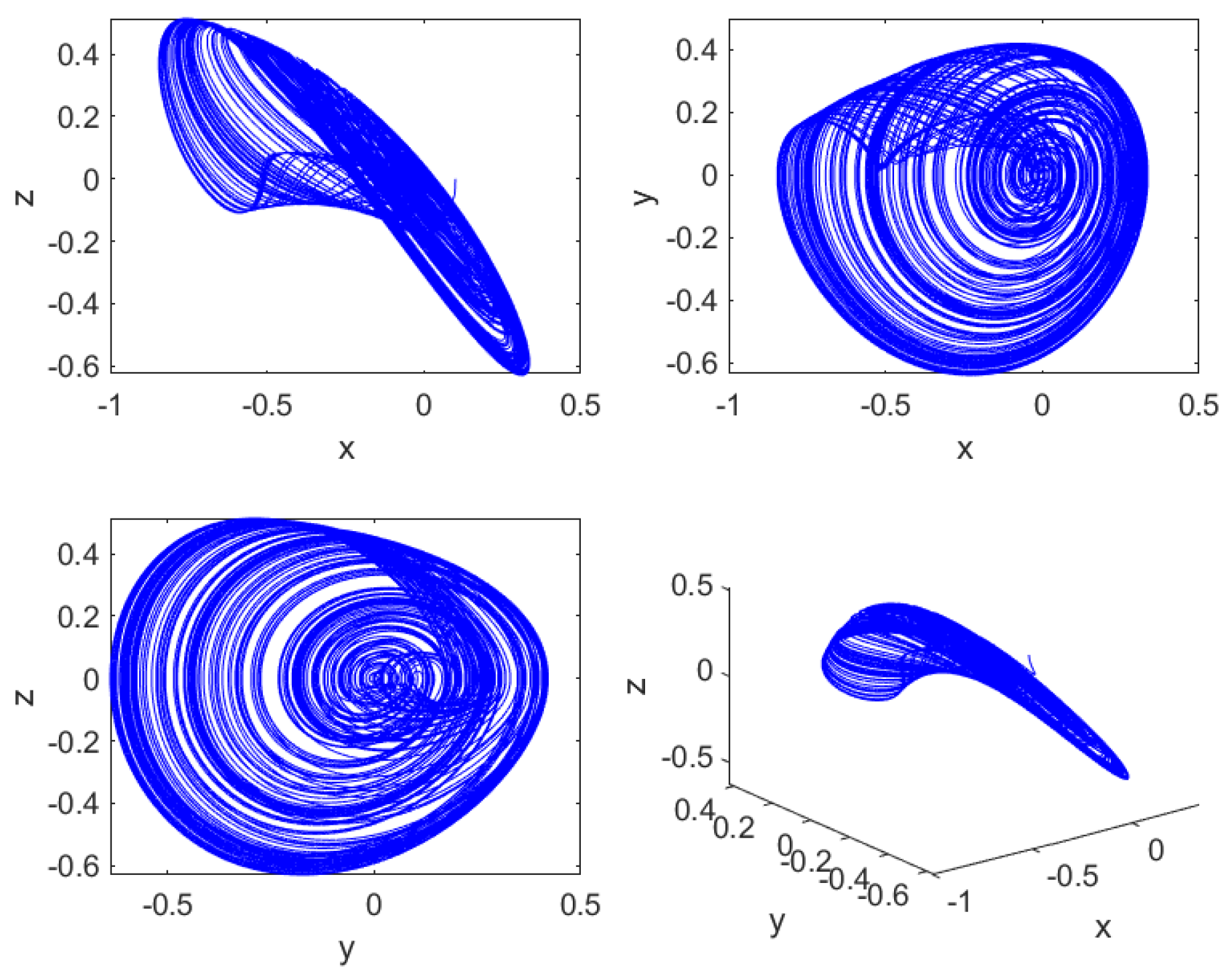
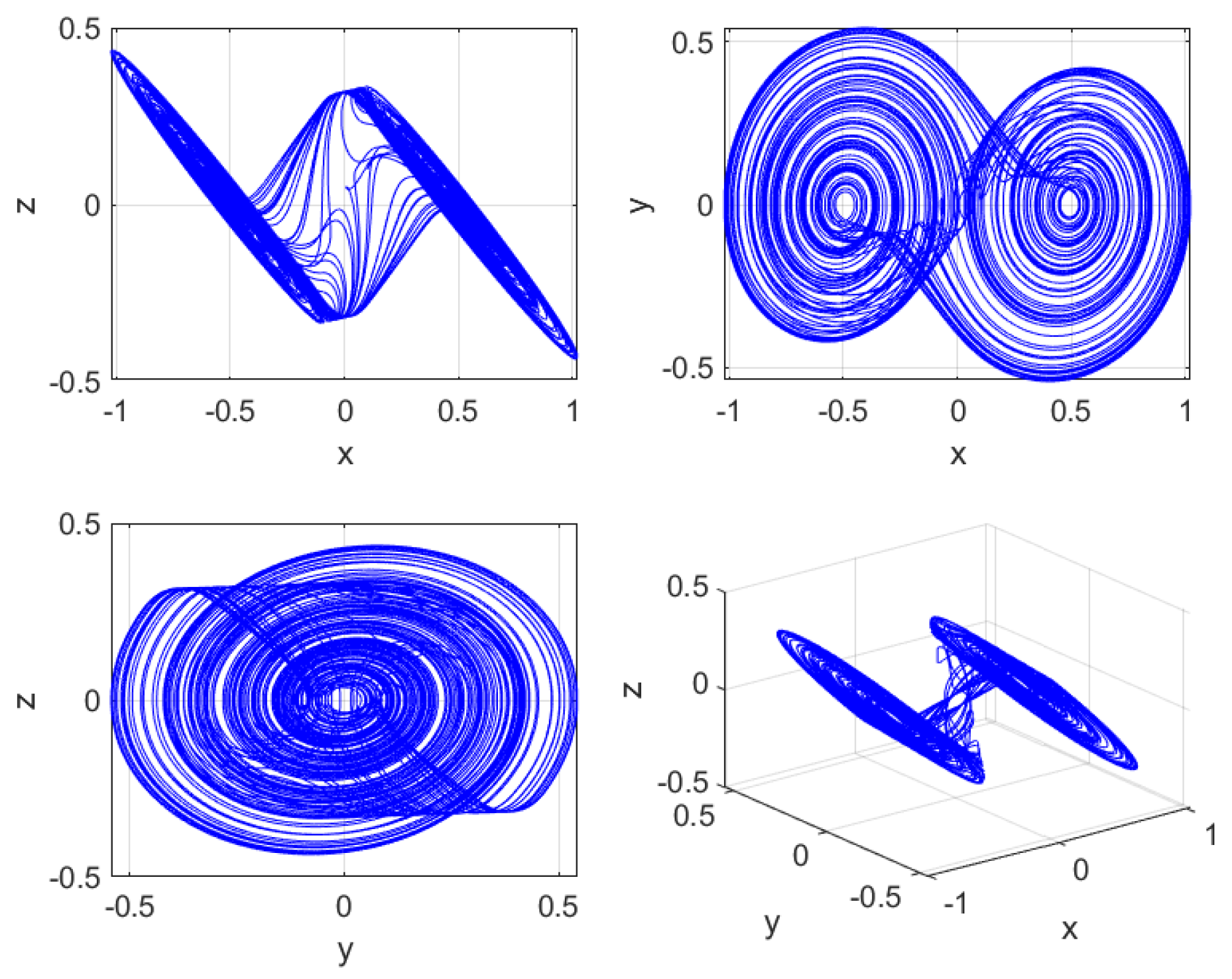
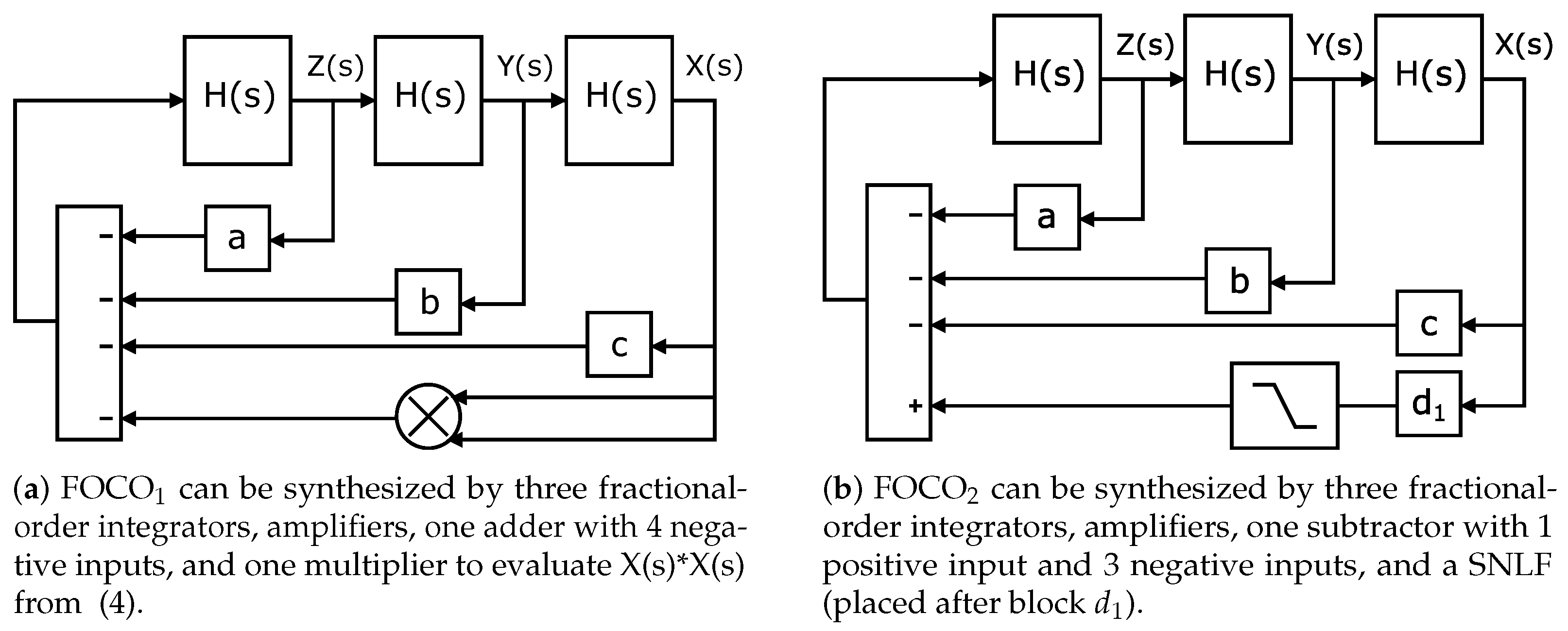
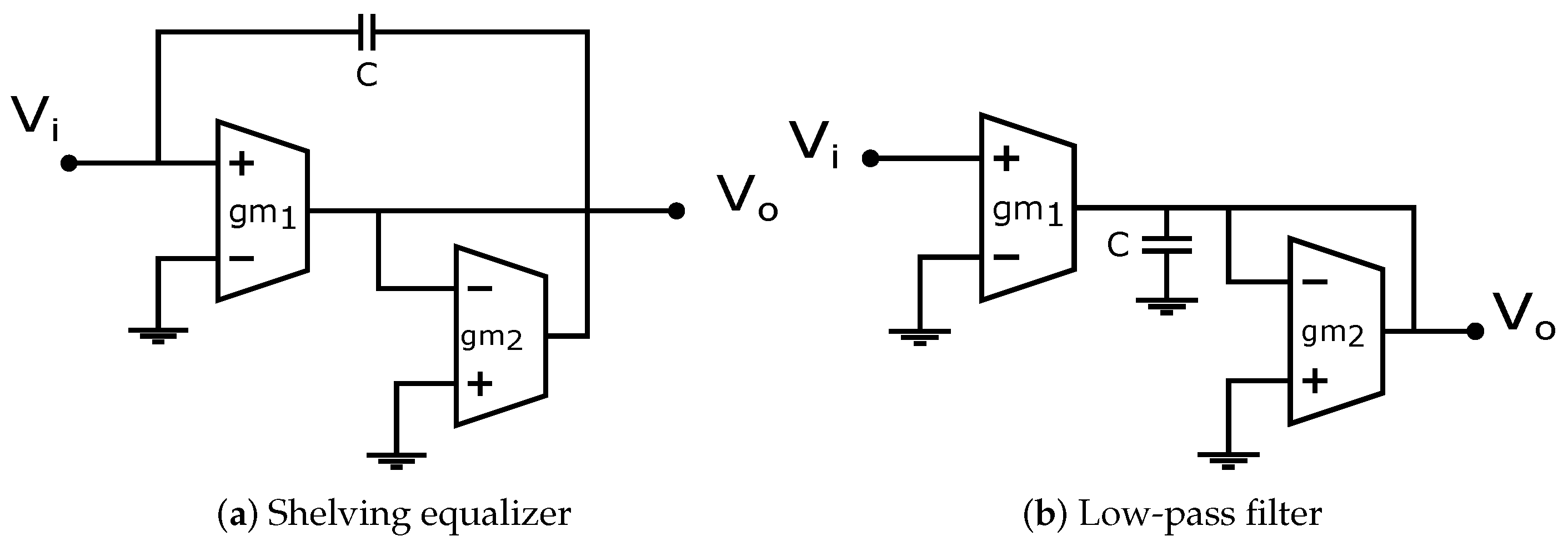
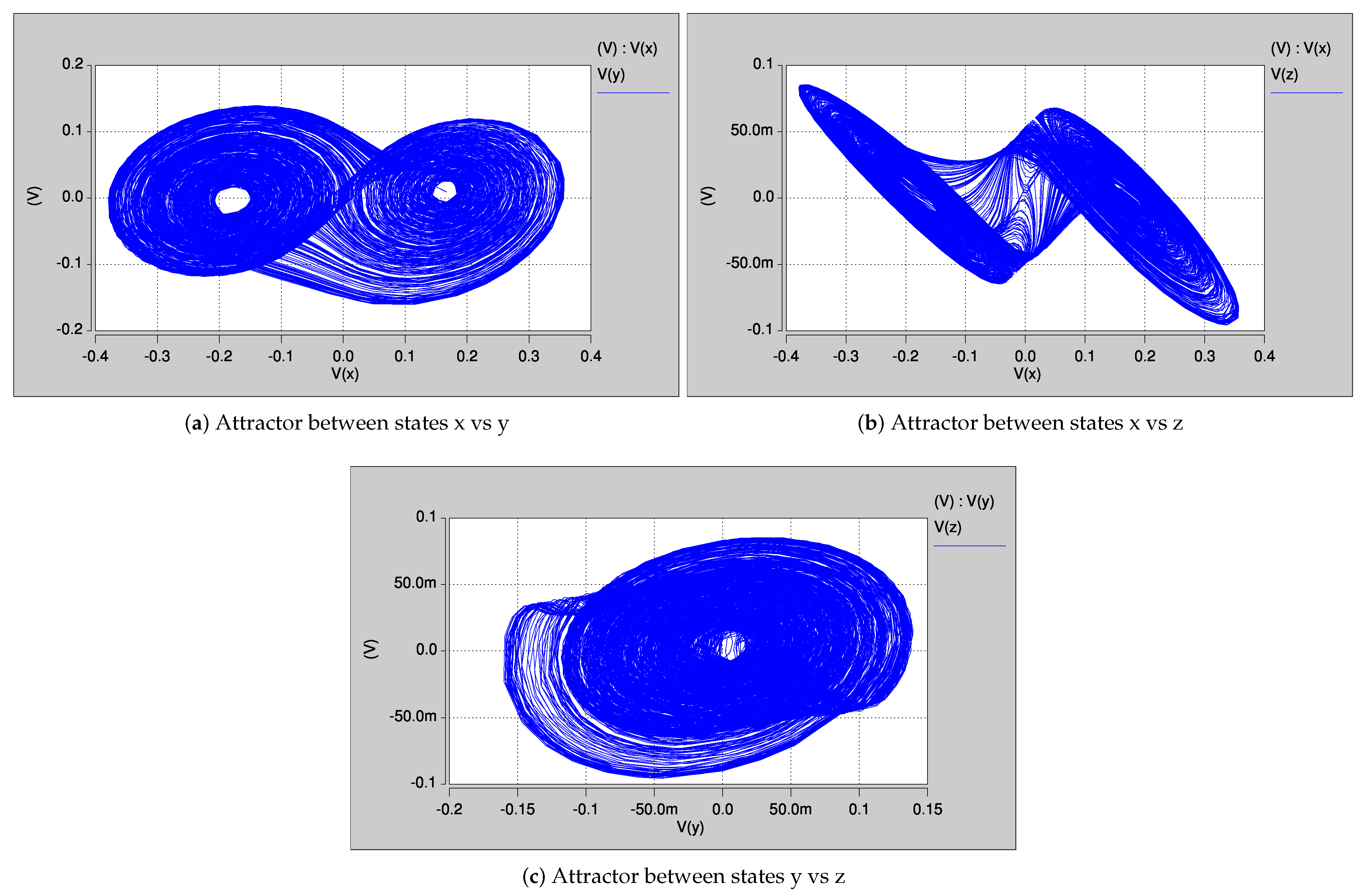


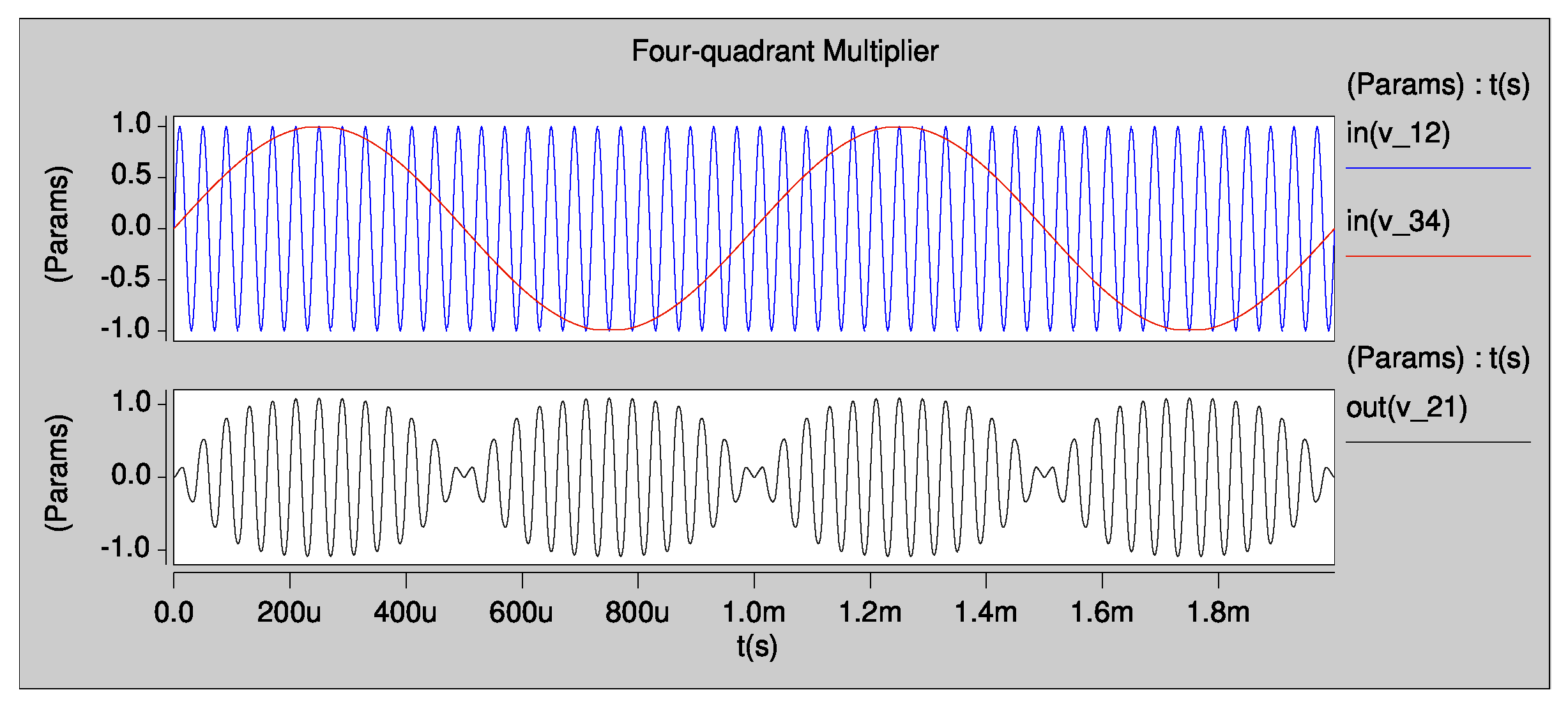
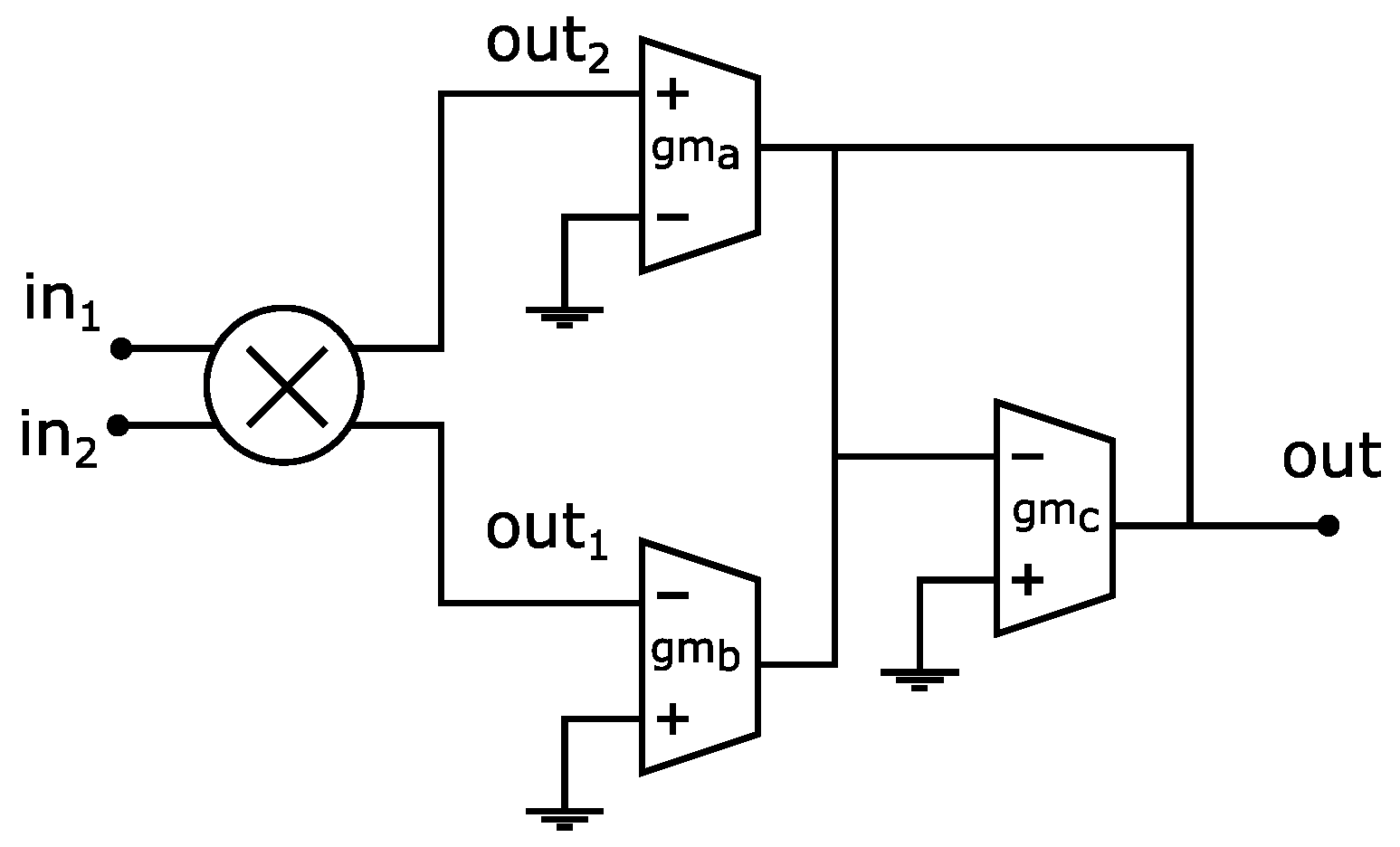
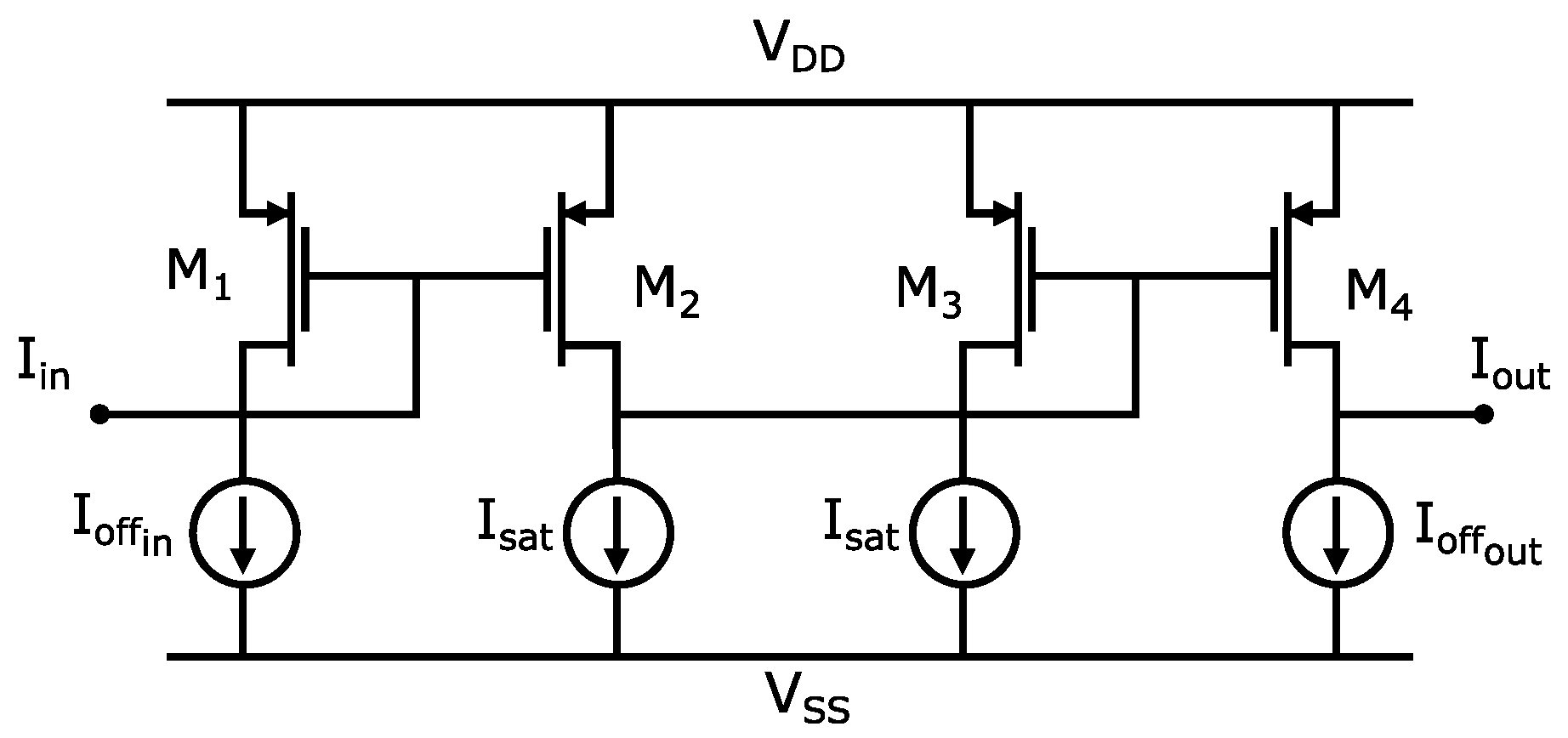

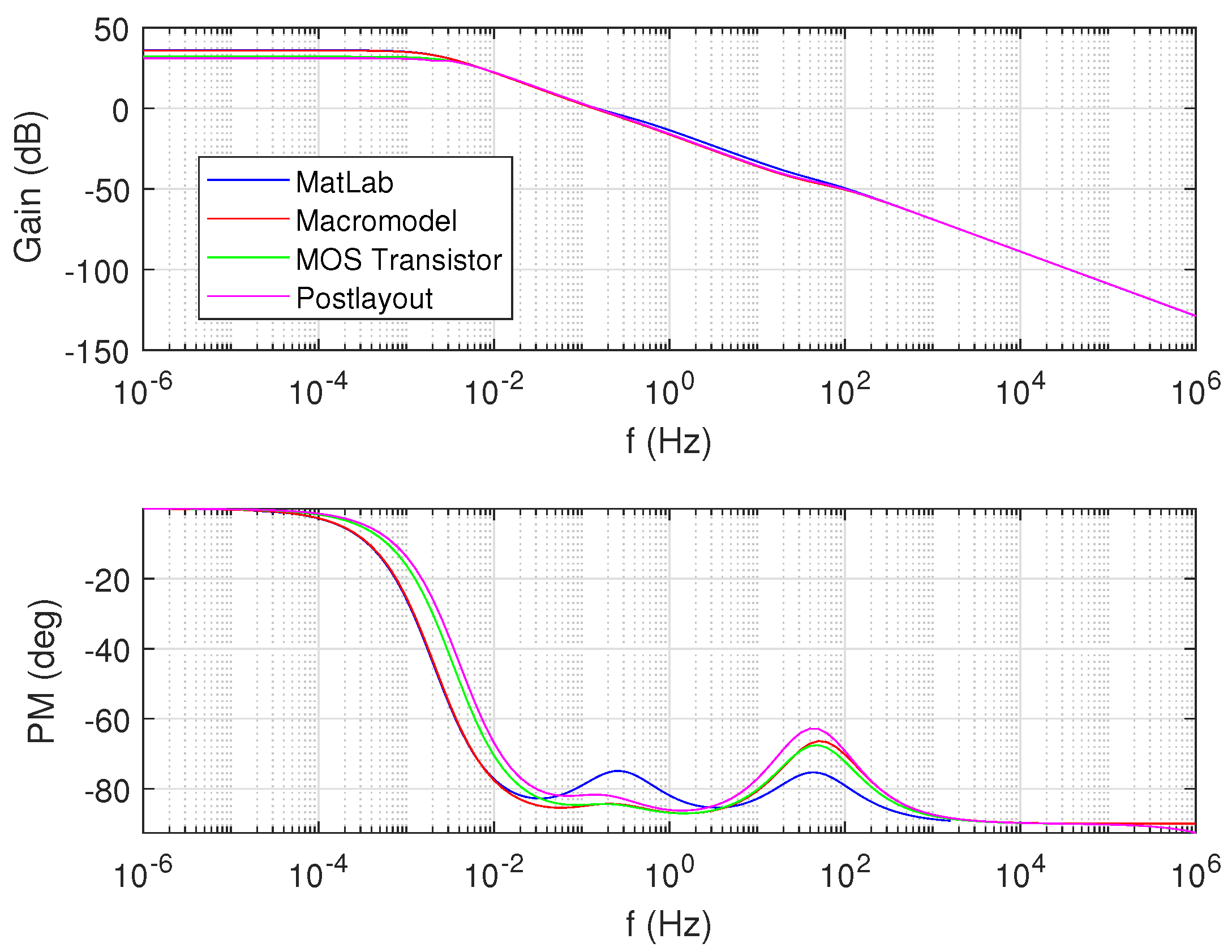
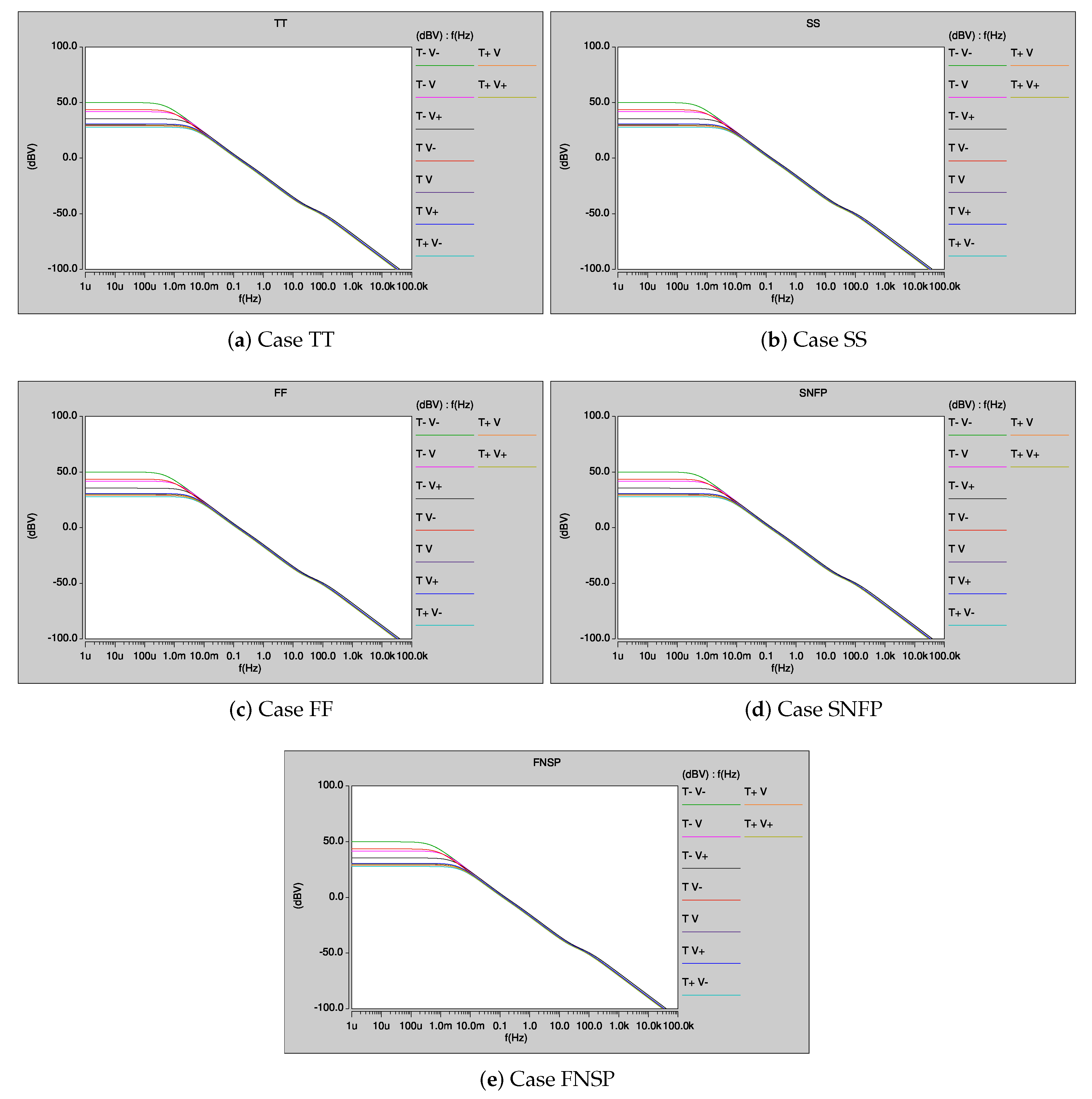
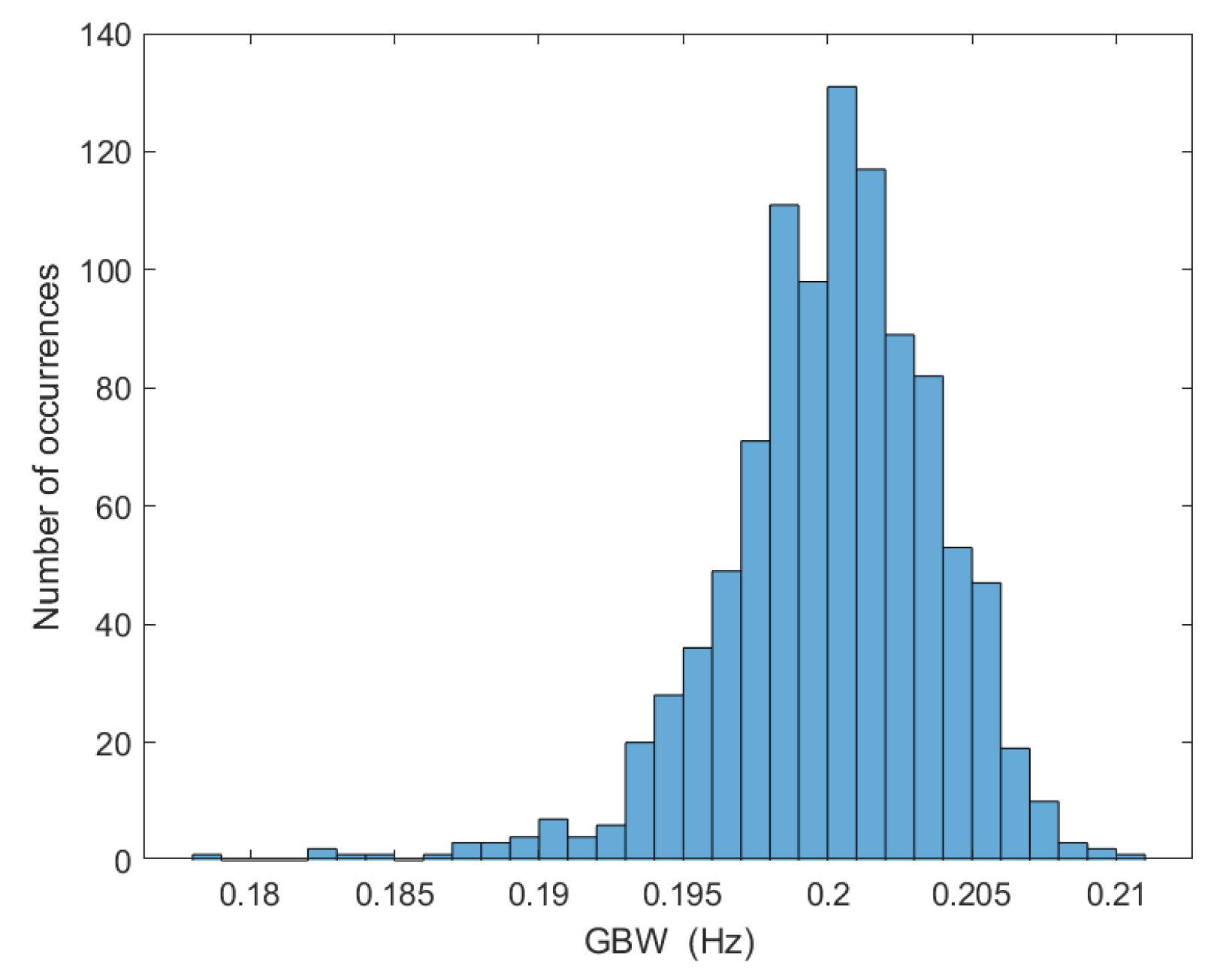

| Parameter | gm = 500 u | gm = 350 u |
|---|---|---|
| DC GAIN (dB) | 61.232 | 61.125 |
| GBW (KHz) | 425 | 419 |
| PM () | 88.96 | 88.943 |
| CMRR (dB) | 73 | 74 |
| SR+ (v/s) | 0.098 | 0.095 |
| SR- (v/s) | 0.106 | 0.105 |
| PSRR+ (dB) | 89 | 89 |
| PSRR- (dB) | 61 | 61 |
| Power dissipation (mW) | 3.19 | 3.18 |
| 1856.8 | 1843.6 | |
| 431.2 | 418 | |
| W(M1,M2) (m) | 20.16 | 20.16 |
| W(M3,M14,M15) (m) | 39.6 | 39.6 |
| W(Mb,M12,M13) (m) | 19.8 | 19.8 |
| W(M4-M9) (m) | 61.2 | 61.2 |
| W(M10,M11)(m) | 122.4 | 122.4 |
| L(m) | 1.8 | 1.8 |
| Ib (A) | 50 | 50 |
| Transistor | m) | m) | Multiplicity |
|---|---|---|---|
| 5.04 | 1.8 | 4 | |
| 9.9 | 1.8 | 4 | |
| 9.9 | 1.8 | 2 | |
| 30.6 | 1.8 | 2 | |
| 30.6 | 1.8 | 4 |
| Transistor | m) | m) | Multiplicity |
|---|---|---|---|
| 1.26 | 1.8 | 4 | |
| 2.52 | 1.8 | 4 | |
| 2.52 | 1.8 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia-Ponce, M.A.; Castañeda-Aviña, P.R.; Tlelo-Cuautle, E.; Carbajal-Gómez, V.H.; González-Díaz, V.R.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.-C. CMOS OTA-Based Filters for Designing Fractional-Order Chaotic Oscillators. Fractal Fract. 2021, 5, 122. https://doi.org/10.3390/fractalfract5030122
Valencia-Ponce MA, Castañeda-Aviña PR, Tlelo-Cuautle E, Carbajal-Gómez VH, González-Díaz VR, Sandoval-Ibarra Y, Nuñez-Perez J-C. CMOS OTA-Based Filters for Designing Fractional-Order Chaotic Oscillators. Fractal and Fractional. 2021; 5(3):122. https://doi.org/10.3390/fractalfract5030122
Chicago/Turabian StyleValencia-Ponce, Martín Alejandro, Perla Rubí Castañeda-Aviña, Esteban Tlelo-Cuautle, Victor Hugo Carbajal-Gómez, Victor Rodolfo González-Díaz, Yuma Sandoval-Ibarra, and Jose-Cruz Nuñez-Perez. 2021. "CMOS OTA-Based Filters for Designing Fractional-Order Chaotic Oscillators" Fractal and Fractional 5, no. 3: 122. https://doi.org/10.3390/fractalfract5030122
APA StyleValencia-Ponce, M. A., Castañeda-Aviña, P. R., Tlelo-Cuautle, E., Carbajal-Gómez, V. H., González-Díaz, V. R., Sandoval-Ibarra, Y., & Nuñez-Perez, J.-C. (2021). CMOS OTA-Based Filters for Designing Fractional-Order Chaotic Oscillators. Fractal and Fractional, 5(3), 122. https://doi.org/10.3390/fractalfract5030122








