Effect of Grain Size on Microscopic Pore Structure and Fractal Characteristics of Carbonate-Based Sand and Silicate-Based Sand

Abstract

In this study, a series of nuclear magnetic resonance (NMR) tests was conducted on calcareous sand, quartz sand, and glass bead with a wide range of grain sizes, to understand the effect of grain size on the micro-pore structure and fractal characteristics of the carbonate-based sand and silicate-based sand. The pore size distribution (PSD) of the tested materials were obtained from the NMR T₂ spectra, and fractal theory was introduced to describe the fractal properties of PSD. Results demonstrate that grain size has a significant effect on the PSD of carbonate-based sand and silicate-based sand. As grain size increases, the PSD of sands evolves from a binary structure with two peaks to a ternary structure with three peaks. The increase in the grain size can cause a remarkable increase in the maximum pore size. It is also found that the more irregular the particle shape, the better the continuity between the large and medium pores. In addition, grain size has a considerable effect on the fractal dimension of the micro-pore structure. The increase of grain size can lead to a significant increase in the heterogeneity and fractal dimension in PSD for calcareous sand, quartz sand and glass bead.

1. Introduction

Carbonate-based sands (i.e., sands with the main component of calcium carbonate) and silicate-based sands (i.e., sands with the main component of quartz) exist extensively in nature, and they have long been used as the two most important granular geomaterials in the construction of geotechnical engineering. Specifically, siliceous-based sand is mainly distributed on the continent [1], which is applied to terrigenous geotechnical projects, such as roads, foundation pits, slopes, tunnels, etc. Calcareous-based sand, formed by the geological deposition of marine biological debris, is widely distributed onshore and offshore. It is commonly used in land reclamation projects. For example, it has been adopted as the filling material for the foundations of wharves, roads, and airport runways and in island reefs. Carbonate-based sand has more complex mechanical properties than silicate-based sand because its particle shape is more irregular [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The microstructure of soils, especially the pore-size distribution (i.e., PSD), has been extensively acknowledged to be related to mechanical properties, such as shear strength, compressibility, and water-retention ability [16,17,18,19,20,21,22]. Therefore, it is essential to investigate the micropore structure of carbonate-based sand and silicate sand for a better understanding of their macroscopic mechanical behaviors.

In the last decade, numerous efforts have been devoted to revealing the pore size distribution of soils, mainly based on several experimental measurement techniques, such as scanning electron microscope (SEM), mercury intrusion porosimetry (MIP), transmission electron microscopy (TEM), X-ray micro-tomography (XR-uCT), and nuclear magnetic resonance (NMR) [10,11,16,23,24,25,26,27]. The previous studies demonstrated that the microscopic pore structure of soils was highly complicated, highlighting the necessity of additional experimental research in this field. Moreover, previous works have provided sufficient evidence that the pore structures of porous media are born with fractal characteristics and could be studied by fractal theory [17,28,29,30,31,32]. Through a series of SEM and NMR tests, Shao et al. [33] observed a rather irregular pore size distribution in tight sandstone which consists of quartz and clay minerals. They found that the pore network of tight sandstones could be recognized as a dual-scale pore system based on fractal theory, and the fractal dimensions could reflect the physical properties. Sun et al. [34] carried out NMR tests on the Lower Cambrian Niutitang formation shale in northern Guizhou, China, and they investigated the relationships between fractal dimensions of micro-pore structure and mineral compositions. Li et al. [35] conducted NMR tests on the organic-rich marine shales of the Lower Cambrian Niutitang Formation in northern Guizhou, China, to explore the pore structures and fractal characteristics. It was found that shale samples with a larger surface fractal dimension have a higher methane adsorption capacity. Although some experimental investigations have been performed on sandstone and shale to investigate the micro-pore structure, few attempts have been made to quantify the microscopic pore structure and fractal characteristics of granular material, such as calcareous sand and siliceous sand. Another challenging problem is that the sands in the field are always heterogeneous with different grain sizes rather than with a single grain size. However, the effect of the grain size on the microstructure of granular material is still poorly understood. Consequently, further investigations are needed to eliminate the gap surrounding the effect of grain size on the microscopic pore structure and fractal characteristics of carbonate-based sand and silicate-based sand.

In this work, a series of nuclear magnetic resonance (NMR) tests was conducted on calcareous sand, quartz sand, and glass bead with a wide range of grain sizes. The effect of grain size on the micropore structure and fractal characteristics of the carbonate-based sand and silicate-based sand was analyzed in detail. Fractal theory was then introduced to describe the fractal properties of PSD, where the fractal dimension was obtained. The relationship between the fractal dimension and grain size was deeply discussed. The present findings might help to achieve a better interpretation and prediction of the macroscopic behavior of sands with different grain sizes from a microscopic structure view.

2. Materials and Methods

2.1. Materials

The carbonate-based sand used in this study was the natural calcareous sand from the South China Sea (as shown in Figure 1a). The South China Sea has a typical dual-structure coral reef stratum due to its complex seabed landform type. The upper layer of coral islands and reefs in the South China Sea is carbonate-based sand, and the lower layer is reef limestone. The carbonate-based sand adopted in this study was obtained from the upper layer of the coral island reef in the South China Sea, which is a good construction filler material widely used in marine reclamation projects. Through additional X-ray diffraction tests already conducted on this carbonated-based sand [2], it was found that this sand is mainly composed of aragonite and calcite, and the calcium carbonate (CaCO₃) content of this sand is about 92%. The silicate sands adopted in this study were quartz sand (see Figure 1b) and glass bead (see Figure 1c) used for comparison experiments. The standard quartz sand was obtained from Fujian, China. It is extensively distributed in various strata in Fujian, China, and it is the most common geotechnical material in the local area. Through further X-ray diffraction tests, this sand was found to have a high silicon dioxide (SiO₂) content of around 98%. The glass bead was a commercial glass bead with artificial round particles and the same particle size as sands. In the sampling process of this study, homogeneous calcareous sand and quartz sand were selected as much as possible in their respective identical locations. Moreover, additional sieving was performed before the NMR test to further ensure the uniformity of the experimental materials. Figure 2 shows the scanning electron microscope (SEM) images of calcareous sand and quartz sand. As can be seen, compared with quartz sand, the particles of calcareous sand have more corners, rougher surfaces and more irregular shapes.

2.2. Test Equipment and Specimen Preparation

The NMR technique has been used to capture the pore size distribution of the adopted specimens. The NMR technique is fast, comprehensive, non-destructive and accurate, which makes it different than the other existing methods like MIT, SEM. Unlike MIT and SEM scanning, NMR can accurately detect the whole pore structures of the sand assembly based on the reliable theoretical relationship between relaxation time and pore size. The device used in this study is the low-field nuclear magnetic resonance device (MesoMR23-060H-I, Shanghai Niumag Corporation, Shanghai, China), as shown in Figure 3. The nuclear magnetic resonance device is composed of five major systems, namely the temperature control system, the magnet system, the spectrometer system, the radiofrequency system and the data acquisition system. The magnet system used 0.5T magnetic field strength, and the magnet temperature was controlled at 32 °C ± 0.01 °C.

The NMR specimens were prepared on a triaxial device. Standard cylindrical specimens with diameters of 50 mm and heights of 100 mm were employed in this study [36,37,38], as shown in Figure 4. The approach of air pluviation was adopted to prepare the specimen to prevent sand particles from breaking during specimen preparation [39]. The prepared specimens were then saturated by passing carbon dioxide and deaired water through the specimens. Subsequently, the specimen was saturated at a back pressure of 200 kPa. After the B-value was detected to be greater than 95%, the saturation operation was stopped. The saturated sample was removed from the triaxial device and then transferred to the sample tube of the NMR device under the protection of the mold. To investigate the effect of grain size on the microstructure and its fractal dimension, NMR tests were carried out on calcareous sand with six single grain sizes (i.e., 0.1–0.25 mm, 0.5–0.71 mm, 0.71–1 mm, 1–2 mm, 2–3 mm, and >5 mm), quartz sands with three single grain sizes (0.1–0.25 mm, 0.5–0.71 mm, and 1–2 mm), and glass beads with four single grain sizes (i.e., 0.5–0.71 mm, 0.71–1.0 mm, 1–2 mm, and 2–3 mm) for comparison. The detailed test program is summarized in

Table 1. Test program of this study.

No.	Material	Grain Size (mm)	Void Ratio
C-D-1	Calcareous sand	0.1–0.25	1.143
C-D-2		0.5–0.71	1.142
C-D-3		0.71–1	1.146
C-D-4		1–2	1.145
C-D-5		2–3	1.144
C-D-6		>5	1.143
S-D-1	Quartz sand	0.1–0.25	0.507
S-D-2		0.5–0.71	0.508
S-D-3		1–2	0.509
G-D-1	Glass sand	0.5–0.71	0.631
G-D-2		0.71–1.0	0.630
G-D-3		1–2	0.632
G-D-4		2–3	0.633

.

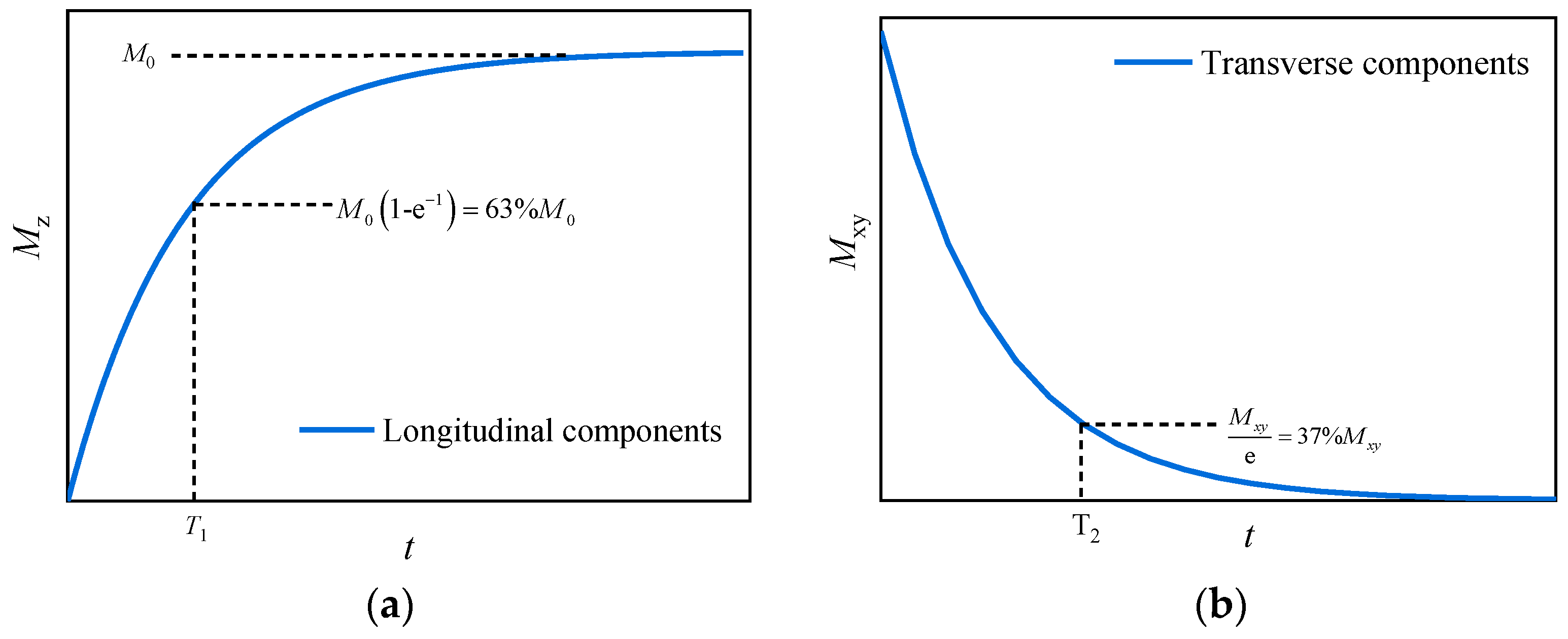
2.3. Calculation Method for Determining Pore Size Distribution Using NMR

After the main magnetic field (B₀) is applied to the nuclei, the spin direction of some nuclei will become the same as the applied magnetic field, while most of the other spin directions are still chaotic. When the applied magnetic field is removed, the non-equilibrium protons at a high energy level will return to the equilibrium state of a low energy level. This process of returning the protons from a high energy level to the equilibrium state is called relaxation. From a macro point of view, the maximum magnetization (M₀) will tend to return to the initial state parallel to B₀ (i.e., the smallest energy and the most stable state). Therefore, attenuation occurs in the xy plane and recovery occurs in the z-direction. The Bloch equation can be used to describe the relaxation phenomenon, as follows:

$$\frac{\mathrm{d}\overrightarrow{M}}{\mathrm{d}t}=\overrightarrow{M}\times \gamma \overrightarrow{B}-\frac{\left(M_z-M_0\right)\overrightarrow{k}}{T_1}-\frac{M_x\overrightarrow{i}+M_y\overrightarrow{j}}{T_2}$$

(1)

which can be transformed into:

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{M}_x\\ M_y\\ M_z\end{array}\right)=\gamma \left(\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ M_x& M_y& M_z\\ B_x& B_y& B_z\end{array}\right)-\frac{\left(M_z-M_0\right)\overrightarrow{k}}{T_1}-\frac{M_x\overrightarrow{i}+M_y\overrightarrow{j}}{T_2}$$

(2)

The solution of the equation with the specific B₀ is given by:

$$\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{M}_x\\ M_y\\ M_z\end{array}\right)=\gamma \left(\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ M_x& M_y& M_z\\ 0& 0& B_0\end{array}\right)-\frac{\left(M_z-M_0\right)\overrightarrow{k}}{T_1}-\frac{M_x\overrightarrow{i}+M_y\overrightarrow{j}}{T_2}\\ =\gamma \left(M_z{B}_0\overrightarrow{i}-M_x{B}_0\overrightarrow{j}\right)-\frac{\left(M_z-M_0\right)\overrightarrow{k}}{T_1}-\frac{M_x\overrightarrow{i}+M_y\overrightarrow{j}}{T_2}\\ =\left(\begin{array}{ccc}-\frac{1}{T_2}& \gamma B_0& 0\\ -\gamma B_0& -\frac{1}{T_2}& 0\\ 0& 0& -\frac{1}{T_1}\end{array}\right)\left(\begin{array}{c}{M}_x\\ M_y\\ M_z\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ \frac{M_0}{T_1}\end{array}\right)\end{array}$$

(3)

where M is the magnetization vector, B is the magnetic field vector, t is the time, γ is the rotation ratio, T₁ is the longitudinal relaxation time, and T₂ is the transverse relaxation time.

T₁ relaxation is the process of energy exchange between hydrogen nuclei and the surrounding environment, that is, T₁ relaxation (i.e., longitudinal relaxation) is spin-lattice relaxation; T₂ relaxation (i.e., transverse relaxation) is the process of energy exchange between hydrogen nuclei and other atomic nuclei, that is, T₂ relaxation is spin-spin relaxation. Figure 5 shows the longitudinal and transverse components of the relaxation process versus time. The equation of longitudinal relaxation is given by:

$$\frac{\mathrm{d}{M}_z}{\mathrm{d}t}=-\frac{M_z-M_0}{T_1}$$

(4)

Then, the solution can be expressed as:

$$M_z\left(t\right)=M_0+\left(M_z\left(0\right)-M_0\right){\mathrm{e}}^{-t/T_1}$$

(5)

The equation of transverse relaxation is given by:

$$\frac{\mathrm{d}{M}_{xy}}{\mathrm{d}t}=-\frac{M_{xy}}{T_2}$$

(6)

Then, the solution can be given by:

$$M_{xy}(t)=M_{xy}\left(0\right){\mathrm{e}}^{-t/T_2}$$

(7)

Because the completion time of T₂ relaxation is much faster than T₁ relaxation, T₂ relaxation is commonly used to study the pore distribution characteristics of the sample in porous fluid media. According to the relaxation mechanism of low-field NMR, there are three different relaxation mechanisms for fluid in porous media. Therefore, the relaxation time of the pore fluid can be expressed as follows [40]:

$$\frac{1}{T_2}=\frac{1}{T_{2\mathrm{B}}}+\frac{1}{T_{2\mathrm{S}}}+\frac{1}{T_{2\mathrm{D}}}$$

(8)

where T₂ is the transverse relaxation time of pore fluid collected by Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence; T_2B is the free transverse relaxation time of the liquid, which is determined by the physical properties of the liquid (such as viscosity and chemical composition); T_2S is the transverse relaxation time caused by surface relaxation; T_2D is the transverse relaxation time of pore fluid caused by diffusion under magnetic field gradient. For water in porous media, the influence of the first and third terms on the equation can be ignored, and the surface relaxation plays the main role as follows:

$$\frac{1}{T_2}=\frac{1}{T_{2\mathrm{S}}}={\rho }_2\left(\frac{S}{V}\right)$$

(9)

where ρ₂ is the surface relaxation coefficient, which is a constant and is not affected by temperature and pressure; the method to determine the ρ₂-value of the sand-gravel mixture is described in detail in Feng, Xu, Chai and Li [23]; S/V is the ratio between the pore surface area (S) to the pore volume (V), which is related to the pore shape. Tian et al. [40] represented that the pore shape in the soil can be approximated as a cylindrical tube shape. Therefore, Equation (9) can be written as such:

$$R=2{\rho }_2{T}_2$$

(10)

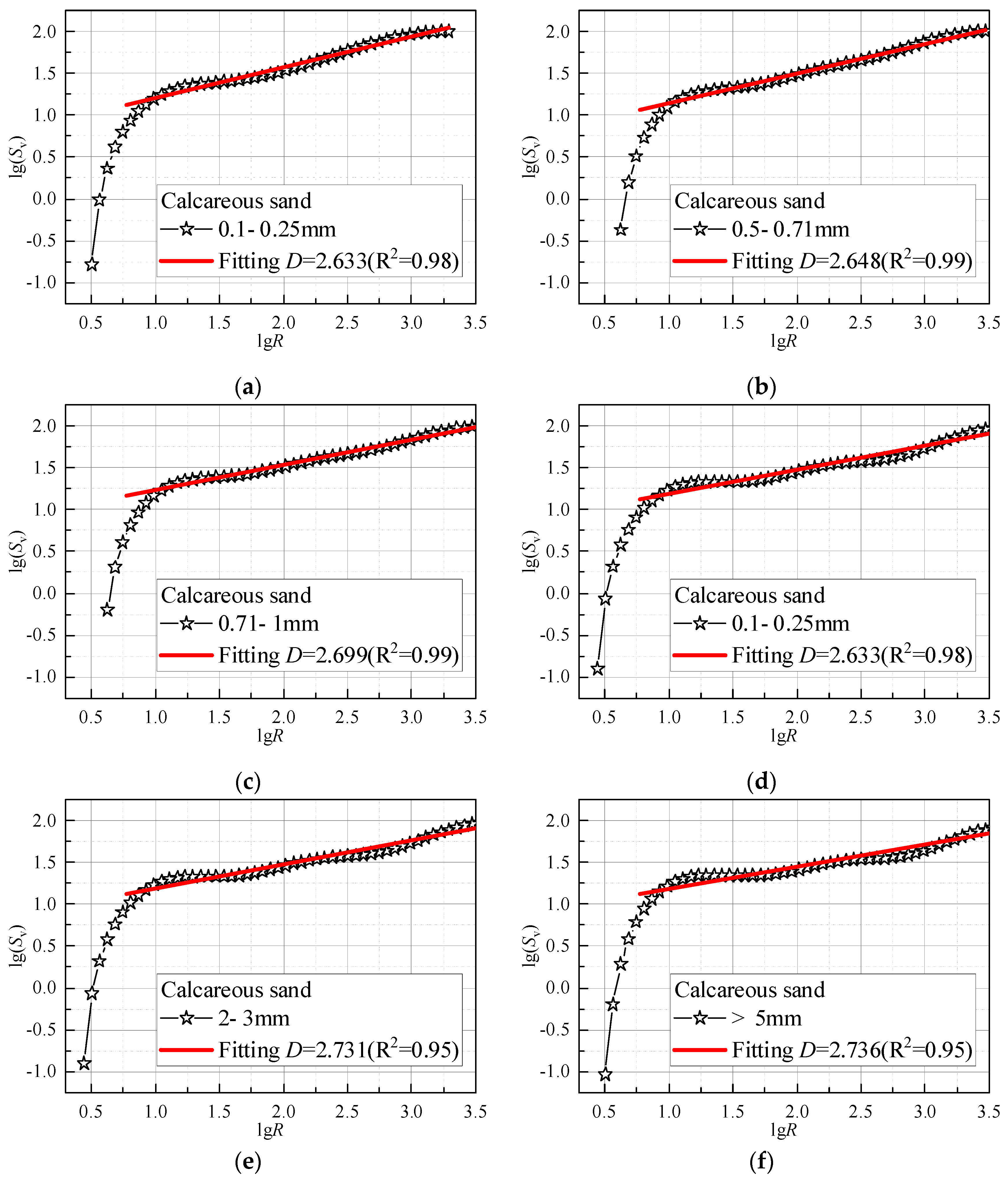
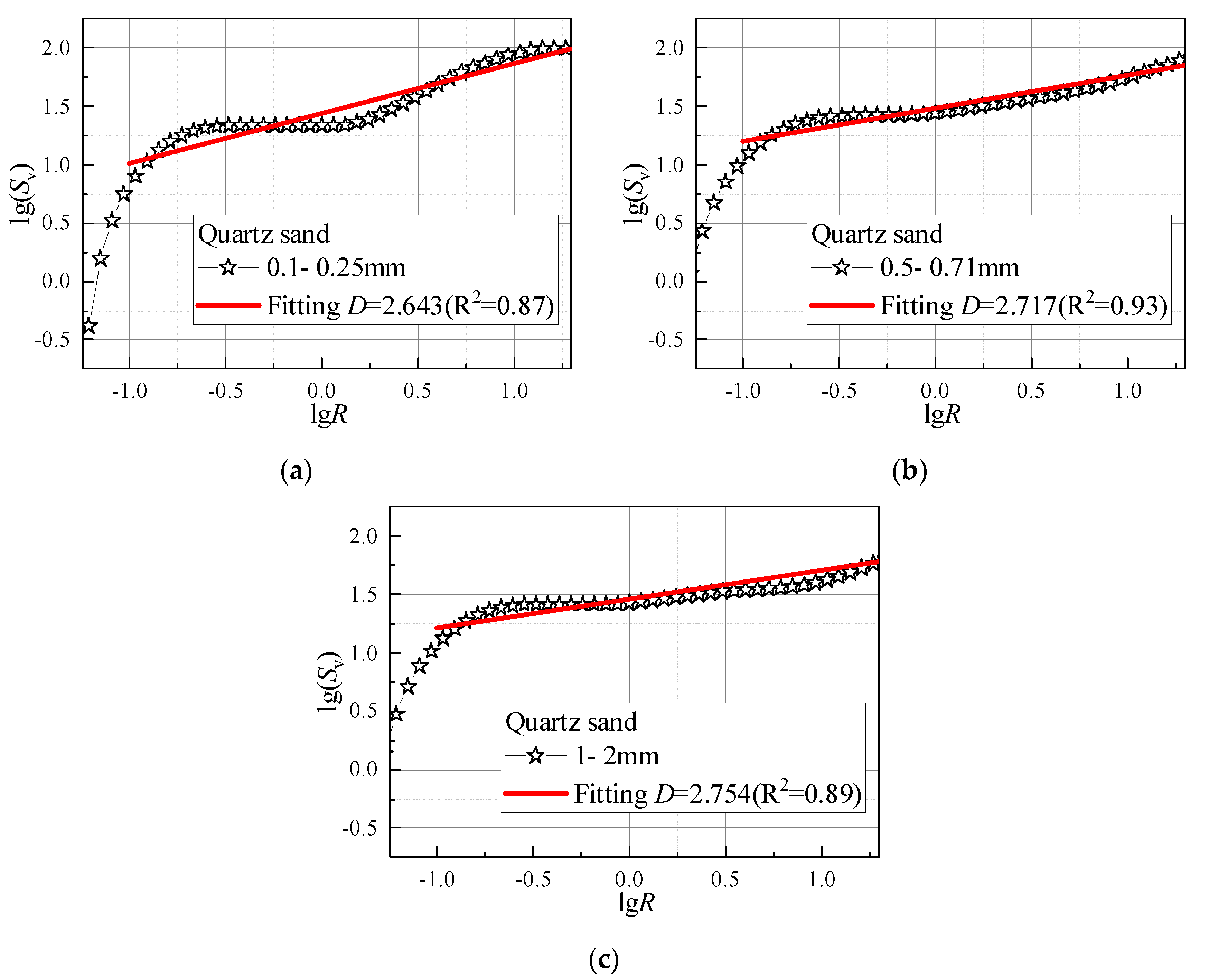
2.4. Calculation Method of Fractal Dimension Using Fractal Theory

Fractal dimension reflects the validity of space occupied by complex shapes, and it is a measure of the irregularity of complex shapes. According to previous works, the pore structures of porous media show fractal characteristics and can be studied by fractal theory [41]. The different fractal dimensions (D) resulted in the mechanisms of pore generation. In recent years, fractal theory has been widely used in quantitatively describing and studying the geometric characteristics of the PSD. The fractal property for the pore size distribution is given by [42]:

$$N(R>R\mathrm{a})\propto R^{-D}$$

(11)

where D is the fractal dimension; N (R > R_a) is the number of pores whose size R is greater than the specific measurement scale R_a. For most geomaterials, counting the number of pores of a given size is not feasible. Instead, it seems more appropriate to use mass to interpret the pore size distribution, which is a more readily measurable quantity. The definition of mass M (R > R_a) is suggested as [43]:

$$M(R>R_{\mathrm{a}})={\rho }_{\mathrm{P}}{C}_{\mathrm{m}}[1-{(R/{\lambda }_{\mathrm{m}})}^{3-D}]$$

(12)

where C_m and λ_m are constants related to pore shape and size, and ρ_P is the pore density under the assumed conditions. The total mass M_T can be determined by setting R = 0 in Equation (12), as given by:

$$M_{\mathrm{T}}={\rho }_{\mathrm{P}}{C}_{\mathrm{m}}$$

(13)

Substitution of Equation (13) into Equation (12) yields:

$$M(R>R_{\mathrm{a}})/M_{\mathrm{T}}=1-{(R/{\lambda }_{\mathrm{m}})}^{3-D}$$

(14)

The constant λ_m is equal to the maximum pore size R_max for the fractal behavior in the case of M (R > R_a)/M_T = 0 with setting R = R_max. For the fractal nature of soil pore size distribution, the fractal dimension D is strictly limited to the range of 0 < D < 3 [44].

On account of the fact M (R > R_a)/M_T + M (R < R_a)/M_T = 1, Equation (8) can be rearranged to display the pore size distribution in a finer percentage by weight, that is, M (R < R_a) by noting that:

$$M(R<R_{\mathrm{a}})/M_{\mathrm{T}}={(R/R_{\max })}^{3-D}$$

(15)

According to the geometric fractal theory [41], the model of fractal dimension D in PSD corresponding to the pore size R obtained by NMR is as follows:

$$\lg S_{\mathrm{v}}=(3-D)\log R+(D-3)\log R_{\max }$$

(16)

where S_v is the percentage of the pore volume. It is calculated by the pore size smaller than the specific pore diameter R to the total pore volume; D is the fractal dimension, and R_max is the maximum pore size.

3. Results and Discussion

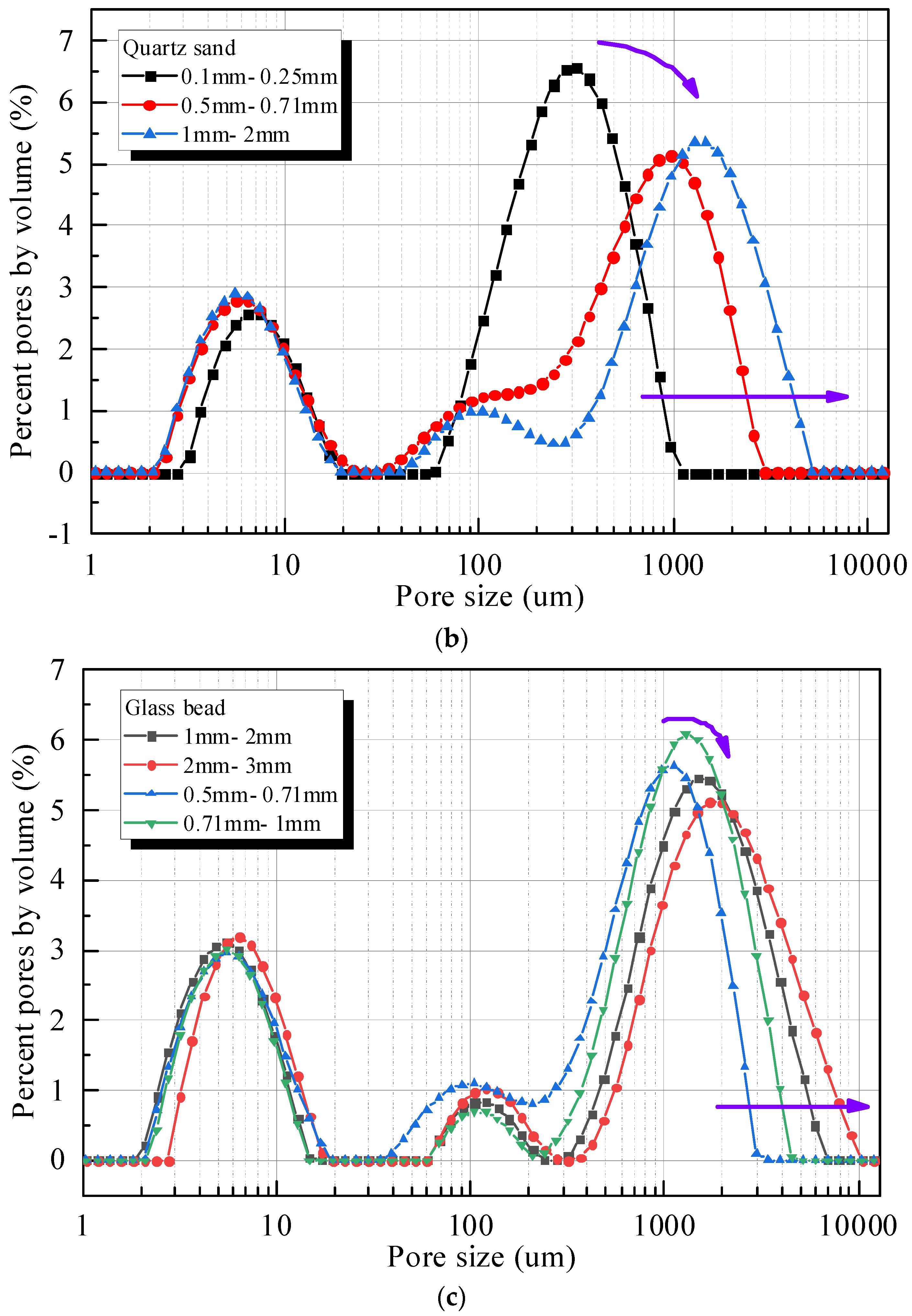
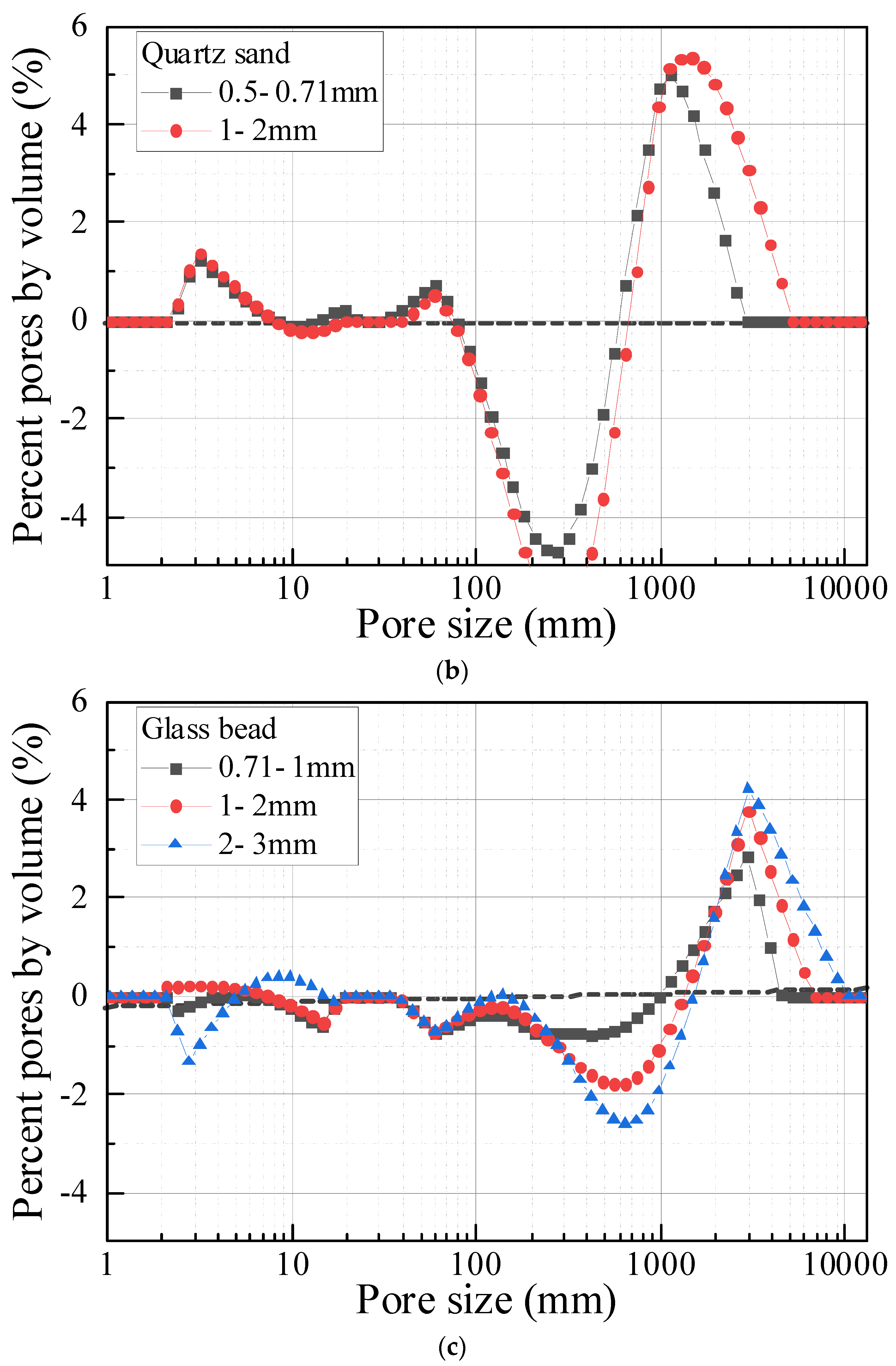
3.1. Effect of Grain Size on the Pore Size Distribution

Figure 6a shows the pore size distribution curve of calcareous sand with different grain sizes obtained from the T₂ relaxation time. It can be observed that the grain size significantly affects the pore size distribution curve of calcareous sand. For specimens with a grain size of 0.1 mm–0.25 mm, the pore size distribution belongs to a binary type with two peaks. With the increase of the grain size, the binary pore size distribution gradually evolves into a ternary pore size distribution with three peaks. The pore diameter corresponding to the turning point where the two peaks evolve into three peaks is around 100 μm. From the pore size distribution curves of the calcareous sands with different grain sizes, it can be inferred that the pore size distribution curve of the specimen with a grain size less than 0.25 mm belongs to a binary type. However, for the specimen with grain size larger than 1 mm, the pore size distribution curve belongs to a ternary type. The pore size distribution curve of the specimen with grain size around 0.25 mm–1 mm is between the binary type and ternary type. In addition to the number of main peaks in the pore size distribution curve of calcareous sand, the grain size also significantly affects the range of the pore size distribution curve. As shown in Figure 6a, the larger the grain size, the larger the maximum pore size and the wider the pore size range.

Figure 6b shows the pore size distribution curves of quartz sands with different grain sizes. It can be seen that, similar to calcareous sand, for quartz sand specimens with a grain size of 0.1 mm–0.25 mm, the pore size distribution also belongs to a binary type with two peaks. As the grain size increases, the pore size distribution curve of quartz sand gradually evolves into a ternary type with three peaks. Figure 6c shows the pore size distribution curves of glass beads. The results show the pore size distribution curves of glass beads all have three peaks. Note that in the pore size range between 100 μm and 1000 μm, carbonate-based sand has a continuous pore size distribution, whereas the pore size distribution of silicate-based sand is discontinuous. This indicates that the more irregular the particle shape, the better the continuity between the large and medium pores. Moreover, for quartz sand and glass bead, as the particle size increases, the maximum pore size also increases significantly.

In order to better understand the relative change of the pore size distribution of the three tested sands with different grain sizes, the difference of the pore size distribution curve under different grain sizes is presented in Figure 7. Figure 7a is the difference between the pore size distribution of calcareous sand with different grain sizes and the pore size distribution of calcareous sand with a grain size of 0.1 mm–0.25 mm. Figure 7b is the difference between the pore size distribution of quartz sand with different grain sizes and the pore size distribution of quartz sand with a grain size of 0.1 mm–0.25 mm. Figure 7c is the difference between the pore size distribution of glass bead with different grain sizes and the pore size distribution of glass beads with a grain size of 0.5 mm–0.71 mm. It can be seen from Figure 7 that the pore size distribution of the three tested materials has a relatively consistent changing trend with the grain size. This indicates that the influence mechanism of grain size on the pore size distribution of the three materials is similar. Specifically, the increase in grain size increases the proportion of large pores with a size larger than 1000 μm, and correspondingly reduces the proportion of medium pores with a size between 100 μm–1000 μm. However, grain size has a minor effect on small pores with a size less than 100 um.

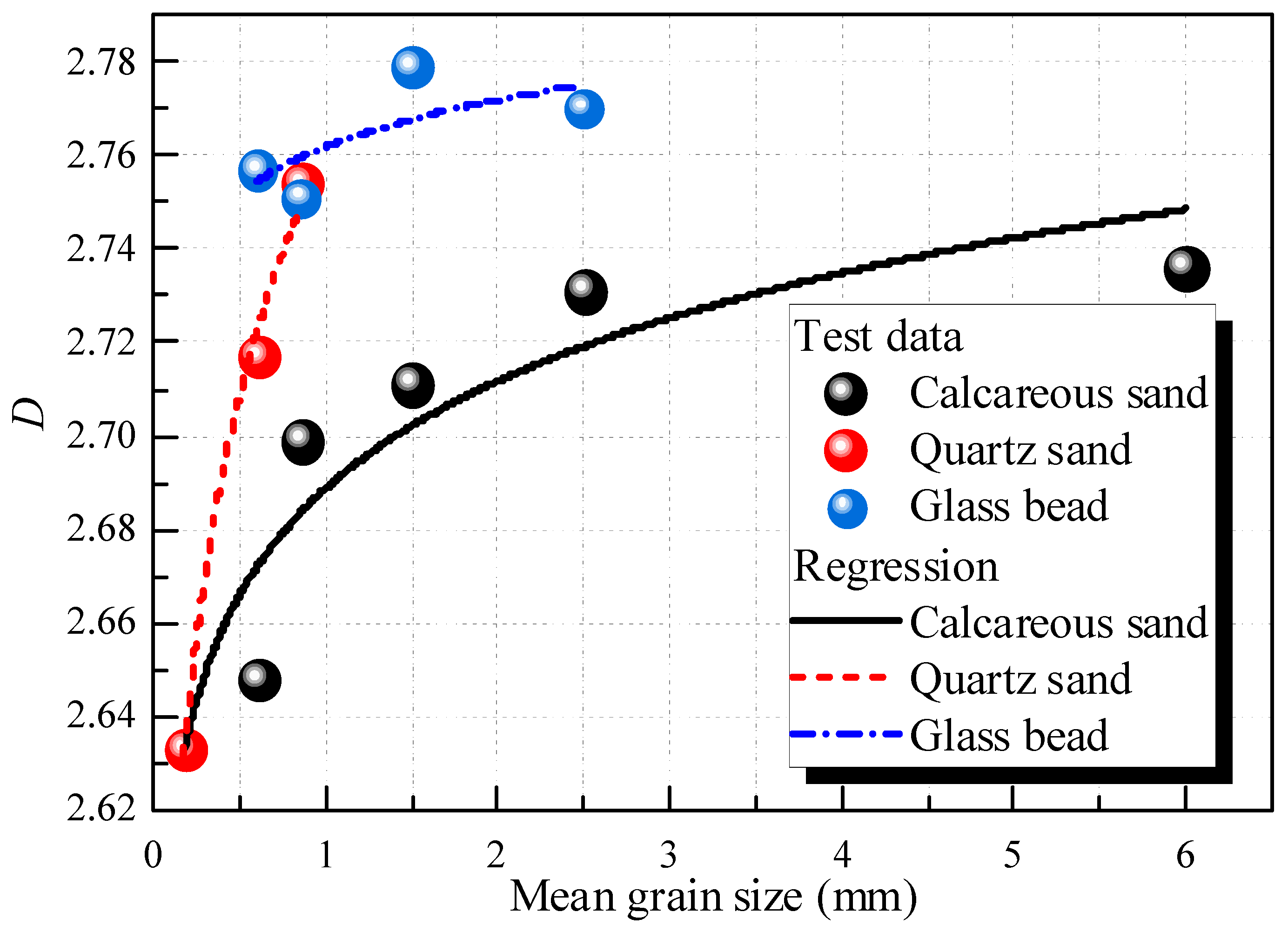
3.2. Effect of Grain Size on the Microsrcture’s Fractal Dimension

Liang et al. [44] reported that the lgS_v-lgR curve of soil included two distinct parts and proposed that the PSD in soils showed multi-fractal characteristics. The lgS_v-lgR curve of calcareous sand, quartz sand, and glass bead are shown in Figure 8, Figure 9 and Figure 10, respectively. There is an obvious inflection point around the pore diameter of 10 um in the lgS_v-lgR curve, indicating that the pore size of about 10 μm is a limitation for the change of pore properties in the carbonate-based sand and silicate-based sand. The dominant pore structure content of carbonate-based sand and silicate-based sand is distributed in the large-size range (i.e., the pore structure with a size greater than 10 μm. Furthermore, the larger pore structure of sand assembly more tends to be a skeleton pore structure with strong contact and control of the mechanical behavior. Therefore, the fractal dimension (D) in a large-size range of pores is supposed to be the dominant parameter reflecting the principal characteristics of the PSD. Based on Equation (16), the fractal dimension of the macropore (i.e., on the right side of the turning point) was obtained through the regression analysis, as shown in Figure 8, Figure 9 and Figure 10. The fitting results of fractal dimensions demonstrate that the pore size distribution of calcareous sand, quartz sand, and glass bead all complies with the fractal law. In addition, the correlation coefficient (R²) of calcareous sand is between 0.95–0.99; the correlation coefficient of quartz sand is between 0.87–0.93 and the correlation coefficient of glass beads is between 0.87–0.94. This indicates that the fractal characteristics of calcareous sand of various particle sizes are more obvious than that of quartz sand and glass beads.

Figure 11 shows the relationship between the fractal dimension and the mean grain size (d₅₀) of the three sands. It can be clearly observed that the fractal dimensions of calcareous sand and quartz sand all increase significantly with the increase of grain size. Compared with calcareous sand and quartz sand, the fractal dimension of glass beads increases more slowly with grain size. This may be due to the single shape (i.e., round shape) of glass beads. Previous studies pointed that the higher fractal dimension of pore size distribution means a more complex pore structure distribution and a stronger heterogeneity of the pore structure distribution [29]. The increase of grain size can lead to a significant increase of D for calcareous sand, quartz sand and glass bead. This indicates that the increase of grain size can cause a more complex pore structure distribution in the sand. Furthermore, under the same grain size, the fractal dimension of calcareous sand is the smallest, the fractal dimension of glass beads is the largest, and quartz sand is somewhere in between. In addition, the fractal dimension of calcareous sand increases more slowly with grain size than quartz sand. The larger the grain size, the greater the gap between the fractal dimensions of the two sands. This indicates that as the grain size increases, the difference in particle shape has a more obvious impact on the pore structure.

It is widely acknowledged that the determination of the fractal dimension plays an important role in predicting the physical and mechanical properties of geomaterials [45,46]. Huang et al. [45] quantified the fractal characteristics of the pore structure of shale and found a significant relationship between the fractal dimension and permeability. Kong et al. [47] established a fractal model of pore size distribution for porous geomaterials based on the fractal characteristics of pores, which could be used to study hydraulic properties. Based on the mercury intrusion test and image analysis, Dou et al. [46] analyzed the effect of different fractal models of pores on the evaluation of sandstone’s permeability and highlighted the role of the fractal dimension in determining the permeability. Therefore, accurate prediction of the fractal dimension is crucial for grasping and analyzing the engineering properties (e.g., permeability) of geomaterials. Considering this, a suitable correlation (see Figure 11) was proposed to capture the fractal dimensions of carbonate-based sand and silicate-based sand with different mean grain sizes, which is as follows:

$$D=\alpha d_{50}{}^{\beta }$$

(17)

where α and β are model parameters, and through regression analysis, the best-fit α and β for carbonate-based sand and silicate-based are summarized in

Table 2. Summaries of model parameters for carbonate-based sand and silicate-based sand.

Parameter	Calcareous Sand	Quartz Sand	Glass Bead
α	2.689	2.761	2.762
β	0.0122	0.0276	0.00524

. The proposed correlation between D and d₅₀ can be applied to the research of a permeability model, water-retention ability analysis, and other related aspects for granular geomaterials, which is useful for guiding the construction of geotechnical engineering.

4. Conclusions

Carbonate-based sand and silicate-based sand are widely used in the construction of geotechnical engineering. To investigate the effect of grain size on the micro-pore structure and fractal characteristics of carbonate-based sand and silicate-based sand, a series of NMR tests were conducted on calcareous sand, quartz sand, and glass bead. The effect of grain size on the pore size distribution and fractal dimension was discussed in detail. The following main conclusions were drawn:

(1)

Grain size had a significant effect on the pore size distribution of carbonate-based sand and silicate-based sand. As the grain size increased, the pore size distribution curve of sands gradually evolved from a binary structure with two peaks to a ternary structure with three peaks. The increase in the grain size could cause a remarkable increase in the maximum pore size. Moreover, the increase in grain size increased the proportion of large pores with a size larger than 1000 μm, and correspondingly reduced the proportion of medium pores with a size between 100 μm–1000 μm. However, grain size had a minor effect on small pores with a size less than 100 um.

(2)

Carbonate-based sand differed significantly from silicate-based sand with respect to the pore size distribution, owing to the significant divergence in particle shapes. In the pore size range between 100 μm and 1000 μm, carbonate-based sand had a continuous pore size distribution, whereas the pore size distribution of silicate-based sand was discontinuous. This indicated that the more irregular the particle shape, the better the continuity between the large and medium pores.

(3)

The pore size distribution of calcareous sand, quartz sand and glass beads all exhibited good fractal characteristics. The fractal dimension (D) of the pore size distribution of the three materials was determined by fractal theory. Compared with the quartz sand and glass beads, the calcareous sand with the most complex particle shape had the most significant fractal characteristics. Moreover, grain size had a considerable effect on the fractal dimension of the carbonate-based sand and the silicate-based sand. The increase of grain size could lead to a significant increase of D for calcareous sand, quartz sand and glass bead, indicating that the increase of grain size would increase the heterogeneity of pore structure distribution in sands. A refined correlation was proposed to determine D for carbonate-based sand and silicate-based sand with different grain sizes.