Novel Numerical Investigations of Fuzzy Cauchy Reaction–Diffusion Models via Generalized Fuzzy Fractional Derivative Operators
Abstract
1. Introduction
2. Basic Notions of Fractional and Fuzzy Calculus
3. Description of the Fuzzy SHPTM
4. Convergence Analysis of Fuzzy SHPTM
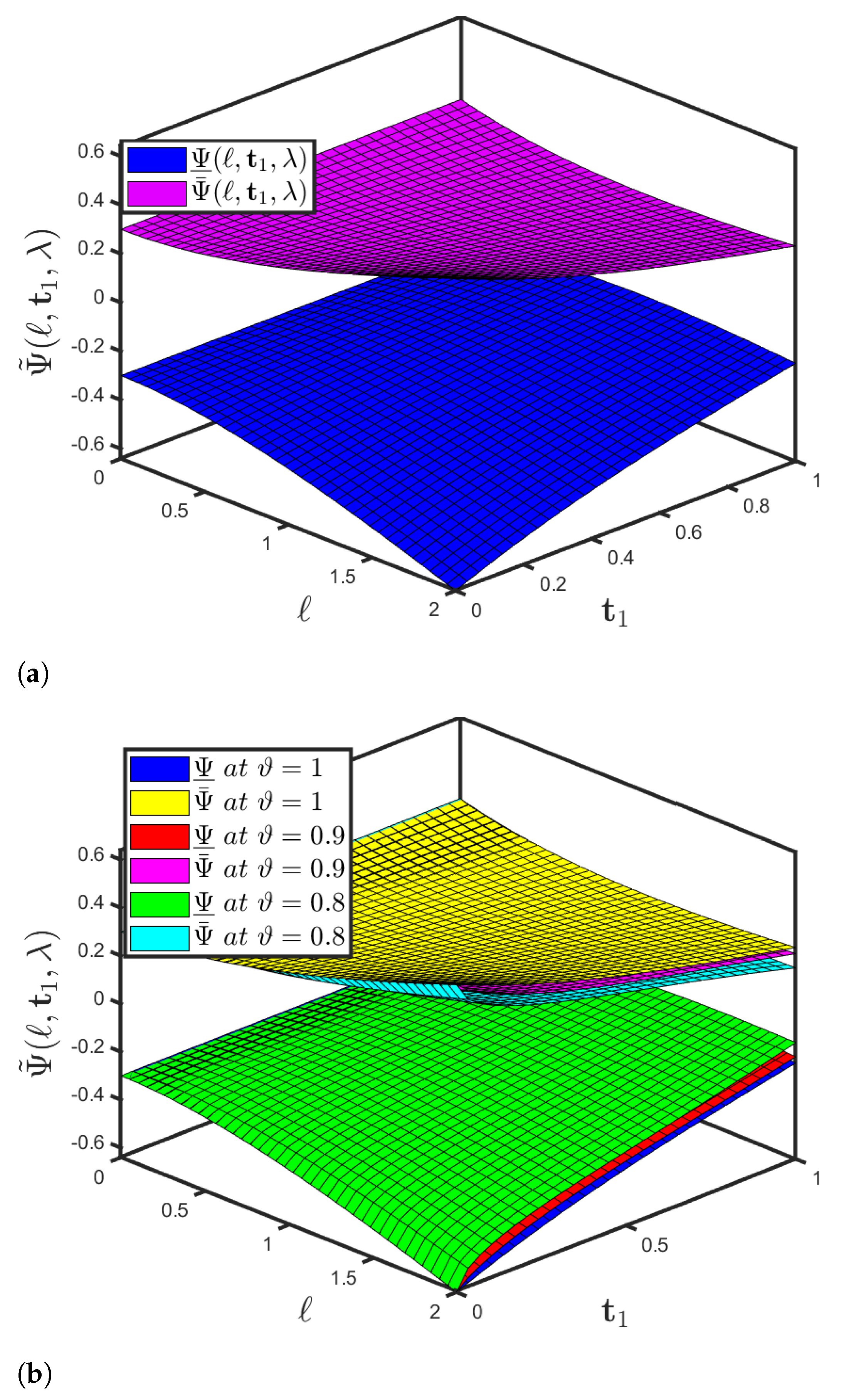
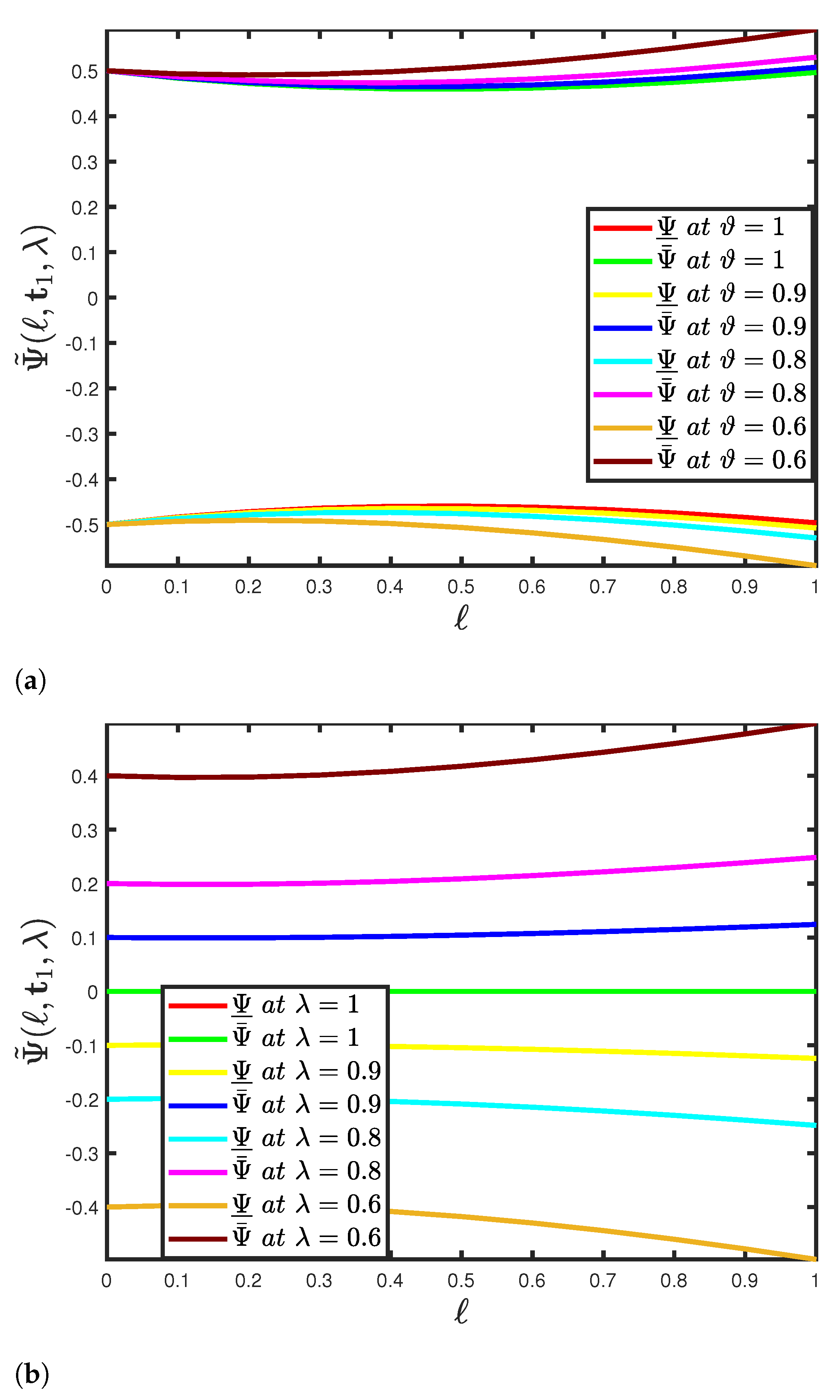
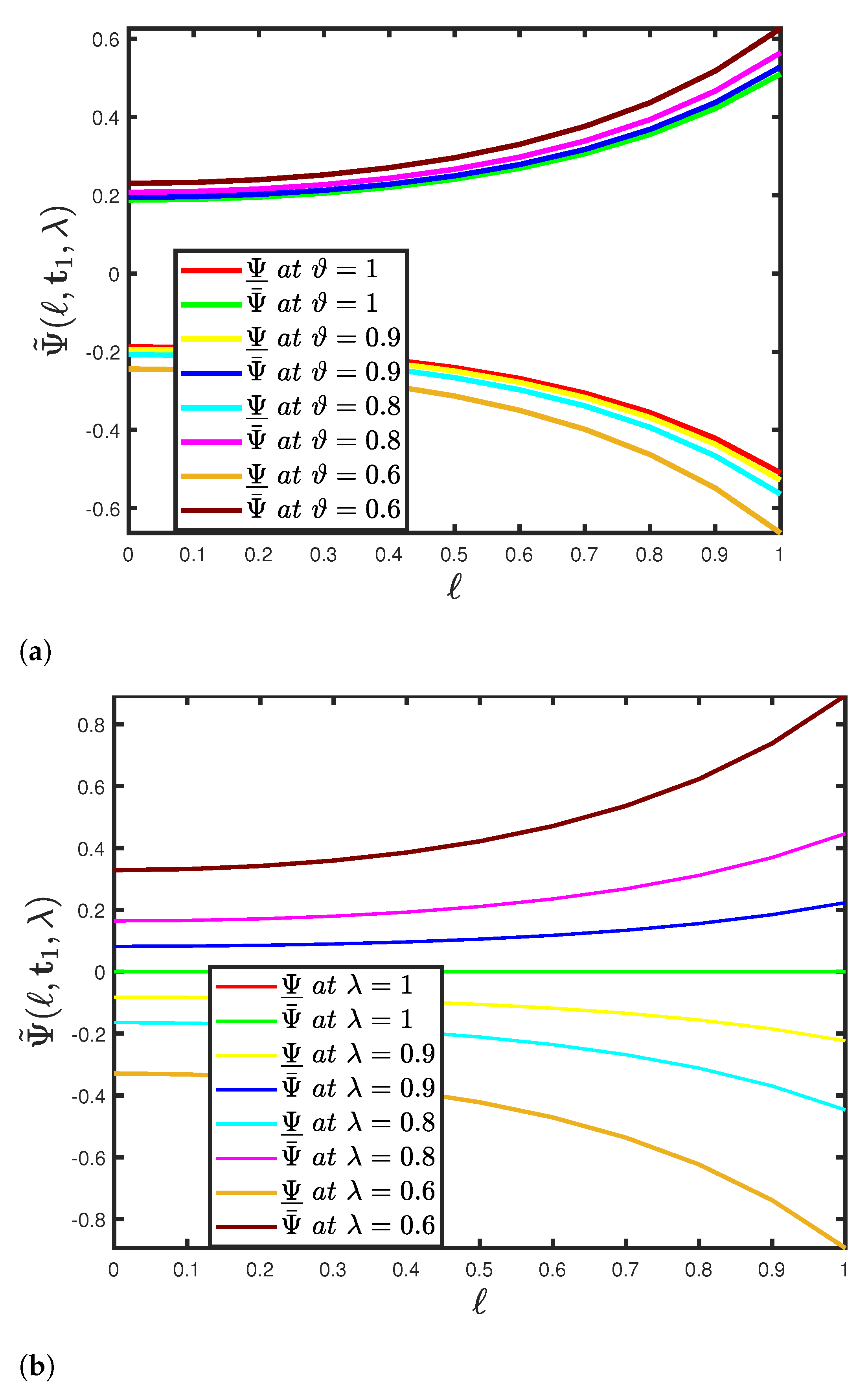
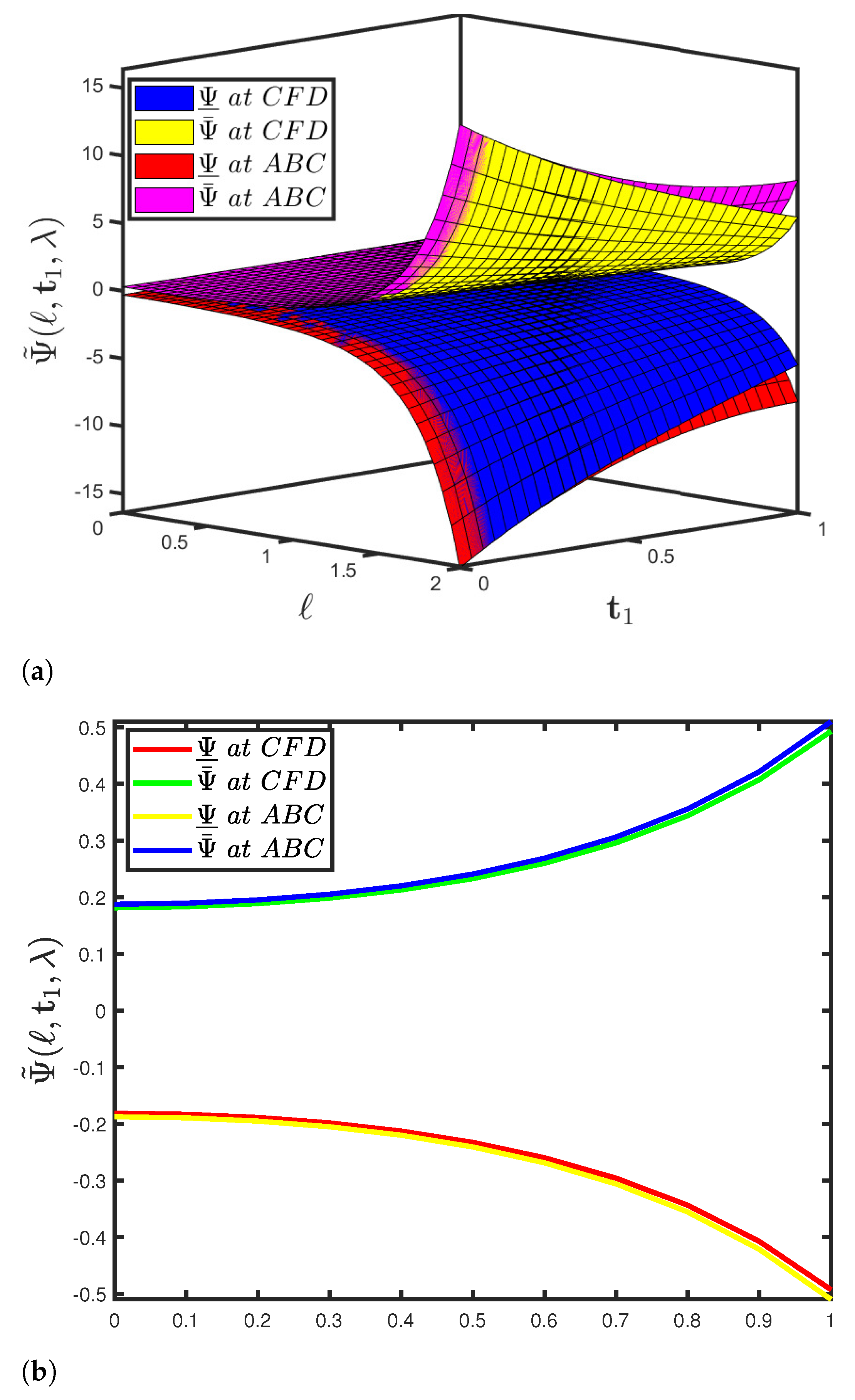
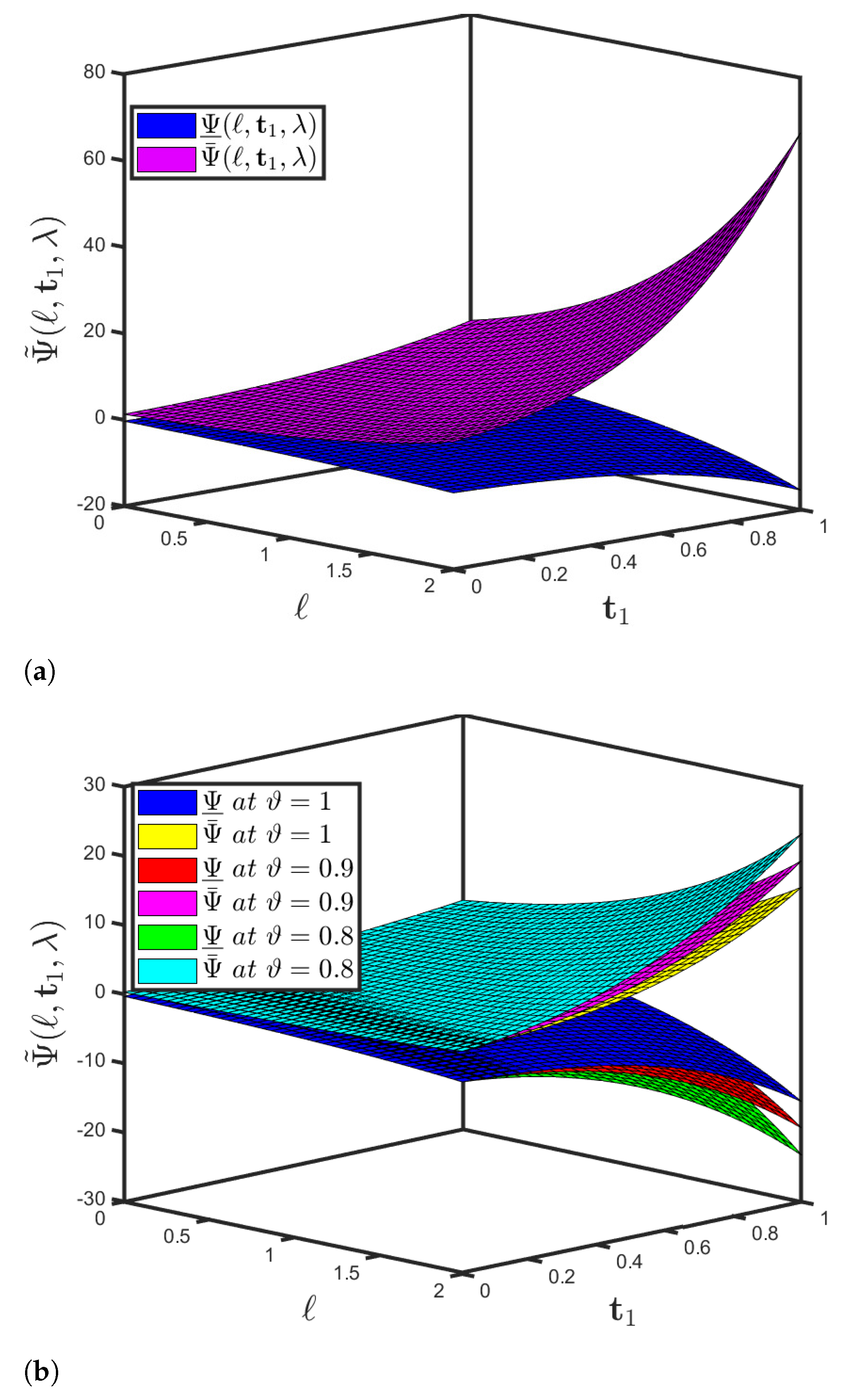
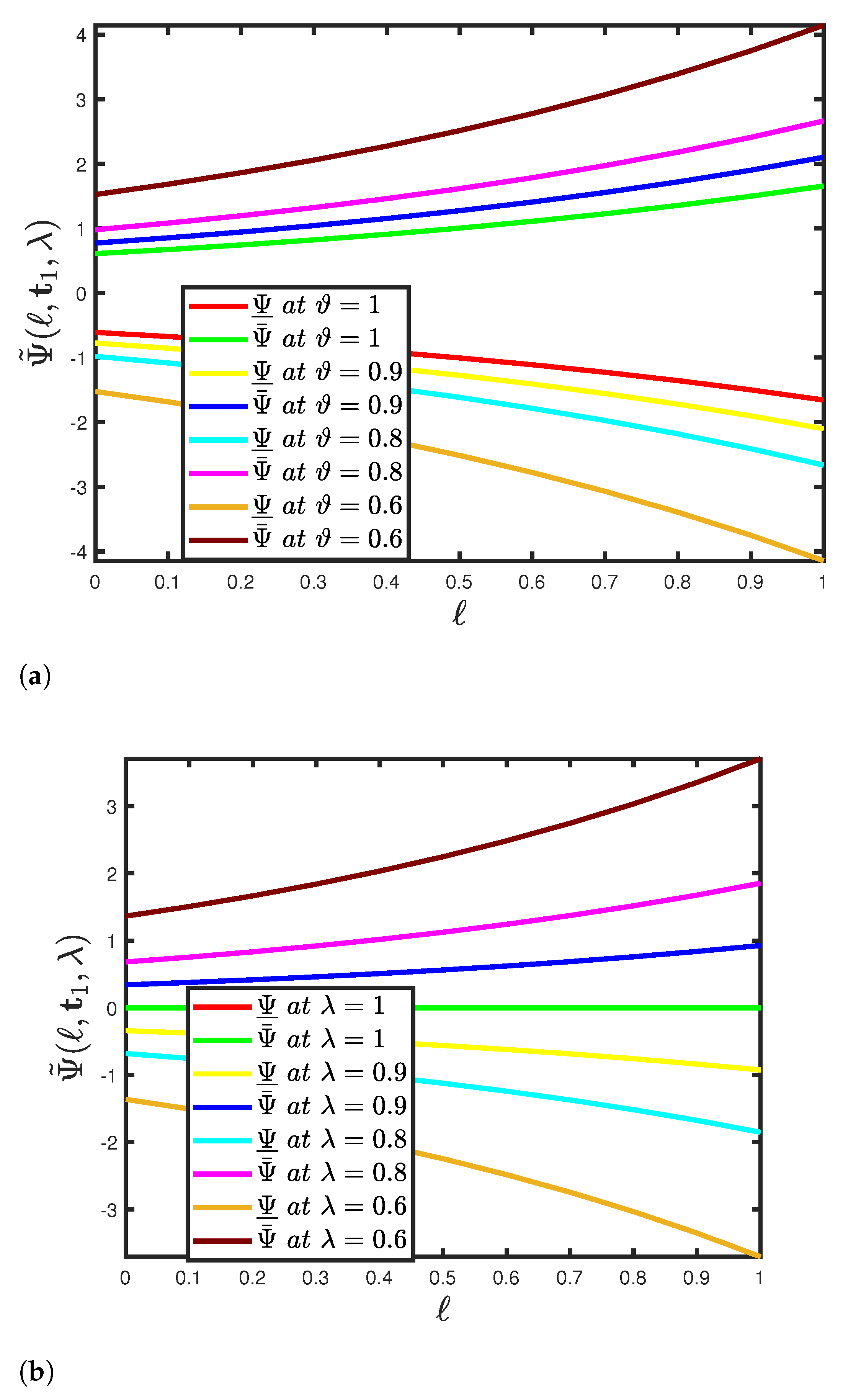
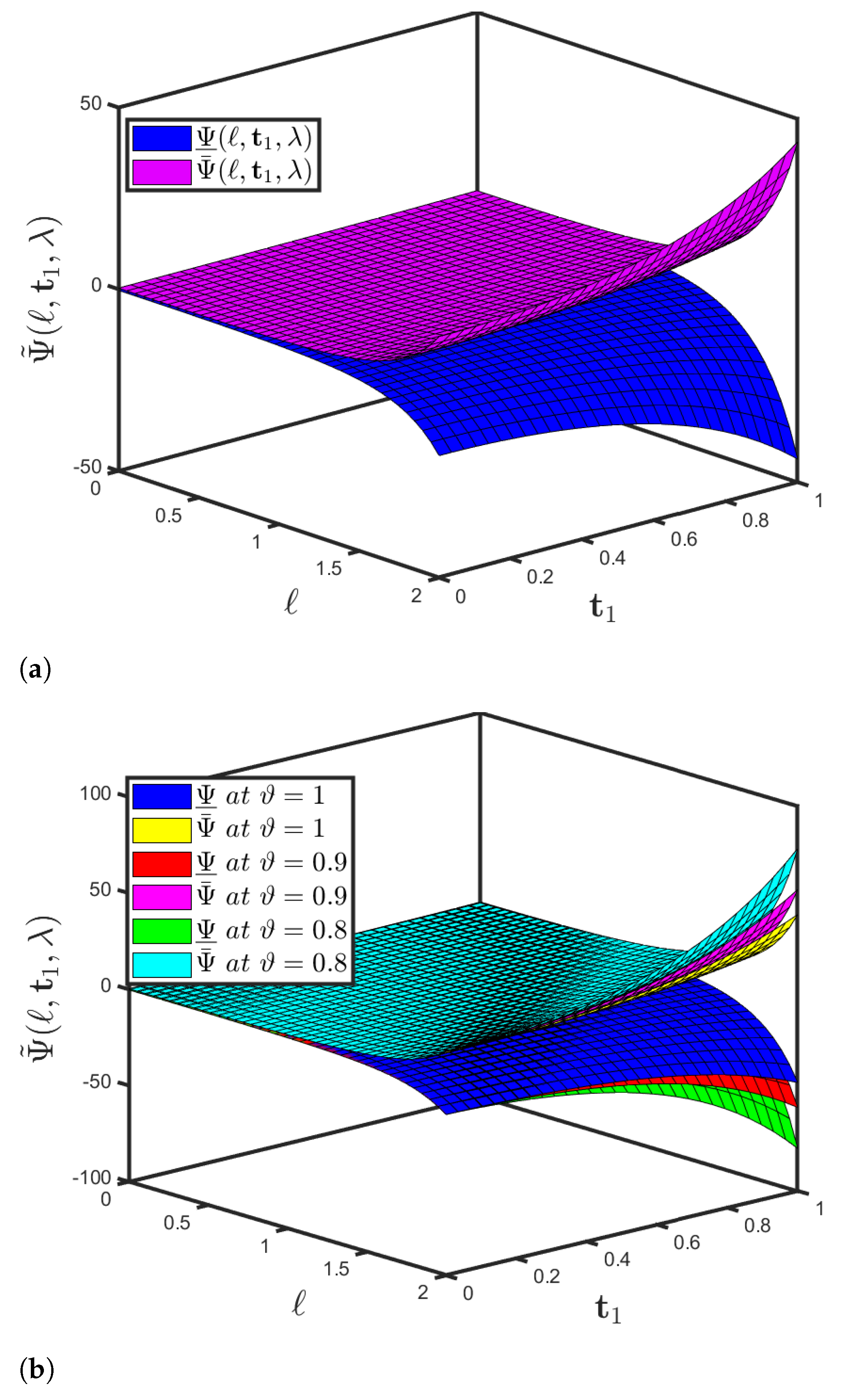
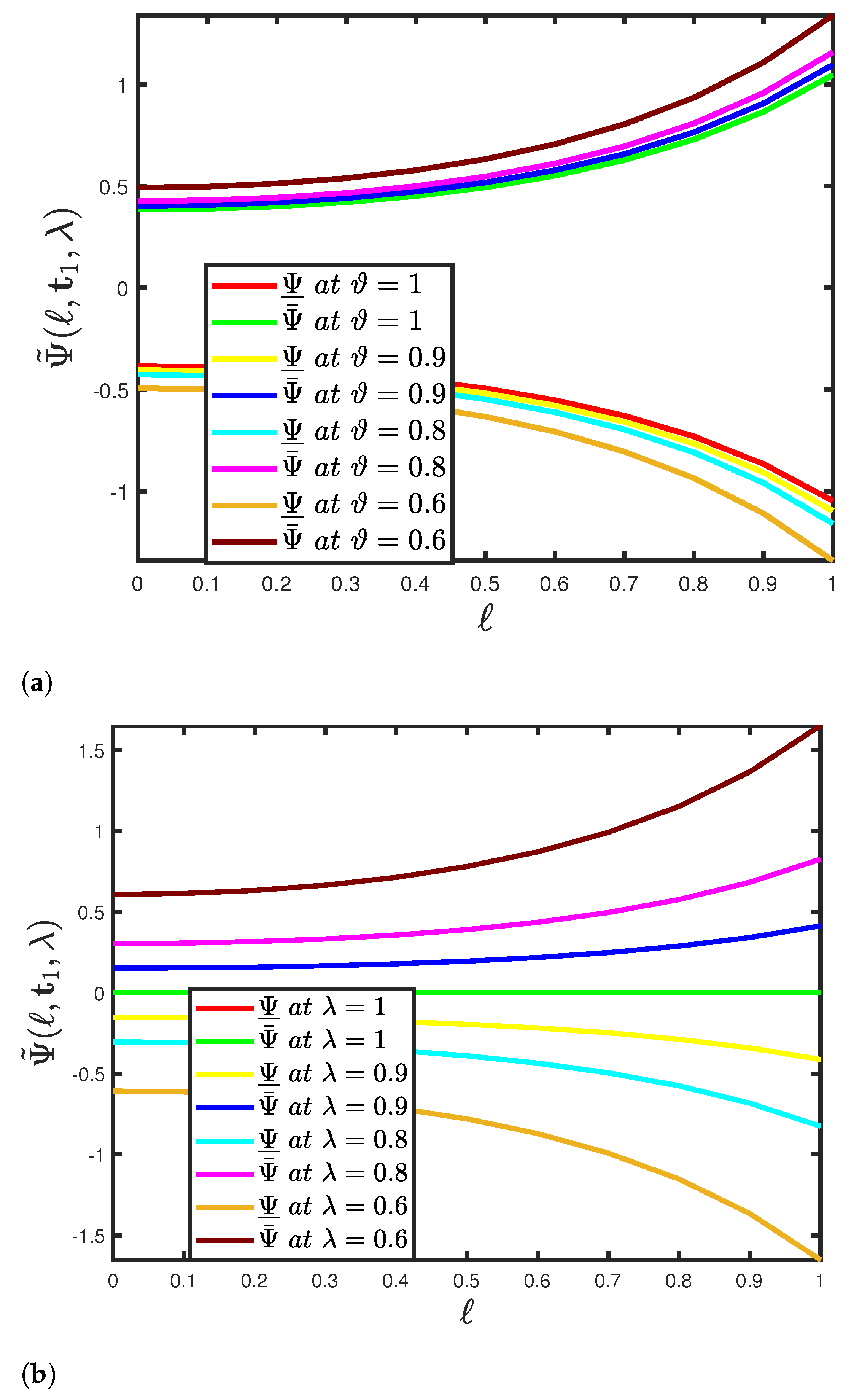
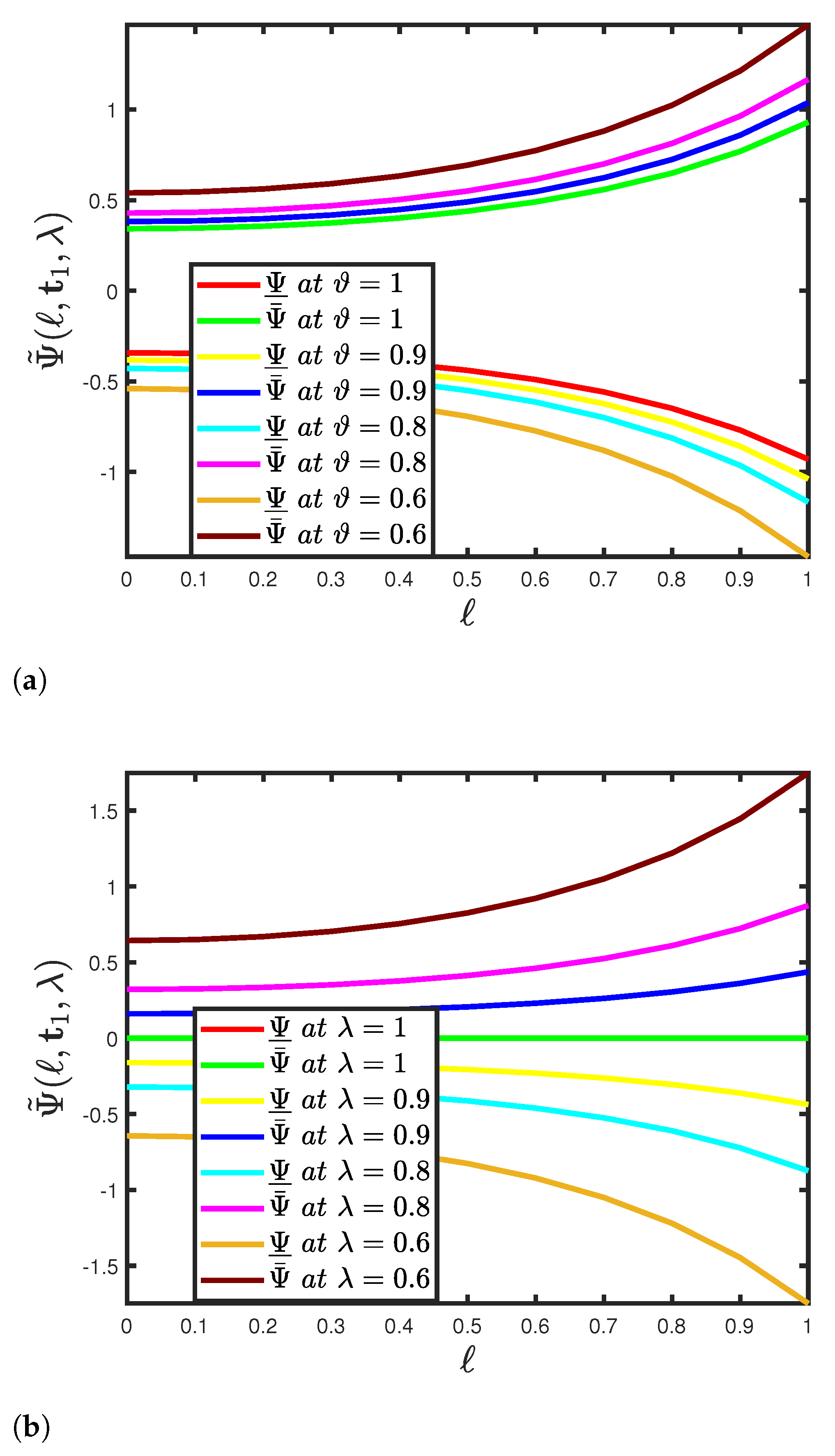
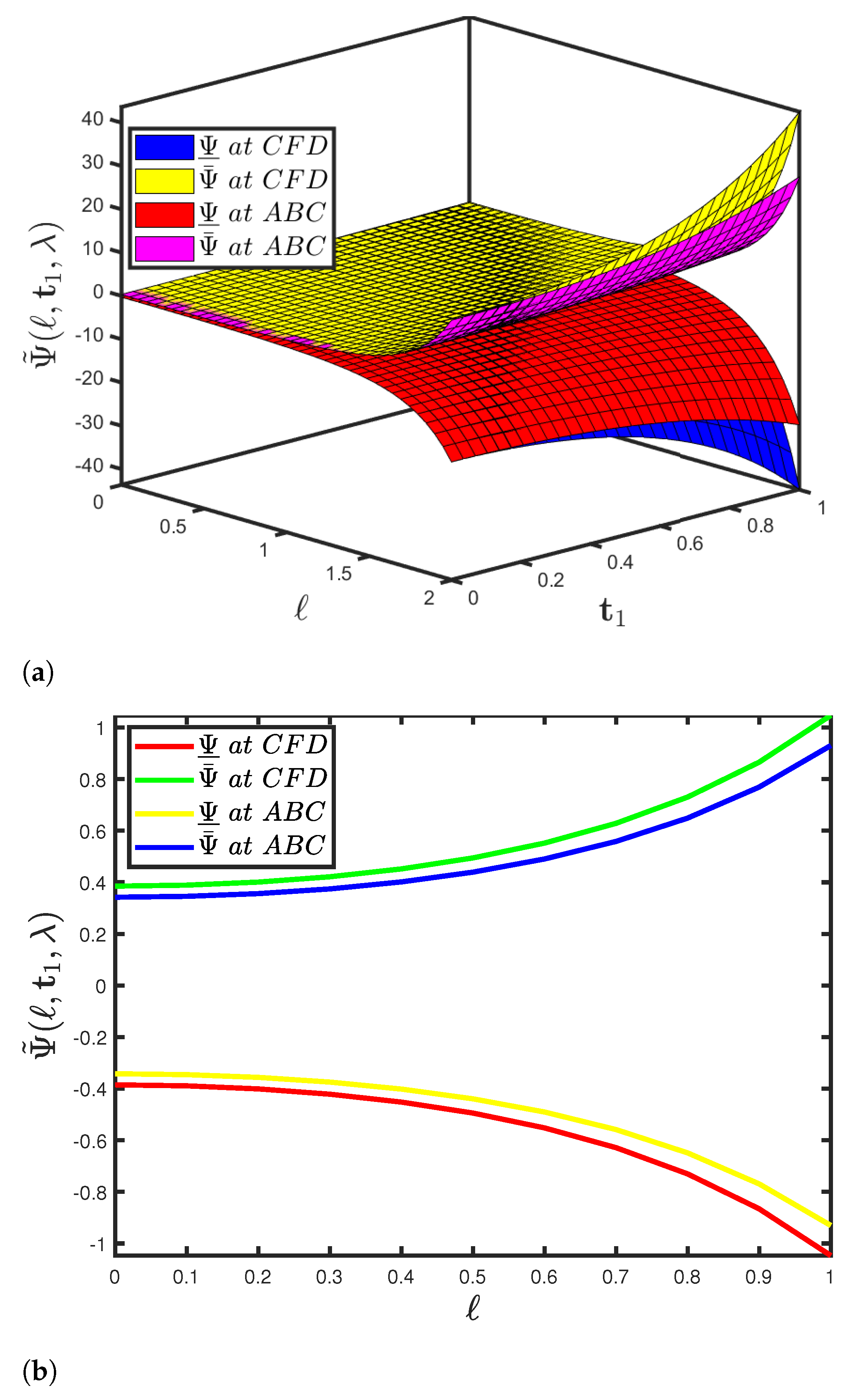
5. Functioning of the SHPTM and Mathematical Findings
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel, Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20, 2. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huanget, J. The Grünwald-Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 3. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y.Q. On Riemann–Liouville and Caputo Derivatives. Dis. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Yepez-Martínez, H.; Baleanu, D.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H. Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Adv. Differ. Equ. 2016, 2016, 164. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana-Baleanu and Caputo-Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. New model of groundwater flowing within a confine aquifer: Application of Caputo-Fabrizio derivative. Arab. J. Geosci. 2016, 9, 1. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. New Laplace-type integral transform for solving steady heattransfer problem. Therm. Sci. 2019, 25, 1–12. [Google Scholar] [CrossRef]
- Zureigat, H.; Izani, A.I.; Sathasivam, S. Numerical solutions of fuzzy fractional diffusion equations by an implicit finite difference scheme. Neural Comput. Appl. 2019, 31, 4085–4094. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T. Fractional spatial diffusion of a biological population model via a new integral transform in the settings of power and Mittag–Leffler nonsingular kernel. Phys. Scr. 2021, 96, 114003. [Google Scholar] [CrossRef]
- Rashid, S.; Ashraf, R.; Akdemir, A.O.; Alqudah, M.A.; Abdeljawad, T.; Mohamed, M.S. Analytic fuzzy formulation of a time-fractional Fornberg-Whitham model with power and Mittag–Leffler kernels. Fractal Fract. 2021, 5, 113. [Google Scholar] [CrossRef]
- Rashid, S.; Hammouch, Z.; Aydi, H.; Ahmad, A.G.; Alsharif, A.M. Novel computations of the time-fractional Fisher’s model via generalized fractional integral operators by means of the Elzaki transform. Fractal Fract. 2021, 5, 94. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Guirao, J.L.G. Construction of an approximate analytical solution for multi-dimensional fractional Zakharov-Kuznetsov equation via Aboodh Adomian decomposition method. Symmetry 2021, 13, 1542. [Google Scholar] [CrossRef]
- Zhou, S.-S.; Rashid, S.; Rauf, A.; Kubra, K.T.; Alsharif, A.M. Initial boundary value problems for a multi-term time fractional diffusion equation with generalized fractional derivatives in time. AIMS Math. 2021, 6, 12114–12132. [Google Scholar] [CrossRef]
- Rashid, S.; Jarad, F.; Abualnaja, K.M. On fuzzy Volterra-Fredholm integrodifferential equation associated with Hilfer-generalized proportional fractional derivative. AIMS Math. 2021, 6, 10920–10946. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Rauf, A.; Chu, Y.-M.; Hamed, Y.S. New numerical approach for time-fractional partial differential equations arising in physical system involving natural decomposition method. Phys. Scr. 2021, 96, 105204. [Google Scholar] [CrossRef]
- Chang, S.S.L.; Zadeh, L. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybern. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. Linguistic variables, approximate reasoning and disposition. Med. Inform. 1983, 8, 173–186. [Google Scholar] [CrossRef]
- Negoita, C.V.; Ralescu, D.A. Applications of Fuzzy Sets to Systems Analysis; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Hukuhara, M. Intégration des applications mesurables dont la valeur est un compact convex. Funkc. Ekvac. 1967, 10, 205–229. [Google Scholar]
- Agarwal, R.P.; Lakshmikantham, V.; Nieto, J.J. On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal. 2020, 72, 59–62. [Google Scholar] [CrossRef]
- Arshad, S.; Lupulescu, V. On the fractional differential equations with uncertainty. Nonlinear Anal. 2011, 74, 85–93. [Google Scholar] [CrossRef]
- Arshad, S.; Luplescu, V. Fractional differential equation with fuzzy initial conditon. Elect. J. Diff. Equ. 2011, 34, 1–8. [Google Scholar]
- Allahviranloo, T.; Salahshour, S.; Abbasbandy, S. Explicit solutions of fractional differential equations with uncertainty. Soft. Comput. 2012, 16, 297–302. [Google Scholar] [CrossRef]
- Salahshour, S.; Allahviranloo, T.; Abbasbandy, S. Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Commun. Nonlin. Sci. Numer. Simul. 2012, 17, 1372–1381. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Abbasbandy, S.; Salahshour, S. Fuzzy fractional differential equations with Nagumo and Krasnoselskii-Krein condition. In Proceedings of the 7th conference of the European Society for Fuzzy Logic and Technology EUSFLAT-LFA 2011, Aix-les-Bains, France, 18–22 July 2011. [Google Scholar]
- Bushnaq, S.; Ullah, Z.; Ullah, A.; Shah, K. Solution of fuzzy singular integral equation with Abel’s type kernel using a novel hybrid method. Adv. Diff. Equ. 2020, 2020, 156. [Google Scholar] [CrossRef]
- Ullah, Z.; Ullah, A.; Shah, K.; Baleanu, D. Computation of semi-analytical solutions of fuzzy nonlinear integral equations. Adv. Diff. Equ. 2020, 2020, 542. [Google Scholar] [CrossRef]
- Salahshour, S.; Ahmadian, A.; Senu, N.; Baleanu, D.; Agarwal, P. On analytical aolutions of the fractional differential equation with uncertainty: Application to the Basset problem. Entropy 2015, 17, 885–902. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; Abdeljawad, T. Semi-analytical solutions of the 3rd order fuzzy dispersive partial differential equations under fractional operators. Alex. Eng. J. 2021, 60, 5861–5878. [Google Scholar] [CrossRef]
- Shah, K.; Seadawy, A.R.; Arfan, M. Evaluation of one dimensional fuzzy fractional partial differential equations. Alex. Eng. J. 2020, 59, 3347–3353. [Google Scholar] [CrossRef]
- Feng, G.; Chen, G. Adaptive control of discrete-time chaotic systems: A fuzzy control approach. Chaos Solitons Fract. 2005, 23, 459–467. [Google Scholar] [CrossRef]
- Jiang, W.; Guo-Dong, Q.; Bin, D. H1 variable universe adaptive fuzzy control for chaotic system. Chaos Solitons Fract. 2005, 24, 1075–1086. [Google Scholar] [CrossRef]
- El-Naschie, M.S. A review of E-infinity theory and the mass spectrum of high energy particle physics. Chaos Solitons Fract. 2004, 19, 209–236. [Google Scholar] [CrossRef]
- Lesnic, D. The decomposition method for Cauchy reaction–diffusion problems. Appl. Math. Lett. 2007, 20, 412. [Google Scholar] [CrossRef][Green Version]
- Dehghan, M.; Shakeri, F. Application of He’s variational iteration method for solving the Cauchy reaction–diffusion problem. J. Comput. Appl. Math. 2008, 214, 435–446. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Abbas, S.; Qurashi, M.A.; Baleanu, D. A modified analytical approach with existence and uniqueness for fractional Cauchy reaction-diffusion equations. Adv. Diff. Equ. 2020, 2020, 28. [Google Scholar] [CrossRef]
- He, J.-H. Homotopy Perturbation Technique. Comp. Meth. Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.-H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fract. 2005, 26, 695–700. [Google Scholar] [CrossRef]
- He, J.-H. Limit cycle and bifurcation of nonlinear problems. Chaos Solitons Fract. 2005, 26, 827–833. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Jafari, H.; Lehre, S.U. A semi-analytical approach for fractional order Boussinesq equation in a gradient unconfined aquifers. Math. Meth. Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Abualnaja, K.M. Fractional view of heat-like equations via the Elzaki transform in the settings of the Mittag–Leffler function. Math. Meth. Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Rashid, S.; Khalid, A.; Sultana, S.; Hammouch, Z.; Shah, R.; Alsharif, A.M. A novel analytical view of time-fractional Korteweg-De Vries equations via a new integral transform. Symmetry 2021, 13, 1254. [Google Scholar] [CrossRef]
- Allahviranloo, T. Fuzzy Fractional Differential Operators and Equation Studies in Fuzziness and Soft Computing; Springer: Berlin, Germany, 2021. [Google Scholar]
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Infor. Cont. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ahmadi, M.B. Fuzzy Lapalce Transform. Soft Comput. 2010, 14, 235–243. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. Homotopy analysis Shehu transform method for solving fuzzy differential equations of fractional and integer order derivatives. Comput. Appl. Math. 2021, 40, 86. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. Int. J. Anal. Appl. 2019, 17, 167–190. [Google Scholar]
- Bokhari, A.; Baleanu, D.; Belgacema, R. Application of Shehu transform to Atangana-Baleanu derivatives. J. Math. Comp. Sci. 2020, 20, 101–107. [Google Scholar] [CrossRef]
- Ghorbani, A. Beyond Adomian polynomials: He polynomials. Chaos Solitons Fract. 2009, 39, 1486–1492. [Google Scholar] [CrossRef]
- Hamoud, A.; Ghadle, K. Modified Adomian decomposition method for solving fuzzy Volterra—Fredholm integral equations. J. Indian Math. Soc. 2018, 85, 52–69. [Google Scholar] [CrossRef]
- Osman, M.; Gong, Z.; Mustafa, A.M.; Yang, H. Solving fuzzy (1+n)-dimensional Burgers’ equation. Adv. Diff. Equ. 2021, 2021, 219. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqudah, M.A.; Ashraf, R.; Rashid, S.; Singh, J.; Hammouch, Z.; Abdeljawad, T. Novel Numerical Investigations of Fuzzy Cauchy Reaction–Diffusion Models via Generalized Fuzzy Fractional Derivative Operators. Fractal Fract. 2021, 5, 151. https://doi.org/10.3390/fractalfract5040151
Alqudah MA, Ashraf R, Rashid S, Singh J, Hammouch Z, Abdeljawad T. Novel Numerical Investigations of Fuzzy Cauchy Reaction–Diffusion Models via Generalized Fuzzy Fractional Derivative Operators. Fractal and Fractional. 2021; 5(4):151. https://doi.org/10.3390/fractalfract5040151
Chicago/Turabian StyleAlqudah, Manar A., Rehana Ashraf, Saima Rashid, Jagdev Singh, Zakia Hammouch, and Thabet Abdeljawad. 2021. "Novel Numerical Investigations of Fuzzy Cauchy Reaction–Diffusion Models via Generalized Fuzzy Fractional Derivative Operators" Fractal and Fractional 5, no. 4: 151. https://doi.org/10.3390/fractalfract5040151
APA StyleAlqudah, M. A., Ashraf, R., Rashid, S., Singh, J., Hammouch, Z., & Abdeljawad, T. (2021). Novel Numerical Investigations of Fuzzy Cauchy Reaction–Diffusion Models via Generalized Fuzzy Fractional Derivative Operators. Fractal and Fractional, 5(4), 151. https://doi.org/10.3390/fractalfract5040151






