Optimal State Control of Fractional Order Differential Systems: The Infinite State Approach

Abstract

Optimal control of fractional order systems is a long established domain of fractional calculus. Nevertheless, it relies on equations expressed in terms of pseudo-state variables which raise fundamental questions. So in order remedy these problems, the authors propose in this paper a new and original approach to fractional optimal control based on a frequency distributed representation of fractional differential equations called the infinite state approach, associated with an original formulation of fractional energy, which is intended to really control the internal system state. In the first step, the fractional calculus of variations is revisited to express appropriate Euler Lagrange equations. Then, the quadratic optimal control of fractional linear systems is formulated. Thanks to a frequency discretization technique, the previous theoretical equations are converted into an equivalent large dimension integer order system which permits the implementation of a feasible optimal solution. A numerical example illustrates the validity of this new approach.

1. Introduction

The calculus of variations [1], a fundamental optimality problem, has been solved by the contributions of renowned mathematicians Bernoulli, Euler, Lagrange, Hamilton, and Jacobi. Optimal control, a direct emanation of fractional calculus, has raised a great interest of automatic control researchers since the works of Pontryaguine, Belman, Kalman, and many others (see the two historical surveys [2,3] and the references therein). These early works were stimulated by the availability of electronic computers and appropriate numerical techniques. Nowadays, optimal state control of integer order systems are a well established and developed topic, presented in many monographs (see for example [4,5]).

Since the seminal monographs of Oldham and Spanier [6] and Podlubny [7], fractional system theory has become an active research field. Quite naturally, optimal control of fractional order systems has given rise to a great interest among fractional calculus researchers during the last 30 years. One can cite the original works of Agrawal [8,9,10,11] and many other contributions (see for example [12,13] and the references therein). In [8], the author generalized classical variational calculus to the fractional order domain and introduced the optimal control of fractional order systems in [9]. Presently, it is accepted by the fractional calculus community that the theory of fractional optimal control has reached maturity. In fact, a fundamental problem of fractional differential systems relies on the definition of state variables and consequently of initial conditions necessary for system initialization. For a long time, researchers have considered that the state of the system $D^n(\underset{-}{X}(t))\hspace{0.17em}=\hspace{0.17em}A\hspace{0.17em}\underset{-}{X}(t)\hspace{0.17em}+\underset{-}{B}\hspace{0.17em}u(t)$ is the state vector $\underset{-}{X}(t)$ as a generalization of the integer order case, since $x(0)$ is usually interpreted as the initial condition of the Caputo derivative [7,14]. In the last approximately 15 years, it has been proved by several researchers with different approaches that the pseudo initial condition $x(0)$ is unable to predict the dynamic behavior of a fractional system for $t\hspace{0.17em}>\hspace{0.17em}0$ [15,16,17,18,19]. Consequently, $\underset{-}{X}(t)$ does not represent system state and it has to be called the pseudo-state. Moreover, since the cost function of optimal state control is generally expressed in terms of a quadratic form of $\underset{-}{X}(t)$, the research works presented in the previous references do not apply to the true state of fractional systems and have to be called pseudo optimal control.

An alternative to the modeling of fractional systems is based on the diffusive representation [20,21] or the frequency distributed representation [22,23]. The internal state $z(\omega ,t)$ of the fractional integrator, which is the basic element for system modeling, is defined by the relation $x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n}(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega$. This relation expresses that the pseudo-state variable $x(t)$ depends on the infinite dimensional distributed state variable $z(\omega ,t)\hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}\infty \hspace{0.17em}]$. It has been proved that the initial state $z(\omega ,0)$ permits the prediction of $x(t)$ for $t\hspace{0.17em}>\hspace{0.17em}0$ [24]; moreover, it has been proved that this modeling technique, known as the infinite state approach [23], is equivalent to the history function approach of Lorenzo and Hartley [25].

Some researchers have applied diffusive representation to the optimal control problem in order to reformulate previous works in a more satisfactory framework [26,27,28,29], i.e., replacing the pseudo-state variable by a distributed variable. Though not directly expressed in terms of the diffusive representation, the works of Tricaud and Chen [30,31] can be associated with this approach.

In fact, a more rigorous formulation of the fractional optimal control problem requires the general representation of fractional systems with the distributed variable $z(\omega ,t)$ and the definition of fractional energy to derive appropriate cost functions [32]. This formulation of fractional energy has already been used to solve the fractional Lyapunov stability problem [33,34]. Moreover, it is necessary to specify what is fractional state control. In chapters 4 and 5 of volume 2 [32], it has been demonstrated that pseudo-state control cannot satisfy integer order state control requirements. Hence it has been proposed to control the internal system state $z(\omega ,t)\hspace{0.17em}$, which is of course a more difficult, though non optimal, control problem.

Consequently, as an extension of this previous work, the objective of this paper is to present an original formulation of fractional optimal control in terms of the infinite state approach where optimal control applies really to the distributed variable $z(\omega ,t)$ instead of the pseudo-state variable $x(t)$. The formulation of this new theory requires the fractional calculus of variations to be revisited in order to apply the reformulated Euler Lagrange equations to the optimal state control of fractional order systems.

The paper is composed of six sections. Section 1 is the introduction. Section 2 deals with the materials and methods required in the understanding of the proposed theory. Section 3 briefly recalls the modeling of fractional systems based on the infinite state approach. The fractional calculus of variations is revisited with the frequency distributed variable in Section 4. Optimal state control of fractional differential systems is derived in Section 5. Finally, we intend to prove the feasibility of this new approach thanks to the numerical implementation of optimal control equations with an academic example in Section 6.

2. Materials and Methods

2.1. The Infinite State Approach

This article relies completely on the infinite state approach, which is an alternative to the conventional modeling of fractional order differential systems. Reading and understanding this article requires knowledge of the basic principles of this technique, essentially those related to the modeling with fractional integrators and the definition of fractional energy.

The fundamental feature of this method is to transform any differential fractional equation into a set of infinite dimensional integer order differential equations. Paradoxically, it does not require extensive knowledge of the usual techniques of the fractional calculus. On the contrary, it requires knowledge of the fundamental principles of integer order system theory and classical calculus of variations. Consequently, this methodology allows the generalization of well established concepts to the fractional domain, however at the price of managing infinite dimensional equations.

The practical implementation of this technique requires the frequency discretization of the fractional integrator, i.e., its approximation by a finite dimension modal model (Section 6).

All of these principles are briefly recalled in Section 3. However, a complete knowledge of this approach requires to refer to the two volumes of the infinite state monograph [32].

2.2. Paper Organization

This paper mainly deals with the presentation of an original theory of fractional optimal control.

The presentation of this theory is articulated around three sections:

• A recall of the basic principles of fractional system modeling based on the infinite state approach (Section 3);
• The derivation of new fractional Euler Lagrange equations (Section 4);
• The application of these variational equations to the optimal state control of fractional linear systems (Section 5).

The results presented in Section 4 and Section 5 are essentially theoretical. Their practical implementation relies on a frequency discretization of theoretical equations, i.e., on a modal expression of the previous optimal control laws which are nothing other than the optimal control of a large dimension integer order system (first part of Section 6).

We do not intend to propose a complete methodology covering all of the theoretical and practical aspects of fractional optimal control. The objective of the second part of Section 6 is only to present a validation of the proposed theory thanks to an academic example and a brief comparison with the original approach proposed in [9] by Agrawal. The numerical implementation of this example Equations (79)–(82) is based on the elementary matrix algebra available in any mathematical solver.

3. Modeling of Fractional Systems

3.1. The Fractional Integrator

Though several definitions of fractional derivatives are available (Riemann-Liouville, Caputo, Grünwald-Letnikov, …), only one definition corresponds to Riemann-Liouville fractional integration [7].

Consider a function $v(t)$; its nth order fractional integral is expressed as:

$$x(t)\hspace{0.17em}=\hspace{0.17em}{I}^n(v(t))\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{{\mu }^{n-1}}{\Gamma (n)}}\hspace{0.17em}v(t-\mu )\hspace{0.17em}d\mu \hspace{0.17em}=\hspace{0.17em}{h}_n(t)\ast v(t)$$

(1)

where

$$h_n(t)\hspace{0.17em}=\hspace{0.17em}\frac{t^{n-1}}{\mathsf{\Gamma }(n)}$$

(2)

The fractional integration operator is defined as:

$$I^n(s)\hspace{0.17em}=\hspace{0.17em}L\left\{h_n(t)\right\}\hspace{0.17em}=\hspace{0.17em}\frac{1}{s^n}$$

(3)

such that

$$x(s)\hspace{0.17em}=\hspace{0.17em}\frac{1}{s^n}\hspace{0.17em}v(s)$$

(4)

Thanks to the inverse Laplace transform, we obtain the diffusive representation [20] or the frequency distributed model [22,32] of the fractional integrator:

$$\left\{\begin{array}{l}\frac{\partial z(\omega ,t)}{\partial t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \hspace{0.17em}z(\omega ,t)\hspace{0.17em}+\hspace{0.17em}v(t) \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\hspace{0.17em}\\ x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}}\\ {\mu }_n(\omega )\hspace{0.17em}=\hspace{0.17em}\frac{\sin \hspace{0.17em}n\pi }{\pi }\hspace{0.17em}{\omega }^{-n} 0\hspace{0.17em}<\hspace{0.17em}n\hspace{0.17em}<\hspace{0.17em}1\hspace{0.17em}\end{array}\right.$$

(5)

Remarks: 

First Equation (5) represents the first order differential equation associated to frequency or mode $\omega$. Its Laplace transform corresponds to $z(\omega ,s)\hspace{0.17em}=\hspace{0.17em}\frac{1}{s\hspace{0.17em}+\hspace{0.17em}\omega }\hspace{0.17em}v(s)$ where the mode $\omega$ is the inverse of a time constant $\tau$.

Second Equation (5) expresses that $x(t)$ is the weighted sum of all the elementary monochromatic contributions $z(\omega ,t)$. Its Laplace transform

$$x(s)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n}(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{{\mu }_n(\omega )}{s\hspace{0.17em}+\hspace{0.17em}\omega }}\hspace{0.17em}d\omega \hspace{0.17em}v(s)\hspace{0.17em}=\hspace{0.17em}\frac{1}{s^n}\hspace{0.17em}v(s)$$

represents the infinite dimensional modal model of the fractional integrator, where the modes $\omega$ are continuously distributed from 0 to infinity. It highlights the long memory behavior of the fractional integrator, which is composed of very slow components ($\omega \hspace{0.17em}\to \hspace{0.17em}0$) and very fast ones ($\omega \hspace{0.17em}\to \hspace{0.17em}\infty$).

Note that first Equation (5) is independent of fractional order $n$ whereas $x(t)$ depends indirectly on $n$ through the weighting term ${\mu }_n(\omega )$ (third Equation (5)).

This distributed model is the basic element of the infinite state approach [23].

Note that $x(t)$, the output of the operator, is not a state variable like in the integer order case: $z(\omega ,t)$ is the true distributed state variable, whereas $x(t)$ is only a pseudo state variable.

3.2. Modeling with Fractional Integrators

Consider the elementary fractional differential equation (FDE):

$$D^n(x(t))\hspace{0.17em}=\hspace{0.17em}f(x,u,t)$$

(6)

The usual approach to fractional modeling is based on the choice of a derivative for $D^n(x(t))\hspace{0.17em}$: generally the Caputo derivative and its pseudo initial condition $x(0)$ are used [7]. Unfortunately, $x(0)$ is unable to predict the behavior of $x(t)$ for $t\hspace{0.17em}>\hspace{0.17em}0$ [14,22].

Thanks to the modeling technique based on the fractional integrator, it is no longer necessary to choose a derivative, which becomes implicit. Moreover, the initial state $z(\omega ,0)$ permits the prediction of $x(t)$ for $t\hspace{0.17em}>\hspace{0.17em}0$.

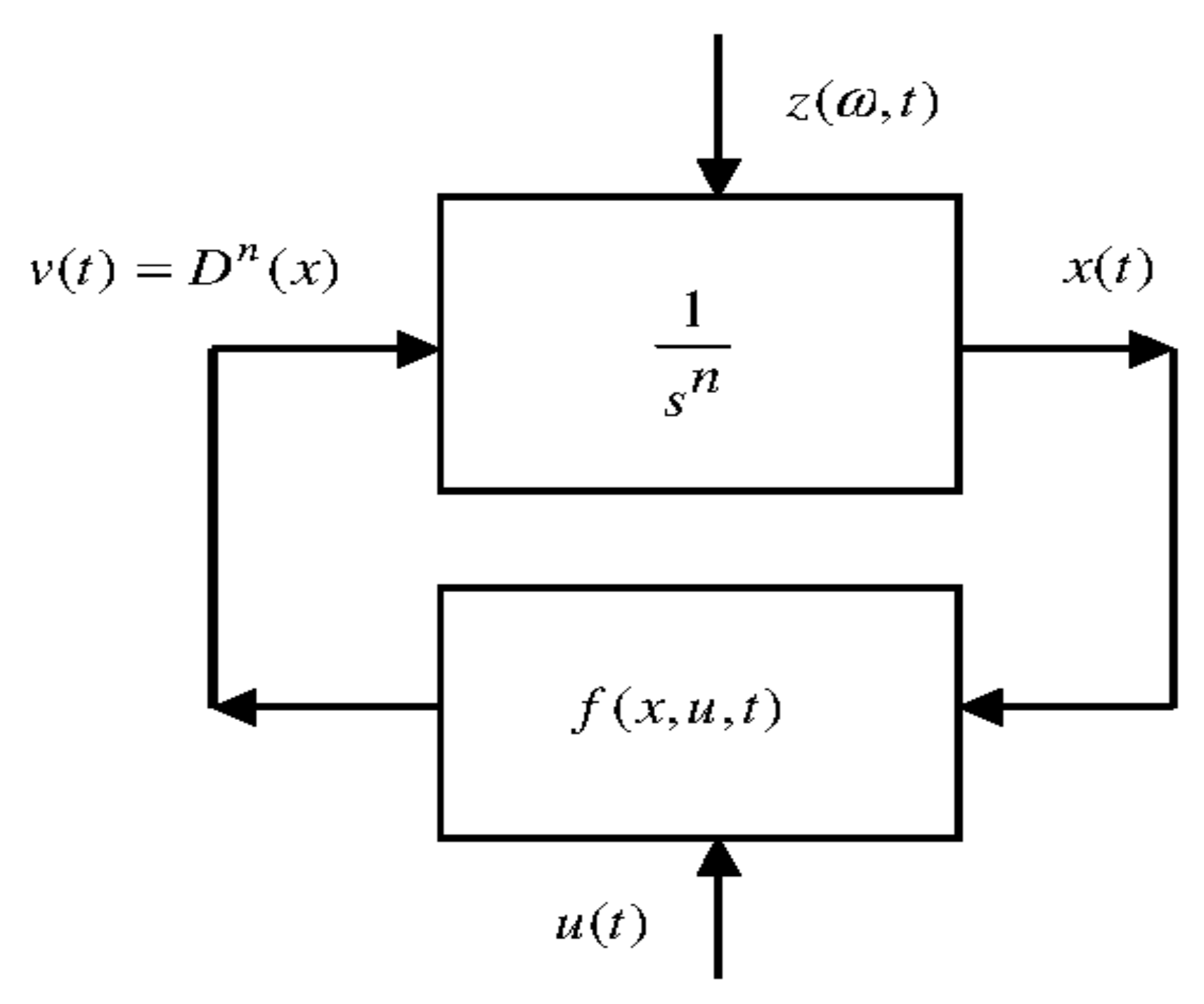
This modeling technique fundamentally corresponds to the graph of Figure 1 [22,23,32]. Note that this modeling technique is not specific to fractional calculus, it is used implicitly by any simulation technique [23]:

The input of the integrator is $v(t)\hspace{0.17em}=\hspace{0.17em}{D}^n(x(t))$ and its internal state $z(\omega ,t)$ corresponds to the system state. The graph of Figure 1 introduces the distributed model of the FDE; the non integer order model has been replaced by an integer order distributed differential system, allowing the use of the integer order system theory.

$$\left\{\begin{array}{l}\frac{\partial z(\omega ,t)}{\partial t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \hspace{0.17em}z(\omega ,t)\hspace{0.17em}+\hspace{0.17em}f(x,u,t) \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\\ x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega }\\ {\mu }_n(\omega )\hspace{0.17em}=\hspace{0.17em}\frac{\sin \hspace{0.17em}n\pi }{\pi }\hspace{0.17em}{\omega }^{-n} 0\hspace{0.17em}<\hspace{0.17em}n\hspace{0.17em}<\hspace{0.17em}1\end{array}\right.$$

(7)

Note that in contrary to Equation (5), the distributed modes $\omega$ are coupled in Equation (7), due to $v(t)\hspace{0.17em}=\hspace{0.17em}f(x,u,t)$: this is an essential feature of the modeling with fractional integrators.

This modeling principle can be directly generalized to the case of N derivatives FDEs [22,32]:

$$D^{\underset{-}{n}}(\underset{-}{X}(t))\hspace{0.17em}=\hspace{0.17em}\underset{-}{F}(\underset{-}{X},u,t)$$

(8)

$z(\omega ,t)$ is replaced by $\underset{-}{Z}(\omega ,t)$

$$\begin{gathered} {\underset{-}{n}}^T\hspace{0.17em}=\hspace{0.17em}[\hspace{0.17em}{n}_1\hspace{0.17em}\dots \hspace{0.17em}{n}_i\hspace{0.17em}\dots \hspace{0.17em}{n}_N\hspace{0.17em}] 0\hspace{0.17em}<\hspace{0.17em}{n}_i\hspace{0.17em}\le \hspace{0.17em}1 \\ {\mu }_{\underset{-}{n}}(\omega )\hspace{0.17em}=\hspace{0.17em}\left[\hspace{0.17em}\begin{array}{ccc}{\mu }_{n1}(\omega )& & 0\\ & {\mu }_{ni}(\omega )& \\ 0& & {\mu }_{nN}(\omega )\end{array}\right] \end{gathered}$$

(9)

and

$$\left\{\begin{array}{l}\frac{\partial \underset{-}{Z}(\omega ,t)}{\partial t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}+\hspace{0.17em}\underset{-}{F}(\underset{-}{X},u,t) \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\\ \underset{-}{X}(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\left[{\mu }_{\underset{-}{n}}(\omega )\right]\hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}d\omega }\end{array}\right.$$

(10)

3.3. Energy of a Fractional Order System

Within the usual fractional approach, $\frac{1}{2}\hspace{0.17em}{x}^2(t)$ is interpreted as an energy, like in the integer order case.

Since $x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n}(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega$, there can be an infinity of $z(\omega ,t)\hspace{0.17em}$ values ($\omega \hspace{0.17em}\in \hspace{0.17em}[0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[$) corresponding to $x(t)\hspace{0.17em}=\hspace{0.17em}0$, although the system is not at rest (refer to counter examples [22,32]).

This means that $\frac{1}{2}{x}^2(t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\left[{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n}(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega \right]}^2$ does not represent an energy, only a pseudo energy.

The fractional energy of the system is based on the distributed variable $z(\omega ,t)\hspace{0.17em}$:

$\frac{1}{2}\hspace{0.17em}z{(\omega ,t)}^2$ is the monochromatic energy density.

$dE\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}z{(\omega ,t)}^2\hspace{0.17em}d\omega$ is the energy in the frequency band $d\omega$ and

$$E(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n}(\omega )\hspace{0.17em}dE\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n}(\omega )\hspace{0.17em}z{(\omega ,t)}^2\hspace{0.17em}d\omega$$

(11)

is the weighted fractional energy of the system [33].

Note that this energy can only be equal to 0 if $z(\omega ,t)\hspace{0.17em}=\hspace{0.17em}0 \forall \omega \hspace{0.17em}\in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[$, i.e., if the system is really at rest.

This definition of energy has been validated by a physical interpretation [32,35].

Fractional energy has been used to derive system stability based on the Lyapunov method [33,34]. It plays a fundamental role in fractional optimal control to define a cost function.

Remark: 

The infinite state fundamentals have already been presented in several conference and journal papers (see for example [19,22,23,24,25,33,34,35]). A two volume monograph [32] provides a “state of the art” of this methodology and its application to different problems arising in fractional system theory.

4. Basic Principles of Fractional Calculus of Variations

4.1. Fractional Lagrangian and Euler Conditions

4.1.1. Integer Order Case

Let $x$ be a function of the $t$ variable.

One defines the Lagrangian $L(x,\dot{x},t)$ and the functional (or cost function) [1,4]:

$$J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}L(x,\dot{x},t)\hspace{0.17em}dt}$$

(12)

The objective of the calculus of variations is to determine the function $x(t)\hspace{0.17em}t\hspace{0.17em}\in \hspace{0.17em}[0\hspace{0.17em},\hspace{0.17em}T]$ which minimizes (or maximizes) the functional J, with the boundary conditions $x(0)$ and $x(T)$.

The fundamental result is that the Lagrangian has to satisfy the Euler condition:

$$\frac{\partial L(x,\dot{x},t)}{\partial x}\hspace{0.17em}-\hspace{0.17em}\frac{d}{dt}\left(\frac{\partial L(x,\dot{x},t)}{d\dot{x}}\right)\hspace{0.17em}=\hspace{0.17em}0$$

(13)

with the boundary conditions $x(0)$ and $x(T)$.

If the final state $x(T)$ is free, we have to satisfy the transversality condition:

$${\left(\frac{\partial L(x,\dot{x},t}{\partial \dot{x}}\right)}_T\hspace{0.17em}=\hspace{0.17em}0$$

(14)

4.1.2. Fractional Order Case

Within the usual fractional order approach, $L(x,\dot{x},t)$ is replaced by $L(x,D^n(x),t)$. Integration by parts, necessary to the derivation of Euler conditions, requires the definition of left and right fractional derivatives [8,9].

However, there are two remaining problems. $x(t)$ is no longer a state variable as in the integer order case, only a pseudo state variable. Moreover, the choice $L(t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}x{(t)}^2$ is no longer an energy, only a pseudo energy.

These problems disappear with the infinite state approach where $x(t)$ is replaced by $z(\omega ,t)$ and $\dot{x}(t)$ by $\dot{z}(\omega ,t)$.

Consequently, we define the monochromatic Lagrangian as $l(\omega ,\dot{z},z,t)$ and the weighted fractional Lagrangian as:

$$L(z,z,t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\omega )\hspace{0.17em}l(\omega ,z,\dot{z},t)\hspace{0.17em}d\omega }$$

(15)

Finally, the functional $J$ is defined as:

$$J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}L(z,\dot{z},t)\hspace{0.17em}dt\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}l(\omega ,z,\dot{z},t)\hspace{0.17em}d\omega \hspace{0.17em}dt}}}$$

(16)

Hence, we can pose the following optimality problem:

Consider the functional $J$ and the function $x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n}(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega$.

Determine the function $x(t)$, i.e., the distributed state variable $z(\omega ,t)$, which minimizes (or maximizes) $J$ with the boundary conditions $z(\omega ,0)$ and $z(\omega ,T) \forall \omega \in \hspace{0.17em}[\hspace{0.17em}0,+\infty [$.

The demonstration is similar to the integer order case, since $\dot{z}(\omega ,t)$ is an integer order derivative.

Then,

$$dJ=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n}(\omega )\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}\left[\hspace{0.17em}\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}z}dz\hspace{0.17em}+\hspace{0.17em}\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}d\dot{z}\right]}\hspace{0.17em}dt\hspace{0.17em}d\omega \hspace{0.17em}$$

(17)

We can use conventional integration by parts technique, i.e.,

$${\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}d\dot{z}\hspace{0.17em}dt}\hspace{0.17em}=\hspace{0.17em}{\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}dz\right]}_0^T\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\frac{\partial }{\partial t}}\hspace{0.17em}\left(\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right)\hspace{0.17em}dz\hspace{0.17em}dt$$

(18)

Since ${\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}dz\right]}_0^T\hspace{0.17em}=\hspace{0.17em}\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}dz(\omega ,T)\hspace{0.17em}-\hspace{0.17em}\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}dz(\omega ,0)\hspace{0.17em}=\hspace{0.17em}0$

because $\left\{\begin{array}{l}dz(\omega ,0)\hspace{0.17em}=\hspace{0.17em}0\\ dz(\omega ,T)\hspace{0.17em}=\hspace{0.17em}0\end{array}\right.\hspace{0.17em}\forall \hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$

we get $dJ=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n}(\omega )\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}\left[\hspace{0.17em}\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\hspace{0.17em}\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]\right]}\hspace{0.17em}dz\hspace{0.17em}dt\hspace{0.17em}d\omega \hspace{0.17em}$.

The optimality condition $dJ\hspace{0.17em}=\hspace{0.17em}0$ is satisfied if:

$$\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\hspace{0.17em}\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]\hspace{0.17em}=\hspace{0.17em}0 \forall \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\hspace{0.17em}$$

(19)

with the boundary conditions $\left\{\begin{array}{l}z(\omega ,0)\hspace{0.17em}\\ z(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$

Remark 1: 

The above condition is the monochromatic Euler condition.

Since $L(z,z,t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\omega )\hspace{0.17em}l(\omega ,z,\dot{z},t)\hspace{0.17em}d\omega }$ we can write for the fractional Lagrangian

$$\frac{\partial \hspace{0.17em}L(z,z,t)}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \hspace{0.17em}L(z,\dot{z},t)}{\partial \hspace{0.17em}\dot{z}}\right]\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]\right]}\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0$$

(20)

This means that this fractional Euler condition is the frequency integral form of the previous monochromatic Euler condition.

Remark 2: 

The transversality condition corresponds to $z(\omega ,0)$ specified and $z(\omega ,T)$ free.

In the integration by parts

$$\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}dz(\omega ,T)\hspace{0.17em}=\hspace{0.17em}0 \forall \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[$$

(21)

$$\mathrm{If}{\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]}_T\hspace{0.17em}=\hspace{0.17em}0 \forall \omega$$

(22)

Then the optimality monochromatic Euler condition is:

$$\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\hspace{0.17em}\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]\hspace{0.17em}=\hspace{0.17em}0 \forall \hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\hspace{0.17em}$$

(23)

with the boundary conditions $\left\{\begin{array}{l}z(\omega ,0)\hspace{0.17em}\\ {\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]}_T\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em}\end{array}\right. \forall \hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$ and for the fractional Lagrangian:

$$\frac{\partial \hspace{0.17em}L}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\hspace{0.17em}\left[\frac{\partial \hspace{0.17em}L}{\partial \hspace{0.17em}\dot{z}}\right]\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em}$$

(24)

with the boundary conditions $z(\omega ,0) \forall \hspace{0.17em}\omega$ and ${\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )}\hspace{0.17em}{\left[\frac{\partial \hspace{0.17em}l}{\partial \hspace{0.17em}\dot{z}}\right]}_T\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0$, i.e.,

$${\left[\frac{\partial \hspace{0.17em}L}{\partial \hspace{0.17em}\dot{z}}\right]}_T\hspace{0.17em}=\hspace{0.17em}0$$

(25)

Remark 3: 

We can note that the fractional Euler condition, within the infinite state approach, is very similar to the integer order case (Equation (13)) where the state variable $x(t)$ is replaced by the distributed variable $z(\omega ,t)$ (Equation (24)). However, there is an important difference; whereas Equation (13) is a classical equation, Equation (24) is a frequency distributed equation, where the monochromatic equation, corresponding to the mode $\omega$ is Equation (19).

4.2. Fractional Lagrange Multiplier

4.2.1. Integer Order Case

Consider the functional $J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}L(x,\dot{x},u,t)\hspace{0.17em}dt}$ where $x(t)$ satisfies the Ordinary Differential Equation (ODE):

$$\dot{x}(t)\hspace{0.17em}=\hspace{0.17em}f(x,u,t)$$

(26)

The objective is to determine $\widehat{u}(t)$ which minimizes (or maximizes) the functional.

The ODE equation is interpreted as an equality constraint $\dot{x}(t)\hspace{0.17em}-\hspace{0.17em}f(x,u,t)\hspace{0.17em}=\hspace{0.17em}0$ and an augmented function $M(x,\dot{x},u,t)$ is defined as:

$$M(x,\dot{x},u,t)\hspace{0.17em}=\hspace{0.17em}L(x,\dot{x},u,t)\hspace{0.17em}-\hspace{0.17em}\lambda (t)\hspace{0.17em}\left(\dot{x}\hspace{0.17em}-\hspace{0.17em}f(x,u,t)\right)$$

(27)

where $\lambda (t)$ is a Lagrange multiplier.

$M(x,\dot{x},u,t)$ has to satisfy the Euler conditions with respect to $x(t)$ and $u(t)$:

$$\left\{\begin{array}{l}\frac{\partial \hspace{0.17em}L}{\partial \hspace{0.17em}x}\hspace{0.17em}+\hspace{0.17em}\lambda (t)\hspace{0.17em}\frac{\partial \hspace{0.17em}f}{\partial \hspace{0.17em}x}\hspace{0.17em}+\hspace{0.17em}\dot{\lambda }(t)\hspace{0.17em}=\hspace{0.17em}0\\ \frac{\partial \hspace{0.17em}L}{\partial \hspace{0.17em}u}\hspace{0.17em}+\hspace{0.17em}\lambda (t)\hspace{0.17em}\frac{\partial \hspace{0.17em}f}{\partial \hspace{0.17em}u}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em}\end{array}\right.$$

(28)

with $\dot{x}(t)\hspace{0.17em}=\hspace{0.17em}f(x,u,t)$ and the boundary conditions $x(0)$ and $x(T)$.

If the final state $x(T)$ is not specified, the transversality condition has to be satisfied:

$${\left[\frac{\partial \hspace{0.17em}M}{\partial \hspace{0.17em}\dot{x}}\right]}_T\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\lambda (T)\hspace{0.17em}=\hspace{0.17em}0$$

(29)

4.2.2. Fractional Order Case

Consider the functional $J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}L(z,\dot{z},u,t)\hspace{0.17em}dt\hspace{0.17em}}$ where $x(t)$ satisfies the FDE

$$D^n(x(t))\hspace{0.17em}=\hspace{0.17em}f(x,u,t)$$

(30)

i.e., the frequency distributed differential system:

$$\left\{\begin{array}{l}\frac{\partial z(\omega ,t)}{\partial t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \hspace{0.17em}z(\omega ,t)\hspace{0.17em}+\hspace{0.17em}f(x,u,t) \omega \in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\\ x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega }\\ {\mu }_n(\omega )\hspace{0.17em}=\hspace{0.17em}\frac{\sin \hspace{0.17em}n\pi }{\pi }\hspace{0.17em}{\omega }^{-n} 0\hspace{0.17em}<\hspace{0.17em}n\hspace{0.17em}<\hspace{0.17em}1\end{array}\right.$$

(31)

with the boundary conditions $\left\{\begin{array}{l}z(\omega ,0)\hspace{0.17em}\\ z(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$.

In order to determine the optimal excitation $\widehat{u}(t)$ which minimizes (or maximizes) the functional $J$, we have to define the frequency distributed Lagrange multipliers $\lambda (\omega ,t)$.

Let $D^n(x(t))\hspace{0.17em}-\hspace{0.17em}f(x,u,t)\hspace{0.17em}=\hspace{0.17em}0$ be an equality constraint which can be also expressed as:

$$\frac{\partial z(\omega ,t)}{\partial \hspace{0.17em}t}\hspace{0.17em}-\hspace{0.17em}g(z,x,u,t)\hspace{0.17em}=\hspace{0.17em}0 \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[$$

(32)

where $g(z,x,u,t)\hspace{0.17em}=\hspace{0.17em}-\omega \hspace{0.17em}z(\omega ,t)\hspace{0.17em}+\hspace{0.17em}f(x,u,t)$.

Then, we can define the augmented function $M(z,\dot{z},u,t)$ such that:

$$M(z,\dot{z},u,t)\hspace{0.17em}=\hspace{0.17em}L(z,\dot{z},u,t)\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}\left[\frac{\partial z(\omega ,t)}{\partial \hspace{0.17em}t}\hspace{0.17em}-\hspace{0.17em}g(z,x,u,t)\right]}\hspace{0.17em}d\omega$$

(33)

As in the case of the fractional Lagrangian, the Lagrange multipliers have to satisfy an integral relation with respect to $\omega$. Note that the second term is not weighted by ${\mu }_n(\omega )$, because of $u(t)$. This particularity will be explained by the fractional cost function (Equation (41)) which is the sum of a fractional order term and an integer order one corresponding to $u(t)$.

Then, as in the integer order case, the function $M(z,\dot{z},u,t)$ has to satisfy the Euler conditions with respect to $z(\omega ,t)$ and $u(t)$:

$$\left\{\begin{array}{l}\frac{\partial \text{}M}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\dot{z}}\right]\hspace{0.17em}=\hspace{0.17em}0\\ \frac{\partial \text{}M}{\partial \hspace{0.17em}u}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\dot{u}}\right]\hspace{0.17em}=\hspace{0.17em}0\end{array}\right.$$

(34)

According to the definition of $M(z,\dot{z},u,t)$, we can write:

$$\frac{\partial \hspace{0.17em}M}{\partial \text{}z}\hspace{0.17em}=\hspace{0.17em}\frac{\partial \hspace{0.17em}L}{\partial \text{}z}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}\frac{\partial \hspace{0.17em}g}{\partial \text{}z}\hspace{0.17em}d\omega$$

and

$$\frac{\partial \hspace{0.17em}M}{\partial \text{}\dot{z}}\hspace{0.17em}=\hspace{0.17em}-{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}d\omega$$

i.e., the first Euler condition is expressed as:

$$\frac{\partial \hspace{0.17em}L}{\partial \text{}z}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}\frac{\partial \hspace{0.17em}g}{\partial \text{}z}\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\frac{\partial \hspace{0.17em}\lambda (\omega ,t)}{\partial \hspace{0.17em}t}}\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0$$

(35)

Moreover:

$$\frac{\partial \hspace{0.17em}M}{\partial \text{}u}\hspace{0.17em}=\hspace{0.17em}\frac{\partial \hspace{0.17em}L}{\partial \text{}u}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}\frac{\partial \hspace{0.17em}g}{\partial \text{}u}\hspace{0.17em}d\omega$$

and $\frac{\partial \hspace{0.17em}M}{\partial \text{}\dot{u}}\hspace{0.17em}=\hspace{0.17em}0$ since $M(z,\dot{z},u,t)$ is independent of $\dot{u}(t)$.

Consequently, the second Euler condition is expressed as:

$$\frac{\partial \hspace{0.17em}L}{\partial \text{}u}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}\frac{\partial \hspace{0.17em}g}{\partial \text{}u}\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0$$

(36)

Conclusion:

The optimal excitation $\widehat{u}(t)$ has to satisfy the two Euler conditions (35) and (36) with the boundary conditions $\left\{\begin{array}{l}z(\omega ,0)\hspace{0.17em}\\ z(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \omega \in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$ and the FDE equation $D^n(x(t))\hspace{0.17em}=\hspace{0.17em}f(x,u,t)$.

If the final state $z(\omega ,T)$ is not specified, the distributed Lagrange multiplier has to satisfy the transversality condition:

$${\left[\frac{\partial \hspace{0.17em}M}{\partial \hspace{0.17em}\dot{z}}\right]}_T\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,T)\hspace{0.17em}d\omega }=\hspace{0.17em}0$$

(37)

The monochromatic transversality condition is derived by differentiation of the previous condition (with respect to $\omega$):

$$\lambda (\omega ,T)\hspace{0.17em}=\hspace{0.17em}0 \forall \hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},+\hspace{0.17em}\infty \hspace{0.17em}[$$

(38)

As previously with the Euler condition, the Euler Lagrange Equations (35) and (36) are again very similar to the integer order case (Equation (28)), where the Lagrange multiplier $\lambda (t)$ has been replaced by a distributed Lagrange multiplier $\lambda (\omega ,t)$. Consequently, the fractional adjoint system is a frequency distributed system, as will be highlighted in the next section.

5. Quadratic Optimal Control of a Fractional Linear System

5.1. Quadratic Optimal Control of the Elementary System

Considering the complexity of the general case with $N$ non-commensurate order derivatives, we present in a first step the one derivative elementary case, which is nevertheless an infinite dimensional quadratic optimal control problem. Moreover, this simple case will permit attention to be paid to the distributed adjoint system.

Consider the time invariant FDE

$$D^n(x(t))\hspace{0.17em}=\hspace{0.17em}a\hspace{0.17em}x(t)\hspace{0.17em}+bu(t)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}<\hspace{0.17em}n\hspace{0.17em}<\hspace{0.17em}1$$

(39)

which is equivalent to the frequency distributed differential system:

$$\left\{\begin{array}{l}\frac{\partial z(\omega ,t)}{\partial t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \hspace{0.17em}z(\omega ,t)\hspace{0.17em}+\hspace{0.17em}ax(t)\hspace{0.17em}+\hspace{0.17em}bu(t) \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\hspace{0.17em}\infty \hspace{0.17em}[\\ x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega }\\ {\mu }_n(\omega )\hspace{0.17em}=\hspace{0.17em}\frac{\sin \hspace{0.17em}n\pi }{\pi }\hspace{0.17em}{\omega }^{-n} 0\hspace{0.17em}<\hspace{0.17em}n\hspace{0.17em}<\hspace{0.17em}1\end{array}\right.$$

(40)

Remember that in the integer order case, with $\dot{x}(t)=\hspace{0.17em}a\hspace{0.17em}x(t)\hspace{0.17em}+bu(t)\hspace{0.17em}$, the functional $J$ is defined as $J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}L(x,\hspace{0.17em}\dot{z},u,t)\hspace{0.17em}dt}$ where $L(x,\hspace{0.17em}\dot{z},\hspace{0.17em}u,t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}x{(t)}^2\hspace{0.17em}+\hspace{0.17em}\frac{1}{2}\hspace{0.17em}u{(t)}^2$.

We have previously highlighted that $\frac{1}{2}\hspace{0.17em}x{(t)}^2$ cannot represent a true energy in the fractional order case. Thus, we have to define the fractional Lagrangian as:

$$L(z,\hspace{0.17em}\dot{z},u,t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}{z}^2(\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}\frac{1}{2}}\hspace{0.17em}{u}^2(t)$$

(41)

and the functional $J$ as:

$$J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}L(z,\hspace{0.17em}\dot{z},\hspace{0.17em}u,t)\hspace{0.17em}dt}$$

(42)

The objective is to determine the optimal excitation $\widehat{u}(t)\hspace{0.17em}t\hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}T]$ which minimizes the functional $J$ with the boundary conditions $\left\{\begin{array}{l}z(\omega ,0)\hspace{0.17em}\\ z(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \omega \in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$.

This problem is solved using the distributed frequency Lagrange multiplier $\lambda (\omega ,t)$ and an augmented function $M(z,\dot{z},u,t)$:

$$M(z,\dot{z},u,t)\hspace{0.17em}=\hspace{0.17em}L(z,\dot{z},u,t)\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}\left[\frac{\partial z(\omega ,t)}{\partial \hspace{0.17em}t}\hspace{0.17em}-\hspace{0.17em}g(z,u,t)\right]}\hspace{0.17em}d\omega$$

(43)

$$\mathrm{where}g(z,u,t)\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \hspace{0.17em}z(\omega ,t)\hspace{0.17em}+\hspace{0.17em}ax(t)\hspace{0.17em}+\hspace{0.17em}bu(t)$$

(44)

$M(z,\dot{z},u,t)$ has to satisfy the two Euler conditions:

$$\left\{\begin{array}{l}\frac{\partial \text{}M}{\partial \hspace{0.17em}z}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\dot{z}}\right]\hspace{0.17em}=\hspace{0.17em}0\\ \frac{\partial \text{}M}{\partial \hspace{0.17em}u}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\dot{u}}\right]\hspace{0.17em}=\hspace{0.17em}0\end{array}\right.$$

(45)

Remark: 

Equation (45) requires differentiation with respect to the distributed variable $z(\omega ,t)$:

$$\frac{\partial }{\partial \hspace{0.17em}z}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}\left[\frac{\partial \hspace{0.17em}z(\omega ,t)}{\partial \hspace{0.17em}t}\hspace{0.17em}-\hspace{0.17em}ax(t)\hspace{0.17em}-\hspace{0.17em}bu(t)\right]\hspace{0.17em}d\omega$$

Note that $x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\xi )\hspace{0.17em}z(\xi ,t)\hspace{0.17em}d\xi }$: in this weighted integral, $x(t)$ depends on the mode $\omega$, but also all the other modes due to the coupling introduced by the term $a\hspace{0.17em}x(t)$ in Equation (44). Consequently, it is important to pay attention to this differentiation which is discussed in the corresponding lemma of Appendix A. Consequently, with $A(t)\hspace{0.17em}=\hspace{0.17em}a$ and $\underset{-}{B}(t)\hspace{0.17em}=\hspace{0.17em}b$, we can write:

$$\begin{array}{l}\frac{\partial \hspace{0.17em}M}{\partial \text{}z}\hspace{0.17em}=\hspace{0.17em}\frac{\partial \hspace{0.17em}L}{\partial \text{}z}\hspace{0.17em}-\frac{\partial }{\partial \hspace{0.17em}z}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}}\left[\frac{\partial \hspace{0.17em}z(\omega ,t)}{\partial \hspace{0.17em}t}\hspace{0.17em}-\hspace{0.17em}ax(t)\hspace{0.17em}-\hspace{0.17em}bu(t)\right]\hspace{0.17em}d\omega \\ \hspace{0.17em}=\hspace{0.17em}\frac{\partial \hspace{0.17em}L}{\partial \text{}z}\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\left[\omega \lambda (\omega ,t)\hspace{0.17em}-\hspace{0.17em}a\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\xi )\hspace{0.17em}\lambda (\xi ,t)\hspace{0.17em}d\xi }\right]}\hspace{0.17em}d\omega \end{array}$$

Since $\frac{\partial L(z,\hspace{0.17em}\dot{z},u,t)}{\partial \hspace{0.17em}z}\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega }$ and $\frac{\partial M(z,\dot{z},u,t)}{\partial \hspace{0.17em}\dot{z}}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}d\omega }$, the first Euler condition can be expressed as:

$${\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega }\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[\omega \lambda (\omega ,t)\hspace{0.17em}-\hspace{0.17em}a\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\xi )\hspace{0.17em}\lambda (\xi ,t)\hspace{0.17em}d\xi }\right]}\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0}$$

i.e.,

$$\frac{\partial }{\partial \hspace{0.17em}t}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[\omega \lambda (\omega ,t)\hspace{0.17em}-\hspace{0.17em}a\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\xi )\hspace{0.17em}\lambda (\xi ,t)\hspace{0.17em}d\xi }\right]}\hspace{0.17em}d\omega \hspace{0.17em}-{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}d\omega }\hspace{0.17em}$$

(46)

This is the integral form (with respect to $\omega$) of the adjoint differential equation related to $\lambda (\omega ,t)$. We obtain the frequency distributed equation of the adjoint system by frequency differentiation of the previous equation, i.e.,:

$$\frac{\partial \lambda (\omega ,t)\hspace{0.17em}}{\partial \hspace{0.17em}t}=\hspace{0.17em}\omega \lambda (\omega ,t)\hspace{0.17em}-\hspace{0.17em}a\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\xi )\hspace{0.17em}\lambda (\xi ,t)\hspace{0.17em}d\xi }\hspace{0.17em}-{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em}$$

(47)

Remark: 

Equation (47) is the monochromatic differential equation of the adjoint system that we can compare to the first equation of Equation (44): note that this equation is unstable, like in the integer order case. Moreover, for the large values of $\omega$, the mode $\lambda (\omega ,t)$ quickly diverges, which is certainly a major difficulty for a practical implementation of fractional optimal control.

Since $\frac{\partial L(z,\hspace{0.17em}\dot{z},\hspace{0.17em}u,t)}{\partial \hspace{0.17em}u}\hspace{0.17em}=\hspace{0.17em}u$ and $\frac{\partial L(z,\hspace{0.17em}\dot{z},u,t)}{\partial \hspace{0.17em}\dot{u}}\hspace{0.17em}=\hspace{0.17em}0$ the second Euler condition is expressed as:

$$u(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0}$$

(48)

This equation provides the optimal excitation $\widehat{u}(t)$.

Conclusion:

The functional $J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\left[\frac{1}{2}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n(\omega )\hspace{0.17em}{z}^2(\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}\frac{1}{2}}\hspace{0.17em}{u}^2(t)\right]}\hspace{0.17em}dt$ is minimal if $z(\omega ,t)$ and $u(t)$ satisfy the optimality conditions:

$$\begin{gathered} \frac{\partial \lambda (\omega ,t)\hspace{0.17em}}{\partial \hspace{0.17em}t}=\hspace{0.17em}\omega \lambda (\omega ,t)\hspace{0.17em}-\hspace{0.17em}a\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\mu }_n(\xi )\hspace{0.17em}\lambda (\xi ,t)\hspace{0.17em}d\xi }\hspace{0.17em}-{\mu }_n(\omega )\hspace{0.17em}z(\omega ,t)\hspace{0.17em} \\ \widehat{u}(t)\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}b\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\lambda (\omega ,t)\hspace{0.17em}d\omega } \end{gathered}$$

where $z(\omega ,t)$ satisfies the frequency distributed differential system (40) with the boundary conditions $\left\{\begin{array}{l}z(\omega ,0)\hspace{0.17em}\\ z(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \omega \in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$

Remark: 

If the final state $z(\omega ,T)$ is not specified, we have to satisfy the transversality condition:

$${\left[\frac{\partial \hspace{0.17em}M}{\partial \hspace{0.17em}\dot{z}}\right]}_T\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\lambda (\omega ,T)\hspace{0.17em}d\omega }=\hspace{0.17em}0$$

(49)

Frequency differentiation of this condition provides the monochromatic transversality condition:

$$\lambda (\omega ,T)\hspace{0.17em}=\hspace{0.17em}0 \forall \hspace{0.17em}\omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},+\hspace{0.17em}\infty \hspace{0.17em}[$$

(50)

5.2. Optimal Control of the Generalized Linear System

Consider the generalized time variant fractional linear system:

$$D^{\underset{-}{n}}(\underset{-}{X}(t))\hspace{0.17em}=\hspace{0.17em}A(t)\hspace{0.17em}\underset{-}{X}(t)\hspace{0.17em}+\hspace{0.17em}\underset{-}{B}(t)\hspace{0.17em}u(t)$$

(51)

and the functional $J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\hspace{0.17em}L(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}dt}$

where the fractional Lagrangian is defined as:

$$L(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{Z}}{(\omega ,t)}^T\hspace{0.17em}\left[R,\mu \right]\hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{u}^2(t)$$

(52)

Thanks to the frequency distributed representation, the system (51) can be expressed as:

$$\left\{\begin{array}{l}\frac{\partial \underset{-}{Z}}{\partial \hspace{0.17em}t}(\omega ,t)\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\omega \underset{-}{Z}(\omega ,t)\hspace{0.17em}+\hspace{0.17em}A(t)\hspace{0.17em}\underset{-}{X}(t)\hspace{0.17em}+\hspace{0.17em}\underset{-}{B}(t)\hspace{0.17em}u(t)\hspace{0.17em}=\hspace{0.17em}\underset{-}{G}(\underset{-}{Z},u,t)\\ \underset{-}{X}(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\mu }_{\underset{-}{n}}(\omega )\right]\hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}d\omega }\end{array}\right.\hspace{0.17em}$$

(53)

with:

$${\mu }_{\underset{-}{n}}(\omega )\hspace{0.17em}=\hspace{0.17em}\left[\hspace{0.17em}\begin{array}{ccc}{\mu }_{n1}(\omega )& & 0\\ & {\mu }_{ni}(\omega )& \\ 0& & {\mu }_{nN}(\omega )\end{array}\right] {\mu }_{ni}(\omega )\hspace{0.17em}=\hspace{0.17em}\frac{\sin \hspace{0.17em}{n}_i\pi }{\pi }\hspace{0.17em}{\omega }^{-n\hspace{0.17em}i}$$

(54)

and

$$\left[R,\mu \right]\hspace{0.17em}=\hspace{0.17em}\left[\hspace{0.17em}\begin{array}{ccc}{R}_1\hspace{0.17em}{\mu }_{n1}(\omega )& & 0\\ & R_i\hspace{0.17em}{\mu }_{ni}(\omega )& \\ 0& & R_N\hspace{0.17em}{\mu }_{nN}(\omega )\end{array}\right] R_{i\hspace{0.17em}}\hspace{0.17em}>\hspace{0.17em}0\hspace{0.17em}$$

(55)

$\dim \hspace{0.17em}\underset{-}{n}\hspace{0.17em}=\hspace{0.17em}\dim \hspace{0.17em}\underset{-}{X}\hspace{0.17em}=\hspace{0.17em}\dim \hspace{0.17em}\underset{-}{Z}\hspace{0.17em}=\hspace{0.17em}N\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}<\hspace{0.17em}{n}_i\hspace{0.17em}\le \hspace{0.17em}1$

The objective is to determine the optimal excitation $\widehat{u}(t) t\hspace{0.17em}\in \hspace{0.17em}[0\hspace{0.17em},\hspace{0.17em}T]$ minimizing the functional $J$ with the boundary conditions $\left\{\begin{array}{l}\underset{-}{Z}(\omega ,0)\hspace{0.17em}\\ \underset{-}{Z}(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \omega \in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$

As with the previous model, we have to define $N$ frequency distributed Lagrange multipliers $\underset{-}{\lambda }(\omega ,t)$ such that:

$$M(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}=\hspace{0.17em}L(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }{(\omega ,t)}^T\hspace{0.17em}\left[\frac{\partial \underset{-}{Z}(\omega ,t)}{\partial \hspace{0.17em}t}\hspace{0.17em}-\hspace{0.17em}\underset{-}{G}(\underset{-}{Z},u,t)\right]}\hspace{0.17em}d\omega$$

(56)

$M(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}$ has to satisfy the two Euler conditions with respect to $\underset{-}{Z}(\omega ,t)$ and $u(t)$:

$$\left\{\begin{array}{l}\frac{\partial \text{}M}{\partial \hspace{0.17em}\underset{-}{Z}}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\underset{-}{\dot{Z}}}\right]\hspace{0.17em}=\hspace{0.17em}0\\ \frac{\partial \text{}M}{\partial \hspace{0.17em}u}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\dot{u}}\right]\hspace{0.17em}=\hspace{0.17em}0\end{array}\right.$$

(57)

Since:

$$\frac{\partial \hspace{0.17em}M}{\partial \text{}\underset{-}{Z}}\hspace{0.17em}=\hspace{0.17em}\frac{\partial \hspace{0.17em}L}{\partial \text{}\underset{-}{Z}}\hspace{0.17em}-\frac{\partial }{\partial \hspace{0.17em}\underset{-}{Z}}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }{(\omega ,t)}^T\hspace{0.17em}}\left[\frac{\partial \hspace{0.17em}\underset{-}{Z}(\omega ,t)}{\partial \text{}t}\hspace{0.17em}-\hspace{0.17em}\underset{-}{G}(\underset{-}{Z},u,t)\right]\hspace{0.17em}d\omega$$

$$\frac{\partial \hspace{0.17em}M}{\partial \text{}\underset{-}{\dot{Z}}}\hspace{0.17em}=\hspace{0.17em}-{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }(\omega ,t)\hspace{0.17em}}d\omega$$

and

$$\frac{\partial \hspace{0.17em}L}{\partial \text{}\underset{-}{Z}}\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[R,\mu \right]}\hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}d\omega$$

we can write, thanks to the differentiation lemma of Appendix A:

$$\begin{array}{l}\frac{\partial \hspace{0.17em}L}{\partial \text{}\underset{-}{Z}}\hspace{0.17em}-\frac{\partial }{\partial \hspace{0.17em}\underset{-}{Z}}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }{(\omega ,t)}^T\hspace{0.17em}}\left[\frac{\partial \hspace{0.17em}\underset{-}{Z}(\omega ,t)}{\partial \text{}t}\hspace{0.17em}-\hspace{0.17em}\underset{-}{G}(\underset{-}{Z},u,t)\right]\hspace{0.17em}d\omega \hspace{0.17em}\\ =\hspace{0.17em}\frac{\partial \hspace{0.17em}L}{\partial \text{}\underset{-}{Z}}\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\left[\omega \hspace{0.17em}\underset{-}{\lambda }\hspace{0.17em}(\omega ,t)\hspace{0.17em}-A(t)\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\mu }_{\underset{-}{n}}\right]\hspace{0.17em}\underset{-}{\lambda }(\xi ,t)\hspace{0.17em}d\xi }\right]}\hspace{0.17em}d\omega \end{array}$$

(58)

Then the first Euler condition can be expressed as:

$${\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\left[R,\mu \right]\hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}d\omega }\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[\omega \underset{-}{\lambda }(\omega ,t)\hspace{0.17em}-\hspace{0.17em}A(t){\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\mu }_{\underset{-}{n}}\right]\hspace{0.17em}\underset{-}{\lambda }(\xi ,t)\hspace{0.17em}d\xi }\right]}\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }(\omega ,t)\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0}$$

(59)

Frequency differentiation of this equation provides the frequency distributed model of the adjoint system:

$$\frac{\partial \underset{-}{\lambda }(\omega ,t)\hspace{0.17em}}{\partial \hspace{0.17em}t}=\hspace{0.17em}\omega \underset{-}{\lambda }(\omega ,t)\hspace{0.17em}-\hspace{0.17em}A(t)\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\mu }_{\underset{-}{n}}\right]\hspace{0.17em}\lambda (\xi ,t)\hspace{0.17em}d\xi }\hspace{0.17em}-\left[R,\mu \right]\hspace{0.17em}\underset{-}{Z}(\omega ,t)\hspace{0.17em}$$

(60)

Moreover, since $\frac{\partial L}{\partial \hspace{0.17em}u}\hspace{0.17em}=\hspace{0.17em}u$ and $\frac{\partial L}{\partial \hspace{0.17em}\dot{u}}\hspace{0.17em}=\hspace{0.17em}0$ the second Euler condition is expressed as:

$$u(t)\hspace{0.17em}+\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }{(\omega ,t)}^T\hspace{0.17em}\underset{-}{B}(t)\hspace{0.17em}d\omega \hspace{0.17em}=\hspace{0.17em}0}$$

(61)

This equation provides the optimal excitation $\widehat{u}(t)$ with the boundary conditions: $\left\{\begin{array}{l}\underset{-}{Z}(\omega ,0)\hspace{0.17em}\\ \underset{-}{Z}(\omega ,T)\hspace{0.17em}\end{array}\right. \forall \omega \in [\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}+\infty \hspace{0.17em}[$

Remark: 

If the final state $\underset{-}{Z}(\omega ,T)$ is not specified, the transversality condition has to be satisfied:

$${\left[\frac{\partial \hspace{0.17em}M}{\partial \hspace{0.17em}\underset{-}{\dot{Z}}}\right]}_T\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}\underset{-}{\lambda }(\omega ,T)\hspace{0.17em}d\omega }=\hspace{0.17em}0$$

(62)

Frequency differentiation of this condition provides the monochromatic transversality condition:

$$\underset{-}{\lambda }(\omega ,T)\hspace{0.17em}=\hspace{0.17em}0 \forall \omega \hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},+\hspace{0.17em}\infty \hspace{0.17em}[$$

(63)

6. Implementation of a Numerical Solution

6.1. Frequency Discretized Model of the Fractional Integrator

Since the optimal solutions derived in Section 5 are based on frequency distributed equations, they are not directly usable. Their practical implementation requires the approximation of these distributed equations by finite dimension equations.

Hence, the solution is to use the finite dimension approximation or frequency discretized model of the fractional integrator.

Several techniques can be used to perform this frequency discretization. However, the success of our approach is based on an approximate model which retains an infinite gain integral action at $\omega =0$ and a fractional behavior in the frequency band $\left[\hspace{0.17em}{\omega }_{\min }\hspace{0.17em};\hspace{0.17em}{\omega }_{\max }\hspace{0.17em}\right]$. This approximation has already been described in several papers, such as [23] and particularly in [32].

Thus, we get the frequency discretized fractional integrator:

$$\left\{\begin{array}{l}\frac{d{z}_j(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{\omega }_j{z}_j(t)\hspace{0.17em}+\hspace{0.17em}v(t) j\hspace{0.17em}=\hspace{0.17em}0 to\hspace{0.17em}J\hspace{0.17em}\\ x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{j=0}^J\hspace{0.17em}{c}_j\hspace{0.17em}{z}_j(t)}\end{array}\right.$$

(64)

Note that for $j\hspace{0.17em}=\hspace{0.17em}0 {\omega }_0\hspace{0.17em}=\hspace{0.17em}0$ and $\frac{d{z}_0(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}v(t)$ which is the model of an integer order integrator.

For more information, refer to [22,32].

6.2. Frequency Discretized Model of the Elementary System

Our objective is to determine the optimal excitation $\widehat{u}(t)$ for the time invariant system:

$$D^n(x(t))\hspace{0.17em}=\hspace{0.17em}a\hspace{0.17em}x(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}u(t)$$

(65)

Its frequency discretization is based on the previous integrator model where $v(t)\hspace{0.17em}=\hspace{0.17em}a\hspace{0.17em}x(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}u(t)$:

$$\left\{\begin{array}{l}\frac{d{z}_j(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{\omega }_j{z}_j(t)\hspace{0.17em}+\hspace{0.17em}a\hspace{0.17em}x(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}u(t)\hspace{0.17em}\\ x(t)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{j=0}^J\hspace{0.17em}{c}_j\hspace{0.17em}{z}_j(t)}\end{array}\right.$$

(66)

Let us define the following vectors:

$$\begin{array}{l}\underset{-}{Z}{(t)}^T\hspace{0.17em}=\hspace{0.17em}\left[z_0(t)\hspace{0.17em}\dots \hspace{0.17em}{z}_j(t)\hspace{0.17em}\dots \hspace{0.17em}{z}_J(t)\right]\\ {\underset{-}{C}}_I\hspace{0.17em}=\hspace{0.17em}\left[c_{0\hspace{0.17em}}\dots \hspace{0.17em}{c}_j\hspace{0.17em}\dots \hspace{0.17em}{c}_J\right]\end{array}$$

(67)

then $x(t)\hspace{0.17em}=\hspace{0.17em}{\underset{-}{C}}_I\hspace{0.17em}\underset{-}{Z}(t)$

Moreover:

$$A_I\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cccc}0& & & 0\\ & -\hspace{0.17em}{\omega }_1& & \\ & & -\hspace{0.17em}{\omega }_j& \\ 0& & & -\hspace{0.17em}{\omega }_J\end{array}\right]\mathrm{and}{\underset{-}{B}}_I\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$$

(68)

Then, the differential system (66) is represented by:

$$\begin{array}{l}\frac{d\underset{-}{Z}(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}{A}_I\hspace{0.17em}\underset{-}{Z}(t)\hspace{0.17em}+\hspace{0.17em}a\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}{\underset{-}{C}}_I\hspace{0.17em}\underset{-}{Z}(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}u(t)\\ =\hspace{0.17em}{A}_{syst}\hspace{0.17em}\underset{-}{Z}(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}u(t)\\ =\hspace{0.17em}\underset{-}{g}(\underset{-}{Z},u,t)\end{array}$$

(69)

with $\left\{\begin{array}{l}{A}_{syst}\hspace{0.17em}=\hspace{0.17em}{A}_I\hspace{0.17em}+\hspace{0.17em}a\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}{\underset{-}{C}}_I\\ \dim \hspace{0.17em}\underset{-}{Z}\hspace{0.17em}=\hspace{0.17em}J\hspace{0.17em}+\hspace{0.17em}1 \dim \hspace{0.17em}{A}_{syst}\hspace{0.17em}=\hspace{0.17em}(J+1)\hspace{0.17em}(J+1)\end{array}\right.\hspace{0.17em}$

Remark: 

Note that the elementary fractional system (65) has been transformed into an equivalent large dimension $(J\hspace{0.17em}+\hspace{0.17em}1)$ integer order system (69). This large dimension is one of the difficulties that the user has to encounter with the practical implementation of the infinite state approach.

6.3. Finite Dimension Optimal Solution

The discretization of the functional $J\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}L(z,\dot{z},u,t)\hspace{0.17em}dt}$ and of the Lagrangian

$L(z,\dot{z},u,t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\displaystyle \underset{0}{\overset{\infty }{\int }}\hspace{0.17em}{\mu }_n}(\omega )\hspace{0.17em}z{(\omega ,t)}^2\hspace{0.17em}d\omega \hspace{0.17em}+\hspace{0.17em}\frac{1}{2}{u}^2(t)$ provides

$$L(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}{\displaystyle \sum _{j=0}^J\hspace{0.17em}{c}_j}{z}_j{(t)}^2\hspace{0.17em}+\hspace{0.17em}\frac{1}{2}{u}^2(t)$$

(70)

Let $\left[\text{}{L}_I\right]\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cccc}{c}_0& & & 0\\ & c_1& & \\ & & c_j& \\ 0& & & c_J\end{array}\right]$

$$\mathrm{Then}L(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\hspace{0.17em}\underset{-}{Z}{(t)}^T\hspace{0.17em}\left[L_I\right]\hspace{0.17em}\underset{-}{\hspace{0.17em}Z}(t)+\hspace{0.17em}\frac{1}{2}{u}^2(t)$$

(71)

The initial optimal problem has been transformed into a classical integer order problem with, nevertheless, a large dimension $J\hspace{0.17em}+\hspace{0.17em}1$.

Consider the Lagrange multipliers:

$$\underset{-}{\lambda }{(t)}^T\hspace{0.17em}=\hspace{0.17em}\left[{\lambda }_0(t)\hspace{0.17em}\dots \hspace{0.17em}{\lambda }_j(t)\hspace{0.17em}\dots \hspace{0.17em}{\lambda }_J(t)\right]$$

(72)

and the augmented function:

$$M(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}=L(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}-\hspace{0.17em}\underset{-}{\lambda }{(t)}^T\hspace{0.17em}\left(\underset{-}{\dot{Z}}(t)\hspace{0.17em}-\hspace{0.17em}\underset{-}{g}(\underset{-}{Z},u,t)\right)$$

(73)

where $M(\underset{-}{Z},\underset{-}{\dot{Z}},u,t)\hspace{0.17em}$ satisfies the Euler conditions:

$$\left\{\begin{array}{l}\frac{\partial \text{}M}{\partial \hspace{0.17em}\underset{-}{Z}}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\underset{-}{\dot{Z}}}\right]\hspace{0.17em}=\hspace{0.17em}0\\ \frac{\partial \text{}M}{\partial \hspace{0.17em}u}\hspace{0.17em}-\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}t}\left[\frac{\partial \text{}M}{\partial \hspace{0.17em}\dot{u}}\right]\hspace{0.17em}=\hspace{0.17em}0\end{array}\right.$$

(74)

Since:

$$\frac{\partial \hspace{0.17em}L}{\partial \hspace{0.17em}\underset{-}{Z}}\hspace{0.17em}=\hspace{0.17em}\left[L_I\right]\hspace{0.17em}\underset{-}{Z}(t)\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}\underset{-}{Z}}\left(\underset{-}{\dot{Z}}(t)\hspace{0.17em}-\hspace{0.17em}\underset{-}{g}(\underset{-}{Z},u,t)\right)\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{A}_{syst}\hspace{0.17em}\frac{\partial }{\partial \hspace{0.17em}\underset{-}{\dot{Z}}}\left(\underset{-}{\dot{Z}}(t)\hspace{0.17em}-\hspace{0.17em}\underset{-}{g}(\underset{-}{Z},u,t)\right)\hspace{0.17em}=\hspace{0.17em}\left[I\right]$$

The first Euler condition provides the differential equation of the adjoint system:

$$\frac{d\underset{-}{\lambda }(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{A}_{syst}{}^T\hspace{0.17em}\underset{-}{\lambda }(t)\hspace{0.17em}-\hspace{0.17em}\left[L_I\right]\hspace{0.17em}\underset{-}{Z}(t)$$

(75)

The second Euler condition expresses the optimal excitation:

$$\widehat{u}(t)\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}b\hspace{0.17em}\underset{-}{\lambda }{(t)}^{T\hspace{0.17em}}{\underset{-}{B}}_I\hspace{0.17em}=\hspace{0.17em}-b\hspace{0.17em}{\displaystyle \sum _{j=0}^J\hspace{0.17em}{\lambda }_j(t)}$$

(76)

Conclusion:

The optimal excitation $\widehat{u}(t)$ is the solution of the differential system:

$$\left\{\begin{array}{l}\frac{d\underset{-}{Z}(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}{A}_{syst}\hspace{0.17em}\underset{-}{Z}(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}\widehat{u}(t)\hspace{0.17em}\\ \frac{d\underset{-}{\lambda }(t)}{d\hspace{0.17em}t}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}{A}_{syst}{}^T\hspace{0.17em}\underset{-}{\lambda }(t)\hspace{0.17em}-\hspace{0.17em}\left[L_I\right]\hspace{0.17em}\underset{-}{Z}(t)\\ \widehat{u}(t)\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}b\hspace{0.17em}\underset{-}{\lambda }{(t)}^T\hspace{0.17em}{\underset{-}{B}}_I\end{array}\right.\hspace{0.17em}$$

(77)

with the boundary conditions: $\left\{\begin{array}{l}\underset{-}{Z}(0)\hspace{0.17em}\\ \underset{-}{Z}(T)\hspace{0.17em}\end{array}\right.\hspace{0.17em}$

If the final state $\underset{-}{Z}(t)$ is not specified, it is replaced by the transversality condition

$$\underset{-}{\lambda }(T)\hspace{0.17em}=\hspace{0.17em}0$$

(78)

Remark: 

Since the frequency elementary system (65) has been replaced by an approximate integer order differential system (69), the solution of the fractional optimal control problem is equivalent to the solution of a large dimension integer order optimal control problem (77).

This result highlights the fact that fractional optimal control requires the optimal control of all the components of $z(\omega ,t)$, contrary to the usual fractional approach, which considers only the pseudo-state $x(t).$

6.4. Numerical Computation of the Optimal Solution

The numerical implementation of the optimal solution (77) would require sophisticated numerical techniques, which are out of the scope of this paper. Note that the usual numerical algorithms cannot be directly used because even with an elementary system like (65), the dimension of (77) is $2\times (J+1)$ with $J\hspace{0.17em}>>\hspace{0.17em}1$. Moreover, since the modes ${\omega }_j$ are distributed on a large spectrum, the problem (77) is very difficult to solve, and it will require adapted algorithms.

In fact, our purpose in the paper is less ambitious. In a first step, we intend to demonstrate that a numerical implementation is feasible, even with an unrealistic approach.

The previous system (77) can be expressed as:

$$\frac{d}{d\hspace{0.17em}t}\left[\begin{array}{c}\underset{-}{Z}(t)\\ \underset{-}{\lambda }(t)\end{array}\right]\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cc}{A}_{syst}& -\hspace{0.17em}b\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}{\underset{-}{B}}_I{}^T\\ -\hspace{0.17em}\left[L_I\right]& -\hspace{0.17em}{A}_{syst}{}^T\end{array}\right]\hspace{0.17em}\left[\begin{array}{c}\underset{-}{Z}(t)\\ \underset{-}{\lambda }(t)\end{array}\right]$$

(79)

Let $\hspace{0.17em}\underset{-}{Y}(t)\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{c}\underset{-}{Z}(t)\\ \underset{-}{\lambda }(t)\end{array}\right] A\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cc}{A}_{syst}& -\hspace{0.17em}b\hspace{0.17em}{\underset{-}{B}}_I\hspace{0.17em}{\underset{-}{B}}_I{}^T\\ -\hspace{0.17em}\left[L_I\right]& -\hspace{0.17em}{A}_{syst}{}^T\end{array}\right]\hspace{0.17em}$

Then $\frac{d}{d\hspace{0.17em}t}\underset{-}{Y}(t)\hspace{0.17em}=\hspace{0.17em}A\hspace{0.17em}\underset{-}{Y}(t)$

Since Equation (79) is a linear system, we can use the matrix exponential $e^{A\hspace{0.17em}t}$, i.e., at $t\hspace{0.17em}=\hspace{0.17em}T$:

$\underset{-}{Y}(T)\hspace{0.17em}=\hspace{0.17em}{e}^{A\hspace{0.17em}T}\hspace{0.17em}\underset{-}{Y}(0)$ (refer to [32] volume 2 chapter 9 for more details) and reciprocally:

$$\underset{-}{Y}(0)\hspace{0.17em}=\hspace{0.17em}{e}^{-A\hspace{0.17em}T}\hspace{0.17em}\underset{-}{Y}(T)\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right]\hspace{0.17em}\underset{-}{Y}(T)$$

(80)

The boundary conditions correspond to $\left\{\hspace{0.17em}\underset{-}{Z}(0)\hspace{0.17em},\hspace{0.17em}\underset{-}{Z}(T)\right\}$ and $\left\{\hspace{0.17em}\underset{-}{\lambda }(0)\hspace{0.17em},\hspace{0.17em}\underset{-}{\lambda }(T)\right\}$.

Moreover, the computation of the optimal solution requires the determination of $\underset{-}{\lambda }(0)$.

For the case of a free final state, the objective is to determine $\underset{-}{\lambda }(0)$ with $\underset{-}{Z}(0)$ and $\underset{-}{\lambda }(T)$.

The final state $\underset{-}{Z}(T)$ is free, thus according to (80):

$$\underset{-}{Z}(T)\hspace{0.17em}=\hspace{0.17em}{M}_{11}{}^{-1}\hspace{0.17em}\left(\underset{-}{Z}(0)\hspace{0.17em}-\hspace{0.17em}{M}_{12}\hspace{0.17em}\underset{-}{\lambda }(T)\right)$$

(81)

Since $\underset{-}{\lambda }(T)\hspace{0.17em}=\hspace{0.17em}0$ we get:

$$\underset{-}{\lambda }(0)\hspace{0.17em}=\hspace{0.17em}{M}_{21}\hspace{0.17em}{M}_{11}{}^{-1}\hspace{0.17em}\underset{-}{Z}(0)$$

(82)

Remark: 

The computation of $\underset{-}{\lambda }(0)$ seems to be a trivial problem relying on a simple matrix inversion.

In fact, the computation of $M_{11}{}^{-1}$ is really a difficult problem.

It is necessary to look at the dimension of matrix $A_{syst}$ since $J$ has to be a large value. Moreover, the modes ${\omega }_j$ of the fractional integrator are spread on a wide range from ${\omega }_{\min }$ to ${\omega }_{\max }$ (with ${\omega }_0\hspace{0.17em}=\hspace{0.17em}0$) which have to satisfy the constraints ${\omega }_{\min }\hspace{0.17em}\to \hspace{0.17em}0$ and ${\omega }_{\max }\hspace{0.17em}\to \hspace{0.17em}\infty$.

Consequently, the matrix $M_{11}$ is very ill conditioned. This problem has already been highlighted in [32].

6.5. Simulation Results

As noted previously, the objective of fractional optimal control is to really control all the components $z_j(t)$ of $x(t)$. Since the optimal solution $\widehat{u}(t)$ is obtained with Equation (76), we have also to compute all the components ${\lambda }_j(t)$ of the adjoint system.

Thus, the visualization of the control problem requires all of the components $z_j(t)$ (for the system) and ${\lambda }_j(t)$ (for the adjoint system) to be taken into account.

Practically, we represent the discretized distribution of $z_j(t)$ and ${\lambda }_j(t)$ at the instants $t\hspace{0.17em}=\hspace{0.17em}0$ and $t\hspace{0.17em}=\hspace{0.17em}T$. Moreover, it is important to represent the dynamics of $z_j(t)$ and ${\lambda }_j(t)$: we have decided to only represent the dynamics corresponding to $j\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}10\hspace{0.17em},\hspace{0.17em}20$. Though the major objective is to compute the optimal components $z_j(t)$, it is obviously interesting to also represent the corresponding pseudo-state $x(t)$, which is the weighted sum of the optimal components $z_j(t)$.

The optimal excitation $\widehat{u}(t)$ is calculated for the system $D^n(x(t))\hspace{0.17em}=\hspace{0.17em}a\hspace{0.17em}x(t)\hspace{0.17em}+\hspace{0.17em}b\hspace{0.17em}u(t) a\hspace{0.17em}=\hspace{0.17em}-1 b\hspace{0.17em}=\hspace{0.17em}1$ with different values of the fractional order $n\hspace{0.17em}=\hspace{0.17em}\left\{\hspace{0.17em}0.5\hspace{0.17em};\hspace{0.17em}0.6\hspace{0.17em};\hspace{0.17em}0.7\hspace{0.17em};\hspace{0.17em}0.8\hspace{0.17em};\hspace{0.17em}0,9\hspace{0.17em}\right\}$ as well as for the integer order case $n\hspace{0.17em}=\hspace{0.17em}1$.

Numerical simulations are performed with the following parameters (refer to [22,32] for more information related to the significance of these parameters):

$$T_e\hspace{0.17em}=\hspace{0.17em}{10}^{-3}s T\hspace{0.17em}=\hspace{0.17em}1.5\hspace{0.17em}s J\hspace{0.17em}=\hspace{0.17em}Ncel\hspace{0.17em}=\hspace{0.17em}20 {\omega }_{\min }\hspace{0.17em}=\hspace{0.17em}{10}^{-7}\hspace{0.17em}rd/s {\omega }_{\max }\hspace{0.17em}=\hspace{0.17em}10\hspace{0.17em}rd/s.$$

As noted previously, matrix inversion of $M_{11}$ is a tough problem; a compromise has been necessary between the values of $a$, $Ncel$, ${\omega }_{\min }$ and ${\omega }_{\max }$.

Initial state $\underset{-}{Z}(0)$ is chosen arbitrarily: $z_j(0)\hspace{0.17em}=\hspace{0.17em}1 \forall \hspace{0.17em}j$, i.e., $x(0)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{j=0}^J\hspace{0.17em}{c}_j}\hspace{0.17em}{z}_j(0)$.

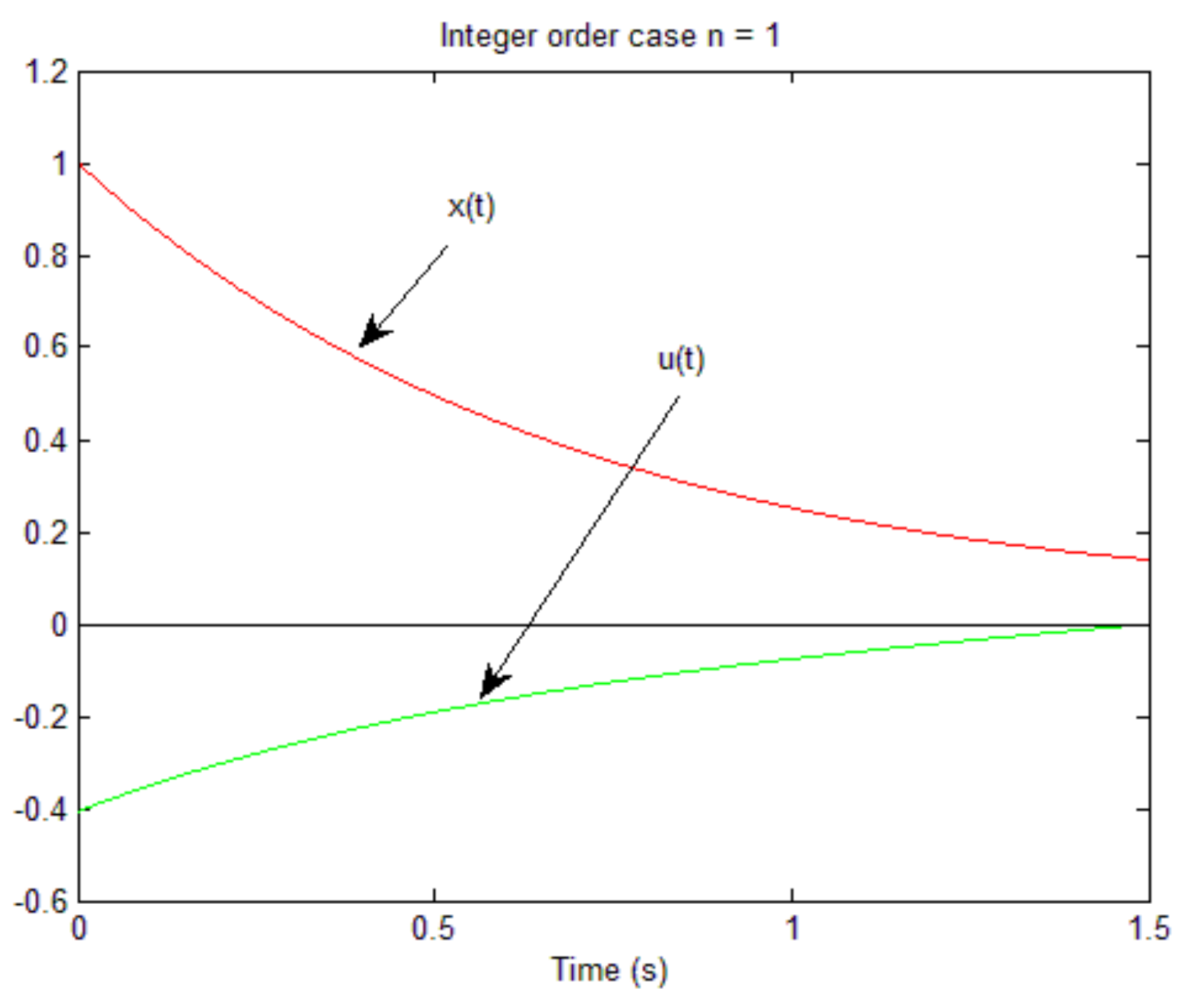
In order to compare the fractional optimal control to the integer order one, Figure 2 presents the graphs of $x(t)$ and $\widehat{u}(t)$ for $n\hspace{0.17em}=\hspace{0.17em}1$ ($x(0)\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}$).

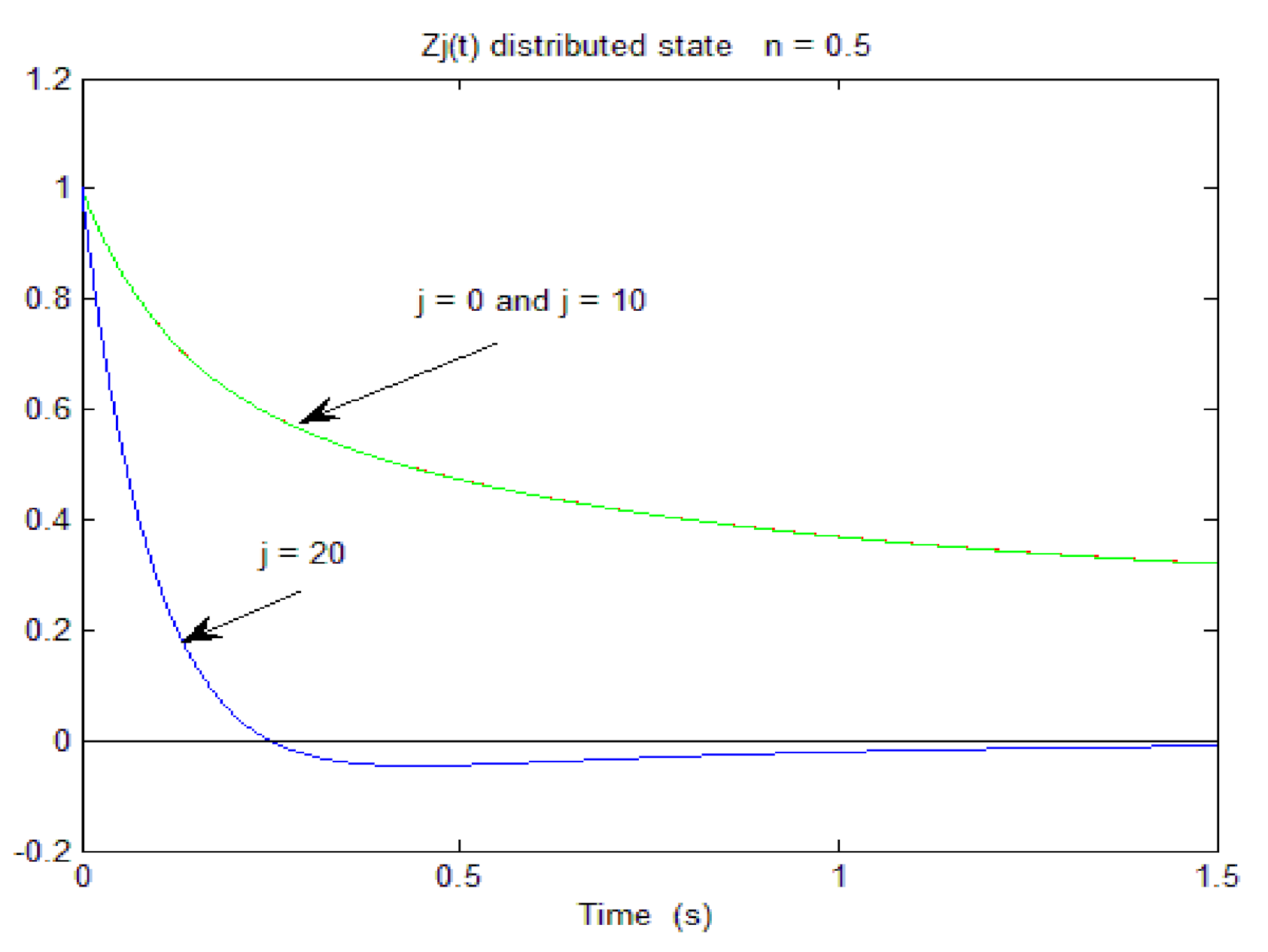
The graphs of $z_j(t)$ and ${\lambda }_j(t)$ are displayed respectively on Figure 3 and Figure 4 for $n\hspace{0.17em}=\hspace{0.17em}0.5 j\hspace{0.17em}=\hspace{0.17em}0 j\hspace{0.17em}=\hspace{0.17em}10 j\hspace{0.17em}=20$.

We can note that the graphs of $z_j(t)$ for $j\hspace{0.17em}=\hspace{0.17em}0$ and $j\hspace{0.17em}=\hspace{0.17em}10$ are very close, which is also verified in the graph of Figure 6 for $n\hspace{0.17em}=\hspace{0.17em}0.5$: since $z_j(0)\hspace{0.17em}=\hspace{0.17em}1 \forall \hspace{0.17em}j$ and according to the dynamics of the modes ${\omega }_j$ for $j\hspace{0.17em}=\hspace{0.17em}0$ and $j\hspace{0.17em}=\hspace{0.17em}10$, the graphs are necessarily very close for $t\hspace{0.17em}\in \hspace{0.17em}[\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}T\hspace{0.17em}]$.

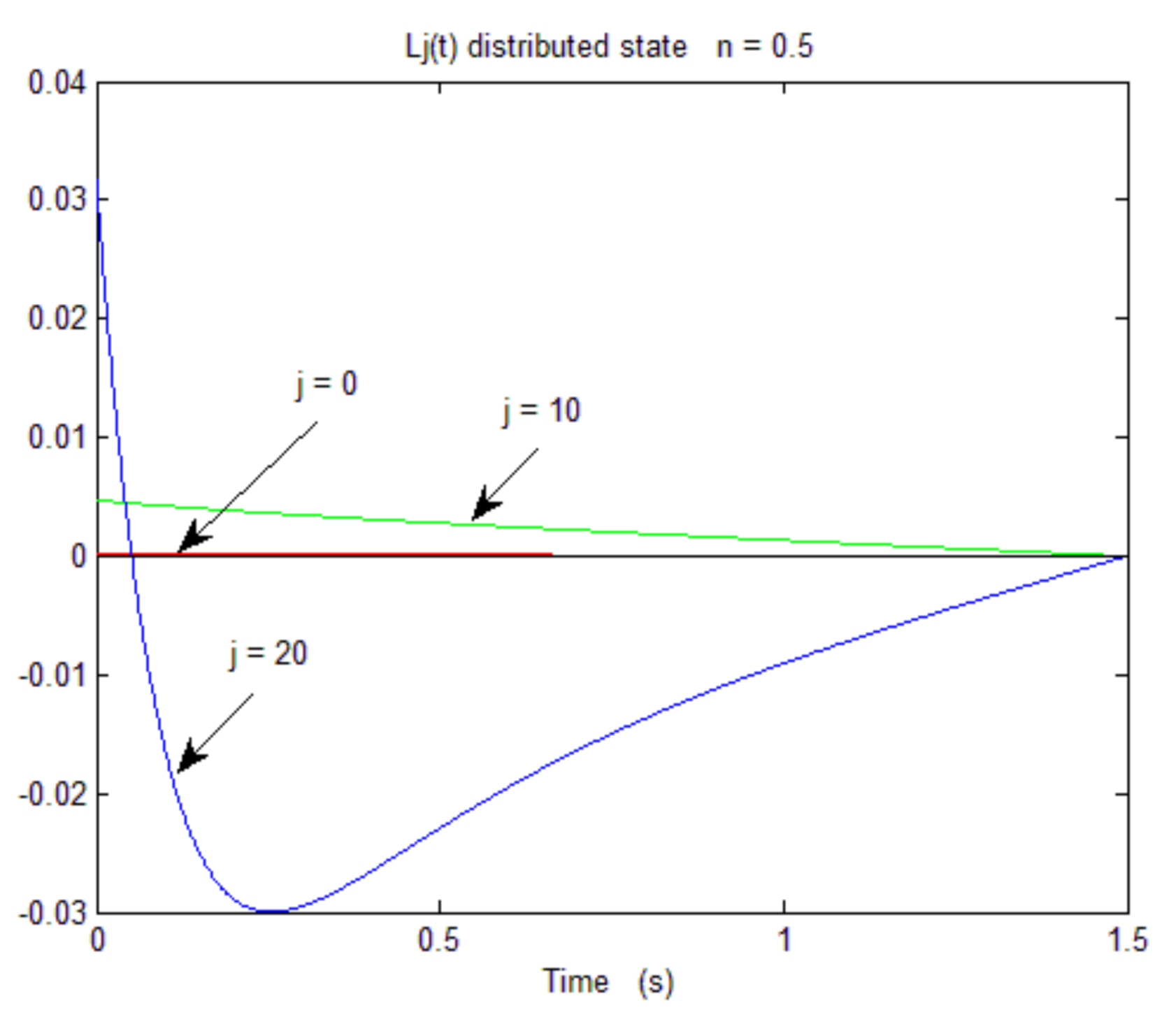
As imposed by the transversality condition (Equation (78)) we can verify that the different graphs of the Lagrange multipliers converge to $0$ for $t\hspace{0.17em}=\hspace{0.17em}T$ on Figure 4, whereas $z_j(T)\hspace{0.17em}\ne \hspace{0.17em}0 \forall \hspace{0.17em}j$ in Figure 3, as expected. This is an illustration of the fractional state control objective as stated in [32] and highlighted in the introduction. Indeed, the transversality condition implies that all of the components ($\lambda (\omega ,t)\hspace{0.17em}\forall \hspace{0.17em}\omega$) of the adjoint system converge to $0$ for $t\hspace{0.17em}=T$. Of course, another objective would be to consider the imposed final state problem, i.e., $z(\omega ,t)\hspace{0.17em}=\hspace{0.17em}z(\omega ,T) \forall \omega \hspace{0.17em}$, which is a classical optimal control problem.

The initial values ${\lambda }_j(0)$, computed by matrix inversion (Equation (82)), are displayed in Figure 5, for j varying from $j\hspace{0.17em}=\hspace{0.17em}0$ to $J\hspace{0.17em}=\hspace{0.17em}Ncel$, for the different values of $n$. We can note in Figure 4 that the graphs of ${\lambda }_j(t)$ are initialized by the corresponding values of ${\lambda }_j(0)$ for $n\hspace{0.17em}=\hspace{0.17em}0.5$.

The final values $z_j(T)$ are displayed on Figure 6 for the different values of $n$: again, we can note as previously for $n\hspace{0.17em}=\hspace{0.17em}0.5$ that the graphs of Figure 3 correspond to $z_j(T)$.

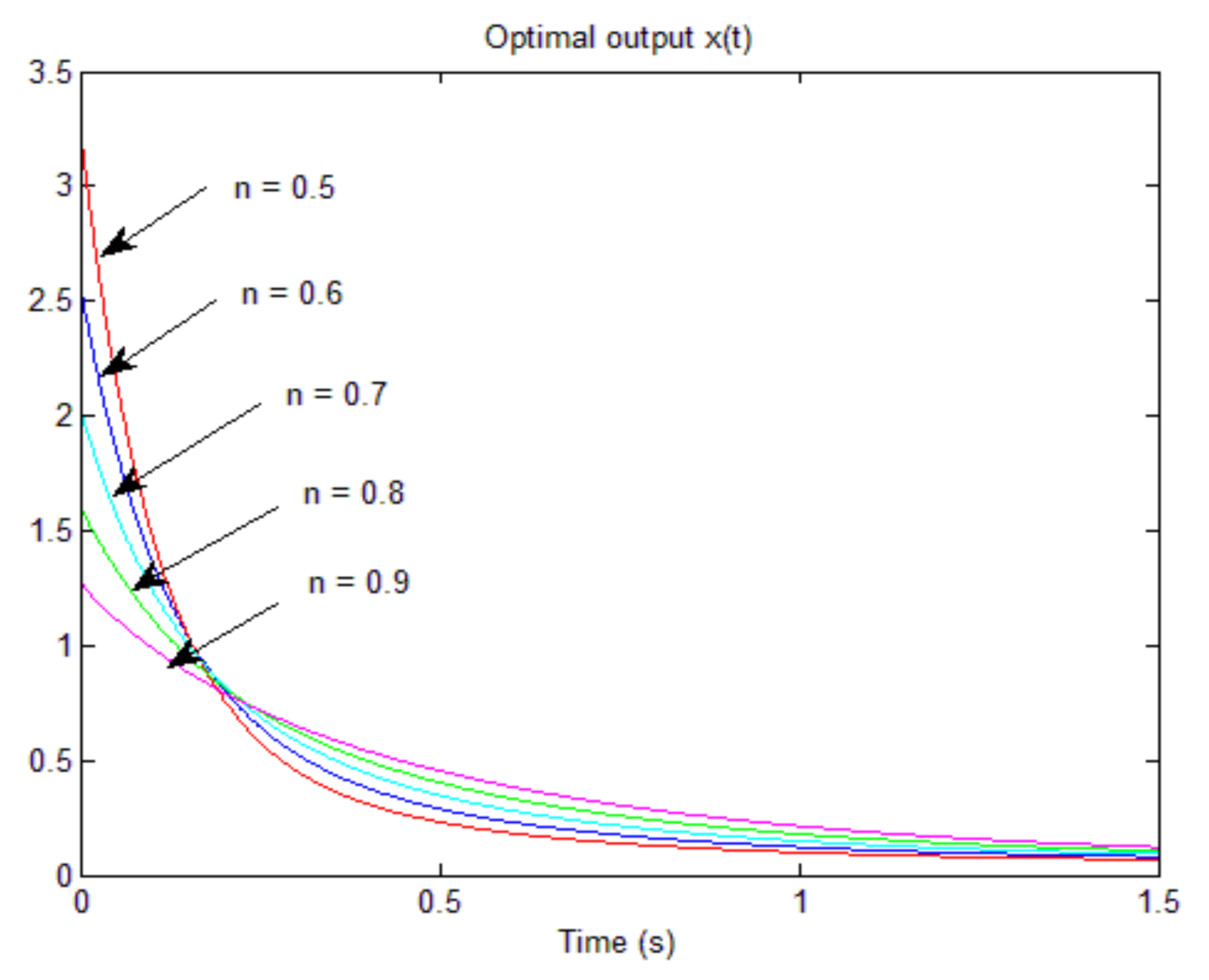
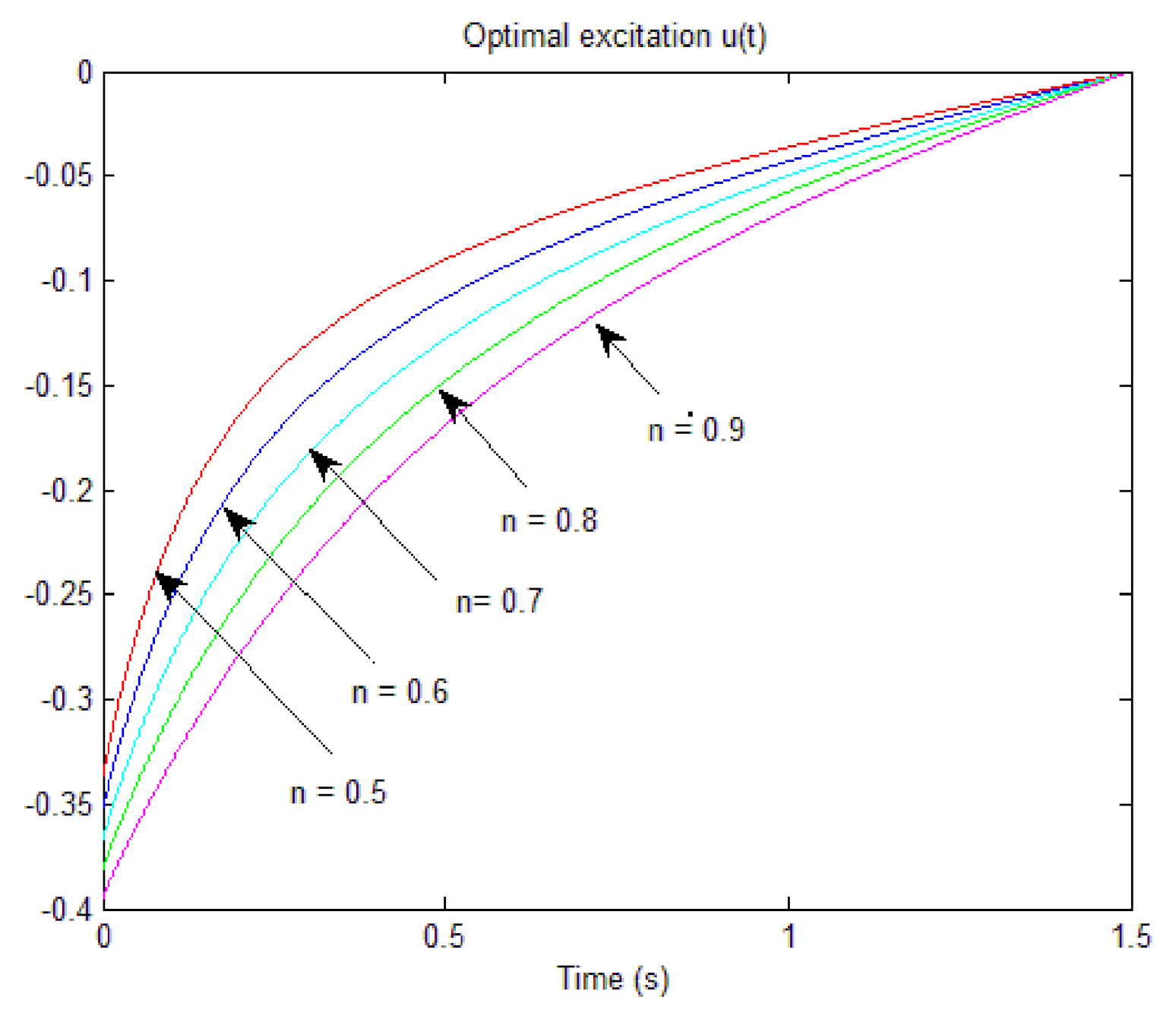
Finally, the graphs of $x(t)$ and $\widehat{u}(t)$ are displayed respectively in Figure 7 and Figure 8 for the different values of $n$. We can note that these graphs (for increasing values of $n$) converge to the corresponding ones of Figure 2 (corresponding to $n\hspace{0.17em}=\hspace{0.17em}1)$.

We can also compare the graphs of $x(t)$ (Figure 3) and $\widehat{u}(t)$ (Figure 4) of the Agrawal paper [9], on page 333, with those obtained by the present approach; we note an important difference between the two methods (particularly for $n\hspace{0.17em}=\hspace{0.17em}0.5$), since the Agrawal technique is based on the pseudo-state variable $x(t)$.

7. Conclusions

Based on the infinite state approach, an alternative theory has been proposed to solve the fractional optimal control problem. The distributed model of the fractional integrator permits to transform any fractional differential equation into a set of infinite dimension integer order differential equations. Contrary to the usual fractional approach, this original formulation is intended to control all the components of the distributed state, instead of the pseudo-state.

The paper develops this new theory in two parts, the first, essentially theoretical part deals with the distributed Euler-Lagrange equations and the optimal control of linear fractional systems, whereas the second part proposes the basics of its practical implementation. A numerical example has demonstrated the feasibility of this alternative theory, but it has also highlighted the difficulties in its practical implementation.

Hence, the solution of many remaining problems will have to be the objective of further research work. The present theory will have to be generalized to the fractional optimal control of nonlinear systems. However, a major research effort will be necessary to provide specific and efficient numerical algorithms for realistic implementation.