Local Convergence and Dynamical Analysis of a Third and Fourth Order Class of Equation Solvers

Abstract

In this article, we suggest the local analysis of a uni-parametric third and fourth order class of iterative algorithms for addressing nonlinear equations in Banach spaces. The proposed local convergence is established using an $\omega$-continuity condition on the first Fréchet derivative. In this way, the utility of the discussed schemes is extended and the application of Taylor expansion in convergence analysis is removed. Furthermore, this study provides radii of convergence balls and the uniqueness of the solution along with the calculable error distances. The dynamical analysis of the discussed family is also presented. Finally, we provide numerical explanations that show the suggested analysis performs well in the situation where the earlier approach cannot be implemented.

1. Introduction

The primary objective of this research is to provide an approximate solution ${\alpha }^{\ast }$ of:

$$\mathcal{F}\left(s\right)=0,$$

(1)

where $\mathcal{F}:\mathcal{O}\subseteq {\mathcal{S}}_1\to {\mathcal{S}}_2$ is a Fréchet derivable operator and $\mathcal{O}\subseteq {\mathcal{S}}_1$ is nonempty, open and convex. ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ are Banach spaces. The requirement for the solutions of nonlinear equations in the form (1) is present in many problems of applied sciences and engineering as a foundation to solve other complicated ones. It is not always possible to determine the exact solutions to this kind of equations, so scientists and researchers frequently use iterative algorithms to approximate the required solution. The most regularly used iterative procedure for addressing (1) is Newton’s scheme that converges quadratically. Over the past several years, numerous authors have developed and are currently improving higher order iterative approaches [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] for solving nonlinear equations.

Local convergence results for different iterative processes have been studied by many authors [18,19,20,21,22,23,24,25,26,27,28], and many important findings have been obtained. In these studies, essential results including convergence radii, measurements on error distances and the extended utility of efficient iterative procedures have been discussed.

In addition, analysis of dynamical characteristics of a class of iterative schemes applied on complex polynomials provides significant results about the stability and reliability of its elements. Researchers such as Amat et al. [29,30], Argyros and Magreñán [19,20], Cordero et al. [31,32,33,34] and others [27,35,36,37] have described complex dynamical behaviors of some famous classes of methods including Jarratt, King, Kim, Chebyshev–Halley, etc.

Recently, Argyros and Magreñán [19] studied the convergence analysis and dynamics of an optimal fourth order family given by:

$$\begin{array}{cc}\hfill t_n& =s_n-\frac{2}{3}\frac{\mathcal{F}\left(s_n\right)}{{\mathcal{F}}^{\prime }\left(s_n\right)},\hfill \\ \hfill s_{n+1}& =s_n-\frac{[({\beta }^2-22\beta -27){\mathcal{F}}^{\prime }\left(s_n\right)+3({\beta }^2+10\beta +5){\mathcal{F}}^{\prime }\left(t_n\right)]\mathcal{F}\left(s_n\right)}{2(\beta {\mathcal{F}}^{\prime }\left(s_n\right)+3{\mathcal{F}}^{\prime }\left(t_n\right))(3(\beta +1){\mathcal{F}}^{\prime }\left(t_n\right)-(\beta +5){\mathcal{F}}^{\prime }\left(s_n\right))},n=0,1,2\dots ,\hfill \end{array}$$

(2)

where $\beta \in \mathbb{C}$. Cordero et al. [34] developed a third and fourth order parametric class of nonlinear equation solvers and studied its stability analysis using a complex dynamics technique.

In this report, our primary aim is to analyze the local convergence and complex dynamical results for a third and fourth order convergent class of iterative procedures. Kou et al. [8] derived a family of iterative algorithms for addressing (1). This family is expressed as follows:

$$\begin{array}{cc}\hfill t_n& =s_n-\frac{2}{3}{\mathcal{F}}^{\prime }{\left(s_n\right)}^{-1}\mathcal{F}\left(s_n\right),\hfill \\ \hfill s_{n+1}& =s_n-\left[I-\frac{3}{4}\mathcal{A}\mathcal{B}\right]{\mathcal{F}}^{\prime }{\left(s_n\right)}^{-1}\mathcal{F}\left(s_n\right),n=0,1,2\dots ,\hfill \end{array}$$

(3)

where $\mathcal{B}={\mathcal{F}}^{\prime }{\left(s_n\right)}^{-1}[{\mathcal{F}}^{\prime }\left(t_n\right)-{\mathcal{F}}^{\prime }\left(s_n\right)]$, $\mathcal{A}=I-\frac{3}{4}\theta \mathcal{B}$ and $\theta \in \mathbb{R}$. The authors [8] also proved that the convergence rate of (3) is at least three, and for $\theta =2$ the convergence order increases to four. Observe that only ${\mathcal{F}}^{\prime }$ is involved in the iterative structure of (3). However, the convergence results of (3) were shown in [8] using conditions on the fourth order derivative. Such convergence criteria [8] restrict the usefulness of these solvers. As an example, we take a function $\mathcal{F}$ defined on $\mathsf{\Omega }=[-\frac{1}{2},\frac{3}{2}]$ by:

$$\mathcal{F}\left(s\right)=\left\{\begin{array}{cc}{s}^{3}ln\left(s^2\right)+s^5-s^4,\hfill & \mathrm{if}s\ne 0\hfill \\ 0,\hfill & \mathrm{if}s=0\hfill \end{array}.\right.$$

(4)

For the above function $\mathcal{F}$, the third derivative ${\mathcal{F}}^{‴}$ is not bounded on its domain $\mathcal{O}$. The convergence theorem for the methods (3) derived in [8] does not work for this problem. Additionally, the authors proved the convergence theorem using the assumption that “if the initial estimation $s_0$ is sufficiently close to the solution $s^{\ast }$, then the sequence of iterates $\left\{s_n\right\}$ converges to $s^{\ast }$”. But how close to the solution $s^{\ast }$ the initial guess $s_0$ should be? The earlier work [8] offers no answer to this question. In other words, no information about the distance between $s_0$ and $s^{\ast }$ was provided for ensuring the convergence of (3). The earlier convergence analysis was established to solve equations only in $\mathbb{R}$. Additionally, complex dynamical analysis was not studied by the authors [8] to extract the stable schemes of the family (3). In this study, we establish the local convergence for the class of methods (3) using a set of conditions only on ${\mathcal{F}}^{\prime }$ in a general Banach space setting. More specifically, the $\omega$-continuity of the first derivative is applied to eliminate the use of higher order derivatives in convergence study. The proposed analysis is useful to address the above discussed problem (4) as well as the problems where higher order derivatives of the involved operator do not exist. This analysis also enables us to apply the methods (3) for solving Banach space valued nonlinear operator equations. Hence, the utility of the family of methods (3) is expanded. This study also provides radii of convergence balls and the uniqueness of the solution along with the calculable error distances. Our technique is so general that it can be used to extend the applicability of other solvers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. These are our motivations for this document. Furthermore, we analyze the dynamical properties of the parametric class (3). This analysis provides an idea to determine such values of the parameter $\theta$ whose corresponding iterative members are numerically stable. Additionally, various chaotic behaviors of the class, such as convergence to n-periodic orbits or attracting strange fixed points and divergence to ∞, are presented using the techniques described in [20,37]. These anomalies are demonstrated with the help of a parameter space and some dynamical planes.

The rest of this document is structured as follows. Section 2 offers the local analysis of the discussed family of methods (3). The dynamical study of this family is explored in Section 3. Numerical illustrations are presented in the final section.

2. Local Convergence Analysis of the Discussed Family of Iterative Algorithms

We establish, with the help of the $\omega$-continuity of ${\mathcal{F}}^{\prime }$, the local convergence of the class of algorithms defined by (3). For $c\in {\mathcal{S}}_1$ and $\rho >0$, we define the following notations:

$$\mathcal{B}(c,\rho )=\{s\in {\mathcal{S}}_1:||c-s||<\rho \},$$

$$\overline{\mathcal{B}}(c,\rho )=\{s\in {\mathcal{S}}_1:\left|\right|c-s\left|\right|\le \rho \}$$

and

$$\mathcal{L}({\mathcal{S}}_1,{\mathcal{S}}_2)=\{\mathcal{T}:{\mathcal{S}}_1\to {\mathcal{S}}_2\mathrm{is}\mathrm{bounded}\mathrm{and}\mathrm{linear}\}.$$

Let $\mathcal{I}=[0,+\infty )$ and suppose there exists a non-decreasing and continuous function ${\omega }_0:\mathcal{I}\to \mathcal{I}$ such that ${\omega }_0\left(0\right)=0$. Let the smallest positive solution ${\mathcal{D}}_0$ of ${\omega }_0\left(y\right)=1$ exist. Set ${\mathcal{I}}_0=[0,{\mathcal{D}}_0)$. Suppose there exist continuous and non-decreasing functions $\omega ,\mathcal{V}:{\mathcal{I}}_0\to \mathcal{I}$ such that $\omega \left(0\right)=0$ and $\frac{1}{3}\mathcal{V}\left(0\right)<1$. We introduce the following functions on the interval ${\mathcal{I}}_0$.

$${\mathcal{J}}_1\left(y\right)=\frac{{\int }_0^1\omega \left((1-\mathcal{X})y\right)d\mathcal{X}+\frac{1}{3}{\int }_0^1\mathcal{V}\left(\mathcal{X}y\right)d\mathcal{X}}{1-{\omega }_0\left(y\right)},$$

(5)

$${\mathcal{H}}_1\left(y\right)={\mathcal{J}}_1\left(y\right)-1,$$

$$\begin{array}{cc}\hfill {\mathcal{J}}_2\left(y\right)& =\frac{1}{1-{\omega }_0\left(y\right)}[{\int }_0^1\omega \left((1-\mathcal{X})y\right)d\mathcal{X}+\frac{3}{4}\left(\frac{\omega \left(({\mathcal{J}}_1\left(y\right)+1)y\right)}{1-{\omega }_0\left(y\right)}\right)\hfill \\ \hfill & \times \left(1+\frac{3}{4}\left|\theta \right|\frac{\omega \left(({\mathcal{J}}_1\left(y\right)+1)y\right)}{1-{\omega }_0\left(y\right)}\right)\times \left({\int }_0^1\mathcal{V}\left(\mathcal{X}y\right)d\mathcal{X}\right)]\hfill \end{array}$$

(6)

and

$${\mathcal{H}}_2\left(y\right)={\mathcal{J}}_2\left(y\right)-1.$$

Then, ${\mathcal{H}}_i\left(0\right)<0$ and ${\mathcal{H}}_i\left(y\right)\to +\infty$ as $y\to {{\mathcal{D}}_0}^{-}$ for $i=1,2$. It is confirmed by applying the intermediate value theorem that the smallest zeros ${\mathcal{D}}_i$ of the functions ${\mathcal{H}}_i$ exist and lie in $(0,{\mathcal{D}}_0)$, where $i=1,2$. Let us denote:

$$\mathcal{R}=min\{{\mathcal{D}}_1,{\mathcal{D}}_2\}.$$

(7)

Hence, we have the following inequalities for each $y\in [0,\mathcal{R})$:

$$0\le {\mathcal{J}}_1\left(y\right)<1$$

(8)

and

$$0\le {\mathcal{J}}_2\left(y\right)<1.$$

(9)

Furthermore, we assume that the following hold true for the Fréchet derivable operator $\mathcal{F}:\mathcal{O}\subset {\mathcal{S}}_1\to {\mathcal{S}}_2$:

$$\mathcal{F}\left({\alpha }^{\ast }\right)=0,{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}\in \mathcal{L}({\mathcal{S}}_2,{\mathcal{S}}_1),$$

(10)

$$\left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }\left(s\right)-{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right))\left|\right|\le {\omega }_0\left(\right||s-{\alpha }^{\ast }\left|\right|),\forall s\in \mathcal{O},$$

(11)

$$\left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }\left(s\right)-{\mathcal{F}}^{\prime }\left(t\right))\left|\right|\le \omega \left(\right||s-t\left|\right|),\forall s,t\in {\mathcal{O}}_0:=\mathcal{O}\cap \mathcal{B}({\alpha }^{\ast },{\mathcal{D}}_0)$$

(12)

and

$$\left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}{\mathcal{F}}^{\prime }\left(s\right)\left|\right|\le \mathcal{V}\left(\right||s-{\alpha }^{\ast }\left|\right|),\forall s\in {\mathcal{O}}_0.$$

(13)

Next, we discuss the local convergence theorem for the family (3).

Theorem 1.

Suppose $\mathcal{F}:\mathcal{O}\subseteq {\mathcal{S}}_1\to {\mathcal{S}}_2$ is Fréchet derivable and ${\alpha }^{\ast }\in \mathcal{O}$. Let $\mathcal{F}$ obey the conditions defined in (10)–(13) and:

$$\overline{\mathcal{B}}({\alpha }^{\ast },\mathcal{R})\subseteq \mathcal{O}.$$

(14)

Then, for any starter $s_0\in \mathcal{B}({\alpha }^{\ast },\mathcal{R})$, the sequence of iterates ${\left\{s_n\right\}}_{n\ge 0}$ constructed by the class of algorithms (3) is well defined, ${\left\{s_n\right\}}_{n\ge 0}\in \mathcal{B}({\alpha }^{\ast },\mathcal{R})$ and ${\displaystyle \underset{n\to \infty }{lim}\left|\right|s_n-{\alpha }^{\ast }\left|\right|=0}$. Moreover, the following items are true for all $n\ge 0$:

$$\left|\right|t_n-{\alpha }^{\ast }\left|\right|\le {\mathcal{J}}_1\left(\right||s_n-{\alpha }^{\ast }\left|\right|\left)\right||s_n-{\alpha }^{\ast }\left|\right|<\left|\right|s_n-{\alpha }^{\ast }\left|\right|<\mathcal{R}$$

(15)

and

$$\left|\right|s_{n+1}-{\alpha }^{\ast }\left|\right|\le {\mathcal{J}}_2\left(\right||s_n-{\alpha }^{\ast }\left|\right|\left)\right||s_n-{\alpha }^{\ast }\left|\right|<\left|\right|s_n-{\alpha }^{\ast }\left|\right|<\mathcal{R},$$

(16)

where the functions ‘$\mathcal{J}$’ are discussed in Equations (5) and (6). In addition, if there exist ${\mathcal{D}}_3\ge \mathcal{R}$ such that:

$${\int }_0^1{\omega }_0\left(\mathcal{X}{\mathcal{D}}_3\right)d\mathcal{X}<1,$$

(17)

then ${\alpha }^{\ast }$ satisfies Equation (1) uniquely in ${\mathcal{O}}_1:=\mathcal{O}\cap \overline{\mathcal{B}}({\alpha }^{\ast },{\mathcal{D}}_3)$.

Proof. 

Let $a\in \mathcal{B}({\alpha }^{\ast },\mathcal{R})$. Using Equations (7) and (11), we obtain:

$$\left|\right|F^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}(F^{\prime }\left(a\right)-F^{\prime }\left({\alpha }^{\ast }\right))\left|\right|\le {\omega }_0\left(\right||a-{\alpha }^{\ast }\left|\right|)<{\omega }_0\left(\mathcal{R}\right)<1.$$

(18)

Equation (18) together with the Banach lemma on invertible operators [1,2,13,16] imply that:

$$\left|\right|{\mathcal{F}}^{\prime }{\left(a\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\le \frac{1}{1-{\omega }_0\left(\right||a-{\alpha }^{\ast }\left|\right|)}<\frac{1}{1-{\omega }_0\left(\mathcal{R}\right)}.$$

(19)

It also follows from Formula (3) for $n=0$ that $t_0$ is well defined. We also have from (3):

$$\begin{array}{cc}{t}_0-{\alpha }^{\ast }\hfill & =s_0-{\alpha }^{\ast }-{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}\mathcal{F}\left(s_0\right)+\frac{1}{3}{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}\mathcal{F}\left(s_0\right)\hfill \\ & =-\left[{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\right]\left[{\int }_0^1{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }({\alpha }^{\ast }+\mathcal{X}(s_0-{\alpha }^{\ast }))-{\mathcal{F}}^{\prime }\left(s_0\right))(s_0-{\alpha }^{\ast })d\mathcal{X}\right]\hfill \\ & +\frac{1}{3}{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}\mathcal{F}\left(s_0\right).\hfill \end{array}$$

(20)

Then, we deduce using (3), (7), (8), (11), (19) (for $a=s_0$) and (20),

$$\begin{array}{cc}\left|\right|t_0-{\alpha }^{\ast }\left|\right|\hfill & \le \left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\left|\right|{\int }_0^1{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }({\alpha }^{\ast }+\mathcal{X}(s_0-{\alpha }^{\ast }))-{\mathcal{F}}^{\prime }\left(s_0\right))(s_0-{\alpha }^{\ast })d\mathcal{X}\left|\right|\hfill \\ & +\frac{1}{3}\left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}\mathcal{F}\left(s_0\right)\left|\right|\hfill \\ & \le \left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\left|\right|{\int }_0^1{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }({\alpha }^{\ast }+\mathcal{X}(s_0-{\alpha }^{\ast }))-{\mathcal{F}}^{\prime }\left(s_0\right))(s_0-{\alpha }^{\ast })d\mathcal{X}\left|\right|\hfill \\ & +\frac{1}{3}\left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}\mathcal{F}\left(s_0\right)\left|\right|\hfill \\ & \le \frac{{\int }_0^1\omega \left((1-\mathcal{X})\right||s_0-{\alpha }^{\ast }\left|\right|\left)d\mathcal{X}\right||s_0-{\alpha }^{\ast }\left|\right|}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}+\frac{1}{3}\frac{{\int }_0^1\mathcal{V}\left(\mathcal{X}\right||s_0-{\alpha }^{\ast }\left|\right|\left)d\mathcal{X}\right||s_0-{\alpha }^{\ast }\left|\right|}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\hfill \\ & =\left[\frac{{\int }_0^1\omega \left((1-\mathcal{X})\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}+\frac{1}{3}{\int }_0^1\mathcal{V}\left(\mathcal{X}\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\right]\left|\right|s_0-{\alpha }^{\ast }\left|\right|\hfill \\ & ={\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|\left)\right||s_0-{\alpha }^{\ast }\left|\right|<\left|\right|s_0-{\alpha }^{\ast }\left|\right|<\mathcal{R}.\hfill \end{array}$$

(21)

Hence, (15) holds for $n=0$. Next, we find a bound for $\left|\right|\mathcal{B}\left|\right|$. We use Equations (12), (19) (for $a=s_0$) and (21) to obtain:

$$\begin{array}{cc}\hfill \left|\right|\mathcal{B}\left|\right|& =\left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}({\mathcal{F}}^{\prime }{\left(t_0\right)}^{-1}-{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1})\left|\right|\hfill \\ \hfill & \le \left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }{\left(t_0\right)}^{-1}-{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1})\left|\right|\hfill \\ \hfill & \le \frac{\omega \left(\right||t_0-s_0|\left|\right)}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\hfill \\ \hfill & \le \frac{\omega \left(\right||t_0-{\alpha }^{\ast }||+||s_0-{\alpha }^{\ast }|\left|\right)}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\hfill \\ \hfill & \le \frac{\omega ({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|\left)\right||s_0-{\alpha }^{\ast }\left|\right|+\left|\right|s_0-{\alpha }^{\ast }\left|\right|)}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\hfill \\ \hfill & =\frac{\omega \left[\right({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|)+1\left)\right||s_0-{\alpha }^{\ast }\left|\right|]}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}.\hfill \end{array}$$

(22)

It follows from the above inequality that:

$$\left|\right|\mathcal{A}\left|\right|\le 1+\frac{3}{4}\left|\theta \right|\frac{\omega \left[\right({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|)+1\left)\right||s_0-{\alpha }^{\ast }\left|\right|]}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}.$$

(23)

Additionally, $s_1$ is well defined by virtue of Equation (19). Next, we use (3), (6), (7), (9), (12), (19) (for $a=s_0$), (21), (22) and (23) to establish:

$$\begin{array}{cc}& \left|\right|s_1-{\alpha }^{\ast }\left|\right|\hfill \\ & \le \left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\left|\right|{\int }_0^1{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}({\mathcal{F}}^{\prime }({\alpha }^{\ast }+\mathcal{X}(s_0-{\alpha }^{\ast }))-{\mathcal{F}}^{\prime }\left(s_0\right))(s_0-{\alpha }^{\ast })d\mathcal{X}\left|\right|\hfill \\ \hfill & +\frac{3}{4}\left|\right|\mathcal{A}\left|\right|\left|\right|\mathcal{B}\left|\right|\left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}\mathcal{F}\left(s_0\right)\left|\right|\hfill \\ \hfill & \le \frac{{\int }_0^1\omega \left((1-\mathcal{X})\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\hfill \\ \hfill & +\frac{3}{4}\left|\right|\mathcal{A}\left|\right|\left|\right|\mathcal{B}\left|\right|\left|\right|{\mathcal{F}}^{\prime }{\left(s_0\right)}^{-1}{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right)\left|\right|\left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}\mathcal{F}\left(s_0\right)\left|\right|\hfill \\ \hfill & \le \frac{{\int }_0^1\omega \left((1-\mathcal{X})\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\hfill \\ \hfill & +\frac{3}{4}\left(1+\frac{3}{4}\left|\theta \right|\frac{\omega \left[\right({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|)+1\left)\right||s_0-{\alpha }^{\ast }\left|\right|]}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\right)\hfill \\ \hfill & \times \left(\frac{\omega \left[\right({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|)+1\left)\right||s_0-{\alpha }^{\ast }\left|\right|]}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\right)\hfill \\ \hfill & \times \left(\frac{{\int }_0^1\mathcal{V}\left(\mathcal{X}\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\right)\hfill \\ \hfill & \le \frac{1}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}[{\int }_0^1\omega \left((1-\mathcal{X})\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}\hfill \\ \hfill & +\frac{3}{4}\left(1+\frac{3}{4}\left|\theta \right|\frac{\omega \left[\right({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|)+1\left)\right||s_0-{\alpha }^{\ast }\left|\right|]}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\right)\hfill \\ \hfill & \times \left(\frac{\omega \left[\right({\mathcal{J}}_1\left(\right||s_0-{\alpha }^{\ast }\left|\right|)+1\left)\right||s_0-{\alpha }^{\ast }\left|\right|]}{1-{\omega }_0\left(\right||s_0-{\alpha }^{\ast }\left|\right|)}\right)\times \left({\int }_0^1\mathcal{V}\left(\mathcal{X}\right||s_0-{\alpha }^{\ast }\left|\right|)d\mathcal{X}\right)]\hfill \\ \hfill & ={\mathcal{J}}_3\left(\right||s_0-{\alpha }^{\ast }\left|\right|\left)\right||s_0-{\alpha }^{\ast }\left|\right|<\left|\right|s_0-{\alpha }^{\ast }\left|\right|<\mathcal{R}.\hfill \end{array}$$

This validates the estimate (16) for $n=0$. The induction for the estimates (15) and (16) is completed for $n=0$. Assuming that (15) and (16) hold true for all $j=1,2,\dots ,n-1$ and then by replacing the estimations, we show the items (15) and (16) are true for $j=n$. From the estimation $\left|\right|s_{n+1}-{\alpha }^{\ast }\left|\right|\le {\mathcal{J}}_2\left(\mathcal{R}\right)\left|\right|s_n-{\alpha }^{\ast }\left|\right|<\mathcal{R}$, we derive that $s_{n+1}\in \mathcal{B}({\alpha }^{\ast },\mathcal{R})$ and ${\displaystyle \underset{n\to \infty }{lim}\left|\right|s_n-{\alpha }^{\ast }\left|\right|=0}$. Let there exist $c^{\ast }(\ne {\alpha }^{\ast })\in {\mathcal{O}}_1$ such that $\mathcal{F}\left(c^{\ast }\right)=0$. Consider $\mathcal{W}={\int }_0^1{\mathcal{F}}^{\prime }({\alpha }^{\ast }+\mathcal{X}(c^{\ast }-{\alpha }^{\ast }))d\mathcal{X}$. From (11) and (17), we obtain:

$$\begin{array}{cc}\hfill \left|\right|{\mathcal{F}}^{\prime }{\left({\alpha }^{\ast }\right)}^{-1}(\mathcal{W}-{\mathcal{F}}^{\prime }\left({\alpha }^{\ast }\right))\left|\right|& \le {\int }_0^1{\omega }_0\left(\mathcal{X}\right||c^{\ast }-{\alpha }^{\ast }\left|\right|)d\mathcal{X}\hfill \\ \hfill & \le {\int }_0^1{\omega }_0\left(\mathcal{X}{\mathcal{D}}_3\right)d\mathcal{X}<1,\hfill \end{array}$$

and this confirms that ${\mathcal{W}}^{-1}\in \mathcal{L}({\mathcal{S}}_2,{\mathcal{S}}_1)$. We obtain ${\alpha }^{\ast }=c^{\ast }$ due to the invertability of $\mathcal{W}$ and the identity $0=\mathcal{F}\left({\alpha }^{\ast }\right)-\mathcal{F}\left(c^{\ast }\right)=\mathcal{W}({\alpha }^{\ast }-c^{\ast })$. □

3. Complex Dynamics of the Discussed Class of Methods

In this section, the complex dynamical analysis of the class (3)is carried out. When analyzing an iterative formula, convergence analysis is not the only required matter to study. The effectiveness of an algorithm also depends on other components, such as verifying how it performs on the basis of the chosen starting points. That is, how large the set of starting points is for which the scheme converges to a solution. For this reason, a wide range of tools are required for a more extensive analysis.

In the research of iterative procedures, the dynamical analysis of a family of iterative algorithms is now gaining increasing interest because it enables separating different iterative approaches in terms of their rate of convergence. It also allows for evaluating their behavior depending on the chosen starting point. This analysis helps one to visualize the set of initial estimates that converge to a root of the equation or other points. Furthermore, it demonstrates the reliability and productiveness of the iterative process.

This research investigates the complex dynamical behavior of the class of methods (3) on a polynomial $N\left(z\right):\mathbb{C}\to \mathbb{C}$ defined by $N\left(z\right)=(z-v_1)(z-v_2)$. We discuss the detailed study of the fixed points and their stability employing MATHEMATICA software [19,20]. In addition, a parameter space and various dynamical planes were constructed and analyzed to show the chaotic nature of the considered family.

We applied the class of schemes (3) on the polynomial $N\left(z\right)=(z-v_1)(z-v_2)$, where $v_1\ne v_2$. Then, we considered the Möbius map $\mathcal{M}\left(z\right)=\frac{z-v_1}{z-v_2}$ with the properties $\mathcal{M}\left(v_1\right)=0$, $\mathcal{M}\left(v_2\right)=\infty$ and $\mathcal{M}(\infty )=1$ to deduce the rational operator:

$${\mathcal{P}}_N(z,\theta )=z^3\frac{z^3+4z^2+5z+2-\theta }{(2-\theta )z^3+5z^2+4z+1},\theta \in \mathbb{C}.$$

(24)

related to the class of algorithms (3).

3.1. Study of Fixed Points and Their Stability

The fixed points of the operator ${\mathcal{P}}_N(z,\theta )$ are obtained by solving the equation ${\mathcal{P}}_N(z,\theta )=z$. The points $z=0$ and $z=\infty$ are superattracting fixed points of ${\mathcal{P}}_N(z,\theta )$ as they are related to $v_1$ and $v_2$, respectively. According to the definition, $z=1$ is a strange fixed point. Moreover, depending on $\theta$, there exist another four strange fixed points. These points can be expressed as follows:

1.

$ex{f}_1\left(\theta \right)=-\frac{5}{4}+\frac{1}{4}\sqrt{1-4\theta }+\frac{1}{4}\sqrt{10-10\sqrt{1-4\theta }-4\theta }$

2.

$ex{f}_2\left(\theta \right)=-\frac{5}{4}+\frac{1}{4}\sqrt{1-4\theta }-\frac{1}{4}\sqrt{10-10\sqrt{1-4\theta }-4\theta }$

3.

$ex{f}_3\left(\theta \right)=-\frac{5}{4}-\frac{1}{4}\sqrt{1-4\theta }+\frac{1}{4}\sqrt{10+10\sqrt{1-4\theta }-4\theta }$

4.

$ex{f}_4\left(\theta \right)=-\frac{5}{4}-\frac{1}{4}\sqrt{1-4\theta }-\frac{1}{4}\sqrt{10+10\sqrt{1-4\theta }-4\theta }$

These strange fixed points are presented in Figure 1 for $ex{f}_j\in \mathbb{R}$, $j=1,2,3,4$.

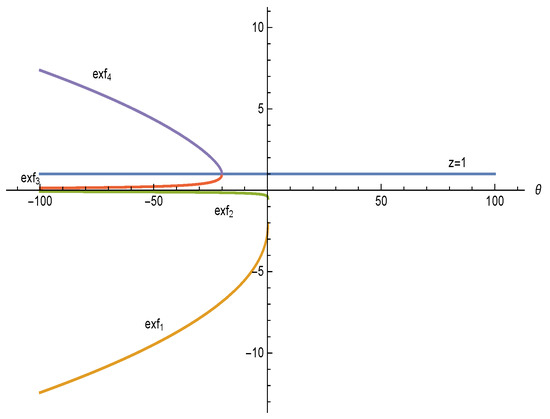
Figure 1. Behavior of the strange fixed points.

The relations among $ex{f}_j\left(\theta \right)$ ($j=1,2,3,4$) are discussed below.

Lemma 1.

The fixed point operator ${\mathcal{P}}_N(z,\theta )$ has five simple strange fixed points except in the following situations:

(i) 

If $\theta =0$, then ${\mathcal{P}}_N(z,\theta )$ has three strange fixed points.

(ii) 

If $\theta =-20$, then $ex{f}_1\left(\theta \right)=ex{f}_2\left(\theta \right)=1$ and the number of strange fixed points is three.

(iii) 

If $\theta =\frac{1}{4}$, then $ex{f}_1\left(\theta \right)=ex{f}_3\left(\theta \right)=-\frac{1}{2}$ and $ex{f}_2\left(\theta \right)=ex{f}_4\left(\theta \right)=-2$. Hence the number of strange fixed points of ${\mathcal{P}}_N(z,\theta )$ is three.

Furthermore, $ex{f}_1\left(\theta \right)=\frac{1}{ex{f}_2\left(\theta \right)}$ and $ex{f}_3\left(\theta \right)=\frac{1}{ex{f}_4\left(\theta \right)}$ for all values of the parameter θ.

To analyze the stability of these strange fixed points and obtain the critical points, we require the first order derivative of ${\mathcal{P}}_N(z,\theta )$. The simplified expression of the differentiated operator is:

$${\mathcal{P}}_N^{\prime }(z,\theta )=-\frac{3z^2{(z+1)}^4((\theta -2)z^2+(-\frac{4}{3}\theta -4)z+\theta -2)}{{(1+(2-\theta )z^3+5z^2+4z)}^2}.$$

(25)

It is easy to observe from Equation (25) that the superattracting fixed points of ${\mathcal{P}}_N(z,\theta )$ are $z=0$ and $z=\infty$. The stability analysis of $z=1$ and $z=ex{f}_j\left(\theta \right),j=1,2,3,4$ will be provided in a different approach. We begin with investigating the stability of $z=1$. This fixed point is associated with the convergence to ∞. We denote the stability function $|{\mathcal{P}}_N^{\prime }(1,\theta )|$ of the fixed point $z=1$ by $S{t}_1\left(\theta \right)$. Using Equation (25), we get:

$$S{t}_1\left(\theta \right)=\left|\frac{32}{\theta -12}\right|$$

(26)

Theorem 2.

The strange fixed point $z=1$ is categorized as follows:

1. 

If $|\theta -12|>32$, then $z=1$ is attracting. In addition, it cannot be superattracting for any value of θ.

2. 

If $|\theta -12|=32$, then $z=1$ is a parabolic fixed point.

3. 

$z=1$ is a repulsor when $|\theta -12|<32$.

Therefore, the stability zone of $z=1$ is the region on $\mathbb{C}$ where $|\theta -12|\ge 32$. This stability zone is presented graphically in Figure 2.

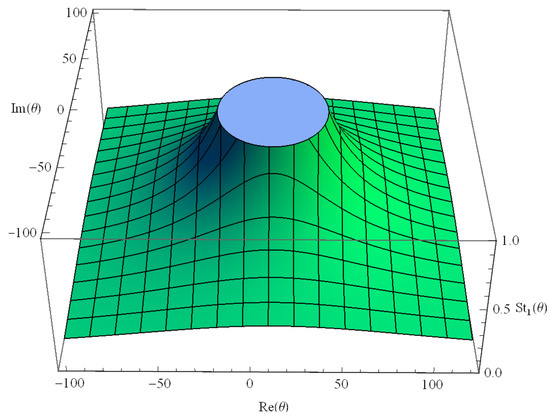
Figure 2. Stability region of $z=1$.

It is incredibly challenging to determine the stability of other fixed points ($ex{f}_j,j=1,2,3,4$) analytically. However, we have used the graphical tool MATHEMATICA to display the stability zones for these points. It is noticed that the stability of $ex{f}_1\left(\theta \right)$ and $ex{f}_2\left(\theta \right)$ is the same. The stability regions of the strange fixed points $ex{f}_1\left(\theta \right)$ and $ex{f}_2\left(\theta \right)$ are presented in the Figure 3a,b, respectively. For the fixed points $ex{f}_3\left(\theta \right)$ and $ex{f}_4\left(\theta \right)$, corresponding stability functions are demonstrated in Figure 4a,b, respectively.

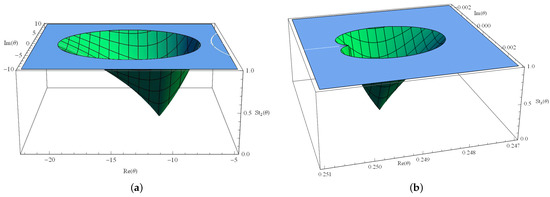
Figure 3. Stability regions. (a) Stability region of $ex{f}_1\left(\theta \right)$ and $ex{f}_2\left(\theta \right)$, (b) Stability region of $ex{f}_1\left(\theta \right)$ and $ex{f}_2\left(\theta \right)$.

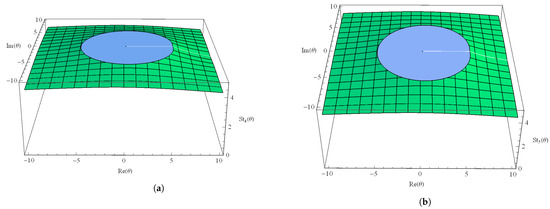
Figure 4. Stability functions. (a) Stability function for $ex{f}_3\left(\theta \right)$, (b) Stability function for $ex{f}_4\left(\theta \right)$.

Considering the stability regions presented in the Figure 3 and Figure 4, the following results are established.

Theorem 3.

In terms of stability, the strange fixed points $ex{f}_j\left(\theta \right),j=1,2,3,4$ are characterized as follows:

1. 

The stability of $ex{f}_1\left(\theta \right)$ and $ex{f}_2\left(\theta \right)$ is the same. In detail,

   * If $\theta \in \{-10.69380\dots ,0.24936\dots \}$, then both fixed points are superattractive fixed points.

    * Additionally, these fixed points are attractors if θ lies in the oval or cardioid presented in Figure 3a,b, respectively.

2. 

The fixed points $ex{f}_3\left(\theta \right)$ and $ex{f}_4\left(\theta \right)$ are always repulsive in nature for any value of θ, and this can be observed in Figure 4a,b, respectively.

3.2. Study of Critical Points and Parameter Spaces

We next discuss the critical points of the class (3) with the parameter space. We obtained the critical points of ${\mathcal{P}}_N(z,\theta )$ by solving ${\mathcal{P}}_N^{\prime }(z,\theta )=0$. It is clear from (25) that 0 and ∞ are critical points of ${\mathcal{P}}_N(z,\theta )$ that are associated with $v_1$ and $v_2$, respectively. The point $z=-1$ is a free critical point of ${\mathcal{P}}_N(z,\theta )$. The other free critical points are represented by $fc{r}_j\left(\theta \right),j=1,2$. The expressions of these free critical points $fc{r}_j\left(\theta \right)$ are as follows:

1.

$fc{r}_1\left(\theta \right)=\frac{1}{3}\frac{2\theta +6+\sqrt{-5{\theta }^2+60\theta }}{\theta -2}$

2.

$fc{r}_2\left(\theta \right)=\frac{1}{3}\frac{2\theta +6-\sqrt{-5{\theta }^2+60\theta }}{\theta -2}$

The number of free critical points of ${\mathcal{P}}_N(z,\theta )$ depends on $\theta$, as summarized below.

Lemma 2.

(i) 

If $\theta \in \{0,2,12\}$, then the number of distinct free critical points of ${\mathcal{P}}_N(z,\theta )$ is one.

(ii) 

For the rest of scenarios, the operator ${\mathcal{P}}_N(z,\theta )$ has three distinct free critical points.

We observe that $fc{r}_1\left(\theta \right)=\frac{1}{fc{r}_2\left(\theta \right)}$. Hence, $fc{r}_1\left(\theta \right)$ and $fc{r}_2\left(\theta \right)$ are not independent. This is why we present the parameter plane related to $fc{r}_1\left(\theta \right)$. The behavior of $z=-1$ and $fc{r}_j\left(\theta \right)$ (when $fc{r}_j\in \mathbb{R}$, $j=1,2$) is provided in Figure 5.

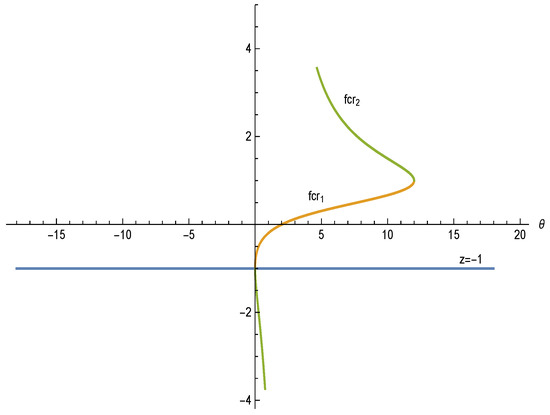
Figure 5. Behavior of free critical points.

The dynamical properties of the considered family (3) were analyzed using the procedure discussed in [19,20]. The parameter space associated to $fc{r}_1\left(\theta \right)$ is given in Figure 6. The detailed views of this parameter space are displayed in Figure 7a,b. The free critical point $z_0=fc{r}_1\left(\theta \right)$ was considered as a stating estimation for the iterative processes of the class. We applied different colors on the initial choice $z_0$ according to the convergence of the corresponding sequence of iterates. Cyan is used to show the convergence of the iteration sequence to 0 (related to $v_1$) or ∞ (related to the $v_2$). We assigned the yellow color to $z_0$ to show the convergence to $z=1$ (related to ∞). We executed a maximum of 2000 iterations with ${10}^{-6}$ as the error tolerance. Moreover, the magenta color indicates the convergence to $ex{f}_j\left(\theta \right),j=1,2,3,4$. Convergences to n-periodic orbits for $n=2,3,4\dots ,8$ are displayed in other colors, including light green, orange, blue, dark orange, dark green, dark red and white, respectively. For $n\ge 9$ the n-periodic orbits are shown in black. In the parameter plane, the points that are not painted with cyan colors are not the appropriate choices for $\theta$ from the numerical point of view. In these zones, the iteration converges to any of the $ex{f}_j\left(\theta \right),j=1,2,3,4$ or to attracting n-periodic orbits or even to ∞. In addition, one can find broad regions where the points are displayed in cyan. This verifies that some iterative procedures of the discussed family are numerically stable.

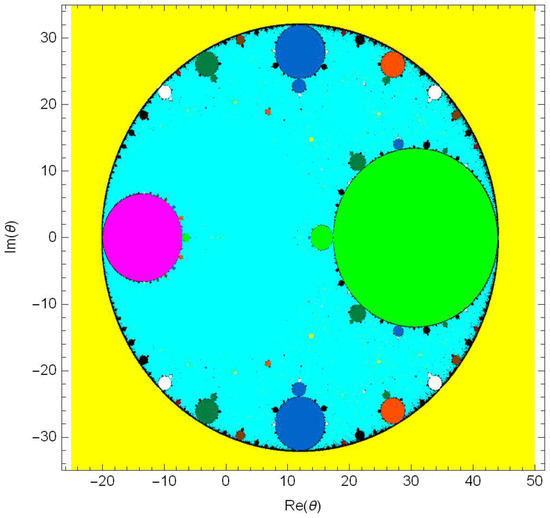
Figure 6. Parameter plane associated with the free critical point $fc{r}_1\left(\theta \right)$.

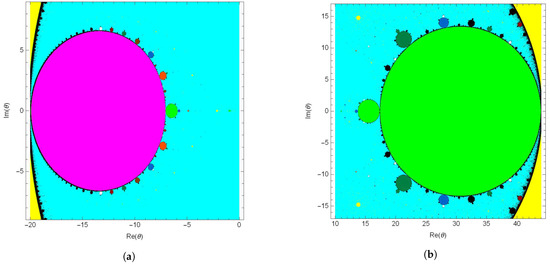
Figure 7. (a,b) Detailed views of the parameter plane associated with $fc{r}_1\left(\theta \right)$.

Next, we provide dynamical planes to display some of the detected anomalies. In these figures, we use cyan and red to demonstrate the convergence to 0 and ∞, respectively. Black indicates that the iterative member of the family (3) does not converge to either 0 or ∞ with the tolerance error ${10}^{-6}$ and at most 1000 iterations. In the dynamical planes shown in Figure 8a,b, we have used yellow to present the convergence of the iterative member to the strange fixed point $z=1$. In Figure 8c,d, attracting strange fixed points $ex{f}_1$ and $ex{f}_2$ appear, which are displayed in magenta and green, respectively.

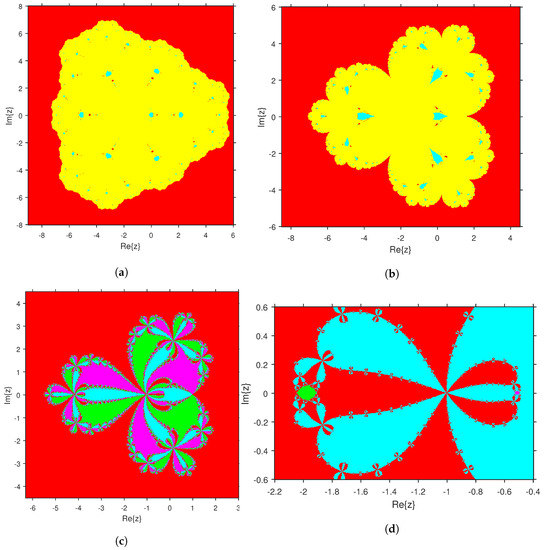
Figure 8. Dynamical Planes. (a) θ = 44.5, (b) θ = −22, (c) θ = −10, (d) θ = 0.249.

In Figure 9a, the dynamical plane related to a scheme of the discussed family (for $\theta =20$) shows the appearance of an attracting 2-cycle $\{0.6143+0.7891i,0.6143-0.7891i\}$. Moreover, various attracting 2-periodic orbits are given in Figure 9b,c. In Figure 9b, the existence of two 2-periodic orbits $\{0.2674-0.9636i,-0.0854-0.9963i\}$ and $\{0.2674+0.9636i,-0.0854+0.9963i\}$ is seen. Additionally, the 2-cycles $\{0.0015-1.0000i,0.9001+0.4357i\}$ and $\{0.0015+1.0000i,0.9001-0.4357i\}$ are presented in Figure 9c. The occurrence of an attracting 3-cycle is provided in Figure 9d. The convergence to n-cycles is presented in black, since this convergence is not related to $v_1$ and $v_2$.

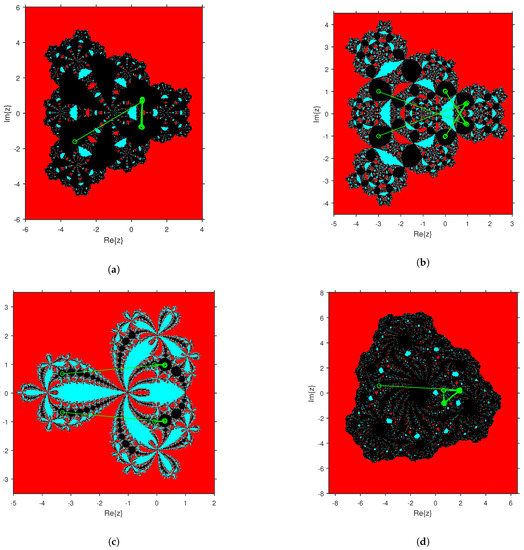
Figure 9. Dynamical Planes. (a) θ = 20, (b) θ = 15.5, (c) θ = −6.5, (d) θ = 25 − 26i.

At the end, we provide dynamical planes for $\theta =-0.5$, $\theta =0$, $\theta =0.2$ and $\theta =2$ in Figure 10a–d, respectively. The attraction basins in these planes are related to $v_1$ or $v_2$ only; as a consequence, the corresponding elements of the considered family are numerically stable. Thus, these methods are preferable over other elements of the family in most numerical applications.

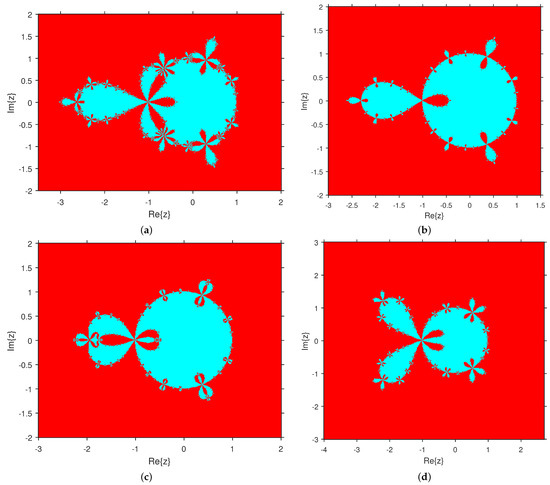
Figure 10. Dynamical planes. (a) $\theta =-0.5$, (b) $\theta =0$, (c) $\theta =0.2$, (d) $\theta =2$.

4. Numerical Examples

In this section, we discuss numerical problems to demonstrate the efficacy of our theoretical findings. In these examples, we apply the proposed results to calculate the convergence radius of four methods derived from the discussed family (3) by using $\theta =-0.5$, $\theta =0$, $\theta =0.2$ and $\theta =2$. Notice that no iterative method is used to find the radius $\mathcal{R}$. However, only Formula (7) is related to the solutions of scalar equations. Iterative method (3) is not used, since the solutions are known. The obtained radii show the degree of difficulty in choosing initial points.

Example 1.

[22] Let $\mathcal{F}$ be defined on ${\mathbb{R}}^3$ for ${(s_1,s_2,s_3)}^t$ by:

$$\mathcal{F}\left(s\right)={(10s_1+sin(s_1+s_2)-1,8s_2-{cos}^2(s_3-s_2)-1,12s_3+sin\left(s_3\right)-1)}^t$$

We have ${\alpha }^{\ast }={(0.0689783491\dots ,0.2464424186\dots ,0.0769289119\dots )}^t$, ${\omega }_0\left(y\right)=\omega \left(y\right)=0.269812y$ and $\mathcal{V}\left(y\right)=2$. The values of $\mathcal{R}$ are presented in Table 1.

Table 1. Radii of convergence balls for Example 1.

$\mathit{\theta }\mathbf{=}\mathbf{-}\mathbf{0.5}$	$\mathit{\theta }\mathbf{=}\mathbf{0}$	$\mathit{\theta }\mathbf{=}\mathbf{0.2}$	$\mathit{\theta }\mathbf{=}\mathbf{2}$
${\mathcal{D}}_1=0.823619$	${\mathcal{D}}_1=0.823619$	${\mathcal{D}}_1=0.823619$	${\mathcal{D}}_1=0.823619$
${\mathcal{D}}_2=0.665576$	${\mathcal{D}}_2=0.722293$	${\mathcal{D}}_2=0.696849$	${\mathcal{D}}_2=0.568151$
$\mathcal{R}=0.665576$	$\mathcal{R}=0.722293$	$\mathcal{R}=0.696849$	$\mathcal{R}=0.568151$

Example 2.

[22] We chose the nonlinear Hammerstein type integral equation given by:

$$\mathcal{F}\left(s\right)\left(x\right)=s\left(x\right)-5{\int }_0^{1}sus{\left(u\right)}^{3}du,$$

where $s\left(x\right)\in C[0,1]$. We have ${\alpha }^{\ast }\left(x\right)=0$, ${\omega }_0\left(y\right)=7.5y$, $\omega \left(y\right)=15y$ and $\mathcal{V}\left(y\right)=2$. The values of $\mathcal{R}$ are provided in Table 2.

Table 2. Radii of convergence balls for Example 2.

$\mathit{\theta }\mathbf{=}\mathbf{-}\mathbf{0.5}$	$\mathit{\theta }\mathbf{=}\mathbf{0}$	$\mathit{\theta }\mathbf{=}\mathbf{0.2}$	$\mathit{\theta }\mathbf{=}\mathbf{2}$
${\mathcal{D}}_1=0.022222$	${\mathcal{D}}_1=0.022222$	${\mathcal{D}}_1=0.022222$	${\mathcal{D}}_1=0.022222$
${\mathcal{D}}_2=0.014295$	${\mathcal{D}}_2=0.015806$	${\mathcal{D}}_2=0.015118$	${\mathcal{D}}_2=0.011853$
$\mathcal{R}=0.014295$	$\mathcal{R}=0.015806$	$\mathcal{R}=0.015118$	$\mathcal{R}=0.011853$

Example 3.

[25] Finally, we address the motivational problem discussed in the introduction part. Then ${\alpha }^{\ast }=1$, ${\omega }_0\left(y\right)=\omega \left(y\right)=96.662907y$ and $\mathcal{V}\left(y\right)=2$. The values of $\mathcal{R}$ are given in Table 3.

Table 3. Radii of convergence balls for Example 3.

$\mathit{\theta }\mathbf{=}\mathbf{-}\mathbf{0.5}$	$\mathit{\theta }\mathbf{=}\mathbf{0}$	$\mathit{\theta }\mathbf{=}\mathbf{0.2}$	$\mathit{\theta }\mathbf{=}\mathbf{2}$
${\mathcal{D}}_1=0.002299$	${\mathcal{D}}_1=0.002299$	${\mathcal{D}}_1=0.002299$	${\mathcal{D}}_1=0.002299$
${\mathcal{D}}_2=0.001945$	${\mathcal{D}}_2=0.002175$	${\mathcal{D}}_2=0.002066$	${\mathcal{D}}_2=0.001613$
$\mathcal{R}=0.001945$	$\mathcal{R}=0.002175$	$\mathcal{R}=0.002066$	$\mathcal{R}=0.001613$