A Characterization of the Dynamics of Schröder’s Method for Polynomials with Two Roots

Abstract

The purpose of this work is to give a first approach to the dynamical behavior of Schröder’s method, a well-known iterative process for solving nonlinear equations. In this context, we consider equations defined in the complex plane. By using topological conjugations, we characterize the basins of attraction of Schröder’s method applied to polynomials with two roots and different multiplicities. Actually, we show that these basins are half-planes or circles, depending on the multiplicities of the roots. We conclude our study with a graphical gallery that allow us to compare the basins of attraction of Newton’s and Schröder’s method applied to some given polynomials.

1. Introduction

In his seminal paper, published in 1870, about the solution of a nonlinear equation in a single unknown,

$$f\left(z\right)=0,$$

(1)

Schröder deals with the problem of characterizing general iterative algorithms to solve (1) with a prefixed order of convergence $\omega \ge 2$ (see the original paper [1] or the commented English translation [2]). The main core of Schröder’s work studies two families of iterative processes, the well-known families of first and second kind [3,4]. The $\omega$-th member of these families is an iterative method that converges with order $\omega$ to a solution of (1). In this way, the second method of both families is Newton’s method. The third method of the first family is Chebyshev’s method. The third method of the second family is Halley’s method. The rest of the methods in both families (with order of convergence $\omega \ge 4$) are not so well known.

Note that Newton’s, Chebyshev’s, and Halley’s methods are also members of another famous family of iterative methods, the known as Chebyshev–Halley family of methods (introduced by Werner [5] and reported by many other authors [6,7]):

$$z_{k+1}=z_k-\left(1+\frac{1}{2}\frac{L_f\left(z_k\right)}{1-\alpha L_f\left(z_k\right)}\frac{f\left(z_k\right)}{f^{\prime }\left(z_k\right)}\right),\alpha \in \mathbb{R},k\ge 0,z_0\in \mathbb{C},$$

(2)

where we have used the notation

$$L_f\left(z\right)=\frac{f\left(z\right)f^{″}\left(z\right)}{f^{\prime }{\left(z\right)}^2}.$$

(3)

In fact, Chebyshev’s method is obtained for $\alpha =0$, Halley’s method appears for $\alpha =1/2$, and Newton’s method can be obtained as a limit case when $\left|\alpha \right|\to \infty$. Except for the limit case of Newton’s method, all the methods in the family have third order of convergence.

In this general context of families of iterative methods for solving nonlinear equations, we would like to highlight a detail that appears in the aforementioned paper by Schröder [1]. Actually, in the third section of this article, Schröder constructs an algorithm by applying Newton’s method to the equation

$$\frac{f\left(z\right)}{f^{\prime }\left(z\right)}=0.$$

The resulting iterative scheme can be written as

$$z_{k+1}=z_k-\frac{f\left(z_k\right)f^{\prime }\left(z_k\right)}{f^{\prime }{\left(z_k\right)}^2-f\left(z_k\right)f^{″}\left(z_k\right)},k\ge 0,z_0\in \mathbb{C},$$

as it is known as Schröder’s method by many authors (see, for instance, in [8,9]). Sometimes, this method is also called Newton’s method for multiple roots.

For our convenience, we denote by $S_f\left(z\right)$ the iteration function of Schröder’s method. Note that it can be written in terms of the function $L_f\left(z\right)$ introduced in (3) in the following way:

$$z_{k+1}=S_f\left(z_k\right)=z_k-\frac{1}{1-L_f\left(z_k\right)}\frac{f\left(z_k\right)}{f^{\prime }\left(z_k\right)}k\ge 0,z_0\in \mathbb{C}.$$

(4)

The same Schröder’s paper [1] compares the resulting algorithm (4) with Newton’s method and says:

“It is an equally worthy algorithm which to my knowledge has not been previously considered. Besides, being almost as simple, this latter algorithm has the advantage that it converges quadratically even for multiple roots.”

Curiously, Schröder’s method (4) does not belong either to the Schröder’s families of first and second kind or the Chebyshev–Halley family (2). It has very interesting numerical properties, such as the quadratic convergence even for multiple roots, but the fact of having a high computational cost (equivalent to the the third order methods in (2)) could be an important handicap for practical purposes.

In this paper, we present a first approach to the dynamical behavior of Schröder’s method. Therefore, we show that for polynomials with two different roots and different multiplicities, it is possible to characterize the basins of attraction and the corresponding Julia set. We can appreciate the influence of the multiplicities in such sets.

2. Preliminaries

In the 14th section of Schröder’s work [1], that has the title The Principal Algorithms Applied to very Simple Examples, we can find the first dynamical study of a couple of rootfinding methods. Actually, Schröder considers those who, in his opinion, are the two most useful methods: Newton’s method, defined by the iterative scheme

$$z_{k+1}=N_f\left(z_k\right)=z_k-\frac{f\left(z_k\right)}{f^{\prime }\left(z_k\right)}k\ge 0,z_0\in \mathbb{C},$$

(5)

and the method $z_{k+1}=S_f\left(z_k\right)$ given in (4).

In the simplest case, namely, equations with only one root, we can assume without loss of generality that $f\left(z\right)=z^n$. It is easy to see that

$$N_f\left(z\right)=\frac{n-1}{n}z,S_f\left(z\right)=0.$$

So Schröder’s method gives the correct root ($z=0$) of the equation in just one step, whereas Newton’s method converges to this root with lineal convergence:

$$z_k={\left(\frac{n-1}{n}\right)}^k{z}_0.$$

Consequently, for equations with a single root Schröder concludes that the convergence regions of these two methods is the entire complex plane.

The next simple case considered by Schröder is the quadratic equation. Again, without loss of generality he assumes $f\left(z\right)=(z-1)(z+1)$. After a series of cumbersome calculus, he states that in this case and for both methods, the entire complex plane decomposes into two regions separated by the imaginary axis. A few years later, Cayley [10] addresses the same problem, only for Newton’s method. In a very elegant way, it can be proved (see in [11] (Theorem 3.2.2) for details) that for polynomials

$$f\left(z\right)=(z-a)(z-b),a,b\in \mathbb{C},a\ne b,$$

(6)

Newton’s iterate converge to the root a if $|z_0-a|<|z_0-b|$ and to the root b if $|z_0-b|<|z_0-a|$.

The behavior of the method in the equidistant line between the two roots is more complicated and gives rise to the idea of Julia set, one of the main concepts in complex dynamics (see in [12], for instance). In this reference, we can find the formal definition of the Julia set related to a rational map $R:\widehat{\mathbb{C}}\to \widehat{\mathbb{C}}$, where $\widehat{\mathbb{C}}$ is the Riemann sphere. Actually, R is said to be normal for a point $z\in \widehat{\mathbb{C}}$, if there exists a neighborhood U of z such that the sequence ${\left\{R^n{|}_U\right\}}_{n\ge 0}$ of mappings from U to $\widehat{\mathbb{C}}$ is equicontinuous. The Julia set of R is the set J of points in $\widehat{\mathbb{C}}$ for which R is not normal. In [12], we can find a list of properties and characterizations of the Julia set as, for instance, J is the frontier of the basin of attraction of the attractive fixed points of R.

The key to prove this result is to consider these methods as rational functions defined in the Riemann sphere $\widehat{\mathbb{C}}$. Therefore, we can prove that Newton iteration function (5) applied to polynomials (6) is conjugate via the Möbius map

$$M\left(z\right)=\frac{z-a}{z-b}$$

(7)

with the function $R\left(z\right)=z^2$, that is, $R\left(z\right)=M\circ N_f\circ M^{-1}\left(z\right)$. The unit circle $S^1=\{z\in \mathbb{C};|z|=1\}$ is invariant by R. Its anti-image by R is the bisector between the roots a and b.

Two functions $f,g:\widehat{\mathbb{C}}\to \widehat{\mathbb{C}}$ are said topologically conjugate if there exists a homeomorphism $\phi$ such that

$$\phi \circ g=f\circ \phi .$$

Topological conjugation is a very useful tool in dynamical systems (see in [13] for more details) because two conjugate functions share the same dynamical properties, from the topological viewpoint. For instance, the fixed points of one function are mapped into the fixed points of the other, the periodic points of one function are mapped into the periodic points of the other function, and so on. Speaking informally, we can say that the two functions are the same from a dynamical point of view. As we have just seen, in some cases one of the functions in a conjugation could be much simpler than the other. In the case of Cayley’s problem, $R\left(z\right)=z^2$ is topologically conjugate (and much simpler) to

$$N_f\left(z\right)=\frac{ab-z^2}{a+b-2z}.$$

In the same way, we have that Schröder’s method (4) applied to polynomials (6)

$$S_f\left(z\right)=\frac{z^2(a+b)-4abz+ab(a+b)}{a^2-2z(a+b)+b^2+2z^2}$$

is conjugated to the function $-R\left(z\right)$ via the Möbius map defined in (7), that is, $M\circ S_f\circ M^{-1}\left(z\right)=-z^2$. Consequently, the dynamical behavior of Schröder’s method for quadratic polynomials mimics the behavior of Newton’s method: the Julia set is the perpendicular bisector between the two roots and the basins of attraction are the corresponding half-planes.

3. Main Results

Now, we consider the case of polynomials with two roots, but with different multiplicities, $m\ge n\ge 1$:

$$f\left(z\right)={(z-a)}^m{(z-b)}^n,a,b\in \mathbb{C},a\ne b.$$

(8)

For our simplicity, and to better appreciate symmetries, we move the roots a and b to 1 and $-1$. To do this, we conjugate with the affine map

$$A\left(z\right)=1+2\frac{z-a}{a-b}$$

(9)

to obtain a simpler function that does not depend on the roots a and b. Let $T_{m,n}\left(z\right)$ be the corresponding conjugate map:

$$T_{m,n}\left(z\right)=A\circ S_f\circ A^{-1}\left(z\right)=\frac{(m-n)z^2+2(m+n)z+m-n}{(m+n)z^2+2(m-n)z+m+n}.$$

(10)

A new conjugation of $T_{m,n}\left(z\right)$ with the Möbius map (7), when $a=1$ and $b=-1$ provides a new rational function whose dynamical are extremely simple. Actually,

$$R_{m,n}\left(z\right)=M\circ T_{m,n}\circ M^{-1}\left(z\right)=-\frac{n{z}^2}{m}.$$

(11)

Note that the circle $C_{m,n}=\{z\in \mathbb{C};|z|=m/n\}$ is invariant by $R_{m,n}\left(z\right)$. After iteration by $R_{m,n}\left(z\right)$, the orbits of the points $z_0$ with $|z_0|<m/n$ go to 0, whereas the orbits of the points $z_0$ with $|z_0|>m/n$ go to ∞. Consequently, $C_{m,n}$ is the Julia set of the map $R_{m,n}\left(z\right)$.

Theorem 1.

Let $T_{m,n}\left(z\right)$ be the rational map defined by (10) and let us denote by $J_{m,n}$ its Julia set. Then, we have

1.

If $m=n$, then $J_{m,m}$ is the imaginary axis.

2.

If $m>n\ge 1$, then $J_{m,n}$ is the circle

$$J_{m,n}=\left\{z\in \mathbb{C};\left|z+\frac{m^2+n^2}{m^2-n^2}\right|=\frac{2mn}{m^2-n^2}\right\}.$$

Proof. 

The proof follows immediately, just by taking into account that $J_{m,n}$ is the pre-image by $M\left(z\right)=(z-1)/(z+1)$ of the circle $C_{m,n}$ and by distinguishing the two situations indicated in the statement of the theorem. □

Theorem 2.

Let $S_f\left(z\right)$ be the rational map defined by applying Schröder’s method to polynomials (8) and let us denote by $J_{m,n,a,b}$ its Julia set. Then, we have

1.

If $m=n$, $J_{m,m,a,b}$ is the locus of points equidistant from a and b.

2.

If $m>n\ge 1$, then $J_{m,n,a,b}$ is the circle

$$J_{m,n,a,b}=\left\{z\in \mathbb{C};\left|z-\frac{b{m}^2-a{n}^2}{m^2-n^2}\right|=\frac{mn|a-b|}{m^2-n^2}\right\}.$$

Proof. 

Now, we deduce this result by calculating the pre-images of $J_{m,n}$ by the affine map $A\left(z\right)$ defined in (9) in the two situations indicated in the previous theorem. □

4. Conclusions and Further Work

We have studied the behavior of Schröder’s method for polynomials with two different complex roots and with different multiplicities (8). Actually, we have proved that the Julia set of the corresponding rational functions obtained in this case is a circle given in Theorem 2.

In addition, Theorem 1 gives us a universal result that characterizes the behavior of Schröder’s method in a very simplified form, depending only of the values of the multiplicities m and n. The influence of the roots a and b is revealed in Theorem 2, and it is just an affine transformation of the situation given in Theorem 1.

Let us consider the points $(x,y)\in {\mathbb{R}}^2$ given by the centers and radius of the circles defined in Theorem 1, that is

$$(x,y)=\left(-\frac{m^2+n^2}{m^2-n^2},\frac{2mn}{m^2-n^2}\right).$$

These points belong to the hyperbola $x^2-y^2=1$ in the real plane ${\mathbb{R}}^2$.

In addition, we appreciate that are polynomials for which Schröder’s method has the same dynamical behavior. Actually, if we introduce the new parameter

$$p=\frac{m}{n},$$

we have that the circles $J_{m,n}$ defined in Theorem 1 can be expressed as

$$J_p=\left\{z\in \mathbb{C};\left|z+\frac{p^2+1}{p^2-1}\right|=\frac{2p}{p^2-1}\right\}.$$

Therefore, Schröder’s method applied to polynomials with multiplicities $(m,n)$ and quotient p gives the same Julia set $J_p$.

We can analyze the dynamics of Schröder’s method applied to polynomials ${(z-1)}^m{(z+1)}^n$, $m>n$ in the following way:

• When $p=m/n\to \infty$, the Julia sets $J_p$ are circles that tend to collapse in the point $z=-1$.
• When $p=m/n\to 1^{+}$, the Julia sets $J_p$ are circles with centers in the negative real line. Note that centers

  $$-\frac{p^2+1}{p^2-1}\to -\infty \mathrm{when}p\to 1^{+}$$

  and radius

  $$\frac{2p}{p^2-1}\to \infty \mathrm{when}p\to 1^{+}.$$
  Therefore, when $p\to 1^{+}$ the Julia set are circles getting bigger and tending to “explode” into the limit case, given by the imaginary axis when $p=1$.

If we consider the presence of the roots a and b, the dynamics of Schröder’s method applied to polynomials ${(z-a)}^m{(z-b)}^n$, $m>n$, can be summarized in a “travel” from a circle concentrated in the root with the smallest multiplicity, b, to circles with the center in the line connecting the roots a and b and radius tending to infinity until the “explosion” into the limit case, given by the bisector of the two roots, when $p=1$.

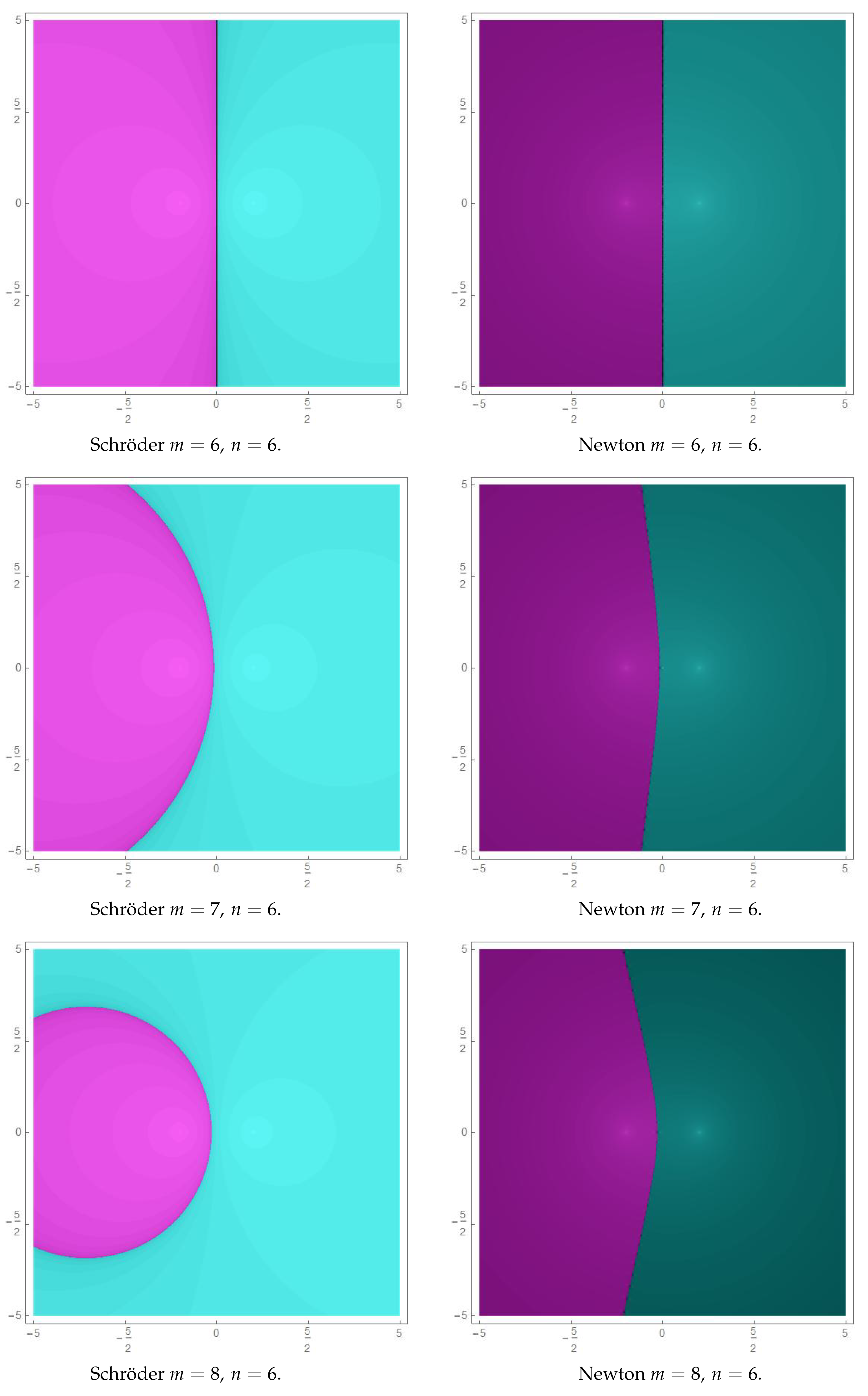
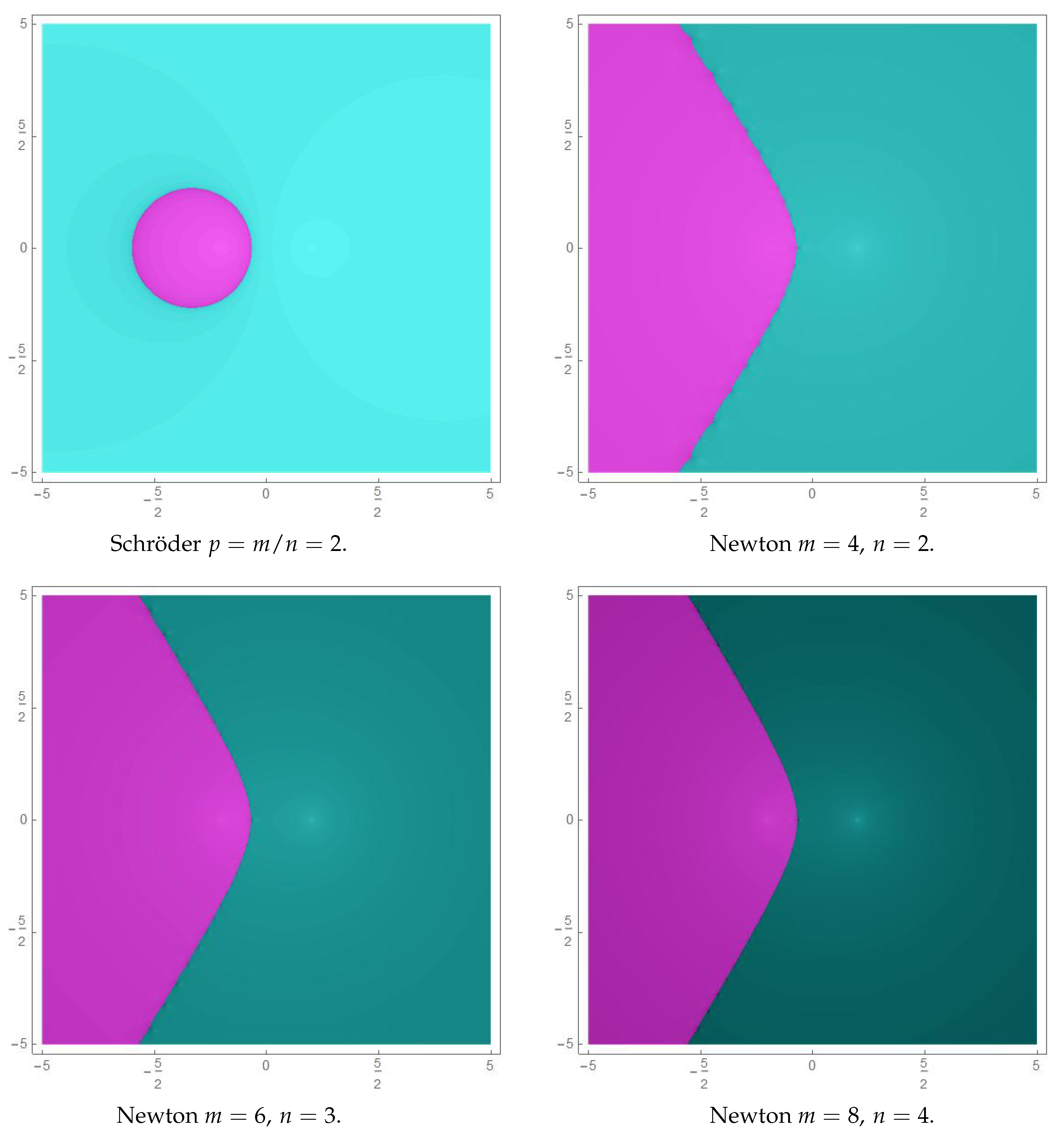
In Figure 1, Figure 2 and Figure 3, we show some graphics of different Julia sets obtained when Schröder’s method is applied to polynomials ${(z-a)}^m{(z-b)}^n$, $m\ge n\ge 1$. We compare these dynamical planes with the ones obtained for Newton’s. For instance, in Figure 1 we show the behavior when $p=m/n$ is increasing. We appreciate how the Julia set for Schröder’s method (a circle) tends to collapse in the point $z=-1$ that in this case is the simple root. In the case of Newton’s method, the Julia set is a kind of “deformed parabola”, whose “axis of symmetry” is the real line, it is open to the left, the “vertex” tends to the simple root $z=-1$, and the “latus rectum” tends to zero. We see how the basin of attraction of the multiple root $z=1$ invades more and more the basin of the simple root $z=-1$, as it was pointed out by Gutiérrez et al. [14].

In Figure 2 we see what happens when $p=m/n\approx 1$. The Julia set for Schröder’s method is circles getting bigger as p approaches the value 1 and exploding into a half-plane limited by the imaginary axis when $p=1$. In the case of Newton’s method, the Julia set is again a “deformed parabola” with the real line as “axis of symmetry” and open to the left. However as p goes to 1, the “vertex” tends to $z=0$ and the “latus rectum” tends to infinity. As a limit case, when $p=1$ this “deformed parabola” becomes a straight line, actually the imaginary axis.

Figure 3 shows the circle corresponding to the Julia set of Schröder’s method applied to polynomials ${(z-1)}^m{(z+1)}^n$ with $p=m/n=2$. We can also see the Julia set of Newton’s method applied to such polynomials. In the case of Newton’s method, we observe that the behavior is not the same for values of m and n such that $p=m/n=2$. The corresponding “deformed parabola” tends to be smoother when the values of m and n increase.

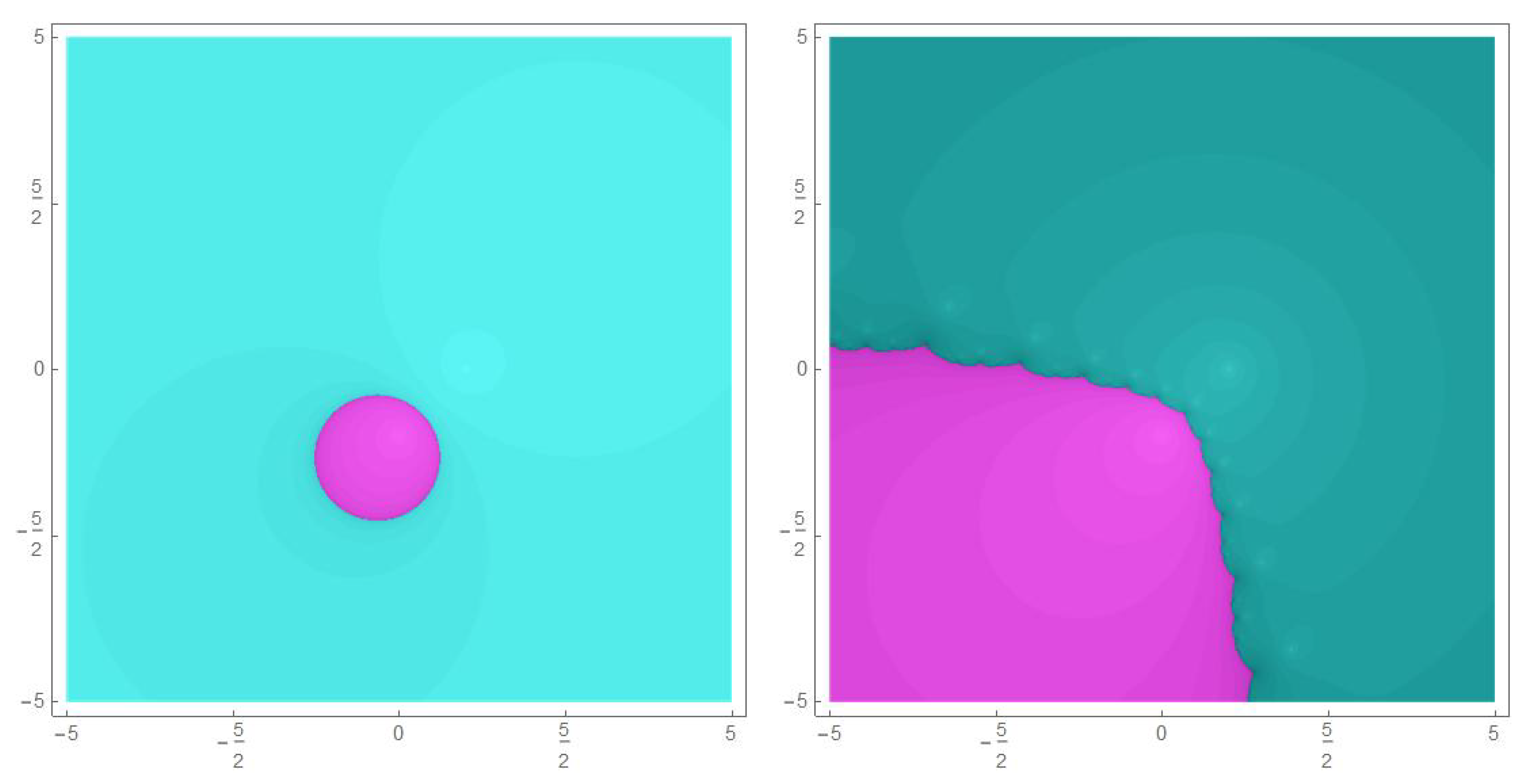
Finally, in Figure 4 we show the Julia set $J_{m,n,a,b}$ defined in Theorem 2 in the case $m=2$, $n=1$, $a=1$, $b=-i$ together with the corresponding Julia set for Newton’s method. In these figures, we appreciate the loss of symmetry respect to the imaginary axis. This role is now played by the equidistant line between the roots a and b.

As a further work, we would like to explore the influence of the multiplicity in the Julia set of Newton’s method applied to polynomials ${(z-a)}^m{(z-b)}^n$, $m\ge n\ge 1$, and its possible relationship between the study of Schröder’s method. In particular, we are interested in characterize the main properties of the “deformed parabolas” that appear in the case of Newton’s method.