A New Approach for Dynamic Stochastic Fractal Search with Fuzzy Logic for Parameter Adaptation
Abstract
1. Introduction
2. Materials and Methods for Stochastic Fractal Search (SFS)
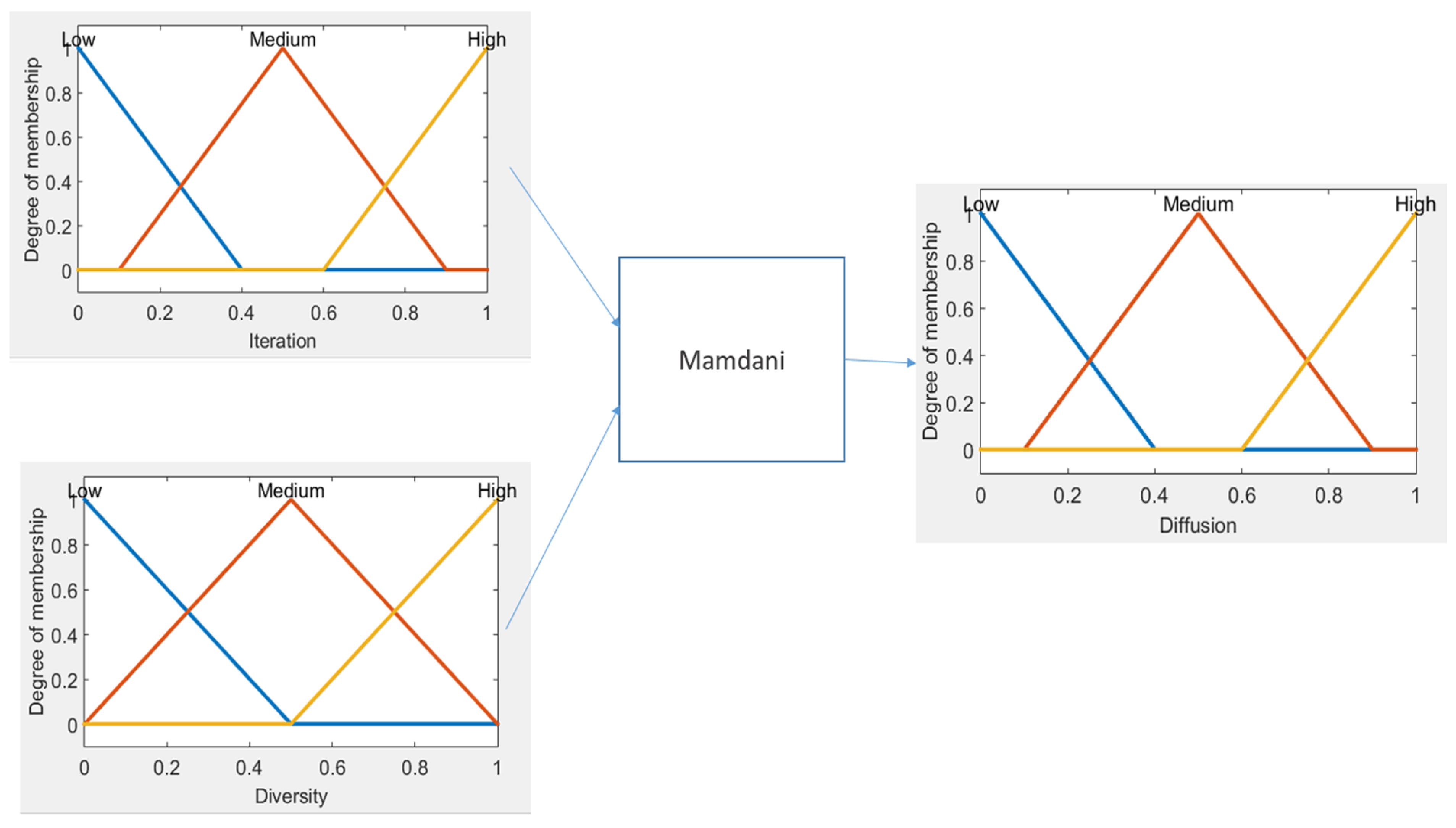
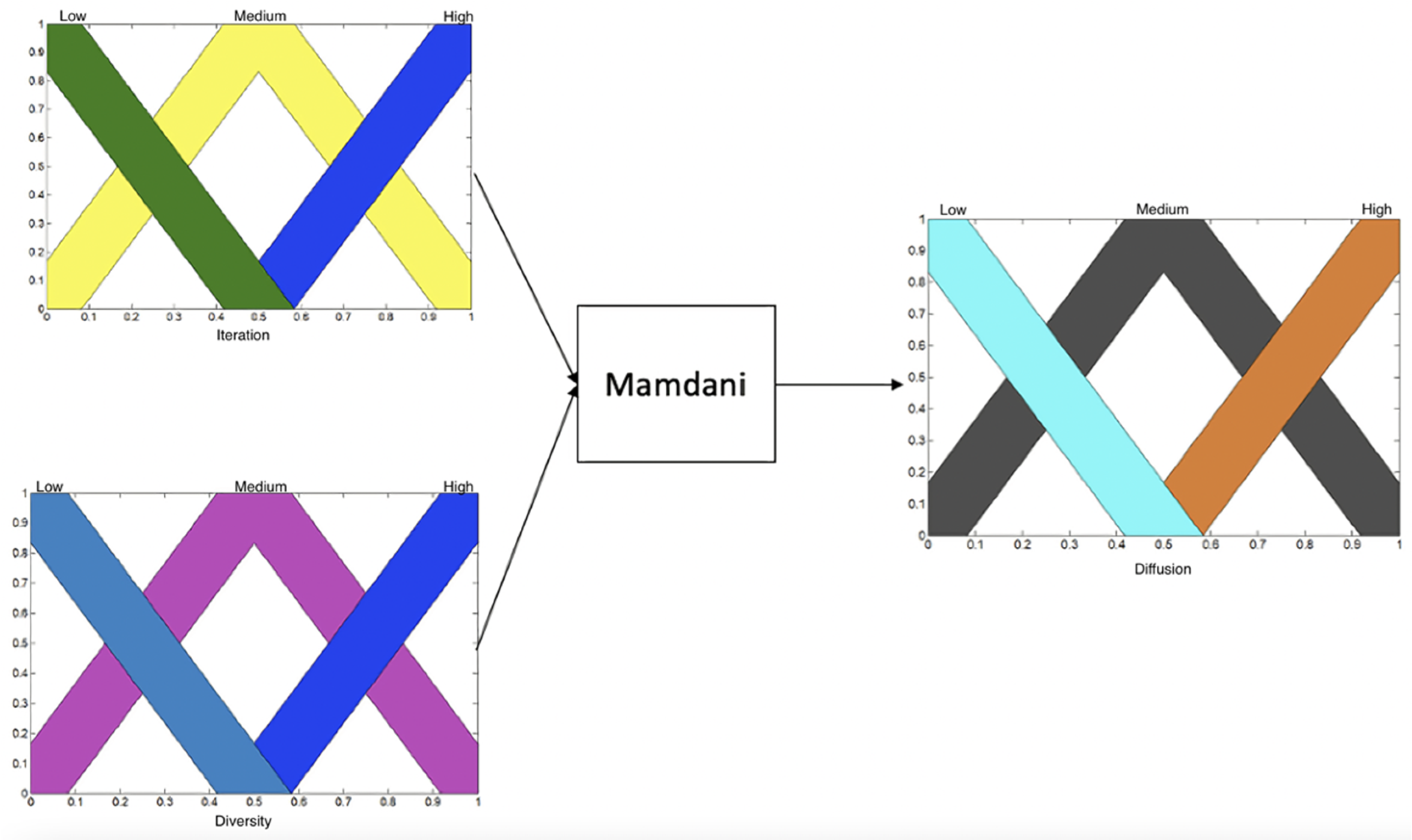
3. Proposed Dynamic Stochastic Fractal Search (DSFS)
- If (Iteration is Low) and (Diversity is Low) then (Diffusion is High).
- If (Iteration is Low) and (Diversity is Medium) then (Diffusion is Medium).
- If (Iteration is Low) and (Diversity is High) then (Diffusion is Medium).
- If (Iteration is Medium) and (Diversity is Low) then (Diffusion is Medium).
- If (Iteration is Medium) and (Diversity is Medium) then (Diffusion is Medium).
- If (Iteration is Medium) and (Diversity is High) then (Diffusion is Medium).
- If (Iteration is High) and (Diversity is Low) then (Diffusion is Medium).
- If (Iteration is High) and (Diversity is Medium) then (Diffusion is Medium).
- If (Iteration is High) and (Diversity is High) then (Diffusion is Low).
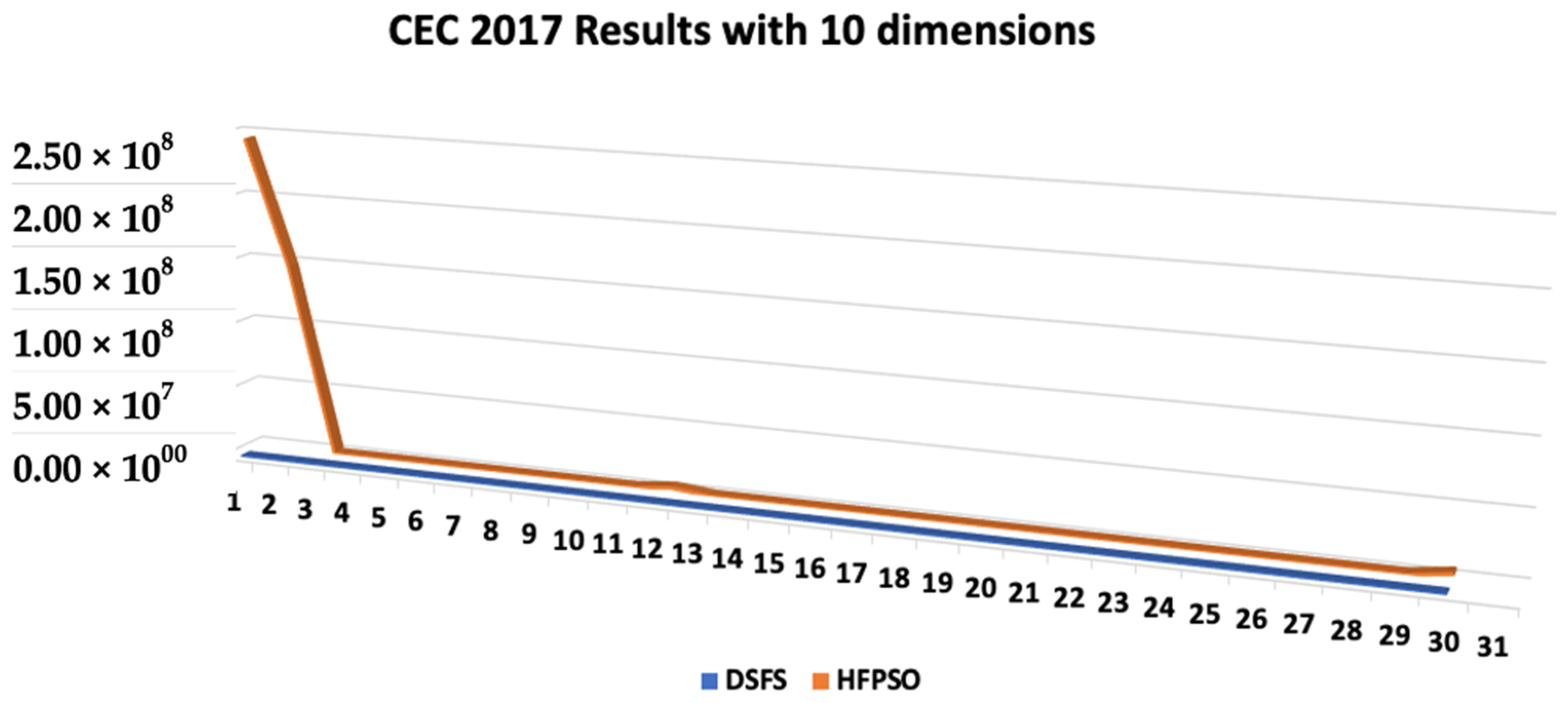
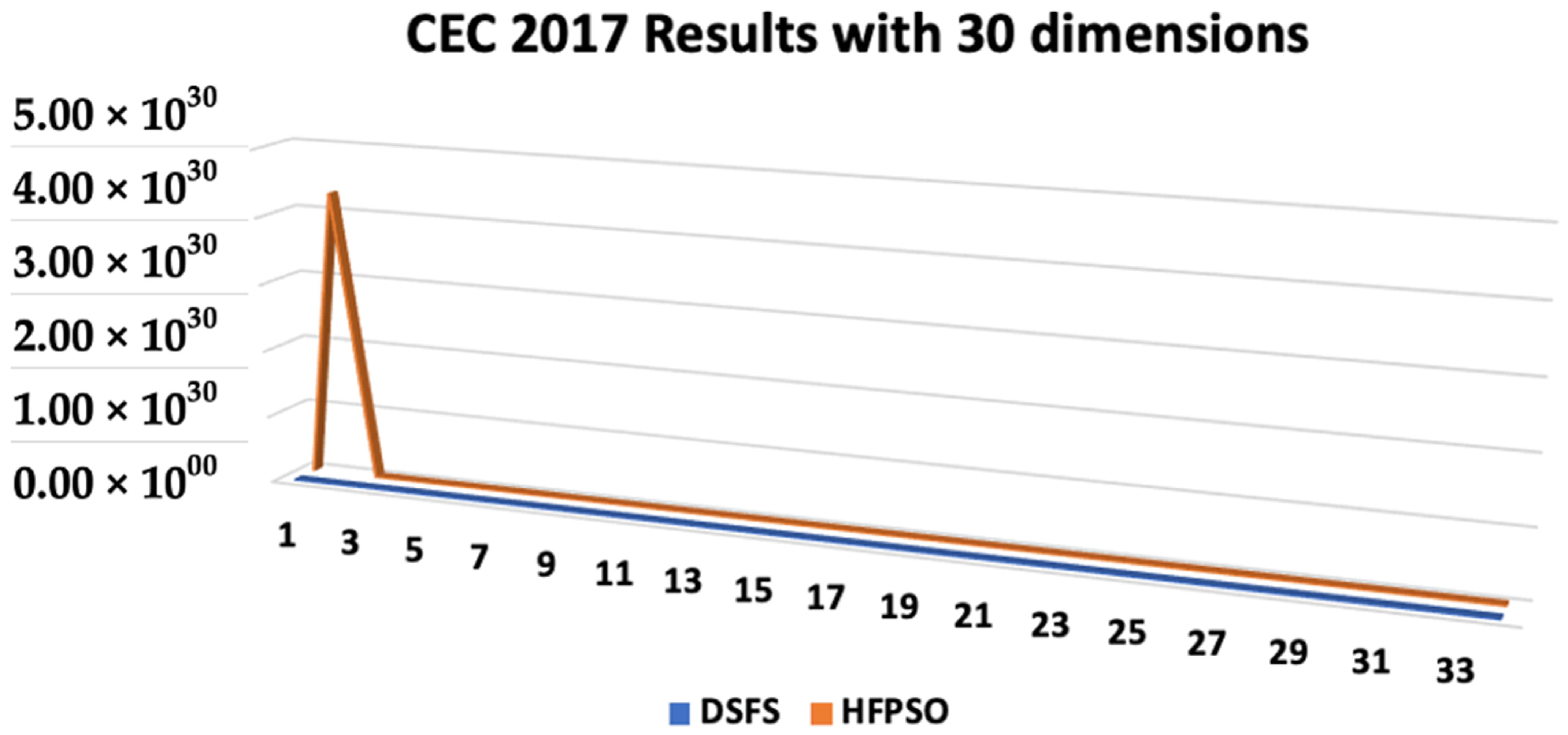
4. Experimental Results
5. Discussion of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Cambridge, UK, 2010. [Google Scholar]
- Holland, J.H. Genetic Algorithms understand Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Garg, H. A hybrid GA-GSA algorithm for optimizing the performance of an industrial system by utilizing uncertain data. In Handbook of Research on Artificial Intelligence Techniques and Algorithms; IGI Global: Seri Iskandar, Malaysia, 2015; pp. 620–654. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Glover, F.; Laguna, M. Tabu Search; Springer: New York, NY, USA, 1997. [Google Scholar]
- Gallego, R.A.; Romero, R.; Monticelli, A.J. Tabu search algorithm for network synthesis. IEEE Trans. Power Syst. 2000, 15, 490–495. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.H.; Tang, F.; Huang, D.X. Improved particle swarm optimization combined with chaos. Chaos Solitons Fractals 2005, 25, 1261–1271. [Google Scholar] [CrossRef]
- Alatas, B.; Akin, E.; Ozer, A.B. Chaos embedded particle swarm optimization algorithms. Chaos Solitons Fractals 2009, 40, 1715–1734. [Google Scholar] [CrossRef]
- Jiao, B.; Lian, Z.; Gu, X. A dynamic inertia weight particle swarm optimization algorithm. Chaos Solitons Fractals 2008, 37, 698–705. [Google Scholar] [CrossRef]
- Yang, D.; Li, G.; Cheng, G. On the efficiency of chaos optimization algorithms for global optimization. Chaos Solitons Fractals 2007, 34, 1366–1375. [Google Scholar] [CrossRef]
- Misaghi, M.; Yaghoobi, M. Improved invasive weed optimization algorithm (IWO) based on chaos theory for optimal design of PID controller. J. Comput. Des. Eng. 2019, 6, 284–295. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Tong, S. Adaptive fuzzy approach to control unified chaotic systems. Chaos Solitons Fractals 2007, 34, 1180–1187. [Google Scholar] [CrossRef]
- Lagunes, M.L.; Castillo, O.; Valdez, F.; Soria, J. Comparative Study of Fuzzy Controller Optimization with Dynamic Parameter Adjustment Based on Type 1 and Type 2 Fuzzy Logic. Int. Fuzzy Syst. Assoc. World Congr. 2019, 1000, 296–305. [Google Scholar]
- Lagunes, M.L.; Castillo, O.; Valdez, F.; Soria, J.; Melin, P. Parameter Optimization for Membership Functions of Type-2 Fuzzy Controllers for Autonomous Mobile Robots Using the Firefly Algorithm. In North American Fuzzy Information Processing Society Annual Conference; Springer: Berlin/Heidelberg, Germany, 2018; pp. 569–579. [Google Scholar]
- Amador-Angulo, L.; Castillo, O. Comparative Analysis of Designing Differents Types of Membership Functions Using Bee Colony Optimization in the Stabilization of Fuzzy Controllers. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 551–571. [Google Scholar]
- Lagunes, M.L.; Castillo, O.; Valdez, F.; Soria, J. Comparison of Fuzzy Controller Optimization with Dynamic Parameter Adjustment Based on of Type-1 and Type-2 Fuzzy Logic. Hybrid Intell. Syst. Control Pattern Recognit. Med. 2020, 827, 47–56. [Google Scholar]
- Pérez, J.; Valdez, F.; Castillo, O. Modification of the Bat Algorithm Using Type-2 Fuzzy Logic for Dynamical Parameter Adaptation. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 343–355. [Google Scholar]
- Bernal, E.; Castillo, O.; Soria, J.; Valdez, F.; Melin, P. A variant to the dynamic adaptation of parameters in galactic swarm optimization using a fuzzy logic augmentation. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–7. [Google Scholar]
- Sánchez, D.; Melin, P.; Castillo, O. Optimization of modular granular neural networks using a firefly algorithm for human recognition. Eng. Appl. Artif. Intell. 2017, 64, 172–186. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman and Company: San Francisco, CA, USA, 1982; Volume 1. [Google Scholar]
- Barnsley, M.F.; Demko, S. Iterated function systems and the global construction of fractals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1985, 399, 243–275. [Google Scholar]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Prusinkiewicz, P. Graphical applications of L−systems. Proc. Graph. Interface 1986, 86, 247–253. [Google Scholar]
- Rushton, B. Subdivision rules for all Gromov hyperbolic groups. arXiv 2017, arXiv:1708.02366. [Google Scholar]
- Falconer, K.J. Random fractals. Math. Proc. Camb. Philos. Soc. 1986, 100, 559–582. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. A Robust Stochastic Fractal Search approach for optimization of the surface grinding process. Swarm Evol. Comput. 2018, 38, 173–186. [Google Scholar] [CrossRef]
- Mellal, M.A.; Zio, E. A penalty guided stochastic fractal search approach for system reliability optimization. Reliab. Eng. Syst. Saf. 2016, 152, 213–227. [Google Scholar] [CrossRef]
- Salimi, H. Stochastic Fractal Search: A powerful metaheuristic algorithm. Knowl. Based Syst. 2015, 75, 1–18. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Naderi, B.; Khalilpourazary, S. Multi-Objective Stochastic Fractal Search: A powerful algorithm for solving complex multi-objective optimization problems. Soft Comput. 2020, 24, 3037–3066. [Google Scholar] [CrossRef]
- Aras, S.; Gedikli, E.; Kahraman, H.T. A novel stochastic fractal search algorithm with fitness-Distance balance for global numerical optimization. Swarm Evol. Comput. 2021, 61, 100821. [Google Scholar] [CrossRef]
- Çelik, E. Incorporation of stochastic fractal search algorithm into efficient design of PID controller for an automatic voltage regulator system. Neural Comput. Appl. 2018, 30, 1991–2002. [Google Scholar] [CrossRef]
- Alomoush, M.I.; Oweis, Z.B. Environmental-economic dispatch using stochastic fractal search algorithm. Int. Trans. Electr. Energy Syst. 2018, 28, e2530. [Google Scholar] [CrossRef]
- Miramontes, I.; Melin, P.; Prado-Arechiga, G. Comparative Study of Bio-inspired Algorithms Applied in the Optimization of Fuzzy Systems. In Hybrid Intelligent Systems in Control, Pattern Recognition and Medicine; Springer: Berlin/Heidelberg, Germany, 2020; Volume 827, pp. 219–231. [Google Scholar]
- Miramontes, I.; Melin, P.; Prado-Arechiga, G. Fuzzy System for Classification of Nocturnal Blood Pressure Profile and Its Optimization with the Crow Search Algorithm. Adv. Intell. Syst. Comput. 2021, 1222, 23–34. [Google Scholar]
- Guzmán, J.; Miramontes, I.; Melin, P.; Prado-Arechiga, G. Optimal Genetic Design of Type-1 and Interval Type-2 Fuzzy Systems for Blood Pressure Level Classification. Axioms 2019, 8, 8. [Google Scholar] [CrossRef]
- Carvajal, O.; Melin, P.; Miramontes, I.; Prado-Arechiga, G. Optimal design of a general type-2 fuzzy classifier for the pulse level and its hardware implementation. Eng. Appl. Artif. Intell. 2021, 97, 104069. [Google Scholar] [CrossRef]
- Miramontes, I.; Guzman, J.C.; Melin, P.; Prado-Arechiga, G. Optimal design of interval type-2 fuzzy heart rate level classification systems using the bird swarm algorithm. Algorithms 2018, 11, 206. [Google Scholar] [CrossRef]
- Biedrzycki, R. A Version of IPOP-CMA-ES Algorithm with Midpoint for CEC 2017 Single Objective Bound Constrained Problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 1489–1494. [Google Scholar]
- Awad, N.H.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P.; Definitions, P. Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Obejective Real-Parameter Numerical Optimization; Technology Report; Nanyang Technological University: Singapore; Jordan Zhengzhou University: Zhengzhou, China, 2016. [Google Scholar]
- Aydilek, İ.B. A Hybrid Firefly and Particle Swarm Optimization Algorithm for Computationally Expensive Numerical Problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
| Type of Function | No | Name of Function | fi |
|---|---|---|---|
| Unimodal Functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 2 | Shifted and Rotated Sum of Different Power Function | 200 | |
| 3 | Shifted and Rotated Zakharov Function | 300 | |
| Simple Multimodal Functions | 4 | Shifted and Rotated Rosenbrock’s Function | 400 |
| 5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| 6 | Shifted and Rotated Expanded Schaffer’s Function | 600 | |
| 7 | Shifted and Rotated Lunacek Bi-Rastrigin Function | 700 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Levy Function | 900 | |
| 10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid Functions | 11 | Hybrid Function 1 (N = 3) | 1100 |
| 12 | Hybrid Function 2 (N = 3) | 1200 | |
| 13 | Hybrid Function 3 (N = 3) | 1300 | |
| 14 | Hybrid Function 4 (N = 4) | 1400 | |
| 15 | Hybrid Function 5 (N = 4) | 1500 | |
| 16 | Hybrid Function 6 (N = 4) | 1600 | |
| 17 | Hybrid Function 6 (N = 5) | 1700 | |
| 18 | Hybrid Function 6 (N = 5) | 1800 | |
| 19 | Hybrid Function 6 (N = 5) | 1900 | |
| 20 | Hybrid Function 6 (N = 6) | 2000 | |
| 21 | Composition Function 1 (N = 3) | 2100 | |
| Composition Functions | 22 | Composition Function 2 (N = 3) | 2200 |
| 23 | Composition Function 3 (N = 4) | 2300 | |
| 24 | Composition Function 4 (N = 4) | 2400 | |
| 25 | Composition Function 5 (N = 5) | 2500 | |
| 26 | Composition Function 6 (N = 3) | 2600 | |
| 27 | Composition Function 7 (N = 6) | 2700 | |
| 28 | Composition Function 8 (N = 3) | 2800 | |
| 29 | Composition Function 9 (N = 3) | 2900 | |
| 30 | Composition Function 10 (N = 3) | 3000 |
| Dynamic Stochastic Fractal Search (DSFS) with 10 Dimensions | |||||
|---|---|---|---|---|---|
| Type-1 Fuzzy Logic | Type-2 Fuzzy Logic | ||||
| Function | fi | Main | Std | Main | Std |
| f1 | 100 | 1.01 × 102 | 4.87 × 10−1 | 1.01 × 102 | 7.85 × 10−1 |
| f2 | 200 | 2.00 × 102 | 0.00 | 2.00 × 102 | 0.00 |
| f3 | 300 | 3.00 × 102 | 3.73 × 10−6 | 3.00 × 102 | 5.04 × 10−6 |
| f4 | 400 | 4.01 × 102 | 7.81 × 10−1 | 4.00 × 102 | 6.19 × 10−1 |
| f5 | 500 | 5.06 × 102 | 2.04 | 5.07 × 102 | 2.64 |
| f6 | 600 | 6.00 × 102 | 7.21 × 10−8 | 6.00 × 102 | 6.24 × 10−8 |
| f7 | 700 | 7.19 × 102 | 3.45 | 7.20 × 102 | 3.32 |
| f8 | 800 | 8.07 × 102 | 3.04 | 8.07 × 102 | 2.44 |
| f9 | 900 | 9.00 × 102 | 0.00 | 9.00 × 102 | 0.00 |
| f10 | 1000 | 1.40 × 103 | 1.70 × 102 | 1.34 × 103 | 1.31 × 102 |
| f11 | 1100 | 1.10 × 103 | 9.31 × 10−1 | 1.10 × 103 | 1.00 |
| f12 | 1200 | 1.50 × 103 | 1.04 × 102 | 1.52 × 103 | 1.02 × 102 |
| f13 | 1300 | 1.31 × 103 | 4.03 | 1.31 × 103 | 4.14 |
| f14 | 1400 | 1.40 × 103 | 1.69 | 1.40 × 103 | 2.01 |
| f15 | 1500 | 1.50 × 103 | 7.24 × 10−1 | 1.50 × 103 | 8.88 × 10−1 |
| f16 | 1600 | 1.60 × 103 | 2.79 × 10−1 | 1.60 × 103 | 3.64 × 10−1 |
| f17 | 1700 | 1.70 × 103 | 2.68 | 1.71 × 103 | 4.41 |
| f18 | 1800 | 1.81 × 103 | 2.56 | 1.81 × 103 | 2.57 |
| f19 | 1900 | 1.90 × 103 | 4.15 × 10−1 | 1.90 × 103 | 4.45 × 10−1 |
| f20 | 2000 | 2.00 × 103 | 1.39 × 10−1 | 2.00 × 103 | 4.73 × 10−3 |
| f21 | 2100 | 2.23 × 103 | 5.08 × 10 | 2.24 × 103 | 5.40 × 10 |
| f22 | 2200 | 2.29 × 103 | 2.17 × 10 | 2.28 × 103 | 3.93 × 10 |
| f23 | 2300 | 2.61 × 103 | 2.80 | 2.60 × 103 | 5.61 × 10 |
| f24 | 2400 | 2.61 × 103 | 1.22 × 102 | 2.63 × 103 | 1.14 × 102 |
| f25 | 2500 | 2.90 × 103 | 1.08 × 10 | 2.90 × 103 | 1.15 × 10 |
| f26 | 2600 | 2.90 × 103 | 2.15 × 10−10 | 2.90 × 103 | 3.02 × 10−10 |
| f27 | 2700 | 3.09 × 103 | 1.97 | 3.09 × 103 | 2.14 |
| f28 | 2800 | 3.09 × 103 | 4.20 × 10 | 3.11 × 103 | 5.69 × 10 |
| f29 | 2900 | 3.16 × 103 | 1.01 × 10 | 3.16 × 103 | 9.65 |
| f30 | 3000 | 3.56 × 103 | 2.30 × 102 | 3.55 × 103 | 1.19 × 102 |
| Dynamic Stochastic Fractal Search (DFSF) with 30 Dimensions | |||||
|---|---|---|---|---|---|
| Type-1 Fuzzy Logic | Type-2 Fuzzy Logic | ||||
| Function | fi | Main | Std | Main | Std |
| f1 | 100 | 3.49 × 103 | 2.76 × 103 | 3.24 × 103 | 2.74 × 103 |
| f2 | 200 | 3.06 × 1016 | 7.11 × 1016 | 7.59 × 1017 | 3.98 × 1018 |
| f3 | 300 | 8.40 × 103 | 3.95 × 103 | 8.79 × 103 | 4.60 × 103 |
| f4 | 400 | 4.87 × 102 | 3.56 × 10 | 4.80 × 102 | 3.39 × 10 |
| f5 | 500 | 6.11 × 102 | 2.27 × 10 | 6.00 × 102 | 2.02 × 10 |
| f6 | 600 | 6.00 × 102 | 1.36 × 10−2 | 6.00 × 102 | 1.13 × 10−2 |
| f7 | 700 | 8.53 × 102 | 1.68 × 10 | 8.60 × 102 | 1.70 × 10 |
| f8 | 800 | 9.05 × 102 | 2.12 × 10 | 9.06 × 102 | 2.27 × 10 |
| f9 | 900 | 9.01 × 102 | 6.89 × 10−1 | 9.04 × 102 | 1.44 × 10 |
| f10 | 1000 | 6.21 × 103 | 6.89 × 10−1 | 6.05 × 103 | 5.03 × 102 |
| f11 | 1100 | 1.19 × 103 | 2.31 × 10 | 1.19 × 103 | 2.90 × 10 |
| f12 | 1200 | 1.56 × 105 | 1.03 × 105 | 1.81 × 105 | 1.48 × 105 |
| f13 | 1300 | 3.56 × 103 | 9.09 × 102 | 4.01 × 103 | 1.00 × 103 |
| f14 | 1400 | 1.50 × 103 | 1.03 × 10 | 1.50 × 103 | 1.06 × 10 |
| f15 | 1500 | 1.70 × 103 | 4.43 × 10 | 1.70 × 103 | 3.95 × 10 |
| f16 | 1600 | 2.45 × 103 | 2.66 × 102 | 2.47 × 103 | 2.14 × 102 |
| f17 | 1700 | 1.85 × 103 | 6.65 × 10 | 1.86 × 103 | 8.06 × 10 |
| f18 | 1800 | 2.87 × 103 | 6.86 × 102 | 2.69 × 103 | 3.69 × 102 |
| f19 | 1900 | 1.99 × 103 | 1.88 × 10 | 1.99 × 103 | 1.87 × 10 |
| f20 | 2000 | 2.39 × 103 | 2.58 × 10 | 2.22 × 103 | 1.12 × 102 |
| f21 | 2100 | 2.40 × 103 | 2.28 × 10 | 2.39 × 103 | 2.51 × 10 |
| f22 | 2200 | 2.30 × 103 | 1.50 × 10−2 | 2.30 × 103 | 7.44 × 10−3 |
| f23 | 2300 | 2.74 × 103 | 2.86 × 10 | 2.73 × 103 | 2.26 × 10 |
| f24 | 2400 | 2.91 × 103 | 3.37 × 10 | 2.90 × 103 | 3.04 × 10 |
| f25 | 2500 | 2.89 × 103 | 1.73 | 2.89 × 103 | 9.76 × 10−1 |
| f26 | 2600 | 4.28 × 103 | 5.50 × 102 | 4.22 × 103 | 6.59 × 102 |
| f27 | 2700 | 3.22 × 103 | 8.08 | 3.22 × 103 | 7.37 |
| f28 | 2800 | 3.21 × 103 | 1.25 × 10 | 3.21 × 103 | 1.27 × 10 |
| f29 | 2900 | 3.63 × 103 | 1.06 × 102 | 3.59 × 103 | 1.13 × 102 |
| f30 | 3000 | 1.32 × 104 | 3.29 × 103 | 1.51 × 104 | 5.55 × 103 |
| Dynamic Stochastic Fractal Search (DSFS) with 50 Dimensions | |||||
|---|---|---|---|---|---|
| Type-1 Fuzzy Logic | Type-2 Fuzzy Logic | ||||
| Function | fi | Main | Std | Main | Std |
| f1 | 100 | 9.00 × 104 | 4.30 × 104 | 8.42 × 104 | 6.69 × 104 |
| f2 | 200 | 1.20 × 1040 | 4.53 × 1040 | 5.08 × 1039 | 1.52 × 1040 |
| f3 | 300 | 6.01 × 104 | 9.72 × 103 | 6.28 × 104 | 1.39 × 104 |
| f4 | 400 | 5.72 × 102 | 4.05 × 10 | 5.69 × 102 | 4.26 × 10 |
| f5 | 500 | 7.68 × 102 | 4.35 × 10 | 7.69 × 102 | 4.59 × 10 |
| f6 | 600 | 6.01 × 102 | 1.35 × 10−1 | 6.01 × 102 | 1.55 × 10−1 |
| f7 | 700 | 1.05 × 103 | 3.18 × 10 | 1.06 × 103 | 2.61 × 10 |
| f8 | 800 | 1.06 × 103 | 3.69 × 10 | 1.06 × 103 | 4.42 × 10 |
| f9 | 900 | 1.13 × 103 | 1.49 × 102 | 1.14 × 103 | 1.22 × 102 |
| f10 | 1000 | 1.13 × 104 | 4.84 × 102 | 1.12 × 104 | 6.53 × 102 |
| f11 | 1100 | 1.36 × 103 | 3.00 × 10 | 1.36 × 103 | 4.30 × 10 |
| f12 | 1200 | 3.54 × 106 | 1.42 × 106 | 3.47 × 106 | 1.96 × 106 |
| f13 | 1300 | 1.48 × 104 | 1.17 × 104 | 1.67 × 104 | 1.36 × 104 |
| f14 | 1400 | 1.50 × 103 | 1.03 × 10 | 1.80 × 103 | 8.36 × 10 |
| f15 | 1500 | 4.14 × 103 | 1.54 × 103 | 3.75 × 103 | 8.43 × 102 |
| f16 | 1600 | 3.52 × 103 | 3.87 × 102 | 3.58 × 103 | 4.80 × 102 |
| f17 | 1700 | 3.05 × 103 | 2.37 × 102 | 3.04 × 103 | 2.56 × 102 |
| f18 | 1800 | 5.42 × 104 | 3.34 × 104 | 5.39 × 104 | 3.20 × 104 |
| f19 | 1900 | 7.10 × 103 | 4.05 × 103 | 7.73 × 103 | 5.45 × 103 |
| f20 | 2000 | 3.10 × 103 | 2.16 × 102 | 3.14 × 103 | 2.36 × 102 |
| f21 | 2100 | 2.55 × 103 | 4.55 × 10 | 2.55 × 103 | 4.99 × 10 |
| f22 | 2200 | 1.10 × 104 | 4.12 × 103 | 1.23 × 104 | 3.40 × 103 |
| f23 | 2300 | 3.00 × 103 | 4.43 × 10 | 2.98 × 103 | 4.91 × 10 |
| f24 | 2400 | 3.14 × 103 | 5.98 × 10 | 3.14 × 103 | 5.85 × 10 |
| f25 | 2500 | 3.07 × 103 | 2.52 × 10 | 3.08 × 103 | 2.22 × 10 |
| f26 | 2600 | 6.07 × 103 | 5.92 × 102 | 6.16 × 103 | 4.77 × 102 |
| f27 | 2700 | 3.41 × 103 | 4.40 × 10 | 3.40 × 103 | 4.09 × 10 |
| f28 | 2800 | 3.36 × 103 | 3.36 × 10 | 3.35 × 103 | 3.44 × 10 |
| f29 | 2900 | 4.15 × 103 | 2.71 × 102 | 4.17 × 103 | 2.55 × 102 |
| f30 | 3000 | 3.25 × 106 | 6.84 × 105 | 3.24 × 106 | 8.20 × 105 |
| Dynamic Stochastic Fractal Search DSFS with 100 Dimensions | |||||
|---|---|---|---|---|---|
| Type-1 Fuzzy Logic | Type-2 Fuzzy Logic | ||||
| Function | fi | Main | Std | Main | Std |
| f1 | 100 | 1.15 × 108 | 4.36 × 107 | 1.08 × 108 | 3.31 × 107 |
| f2 | 200 | 1.34 × 10108 | 8.85 × 10108 | 1.14 × 10111 | 5.81 × 10111 |
| f3 | 300 | 2.53 × 105 | 2.78 × 104 | 2.56 × 105 | 2.78 × 104 |
| f4 | 400 | 9.23 × 102 | 4.74 × 10 | 9.37 × 102 | 6.10 × 10 |
| f5 | 500 | 1.29 × 103 | 9.15 × 10 | 1.29 × 103 | 7.11 × 10 |
| f6 | 600 | 6.07 × 102 | 1.33 | 6.07 × 102 | 1.02 |
| f7 | 700 | 1.72 × 103 | 5.61 × 10 | 1.73 × 103 | 5.30 × 10 |
| f8 | 800 | 1.58 × 103 | 7.70 × 10 | 1.59 × 103 | 8.69 × 10 |
| f9 | 900 | 1.19 × 104 | 3.07 × 103 | 1.28 × 104 | 4.21 × 103 |
| f10 | 1000 | 2.71 × 104 | 1.04 × 103 | 2.72 × 104 | 9.91 × 102 |
| f11 | 1100 | 1.62 × 104 | 3.86 × 103 | 1.63 × 104 | 4.35 × 103 |
| f12 | 1200 | 6.66 × 107 | 2.09 × 107 | 7.05 × 107 | 1.74 × 107 |
| f13 | 1300 | 5.66 × 103 | 1.80 × 103 | 6.16 × 103 | 2.89 × 103 |
| f14 | 1400 | 3.36 × 105 | 2.50 × 105 | 2.36 × 105 | 1.44 × 105 |
| f15 | 1500 | 4.46 × 103 | 4.66 × 103 | 4.39 × 103 | 3.13 × 103 |
| f16 | 1600 | 7.97 × 103 | 8.58 × 102 | 7.70 × 103 | 7.93 × 102 |
| f17 | 1700 | 6.04 × 103 | 3.39 × 102 | 5.90 × 103 | 5.76 × 102 |
| f18 | 1800 | 5.97 × 105 | 3.86 × 105 | 6.45 × 105 | 3.99 × 105 |
| f19 | 1900 | 3.60 × 103 | 1.65 × 103 | 3.49 × 103 | 1.56 × 103 |
| f20 | 2000 | 2.18 × 103 | 8.28 × 10 | 6.27 × 103 | 4.30 × 102 |
| f21 | 2100 | 3.11 × 103 | 6.75 × 10 | 3.11 × 103 | 6.06 × 10 |
| f22 | 2200 | 2.96 × 104 | 8.67 × 102 | 2.97 × 104 | 8.23 × 102 |
| f23 | 2300 | 3.59 × 103 | 5.69 × 10 | 3.57 × 103 | 7.87 × 10 |
| f24 | 2400 | 4.09 × 103 | 9.76 × 10 | 4.08 × 103 | 1.19 × 102 |
| f25 | 2500 | 3.63 × 103 | 6.17 × 10 | 3.63 × 103 | 5.46 × 10 |
| f26 | 2600 | 1.41 × 104 | 1.04 × 103 | 1.42 × 104 | 8.28 × 102 |
| f27 | 2700 | 3.72 × 103 | 7.06 × 10 | 3.73 × 103 | 5.89 × 10 |
| f28 | 2800 | 3.96 × 103 | 1.11 × 102 | 3.96 × 103 | 1.35 × 102 |
| f29 | 2900 | 7.96 × 103 | 5.34 × 102 | 7.96 × 103 | 5.11 × 102 |
| f30 | 3000 | 3.04 × 105 | 1.27 × 105 | 3.18 × 105 | 1.68 × 105 |
| HFPSO [40] | DSFS Type-1 Fuzzy Logic | DSFS Type-2 Fuzzy Logic | |||||
|---|---|---|---|---|---|---|---|
| Function | fi | Mean | Std | Mean | Std | Mean | Std |
| f1 | 100 | 9.81 × 108 | 1.01 × 102 | 1.01 × 102 | 4.87 × 10−1 | 1.01 × 102 | 7.85 × 10−1 |
| f2 | 200 | 4.91 × 108 | 2.00 × 102 | 2.00 × 102 | 0.00 | 2.00 × 102 | 0.00 |
| f3 | 300 | 5.96 × 103 | 3.00 × 102 | 3.00 × 102 | 3.73 × 10−6 | 3.00 × 102 | 5.04 × 10−6 |
| f4 | 400 | 4.55 × 10 | 4.01 × 102 | 4.01 × 102 | 7.81 × 10−1 | 4.00 × 102 | 6.19 × 10−1 |
| f5 | 500 | 1.84 × 10 | 5.06 × 102 | 5.06 × 102 | 2.04 | 5.07 × 102 | 2.64 |
| f6 | 600 | 1.35 × 10 | 6.00 × 102 | 6.00 × 102 | 7.21 × 10−8 | 6.00 × 102 | 6.24 × 10−8 |
| f7 | 700 | 1.73 × 10 | 7.19 × 102 | 7.19 × 102 | 3.45 | 7.20 × 102 | 3.32 |
| f8 | 800 | 1.44 × 10 | 8.07 × 102 | 8.07 × 102 | 3.04 | 8.07 × 102 | 2.44 |
| f9 | 900 | 3.07 × 102 | 9.00 × 102 | 9.00 × 102 | 0.00 | 9.00 × 102 | 0.00 |
| f10 | 1000 | 3.79 × 102 | 1.40 × 103 | 1.40 × 103 | 1.70 × 102 | 1.34 × 103 | 1.31 × 102 |
| f11 | 1100 | 5.24 × 10 | 1.10 × 103 | 1.10 × 103 | 9.31 × 10−1 | 1.10 × 103 | 1.00 |
| f12 | 1200 | 4.13 × 106 | 1.50 × 103 | 1.50 × 103 | 1.04 × 102 | 1.52 × 103 | 1.02 × 102 |
| f13 | 1300 | 7.68 × 103 | 1.31 × 103 | 1.31 × 103 | 4.03 | 1.31 × 103 | 4.14 |
| f14 | 1400 | 4.18 × 103 | 1.40 × 103 | 1.40 × 103 | 1.69 | 1.40 × 103 | 2.01 |
| f15 | 1500 | 2.37 × 104 | 1.50 × 103 | 1.50 × 103 | 7.24 × 10−1 | 1.50 × 103 | 8.88 × 10−1 |
| f16 | 1600 | 1.59 × 102 | 1.60 × 103 | 1.60 × 103 | 2.79 × 10−1 | 1.60 × 103 | 3.64 × 10−1 |
| f17 | 1700 | 8.40 × 10 | 1.70 × 103 | 1.70 × 103 | 2.68 | 1.71 × 103 | 4.41 |
| f18 | 1800 | 1.79 × 104 | 1.81 × 103 | 1.81 × 103 | 2.56 | 1.81 × 103 | 2.57 |
| f19 | 1900 | 3.83 × 104 | 1.90 × 103 | 1.90 × 103 | 4.15 × 10−1 | 1.90 × 103 | 4.45 × 10−1 |
| f20 | 2000 | 1.08 × 102 | 2.00 × 103 | 2.00 × 103 | 1.39 × 10−1 | 2.00 × 103 | 4.73 × 10−3 |
| f21 | 2100 | 4.78 × 10 | 2.23 × 103 | 2.23 × 103 | 5.08 × 10 | 2.24 × 103 | 5.40 × 10 |
| f22 | 2200 | 5.88 × 102 | 2.29 × 103 | 2.29 × 103 | 2.17 × 10 | 2.28 × 103 | 3.93 × 10 |
| f23 | 2300 | 2.87 × 10 | 2.61 × 103 | 2.61 × 103 | 2.80 | 2.60 × 103 | 5.61 × 10 |
| f24 | 2400 | 1.47 × 102 | 2.61 × 103 | 2.61 × 103 | 1.22 × 102 | 2.63 × 103 | 1.14 × 102 |
| f25 | 2500 | 5.02 × 10 | 2.90 × 103 | 2.90 × 103 | 1.08 × 10 | 2.90 × 103 | 1.15 × 10 |
| f26 | 2600 | 3.42 × 102 | 2.90 × 103 | 2.90 × 103 | 2.15 × 10−10 | 2.90 × 103 | 3.02 × 10−10 |
| f27 | 2700 | 3.94 × 10 | 3.09 × 103 | 3.09 × 103 | 1.97 | 3.09 × 103 | 2.14 |
| f28 | 2800 | 1.08 × 102 | 3.09 × 103 | 3.09 × 103 | 4.20 × 10 | 3.11 × 103 | 5.69 × 10 |
| f29 | 2900 | 9.40 × 10 | 3.16 × 103 | 3.16 × 103 | 1.01 × 10 | 3.16 × 103 | 9.65 |
| f30 | 3000 | 3.75 × 106 | 3.56 × 103 | 3.56 × 103 | 2.30 × 102 | 3.55 × 103 | 1.19 × 102 |
| HFPSO [40] | DSFS Type-1 Fuzzy Logic | DSFS Type-2 Fuzzy Logic | |||||
|---|---|---|---|---|---|---|---|
| Function | fi | Mean | Std | Mean | Std | Mean | Std |
| f1 | 100 | 9.81 × 108 | 1.01 × 102 | 3.49 × 103 | 2.76 × 103 | 3.24 × 103 | 2.74 × 103 |
| f2 | 200 | 4.91 × 108 | 2.00 × 102 | 3.06 × 1016 | 7.11 × 1016 | 7.59 × 1017 | 3.98 × 1018 |
| f3 | 300 | 5.96 × 103 | 3.00 × 102 | 8.40 × 103 | 3.95 × 103 | 8.79 × 103 | 4.60 × 103 |
| f4 | 400 | 4.55 × 10 | 4.01 × 102 | 4.87 × 102 | 3.56 × 10 | 4.80 × 102 | 3.39 × 10 |
| f5 | 500 | 1.84 × 10 | 5.06 × 102 | 6.11 × 102 | 2.27 × 10 | 6.00 × 102 | 2.02 × 10 |
| f6 | 600 | 1.35 × 10 | 6.00 × 102 | 6.00 × 102 | 1.36 × 10−2 | 6.00 × 102 | 1.13 × 10−2 |
| f7 | 700 | 1.73 × 10 | 7.19 × 102 | 8.53 × 102 | 1.68 × 10 | 8.60 × 102 | 1.70 × 10 |
| f8 | 800 | 1.44 × 10 | 8.07 × 102 | 9.05 × 102 | 2.12 × 10 | 9.06 × 102 | 2.27 × 10 |
| f9 | 900 | 3.07 × 102 | 9.00 × 102 | 9.01 × 102 | 6.89 × 10−1 | 9.04 × 102 | 1.44 × 10 |
| f10 | 1000 | 3.79 × 102 | 1.40 × 103 | 6.21 × 103 | 6.89 × 10−1 | 6.05 × 103 | 5.03 × 102 |
| f11 | 1100 | 5.24 × 10 | 1.10 × 103 | 1.19 × 103 | 2.31 × 10 | 1.19 × 103 | 2.90 × 10 |
| f12 | 1200 | 4.13 × 106 | 1.50 × 103 | 1.56 × 105 | 1.03 × 105 | 1.81 × 105 | 1.48 × 105 |
| f13 | 1300 | 7.68 × 103 | 1.31 × 103 | 3.56 × 103 | 9.09 × 102 | 4.01 × 103 | 1.00 × 103 |
| f14 | 1400 | 4.18 × 103 | 1.40 × 103 | 1.50 × 103 | 1.03 × 10 | 1.50 × 103 | 1.06 × 10 |
| f15 | 1500 | 2.37 × 104 | 1.50 × 103 | 1.70 × 103 | 4.43 × 10 | 1.70 × 103 | 3.95 × 10 |
| f16 | 1600 | 1.59 × 102 | 1.60 × 103 | 2.45 × 103 | 2.66 × 102 | 2.47 × 103 | 2.14 × 102 |
| f17 | 1700 | 8.40 × 10 | 1.70 × 103 | 1.85 × 103 | 6.65 × 10 | 1.86 × 103 | 8.06 × 10 |
| f18 | 1800 | 1.79 × 104 | 1.81 × 103 | 2.87 × 103 | 6.86 × 102 | 2.69 × 103 | 3.69 × 102 |
| f19 | 1900 | 3.83 × 104 | 1.90 × 103 | 1.99 × 103 | 1.88 × 10 | 1.99 × 103 | 1.87 × 10 |
| f20 | 2000 | 1.08 × 102 | 2.00 × 103 | 2.39 × 103 | 2.58 × 10 | 2.22 × 103 | 1.12 × 102 |
| f21 | 2100 | 4.78 × 10 | 2.23 × 103 | 2.40 × 103 | 2.28 × 10 | 2.39 × 103 | 2.51 × 10 |
| f22 | 2200 | 5.88 × 102 | 2.29 × 103 | 2.30 × 103 | 1.50 × 10−2 | 2.30 × 103 | 7.44 × 10−3 |
| f23 | 2300 | 2.87 × 10 | 2.61 × 103 | 2.74 × 103 | 2.86 × 10 | 2.73 × 103 | 2.26 × 10 |
| f24 | 2400 | 1.47 × 102 | 2.61 × 103 | 2.91 × 103 | 3.37 × 10 | 2.90 × 103 | 3.04 × 10 |
| f25 | 2500 | 5.02 × 10 | 2.90 × 103 | 2.89 × 103 | 1.73 | 2.89 × 103 | 9.76 × 10−1 |
| f26 | 2600 | 3.42 × 102 | 2.90 × 103 | 4.28 × 103 | 5.50 × 102 | 4.22 × 103 | 6.59 × 102 |
| f27 | 2700 | 3.94 × 10 | 3.09 × 103 | 3.22 × 103 | 8.08 | 3.22 × 103 | 7.37 |
| f28 | 2800 | 1.08 × 102 | 3.09 × 103 | 3.21 × 103 | 1.25 × 10 | 3.21 × 103 | 1.27 × 10 |
| f29 | 2900 | 9.40 × 10 | 3.16 × 103 | 3.63 × 103 | 1.06 × 102 | 3.59 × 103 | 1.13 × 102 |
| f30 | 3000 | 3.75 × 106 | 3.56 × 103 | 1.32 × 104 | 3.29 × 103 | 1.51 × 104 | 5.55 × 103 |
| HFPSO [40] | DSFS | |||||
|---|---|---|---|---|---|---|
| Type-1 Fuzzy Logic | ||||||
| Function | fi | Mean | Std | Mean | Std | z |
| f1 | 100 | 9.81 × 108 | 1.01 × 102 | 1.01 × 102 | 4.87 × 10−1 | 3.76 × 107 |
| f2 | 200 | 4.91 × 108 | 2.00 × 102 | 2.00 × 102 | 0.00 | 9.51 × 106 |
| f3 | 300 | 5.96 × 103 | 3.00 × 102 | 3.00 × 102 | 3.73 × 10−6 | 7.31 × 10 |
| f4 | 400 | 4.55 × 10 | 4.01 × 102 | 4.01 × 102 | 7.81 × 10−1 | −3.43 |
| f5 | 500 | 1.84 × 10 | 5.06 × 102 | 5.06 × 102 | 2.04 | −3.73 |
| f6 | 600 | 1.35 × 10 | 6.00 × 102 | 6.00 × 102 | 7.21 × 10−8 | −3.79 |
| f7 | 700 | 1.73 × 10 | 7.19 × 102 | 7.19 × 102 | 3.45 | −3.78 |
| f8 | 800 | 1.44 × 10 | 8.07 × 102 | 8.07 × 102 | 3.04 | −3.80 |
| f9 | 900 | 3.07 × 102 | 9.00 × 102 | 9.00 × 102 | 0.00 | −2.55 |
| f10 | 1000 | 3.79 × 102 | 1.40 × 103 | 1.40 × 103 | 1.70 × 102 | −2.82 |
| f11 | 1100 | 5.24 × 10 | 1.10 × 103 | 1.10 × 103 | 9.31 × 10−1 | −3.69 |
| f12 | 1200 | 4.13 × 106 | 1.50 × 103 | 1.50 × 103 | 1.04 × 102 | 1.07 × 104 |
| f13 | 1300 | 7.68 × 103 | 1.31 × 103 | 1.31 × 103 | 4.03 | 1.88 × 10 |
| f14 | 1400 | 4.18 × 103 | 1.40 × 103 | 1.40 × 103 | 1.69 | 7.69 |
| f15 | 1500 | 2.37 × 104 | 1.50 × 103 | 1.50 × 103 | 7.24 × 10−1 | 5.73 × 10 |
| f16 | 1600 | 1.59 × 102 | 1.60 × 103 | 1.60 × 103 | 2.79 × 10−1 | −3.49 |
| f17 | 1700 | 8.40 × 10 | 1.70 × 103 | 1.70 × 103 | 2.68 | −3.68 |
| f18 | 1800 | 1.79 × 104 | 1.81 × 103 | 1.81 × 103 | 2.56 | 3.44 × 10 |
| f19 | 1900 | 3.83 × 104 | 1.90 × 103 | 1.90 × 103 | 4.15 × 10−1 | 7.42 × 10 |
| f20 | 2000 | 1.08 × 102 | 2.00 × 103 | 2.00 × 103 | 1.39 × 10−1 | −3.66 |
| f21 | 2100 | 4.78 × 10 | 2.23 × 103 | 2.23 × 103 | 5.08 × 10 | −3.79 |
| f22 | 2200 | 5.88 × 102 | 2.29 × 103 | 2.29 × 103 | 2.17 × 10 | −2.88 |
| f23 | 2300 | 2.87 × 10 | 2.61 × 103 | 2.61 × 103 | 2.80 | −3.83 |
| f24 | 2400 | 1.47 × 102 | 2.61 × 103 | 2.61 × 103 | 1.22 × 102 | −3.65 |
| f25 | 2500 | 5.02 × 10 | 2.90 × 103 | 2.90 × 103 | 1.08 × 10 | −3.81 |
| f26 | 2600 | 3.42 × 102 | 2.90 × 103 | 2.90 × 103 | 2.15 × 10−10 | −3.42 |
| f27 | 2700 | 3.94 × 10 | 3.09 × 103 | 3.09 × 103 | 1.97 | −3.82 |
| f28 | 2800 | 1.08 × 102 | 3.09 × 103 | 3.09 × 103 | 4.20 × 10 | −3.74 |
| f29 | 2900 | 9.40 × 10 | 3.16 × 103 | 3.16 × 103 | 1.01 × 10 | −3.76 |
| f30 | 3000 | 3.75 × 106 | 3.56 × 103 | 3.56 × 103 | 2.30 × 102 | 4.08 × 103 |
| HFPSO [40] | DSFS | |||||
|---|---|---|---|---|---|---|
| Type-1 Fuzzy Logic | ||||||
| Function | fi | Mean | Std | Mean | Std | z |
| f1 | 100 | 9.81 × 108 | 1.01 × 102 | 3.49 × 103 | 2.76 × 103 | 1.95 × 106 |
| f2 | 200 | 4.91 × 108 | 2.00 × 102 | 3.06 × 1016 | 7.11 × 1016 | −2.36 |
| f3 | 300 | 5.96 × 103 | 3.00 × 102 | 8.40 × 103 | 3.95 × 103 | −3.37 |
| f4 | 400 | 4.55 × 10 | 4.01 × 102 | 4.87 × 102 | 3.56 × 10 | −6.01 |
| f5 | 500 | 1.84 × 10 | 5.06 × 102 | 6.11 × 102 | 2.27 × 10 | −6.41 |
| f6 | 600 | 1.35 × 10 | 6.00 × 102 | 6.00 × 102 | 1.36 × 10−2 | −5.35 |
| f7 | 700 | 1.73 × 10 | 7.19 × 102 | 8.53 × 102 | 1.68 × 10 | −6.36 |
| f8 | 800 | 1.44 × 10 | 8.07 × 102 | 9.05 × 102 | 2.12 × 10 | −6.04 |
| f9 | 900 | 3.07 × 102 | 9.00 × 102 | 9.01 × 102 | 6.89 × 10−1 | −3.61 |
| f10 | 1000 | 3.79 × 102 | 1.40 × 103 | 6.21 × 103 | 6.89 × 10−1 | −2.28 × 10 |
| f11 | 1100 | 5.24 × 10 | 1.10 × 103 | 1.19 × 103 | 2.31 × 10 | −5.66 |
| f12 | 1200 | 4.13 × 106 | 1.50 × 103 | 1.56 × 105 | 1.03 × 105 | 2.11 × 102 |
| f13 | 1300 | 7.68 × 103 | 1.31 × 103 | 3.56 × 103 | 9.09 × 102 | 1.42 × 10 |
| f14 | 1400 | 4.18 × 103 | 1.40 × 103 | 1.50 × 103 | 1.03 × 10 | 1.05 × 10 |
| f15 | 1500 | 2.37 × 104 | 1.50 × 103 | 1.70 × 103 | 4.43 × 10 | 8.03 × 10 |
| f16 | 1600 | 1.59 × 102 | 1.60 × 103 | 2.45 × 103 | 2.66 × 102 | −7.74 |
| f17 | 1700 | 8.40 × 10 | 1.70 × 103 | 1.85 × 103 | 6.65 × 10 | −5.69 |
| f18 | 1800 | 1.79 × 104 | 1.81 × 103 | 2.87 × 103 | 6.86 × 102 | 4.25 × 10 |
| f19 | 1900 | 3.83 × 104 | 1.90 × 103 | 1.99 × 103 | 1.88 × 10 | 1.05 × 102 |
| f20 | 2000 | 1.08 × 102 | 2.00 × 103 | 2.39 × 103 | 2.58 × 10 | −6.25 |
| f21 | 2100 | 4.78 × 10 | 2.23 × 103 | 2.40 × 103 | 2.28 × 10 | −5.78 |
| f22 | 2200 | 5.88 × 102 | 2.29 × 103 | 2.30 × 103 | 1.50 × 10−2 | −4.09 |
| f23 | 2300 | 2.87 × 10 | 2.61 × 103 | 2.74 × 103 | 2.86 × 10 | −5.69 |
| f24 | 2400 | 1.47 × 102 | 2.61 × 103 | 2.91 × 103 | 3.37 × 10 | −5.80 |
| f25 | 2500 | 5.02 × 10 | 2.90 × 103 | 2.89 × 103 | 1.73 | −5.36 |
| f26 | 2600 | 3.42 × 102 | 2.90 × 103 | 4.28 × 103 | 5.50 × 102 | −7.31 |
| f27 | 2700 | 3.94 × 10 | 3.09 × 103 | 3.22 × 103 | 8.08 | −5.64 |
| f28 | 2800 | 1.08 × 102 | 3.09 × 103 | 3.21 × 103 | 1.25 × 10 | −5.50 |
| f29 | 2900 | 9.40 × 10 | 3.16 × 103 | 3.63 × 103 | 1.06 × 102 | −6.13 |
| f30 | 3000 | 3.75 × 106 | 3.56 × 103 | 1.32 × 104 | 3.29 × 103 | 4.22 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagunes, M.L.; Castillo, O.; Valdez, F.; Soria, J.; Melin, P. A New Approach for Dynamic Stochastic Fractal Search with Fuzzy Logic for Parameter Adaptation. Fractal Fract. 2021, 5, 33. https://doi.org/10.3390/fractalfract5020033
Lagunes ML, Castillo O, Valdez F, Soria J, Melin P. A New Approach for Dynamic Stochastic Fractal Search with Fuzzy Logic for Parameter Adaptation. Fractal and Fractional. 2021; 5(2):33. https://doi.org/10.3390/fractalfract5020033
Chicago/Turabian StyleLagunes, Marylu L., Oscar Castillo, Fevrier Valdez, Jose Soria, and Patricia Melin. 2021. "A New Approach for Dynamic Stochastic Fractal Search with Fuzzy Logic for Parameter Adaptation" Fractal and Fractional 5, no. 2: 33. https://doi.org/10.3390/fractalfract5020033
APA StyleLagunes, M. L., Castillo, O., Valdez, F., Soria, J., & Melin, P. (2021). A New Approach for Dynamic Stochastic Fractal Search with Fuzzy Logic for Parameter Adaptation. Fractal and Fractional, 5(2), 33. https://doi.org/10.3390/fractalfract5020033









