Improving Real Estate Rental Estimations with Visual Data
Abstract
1. Introduction
Research Question
- Does the performance of a neural network that uses tabular features for predicting rental prices improve with additional training data that are non-structured, including advertised property images and satellite views?
- Does such a neural network outperform models trained solely on structured features?
2. Swiss Real Estate Dataset
2.1. Tabular Data
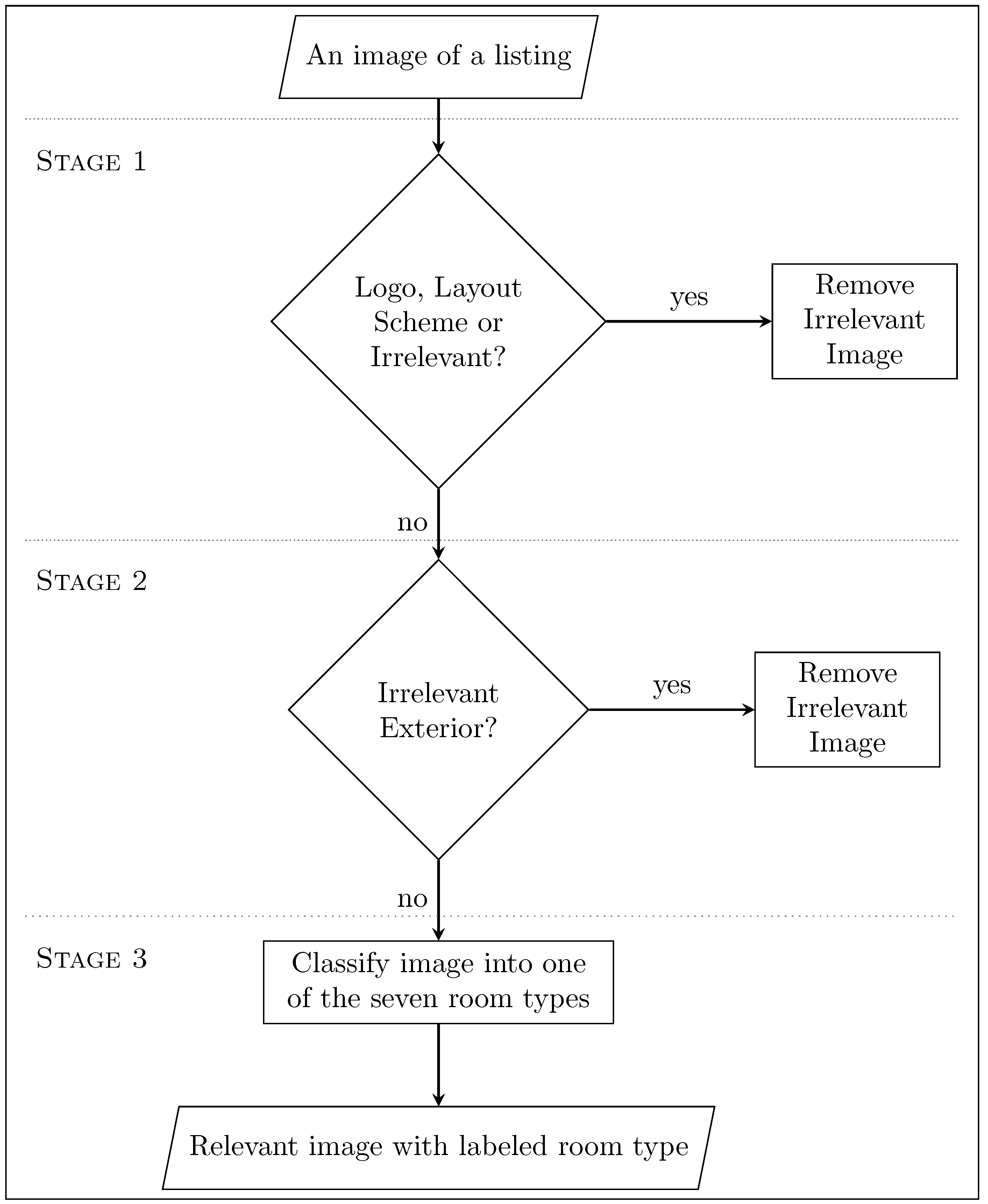
2.2. Image Data
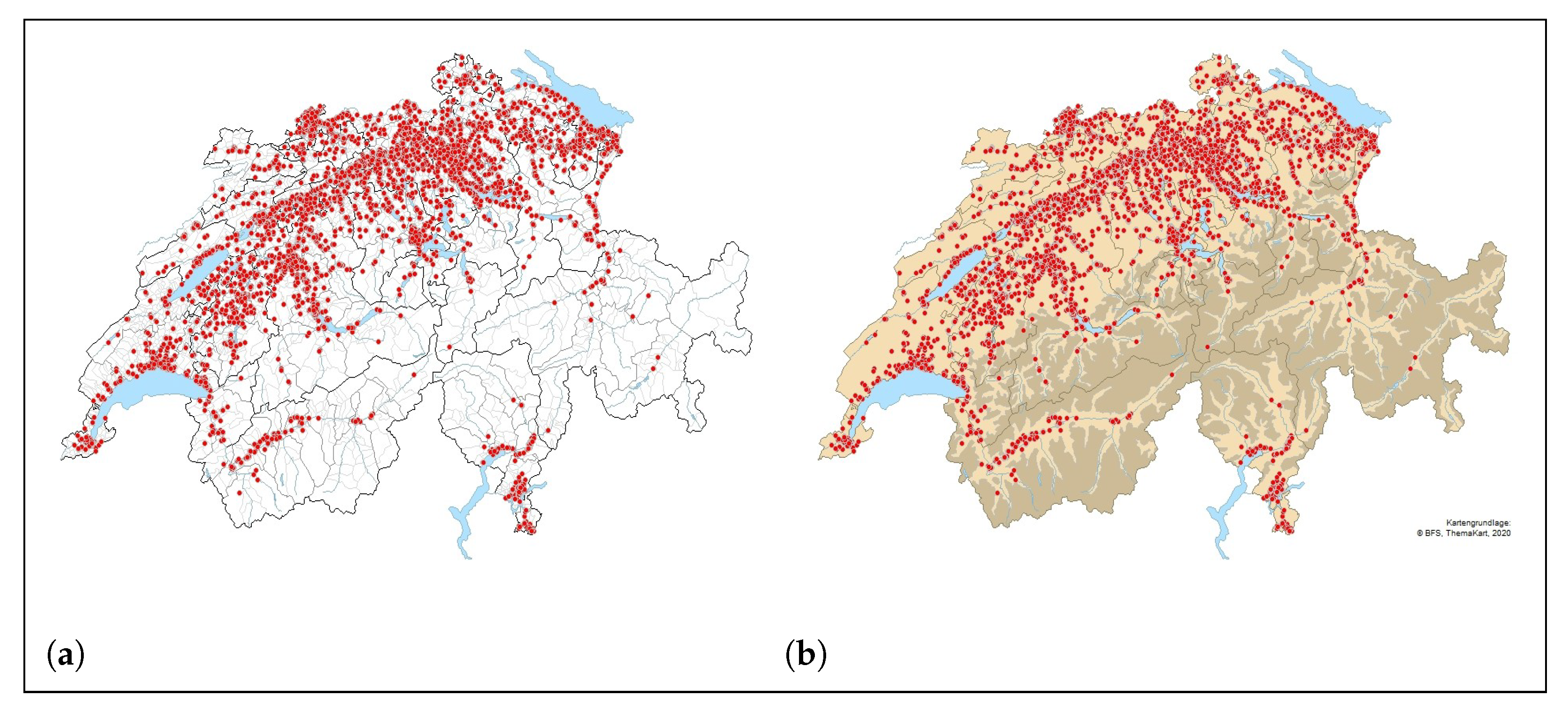
2.3. Satellite Data
2.4. Descriptive Statistics of the Final Dataset
3. Predictive Modeling
3.1. Performance Metrics
3.2. Classical Machine Learning Models
3.3. Artificial Neural Networks
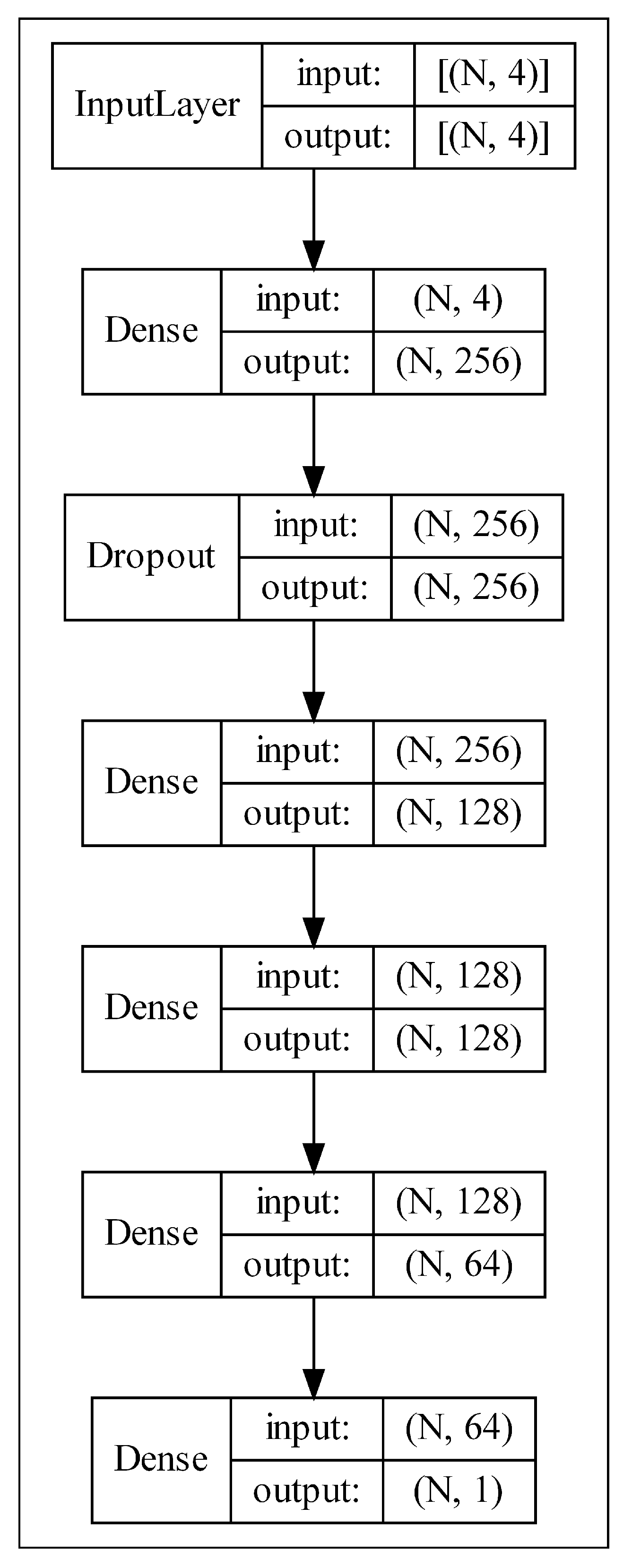
3.3.1. Multi-Layer Perceptron for Tabular Data
3.3.2. Feeding Multiple Images to NNs
- (1)
- Feeding all images one by one and using the same property price as the outcome for each image. The least challenging approach is arguably passing each image from the listing one at a time through a neural network while directly setting the price as the outcome for each image. Such an approach replicates many current observations with only the image differing. There are two main limitations to this approach. The first is the possibility of such a model becoming confused and ineffective, as it is missing the context from the other images, which impacts its ability to build the bigger picture. For instance, it may be that the bathrooms are the main driver of the price among all properties. Such a model would not be able to identify that since it is not comparing a bathroom against bathrooms but a bathroom against every other kind of room. Conceivably, we could classify the room type and only feed images from a selected number of categories. Nonetheless, the problem of comparison against widely different room types remains. The second issue with this approach is that the number of images of a given listing may impact the overall model prediction, hence biasing the outcome. For instance, a listing with eight images will have eight replicated entries, and, as opposed to a listing with one image, it may mislead the regression model and dilute the results.
- (2)
- Designingnindependent NNs for each of theximages whereby all the outputs fuse (e.g., concatenate) to predict a single price. The second option is to design n multiple NNs for the images, whereby n is either set as the maximum number of images found in all listings or fixed at the desired number. The former case is not feasible, as if x is the number of images for a given listing, and then for the difference , we would have to duplicate some of the x images or pass i as blank images (e.g., black or white images). Moreover, fixing the n could also work, and we could, for example, decide on setting , assuming that we have four types of images; however, we would need to feed the same kind of room type into the branches to make sure the images are directly cross-comparable. In addition, another issue with designing multiple models is that it may be computationally inefficient. We also suspect that since training configurations such as the optimizer and learning rate are kept constant among all variations of NNs, it may be more difficult for a model with multiple n branches to converge than a simpler model with fewer branches; however, this remains merely a hypothesis, and its validation goes beyond the scope of this thesis. Finally, an advantage of using n models is the ability to experiment with different branches by temporarily disabling inputs (one or more room types) to understand better what image/room types have the most significant impact on the prices.
- (3)
- Create montages that combinenimages of the same listing into one image. One possible way of feeding multiple images into a neural network is combining them into a montage with the room types. The work that closely resembles our intended methodology is [8], where the authors used generated montages of wheat plots to predict numerical outcomes related to plants, such as their plant height. Creating a montage of room types over the two previous methods is preferred, as an initial model (not presented in this paper) revealed that this approach outperforms the technique where the images are fed into the network one at a time. Moreover, the montage approach has been favored due to the simplicity of this approach compared to designing n independent models, as well as the possibility of assessing organized as opposed to randomly designed montages.
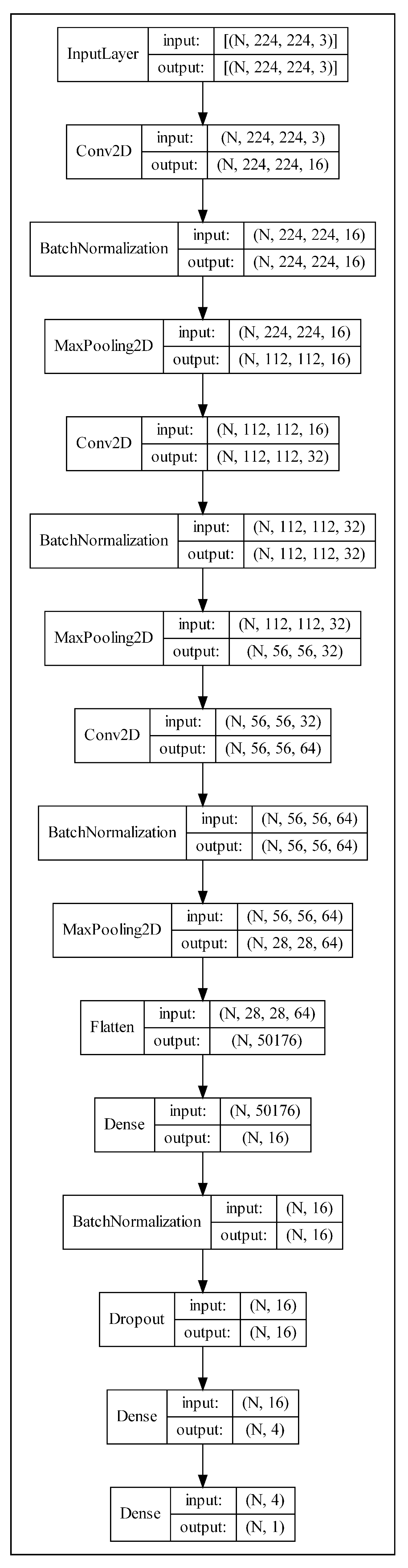
3.3.3. Gradient Boosting Machine for Visual Data
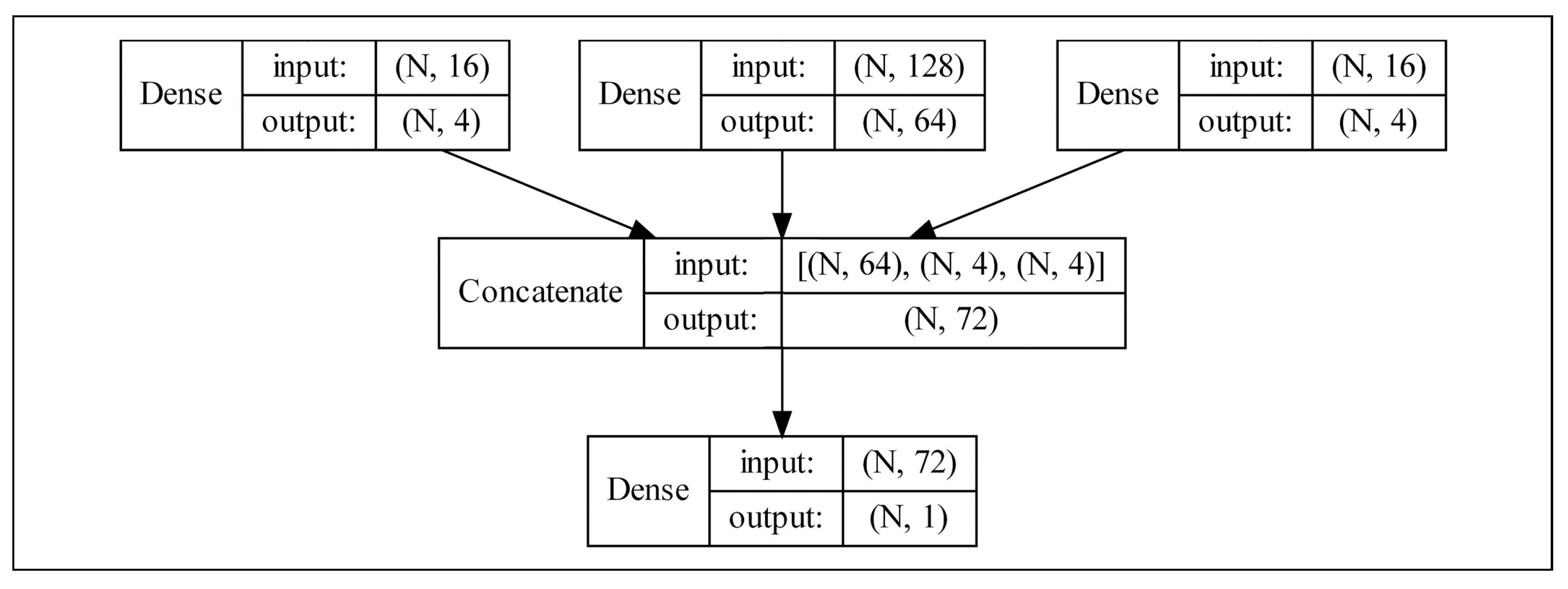
3.4. Multi-Modal Learning
3.4.1. Ablation Study
3.4.2. Performance Validation
4. Results and Discussion
5. Conclusions
- Additional input data, such as the advertisement description—another form of unstructured data—may benefit rental estimations. Two examples of applications may be in the forms of the information extraction (IE) of relevant features, where those features exist in an unstructured form, or providing all the descriptions as a new branch to NN T+OPI+SI without any intermediate feature extraction.
- Instead of one montage of property images with the chosen room types, it is possible to create a branch for each room type, allowing for ablation studies whereby branches are added to or removed from the model.
- It would be beneficial to perform a similar study on the sales prices and observe similarities and differences with the rental estimations. Such an experiment can be carried out either with the sales data gathered by us (not presented in this paper) or through an external dataset.
- Our dataset is based on the Swiss real estate market. However, further investigation is needed to know whether our findings can extend to other countries and markets.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | artificial neural network |
| AVM | automated valuations model |
| AdaMax | extension to the adaptive movement estimation optimization algorithm |
| CNN | convolutional neural network |
| GBM | gradient boosting machines |
| GBM T | gradient boosting machines with tabular features |
| IE | information extraction |
| LR T | linear regression with tabular features |
| MAE | mean absolute error |
| ML | classical machine learning models used throughout this paper: linear regression, random forest, gradient boosting machines, and eXtreme gradient boosting |
| MLP | multi-layer perceptron |
| MSE | mean squared error |
| NN | neural network |
| NN T | neural network with tabular features |
| NN T+CI | neural network with tabular features and cat images |
| NN T+OPI | neural network with tabular features and organized property images (interior and exterior) |
| NN T+OPI+SI | neural network with tabular features and organized property and satellite images |
| NN T+RPI | neural network with tabular features and randomly placed property images (interior and exterior) |
| NN T+SI | neural network with tabular features and satellite images |
| RF T | random forest with tabular features |
| RMSE | root mean squared error |
| ReLU | rectified linear unit (activation function) |
| SAR | spatial auto-regressions |
| SRED | Swiss Real Estate Dataset |
| SURF | speeded up robust features |
| SVM | support-vector machine |
| tanh | hyperbolic tangent (activation function) |
| XGB | eXtreme gradient boosting |
| XGB T | eXtreme gradient boosting with tabular features |
References
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models from Natural Language Supervision. In Proceedings of the 38th International Conference on Machine Learning, ICML 2021, Virtual Event, 18–24 July 2021; Meila, M., Zhang, T., Eds.; PMLR: Groveland, CA, USA, 2021; Volume 139, pp. 8748–8763. [Google Scholar]
- Ofli, F.; Alam, F.; Imran, M. Analysis of Social Media Data using Multimodal Deep Learning for Disaster Response. arXiv 2020, arXiv:2004.11838. [Google Scholar]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Baltrusaitis, T.; Ahuja, C.; Morency, L.P. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Sun, S. A survey of multi-view machine learning. Neural Comput. Appl. 2013, 23, 2031–2038. [Google Scholar] [CrossRef]
- Li, Y.; Yang, M.; Zhang, Z. A Survey of Multi-View Representation Learning. IEEE Trans. Knowl. Data Eng. 2019, 31, 1863–1883. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Shelter Island, NY, USA, 2017; Chapter 7; pp. 234–240. [Google Scholar]
- Apolo-Apolo, O.E.; Pérez-Ruiz, M.; Martínez-Guanter, J.; Egea, G. A mixed data-based deep neural network to estimate leaf area index in wheat breeding trials. Agronomy 2020, 10, 175. [Google Scholar] [CrossRef]
- Chau, K.; Chin, T.L. A Critical Review of Literature on the Hedonic Price Model. Int. J. Hous. Sci. Its Appl. 2003, 2, 145–165. [Google Scholar]
- Bourassa, S.C.; Cantoni, E.; Hoesli, M. Predicting house prices with spatial dependence: A comparison of alternative methods. J. Real Estate Res. 2010, 32, 139–159. [Google Scholar] [CrossRef]
- Law, S.; Paige, B.; Russell, C. Take a look around: Using street view and satellite images to estimate house prices. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Wittowsky, D.; Hoekveld, J.; Welsch, J.; Steier, M. Residential housing prices: Impact of housing characteristics, accessibility and neighbouring apartments—A case study of Dortmund, Germany. Urban Plan. Transp. Res. 2020, 8, 44–70. [Google Scholar] [CrossRef]
- Poursaeed, O.; Matera, T.; Belongie, S. Vision-based real estate price estimation. Mach. Vis. Appl. 2018, 29, 667–676. [Google Scholar] [CrossRef]
- Ahmed, E.H.; Moustafa, M. House price estimation from visual and textual features. In Proceedings of the 8th International Joint Conference on Computational Intelligence—NCTA, Porto, Portugal, 9–11 November 2016; Volume 3, pp. 62–68. [Google Scholar] [CrossRef][Green Version]
- Lee, C.; Park, K.H. Using photographs and metadata to estimate house prices in South Korea. Data Technol. Appl. 2020, 55, 280–292. [Google Scholar] [CrossRef]
- Zhao, Y.; Chetty, G.; Tran, D. Deep Learning with XGBoost for Real Estate Appraisal. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence, SSCI 2019, Xiamen, China, 6–9 December 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 1396–1401. [Google Scholar] [CrossRef]
- Murray, N.; Marchesotti, L.; Perronnin, F. AVA: A large-scale database for aesthetic visual analysis. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2408–2415. [Google Scholar] [CrossRef]
- Kucklick, J.P.; Oliver, M.; Str, W. A Comparison of Multi-View Learning Strategies for Satellite Image-Based Real Estate Appraisal. arXiv 2021, arXiv:2105.04984. [Google Scholar]
- Bency, A.J.; Rallapalli, S.; Ganti, R.K.; Srivatsa, M.; Manjunath, B.S. Beyond spatial auto-regressive models: Predicting housing prices with satellite imagery. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision, WACV 2017, Santa Rosa, CA, USA, 24–31 March 2017; pp. 320–329. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgo, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Nica, I.; Alexandru, D.B.; Crăciunescu, S.L.P.; Ionescu, Ș. Automated Valuation Modelling: Analysing Mortgage Behavioural Life Profile Models Using Machine Learning Techniques. Sustainability 2021, 13, 5162. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training; R Package Version 6.0-92; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- LeDell, E.; Gill, N.; Aiello, S.; Fu, A.; Candel, A.; Click, C.; Kraljevic, T.; Nykodym, T.; Aboyoun, P.; Kurka, M.; et al. h2o: R Interface for the ‘H2O’ Scalable Machine Learning Platform; R Package Version 3.36.1.2; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. xgboost: Extreme Gradient Boosting; R Package Version 1.6.0.1; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; Babenko, A. Revisiting Deep Learning Models for Tabular Data. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 18932–18943. [Google Scholar]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E.; Andina, D. Deep Learning for Computer Vision: A Brief Review. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 604–624. [Google Scholar] [CrossRef] [PubMed]
- Allaire, J.; Chollet, F. keras: R Interface to ‘Keras’; R Package Version 2.9.0; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Allaire, J.; Tang, Y. tensorflow: R Interface to ‘TensorFlow’; R Package Version 2.9.0; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Riordan, D.; Walsh, J. Deep learning vs. traditional computer vision. In Proceedings of the Science and Information Conference, Tokyo, Japan, 16–19 March 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 128–144. [Google Scholar]
- Feng, J.; Lu, S. Performance Analysis of Various Activation Functions in Artificial Neural Networks. J. Phys. Conf. Ser. 2019, 1237, 111–122. [Google Scholar] [CrossRef]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient BackProp. In Neural Networks: Tricks of the Trade, 2nd ed.; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–48. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-ResNet and the impact of residual connections on learning. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, AAAI 2017, San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, Conference Track Proceedings, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Meyes, R.; Lu, M.; de Puiseau, C.W.; Meisen, T. Ablation Studies in Artificial Neural Networks. arXiv 2019, arXiv:1901.08644. [Google Scholar]
- Zhang, W.; Sun, J.; Tang, X.; Zhang, W.; Sun, J.; Tang, X. Cat Head Detection— How to Effectively Exploit Shape and Texture Features. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Forsyth, D., Torr, P., Zisserman, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 802–816. [Google Scholar]
- Liu, T.; Abd-Elrahman, A.; Jon, M.; Wilhelm, V. Comparing Fully Convolutional Networks, Random Forest, Support Vector Machine, and Patch-based Deep Convolutional Neural Networks for Object-based Wetland Mapping using Images from small Unmanned Aircraft System. GIScience Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
- Gupta, S.; Arbeláez, P.; Malik, J. Perceptual Organization and Recognition of Indoor Scenes from RGB-D Images. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 564–571. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J. Diabetic Retinopathy Detection via Deep Convolutional Networks for Discriminative Localization and Visual Explanation. In Proceedings of the 2018 International Conference on Virtual Reality and Visualization (ICVRV), Qingdao, China, 22–24 October 2018. [Google Scholar]




| Class | No Test | Balanced | F1 | Sensitivity | Specificity |
|---|---|---|---|---|---|
| Samples | Accuracy | ||||
| Living room | 1210 | 0.905 | 0.828 | 0.850 | 0.960 |
| Kitchen | 1217 | 0.937 | 0.899 | 0.892 | 0.982 |
| Interior | 950 | 0.946 | 0.907 | 0.905 | 0.987 |
| Exterior | 1315 | 0.970 | 0.956 | 0.947 | 0.993 |
| Dining room | 975 | 0.920 | 0.860 | 0.862 | 0.979 |
| Bedroom | 1206 | 0.942 | 0.910 | 0.898 | 0.986 |
| Bathroom | 542 | 0.955 | 0.907 | 0.919 | 0.992 |
| Variable | Mean | SD | Min | Q1 | Median | Q3 | Max |
|---|---|---|---|---|---|---|---|
| price (CHF) | 1730 | 598 | 495 | 1385 | 1620 | 1935 | 7400 |
| living_space () | 86 | 31 | 19 | 68 | 83 | 100 | 1502 |
| rooms | 3.589 | 0.941 | 1.5 | 3 | 3.5 | 4.5 | 14 |
| lon | 8.018 | 0.812 | 6.043 | 7.456 | 7.899 | 8.633 | 9.869 |
| lat | 47.156 | 0.396 | 45.832 | 46.960 | 47.265 | 47.443 | 47.794 |
| Model | Hyperparameter | Value |
|---|---|---|
| GBM | Number of trees | 200 |
| Minimum number of observations in terminal nodes | 10 | |
| Column sampling rate | 1 | |
| Learning rate | 0.15 | |
| Maximum tree depth | 7 | |
| XGBoost | Maximum number of boosting iterations | 150 |
| Maximum tree depth | 15 | |
| Learning rate | 0.15 | |
| Lagrangian multiplier | 0 | |
| Subsample ratio of columns when constructing each tree | 0.75 | |
| Minimum sum of instance weight needed in a child | 1 | |
| Subsample ratio of the training instance | 1 |
| Model | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | Mean | Median | |
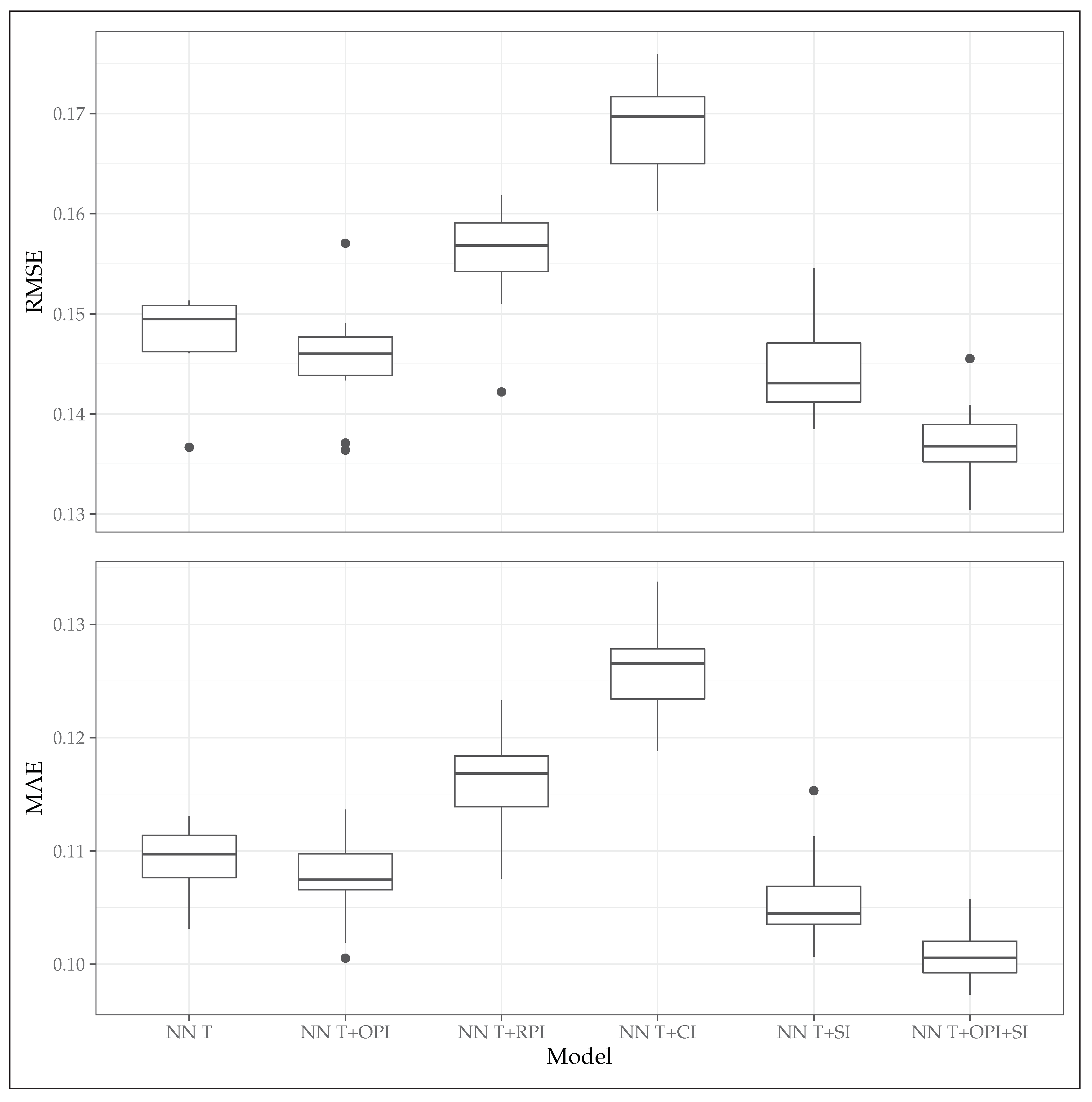
| NN T * | 0.148 | 0.149 | 0.109 | 0.110 | 0.744 | 0.741 |
| NN T+OPI † | 0.146 | 0.146 | 0.107 | 0.107 | 0.752 | 0.757 |
| NN T+RPI ‡ | 0.156 | 0.157 | 0.116 | 0.117 | 0.716 | 0.708 |
| NN T+CI § | 0.168 | 0.170 | 0.126 | 0.127 | 0.668 | 0.668 |
| NN T+SI †† | 0.144 | 0.143 | 0.106 | 0.105 | 0.756 | 0.754 |
| NN T+OPI+SI ‡‡ | 0.137 | 0.137 | 0.101 | 0.101 | 0.779 | 0.776 |
| Model | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| LR T a | 0.228 | 0.221 | 0.163 | 0.159 | 0.391 | 0.422 |
| RF T b | 0.065 | 0.144 | 0.047 | 0.105 | 0.955 | 0.753 |
| GBM T c | 0.100 | 0.139 | 0.076 | 0.103 | 0.884 | 0.770 |
| XGB T d | 0.026 | 0.137 | 0.017 | 0.099 | 0.993 | 0.775 |
| NN T e | 0.136 | 0.149 | 0.102 | 0.113 | 0.789 | 0.736 |
| NN T+OPI+SI f | 0.044 | 0.136 | 0.034 | 0.101 | 0.985 | 0.783 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azizi, I.; Rudnytskyi, I. Improving Real Estate Rental Estimations with Visual Data. Big Data Cogn. Comput. 2022, 6, 96. https://doi.org/10.3390/bdcc6030096
Azizi I, Rudnytskyi I. Improving Real Estate Rental Estimations with Visual Data. Big Data and Cognitive Computing. 2022; 6(3):96. https://doi.org/10.3390/bdcc6030096
Chicago/Turabian StyleAzizi, Ilia, and Iegor Rudnytskyi. 2022. "Improving Real Estate Rental Estimations with Visual Data" Big Data and Cognitive Computing 6, no. 3: 96. https://doi.org/10.3390/bdcc6030096
APA StyleAzizi, I., & Rudnytskyi, I. (2022). Improving Real Estate Rental Estimations with Visual Data. Big Data and Cognitive Computing, 6(3), 96. https://doi.org/10.3390/bdcc6030096







