1. Introduction
During operation of a jet engine, deterioration occurs and continually reduces the engine performance. As a result, the specific fuel consumption (SFC)and exhaust gas temperature (EGT) are increasing with on-wing time of the engine, which also leads to an increase in direct operating costs (DOCs). When the EGT reaches a given limit, the engine has to be removed from the airplane and to be overhauled by an MRO (Maintenance, Repair and Overhaul) company. For a long time the time-based maintenance was standard procedure of repairing an engine. Thereby, no special attention to the operational and maintenance history is given, and the engine components receive more or less standard repairs. Time-based maintenance is now being replaced by condition-based maintenance. The condition-based maintenance is characterized by the requirement of a detailed prediction and an examination of the engine components and its piece parts at the incoming inspection of the overhaul and tailored maintenance actions, depending on the engine history and condition.
For further improvement of the condition-based maintenance, the influence of each engine component and its piece parts to the engine performance needs to be known. Using the example of the high pressure compressor (HPC) , the aerodynamics of its individual blading has to be determined to predict the changes of the resulting compressor map. Thus, the MRO companies would be able to repair and rearrange the blading in such that the customer demands for the next planned operation are met as cost-effectively as possible, while respecting the given limits of the Engine Manual (EM).
In order to determine the geometric variances of deteriorated HPC airfoils, a multitude of HPC airfoils has been digitized. This paper focuses on modified front and rear stages of the HPC. Therefore, more than two complete rotor bladings of operated jet engines [
1] and additionally 40 stator vanes for each of the analyzed HPC stages have been digitized by a structured light 3D-scanner in conjunction with a photogrammetric system. To determine manufacturing tolerances, 30 new airfoils of each analyzed compressor row have been digitized. Afterward, the airfoils were analyzed with respect to their geometric parameters by an in-house programmed algorithm [
2]. Subsequently, aerodynamic sensitivities of the geometric properties were investigated using computational fluid dynamic (CFD)-methods. Therefore, extensive Design of Experiments (DoE) for the front and rear stages have been carried out [
3,
4]. To reduce the number of independent geometric properties, the geometric parameters have previously been scanned for possible correlations [
5].
This paper takes the next step of this field of research and focuses on the changes of the jet engine performance due to compressor deterioration. Therefore, a modular performance synthesis model of a popular two-shaft bypass jet engine was set up and validated by test cell data. To analyze the impact of deteriorated HPC bladings, the geometric parameters of front and rear stages of the HPC are modified and implemented in a full HPC model. Thereby, results of the previous DoEs [
3,
4] were used to change the geometric parameters of the corresponding compressor stages to achieve stage setups with low- and high-stage efficiency. Therefore, the leading edge geometry, the stagger angle, and the profile camber were modified. The aerodynamics of the HPC is simulated using methods of CFD. With the deteriorated throttle lines, the reference HPC map is scaled and implemented in the performance model of the jet engine. Thus, it is possible to identify the more relevant HPC stage in order to predict the possible performance range (by repairing the stage) and to analyze the interactions between the engine components.
2. Generation of Deteriorated Stage Setups
To determine the aerodynamic sensitivities to the geometric parameters of the regarded compressor stages, two extensive DoEs were created [
3,
4]. The geometric properties of the rotor blades and stator vanes were modified in a range of
(standard deviation of the deteriorated airfoils) around the new part mean value. The used standard deviation of the geometric properties was calculated by analyzing more than two HPC bladings [
1]. Thereby, the geometric properties were analyzed on 19 profile sections of the airfoils. Afterward, for each profile section, the mean value and the corresponding standard deviation were calculated. Generating the modified geometries, each geometric property was changed in a range of
homogeneously over the blade height.
The throttle lines of the modified stage geometries were simulated by methods of CFD. Afterward, these throttle lines were analyzed at a reference mass flow. The aerodynamic results such as efficiency and pressure rise were used in conjunction with the corresponding geometric values to train a meta-model using the
Kriging-Method [
6]. After validating the prediction quality of the meta-model, the user is able to predict the aerodynamic performance of unknown geometric variations without using further CFD calculations.
2.1. Front Stage Sensitivities
Using the trained meta-models,
Pareto charts were used to identify the aerodynamic sensitivities to the geometric parameters. Therefore, all geometric properties were changed independently by about
, and the aerodynamic performance parameters were calculated by the meta-model. The aerodynamic changes for one performance parameter, influenced independently by all geometric properties successively, were summed and plotted in a
Pareto chart.
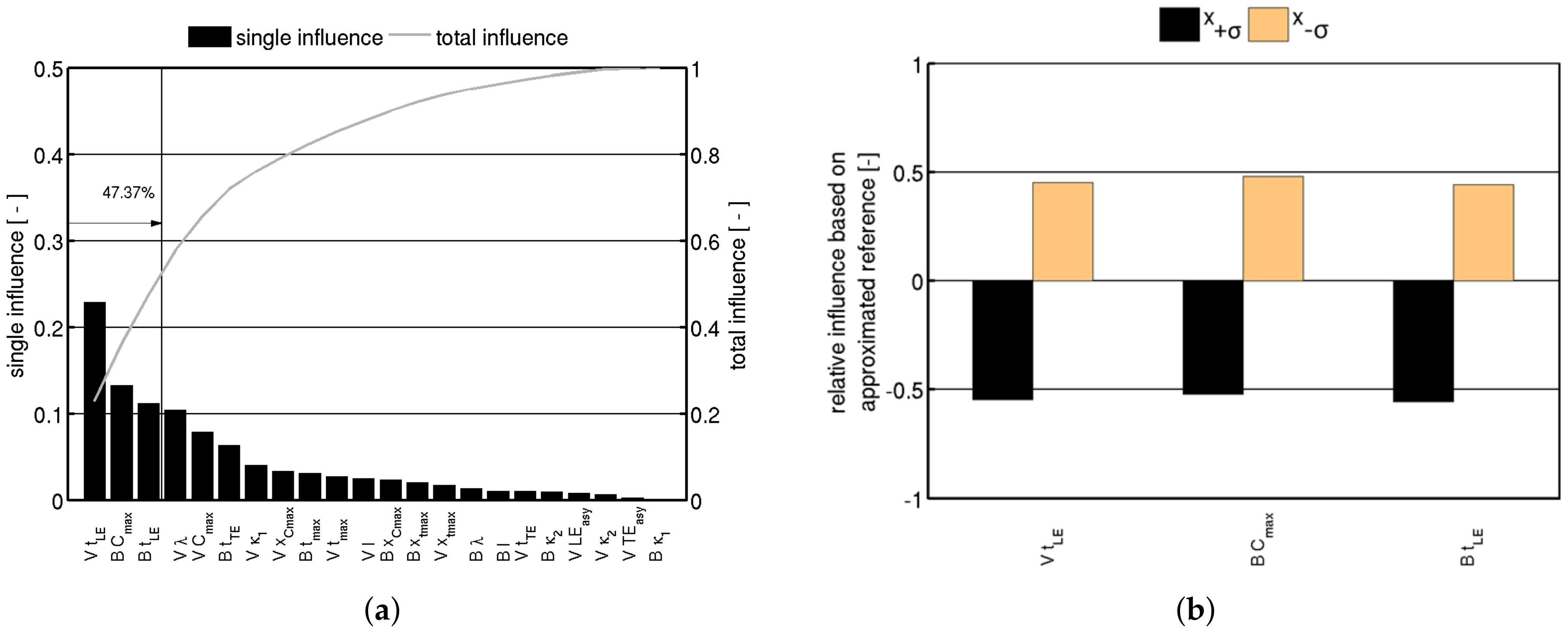
Figure 1a shows the
Pareto chart for the isentropic efficiency
of the front stage, analyzed at the reference mass flow. As can be seen, the most relevant geometric parameters are the leading edge thickness of the stator vane
as well asthe maximum profile camber of the rotor blade
and the leading edge thickness of the rotor blade
. The accumulated impact of the three most important parameters is almost half of the overall changes caused by 22 geometric properties.
A closer look at the three dominating geometric properties is given in
Figure 1a. Here, the direction of the aerodynamic performance parameter changes caused by the geometric variations is shown. Black bars indicate an increased geometric property by
and orange bars indicate decreased values of the same amount. Thus, the geometric parameters vary symmetrically around the reference value, and an equal change of the isentropic efficiency
is expected. Thereby, bars above zero indicate an increased value for the isentropic efficiency
and vice versa. This illustration is only visualizing the directional dependency and its sensitivity of the isentropic efficiency
toward the geometric property and not the magnitude of change. For the front stage, the isentropic efficiency
is increasing as leading edge thicknesses of the rotor blade
and stator vane
decrease and as the maximum profile camber of the rotor blade
decreases.
2.2. Rear-Stage Sensitivities
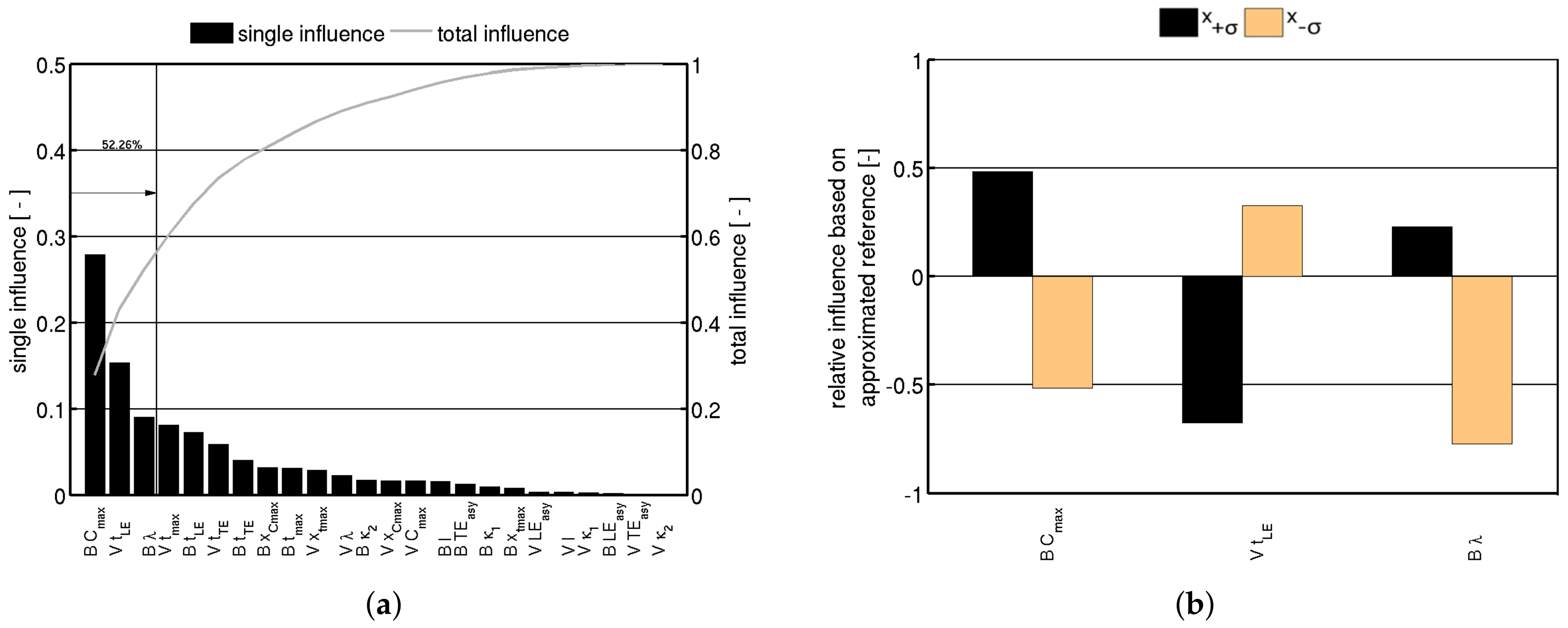
A similar analysis was conducted for the rear stage.
Figure 2a illustrates the
Pareto chart for the isentropic efficiency
of the rear stage, analyzed at the reference mass flow. The three dominating geometric values are the maximum camber of the rotor blade
, the leading edge thickness of the stator vane
, and the stagger angle of the rotor blade
. Comparable to the front stage, the first three parameters have an accumulated impact of about half of the overall changes caused by 24 geometric properties (the number of geometric properties is higher because, at front stage, the rear stage has fewer correlations between the properties [
3,
4]).
A detailed look at the three dominating geometric properties is given in
Figure 2b. In contrast to the sensitivities of the front stage, the isentropic efficiency
is decreasing as the maximum profile camber of the rotor blade
decreases. The changes caused by changing the leading edge thicknesses of the stator vane
are similar to the front stage: decreasing the thickness results in an increased efficiency. Nevertheless, a strong dependency on the direction of the geometric change can be noticed. Increasing the leading edge thickness results in a decrease in efficiency that is stronger than the decrease in thickness of about the same amount. Such a dependency can be seen for the stagger angle of the rotor blade
as well. Decreasing the stagger angle results in a steeper drop in efficiency compared to the efficiency gain of increased stagger angles (cf. [
4]).
Although there is no experimental validation for this studies, the results are in a good agreement with publications of other researchers. Lange et al. [
7] analyzed manufacturing variability of HPC rotor blades and ranked the geometric properties for their aerodynamic impact. Although manufacturing tolerances instead of deterioration were investigated, the thickness-related parameters have a dominant impact—especially the leading edge thickness, which is similar to this study.
2.3. Stage Setups for Full HPC Calculations
In this section, geometries that show maximally high aerodynamic deviations from the reference airfoils are determined. Thereby, the geometric properties of the airfoils shall lay in between the range of the analyzed deteriorated ones. In doing so, the results of the previous DoEs were used. Because there is no physical airfoil that satisfies the desired requirements, the airfoils have to be generated by an in-house programmed algorithm [
2]. As a result, artificially deteriorated front and rear stages were generated and implemented into the full HPC model. To compare the aerodynamics of deteriorated front and rear stages to the reference geometry, all geometric properties were set to the mean values of the deteriorated airfoils [
1]. Thereby, the leading edges of the front stage become thinner, while the rear stage tends toward thicker leading edges. Furthermore, the airfoils open, and the stagger angles decrease.
Moreover, to achieve aerodynamic deviations that are as wide as possible, stage setups for minimum and maximum isentropic efficiency were generated. Therefore, the previously shown aerodynamic sensitivities to geometric changes were used. Thus, the geometric properties that are mainly influencing the isentropic efficiency—in addition to the mean value of the deteriorated airfoils—were changed by
in the direction for minimum and maximum efficiency.
Table 1 shows the direction of chosen geometric properties for maximum isentropic efficiency. As can be seen, the front stage setup for maximum efficiency is characterized by decreased values of
,
,
, and
, whereas the values for
and
are increased. The rear stage is characterized by decreased values of
and
. The values for
,
,
, and
are increased to achieve a rise in efficiency. The behavior for minimum efficiency is vice versa.
After defining the values of the geometric airfoil properties, the airfoils are generated and meshed with an in-house programmed algorithm [
2] and integrated into the full HPC CFD-model. In doing so, all compressor rows were meshed with uniform blade sets across the circumference, which is not a realistic condition. Nevertheless, the impact of a completely changed compressor row can be analyzed by this method. Lange et al. carried out CFD calculations for non axis-symmetric compressor bladings [
8]. Thereby, Lange et al. simulated passages with 1, 2, 4, and 8 individual changed blades. As a result, they showed the high spreading of the stage efficiency for the single passage, caused by the high spreading of geometries. Furthermore, two passage blade pairs can negatively influence each other, which results in lower stage efficiencies, compared to the single passage. If the number of passages is increasing, the efficiencies show a narrowed distribution around a mean value.
3. CFD Setup
The full HPC CFD-model contains all 21 compressor rows, bleed-ports, and cavities. Adjusting the integrated VSV system, it is possible to simulate the compressor behavior to generate a compressor map. Nevertheless, for this study, only the throttle line for the operating condition cruise was simulated with the deteriorated front and rear stage. The behavior of the remaining parts of the compressor map was generated by scaling the reference map.
The CFD simulations have been carried out with the RANS (Reynolds Averaged Navier Stokes) solver
TRACE [
9,
10,
11,
12] from DLR (German Aerospace Center). As has already been mentioned, the operation point cruise was chosen for the generation of the deteriorated full HPC CFD-calculations. As inlet boundary condition the total pressure
, total temperature
, flow angle in circumferential direction
, the radial distribution of the flow angle in radial direction
, Mach Number
, turbulent intensity
and turbulent length scale
are chosen. As an exit boundary condition, the averaged static pressure was chosen and varied to simulate the throttle line. Because the throttle lines are calculated as a steady-state condition, the last converged point only represents a kind of numerical point of stall and does not represent the physical one. Further solver settings are summarized in
Table 2.
Subsequently to the simulations, the CFD results are analyzed for the isentropic efficiency
and the total pressure ratio
. The isentropic efficiency is calculated by the total pressure ratio,
and the total temperature ratio
,
with the following equation:
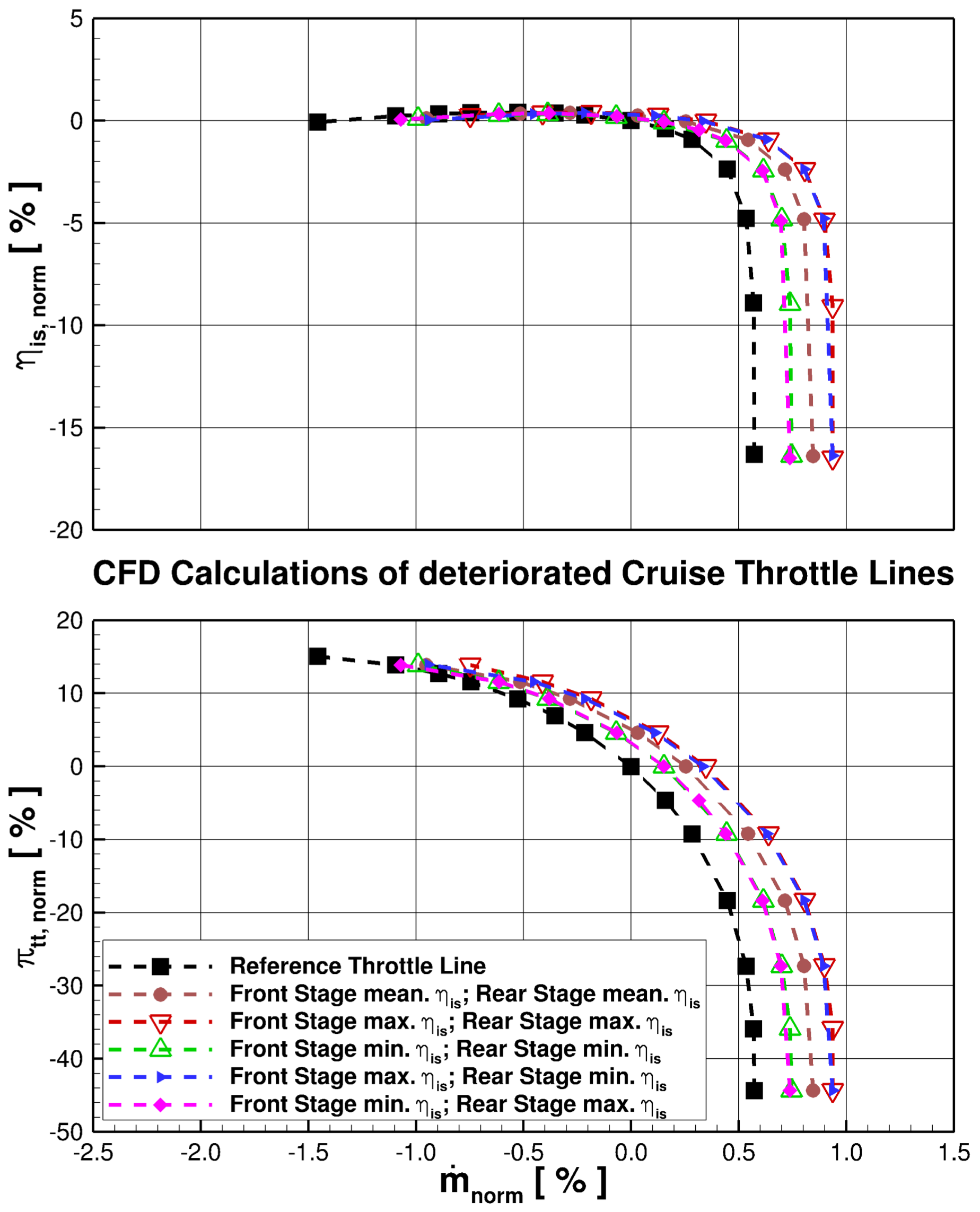
The results of the deteriorated full HPC CFD-calculations are visualized in
Figure 3. Here, the reference throttle line for cruise condition is shown as well as different deterioration combinations of the front and rear stage. The lower part of the figure illustrates the normalized pressure ratio, and the upper part illustrates the normalized isentropic efficiency. For the normalization, the operating point of the cruise was chosen. The throttle line of the front and rear stage setups with all geometric properties set to the mean value of the statistical analysis of the deteriorated airfoils is shown as line with circle symbols. As can be seen, the throttle line is shifted toward higher massflows, which results for the reference mass flow in higher efficiency. Thereby, the shifting toward higher massflows is mainly caused by decreased stagger angles of the deteriorated front blades. For the deterioration combination of maximum
in the front and rear stage, this effect is even strengthened (see
Table 1) and the shifting toward lower loadings is increasing. For the deterioration combination of minimum
, this effect is weakened.
Another effect which is strengthening the increase in efficiency of the changed stage geometries is the influence of the leading edges. Because the modified airfoils have thinner leading edges, compared to the reference airfoils, the efficiency is increased (see
Figure 1b and
Figure 2b). Nevertheless, it has to be mentioned that effects such as increased gaps or roughness have not been taken into account.
Another observation is that the aerodynamic changes of the deteriorated HPC are mainly caused by the front stage. As can be seen, the throttle lines with the combination of the maximum in the front and rear stages and the throttle line with maximum in the front stage and minimum in the rear stage are overlapping. The same behavior can be observed for the combinations of minimum in the front and rear stages and the throttle line with minimum in the front stage and maximum in the rear stage.
4. Compressor Map Scaling
Because it is not feasible to simulate a complete compressor map for each deterioration combination in the front and aft stage, a scaling of the reference compressor map was chosen. Therefore, scaling factors at the cruise condition point were generated by referencing the deteriorated operating point to the reference one [
13]. Using this method, scaling factors for the massflow
,
the total pressure ratio
,
and the isentropic efficiency
,
were generated. Afterward, the reference compressor map parameters were multiplied with these scaling factors. As an example,
Table 3 states the scaling factor values for the deterioration combination of maximum
as well as the minimum
in the front and rear stages. Because of the shifting of the throttle lines toward higher mass flows (see
Figure 3), the scaling factor for the massflow
is noticeably increased. In addition, the scaling factors for efficiency
and the pressure ratio
are slightly higher than 1.
Because the scaling factors are only constants generated at the operating point of cruise, the functionality of the used method must be validated. This was done by additional CFD calculations at the left limit of the compressor map. This limit is represented by the throttle line with the rotational speed of the ground-idle operating point. Therefore, the full HPC CFD model was trimmed to this operating line by changing the rotational speed, the bleed and VSV system, as well as the in- and outlet boundary conditions. To minimize the additional numerical effort, the validation was done for the deterioration level with the highest aerodynamic deviations to the reference throttle line of the cruise. The chosen deterioration combination is maximum
in the front and rear stages (see
Figure 3 and
Table 3).
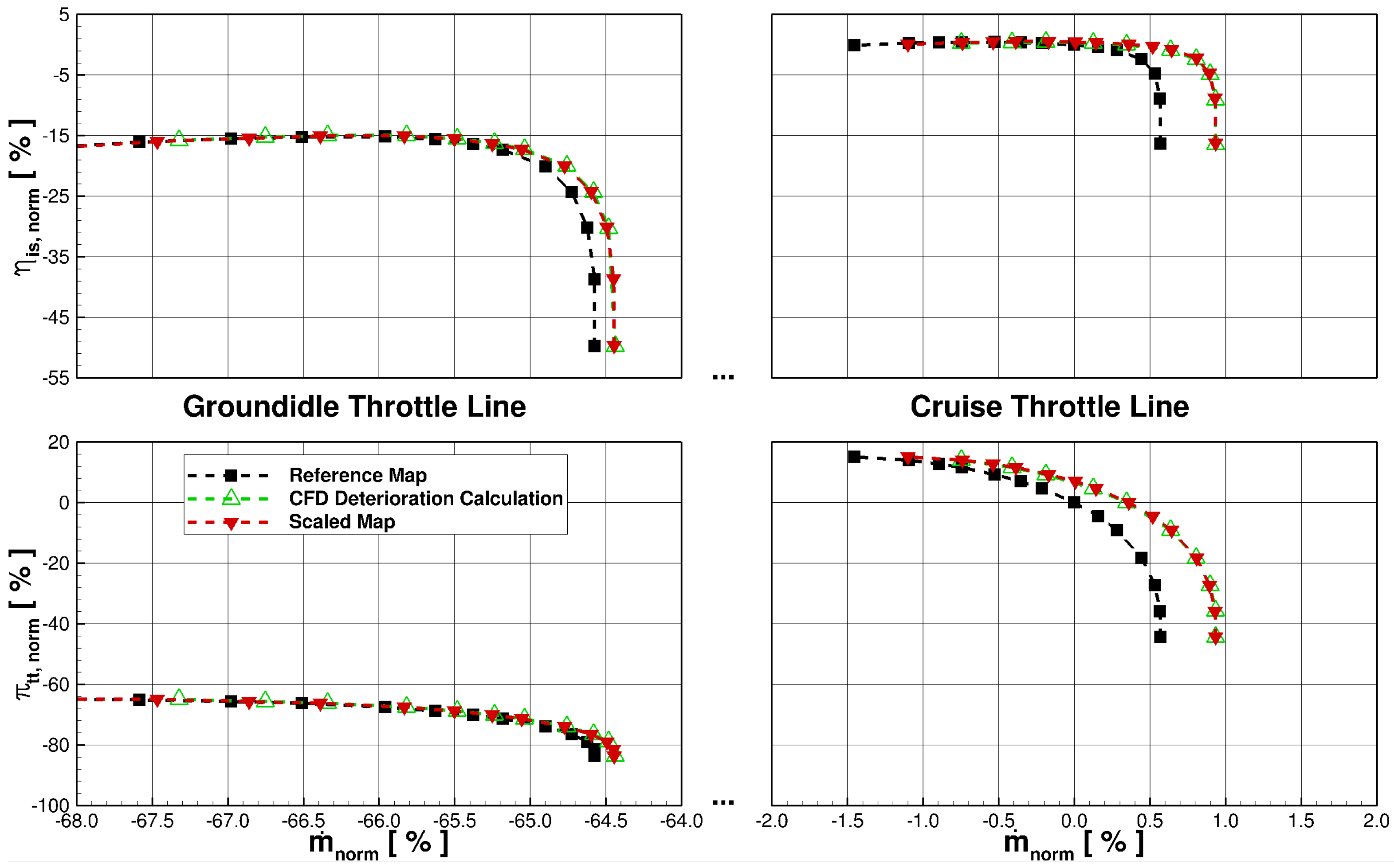
Figure 4 shows the sections for ground-idle and cruise of the compressor map. The reference map is characterized by the black, the CFD calculations of the deteriorated compressor geometry by the green, and the scaled compressor map by the red. Again, the lower part of the figure illustrates the normalized pressure ratio and the upper part the normalized isentropic efficiency. For the normalization, the operating point of cruise was chosen, which has also been used for scaling the reference to the deteriorated map. On the right hand side, a good agreement of the scaled to the CFD throttle line can be noticed. On the left hand side, the comparison for ground-idle is shown. As can be seen, the map scaling works at the left limit of the map as well. Comparing the operating point on the ground-idle throttle line which represents the ground-idle working point, the deviations between the CFD calculation and the scaled map have the following values:
= −0.035%
= −0.056%
= −0.018%
As can be seen, the deviations between the CFD and scaled throttle line are quite small and, therefore, negligible.
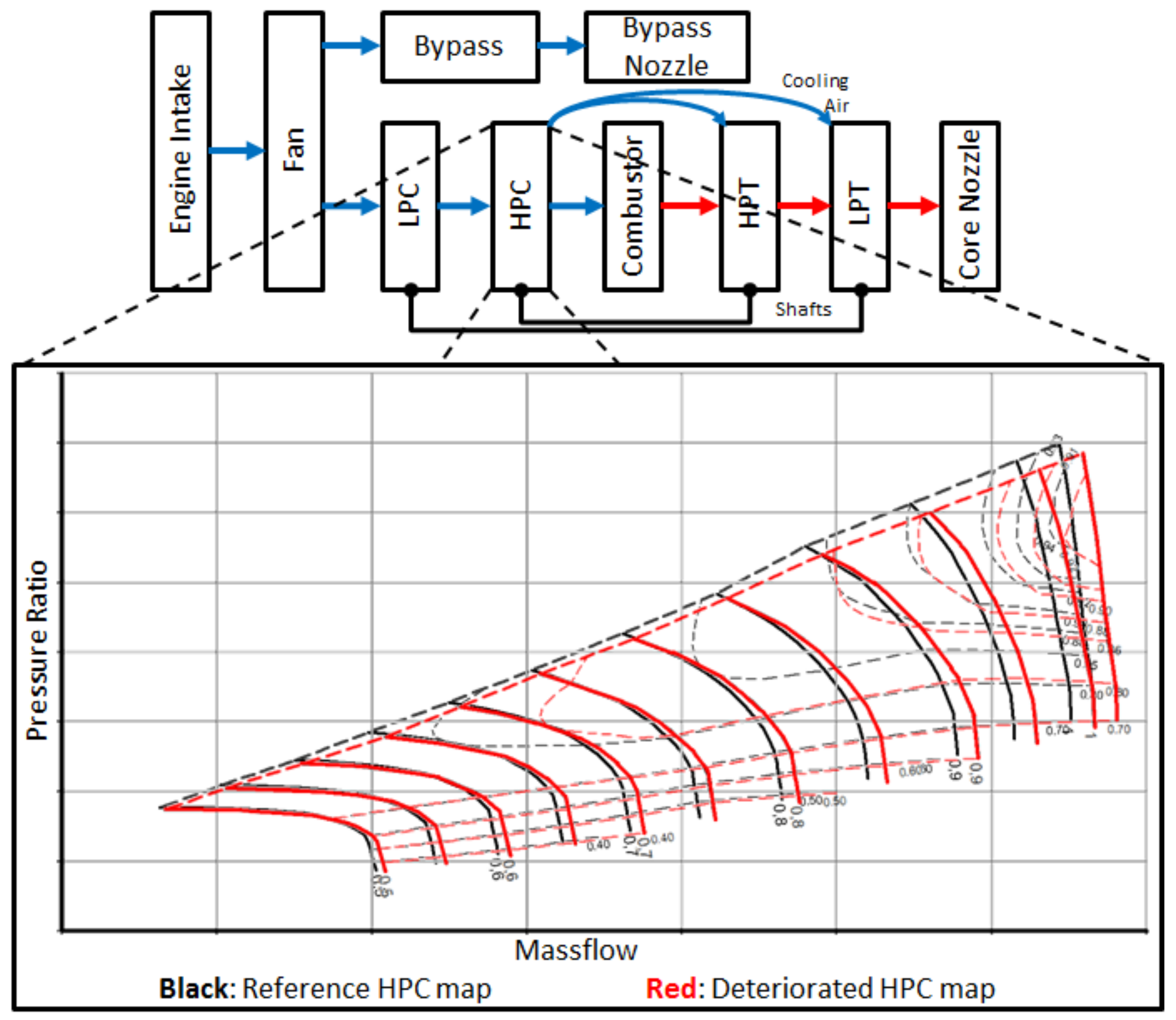
5. Modular Performance Synthesis Model
To determine the changes of the engine performance due to changed HPC aerodynamics, a modular performance synthesis model of the analyzed jet engine was set up and validated by test cell data. For setting up the model, the software
GasTurb [
14] was used. The technique of modular performance synthesis was characterized by splitting up the thermodynamic cycle of a jet engine into its individual components (see
Figure 5 upper part). Thereby, the flow was calculated successively in each component independently from the other components. The component behavior can be described by simple equations (i.e. the pressure drop in a tube) or by complex component maps for the turbo-components (see
Figure 5 lower part). The modular performance synthesis is characterized by a 1D-calculation method, which averages the flow parameters such as total pressure and temperature over the cross section. As a result, the modular performance synthesis is able to predict performance parameters such as EGT or SFC.
In the modular performance synthesis model, the reference HPC map was replaced by the deteriorated ones (see
Figure 5 lower part), while leaving the rest of the model in its original configuration. To prepare the scaled CFD maps, the software
Smooth C was used [
15]. With this software, it is possible to inter- and extrapolate further throttle lines inside the compressor map and to transfer the data in a consistent input format for
GasTurb.
6. Jet Engine Performance Calculations
For evaluating the impact of modified stage geometries to the engine performance parameters, the HPC map of the modular performance synthesis model was replaced by the scaled ones. To guarantee an adjustment of the same engine operating condition despite the changed HPC maps, the model was regulated by the engine pressure ratio (EPR). This is the same engine control philosophy as for the real one. Afterward, typical performance parameters are analyzed at the operating condition cruise.
Table 4 summarizes chosen parameters, defining the compressor performance and the jet engine efficiency. As can be seen, the pressure ratio and efficiency of the HPC are increasing. This behavior can be explained by the scaling factors presented in
Table 3. Again, it has to be mentioned that, because of the thinner leading edges in conjunction with an opening of the rows, the chosen geometric deterioration combinations result in a higher efficiency at the regarded massflow. Thereby, the higher scaling factors of the deterioration combination of maximum
in the front and rear stages result in higher changes of
and
, compared to the deterioration combination of minimum
in these stages. Although only two compressor stages have been modified for the CFD-calculations, a noticeable effect on engine fuel economy can be observed: The given deterioration combinations result in a decrease in SFC by 0.1% and 0.04%. Consequently, the EGT is decreased as well, and the gain in EGT is about 1.12 and 0.52 K.
Due to the small geometric changes in only two of the compressor stages, the deviations caused by the scaled HPC maps are quite small and do not represent the reality. As already mentioned, the airfoil gaps and roughness did not change during these investigations. Specifically, these effects would result in decreased compressor performance. Nevertheless, the process is able to reflect even these small changes in engine performance parameters such as EGT and SFC, caused by small geometric changes inside only a few HPC rows.
To evaluate the impact of a strongly deteriorated HPC, a third HPC map modification was made. Therefore, all scaling factors were set to 0.98, which is a realistic range of deteriorated HPCs coming to a shop visit. Thereby, geometric variations of all HPC stages in conjunction with increased airfoil gaps and surface roughness reduce the HPC performance. For such an HPC, the increase in SFC is about 0.88% and in EGT about 9.71 K.
To give the reader a feeling for the provoked changes by the strongly deteriorated HPC, its impact to the fuel consumption of a typical civil flight mission is calculated. Thereby, the mission is characterized by taxiing on the ground followed by the take-off and the succeeding cruise flight. Afterwards, the airplane approaches and lands. With four hours, the operating condition of cruise is the longest flight period. For this magnitude of deterioration, the integrated fuel consumption of one engine is increased by about 88.95 kg, which is an increase of 1.12%.
7. Conclusions
In this paper, changes in jet engine performance caused by deteriorated HPCs were evaluated. The front and rear stages of an HPC were modified, and the performance was simulated by methods of CFD. The results of two previous DoEs were used to change the stage geometry in a manner for maximum and minimum efficiency. To lower the number of required numerical simulations, a compressor map scaling method was introduced and validated by an exemplary deterioration condition of the HPC. Using this scaling method, the calculation of only one deteriorated point on the throttle line would be sufficient to scale the complete reference map to a deteriorated one. Nevertheless, the complete deteriorated throttle line was calculated to evaluate its possible shape changes. Afterward, the changed compressor maps were embedded in the modular performance synthesis model of the analyzed jet engine to evaluate its performance changes. The main results of the paper can be summarized as follows:
Because deterioration leads to thinner airfoils, the efficiency shows a trend toward higher values. Additionally, the decreased stagger angle inside the front stage results in a throttle line shifting toward higher massflows. Nevertheless, it has to be mentioned that effects such as increased gaps or roughness have not been taken into account.
The investigated compressor behavior is mainly driven by the front stage. An HPC setup with installed front and rear stages with maximum efficiency shows nearly the same performance as an HPC setup with an installed front stage for maximum efficiency and a rear stage with minimum efficiency.
The presented compressor map scaling method—which works with constant multipliers for massflow, efficiency, and pressure ratio, respectively—works well for the complete area of the map.
By modifying only two stages of the HPC, a significant influence on jet engine performance was proven. Because of the already explained higher efficiency, the impact is positive. For the example maximum efficiency in the front and rear stages, the SFC decreases by about 0.1% and the EGT is approximately 1.1 K colder.
To show the impact of an overall deteriorated HPC, the scaling factors were all set to values representing an engine coming to the shop. For this example, a massive increase in the SFC was observed. Its value rises up to about 0.9%, and the EGT is 9.7 K hotter. The increased SFC results in an increase of integrated mission fuel consumption (with a duration in cruise condition of 4 h) about 89 kg per engine which is 1.1% more than the reference value.
All in all, the presented process is able to reflect changes in engine performance parameters, such as EGT and SFC, caused by small geometric changes inside the HPC. Thus, with this process, the MRO companies would be able to evaluate the compressor performance at incoming inspections and to identify sensitive compressor areas, which can lead to an increase in its performance.
In the future, MRO companies will be able to classify serviceable airfoils with respect to their aerodynamics and impact on the HPC and jet engine performance. With detailed knowledge of the varying airfoil aerodynamics, HPC repair could be adjusted to given HPC efficiencies to meet customers requirements as cost-effectively as possible. Furthermore, expensive troubleshooting due to a poor contracted engine performance can be avoided.
Nevertheless, further work must be undertaken. Additional compressor stages should be adjusted in their geometry to generate a fully changed HPC. Furthermore, the airfoils gaps and roughness could be increased to meet the true deteriorated compressor appearance.