1. Introduction
Wear occurs during the on-wing time of jet engines, and leads to a decreased performance. This is why they are overhauled regularly, maintaining safety level and high efficiency. Currently, efficiency is increasingly important, and maintenance companies must therefore provide exact performance parameters such as exhaust gas temperature (EGT) and thrust-specific fuel consumption (TSFC). To reach these goals, they often use customized maintenance actions for each engine. To improve this approach, tailored repairs for each blade can be a choice.
Special attention is given to the high-pressure compressor (HPC) because of its comparatively large influence on the overall engine performance. Therefore, detailed knowledge about the aerodynamic behavior of deteriorated blades is necessary. For BLISKs (blade-integrated-disks) the aerodynamic behavior is even more complex because individual blades cannot be replaced or rearranged in a reasonable manner. Thus, coupled deteriorated blades have a high significance and a more complex behavior due to the blade interaction. To ensure an effective maintenance for BLISKs, the impact on the aerodynamic performance of coupled misshaped blades are the key factor.
The heterogeneous deterioration of BLISK blades around the circumference and their effects on the flow behavior were shown in a previous publication [
1]). The maximum leading edge thickness on one blade was combined with the stagger angle deviation of the adjacent blade. The resulting throttle-line was compared to a newly-manufactured blade and the standalone variances to show the interaction between two different shaped airfoils. Compared to standalone ones, coupled deteriorated blades have a lower performance level, which indicates an interaction. These findings are backed up by the results of the wake, which also give an indication of the fluid mechanical changes due to the interaction.
In order to improve the understanding of the complex system behavior of deterioration-afflicted turbomachinery, probabilistic methods are a possibility to significantly increase the knowledge gain. Lange et al. [
2,
3,
4] investigated the influence of manufacturing tolerances on HPC performance by means of a probabilistic approach. They developed a parametric model for compressor blades to reproduce the manufacturing tolerances by a transformation of blade profile parameters [
2]. This model was used for a computational fluid dynamics (CFD)-based probabilistic method to rank the changed parameters due to their effect on the HPC performance. They used a Monte Carlo simulation method using an optimized Latin hypercube sampling. Their results showed that the thickness related parameters—leading and trailing edge, as well as the max. thickness—are ranked as the highest parameters with regard to the loss coefficient, followed by the stagger angle [
3]. Additionally, Lange et al. [
4] carried out a non-axis-symmetric blade arrangement by investigating 1, 2, 4, and 8 passages with individual blades. They presented a high drop of stage efficiency for simulating two passages, whereas by increasing the number of passages the efficiency tended towards a mean value.
A sensitivity investigation on the influence of deterioration on high-pressure compressor performance was done by Reitz et al. [
5]. They analyzed a deteriorated HPC front stage by means of a design of experiments (DoE) at cruise condition. The base of this investigation was a set of two used full HPC bladings (approx. 1200 blades), which were digitized by Marx et al. [
6]. The influence on the performance was categorized by work and pressure coefficient. Both were mainly affected by the stagger angle, the max. profile camber, and its position. The loss coefficient was mostly influenced by the thickness-related parameters of the leading edge. A comparison of different deteriorated stages and their influence was also done by Reitz et al. [
7]. Here they showed that the sensitivities changed because of different Mach number of the incoming flow. Due to the transonic flow regime for high Mach numbers at the front stage, the profile camber as well as its position was highly ranked within the Pareto analysis. In an aft stage with low incoming Mach numbers, the thickness-related parameters and the stagger angle were more important.
An investigation which included three different operating points was done by Ernst et al. [
8]. Their research was based on a quasi-3D (Q3D) CFD simulation of the final low-pressure turbine stage with regards to the effect of regeneration-induced geometric variances. They showed a dependency of the effect of regeneration-induced variances on the operating point. Cruise and takeoff conditions had a similar behavior, whereas the approach condition showed the highest sensitivities regarding the isentropic efficiency.
The present study addresses the effects of coupled deteriorated blades on the aerodynamic behavior of the first stage of a high-pressure compressor regarding three different operating points. Therefore, a DoE was done to identify the geometric properties leading to a change in performance. The DoE was performed by an in-house tool, introduced by Reitz et al. [
5]. The data base of this investigation was based on ten first-stage HPC BLISKs with 26 blades each. Within this population, correlations between geometric parameters were taken into account. This data base was concluded in a design space filled with 1400 differently-shaped blades, resulting in 700 different computational domains. These blade geometries were fully automatically generated and the computational domains were meshed with a procedure also introduced by Reitz et al. [
9]. To reduce the computational effort of CFD calculations, similar to Ernst et al. [
8], Q3D simulations of the
blade height were carried out. Furthermore, by limitation to Q3D simulations, the investigation was focused on the interaction between coupled geometric variances without the influence of 3D effects. The performances of the geometrically-deteriorated blades were stored in conjunction with their geometrical properties in a data matrix. By means of this data matrix, a meta-model was trained with a Kriging Method [
10]. By this method, a fast prediction of characteristic performances of coupled deteriorated blades was done without using further CFD-simulations.
2. BLISK Blade Deterioration
The statistical base of deteriorated blades was determined by examination of ten first-stage BLISKs with 26 blades each, installed in an HPC. The BLISK was operated in a medium bypass engine ( ) which was installed as a rear-mounted engine in regional and business jets. The BLISKs were in operation for about 20,000 cycles, and thus regeneration procedures were done which can effect the geometrical properties as well as the operational wear. Overall, the statistical data base was set to 260 single blades.
To examine the geometrical properties for each blade, each BLISK was scanned by a structured light 3D-scanner in conjunction with a photogrammetric system. This technique resulted in a point cloud of each entire BLISK. To reach a high point cloud density of the BLISK, a measurement volume of
mm for the blade was chosen. The edges of each blade were measured with a higher resolution to take the highly-critical edges into account. Therefore, the measurement volume was reduced to
mm. The resulting point cloud was analyzed by an in-house programmed tool (cf. Reitz et al. [
9]). The geometric properties were determined on 19 2D-profile sections from
to
blade height. This process resulted in statistical data with parameters listed in
Table 1 for every profile section of each blade.
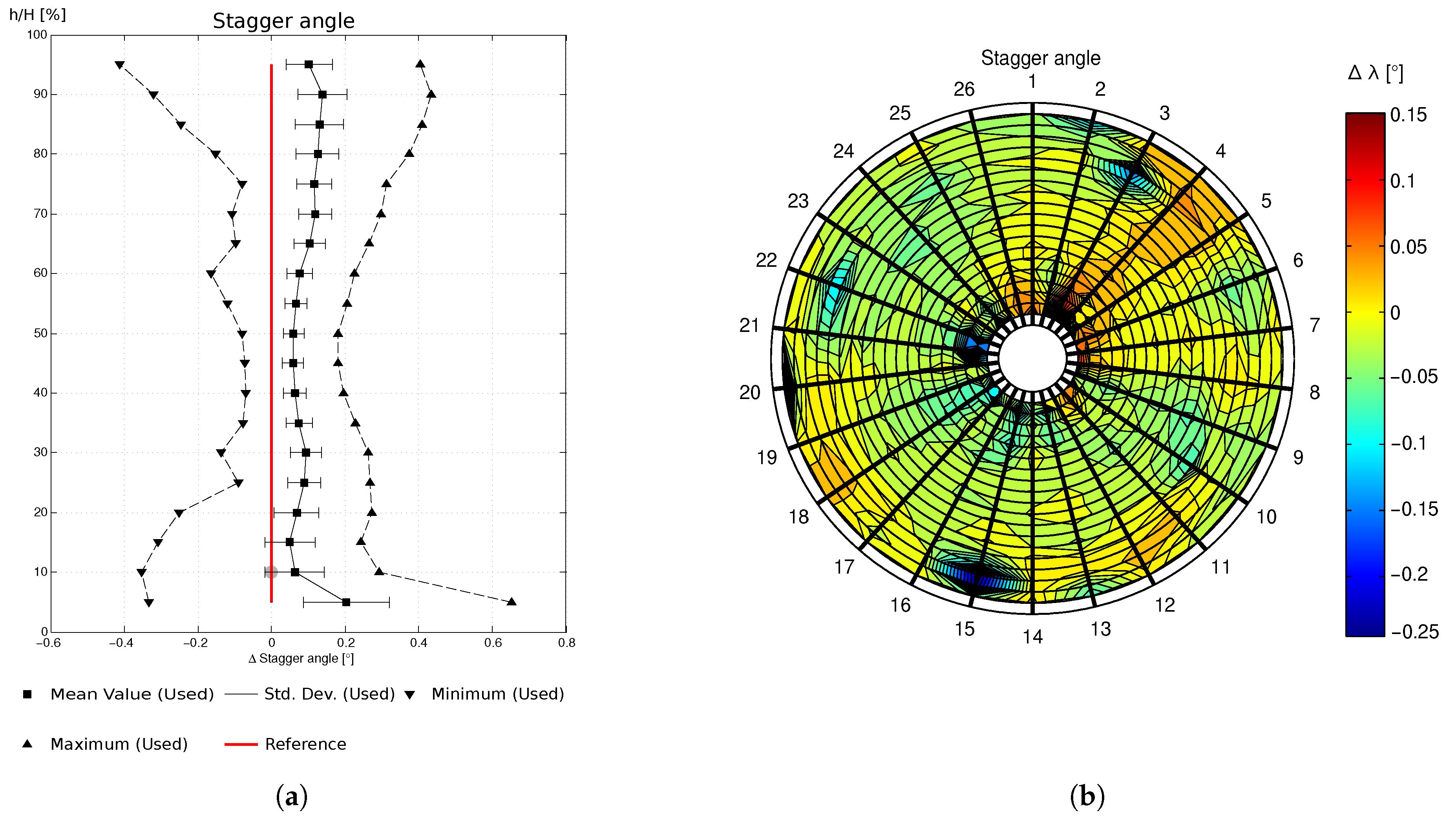
The resulting statistics are shown in
Figure 1 in the forms of the geometrical parameter stagger angle regarding ten BLISKs and the spreading of BLISK No. 9. The radial distribution of the stagger angle (
Figure 1a) based on ten BLISKs showed a maximum deviation of
, a standard deviation of
at
blade height, and
at mid-span. The standard deviation of all 12 geometric properties at
blade height was the base of the design space used for the DoE. In
Figure 1b, the variation of the stagger angle along the blade height for every blade on BLISK No. 9 is shown. Here, the stagger angle had a spreading of about
overall. The important aspect to be considered is the inhomogeneous wear at adjacent blades. Especially blades 3 and 4 stand out with contrary trends of the stagger angle. While blade 3 had an opening characteristic, blade 4 showed a closing trend for the stagger angle. Additionally, highly inhomogeneous locations could be detected for blade 15.
It has to be mentioned that no newly-manufactured BLISK was analyzed. Therefore, both plots show the variation of the statistical data to a chosen blade, representing the mean value. A comparison with Marx et al. [
6] and Reitz et al. [
7], it shows that the wear distribution was of the same magnitude and was therefore considered to be representative.
3. Design of Experiments
In order to rank the effect of coupled geometric properties, a sensitivity analysis was done by means of a DoE. The work of Reitz et al. [
5] was extended by focusing on circumferentially-coupled deteriorated blades, their interaction, and effects considering three different operating points.
Figure 2 shows the non-dimensional pressure distribution for three operating points at
blade height compared to their complementary full 3D simulations. All three operating points showed a good match between the full 3D simulations and their corresponding Q3D simulations. By using Q3D simulations, the focus of this investigation was on sensitivities regarding the interaction between coupled geometric variances. Furthermore, the
profile section represents a critical profile height in terms of aerodynamic loads and transferred work. In terms of the aerodynamic effects of geometric variances, the
profile section is representative. Reitz et al. [
5] investigated a full 3D blade. With respect to this study, the results of the
profile section presented here are comparable. Additionally, the computational effort was reduced. For the CFD calculations, the
profile section of a representative front stage rotor blade was used because a newly-manufactured BLISK was missing.
The geometries were generated by an in-house programmed tool [
9] by manipulating a reference blade geometry on 19 profile sections for each of the 12 geometric parameters. To fill the data space, a set of 700 coupled geometric variances and therefore with two different blade passages was created. To ensure an equally distributed data set, a Latin hypercube sampling algorithm [
10] was used. The parameter space was limited by
, whereas
was the standard deviation regarding the wear characteristics of the analyzed BLISKs (
Figure 1a). To reduce the number of parameters shown in
Table 1 and to avoid mistakes in the meta-model, correlations within the geometric parameters were taken into account. The correlations were built after a process Reitz et al. developed in [
11], which is based on the coefficients of Bravais and Pearson [
12,
13]. The evaluation was done by linear regression. For the BLISK geometry data set, the following correlations were found:
Correlations (
1) and (
2) show the coherence between edge parameter at the leading and trailing edge. LE and TE. The parameter
defines the behavior of
and
. The same applies to the trailing edge. If a thicker edge appears, the edge stretching is decreasing. The stretching again provides higher radii. Thus, the correlation between the edge parameters reproduces blunted edges as well as sharpened edges.
Computation Method
To train the meta-model, the data set was simulated with the numerical CFD-solver TRACE of DLR Cologne. The CFD-code solves three-dimensional Reynolds-averaged Navier–Stokes equations on multi-block meshes by finite volume method, Nürnberger [
14], Kügeler [
15], Marciniak et al. [
16], Becker et al. [
17]. The discretization method for the convective fluxes was the second-order TVD upwind scheme of Roe [
18]. The diffusive fluxes were discretized by a central differencing scheme. An implicit predictor–corrector time integration algorithm was used for steady state simulations. As turbulence model, the two-equation
-model of Wilcox [
19] with the stagnation point anomaly fix of Kato–Launder [
20] was used. To capture the rotational effects, an extension of Bardina was implemented [
21]. The inlet and outlet boundaries were applied after the method of Saxer and Giles [
22]. The boundary layer transition was modelled by the two-equation
-model of Langtry and Menter [
23]. This model evaluates the local flow features to facilitate natural-, bypass-, and separation-induced transition. The correlation constants used in the transition extension of TRACE were modified, but the general formulation was applied from Langtry et al. [
23].
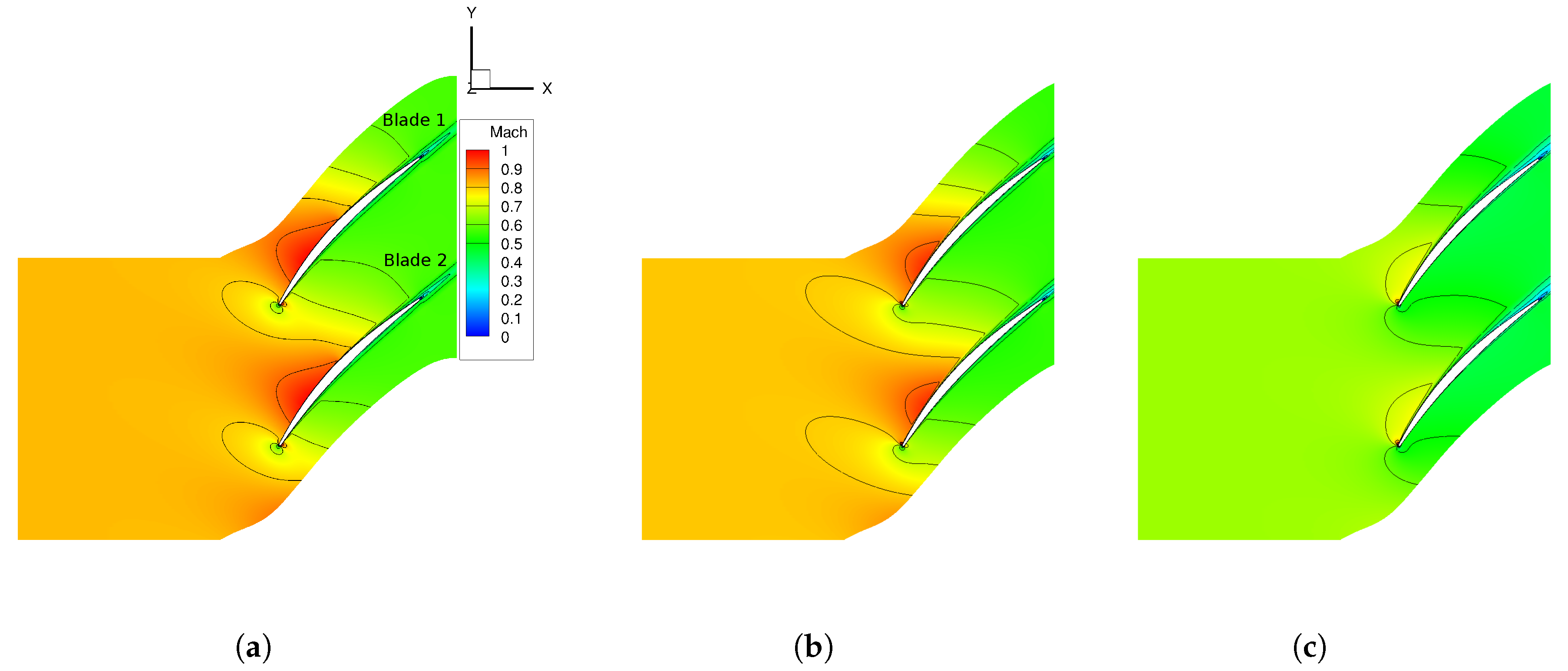
The computational domain consisted of two sectors to capture the effects of both deteriorated blades independently (cf.
Figure 3). The domain consisted of approximately 400,000 grid points, and all no-slip boundaries had a dimensionless wall distance of the wall-adjacent cell below
. A grid study was done which resulted in the given mesh. Depending on the test case blade condition, the convergence of steady state simulations was achieved after 9000–14,000 iterations, which was characterized by a relative difference of in- and outlet massflow of ≤0.02% within 2000 iterations.
To ensure that the Q3D simulations were in line with the 3D results of every operational point, the boundary conditions and the influence of the axial velocity density ratio (AVDR) had to be adapted. The boundary conditions are listed in
Table 2. The influence of the AVDR was taken into account by varying the domain height of the mesh to capture the stream tube contraction. The method used was proposed by Stark and Hoheisel [
24]. By means of this method, the Q3D simulations reached similar results, and especially the boundary layer effects and the pressure distribution were similar to the full 3D simulation. Through this approach, it is possible to detect the fluid dynamic effects of geometric blade variances of coupled blades without superimpositions of 3D effects like tip clearance vortex.
4. Validation of Meta-Model
The Kriging method according to Lophaven et al. [
10] based on 700 CFD simulations was used to train the meta model. To ensure that the meta-model was working in a reasonable interpolation range, the parameter value was limited between
independently. To validate the meta model, the aerodynamic performance for every data sample was predicted by means of the meta model and was compared to the CFD simulation. By means of conventional cross-validation (i.e., successive deletion of values for modeling and estimation), the quality of the Kriging method and therefore the meta model can be given (Kienitz [
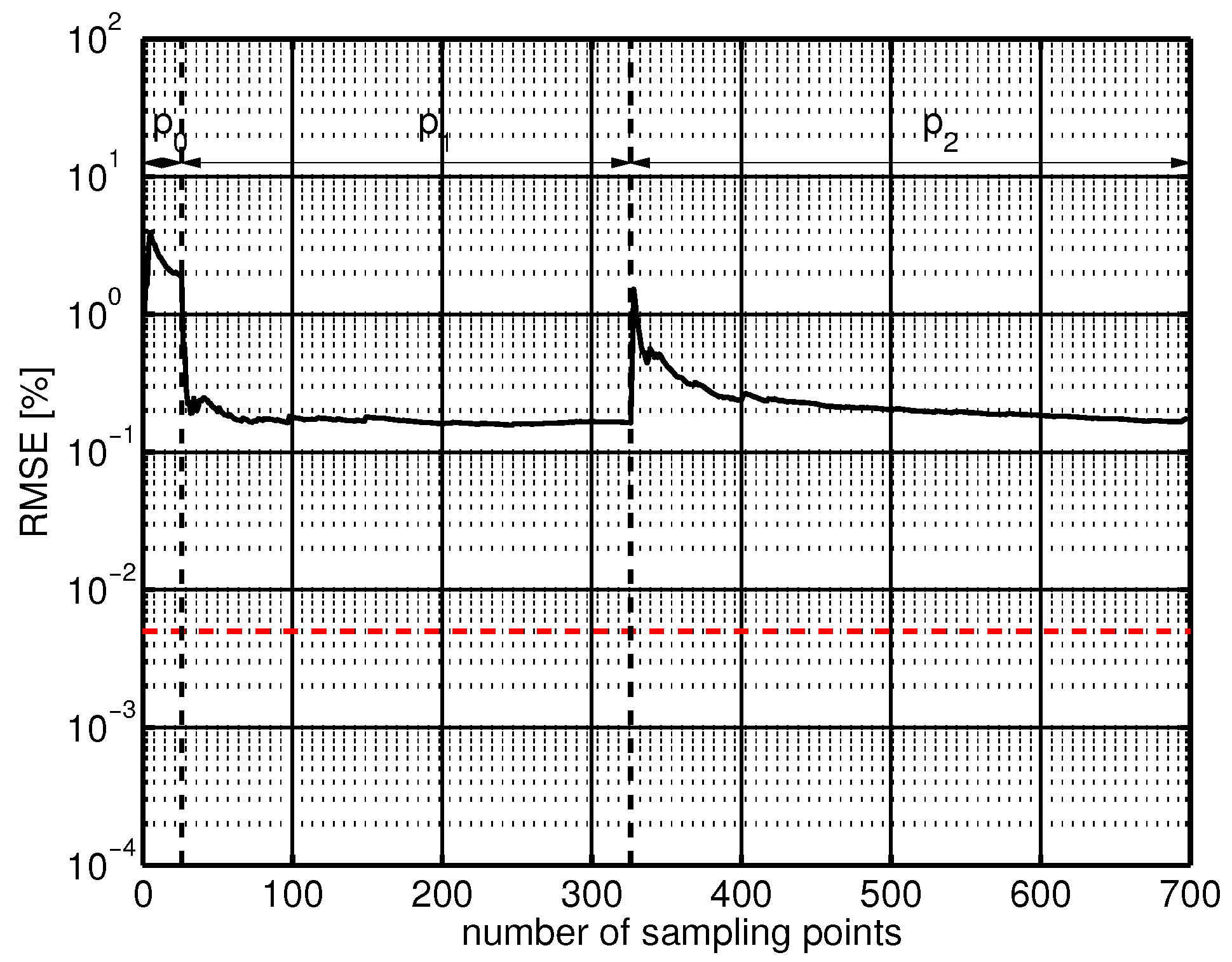
25]). In
Figure 4 the root mean square error (RMSE) is shown for the prediction of the loss coefficient at takeoff condition. The chart can be divided into three subareas: The first,
, shows the error with a constant prediction value for the Kriging method. Here a high error of approx.
was calculated. For the second area,
, the Kriging method worked on a linear interpolation and, as can be seen, the error was in the region of
. The third area
describes the error of the Kriging interpolation working with a quadratic analysis. Here the error reached
. The quadratic interpolation method is best suited for the problem definition because it can be assumed that relations between geometric parameters and aerodynamic flow field cannot be mapped with a linear approach (Reitz et al. [
5]).
5. Influence of Wear Parameters
The performance impact of differently deteriorated coupled blades was described by Pareto charts which show the influence of each geometric parameter and sensitivities which allow insight into the aerodynamic behavior. Due to dividing the domain, the coupled blades could be investigated independently, and therefore the interaction could be detected. The massflow deflection which occurred due to differently shaped blades was covered by taking the specific massflow of each border of both domains into account. Thus, it is assured that each airfoil was accounting for its influence on the flow field. Note that periodic boundary conditions for the whole domain indicate an alternating blade arrangement (
Figure 3). Therefore, this study cannot reproduce the the found circumferential pattern but addresses the effects of coupled blades on their performance in an conservative assumption.
Both blades were investigated by means of pressure rise coefficient
and loss coefficient
The Pareto chart shows all three operating points (cruise, takeoff, touchdown) and the influence of twelve geometric parameters for each blade representing the deterioration found in the statistics (
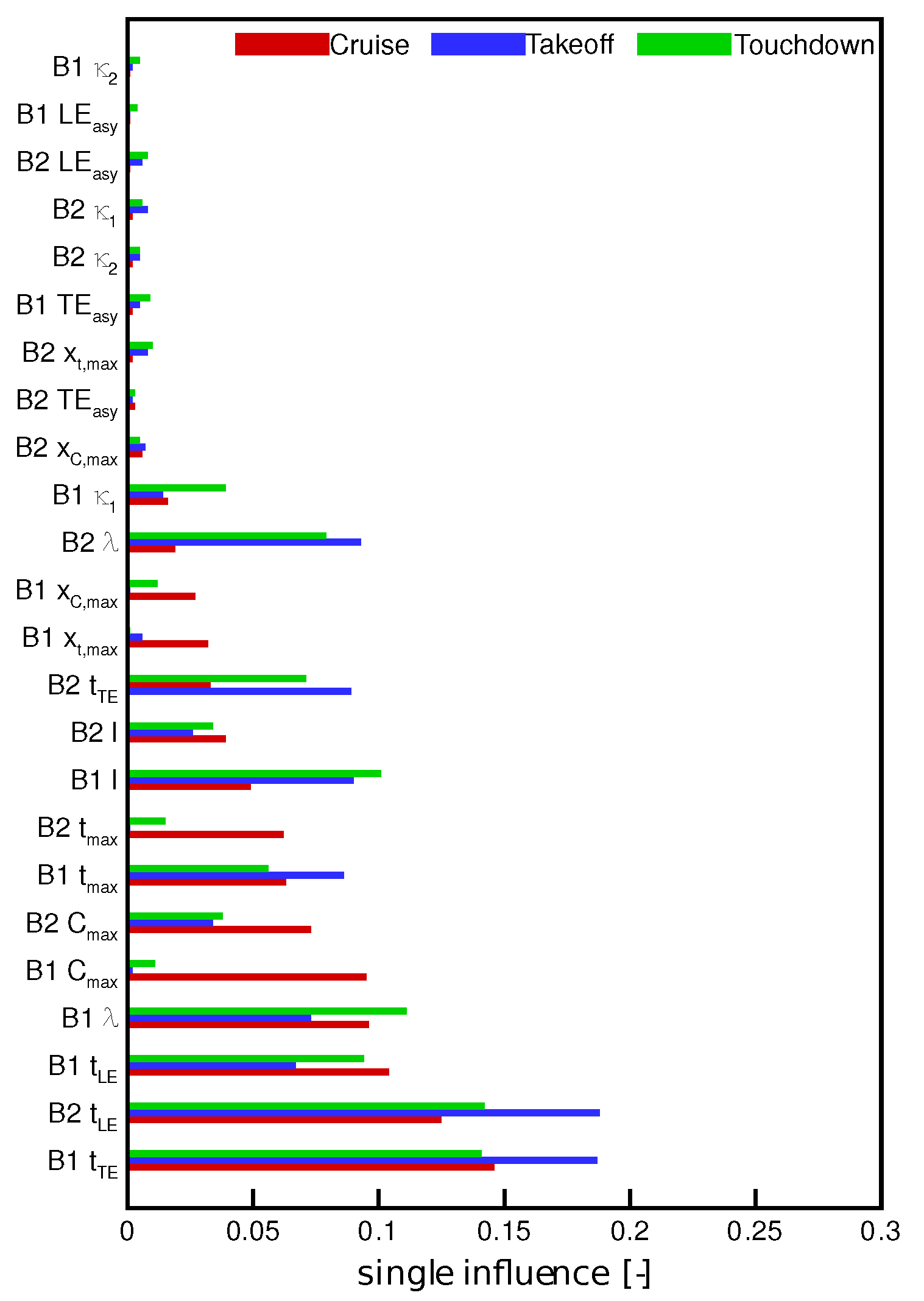
Figure 1). The figure presents the order of parameters based on the influence of the operating condition and the influence of every parameter on blade one. Thus, it can be seen that the parameters of blade two influenced the flow behavior of blade one.
5.1. Pressure Rise Coefficient
In
Figure 5, the Pareto chart of the pressure rise coefficient
is shown. The geometric parameters of both blades
are presented on the ordinate, whereas the influence is shown on the abscissa. The biggest influence on the pressure rise for the cruise condition is from the trailing edge of blades two
and one
, followed by the stagger angle for blades two
and one
. For both parameters, blade two had a higher influence on the aerodynamic performance of blade one than the parameters of blade one itself. This indicates a strong flow field change due to the deterioration. Looking at the takeoff condition, the influence of
,
,
, and
changed. The stagger angle of blade two
and
were the most important wear parameters, followed by
and
.
This similar behavior can be explained by comparable flow conditions (
Figure 2 and
Figure 3). Both conditions had a transonic flow region on the suction side in common. This region was therefore mainly influenced by the stagger angle. Additionally, the trailing edge parameter influenced the passage between both blades. Due to this, a high influence on flow field could be detected.
The wear parameter showed a different behavior for the touchdown condition. Again, the trailing edge parameters of
and
had the highest influence. The second-ranked parameter was the stagger angle for both blades. Here, the stagger angle of blade two had a higher impact (
) on the adjacent blade than blade one itself (
). The leading edge wear parameter of blade two
also had a high influence on the pressure rise of the adjacent airfoil compared to both other operating points, although this can be explained by the flow condition at touchdown. The blades had no transonic region and therefore had a clear subsonic flow which indicates a higher sensitivity to leading edge deterioration (
Figure 3).
Figure 6 gives a detailed look at the sensitivities of the most important wear parameters. By means of the meta model, the sensitivities of the wear parameter were investigated. Therefore, the range of the changed parameters is
like the Pareto chart. The influence was compared to a reference value. Thereby, a positive value represents an increasing performance parameter and vice versa.
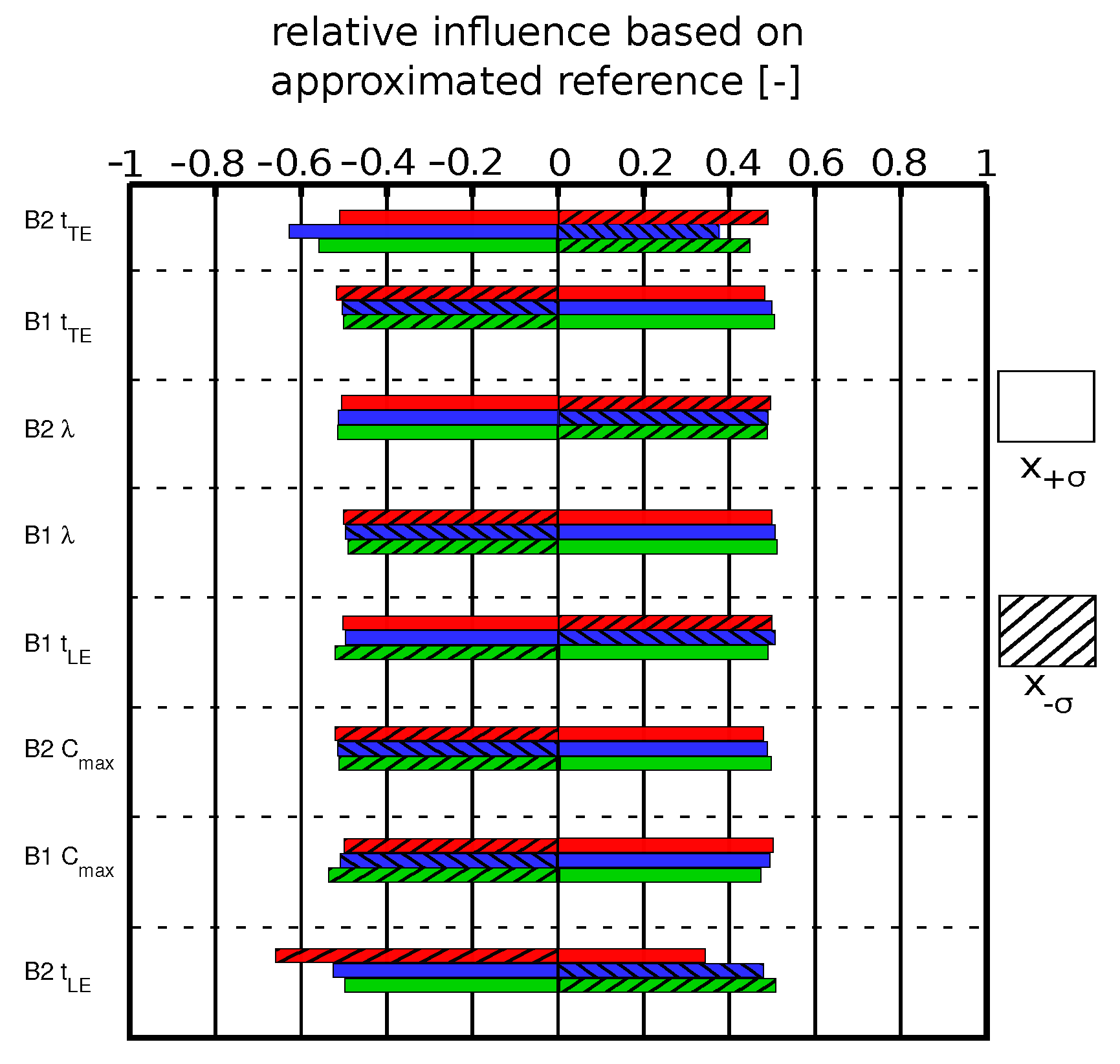
Regarding the effects on the pressure rise, the trailing edge and the stagger angle had a contrary behavior for blades one and two. A thicker trailing edge for blade one led to an increasing pressure rise, whereas a thicker trailing edge for blade two led to a lower pressure rise for blade one. The same behavior was detected for the stagger angle. For blade one, the leading edge sensitivity for the touchdown condition had a contrary behavior. A thicker leading edge led to a higher pressure rise coefficient due to the subsonic incoming flow. Additionally, for blade two the touchdown and the takeoff conditions had a contrary behavior compared to the cruise condition. The max. profile camber for both blades for all flow conditions showed a similar behavior. A higher profile camber led to a higher pressure recovery.
5.2. Loss Coefficient
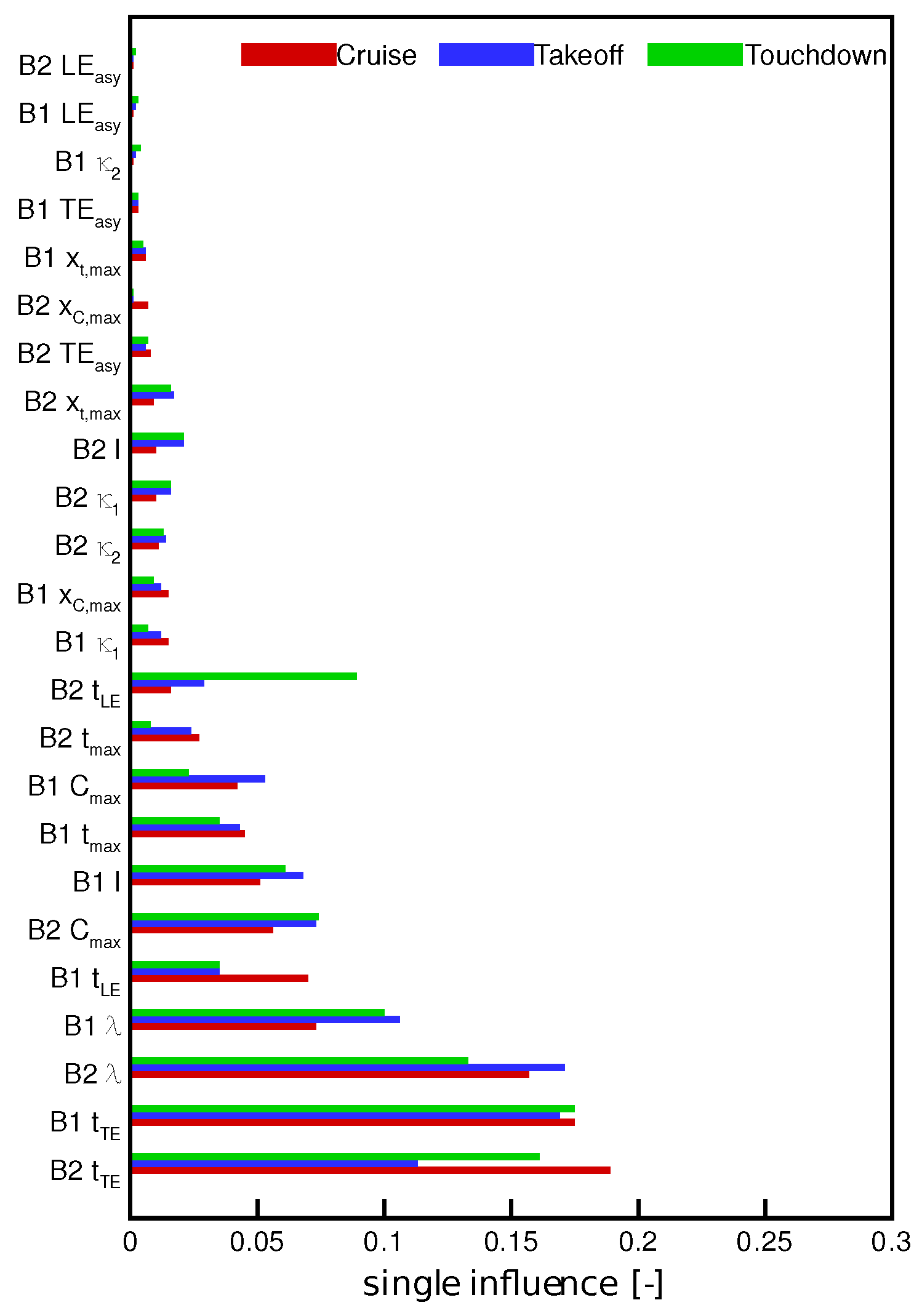
In
Figure 7 the influence of wear parameters on the loss coefficient is shown. As before, the influence of the wear parameter is presented regarding blade one. The parameter
has the highest influence on the loss coefficient for the touchdown condition. Also for touchdown, the influence of this parameter had the highest (
) influence, followed by the cruise condition
which was second-ranked among all wear parameters in cruise condition. Here the interaction between both coupled deteriorated blades can be seen. The adjacent blade two had a very high influence due to the flow field changes which affected the flow field of the adjacent blade.
The trailing edge of blade one was the next-ranked parameter and was highest ranked for the cruise condition. The stagger angle for had a much higher influence for takeoff and touchdown conditions than for the cruise condition. Additionally, the trailing edge of blade two had a higher influence on both takeoff and touchdown conditions compared to cruise. Contrary to this, the max. profile camber only had a significant influence for the cruise condition.
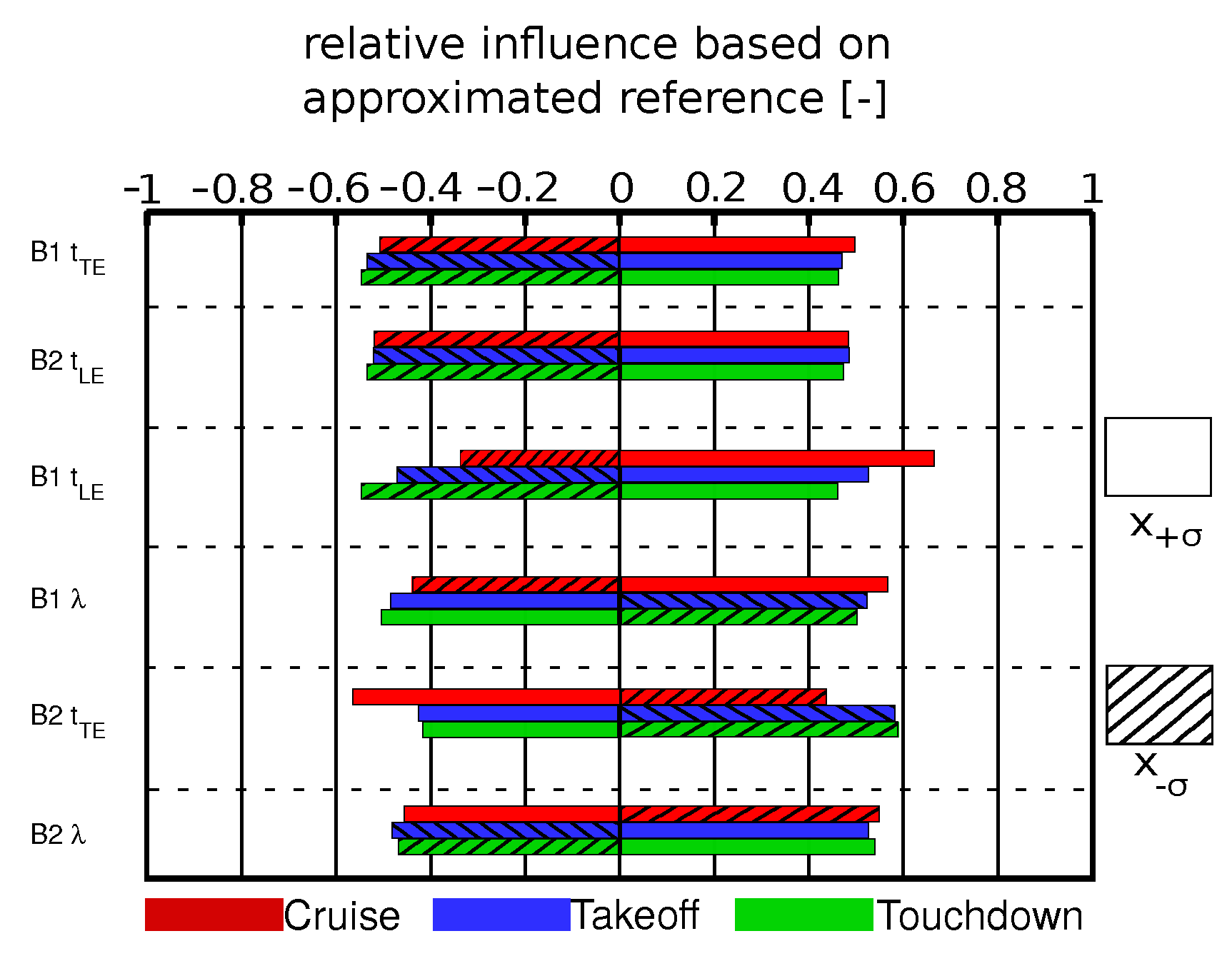
The sensitivities of the loss coefficient are presented in
Figure 8 in the same manner as for the pressure rise coefficient. Here, thicker leading edges led to higher losses for both blades. The sensitivities showed a higher influence for a
at cruise condition by increasing the thickness up to
. A descending tendency for takeoff and touchdown conditions can be seen. For
, the leading edge thickness had an ascending tendency. This behavior can also be explained by the flow field conditions. Additionally, a thicker trailing edge for blade one led to higher losses, whereas the influence of the blade two trailing edge was contrary. Furthermore, the stagger angle showed different behavior for the cruise condition. An increased stagger angle for blade one resulted in higher losses, whereas an increased stagger angle for blade two led to decreased losses on blade one. The contrary behavior was seen for the takeoff and touchdown conditions.
Overall, the wear behavior of blade one was similar to the results of Reitz et al. [
5]. The circumferential placed blade two had a high influence on the pressure rise as well as on the loss coefficient of blade one. Furthermore, unfavorable combinations of high-ranked wear parameters can lead to strengthened effects on the aerodynamic performance.
6. Conclusions
The statistical analysis of 10 flown first-stage high-pressure compressor BLISKs with 26 blades each showed significant geometric variances. Additionally, the blades showed a heterogeneous geometrical behavior around the circumference, caused by operation and regeneration. For example, the stagger angle had a max. variation of and could change between two adjacent blades of the BLISK up to . To investigate the effects of changed blade geometry on the circumference, a DoE for three operating points (cruise, takeoff, and touchdown) was done. The profile section of an HPC front stage was used to generate coupled blades to gain insight into the interaction between differently-shaped geometries. Therefore, a design space of 700 coupled, differently-shaped blades using a Latin hypercube sampling method was generated. The geometric parameters of these coupled blades varied between of the found wear characteristics. To train the meta model based on the design space, numerical simulations of the coupled blades were performed. The blade loading of the Q3D blade simulations were adjusted by using the AVDR to match the flow phenomena of a simulated 3D blade. The meta model was used to create Pareto charts and sensitivity analysis. The investigation showed a strong interaction between the coupled wear parameters for all three operating points.
- (a)
The pressure coefficient was mainly influenced by changes of the trailing edge, stagger angle, and leading edge. All three parameters influenced not only the changed blade, but also the adjacent blade by the same order of magnitude.
- (b)
A sensitivity analysis of the pressure coefficient showed nearly the same behavior for all three operating points. A thicker trailing edge led to a higher pressure coefficient on the affected blade and a lower pressure coefficient for the adjacent blade. The same behavior could be seen for the stagger angle. The leading edge influence depended on the operating condition.
- (c)
The loss coefficient showed strong dependencies on the operating condition. While the thickness-related edge parameter and stagger angle of both blades had a high influence, the max. profile camber only had a strong impact for the cruise condition.
- (d)
The sensitivity analysis of the loss coefficient showed similar behavior for all operating conditions for the presented wear parameters, apart from the stagger angle. Here the stagger angle showed a contrary behavior for the cruise condition.
To summarize, the operating condition changed the impact of the wear parameters significantly. Furthermore, sensitivities of wear parameters were changed between different operating conditions. Additionally, it was shown that the adjacent blade had a significant influence on the flow behavior of the adjacent blade, and this behavior also changed due to the operating condition. The shift of the influence was a result of different flow fields, and therefore their characteristic blade loading. Cruise condition had transonic flow conditions, whereas the takeoff condition had a slightly slower incoming flow Mach number. The touchdown condition was in a subsonic region. Therefore, the blade loading was different for all three operating points and because of this, the influence of wear parameters differed.
In addition, the outcome outlines that coupled geometric variances not only affect the blade row itself, but also the the following stator row due to the changed outlet flow. So, the stage matching of coupled deteriorated blades needs to be the subject of further investigations.
It can be concluded that unfavorable coupled wear parameters lead to higher effects on the performance due to the interaction of different wear parameters. Based on this, the maintenance process of BLISK blades should not only address a damaged blade but also the adjacent blades to avoid a drop of performance due to the unfavorable effects of coupled deteriorated blades.