A Cross-National Study on Sustainable Smart City Indicators and Their Influence on Life Expectancy—A Cluster Analysis of EU Countries

Abstract

As a consequence of climate change and its negative impacts on the environment and on human health, the topic of sustainability has become an integral part of urban policy. Smart city initiatives around the world are focusing on different aspects of sustainability in order to provide better living conditions for their residents. The aim of this study is to investigate the impact of selected smart city indicators on the average life expectancy as a variable for quality of life and well-being. Based on a Common Correlated Effects (CCE) model, Instrumental Variable Estimator with Common Factors (2SIV), and clustering regression model, EU countries were divided into three distinct clusters indicating common elements but also specificities of each group. The analysis confirmed the positive impact of GDP growth, renewable energy consumption, and the proportion of the population with a tertiary level of education on life expectancy. On the other hand, CO₂ emissions and transport pollution have an adverse effect. The analysis provides valuable insights into the complex relationship between smart city variables and quality of life, and it may serve as a basis for informed and responsible decision-making by relevant urban stakeholders aimed at designing more sustainable, resilient, and healthier cities.

1. Introduction

Modern cities currently face numerous issues arising from the increasing number of people living in them, environmental impacts, limited resources, and the intricate dynamics of social and economic factors. The rising population density strains infrastructure, resulting in traffic jams, strained public services, and heightened pollution levels. Climate change further threatens cities’ resilience as increasing temperatures impact sustainability and liveability. Moreover, socio-economic gaps worsen disparities in accessing education, healthcare, and job opportunities. In addressing these challenges, smart cities are transitioning towards a strategy that utilises technology- and data-driven solutions to enhance efficiency, sustainability, and overall well-being. As countries worldwide embark on urbanisation endeavours, the influence of these advancements on citizens’ quality of life gains significance. This study aims to investigate the correlation between socio-economic and environmental factors and life expectancy at a European Union (EU) scale.

From the urban science perspective, cities can be perceived through various lenses, including spatial, socio-economic, and environmental dimensions. Spatially, different methodologies and approaches can be used to delineate city boundaries. Core-based statistical areas, urban areas, or administrative boundaries can lead to different city characteristics and spatial distributions [1]. However, Sahasranaman and Bettencourt [2] and Lobo et al. [3] suggest that cities are not only geographical entities but complex systems that facilitate economic and social interactions. With growing recognition of environmental challenges such as the consequences of climate change or limited natural resources, ecological footprints and environmental sustainability aspects have become integral components in defining cities. Dias et al. [4] emphasise the holistic approach that seeks a balance between economic development, quality of the environment, and citizens’ quality of life. Ensuring the efficient and sustainable management of resources and consideration of environmental and social aspects in decision-making processes is necessary to incorporate these aspects into urban governance [5]. In order to enhance multifaceted urban sustainability and improve citizens’ quality of life, many cities are turning to the concept of smart cities.

Smart city programmes and initiatives incorporate information and communication technologies (ICT) to improve energy efficiency and the use of renewable energy, optimise transportation systems, enhance recycling and circularity, and improve public services. These efforts not only enhance efficiency in using resources and supporting environmental sustainability but also encourage inclusivity, incentivise citizen involvement, and strengthen overall city resilience. However, the relationship between smart cities’ development and public health on a national scale is an aspect that warrants further attention from decision-makers, researchers, and practitioners. As a result, global organisations like the United Nations (UN) and the European Union (EU) have stressed the importance of plans that focus on promoting health and quality of life within the larger framework of sustainable development.

The global importance of resilient and sustainable urban environments and inclusive communities is highlighted in the UN’s key documents and initiatives, such as Agenda 2030 and the Sustainable Development Goals, where SDG 11 in particular addresses this issue. This area is of utmost importance at the EU level. For instance, the EU supports smart, green, and integrated urban development through the EU Smart Cities programme, under Horizon 2020 [6]. The role of digital transformation as a vehicle for improving the lives of citizens is further underlined in the EU’s Digital Agenda [7]. Moreover, the transformative potential of ICT in creating more sustainable and efficient cities is recognised in the European Commission’s Smart Cities and Communities initiative [8], which enhances and supports the overall objectives of the European Urban Agenda.

This study aligns well with the international commitments set by the UN and the EU to leverage technological advances to improve public health and well-being. As the UN emphasises, sustainable development can only be achieved when there is a balance between the ways we develop and manage urban areas [9].

The cross-national focus of this study resonates with the wider global community aiming towards the SDGs. As the UN points out, “cities are hubs for ideas, commerce, social development and more” [10]. In addition, smart cities have the potential to improve the living conditions of their citizens by helping to reduce emissions, increase efficiency, promote sustainable economic growth, and improve overall urban life [11,12]. The aim of this study is to explore the relationships among a diverse set of variables, such as GDP, CO₂ emissions, renewable energy use, education, recycling rates, and transport-related emissions, and examine how they interact with life expectancy in the European Union. While our research focuses on city issues, we opted to use national data from EU member states, due to the unavailability of reliable and comparable data at the city level. This approach allows us to explore wider patterns that may reflect the urban dynamics at a national scale. Given the complexity and heterogeneity of cities within EU countries, national-level analysis helps us understand the overall patterns and identify commonalities and disparities in urban issues across EU countries. This research intends to employ regression clustering analysis to approach the unique segmentation of EU countries as clusters based on common characteristics, allowing us to account for regional specificities and heterogeneities. This innovative methodology is anticipated to not only enhance the accuracy of our findings but also to enable us to provide more tailored and effective urban management recommendations that reflect the distinct contexts of different EU member states.

The rest of the paper is structured as follows: Section 2 is devoted to reviewing current literature and provides a rationale for choosing variables. In Section 3, we formulate our research hypothesis and present the data. Results are summarized in Section 4 and discussed in Section 5. The last part concludes the findings and outlines the policy implications. The paper has an ambition to extend our academic knowledge, but also contribute to the ongoing international dialogue on urban development and its impact on the health and well-being of populations in different country-specific conditions.

2. Literature Review and Rationale for Selecting Variables

As cities become centrepieces of human development, smart city initiatives focused on improving the urban living conditions and quality of life of citizens have gained increasing attention in recent years. In this context, life expectancy has become a critical indicator of the population´s wellbeing. The literature consistently supports the assertion that life expectancy is influenced by various interconnected socio-economic, environmental, and health factors that collectively shape the quality of life within society.

Socio-economic factors, such as income and education, play a crucial role in determining life expectancy. Studies by Gilligan & Skrepnek [13] and Miladinov [14] suggest that higher income levels correlate positively with increased life expectancy, as wealthier individuals typically have better access to healthcare, nutrition, and living conditions. Research has also indicated that greater economic prosperity can result in increased investments in environmental protection and programs aimed at improving public health [15,16]. Education also plays a critical role as individuals with higher educational attainment tend to engage in healthier lifestyles and have better access to health resources, which in turn enhances their longevity [17,18]. Additionally, education is a strong predictor of health literacy, enabling individuals to make informed health choices that can enhance their longevity [19]. Furthermore, social policies that allocate resources towards education and healthcare have been linked to improved life expectancy outcomes, particularly in high-income countries [20]. Higher educational attainment is also associated with higher income and better employment opportunities, which can consequently lead to improved health and well-being [21]. On the other hand, the disparities in life expectancy among different socio-economic groups highlight the importance of addressing social determinants of health to improve overall population well-being [19].

CO₂ emissions are a primary contributor to climate change and are linked to negative impacts on health, which can further negatively affect life expectancy. Higher concentrations of CO₂ emissions and long-term exposure to pollutants are associated with respiratory diseases and other negative health effects [22,23], that further reduce life expectancy. For example, research by Chang [24] indicates that the negative impact of CO₂ emissions on life expectancy is particularly pronounced in countries, where industrial activities and urbanization contribute significantly to air quality deterioration. Implementing smart city initiatives such as green mobility [25,26] and the use of renewable energy [27,28], have the potential to reduce these emissions and hence related health risks [29]. Renewables as a percentage of equivalent primary energy consumption is an indicator representing a green energy transition, reducing dependence on fossil fuels and mitigating the effects of climate change [30,31]. Fossil fuel combustion is a main source of air pollution, emitting harmful pollutants such as particulate matter (PM 2.5; 10), sulphur dioxide (SO₂), nitrogen oxides (NOx), and volatile organic compounds (VOCs). These pollutants can negatively affect respiratory health, the cardiovascular system, and general well-being [32,33]. In contrast, renewable energy sources do not emit pollutants during energy production and thus significantly reduce air pollution levels in urban environments [28,34]. Studies have shown the health co-benefits of using renewable energy, including reducing air pollution-related diseases and premature mortality [35]. Similar findings were confirmed by Zhang et al. [32] investigated the impact of foreign direct investment inflow, carbon emissions, and renewables on health quality in China. Results suggest that the CO₂ emissions hurt health quality. Moreover, a significant and positive impact was reported in the case of renewable energy consumption. The study showed that higher shares of renewable energy tend to have better health outcomes and longer life expectancies due to reduced exposure to harmful pollutants associated with fossil fuel combustion.

Another critical factor influencing life expectancy is urbanization. As urban areas are often characterized by higher population density and higher pollution levels, this tends to cause lifestyle-related health risks [36,37]. Especially rapid urbanization and increased population density has been linked to high levels of pollution, inadequate infrastructure, and limited access to health services [38,39]. However, urbanization also promotes economic growth and innovation [40]. In this term, urbanization can provide opportunities for improved healthcare access and social services, enhancing life expectancy if managed effectively. Highlighting the dual nature of urbanization, Zeng et al. [38] call for sustainable urban planning that prioritizes health and well-being, such as creating green spaces and improving public transportation to reduce emissions.

Finally, transport-related emissions, particularly from fossil-fuelled vehicles, are a significant source of air pollution in urban areas [41]. These emissions release harmful pollutants such as NOx, PM, and VOCs [25,42]. Exposure to emissions has been linked to a range of adverse health outcomes, including aggravation of asthma, lung cancer, and cardiovascular disease. Vulnerable populations are particularly susceptible to the health effects of transport-related pollution [43]. Health issues related to high concentrations and long exposure to these pollutants can reduce life expectancy [44].

The concept of smart cities concentrates on a wide spectrum of aspects. For instance, Abu-Rayash and Dincer [12] address smart energy systems. They propose a model for evaluating smart cities based on a complex system of smart city characteristics. The study, in particular, highlights the positive role of smart energy systems and their correlation with economic performance and smart city governance. Similarly, Ji et al. [45] performed a case study among citizens in Taiwan, investigating their perceptions and preferences for smart city services. The study underlines the need to align technological advances with the needs of residents. From citizens’ perspectives, smart energy systems and smart mobility were the highly preferred areas, with the potential to improve the quality of life and well-being of citizens. This perspective is complemented by Macke et al. [46], who examine citizens’ perceptions of quality of life in smart cities. The factors that influence the perceptions of quality of life are identified. The study emphasises the importance and advocates for an integrated approach that combines both objective and subjective aspects of quality of life and provides valuable insight for policymakers and urban planners who are concerned about improving the living conditions of citizens in smart cities.

The social and cultural aspects of smart cities are explored by Han and Hawken [47], who highlight the importance of a more holistic approach and the necessity to take cultural nuances, social identity and human behaviour into consideration when designing smart cities. They criticize the common metrics for assessing smart cities and advocate for balancing urban innovations and technology integration with cities’ unique historical and cultural contexts and the needs of citizens.

The ample evidence from the literature provides significant insights into the multifaceted nature of smart cities, particularly regarding sustainability and quality of life. However, there remains a critical gap in understanding how the specific mechanisms influence life expectancy—an important variable referencing health outcomes. While previous studies have often focused on singular aspects such as city governance, environmental sustainability, energy issues and urban livability, they haven´t fully explored the multidimensional relationships between smart city variables and life expectancy. Also, although some research has linked environmental factors like CO₂ emissions and renewable energy with health impacts, the interplay between these and other socio-economic factors, such as urbanization, education, and economic growth, is still unexplored.

Focusing on a comprehensive set of variables derived from theoretical frameworks and empirical studies, this research seeks to address these gaps and contribute to a deeper understanding of the complex interplay between smart city indicators and public health outcomes. The novelty of this study lies in its holistic approach to examining the relationship between smart city characteristics and life expectancy. Through rigorous analysis and interpretation of national-level data, we aim to provide actionable insights for policymakers, urban planners and public health professionals aiming to create healthier and more resilient cities.

These variables were selected as input for our analysis to help us better understand complex relations between smart city indicators and life expectancy and identify key drivers of public health in a smart city context. Each variable represents a different aspect of urban development, environmental sustainability or socio-economic well-being, with the potential to influence life expectancy through different pathways.

By examining these smart city indicators in conjunction with life expectancy, this research aims to elucidate the complex interactions between urbanisation, economic activities, environmental quality and socio-economic inequalities on public health outcomes.

3. Theoretical Framework and Hypothesis Development

Our research on the impact of variables such as GDP, CO₂ emissions, urbanisation, renewable energy, education and recycling on life expectancy is based on several theoretical frameworks. First, sustainable development theory, suggesting the harmonious development of economic, social and environmental dimensions, represents the holistic approach to development. It is highly applicable for urban planning and resource management focused on the improvement of the quality of life of citizens. Studies on renewable energy and recycling initiatives are often grounded on this framework, highlighting the importance of sustainable practices for increased quality of life due to reduced pollution [48,49]. Second, human capital theory suggests that investments in education enhance individuals´ productivity and economic outcomes. It posits that better education leads to better job opportunities and higher income, which also contributes to better health outcomes and longer life expectancy. As mentioned before, research consistently declares a positive correlation between education and health [50,51]. Third, the smart city concept encompasses various frameworks focused on the integration of technology, sustainability and citizen engagement to enhance urban living conditions. According to Sharif and Pokharel [52], the smart city concept was introduced in the early 1990s to enhance urban processes and services to improve economic development, quality of life and sustainable environment.

In recent decades, we have witnessed the transition of cities worldwide towards more sustainable and smarter urban conditions. Adopting technological innovations and striving for environmental sustainability, these initiatives have various positive effects on the economy, environment and community. However, there are also critical voices pointing to the negative aspects and calling for a more holistic approach to assessing the performance of smart cities. This study aims to fill this gap by investigating how key smart city indicators influence life expectancy at birth as a proxy for the quality of life. Identifying drives that can positively or negatively affect life expectancy can serve as valuable input for responsible, evidence-based policies and urban planning strategies that promote healthier and more resilient cities.

The study that certain smart city indicators will significantly impact life expectancy at birth. In particular, the study assumes that higher GDP per capita, renewable energy (% primary energy equivalent), tertiary education attainment and municipal waste recycling rate for municipal waste are positively associated with higher life expectancy. Conversely, the study expects higher per capita CO₂ levels and a higher proportion of urban population to be negatively associated with life expectancy, reflecting the potential health consequences of environmental degradation and urbanisation. Through rigorous statistical analysis, the study aims to validate these hypotheses and uncover nuanced relationships between smart city indicators and public health outcomes.

4. Data and Methods

Using annual data from 2000 to 2021, the impact of various smart city indicators, including GDP per capita in PPP, annual CO₂ emissions per capita, share of urban population, renewable energy (% primary energy equivalent), tertiary education attainment, municipal waste recycling rate and transportation emissions, on life expectancy at birth is examined. The analysis focused on twenty-five European countries, namely Austria (AUT), Belgium (BEL), Bulgaria (BGR), Croatia (HRV), the Czech Republic (CZE), Denmark (DNK), Estonia (EST), France (FRA), Finland (FIN), Germany (GER), Greece (GRC), Hungary (HUN), Ireland (IRL), Italy (IT) Ireland (IRL), Italy (ITA), Lithuania (LTU), Latvia (LVA), Luxembourg (LUX), the Netherlands (NLD), Poland (POL), Portugal (PRT), Romania (ROU), Slovakia (SVK), Slovenia (SVN), Spain (ESP) and Sweden (SWE).

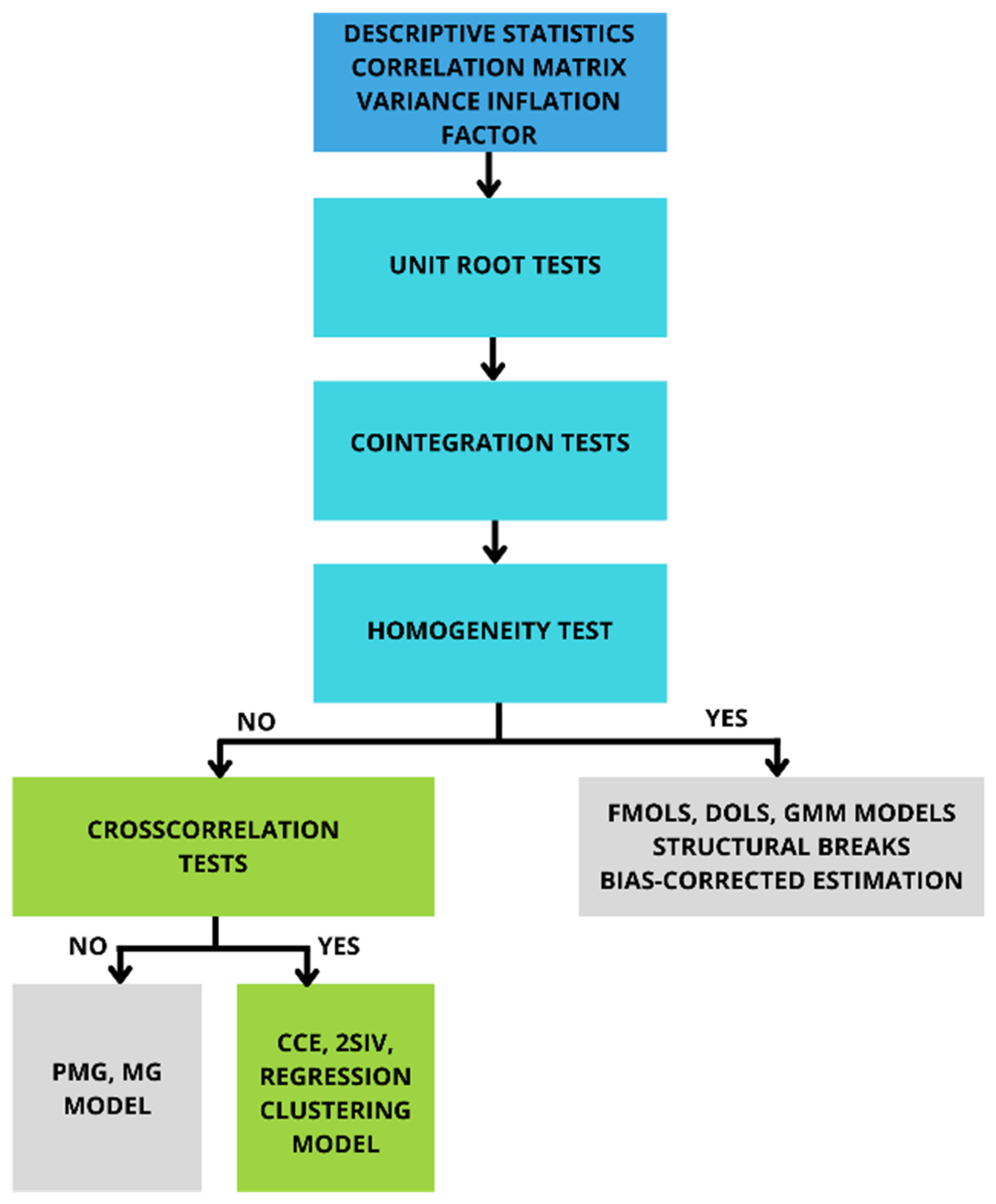
Based on the literature review, the eight variables were selected as input into the econometric models, as shown in

Table 1. Variable definition.

Variable	Unit	Abbreviation
Average lifespan	Years	LIFE
Gross Domestic Product	Eur per capita	GDP
CO2 emissions	Tonnes per capita	CO2
Urban population	% of total population	URBAN
Energy produced from renewable sources	MWh per capita	RES
Tertiary educational attainment	% of total population	EDU
Recycling rate of municipal waste	% of total waste generated	RECY
Transport-related emissions	gCO2/km	TRANS

. The models are developed using Stata 15.1.

Table 2. Descriptive statistics of analysed variables.

Variable	Mean	Std. Dev	Min	Country	Max	Country
LIFE	78.33282	3.281492	69.5031	ROU	83.552	IT
GDP	31,000.96	22,555.37	1617.164	BGR	134,712.8	LUX
CO2	8.073056	3.570993	2.96028	LVA	25.98496	LUX
URBAN	71.87019	11.8938	50.754	SVN	98.117	BEL
RES	17.33377	11.77908	1.28	LUX	62.686	SWE
EDU	34.60971	11.38074	9.2	ROU	62.6	LUX
RECY	30.83254	18.20051	0	LTU, LVA, ROU	70.3	DEU
TRANS	140.8825	22.86912	85.7	NLD	200.2	SWE

shows descriptive statistics. The average CO₂ per capita is 8.07 tons, with a standard deviation of 3.57 tons, indicating relatively high variability in CO₂ emissions between countries. The wide range among countries indicates different levels of industrial activities, composition of energy mixes and policy regulations. Life expectancy (LIFE) ranges from a minimum of 69.5 years in Romania (ROU) to a maximum of 83.55 years in Italy (IT). This 14-year difference reflects possible variations in healthcare quality, socio-economic and environmental conditions, as well as lifestyle factors.

Table 3. Correlation matrix.

Log	LIFE	GDP	CO2	Urban	RES	EDU	RECY	TRANS
LIFE
GDP	0.835 ***
CO2	0.259 ***	0.419 ***
Urban	0.408 ***	0.504 ***	0.311 ***
RES	0.0002	−0.0819 *	−0.5649 ***	−0.160 ***
EDU	0.482 ***	0.560 ***	0.004	0.412 ***	0.134 ***
RECY	0.664 ***	0.706 ***	0.225 ***	0.437 ***	0.097 **	0.567 ***
TRANS	−0.459 ***	−0.215 ***	0.331 ***	−0.062	−0.299 ***	−0.415 ***	−0.324 ***

Note: *—sig. level 0.1, **—sig. level 0.05, ***—sig. level 0.01.

shows the correlation matrix. Most of the correlation coefficients are statistically significant. Zooming in on life expectancy, we observe a strong positive correlation between GDP and life expectancy, suggesting that economic welfare positively correlates with longer life expectancy. Similarly, a strong positive correlation exists between recycling rate and life expectancy, suggesting positive impacts of efficient waste management and cleaner environment. A positive correlation can also be observed in the case of urban population rate and education. In contrast, there is a negative correlation between life expectancy and transport-related emissions.

First, a multiple regression analysis is performed with life expectancy at birth (LIFE) as the dependent variable and all other variables as input variables.

The resulting regression coefficients are shown in

Table 4. Multiple regression.

	Coef.
	Reg	Ivreg (2-IV)	Ivreg (3-IV)
Log_GDP	0.04189 ***	0.05075 ***
Log_CO2	−0.00387	−0.03313 ***	0.01573 ***
Log_URBAN	0.00038	−0.00017	0.01652
Log_RES	−0.00108
Log_EDU	−0.01438 ***	−0.01190 ***	0.01422 ***
Log_RECY	0.00409 **	0.00828 ***	0.02339 ***
Log_TRANS	−0.07404 ***
constant	2.01504 ***	1.85923 ***	1.79651 ***
R2	0.693	0.6017	0.3554
Test	Statistic	p-value	p-value
Tests of endogeneity	Durbin (score) chi2 (1)	0.000	0.0080
First stage tests	Minimum eigenvalue statistic	Test statistics F (2481) = 160.929 is much larger then any critical values	Test statistics F (3481) = 151.212 is much larger then any critical values
Tests of overidentifying restrictions:	Sargan (score) chi2 (2) Basmann chi2 (2)	0.000 0.000	0.000 0.000
Instrumental variables		Log_RES,TRANS	Log_GDP,RES,TRANS

Note: p < 0.05 (**), p < 0.01 (***).

. This analytical approach allows us to comprehensively examine the relationships between LIFE and the different input variables. By assessing the magnitude and direction of these coefficients, the study gains insight into how factors such as GDP, urbanisation, CO₂ emissions, education and renewable energy influence LIFE in the context of smart cities.

The coefficient of determination (R-squared = 0.693) indicates that about 69.3% of the variability of the dependent variable can be explained by the independent variables included in the model. To ensure the robustness of the analysis, it is important to check for multicollinearity between the independent variables. In the study, a thorough check of multicollinearity is conducted using the variance inflation factor (VIF). Identifying and dealing with multicollinearity is crucial to ensure the reliability and interpretability of the regression results.

The next two columns show models where Log_CO₂ is treated as an endogenous variable. The instrumental variables are Log_RES, Log_TRANS column Ivreg (2-IV). In the Ivreg (3-IV) column, three instrumental variables are considered: Log_RES, Log_TRANS and Log_GDP. However, in both cases, good results were not obtained in the Test of overidentifying restrictions. This means that these models are not correctly specified. Also, the R-squared is very low in the case of Ivreg (3-IV).

To examine the presence of multicollinearity among variables, we calculated variance inflation factor (VIF). The results are presented in

Table 5. Variance Inflation Factor.

Variables	VIF	Variables	VIF
Log_GDP	2.33	Log_TRANS	1.59
Log_CO2	2.32	Log_URBAN	1.54
Log_RECY	1.98	Log_EDU	1.47
Log_RES	1.69	Mean VIF	1.85

.

There are different recommendations for acceptable values of the VIF in the literature. While a maximum VIF value of 10 is generally advocated [53], some researchers suggest stricter thresholds, e.g., VIF values that do not exceed 5 [54] or even 4 [55]. The analysis shows that the VIF values obtained are below these recommended thresholds. Moreover, Zuur et al. [56] suggest, that VIF of 3 or more may no longer be considered suitable. The achieved VIF values are below the recommended values, so we can work with all variables in the following procedure.

Moreover, we use the LASSO (Least Absolute Shrinkage and Selection Operator) method to confirm this conclusion. LASSO reduces the number of explanatory variables and can be a tool for selecting appropriate regressors. Lambda λ is a penalty parameter that determines the magnitude of regularisation, Knots are the values of λ at which variables in the model change. The method involves adding variables step-by-step (see Action column), while minimising Akaike Information Criterion (AIC) and taking into account model goodness-of-fit (R-square), as captured in

Table 6. Results of LASSO (Least Absolute Shrinkage and Selection Operator).

Knot	Lambda	AIC	R-Squared	Action
1	12.12170	−4022.734	0.000	Added _cons
2	11.04484	−4072.128	0.1000	Added Log_GDP
3	5.75879	−4319.461	0.4601	Added Log_TRANS
4	2.49284	−4513.398	0.6386	Added Log_RECY
5	0.81629	−4566.429	0.6772	Added Log_EDU
6	0.16787	−4586.749	0.6917	Added Log_CO2
7	0.10543	−4585.748	0.6923	Added Log_RES
8	0.01640	−4584.676	0.6930	Added Log_Urban

.

The regression coefficients obtained by the LASSO method are shown in

Table 7. LASSO regression coefficients.

Selected	LASSO	Post-Est OLS
Log_GDP	0.04035	0.04116
Log_EDU	−0.01082	−0.01391
Log_RECY	0.00335	0.00372
Log_TRANS	−0.07231	−0.07631
cons	2.00521	2.01684

. According to the regression coefficients, Log_GDP, Log_TRANS, Log_RECY, and Log_EDU are the most impactful variables, while others (Log_CO₂, Log_RES, and Log_Urban) have minor effects.

Comparing the LASSO and Post-est OLS, the magnitude and direction of relations are consistent, with only slight variations.

Consequently, the study continues with all variables in the subsequent analysis as their intercorrelations are within acceptable limits. This ensures the reliability and validity of the regression model and facilitates a comprehensive examination of the relationships between the variables of interest. Subsequently, a wide range of mathematical and statistical techniques are used in the analysis. The methodological procedure is illustrated in Figure 1.

5. Results and Discussion

Fisher ADF, Fisher PP and CIPS unit root test of [57] are used to investigate the stationarity of the variables. With the results of these tests, it is determined that the series is stationary at the first difference, I (1) (

Table 8. Panel unit root tests.

Panel Unit Root Test
	1st Generation—p-Value				2nd Generation
Variables	Fisher (ADF)		Fisher (PP)	IPS	CIPS
Log_LIFE	P	1	0.9995	1	−3.081 ***
	Z	1	1
	L *	1	1
	Pm	1	0.9959
D.Log_LIFE	P	0.000	0.000	0.002	−4.419 ***
	Z	0.000	0.000
	L *	0.000	0.000
	Pm	0.000	0.000
Log_GDP	P	0.0528	0.9999	0.0069	−2.66 *
	Z	0.0013	0.9884
	L *	0.0036	0.9783
	Pm	0.0429	0.9982
D. Log_GDP	P	0.000	0.000	0.000	−3.333 ***
	Z	0.000	0.000
	L *	0.000	0.000
	Pm	0	0
Log_CO2	P	0.0601	0.0002	0.0762	−2.426
	Z	0.0470	0.0001
	L *	0.0545	0.0001
	Pm	0.0505	0.000
D.Log_CO2	P	0.000	0.000	0.000	−4.876 ***
	Z	0.000	0.000
	L *	0.000	0.000
	Pm	0.000	0.000
Log_Urban	P	0.000	0.0620	0.6313	−1.534
	Z	0.0003	1
	L *	0.000	0.9994
	Pm	0.000	0.0525
D.Log_Urban	P	0.000	0.000	0.0005	−3.5 ***
	Z	0.0004	0.000
	L *	0.000	0.000
	Pm	0.000	0.000
Log_RES	P	0.0023	0.000	0.2126	−2.86 ***
	Z	0.2278	0.0191
	L *	0.0700	0.0009
	Pm	0.0005	0.000
D.LOG_RES	P	0.000	0.000	0.000	−4.939 ***
	Z	0.000	0.000
	L *	0.000	0.000
	Pm	0.000	0.000
Log_EDU	P	0.0030	0.0053	0.4287	Not balanced panel
	Z	0.1755	0.3645
	L *	0.0644	0.2812
	Pm	0.0007	0.0017
D.Log_EDU	P	0.000	0.000	0.000	Not balanced panel
	Z	0.000	0.000
	L *	0.000	0.000
	Pm	0.000	0.000
Log_RECY	P	0.000	0.5196	0.0221	Not balanced panel
	Z	0.0386	0.5749
	L *	0.000	0.6048
	Pm	0.000	0.5458
D.Log_RECY	P	0.000	0.000	0.000	Not balanced panel
	Z	0.000	0.000
	L *	0.000	0.000
	Pm	0.000	0.000
Log_TRANS	P	1	1	1	Not balanced panel
	Z	1	1
	L *	1	1
	Pm	1	0.99
D.Log_TRANS	P	0.2461	0.000	0.3663	Not balanced panel
	Z	0.3528	0.000
	L *	0.3283	0.000
	Pm	0.2590	0.000

Note: p < 0.10 (*), p < 0.01 (***).

).

The p-values are reported for most tests, except for the CIPS test, where the test statistic is calculated. The critical values for the CIPS test at different significance levels (1%, 5%, and 10%) are −2.81, −2.66, and −2.58. The majority of tests, except Fisher (ADF) for the Log_TRANS variable, show that the variables are integrated of the first degree (I (1)). Some tests even label the variables as stationary.

Moving on to cointegration tests, these tests aim to determine whether there exists a long-term stable relationship between variables. Cointegration implies that economic time series, after short-term fluctuations, converge back to an equilibrium state.

The cointegration tests proposed by [58,59,60] are applied to panel data in this study. The results, which are presented in

Table 9. Cointegration tests.

Panel Cointegration Test	No	Test Type	p-Value
Kao tests	1	MDF	0.0000
	2	Dickey Fuller (DF)	0.0066
	3	ADF	0.0571
	4	Unadjusted modified Dickey-Fuller	0.000
	5	Unadjusted DF	0.0069
Pedroni tests	1	MPP	0.000
	2	PP	-
	3	ADF	0.000
Westerlund tests for cointegration	1	All panels are cointegrated	0.0029
	2	Some panels are cointegrated	0.0426

, predominantly support the hypothesis of cointegration among the variables.

In the following analysis, the study estimates the coefficients for both fixed-effects (FE) and random-effects models. The coefficients derived from the FE model are shown in

Table 10. Fixed effect coefficients.

Log_LIFE	Coef.
	FE	Xtivreg (2-IV)	Xtivreg (3-IV)
Log_GDP	0.01722 ***	0.02238 ***
Log_CO2	−0.00664 *	−0.06636 ***	−0.06466 ***
Log_Urban	−0.02350	−0.01679	0.02469
Log_RES	0.00301 **
Log_EDU	0.00929 ***	0.00619 *	0.01626 ***
Log_RECY	0.00459 ***	0.00704 ***	0.00907 ***
Log_TRANS	−0.04989 ***
constant	2.00386 ***
R2	0.9428 (within)	0.7539	0.7026
F statistic	F (7456) = 386.86	F (5458) = 311.63	F (4459) = 301.43
AIC	−4365.025	−4129.718	−4039.332
BIC	−4331.502	−4108,767	−4022.571
Test	Statistic	p-value	p-value
Underidentification test	Anderson canon. corr. LM statistic) Chi-sq (2), Chi-sq (3)	0.000	0.000
Weak identification test	Cragg-Donald		Weak identification test
Overidentification test of all instruments	Sargan statistic Chi-sq (1), Chi-Sq (2)	0.000	0.000
Endogeneity test of endogenous regressors	Chi-sq (1)	0.000	0.000
Instrumental variables		Log_RES,TRANS	Log_GDP,RES,TRANS

Note: p < 0.10 (*), p < 0.05 (**), p < 0.01 (***).

. When we compare the coefficients from multiple regression analysis, we can observe more significant coefficients. In particular, overall CO₂ emissions and transport emissions negatively affect life expectancy, while GDP, renewable energy sources, education and recycling rates have a positive effect on life expectancy. However, the coefficients for the Urban variable are not statistically significant, according to our models.

The next two columns show models where Log_CO₂ is treated as an endogenous variable. The instrumental variables are Log_RES, Log_TRANS column xtIvreg (2-IV). In column xtIvreg (3-IV) three instrumental variables are considered: Log_RES, Log_TRANS and Log_GDP.

The choice of the FE model over the random effects model is supported by the results of the Hausman test and the Breusch-Pagan-Lagrange multiplier test for random effects, indicating the suitability of the FE model for the analysis. The results of these diagnostic tests are presented with the residual tests for the FE model in

Table 11. Fixed effect tests.

Test	p-Value
Hausman test (Fixed Effects, Random Effects)	0.000
Breusch and Pagan Lagrangian multiplier test	0.000
Pesaran’s test	0.000
Friedman’s test	0.000
Modified Wald test	0.000

.

The test statistic for Frees’ test of cross-sectional independence is 5.749, significantly exceeding the critical values derived from the Frees’ Q distribution at different significance levels: for α = 0.10, a critical value of 0.2559, for α = 0.05, a critical value of 0.3429 and for α = 0.01, a critical value of 0.5198. These results of the analysis of the residuals of the FE model indicate the presence of cross-sectional dependence (CSD) and heteroscedasticity in the data.

The study uses two advanced estimation methods to mitigate these econometric problems: the Common Correlated Effects (CCE) estimator and the instrumental variable estimator with common factors (2SIV). The CCE estimator is specifically designed to address the problem of cross-sectional dependence as it accounts for unobserved common factors that may influence the dependent variable across different cross-sections. Meanwhile, the 2SIV method addresses endogeneity concerns by using common factors as instrumental variables. This helps us deal with the correlation between the predictors and the error term while also considering heteroscedasticity.

Evaluating the analysed variables for CSD is an essential step in the analysis. For this purpose, the study uses the estimation of the exponent of CSD alpha (α) and the CD test developed by Pesaran [60]. In addition, Chudik et al. [61], cited in Ditzen [62], distinguish four categories of CSD: weak (α = 0, α = 0), semi-weak (0 < α < 0.5, 0 < α < 0.5), semi-strong (0.5 ≤ α < 1, 0.5 ≤ α < 1) and strong (α = 1, α= 1) CSD. The hypotheses for the CD test are formulated as follows: The null hypothesis (H0) states that a variable has a weak CSD. In contrast, the alternative hypothesis (H1) states that a variable has a strong CSD. The CSD outcomes are shown in

Table 12. CSD results.

Variable	Alpha (α)	CD	p-Value
Log_LIFE	1.0072	76.968	0.000
Log_GDP	1.0072	75.472	0.000
Log_CO2	0.9946	45.366	0.000
Log_Urban	0.9465	28.116	0.000
Log_RES	1.0072	73.058	0.000
Log_EDU	1.0074	72.126	0.000
Log_RECY	0.9857	72.841	0.000
Log_TRANS	1.0091	11.439	0.000

.

The estimated alpha coefficients (α) for all variables analysed are significantly above the established threshold of 0.5, indicating the prevalence of a strong CSD. In addition, the p-values associated with the null hypothesis in the CD test are sufficiently low to support the conclusion that the variables analysed have a strong CSD. This observation suggests that the variables are influenced by common factors or common shocks that affect multiple units within the panel, implying that the individual observations are not completely independent of each other.

Determining whether the slope coefficients are homogeneous (uniform across units) or heterogeneous (varying across units) is fundamental to econometric analysis as it directly influences the choice of estimation methods. In scenarios where the slope coefficients are homogeneous, several econometric techniques are applicable, including FE, RE, the generalised method of moments, and methods that account for structural breaks. Conversely, alternative methods are justified for models with heterogeneous slope coefficients. Neglecting to account for the heterogeneity in the slope, if it exists, can result in unreliable outcomes, as pointed out by Pesaran and Smith [63]. Therefore, accurately identifying whether there is heterogeneity or homogeneity in the slope is essential for choosing the econometric model.

To determine whether there is heterogeneity or homogeneity in the slope within the dataset, this study utilises the Blomquist and Westerlund test [64], as explained by Bersvendsen and Ditzen [65]. This method enables us to thoroughly examine slope homogeneity while adjusting for CSD, heteroscedasticity and autocorrelation through applying CR and HAC options for error estimation. The test yields a delta statistic of 15.994 with a p-value of 0.000, strongly suggesting that the slope coefficients are heterogeneous across units.

Given the rejection of the null hypothesis (H₀) of slope homogeneity, the analysis requires estimation techniques that can account for slope heterogeneity. For this purpose, the heterogenous panel estimation technique is required, especially in MG type models. This technique is designed to effectively address the issue of variability of coefficients across the panels.

Statistical procedure for factor estimation was employed to accurately estimate the number of common factors. The estimation results, showcasing the calculated number of factors considering up to eight possible factors, are detailed in

Table 13. Estimates of the number of factors.

IC	No. of Factors	IC	No. of Factors
PC_{p1}	8	IC_{p1}	8
PC_{p2}	8	IC_{p2}	8
PC_{p3}	8	IC_{p3}	8
ER	1	GR	1
GOS	1	ED	3

.

The initial estimates, as given in the first three rows of Table 13, are based on different penalty functions: PC_{p1}, IC_{p1}, through IC_{p3}, as introduced by Bai and Ng [66]. These researchers developed three different penalty functions to estimate the number of factors in factorial models, namely PC_{p1}, PC_{p2}, and PC_{p3}. The basic idea behind these functions is to achieve an optimal balance between the goodness of fit of the model and its complexity and thus determine an appropriate number of factors. However, it should be noted that, as suggested by Ditzen [67], these estimates tend to overestimate the true number of factors. In addition, the GOL estimator is not included in the analysis, although it is well suited for testing residuals. Therefore, the study primarily focuses on identifying a more conservative estimate of the number of factors between one and three.

To meet the challenge of a strong CSD within panel data, the study employs a CCE estimator as developed and refined by Ditzen [68]. This approach operationalises the procedures described in the seminal work of Chudik and Pesaran [69] and the basic principles outlined by Pesaran et al. [70]. The CCE estimator, an integral part of this command, requires the inclusion of a sufficient number of lags of the cross-sectional averages in each panel equation. Importantly, these means must be at least as large as the number of unobserved common factors affecting the panel. A key advantage of the CCE estimator is its ability to effectively account for unobserved common factors without requiring precise information about their total number.

In parallel, the study employs the 2SIV method, a recent development described in detail in the works of Norkutė et al. [71] and Cui et al. [72]. The 2SIV method separates common factors from the error term and the regression variables in two steps. The 2SIV algorithm, introduced by Kripfganz and Sarafidis [73], first uses PCA to remove common factors from the regressors. In the second stage, the model residuals are then calculated using the first-stage parameters. The model is further adjusted for the factor residuals before another IV regression is run with the obtained instrumental variables. The comparative effectiveness of these approaches—CCE and 2SIV—Is shown in

Table 14. Comparison of CCE and 2SIV.

	CCE (7 + 8)	IVCCE (7 + 8) (2-IV)	IVCCE (7 + 8) (3-IV)	2SIV (MG)
Log_GDP	0.01482	0.02119 ***		0.00756
Log_CO2	−0.00778	−0.01777 **	0.00685	−0.02573 ***
Log_Urban	−0.38390 *	0.27800	−0.18112	−0.10837
Log_RES	0.00893			−0.00213
Log_EDU	0.00232	0.01151	0.00333	0.01038
Log_RECY	0.00321	0.00381	0.00851	0.00411
Log_TRANS	0.00169			−0.03864 **
constant				2.174 ***
F statistics	F (7456) = 386.86	F (5458) = 311.63	F (4459) = 301.43
AIC	−4365.025	−4129.718	−4039.332
BIC	−4331.502	−4108.767	−4022.571
CD (p-value)	0.2614	0.5455	0.0020
Alpha (CSD)	0.5487	0.5264	0.5922
Instrumental variables	Log_RES, TRANS	Log_GDP, RES, TRANS

Note: *—sig. level 0.1, **—sig. level 0.05, ***—sig. level 0.01.

.

In the first column, all the regressors were chosen as mean group variables (7), and all the variables were chosen as cross-sectional mean variables (8). The second column contains the coefficients of the CCE model, where the endogenous variable Log_CO₂ and the two instrumental variables Log_RES and log_TRANS have been selected. The fourth column presents the parameters of the 2SIV mean group estimator, where factmax = 3, the number of instruments is 24, and there is 1 factor in X. The lag (0–2) of all regressors was used to calculate the instrumental variables in the fourth column. All models have a small number of significant coefficients. The third model has no significant coefficient. The CD test and the alpha coefficient were used to test the cross-sectional dependence of the CCE model residuals. Acceptable results in terms of weak cross-sectional dependence are obtained in the first and second columns. Since the results obtained from the CCE and 2SIV models are not satisfactory, a partial heteroskedastic approach addresses the issue.

The second column presents the parameters of the Mean-group estimator, where factmax = 3, the number of instruments is 24, and 1 factor in X. Lag (0–2) of all regressors are utilised in the calculation of instrumental variables in the second column.

Despite the rigorous application of these models, only a limited number of coefficients were found to be statistically significant. Within the CCE framework, only the coefficient for Log_Urban is significant, while the 2SIV approach identified significant coefficients for Log_CO₂ and Log_Trans, all of which hurt life expectancy.

Further examination of CSD within the CCE model residuals, using the CD test and estimation of the alpha coefficient, indicated only weak CSD. Despite these nuanced approaches, the results obtained from the CCE and 2SIV models are not entirely satisfactory, leading us to consider a partially heterogeneous approach as a possible solution.

The traditional assumption that model coefficients are homogeneous across entities in a panel data model is often theoretically and practically difficult to justify. Conversely, the assumption of complete heterogeneity—Where each entity has its regression coefficients—may not always be appropriate, as it overlooks the potential for generalisable patterns across entities. Sarafidis and Weber [74] critique these conventional approaches, suggesting that both the homogeneous (pooling) and fully heterogeneous models represent polar extremes. They argue for exploring intermediate solutions, which are likely to provide more realistic and nuanced insights in many practical scenarios.

In this vein, Sarafidis and Weber [74] propose a partial heterogeneity framework for panel data analysis. This framework allows for varying degrees of heterogeneity across units, recognising that while differences exist, they may not be as pronounced or uniform as the extremes of complete homogeneity or heterogeneity suggest. Christodoulou and Sarafidis [75] further operationalise this concept by introducing the command (xtregcluster) in Stata, which implements a panel regression clustering approach. This method segments entities into Ω clusters, within which regression coefficients are assumed to be homogeneous. The residual sum of squares (RSS) for each cluster ω is denoted as RSSω, and the total RSS is calculated as the sum of the RSSω for all clusters, i.e., RSS = ${\sum }_{\mathsf{\omega }=1}^{\Omega }\mathrm{RSS}\mathsf{\omega }$. The optimal number of clusters, Ω, is determined by minimising the Model Information Criterion (MIC), which can be shown in Equation (1):

$$\mathrm{MIC}=\mathrm{N}\log \left({\displaystyle \frac{\mathrm{RSS}}{\mathrm{N}\stackrel{-}{\mathrm{T}}}}\right)+\mathrm{f}\left(\Omega \right){\mathsf{\Theta }}_{\mathrm{N}}$$

(1)

where $\stackrel{-}{\mathrm{T}}={\displaystyle \frac{1}{\stackrel{-}{\mathrm{N}}}}{\sum }_{i=1}^{\mathrm{N}}{\mathrm{T}}_i$ represents the average length of the time series for the panel. For panels with equal time-series length, it simplifies to $\stackrel{-}{\mathrm{T}}$ = T. The term f(Ω) Θ_N serves as a penalty function to prevent overfitting by penalising the inclusion of excessive clusters. Here, f(Ω) is a strictly increasing function of the number of clusters, with the default setting f(Ω) = Ω and Θ_N = 13 log N + 23 N. Other common values for Θ_N are ln (N) and $\sqrt{\mathrm{N}}$.

The next step is identifying the most appropriate regression clustering model for the panel data. The MIC values for potential clustering configurations, ranging from 1 to 10 clusters, are presented in

Table 15. MIC outcomes.

Omega	Total RSS	MIC
1	0.004	−290.979
2	0.002	−297.067
3	0.002	−297.344
4	0.002	−297.297
5	0.002	−294.820
6	0.002	−290.602
7	0.001	−288.381
8	0.001	−285.934
9	0.001	−282.476
10	0.001	−280.104

.

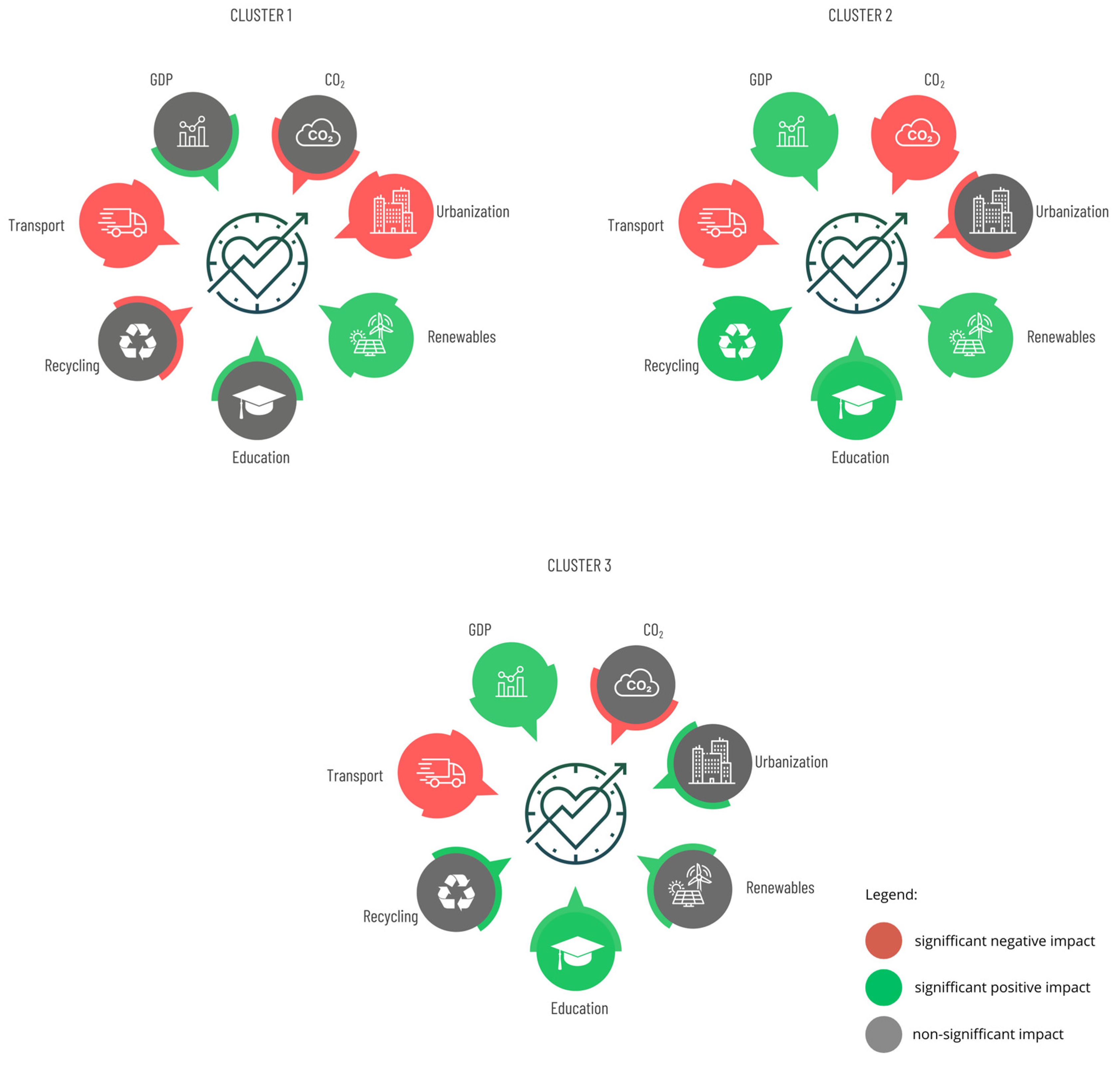
The lowest MIC value (−297.344) is obtained for 3 clusters. The values of the model coefficients for each cluster the overall model (Pooled), and other model characteristics and tests are shown in

Table 16. Panel data estimates by omega.

Variable	Cluster 1	Cluster 2	Cluster 3	Pooled
Log_GDP	0.00691	0.01110 ***	0.01625 ***	0.01722 ***
Log_CO2	−0.00621	−0.01969 ***	−0.00206	−0.00664 *
Log_Urban	−1.06465 ***	0.01478	0.00402	−0.02350
Log_RES	0.02877 ***	0.00940 ***	−0.00080	0.00301 **
Log_EDU	0.01462	0.01018 ***	0.01445 ***	0.00929 ***
Log_RECY	−0.00462	0.00923 ***	0.00060	0.00459 ***
Log_TRANS	−0.13458 ***	−0.01091 **	−0.06822 ***	−0.04989 ***
constant	4.06908 ***	1.85559 ***	1.99413 ***	2.00386 ***
Nc	3	10	12	25
T	17.00	19.90	19.83	19.52
R2 within	0.9428	0.9161	0.9107	0.8499
R2 between	0.0014	0.0710	0.5594	0.5729
R2 overall	0.0952	0.2319	0.5748	0.5053
Corr (ui, Xb)	−0.8679	−0.1026	0.2251	0.3109
rho	0.9919	0.98079	0.95177	0.94919
F test (p-value)	0.000	0.000	0.000	0.000

Note: *—sig. level 0.1, **—sig. level 0.05, ***—sig. level 0.01.

.

The composition of the clusters is as follows: First cluster: Comprising only three EU countries, BGR, EST and LVA, this cluster is characterised by the significant influence of urbanisation and transport (specifically the average CO₂ emissions per km of new passenger cars) on life expectancy, both of which have a negative effect. Conversely, the use of renewable energy sources has a significant positive effect. GDP and education also contribute positively, but their effects are not statistically significant in this cluster. CO₂ emissions and recycling rates show negative tendencies, which are not significant either.

Second cluster: Comprising AUT, BEL, CYP, DEU, GRC, HUN, LTU, NLD, IRL, and SWE, this cluster is the most significant. All variables, except urbanisation, have a significant impact on life expectancy. In particular, GDP, recycling rate, renewable energy consumption and education level increase life expectancy. On the other hand, CO₂ emissions and transport emissions contribute to decreased life expectancy. Urbanisation shows a positive trend but does not reach statistical significance.

Third cluster: This cluster is the greatest, comprising 12 countries, namely CZE, DNK, ESP, FIN, FRA, ITA, LUX, POL, PRT, ROU, SVK, and SVN. Within this cluster, we can observe significant positive effects of GDP and education on life expectancy. Similarly, as in previous clusters, transport emissions hurt life expectancy. Visualisation of the cluster analysis results is captured in Figure 2.

The impact of smart city indicators depicted in Figure 2 is distinguished by different colours. In particular, green signifies that the variable leads to an increase in life expectancy at birth, red indicates that the variable decreases life expectancy at birth and grey denotes variables whose impact is statistically insignificant.

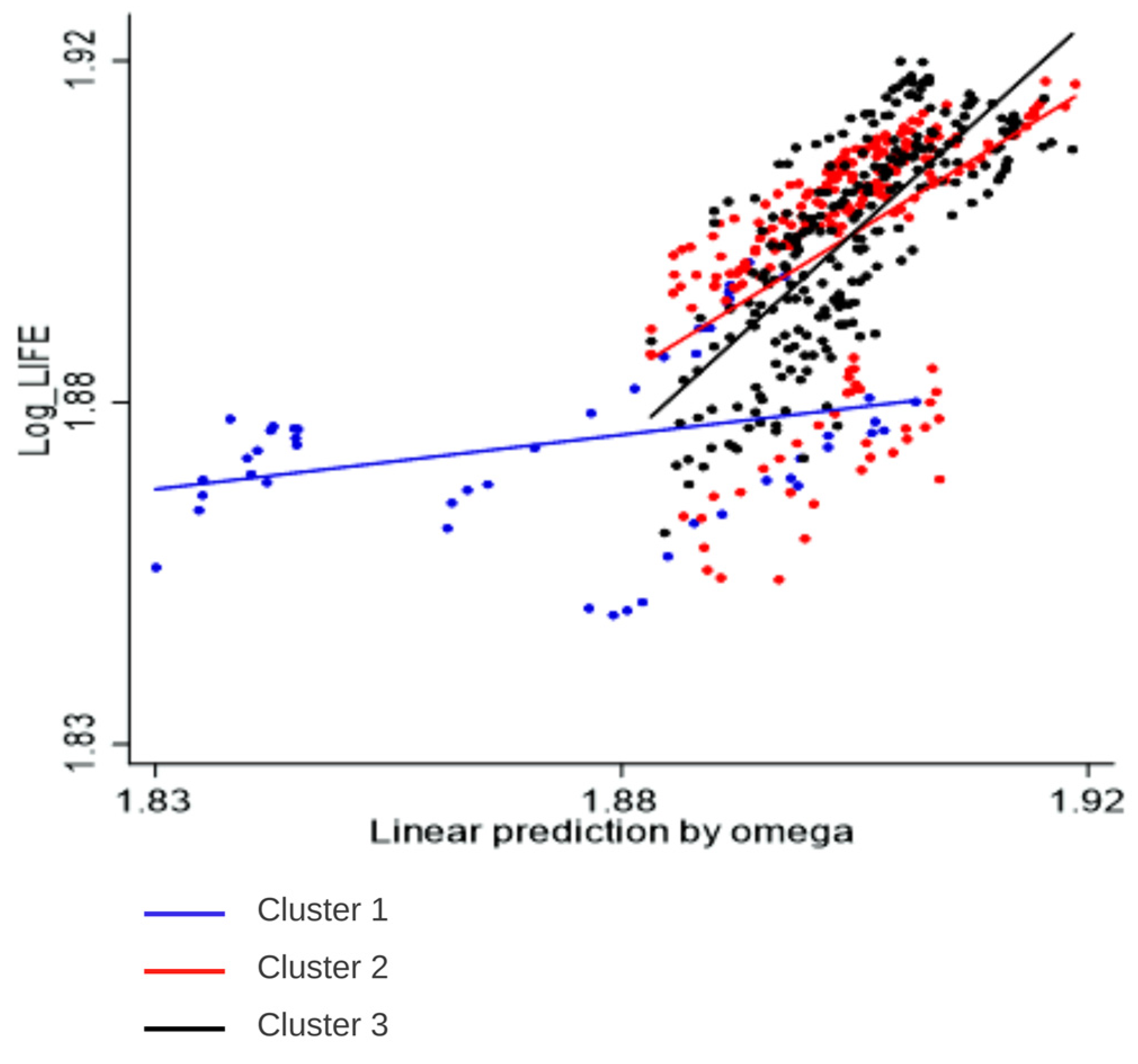
The scatter plot between ROA and linear prediction is shown in Figure 3, with different clusters indicated by different colours and each cluster associated with a line segment.

Figure 4 shows the geographical distribution of countries into the three clusters based on the performed analysis.

The coefficients of determination are remarkably high in all cases. In particular, the coefficients of determination for individual clusters exceed the coefficient of determination for the pooled model. This means that the regression models fitted to each cluster explain a greater proportion of the variance in the dependent variable than the model that includes all clusters together. These findings suggest that commonly used panel data approaches can derive general results that do not reflect the specificities of analysed units and the heterogeneity in the relationships between variables across clusters. On the other hand, cluster analysis provides more accurate results as it considers cluster-specific characteristics that more effectively reflect the context of analysed countries.

6. Discussion

The benefits of using green energy are seen in groups 1 and 2 which is confirmed by the pooled model. Renewable energy sources have significantly lower negative impacts on the environment compared to fossil fuels. They have a lower carbon footprint and emit fewer greenhouse gases that directly contribute to climate change and harm the environment. Consequently, by reducing air pollution, we can, in the long run, improve public health by decreasing respiratory and cardiovascular diseases aggravated by polluted air [76]. Shifting towards cleaner energy can lead to more resilient communities and support global efforts to combat climate change and mitigate its adverse effects [77,78]. Moreover, investing in renewable energy brings not only health and environmental benefits but also economic advantages [79]. The expanding renewable energy industry creates job opportunities [80], which can boost economies and help alleviate poverty, indirectly enhancing life expectancy through better social and economic conditions.

The consistent positive impact of education across all groups of countries underlines the role of educational achievement in promoting health and extending life expectancy [81]. This indicates that national and regional policies aimed at enhancing access to quality education could significantly contribute to improving the health of inhabitants [82]. Higher education plays a crucial role in determining socioeconomic status, such as better job opportunities, increased income and better living standards [83], which tend to have positive spill-over effects regarding better health outcomes and increased life expectancy.

The detrimental effects of emissions from transportation on life expectancy across clusters highlight an issue that impacts countries globally irrespective of their specific grouping in clusters. These emissions, primarily originating from vehicles running on fossil fuels, release a range of different air pollutants. Related studies by Chaix et al. [84] and Krzyzanowski [85] have extensively detailed the health consequences of these pollutants. The broad negative impact of emissions on life expectancy observed in country clusters underscores a common challenge that transcends borders and regional distinctions.

The study identifies an adverse impact of rapid urbanisation in cluster one while showing a positive but insignificant effect in clusters two and three. These findings align with current research by Ahmad et al. [39] and Gracia-de-Rentería [86], indicating that urbanisation´s influence on life expectancy varies in strength and direction, reflecting a multifaceted interplay of positive and negative factors. While urban areas offer benefits like improved healthcare access, education opportunities and economic growth, they pose challenges that can detrimentally affect health. Urban regions often face heightened levels of air and noise pollution due to traffic congestion and industrial operations.

Our study presumed that increased recycling rates can benefit public health. However, the findings of our analysis show equivocal results. In cluster one, the recycling rate shows a negative impact on life expectancy, though not statistically significant. Conversely, in cluster two, the effect is positive and significant. Similarly, in cluster three, the impact is positive but lacks statistical significance. Given that the second and third clusters encompass most of the analysed countries, we can conclude that recycling efforts and embracing circular economy practices have a positive influence.

7. Conclusions

Examining sustainable smart city indicators and their impact on life expectancy in 25 European countries from 2000 to 2021 reveals profound insights into urban sustainability. The study shows that factors such as GDP per capita, renewable energy consumption and tertiary education attainment are key drivers of increased life expectancy, highlighting the benefits of economic prosperity, clean energy and education. However, it is important to note that the impact of CO₂ emissions and pollutants from transportation emphasises the necessity for efficient and reasonable environmental policies. The performed cluster analysis of EU countries reveals three groups showcasing how smart city components interact with each other in different national contexts. This underscores the importance of targeted strategies that take into account the characteristics of each group leading to effective people-centric urban planning and decision/policy making that aims to achieve sustainability and public health goals with precision.

To leverage the power of smart city indicators and enhance life expectancy, the study puts forth a series of policy recommendations to promote sustainability and public health. These recommendations include overarching suggestions for all groups and tailored suggestions for each cluster.

Key suggestions for all clusters:

-

Develop and enforce policies and incentives supporting more sustainable transportation systems (such as public transport and cycling infrastructure) to reduce transport emissions, improve urban air quality and enhance public health.

-

Foster the adoption of clean/renewable energy sources to lower carbon footprints and address adverse health effects. Investments in innovations, research and development in advanced renewable energy technologies are highly recommended.

-

Enhancements in the quality and accessibility of education, breaking barriers to attaining higher education and supporting lifelong learning can play a vital role in reducing health disparities and enhancing overall health outcomes.

-

Implementing regulations to reduce carbon emissions and other harmful pollutants is crucial for combating their negative effects on health and life expectancy.

-

Specific recommendations for each cluster:

-

Cluster 1: Addressing the challenges of urbanisation and transportation emissions while maximising the benefits of greener energy usage. Countries in this group should focus on promoting transportation improving planning to alleviate congestion and enhance air quality and wider adoption of renewable energy sources.

-

Cluster 2: Building upon the impacts of economic development, education, renewable energy and waste management while striving to decrease carbon footprints. These nations are encouraged to expand their green energy infrastructure and settings, bolster recycling efforts and circular economy practices, and implement effective strategies to reduce emissions from transportation.

-

Cluster 3: Balancing economic growth and educational advancement with efforts to mitigate transport related issues. Countries within this cluster should prioritize investments in transport systems—public transportation, micro-transport—and adopt urban planning practices focused on environmental and social sustainability and well-being. Alongside the adoption of cleaner technologies aimed at improving air quality, it should be prioritised.

By putting these customised, data-driven policies and strategies into practice, decision-makers and urban key players can successfully tackle the challenges of sustainability and public health, fostering cities that are not only smart but also environmentally sustainable, climate resilient, inclusive and healthy for all residents.