Islanding Detection in Grid-Connected Urban Community Multi-Microgrid Clusters Using Decision-Tree-Based Fuzzy Logic Controller for Improved Transient Response
Abstract
1. Introduction
2. Description and Modeling of Multi-Microgrid (MMG) System under Study
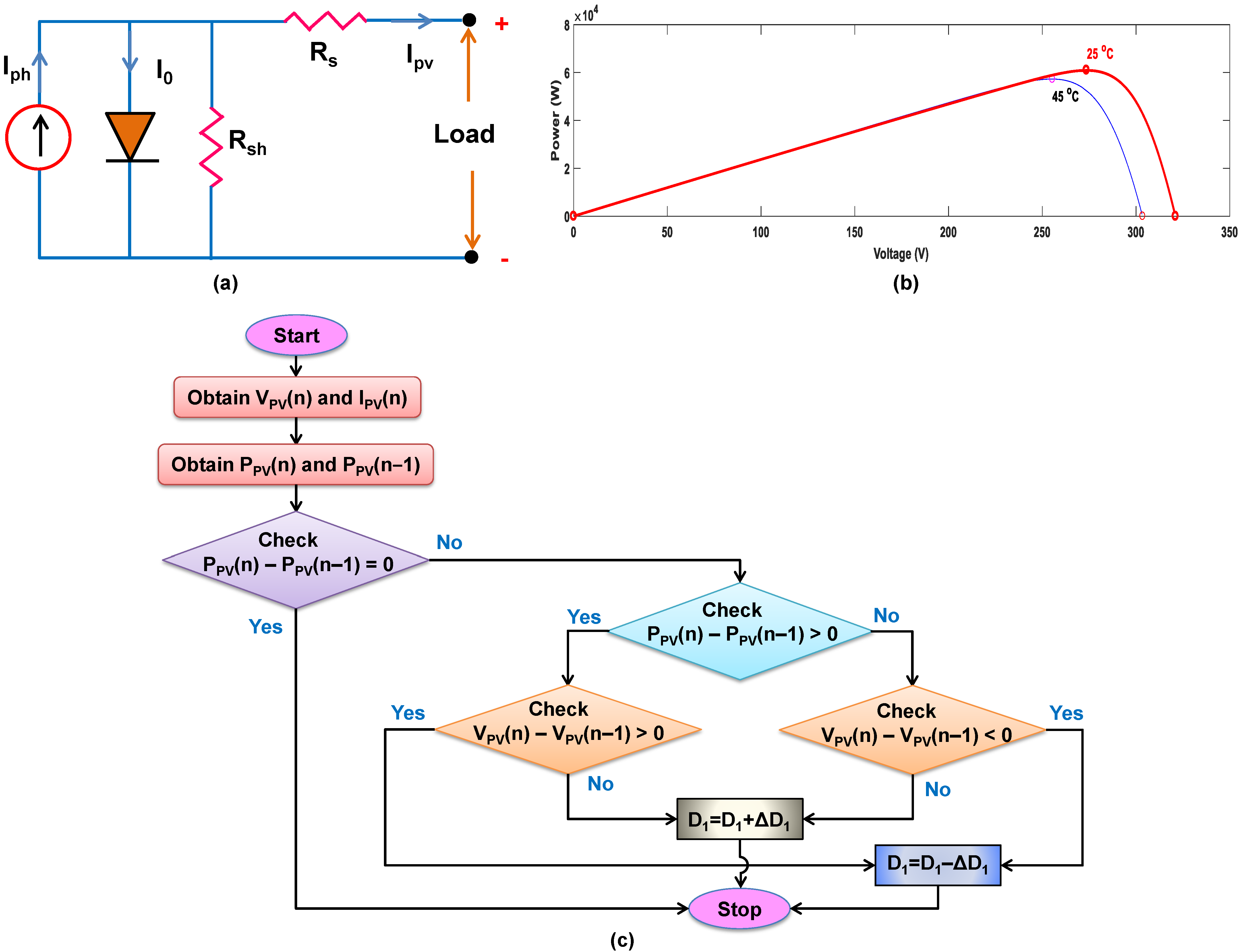
2.1. Solar PV System Modeling
2.2. Proton Exchange Membrane Fuel Cell (PEMFC) Modeling
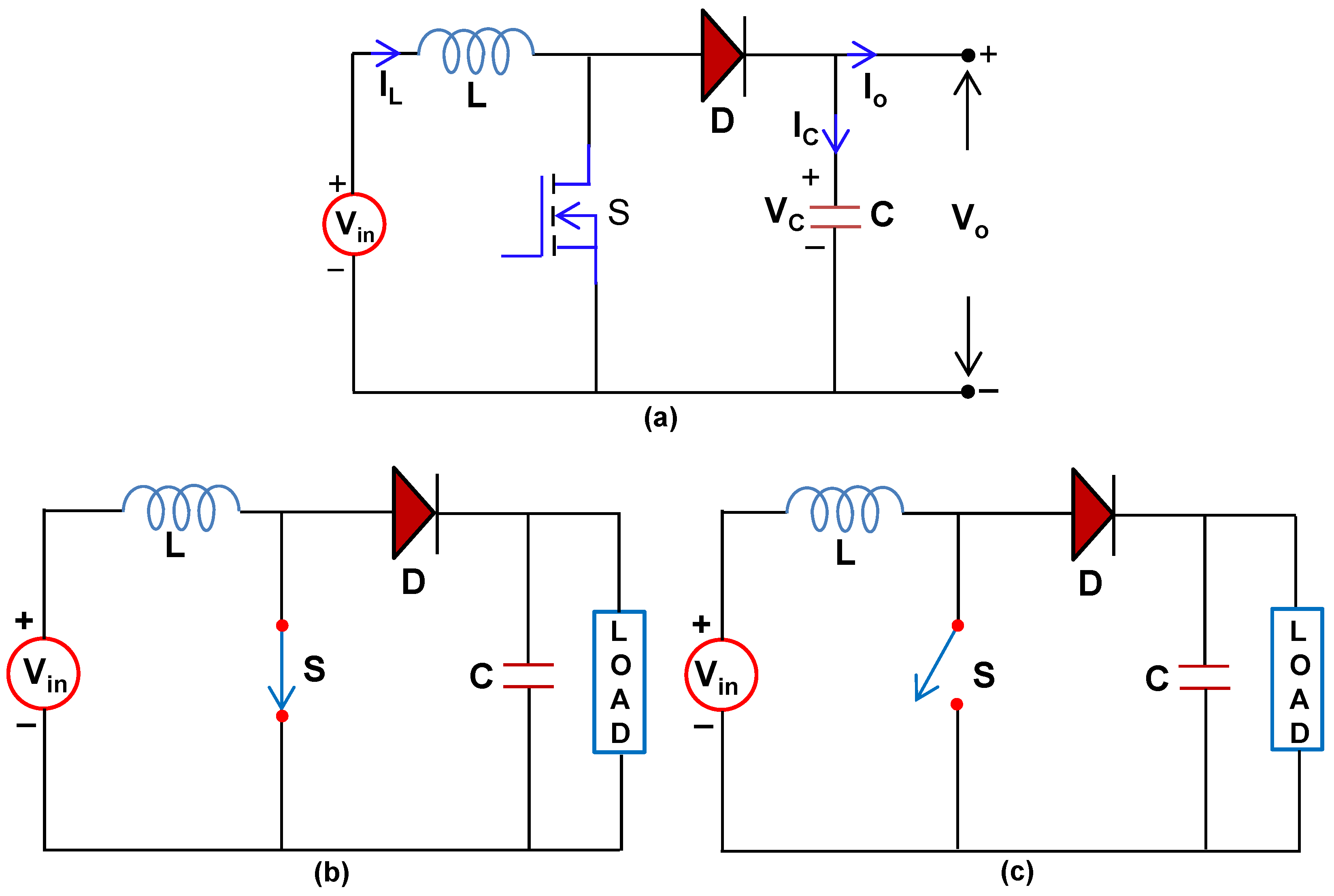
2.3. DC to DC Converter Modeling
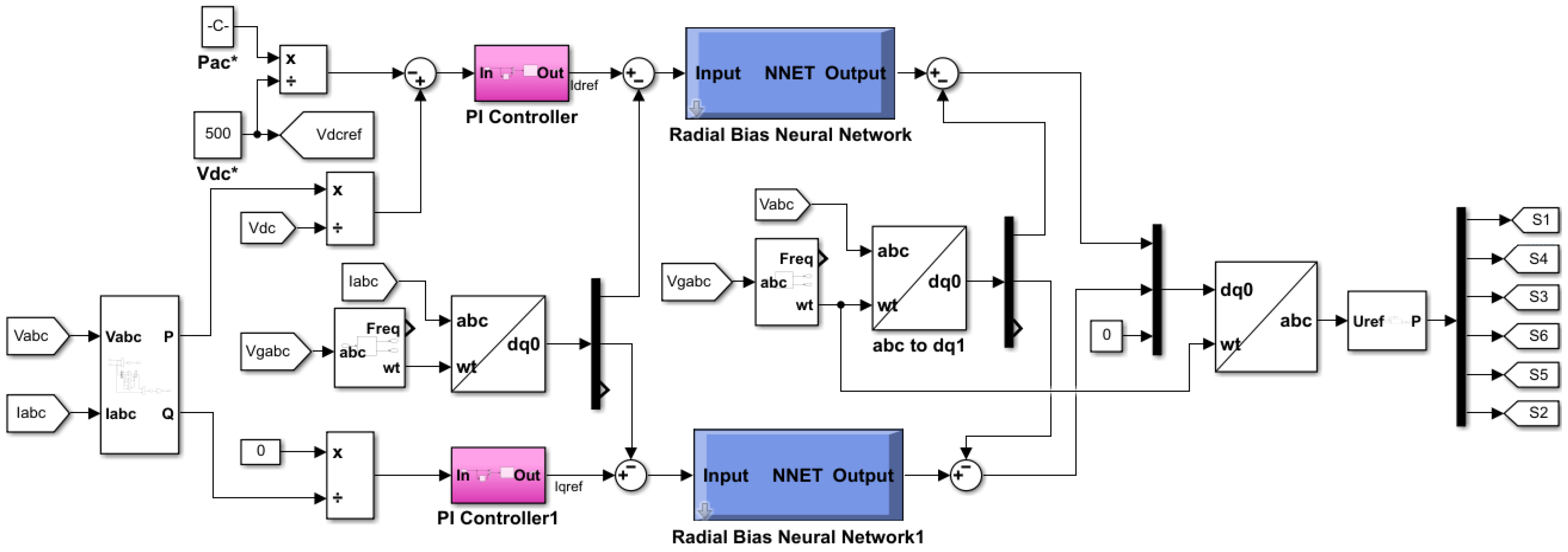
2.4. Control Circuit for DC to AC Converter (Three-Phase Inverter) Modeling
2.5. Load Profiles Considered for Modeling of MG-1 and MG-2
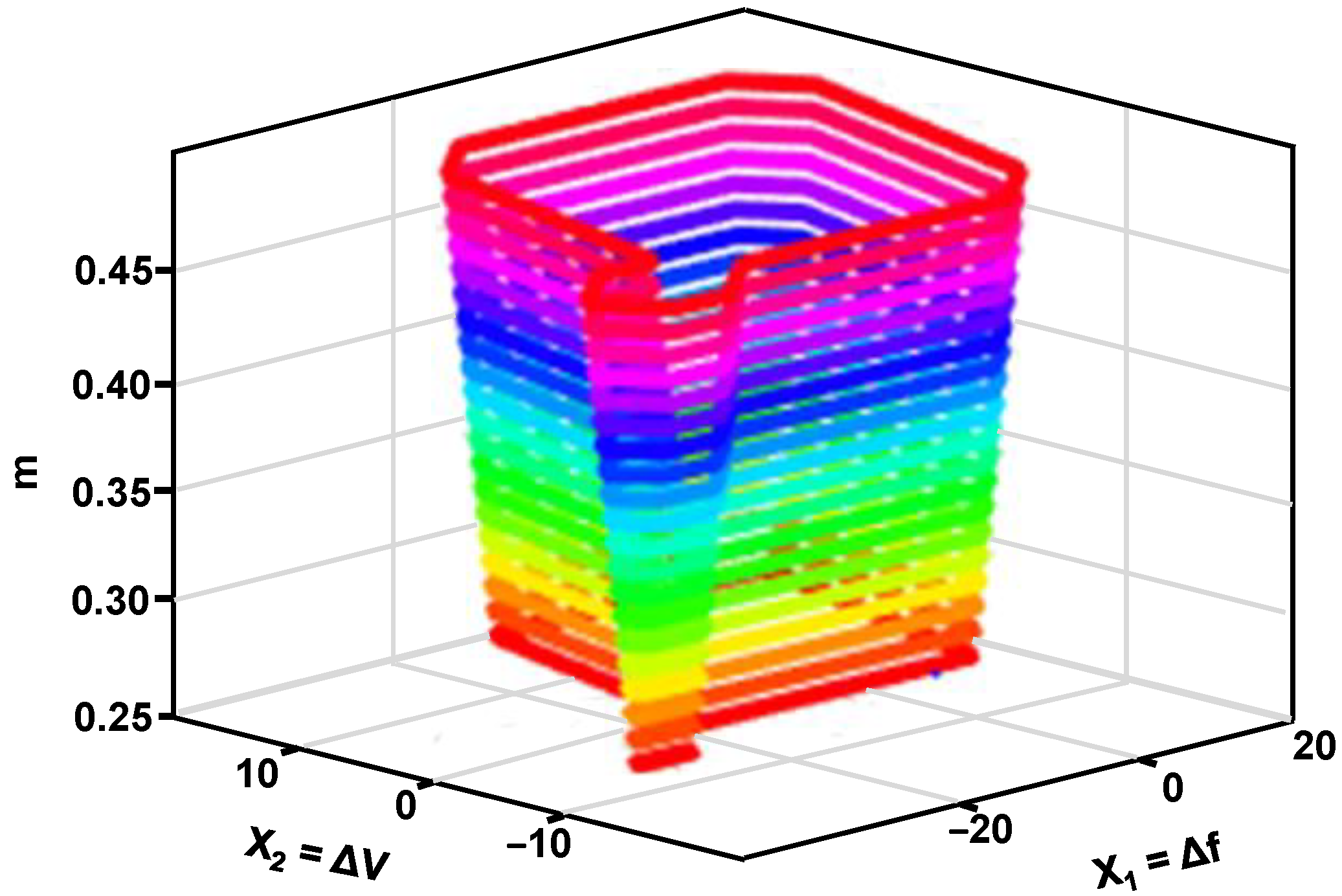
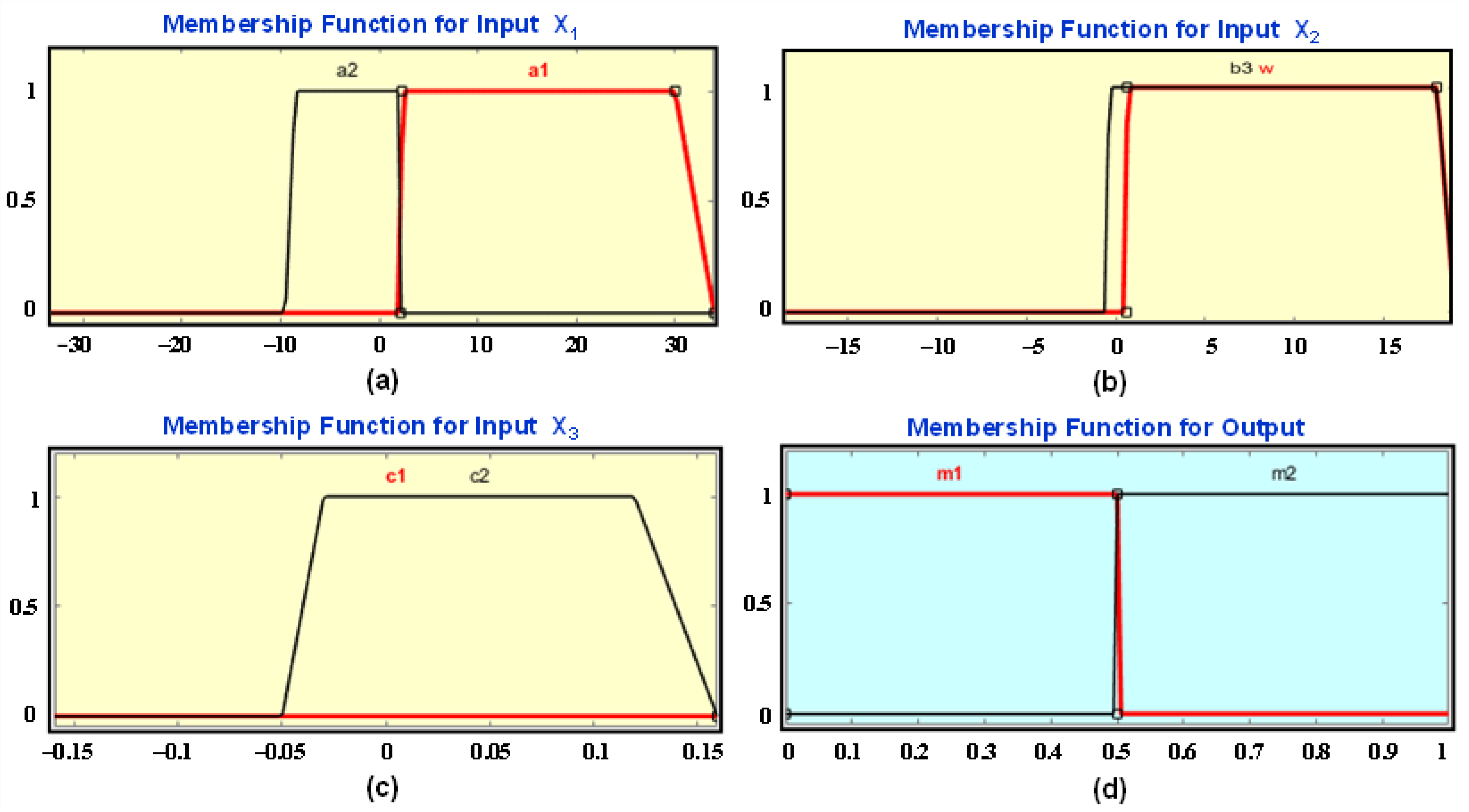
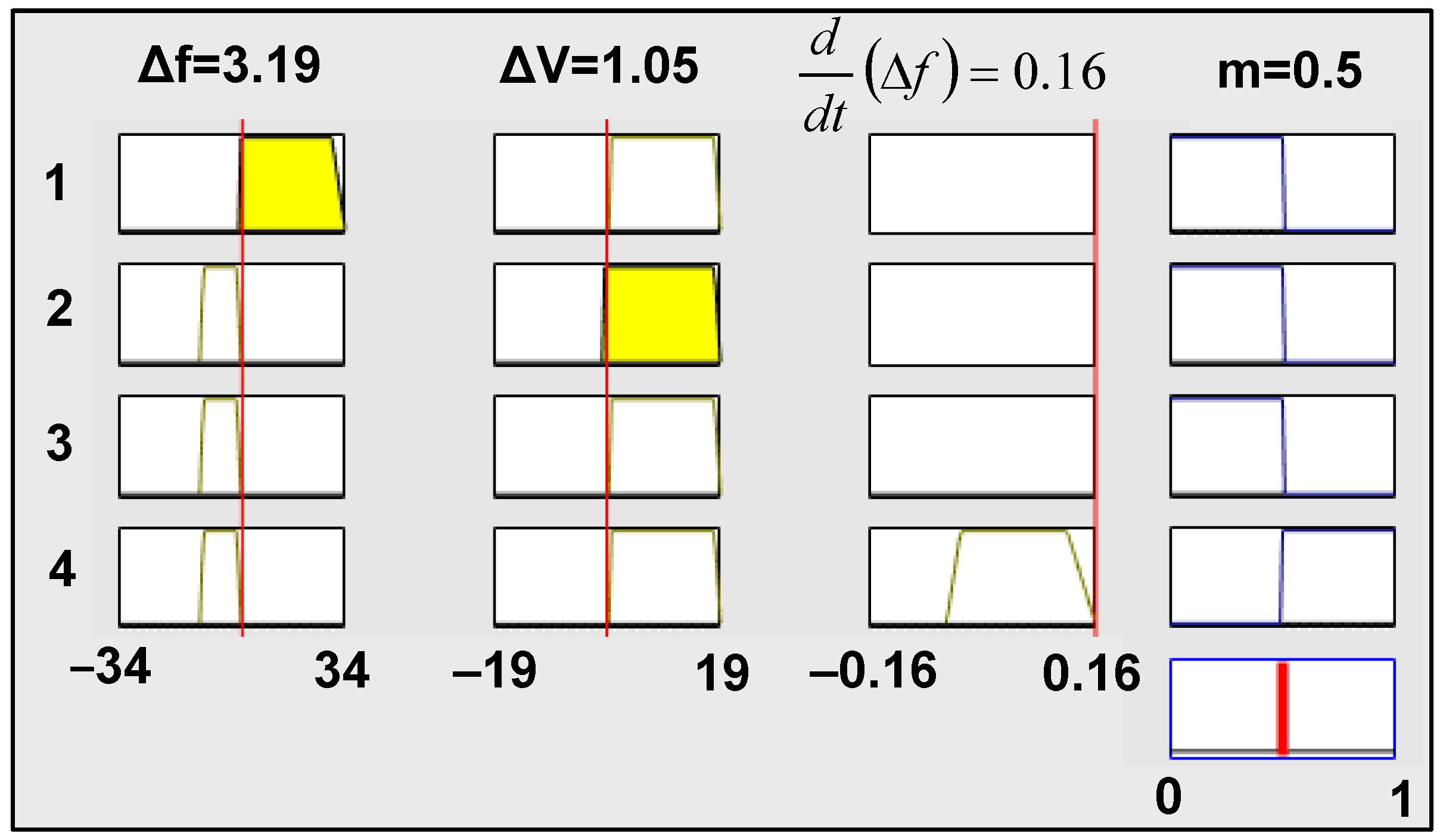
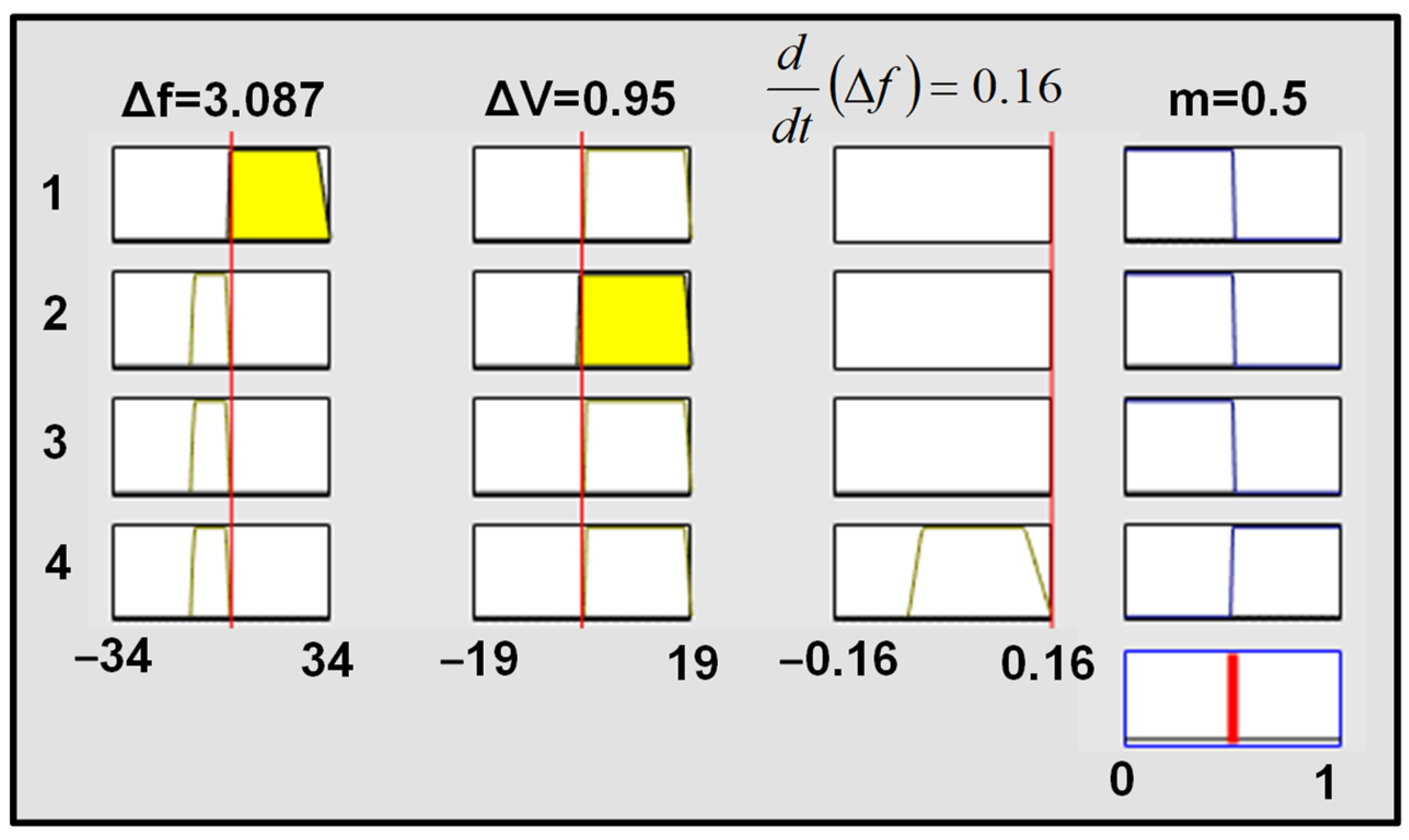
3. Proposed Decision-Tree-Based Fuzzy Logic (DT-FL) Controller
- –
- Rule 1: if X1 is P1 and X2 is Q2, then an island occurs.
- –
- Rule 2: if X1 is P2 and X2 is Q3, then an island occurs.
- –
- Rule 3: if X1 is P2 and X2 is Q1 and X3 is R1, then an island occurs.
- –
- Rule 4: if X1 is P2 and X2 is Q1 and X3 is R2, then no island occurs.
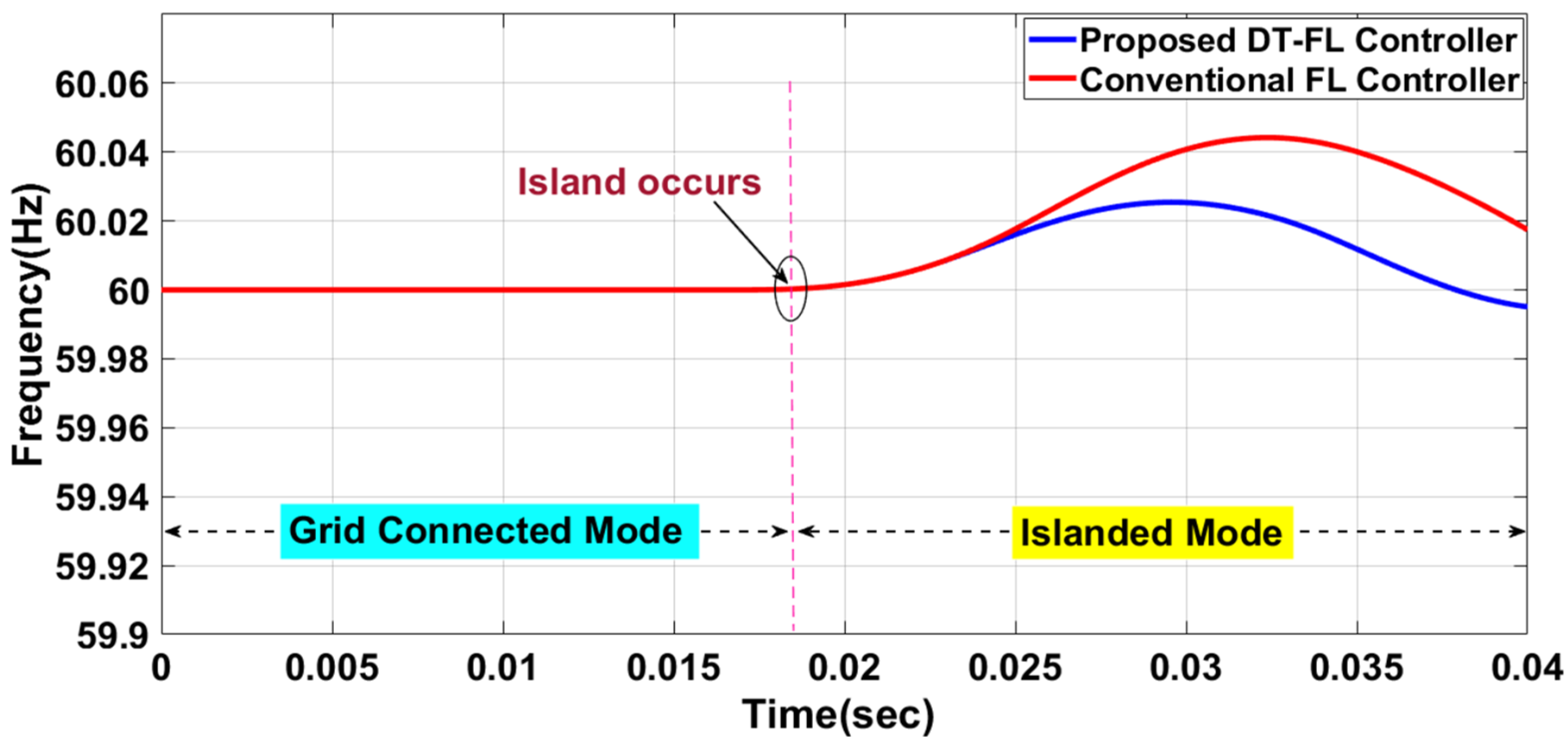
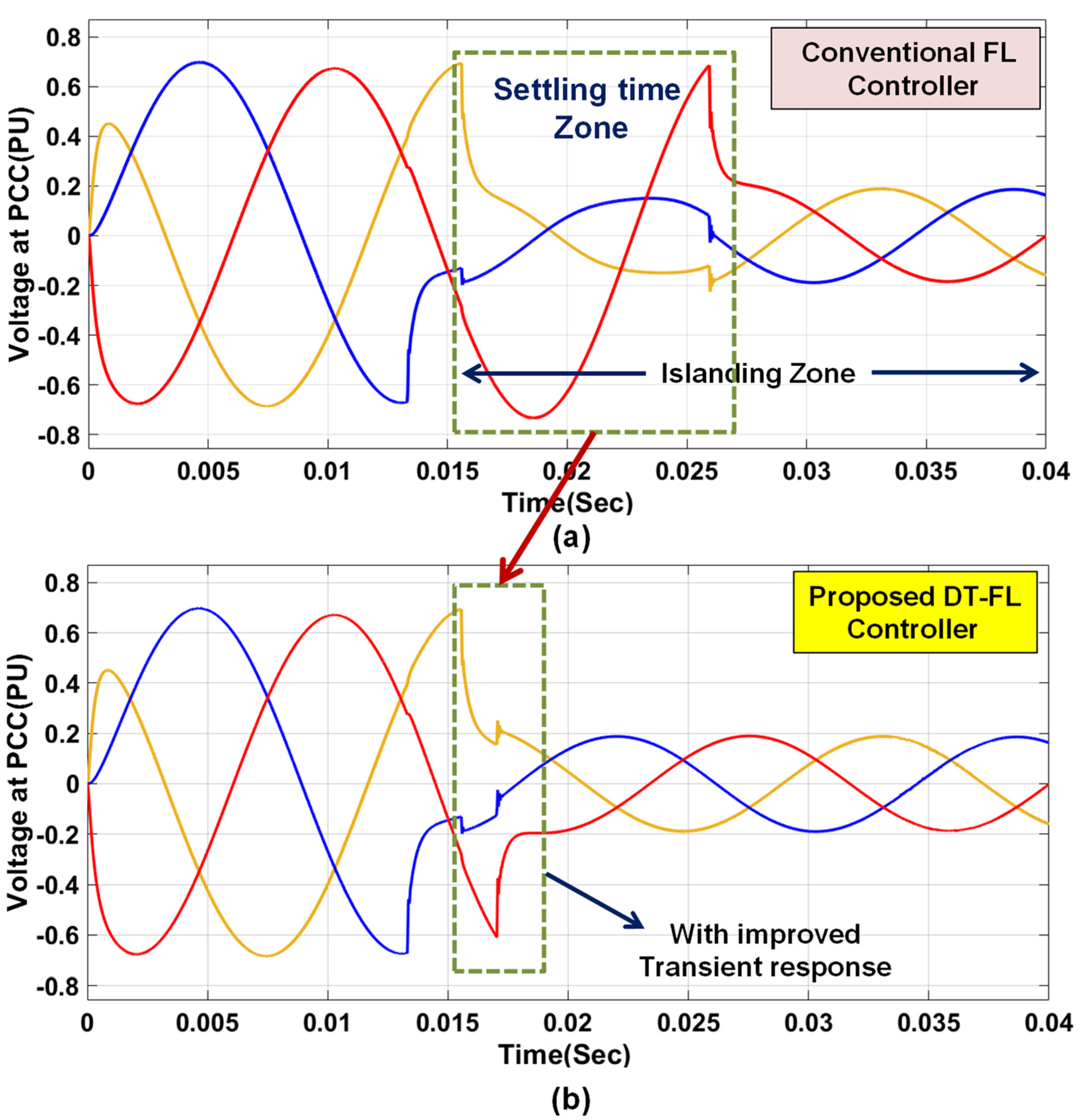
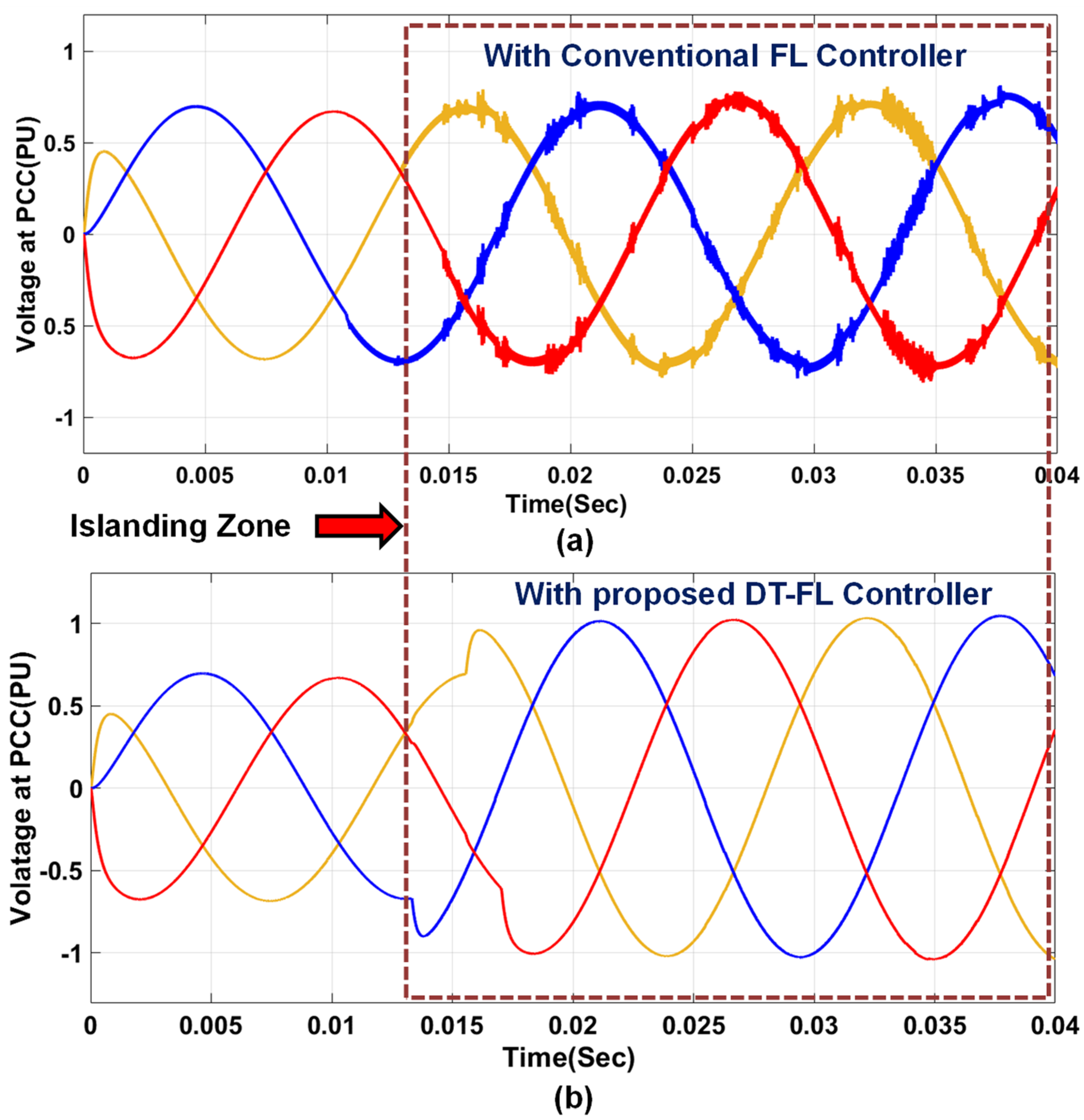
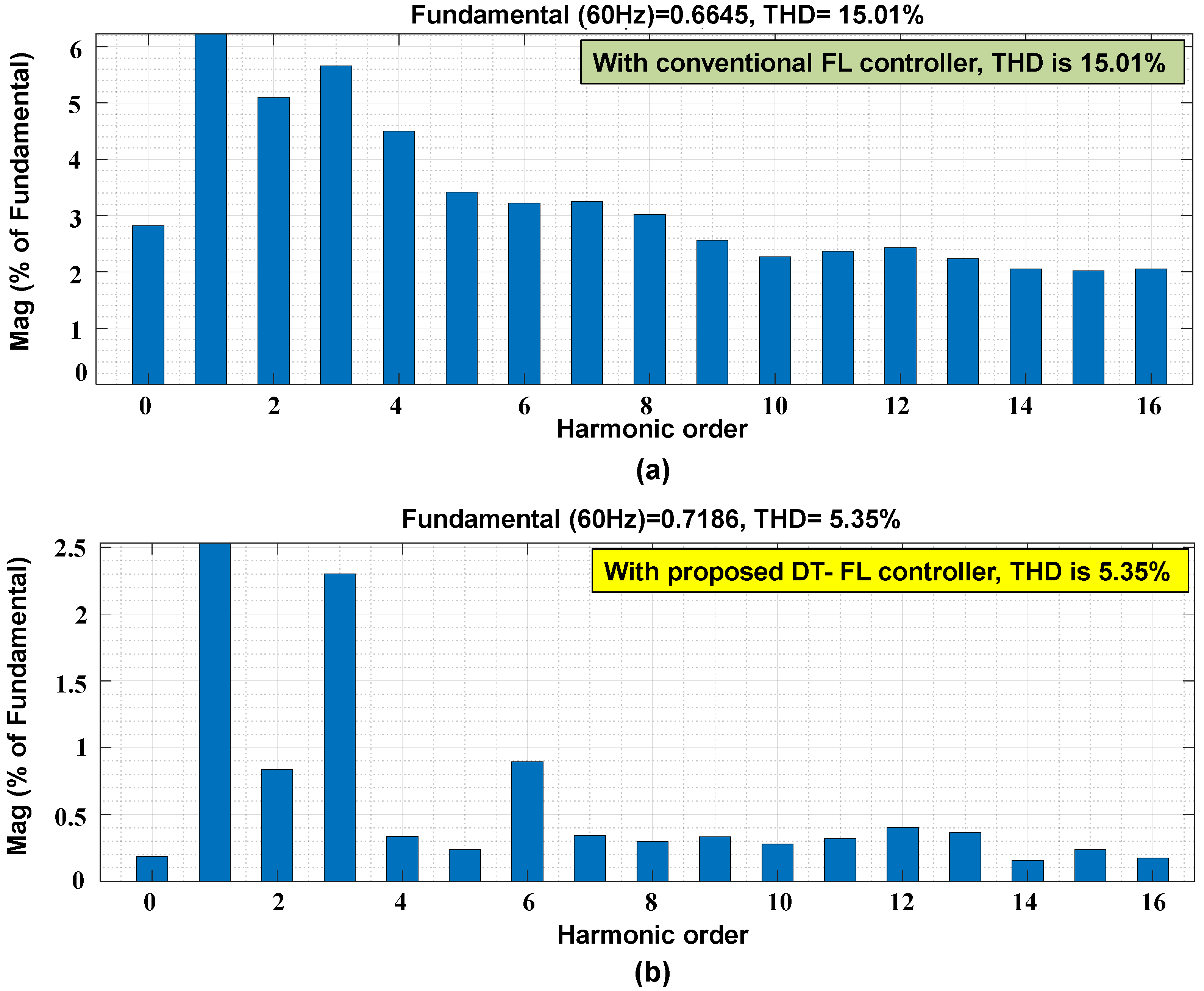
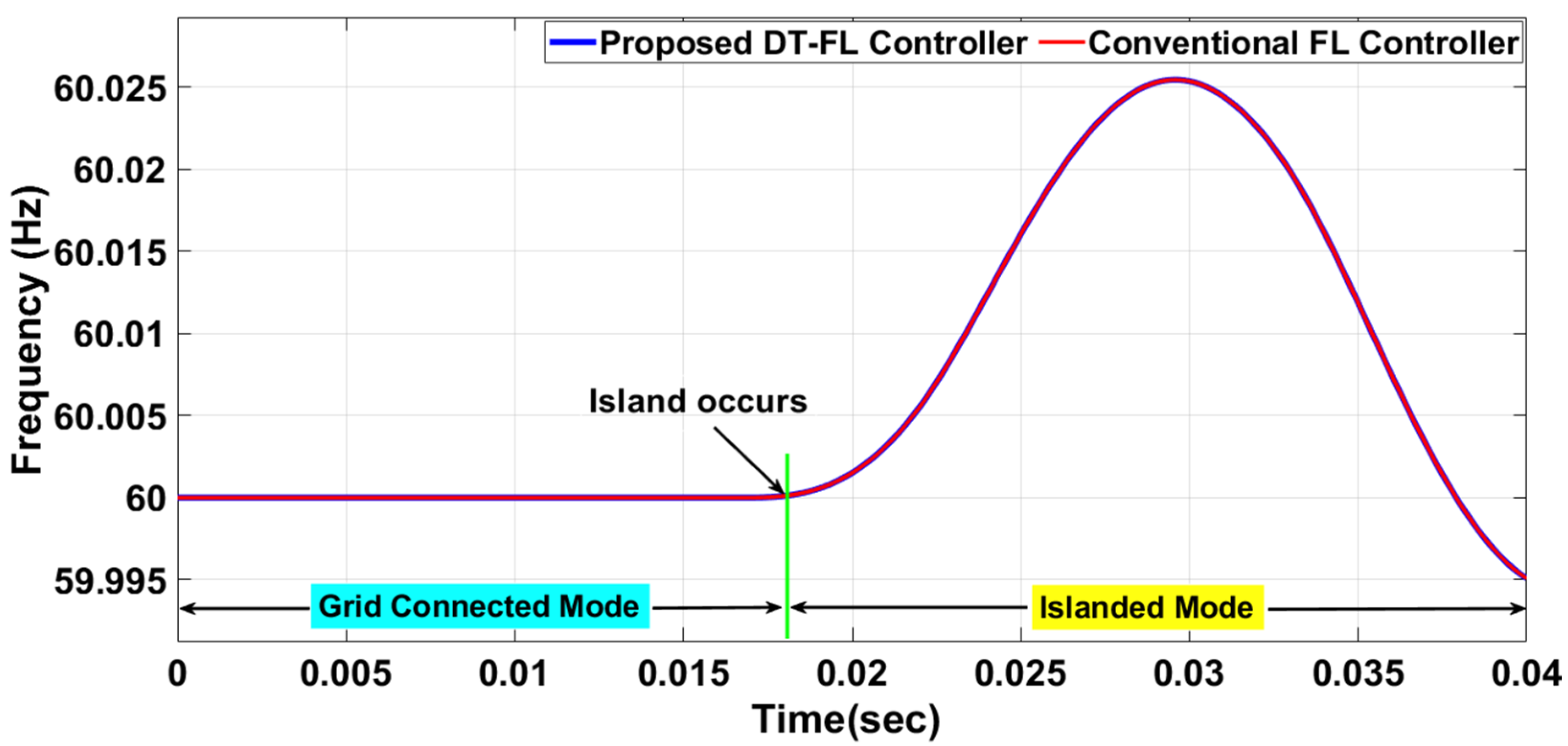
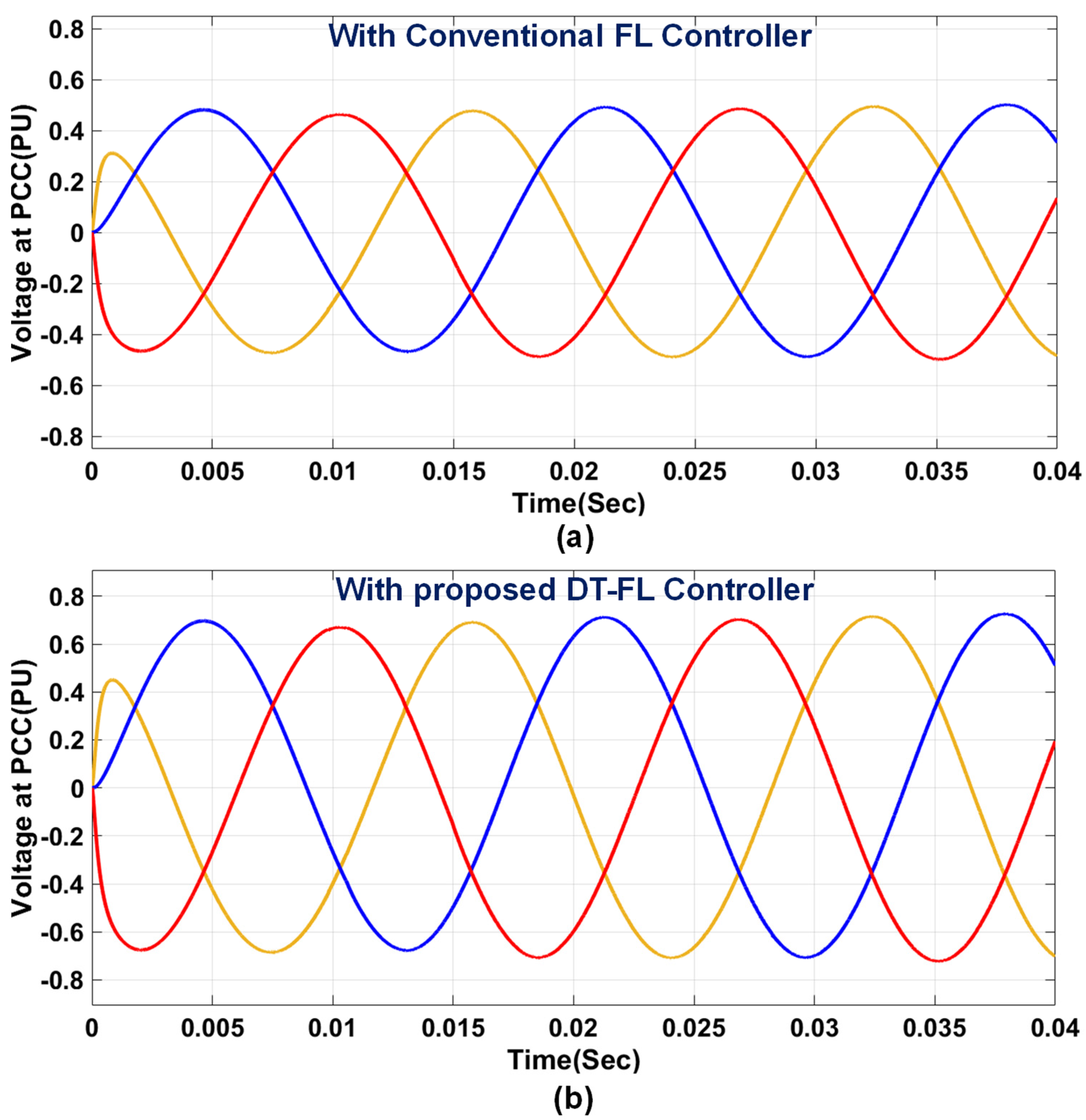
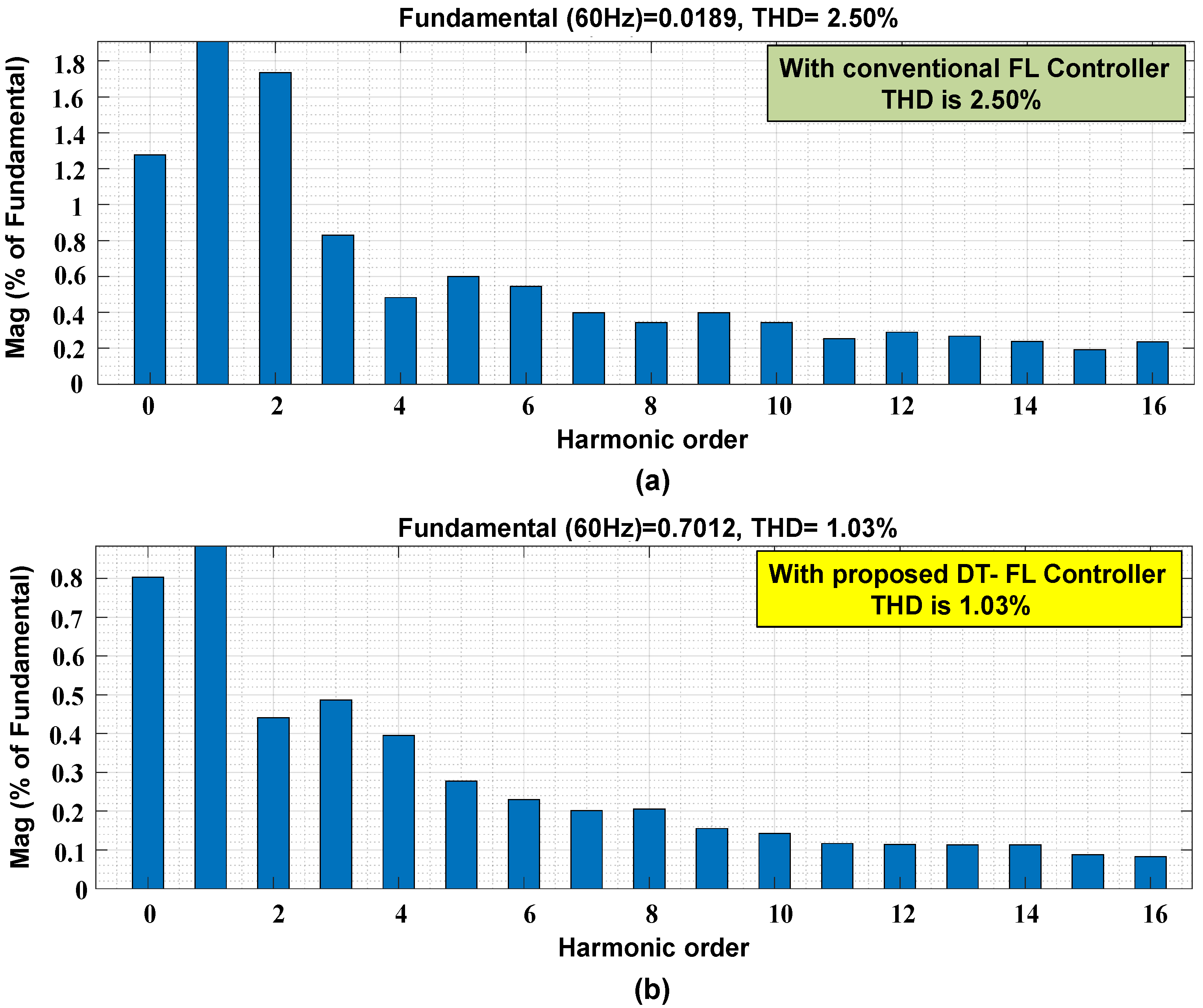
4. Simulation Results and Discussion
4.1. Analysis of the System under Test Condition A
4.2. Analysis of the System under Test Condition B
4.3. Analysis of the System under Test Condition C
5. Conclusions
- ▪
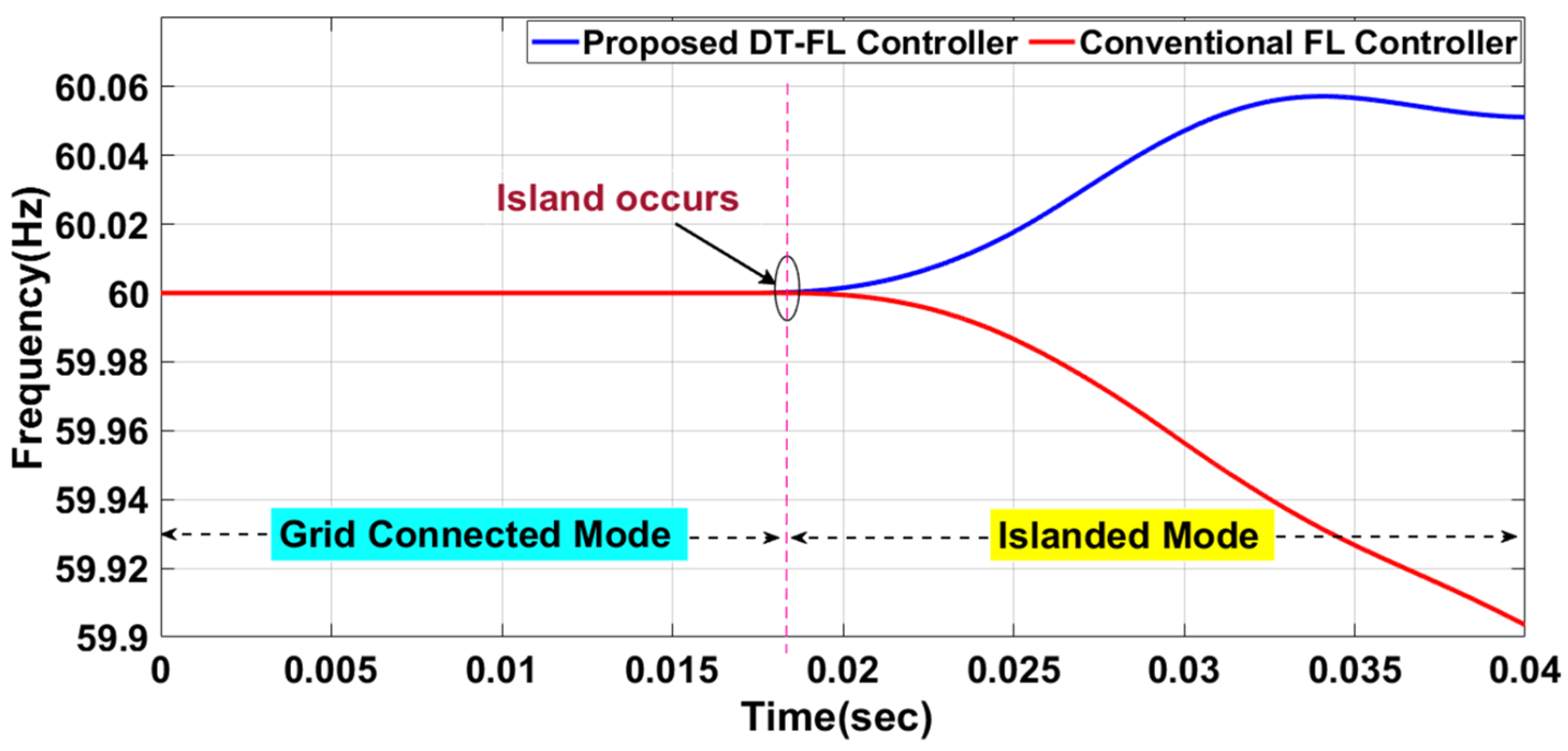
- Islanding detection is achieved satisfactorily, with better transient response characteristics for the voltage and frequency.
- ▪
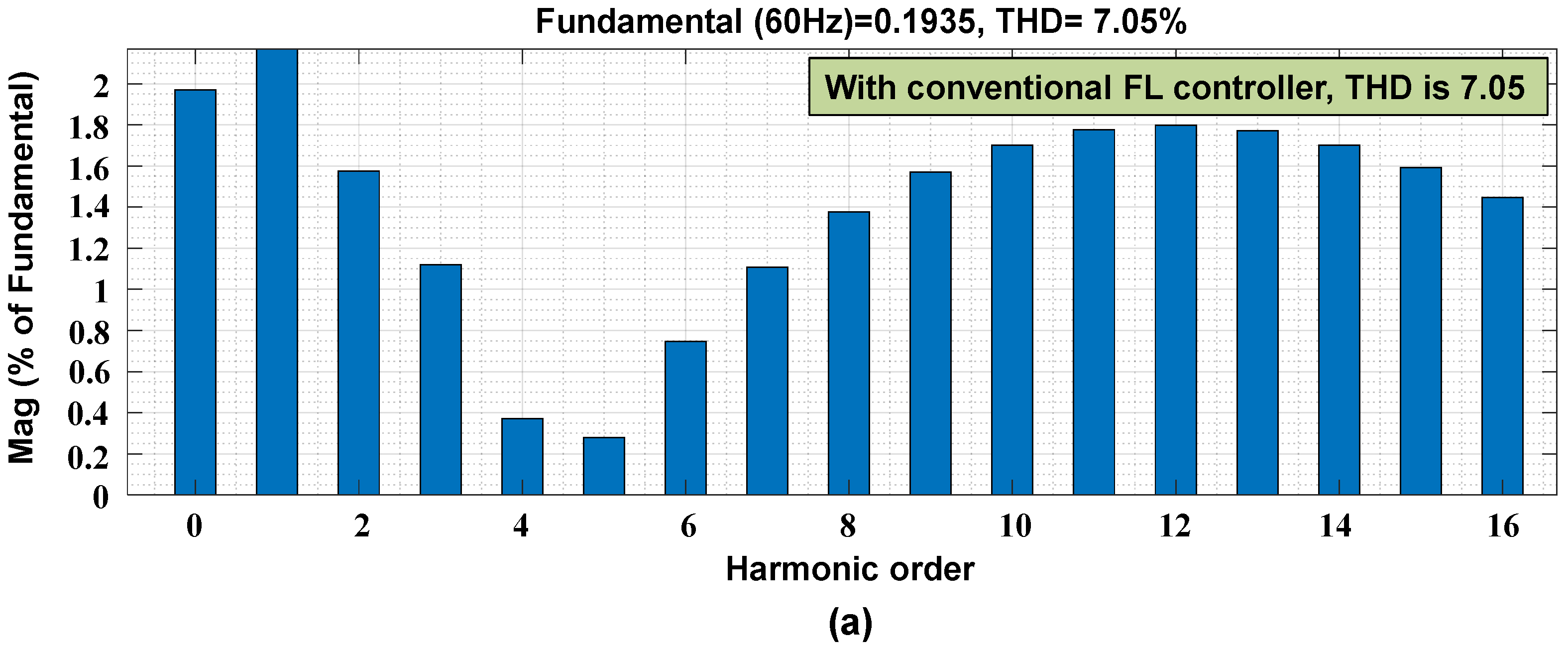
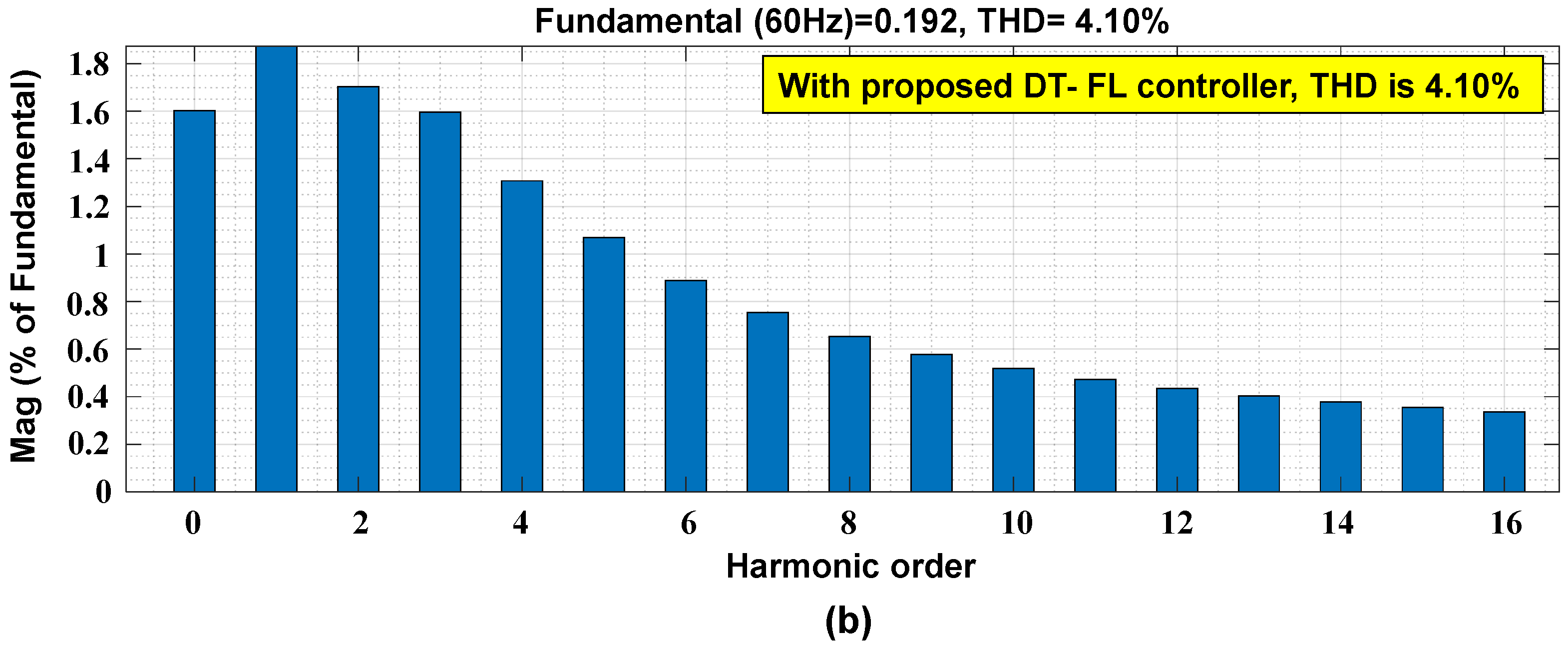
- The THD limits are also maintained as per the IEEE standards.
- ▪
- The frequency response is maintained within the limits suggested by the IEEE standards, using the proposed DT-FL controller.
- ▪
- The transient response of the system is improved by reducing the settling time after the occurrence of the island.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Typical Ratings |
|---|---|
| AC voltage of MG-1 and MG-2 | 415 V |
| DC voltage of MG-1 and MG-2 | 500 V |
| Transformer T1 | 415 (Δ)/13.8 kV (Y-Gnd), 60 Hz |
| Transformer T2 | 13.8 kV (Y-Gnd)/69 kV (Δ), 60 Hz |
| Length of distributed transmission line | 20 kM |
| Load A | 10 MW + j3.5MVAR |
| Load B | 7.5 MW + j12MVAR |
| Solar PV open circuit voltage | 50 V |
| Solar PV short circuit current | 4.5 A |
| Fuel cell stack temperature | 343 K |
| Fuel cell no-load voltage | 0.75 V |
| Frequency limits | 59.95 Hz–60.05 Hz |
| Voltage limits | 0.8 PU to 1.2 PU |
| THD limits | 5% |
| M.F. P1 | [2.18, 2.3, 30, 34] |
| M.F. P2 | [−9.5, −8.5, 1.95, 2.18] |
| M.F. Q1 | [0.64, 0.6, 18, 19] |
| M.F. Q2 | [−0.5, −0.4, 18, 19] |
| M.F. Q3 | [−0.5, −0.4, 0.55, 0.64] |
| M.F. R1 | [0.16, 0.2, 0.5, 0.6] |
| M.F. R2 | [−0.05, −0.03, 0.12, 0.16] |
| FIS output: Islanding | 0.5 |
| FIS output: Non-Islanding | 0 |
| Utility grid power | 100 MVA |
| Utility grid voltage | 69 kV |
| Frequency | 60 Hz |
References
- Rao, S.N.V.B.; Yellapragada, V.P.K.; Padma, K.; Pradeep, D.J.; Reddy, C.P.; Amir, M.; Refaat, S.S. Day-Ahead Load Demand Forecasting in Urban Community Cluster Microgrids Using Machine Learning Methods. Energies 2022, 15, 6124. [Google Scholar] [CrossRef]
- Reddy, G.P.; Kumar, Y.V.P.; Chakravarthi, M.K. Communication Technologies for Interoperable Smart Microgrids in Urban Energy Community: A Broad Review of the State of the Art, Challenges, and Research Perspectives. Sensors 2022, 22, 5881. [Google Scholar] [CrossRef] [PubMed]
- Pavan Kumar, Y.V.; Bhimasingu, R. Review and retrofitted architectures to form reliable smart microgrid networks for urban buildings. IET Netw. 2015, 4, 338–349. [Google Scholar] [CrossRef]
- Pavan Kumar, Y.V.; Bhimasingu, R. Optimal Sizing of Microgrid for an Urban Community Building in South India using HOMER. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Mumbai, India, 16–19 December 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Pavan Kumar, Y.V.; Ravikumar, B. Integrating Renewable Energy Sources to an Urban Building in India: Challenges, Opportunities, and Techno-Economic Feasibility Simulation. Technol. Econ. Smart Grids Sustain. Energy 2016, 1, 1. [Google Scholar] [CrossRef]
- Rao, S.N.V.B.; Pavan Kumar, Y.P.; Amir, M.; Ahmad, F. An Adaptive Neuro-Fuzzy Control Strategy for Improved Power Quality in Multi-Microgrid Clusters. IEEE Access 2022, 10, 128007–128021. [Google Scholar] [CrossRef]
- Rao, S.N.V.B.; Narayana, N.R.; Prasanna, T.D.; Rao, M.S.N.L.N.; Chand, P.G. Fault Detection in Cluster Microgrids of Urban Community using Multi-Resolution Technique based Wavelet Transforms. Int. J. Renew. Energy Res. 2022, 12, 1204–1215. [Google Scholar] [CrossRef]
- IEEE 1547; IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems. IEEE Standard: New York, NY, USA, 2003; pp. 1547–2003.
- Pouryekta, A.; Murthy, V.K.R.; Mithulananthan, N.; Arulampalam, A. Islanding Detection and Enhancement of Microgrid Performance. IEEE Syst. J. 2018, 12, 3131–3141. [Google Scholar] [CrossRef]
- Mlakic, D.; Baghaee, H.R.; Nikolovski, S. A Novel ANFIS-Based Islanding Detection for Inverter-Interfaced Microgrids. IEEE Trans. Smart Grid 2019, 10, 4411–4424. [Google Scholar] [CrossRef]
- Murugesan, S.; Murali, V. Hybrid Analyzing Technique Based Active Islanding Detection for Multiple DGs. IEEE Trans. Ind. Inform. 2019, 15, 1311–1320. [Google Scholar] [CrossRef]
- Abde, A.A.; Salem, A.A.; Oda, E.S.; Eldesouky, A.A. Islanding Detection of Microgrid Incorporating Inverter Based DGs Using Long Short-Term Memory Network. IEEE Access 2020, 8, 106471–106486. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, V.; Pratap, R. Rate of Change of Frequency Deviation Based Unintentional Islanding Detection for Microgrids. In Proceedings of the International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 90–95. [Google Scholar] [CrossRef]
- Ahmed, Y.E.; Dalal Hussien, H.; Abd-Elhaleem, S.; Abozalam, B.A.; Asham, A.D. Fast and accurate islanding detection technique for microgrid connected to photovoltaic system. J. Radiat. Res. Appl. Sci. 2021, 14, 210–221. [Google Scholar] [CrossRef]
- Ran, C.; Li, Z.; Xiong, C.; Hanping, X.; Zhang, Z.; Xuhui, H.; Qingguo, D.; Can, W. Islanding detection method for microgrids based on CatBoost. Front. Energy Res. 2023, 10, 1016754. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, V.; Tyagi, B. Islanding detection for reconfigurable microgrid with RES. IET Gener. Transm. Distrib. 2021, 15, 1187–1202. [Google Scholar] [CrossRef]
- Dixit, V.; Jadhwani, M.; Pandey, A.; Kazi, F. A Hybrid Islanding Detection Scheme for Grid-Tied PV Microgrid. In Proceedings of the IEEE 18th India Council International Conference, Guwahati, India, 19–21 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yasser, A.E.; Amin, D.A.; Belgacem, B.; Abdelmoty, A.; Dalal, H.H.; Belal, A.A.; Abd-Elhaleem, S. An innovative hybrid method for islanding detection using fuzzy classifier for different circumstances including NDZ. J. Radiat. Res. Appl. Sci. 2022, 15, 129–142. [Google Scholar] [CrossRef]
- Soham, D.; Sachin, O.; Pradip Kumar, S. A secured, reliable and accurate unplanned island detection method in a renewable energy based microgrid. Eng. Sci. Technol. Int. J. 2021, 24, 1102–1115. [Google Scholar] [CrossRef]
- Salman, S.; Ai, X.; Wu, Z. Design of a P-&-O algorithm based MPPT charge controller for a stand-alone 200W PV system. Prot. Control. Mod. Power Syst. 2018, 3, 25. [Google Scholar] [CrossRef]
- Rao, S.N.V.B.; Padma, K. ANN based Day-Ahead Load Demand Forecasting for Energy Transactions at Urban Community Level with Interoperable Green Microgrid Cluster. Int. J. Renew. Energy Res. 2021, 11, 147–157. [Google Scholar]
- Shaik, M.; Shaik, A.G.; Yadav, S.K. Hilbert–Huang transform and decision tree based islanding and fault recognition in renewable energy penetrated distribution system. Sustain. Energy Grids Netw. 2022, 30, 100606. [Google Scholar] [CrossRef]
- Rabcan, J.; Zaitseva, E.; Levashenko, V.; Kvassay, M.; Surda, P.; Macekova, D. Fuzzy Decision Tree Based Method in Decision-Making of COVID-19 Patients’ Treatment. Mathematics 2021, 9, 3282. [Google Scholar] [CrossRef]
- Chakravorti, T.; Patnaik, R.K.; Dash, P.K. Detection and classification of islanding and power quality disturbances in microgrid using hybrid signal processing and data mining techniques. IET Signal Process. 2018, 12, 82–94. [Google Scholar] [CrossRef]
- Rao, S.N.V.B.; Kumar, Y.V.P.; Pradeep, D.J.; Reddy, C.P.; Flah, A.; Kraiem, H.; Al-Asad, J.F. Power Quality Improvement in Renewable-Energy-Based Microgrid Clusters Using Fuzzy Space Vector PWM Controlled Inverter. Sustainability 2022, 14, 4663. [Google Scholar] [CrossRef]



| S. No. | Load Name | Load Type | Rating (kW + jkVAR) |
|---|---|---|---|
| 1 | Fan | Load-1 | 0.07 + j0.019 |
| 2 | Light | Load-2 | 0.03 + j0.006 |
| 3 | AC_type1 | Load-3 | 1.3 + j0.429 |
| 4 | TV | Load-5 | 0.07 + j0.019 |
| 5 | Refrigerator | Load-6 | 0.4 + j0.14 |
| 6 | Grinder | Load-7 | 0.5 + j0.17 |
| 7 | Washing machine | Load-8 | 0.51 + j0.16 |
| 8 | Computer | Load-9 | 0.46 + j0.148 |
| 9 | Water cooler | Load-10 | 0.51 + j0.16 |
| 10 | Machine_type1 | Load-11 | 2.2 + j0.724 |
| Load Particulars | Load Distribution in a Day | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Load Type | Qty/Flat | Qty/ 20 Flats | 0–4 h | 4–8 h | 8–12 h | 12–16 h | 16–20 h | 20–24 h | ||||||||||||
| Qty ON | Load | Qty ON | Load | Qty ON | Load | Qty ON | Load | Qty ON | Load | Qty ON | Load | |||||||||
| kW | kVAR | kW | kVAR | kW | kVAR | kW | kVAR | kW | kVAR | kW | kVAR | |||||||||
| Load-1 | 3 | 60 | 60 | 3.61 | 1.15 | 60 | 3.61 | 1.14 | 40 | 2.42 | 0.76 | 40 | 2.4 | 0.77 | 45 | 2.7 | 0.86 | 30 | 1.8 | 0.57 |
| Load-2 | 4 | 80 | 20 | 0.4 | 0.12 | 40 | 0.8 | 0.24 | 25 | 0.5 | 0.15 | 10 | 0.2 | 0.06 | 60 | 1.2 | 0.36 | 70 | 1.4 | 0.42 |
| Load-3 | 1 | 20 | 16 | 20.8 | 6.83 | 12 | 15.6 | 5.12 | 8 | 10.4 | 3.42 | 18 | 23.4 | 7.69 | 9 | 11.7 | 3.84 | 17 | 22.1 | 7.26 |
| Load-5 | 1 | 20 | 2 | 0.12 | 0.04 | 12 | 0.72 | 0.23 | 15 | 0.9 | 0.29 | 15 | 0.9 | 0.29 | 16 | 0.96 | 0.3 | 15 | 0.9 | 0.29 |
| Load-6 | 1 | 20 | 20 | 8 | 2.6 | 20 | 8 | 2.6 | 20 | 8 | 2.6 | 20 | 8 | 2.6 | 20 | 8 | 2.6 | 20 | 8 | 2.6 |
| Load-7 | 1 | 20 | 2 | 1 | 0 | 14 | 7 | 1.12 | 14 | 7 | 2.24 | 4 | 2 | 0.64 | 5 | 2.5 | 0.8 | 10 | 5 | 1.6 |
| Load-8 | 1 | 20 | 0 | 0 | 0 | 10 | 5 | 0.8 | 15 | 7.5 | 2.4 | 6 | 3 | 0.96 | 8 | 4 | 1.28 | 8 | 4 | 1.28 |
| Total Load | 33.9 + j10.73 | 40.72 + j11.25 | 36.7 + j11.86 | 39.9 + j13 | 31.06 + j10 | 47.1 + j14.02 | ||||||||||||||
| Load Details | Load Distribution over a Day | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Load Type | Qty/Flat | 0–4 h | 4–8 h | 8–12 h | 12–16 h | 16–20 h | 20–24 h | ||||||||||||
| Qty ON | Load | Qty ON | Load | Qty ON | Load | Qty ON | Load | Qty ON | Load | Qty ON | Load | ||||||||
| kW | kVAR | kW | kVAR | kW | kVAR | kW | kVAR | kW | kVAR | kW | kVAR | ||||||||
| Load-1 | 200 | 20 | 1.2 | 0.38 | 40 | 2.4 | 0.76 | 150 | 9 | 2.85 | 180 | 10.8 | 3.42 | 70 | 4.2 | 1.33 | 50 | 3 | 0.95 |
| Load-2 | 300 | 50 | 1 | 0.3 | 25 | 0.5 | 0.15 | 150 | 3 | 0.9 | 150 | 3 | 0.9 | 50 | 1 | 0.3 | 120 | 2.4 | 0.72 |
| Load-3 | 25 | 5 | 6.5 | 2.14 | 5 | 6.5 | 2.14 | 10 | 13 | 4.27 | 15 | 19.5 | 6.41 | 10 | 13 | 4.27 | 7 | 9.1 | 2.99 |
| Load-9 | 150 | 20 | 9 | 2.96 | 40 | 18 | 5.92 | 75 | 33.75 | 11.1 | 100 | 45 | 14.8 | 80 | 36 | 11.84 | 50 | 22.5 | 7.4 |
| Load-11 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 15.4 | 5.06 | 7 | 15.4 | 5.06 | 0 | 0 | 0 | 0 | 0 | 0 |
| Load-10 | 20 | 10 | 5 | 1.6 | 10 | 5 | 1.6 | 20 | 10 | 3.2 | 20 | 10 | 3.2 | 10 | 5 | 1.6 | 10 | 5 | 1.6 |
| Total Load | 22.7 + j7.38 | 32.4 + j10.57 | 84.15 + j27.38 | 103.7 + j33.79 | 59.2 + j19.34 | 22 + j13.66 | |||||||||||||
| Extracted Feature at PCC | Notation | Units |
|---|---|---|
| Change in frequency | Hz | |
| Change in voltage | PU | |
| Rate of change in frequency | Hz/s | |
| Rate of change in voltage | PU/s | |
| Rate of change in power | MW/s | |
| Ratio of change in frequency to change in power | Hz/MW | |
| Current THD | PU | |
| Voltage THD | PU | |
| Change in power factor | -- | |
| Absolute phase voltage times of power factor | -- | |
| Rate of change of absolute phase voltage times of power factor | -- |
| S. No. | Condition | Description of Procedure |
|---|---|---|
| 1 | A | Trip the circuit breaker (CB1) of MG-1 by connecting a PCC load of 7.5 MW + j12.5MVAR |
| 2 | B | A sudden drop in the loads connected at the PCC by 25%, i.e., 1.89 MW + j3MVAR |
| 3 | C | Trip the circuit breaker (CB2) of MG-2 by isolating the PCC loads |
| Test Cases | Actual Class | Conventional FL Controller without Noise | ||
|---|---|---|---|---|
| FIS-0.5 (Island) | FIS-0 (Non-Island) | Accuracy (%) | ||
| 10 | Island | 8 | 0 | 80 |
| Non-island | 0 | 8 | 80 | |
| Proposed DT-FL Controller without Noise | ||||
| FIS-0.5 (Island) | FIS-0 (Non-Island) | Accuracy (%) | ||
| Island | 10 | 0 | 100 | |
| Non-island | 0 | 10 | 100 | |
| Conventional FL Controller with Noise (20 dB) | ||||
| FIS-0.5 (Island) | FIS-0 (Non-Island) | Accuracy (%) | ||
| Island | 7 | 0 | 70 | |
| Non-island | 0 | 7 | 70 | |
| Proposed DT-FL Controller with Noise (20 dB) | ||||
| FIS-0.5 (Island) | FIS-0 (Non-Island) | Accuracy (%) | ||
| Island | 9 | 0 | 90 | |
| Non-island | 0 | 9 | 90 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkata Pavan Kumar, Y.; Naga Venkata Bramareswara Rao, S.; Kannan, R. Islanding Detection in Grid-Connected Urban Community Multi-Microgrid Clusters Using Decision-Tree-Based Fuzzy Logic Controller for Improved Transient Response. Urban Sci. 2023, 7, 72. https://doi.org/10.3390/urbansci7030072
Venkata Pavan Kumar Y, Naga Venkata Bramareswara Rao S, Kannan R. Islanding Detection in Grid-Connected Urban Community Multi-Microgrid Clusters Using Decision-Tree-Based Fuzzy Logic Controller for Improved Transient Response. Urban Science. 2023; 7(3):72. https://doi.org/10.3390/urbansci7030072
Chicago/Turabian StyleVenkata Pavan Kumar, Yellapragada, Sivakavi Naga Venkata Bramareswara Rao, and Ramani Kannan. 2023. "Islanding Detection in Grid-Connected Urban Community Multi-Microgrid Clusters Using Decision-Tree-Based Fuzzy Logic Controller for Improved Transient Response" Urban Science 7, no. 3: 72. https://doi.org/10.3390/urbansci7030072
APA StyleVenkata Pavan Kumar, Y., Naga Venkata Bramareswara Rao, S., & Kannan, R. (2023). Islanding Detection in Grid-Connected Urban Community Multi-Microgrid Clusters Using Decision-Tree-Based Fuzzy Logic Controller for Improved Transient Response. Urban Science, 7(3), 72. https://doi.org/10.3390/urbansci7030072








