A Geometric Classification of World Urban Road Networks
Abstract
:1. Introduction
2. Network Science
3. Materials and Methods
3.1. Data
3.2. Methodology
3.2.1. Degree Distribution
3.2.2. Link Length Distribution
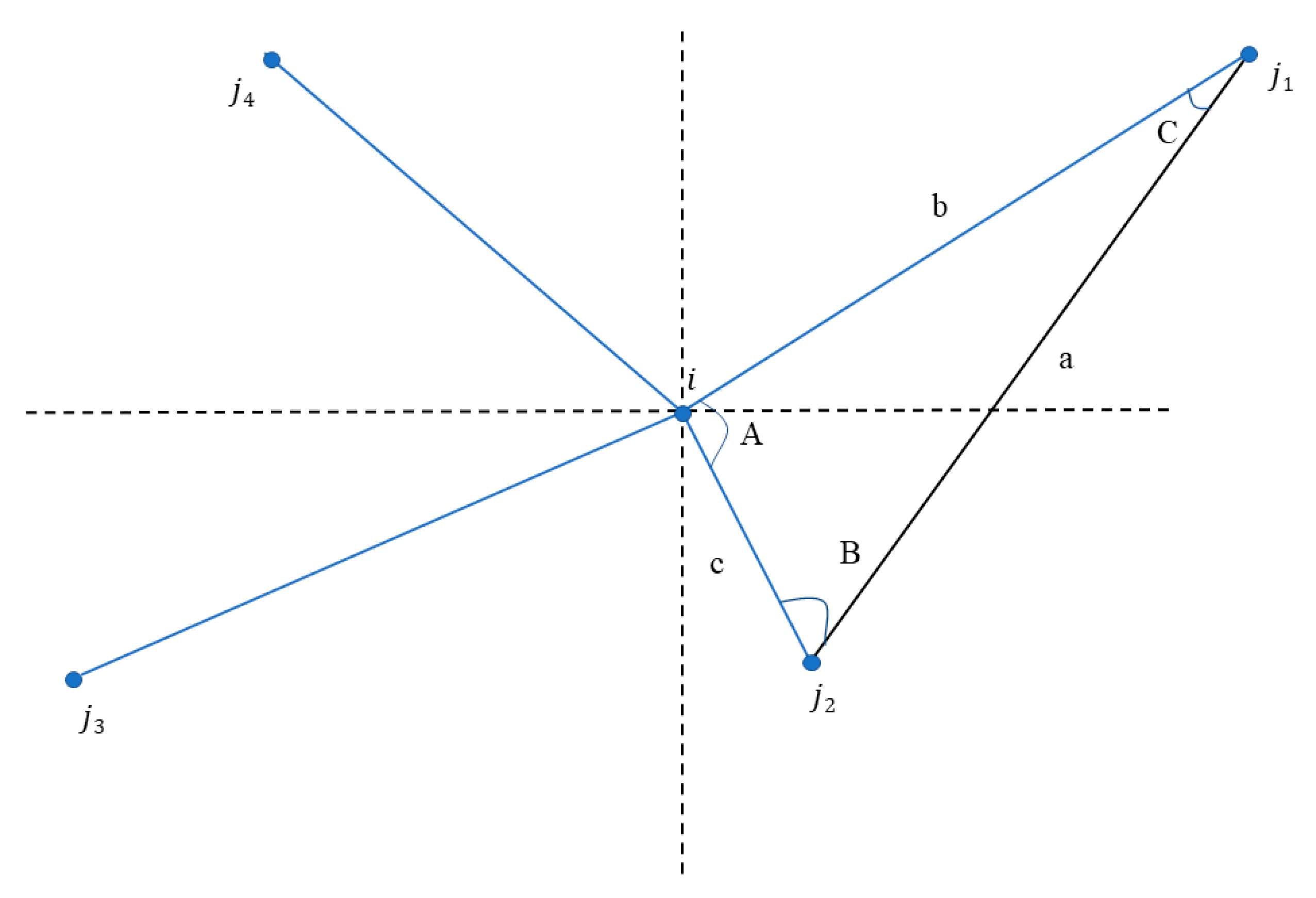
3.2.3. Intersection Angle Distribution
3.2.4. Clustering
4. Results
4.1. Universal Pattern
4.2. Road Network Analysis
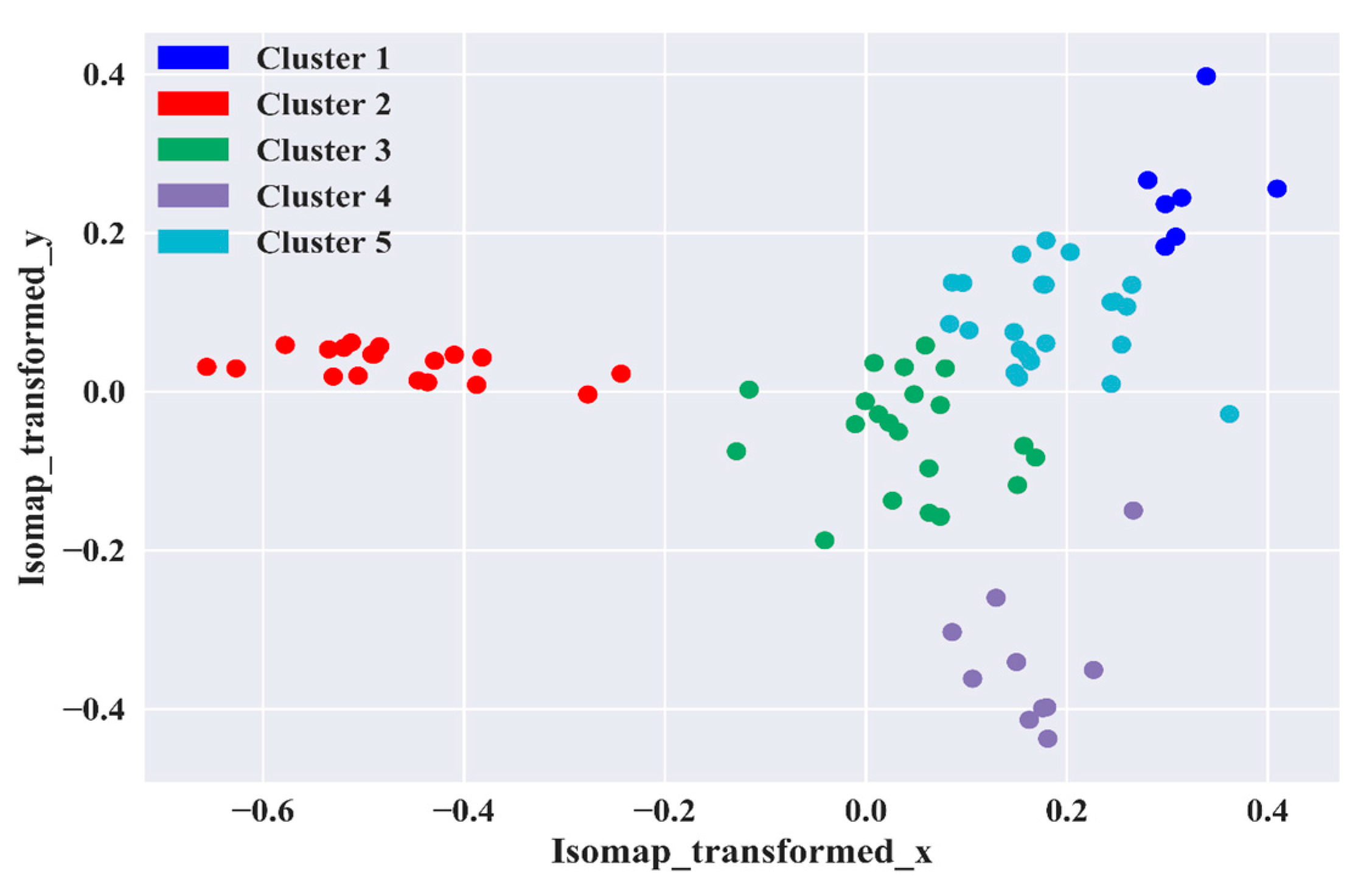
5. Discussion
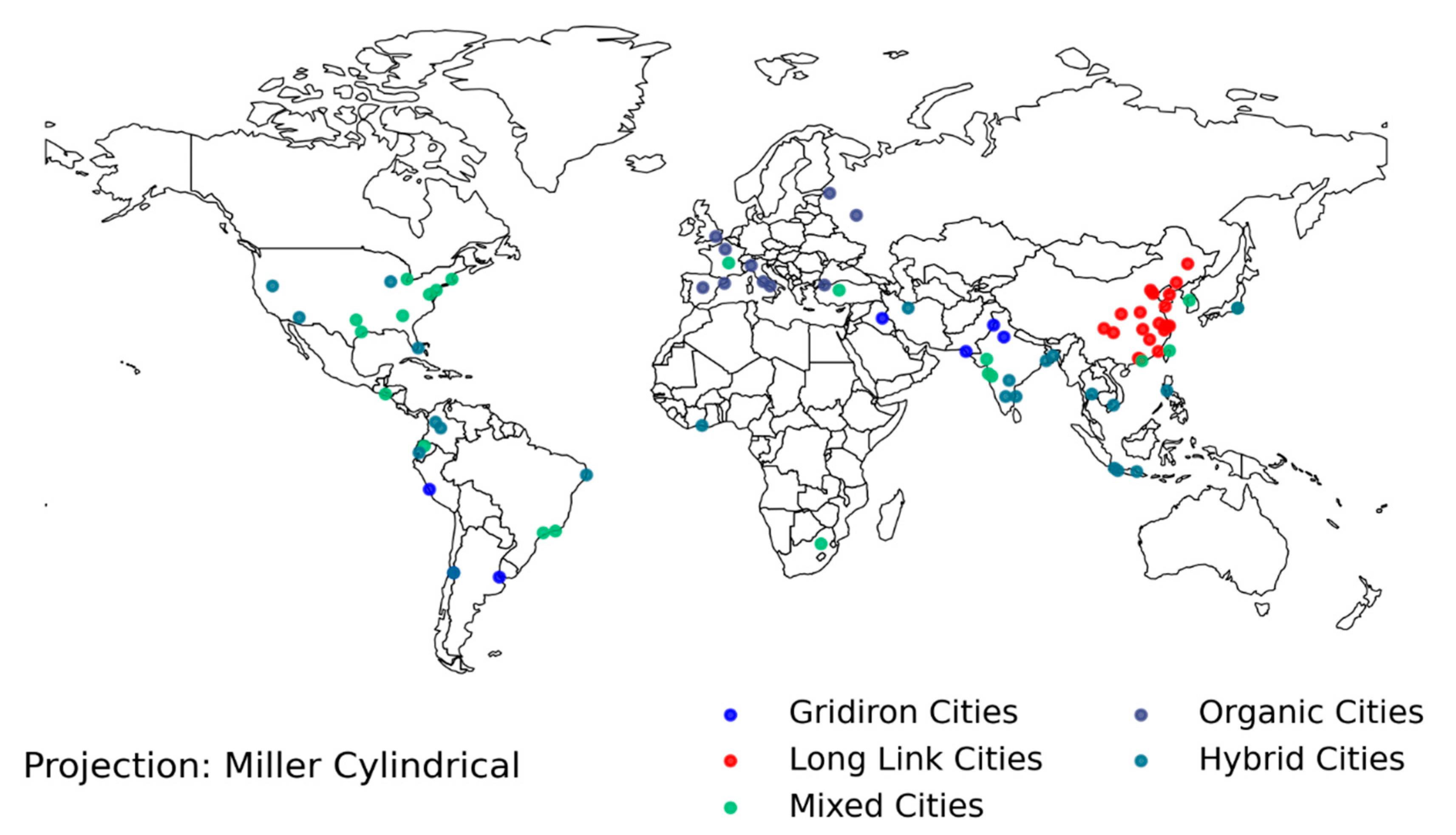
5.1. Cities Classification
5.2. Research and Policy Implications
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Derrible, S. Complexity in future cities: The rise of networked infrastructure. Int. J. Urban Sci. 2017, 21, 68–86. [Google Scholar] [CrossRef]
- Derrible, S. Urban Engineering for Sustainability; The MIT Press: Cambridge, MA, USA, 2019; Available online: https://mitpress.mit.edu/books/urban-engineering-sustainability (accessed on 11 May 2021).
- McKenzie, G. Urban mobility in the sharing economy: A spatiotemporal comparison of shared mobility services. Comput. Environ. Urban Syst. 2020, 79, 101418. [Google Scholar] [CrossRef]
- Batty, M.; Marshall, S. Thinking organic, acting civic: The paradox of planning for Cities in Evolution. Landsc. Urban Plan. 2017, 166, 4–14. [Google Scholar] [CrossRef]
- Barthelemy, M.; Bordin, P.; Berestycki, H.; Gribaudi, M. Self-organization versus top-down planning in the evolution of a city. Sci. Rep. 2013, 3, 2153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martínez-Mendoza, R. Analyzing Urban Spaces: A Comparative Study of Sociability in Two Plazas in Santiago de Querétaro City, Mexico. 2001. Available online: https://ttu-ir.tdl.org/handle/2346/61606 (accessed on 20 October 2021).
- Amini, B.; Peiravian, F.; Mojarradi, M.; Derrible, S. Comparative Analysis of Traffic Performance of Urban Transportation Systems. Transp. Res. Rec. J. Transp. Res. Board 2016, 2594, 159–168. [Google Scholar] [CrossRef]
- Derrible, S. An approach to designing sustainable urban infrastructure. MRS Energy Sustain. 2018, 5, E15. [Google Scholar] [CrossRef] [Green Version]
- Marshall, S. Streets and Patterns; Routledge: London, UK, 2004; p. 328. ISBN 978-1-134-37075-7. [Google Scholar]
- Cervero, R.; Kockelman, K. Travel demand and the 3Ds: Density, diversity, and design. Transp. Res. Part D Transp. Environ. 1997, 2, 199–219. [Google Scholar] [CrossRef]
- Handy, S.L.; Boarnet, M.G.; Ewing, R.; Killingsworth, R.E. How the built environment affects physical activity: Views from urban planning. Am. J. Prev. Med. 2002, 23, 64–73. [Google Scholar] [CrossRef]
- Uchida, K. Estimating the value of travel time and of travel time reliability in road networks. Transp. Res. Part B Methodol. 2014, 66, 129–147. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Comparative Analysis on Topological Structures of Urban Street Networks. ISPRS Int. J. Geo-Inf. 2017, 6, 295. [Google Scholar] [CrossRef] [Green Version]
- Akbarzadeh, M.; Memarmontazerin, S.; Derrible, S.; Salehi Reihani, S.F. The role of travel demand and network centrality on the connectivity and resilience of an urban street system. Transportation 2019, 46, 1127–1141. [Google Scholar] [CrossRef]
- Marshall, W.E.; Piatkowski, D.P.; Garrick, N.W. Community design, street networks, and public health. J. Transp. Health 2014, 1, 326–340. [Google Scholar] [CrossRef]
- Frizzelle, B.G.; Evenson, K.R.; Rodriguez, D.A.; Laraia, B.A. The importance of accurate road data for spatial applications in public health: Customizing a road network. Int. J. Health Geogr. 2009, 8, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, M.A.P.; Sekhar, S.V.C.; D’Este, G.M. Application of Accessibility Based Methods for Vulnerability Analysis of Strategic Road Networks. Netw. Spat. Econ. 2006, 6, 267–291. [Google Scholar] [CrossRef]
- Taylor, M.A.P. Susilawati Remoteness and accessibility in the vulnerability analysis of regional road networks. Transp. Res. Part A Policy Pract. 2012, 46, 761–771. [Google Scholar] [CrossRef]
- Fancello, G.; Carta, M.; Fadda, P. A Modeling Tool for Measuring the Performance of Urban Road Networks. Procedia Soc. Behav. Sci. 2014, 111, 559–566. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wang, N. Resilience-based risk mitigation for road networks. Struct. Saf. 2016, 62, 57–65. [Google Scholar] [CrossRef] [Green Version]
- Wang, J. Resilience of Self-Organised and Top-Down Planned Cities—A Case Study on London and Beijing Street Networks. PLoS ONE 2015, 10, e0141736. [Google Scholar] [CrossRef]
- Sharifi, A. Resilient urban forms: A review of literature on streets and street networks. Build. Environ. 2019, 147, 171–187. [Google Scholar] [CrossRef]
- Kermanshah, A.; Derrible, S.; Berkelhammer, M. Using Climate Models to Estimate Urban Vulnerability to Flash Floods. J. Appl. Meteorol. Climatol. 2017, 56, 2637–2650. [Google Scholar] [CrossRef]
- Xie, F.; Levinson, D. Measuring the Structure of Road Networks. Geogr. Anal. 2007, 39, 336–356. [Google Scholar] [CrossRef]
- Sharifi, A. A typology of smart city assessment tools and indicator sets. Sustain. Cities Soc. 2020, 53, 101936. [Google Scholar] [CrossRef]
- Gauthier, P.; Furno, A.; El Faouzi, N.-E. Road Network Resilience: How to Identify Critical Links Subject to Day-to-Day Disruptions. Transp. Res. Rec. 2018, 2672, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Henry, E.; Furno, A.; Faouzi, N.-E.E. Approach to Quantify the Impact of Disruptions on Traffic Conditions using Dynamic Weighted Resilience Metrics of Transport Networks. Transp. Res. Rec. 2021, 2675, 61–78. [Google Scholar] [CrossRef]
- Boeing, G. Street Network Models and Indicators for Every Urban Area in the World. Geogr. Anal. 2021. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1111/gean.12281 (accessed on 9 March 2021). [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010; p. 789. ISBN 978-0-19-920665-0. [Google Scholar]
- Barabási, A.-L.; Pósfai, M. Network Science; Cambridge University Press: Cambridge, UK, 2016; p. 477. ISBN 978-1-107-07626-6. [Google Scholar]
- Ahmad, N.; Derrible, S. Evolution of Public Supply Water Withdrawal in the USA: A Network Approach. J. Ind. Ecol. 2015, 19, 321–330. [Google Scholar] [CrossRef]
- Derrible, S.; Ahmad, N. Network-Based and Binless Frequency Analyses. PLoS ONE 2015, 10, e0142108. [Google Scholar] [CrossRef]
- Chalasani, V.S.; Denstadli, J.M.; Engebretsen, O.; Axhausen, K.W. Precision of geocoded locations and network distance estimations. J. Transp. Stat. 2005, 8, 1–15. [Google Scholar]
- Crucitti, P.; Latora, V.; Porta, S. Centrality measures in spatial networks of urban streets. Phys. Rev. E 2006, 73, 036125. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Claramunt, C. Topological Analysis of Urban Street Networks. Environ. Plan. B Plan. Des. 2004, 31, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Boeing, G. Urban spatial order: Street network orientation, configuration, and entropy. Appl. Netw. Sci. 2019, 4, 67. [Google Scholar] [CrossRef] [Green Version]
- Akbarzadeh, M.; Memarmontazerin, S.; Soleimani, S. Where to look for power Laws in urban road networks? Appl. Netw. Sci. 2018, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Tsiotas, D.; Polyzos, S. The topology of urban road networks and its role to urban mobility. Transp. Res. Procedia 2017, 24, 482–490. [Google Scholar] [CrossRef]
- Dumedah, G.; Garsonu, E.K. Characterising the structural pattern of urban road networks in Ghana using geometric and topological measures. Geo Geogr. Environ. 2021, 8, e00095. [Google Scholar] [CrossRef]
- Martínez Mori, J.C.; Samaranayake, S. Bounded Asymmetry in Road Networks. Sci. Rep. 2019, 9, 11951. [Google Scholar] [CrossRef]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef] [Green Version]
- Hillier, W.R.G.; Turner, A.; Yang, T.; Park, H. Metric and topo-geometric properties of urban street networks: Some convergencies, divergencies and new results. J. Space Syntax 2010, 1, 258–279. [Google Scholar]
- Nicosia, V.; Criado, R.; Romance, M.; Russo, G.; Latora, V. Controlling centrality in complex networks. Sci. Rep. 2012, 2, 218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Merchán, D.; Winkenbach, M.; Snoeck, A. Quantifying the impact of urban road networks on the efficiency of local trips. Transp. Res. Part A Policy Pract. 2020, 135, 38–62. [Google Scholar] [CrossRef] [Green Version]
- Batty, M. The New Science of Cities; MIT Press: Cambridge, MA, USA, 2013; p. 520. ISBN 978-0-262-01952-1. [Google Scholar]
- Buhl, J.; Gautrais, J.; Reeves, N.; Solé, R.V.; Valverde, S.; Kuntz, P.; Theraulaz, G. Topological patterns in street networks of self-organized urban settlements. Eur. Phys. J. B 2006, 49, 513–522. [Google Scholar] [CrossRef]
- Barthelemy, M. From paths to blocks: New measures for street patterns. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 256–271. [Google Scholar] [CrossRef]
- Boeing, G. The Morphology and Circuity of Walkable and Drivable Street Networks. In The Mathematics of Urban Morphology; D’Acci, L., Ed.; Modeling and Simulation in Science, Engineering and Technology; Springer: Cham, Switzerland, 2019; pp. 271–287. ISBN 978-3-030-12381-9. [Google Scholar]
- Porta, S.; Crucitti, P.; Latora, V. The Network Analysis of Urban Streets: A Primal Approach. Environ. Plan. B Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef] [Green Version]
- Kirkley, A.; Barbosa, H.; Barthelemy, M.; Ghoshal, G. From the betweenness centrality in street networks to structural invariants in random planar graphs. Nat. Commun. 2018, 9, 2501. [Google Scholar] [CrossRef]
- Furno, A.; El Faouzi, N.-E.; Sharma, R.; Zimeo, E. Fast Computation of Betweenness Centrality to Locate Vulnerabilities in Very Large Road Networks. 2018. Available online: https://trid.trb.org/view/1496091 (accessed on 23 July 2021).
- Shang, W.-L.; Chen, Y.; Song, C.; Ochieng, W.Y. Robustness Analysis of Urban Road Networks from Topological and Operational Perspectives. Math. Probl. Eng. 2020, 2020, e5875803. [Google Scholar] [CrossRef]
- Han, Z.; Cui, C.; Miao, C.; Wang, H.; Chen, X. Identifying Spatial Patterns of Retail Stores in Road Network Structure. Sustainability 2019, 11, 4539. [Google Scholar] [CrossRef] [Green Version]
- LOBsang, T.; Zhen, F.; Zhang, S. Can Urban Street Network Characteristics Indicate Economic Development Level? Evidence from Chinese Cities. ISPRS Int. J. Geo-Inf. 2020, 9, 3. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B. A topological pattern of urban street networks: Universality and peculiarity. Phys. A Stat. Mech. Its Appl. 2007, 384, 647–655. [Google Scholar] [CrossRef] [Green Version]
- Masucci, A.P.; Stanilov, K.; Batty, M. Exploring the evolution of London’s street network in the information space: A dual approach. Phys. Rev. E 2014, 89, 012805. [Google Scholar] [CrossRef] [Green Version]
- Hacar, M.; Kılıç, B.; Şahbaz, K. Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey. ISPRS Int. J. Geo-Inf. 2018, 7, 400. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Chen, Z.; Mu, L.; Zhang, X. Road network structure and ride-sharing accessibility: A network science perspective. Comput. Environ. Urban Syst. 2020, 80, 101430. [Google Scholar] [CrossRef]
- Barthélemy, M. Betweenness centrality in large complex networks. Eur. Phys. J. B 2004, 38, 163–168. [Google Scholar] [CrossRef]
- Chan, S.H.Y.; Donner, R.V.; Lämmer, S. Urban road networks—Spatial networks with universal geometric features? Eur. Phys. J. B 2011, 84, 563–577. [Google Scholar] [CrossRef] [Green Version]
- Strano, E.; Viana, M.; da Fontoura Costa, L.; Cardillo, A.; Porta, S.; Latora, V. Urban Street Networks, a Comparative Analysis of Ten European Cities. Environ. Plan. B Plan. Des. 2013, 40, 1071–1086. [Google Scholar] [CrossRef] [Green Version]
- Karduni, A.; Kermanshah, A.; Derrible, S. A protocol to convert spatial polyline data to network formats and applications to world urban road networks. Sci. Data 2016, 3, 160046. [Google Scholar] [CrossRef] [PubMed]
- Sinnott, R.W. Virtues of the haversine. Sky Telesc. 1984, 68, 158–159. [Google Scholar]
- Steinbach, M.; Ertöz, L.; Kumar, V. The Challenges of Clustering High Dimensional Data. In New Directions in Statistical Physics; Wille, L.T., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 273–309. ISBN 978-3-642-07739-5. [Google Scholar]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems 14; MIT Press: Cambridge, MA, USA, 2002; pp. 849–856. ISBN 978-0-262-04207-9. [Google Scholar]
- Nasri, A.; Zhang, L. A multi-dimensional multi-level approach to measuring the spatial structure of U.S. metropolitan areas. J. Transp. Land Use 2018, 11, 49–65. [Google Scholar] [CrossRef]
- Xu, W. Urban Explorations: Analysis of Public Park Usage using Mobile GPS Data. arXiv 2018, arXiv:1801.01921. [Google Scholar]
- Spadon, G.; Gimenes, G.; Rodrigues, J.F. Topological Street-Network Characterization Through Feature-Vector and Cluster Analysis. In Computational Science—ICCS 2018; Shi, Y., Fu, H., Tian, Y., Krzhizhanovskaya, V.V., Lees, M.H., Dongarra, J., Sloot, P.M.A., Eds.; Springer: Cham, Switzerland, 2018; pp. 274–287. [Google Scholar]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.-H.; Jung, W.-S. Analysis on the urban street network of Korea: Connections between topology and meta-information. Phys. A Stat. Mech. Its Appl. 2018, 497, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Louf, R.; Barthelemy, M. A typology of street patterns. J. R. Soc. Interface 2014, 11, 20140924. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alobaydi, D. A study of the morphological evolution of the urban cores of baghdad in the 19th and 20th century. In Proceedings of the 11th International Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017; Volume 12. [Google Scholar]
- Yue, W.; Liu, Y.; Fan, P. Measuring urban sprawl and its drivers in large Chinese cities: The case of Hangzhou. Land Use Policy 2013, 31, 358–370. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, W.; Fan, P. Spatial Determinants of Urban Land Conversion in Large Chinese Cities: A Case of Hangzhou. Environ. Plan. B Plan. Des. 2011, 38, 706–725. [Google Scholar] [CrossRef]
- Wang, S.; Yu, D.; Kwan, M.-P.; Zheng, L.; Miao, H.; Li, Y. The impacts of road network density on motor vehicle travel: An empirical study of Chinese cities based on network theory. Transp. Res. Part A Policy Pract. 2020, 132, 144–156. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, B. Defining and generating axial lines from street center lines for better understanding of urban morphologies. Int. J. Geogr. Inf. Sci. 2012, 26, 1521–1532. [Google Scholar] [CrossRef]
- Kaoru, Y.; Yusuke, K.; Yuji, Y. Local Betweenness Centrality Analysis of 30 European Cities. arXiv 2021, arXiv:2103.1143726. [Google Scholar]
- Mohajeri, N.; French, J.R.; Batty, M. Evolution and entropy in the organization of urban street patterns. Ann. GIS 2013, 19, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Levinson, D.; Huang, A. A Positive Theory of Network Connectivity. Environ. Plan. B Plan. Des. 2012, 39, 308–325. [Google Scholar] [CrossRef] [Green Version]
- Marshall, W.E.; Garrick, N.W. Street network types and road safety: A study of 24 California cities. Urban Des. Int. 2010, 15, 133–147. [Google Scholar] [CrossRef]
- Casali, Y.; Heinimann, H.R. A topological analysis of growth in the Zurich road network. Comput. Environ. Urban Syst. 2019, 75, 244–253. [Google Scholar] [CrossRef]
- Langeland, A. Sustainable Transport in Cities: Learning from Best and Worst Practice? MIT Press: Cambridge, MA, USA, 2015; pp. 93–103. Available online: http://library.witpress.com/viewpaper.asp?pcode=UT15-008-1 (accessed on 5 January 2022).
- Angelidou, M. Smart city policies: A spatial approach. Cities 2014, 41, S3–S11. [Google Scholar] [CrossRef]
- Angelidou, M. The Role of Smart City Characteristics in the Plans of Fifteen Cities. J. Urban Technol. 2017, 24, 3–28. [Google Scholar] [CrossRef]
- Hodgkinson, S. Is Your City Smart Enough? Report No. OI00130-007; Ovum: London, UK, 2011. [Google Scholar]
- Tranos, E.; Gertner, D. Smart networked cities? Innov. Eur. J. Soc. Sci. Res. 2012, 25, 175–190. [Google Scholar] [CrossRef]
- Guo, Y.; Tang, Z.; Guo, J. Could a Smart City Ameliorate Urban Traffic Congestion? A Quasi-Natural Experiment Based on a Smart City Pilot Program in China. Sustainability 2020, 12, 2291. [Google Scholar] [CrossRef] [Green Version]

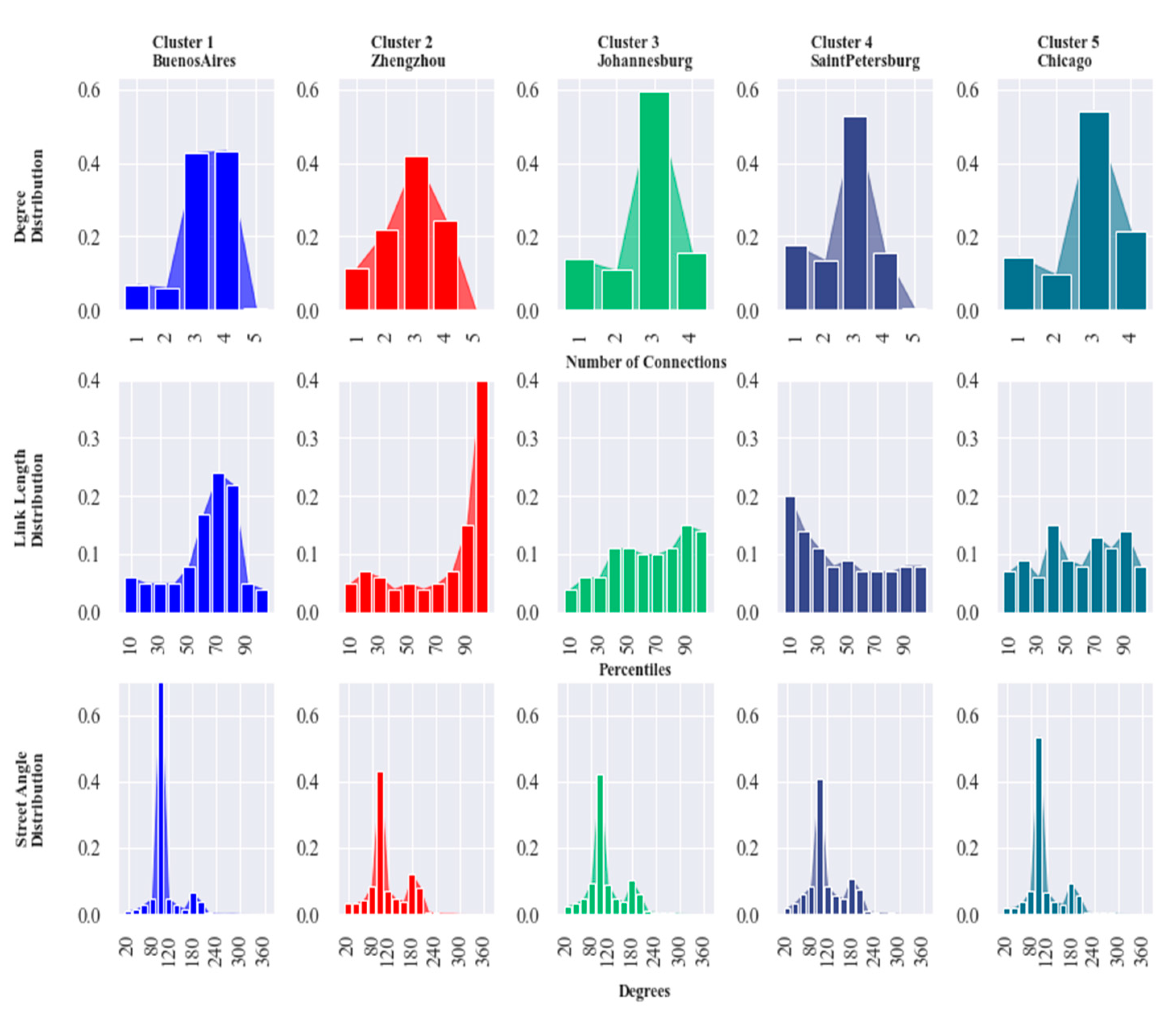
| Percentiles | Length (m) |
|---|---|
| 10 | 15 |
| 20 | 27 |
| 30 | 41 |
| 40 | 55 |
| 50 | 73 |
| 60 | 93 |
| 70 | 121 |
| 80 | 170 |
| 90 | 279 |
| Clustering Techniques | Silhouette Scores |
|---|---|
| K-means | 0.69 |
| Spectral K-means | 0.66 |
| Hierarchical | 0.63 |
| HDBSCAN | 0.47 |
| Group | Cities |
|---|---|
| Class 1: Gridiron (many 90° angles) | Baghdad, Buenos Aires, Delhi, Karachi, Lahore, Lima, Santiago. |
| Class 2: Long Link (disproportionate number of long links) | Beijing, Chengdu, Chongqing, Dalian, Dongguan, Fuzhou, Guangzhou, Hangzhou, Harbin, Nanjing, Qingdao, Quanzhou, Shanghai, Shenyang, Suzhou, Tianjin, Wuhan, Xianyang, Zhengzhou. |
| Class 3: Organic (short links and more non-90° and 180° angles) | Barcelona, Istanbul, London, Madrid, Milan, Moscow, Naples, Paris, Rome, Saint Petersburg. |
| Class 4: Hybrid (historical and recently developed with both short and long links) | Abidjan, Bangdung, Bangkok, Belo Horizonte, Bengaluru, Bogota, Calcutta, Chennai, Chicago, Dhaka, Ho Chi Minh, Hyderabad, Jakarta, Los Angeles, Manila, Medellin, Miami, Phoenix, Porto Alegre, Recife, Surabaya, Tehran, Tokyo. |
| Class 5: Mixed (shares similarity with all other classes) | Ahmedabad, Ankara, Atlanta, Boston, Dallas, Detroit, Houston, Johannesburg, Mumbai, New York, Philadelphia, Pune, Rio de Janeiro, Salvador, San Francisco, Sao Paolo, Seoul, Shenzhen, Surat, Taipei, Washington DC. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badhrudeen, M.; Derrible, S.; Verma, T.; Kermanshah, A.; Furno, A. A Geometric Classification of World Urban Road Networks. Urban Sci. 2022, 6, 11. https://doi.org/10.3390/urbansci6010011
Badhrudeen M, Derrible S, Verma T, Kermanshah A, Furno A. A Geometric Classification of World Urban Road Networks. Urban Science. 2022; 6(1):11. https://doi.org/10.3390/urbansci6010011
Chicago/Turabian StyleBadhrudeen, Mohamed, Sybil Derrible, Trivik Verma, Amirhassan Kermanshah, and Angelo Furno. 2022. "A Geometric Classification of World Urban Road Networks" Urban Science 6, no. 1: 11. https://doi.org/10.3390/urbansci6010011
APA StyleBadhrudeen, M., Derrible, S., Verma, T., Kermanshah, A., & Furno, A. (2022). A Geometric Classification of World Urban Road Networks. Urban Science, 6(1), 11. https://doi.org/10.3390/urbansci6010011







