Insights from Self-Organizing Maps for Predicting Accessibility Demand for Healthcare Infrastructure
Abstract
1. Introduction
2. Methods
2.1. Study Area
2.2. Data Sources
2.3. Data Preparation
2.4. Principal Component Analysis and Hierarchical Clustering
2.5. Self-Organizing Maps
2.6. Accessibility Analysis
3. Results and Discussion
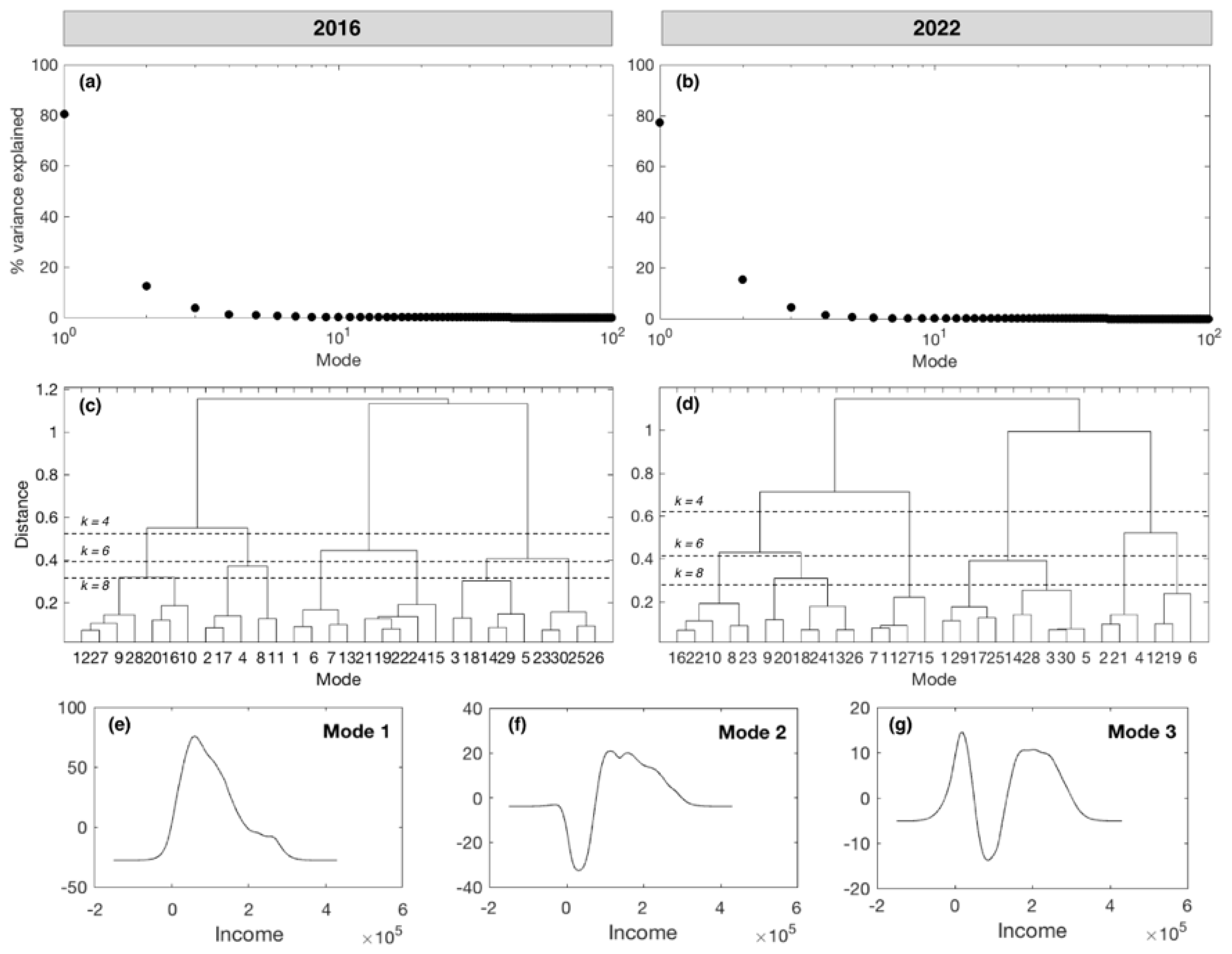
3.1. Insights from Principal Component Analysis
3.2. Self-Organising Maps
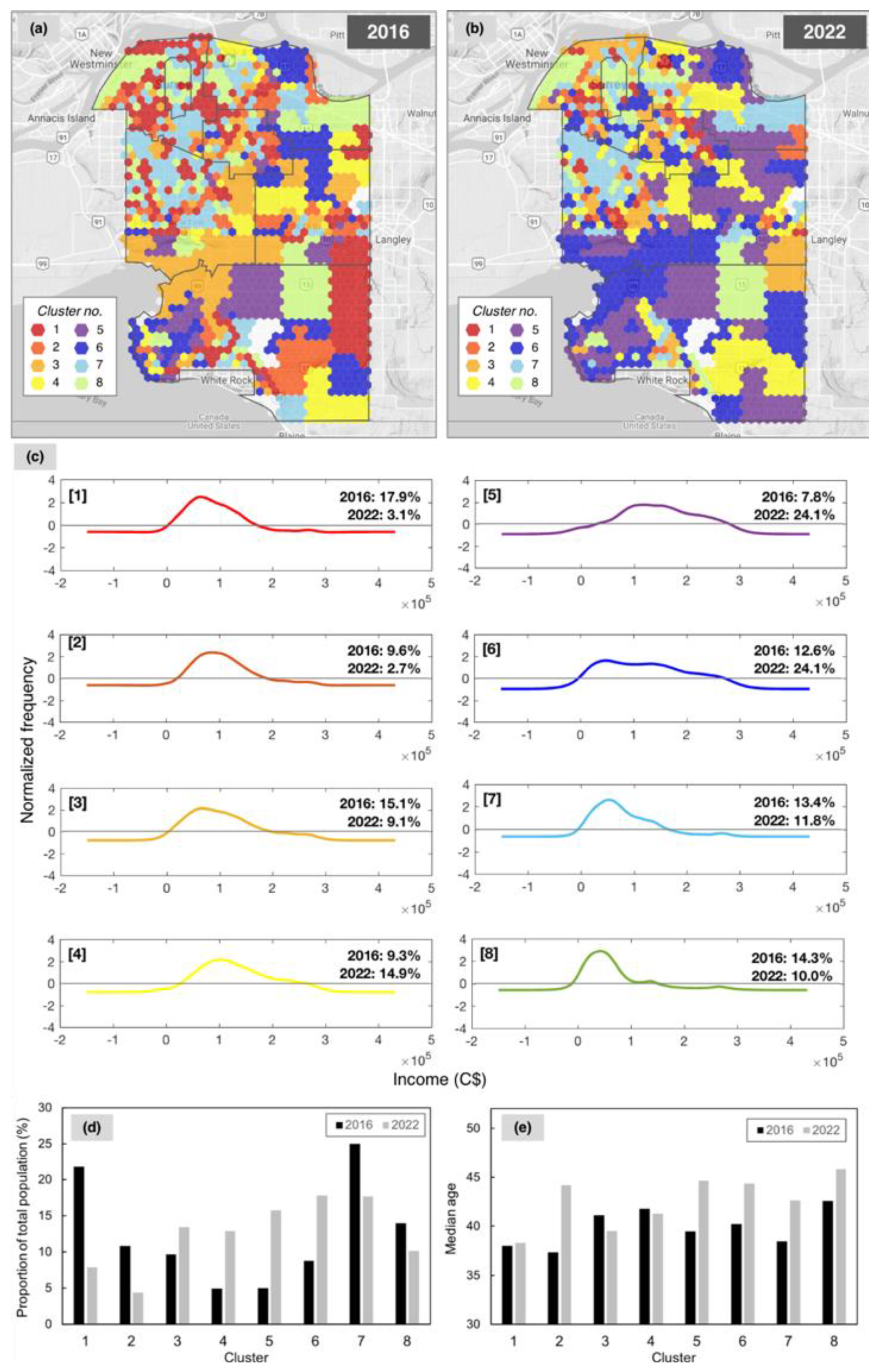
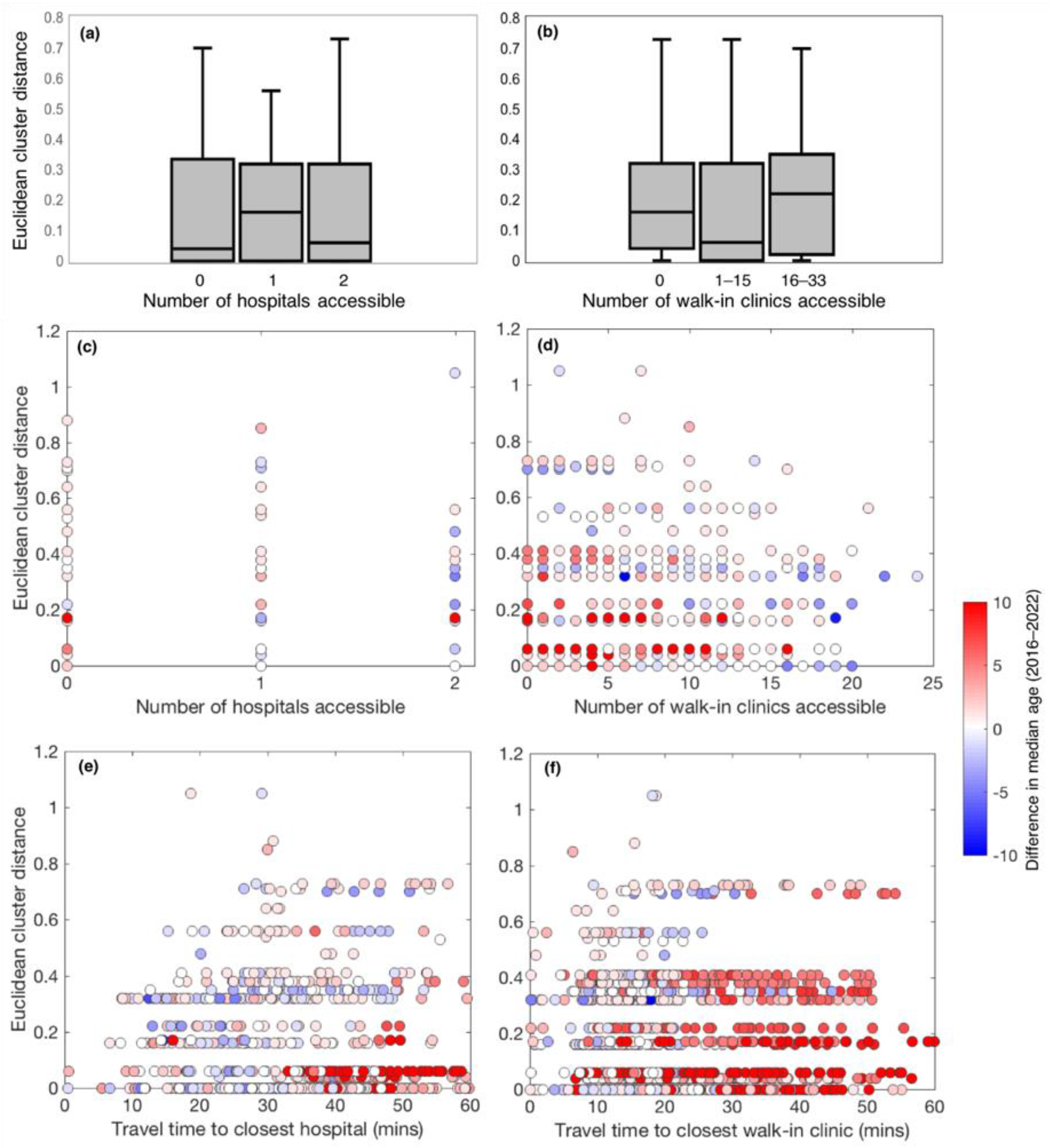
3.2.1. Relating SOM Topology to Accessibility and Travel-Time
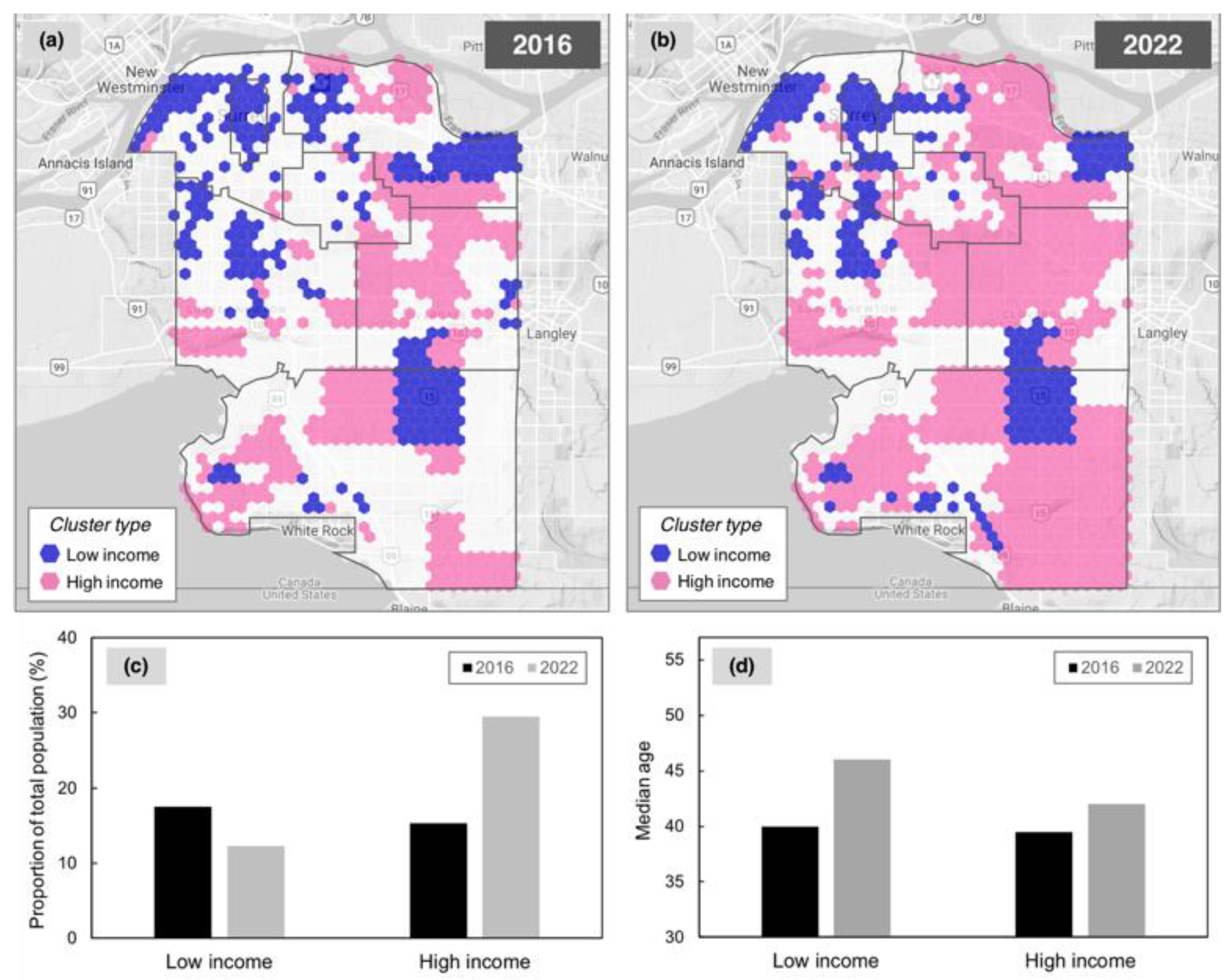
3.2.2. Attribution of Differences over Time
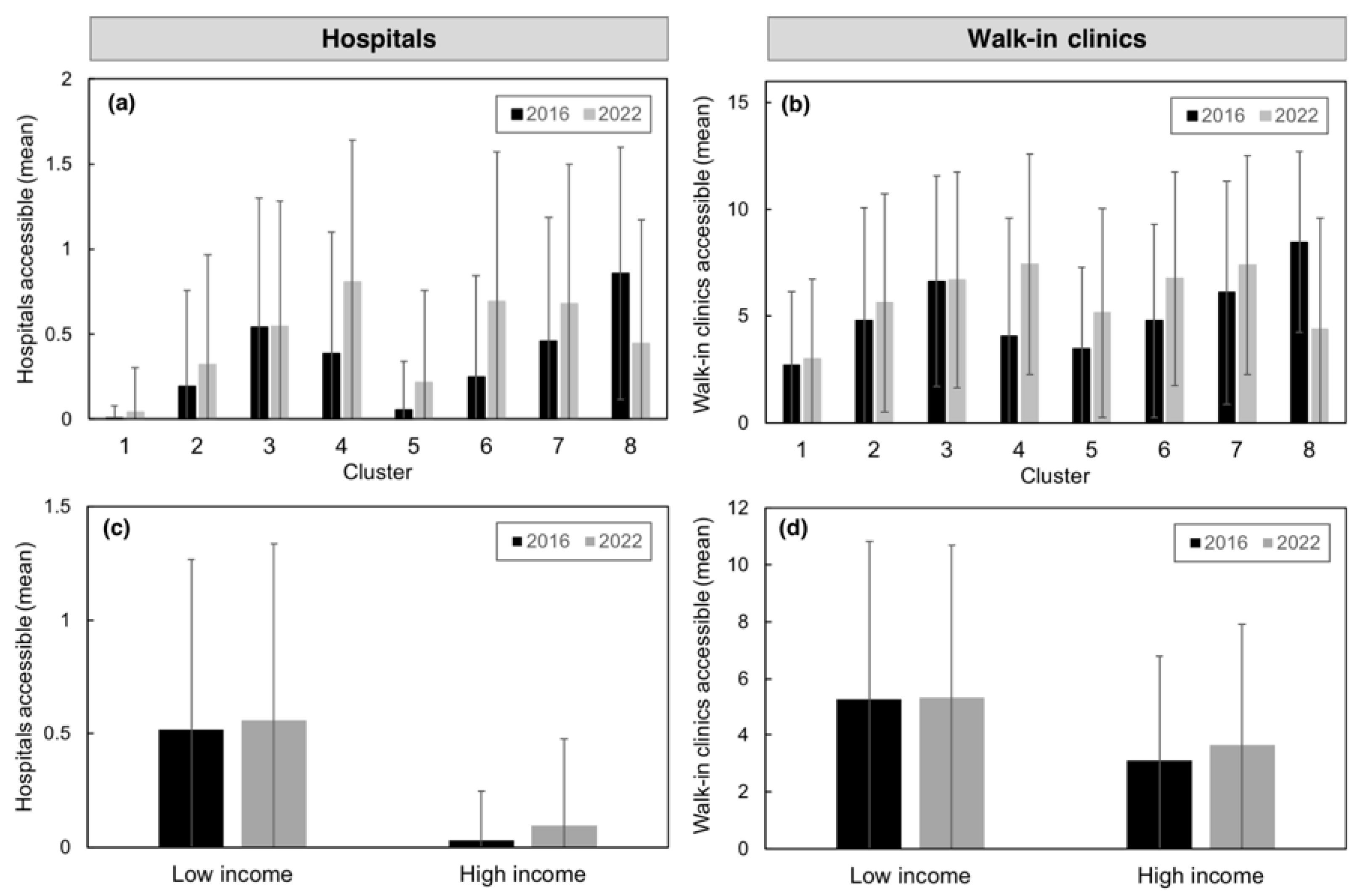
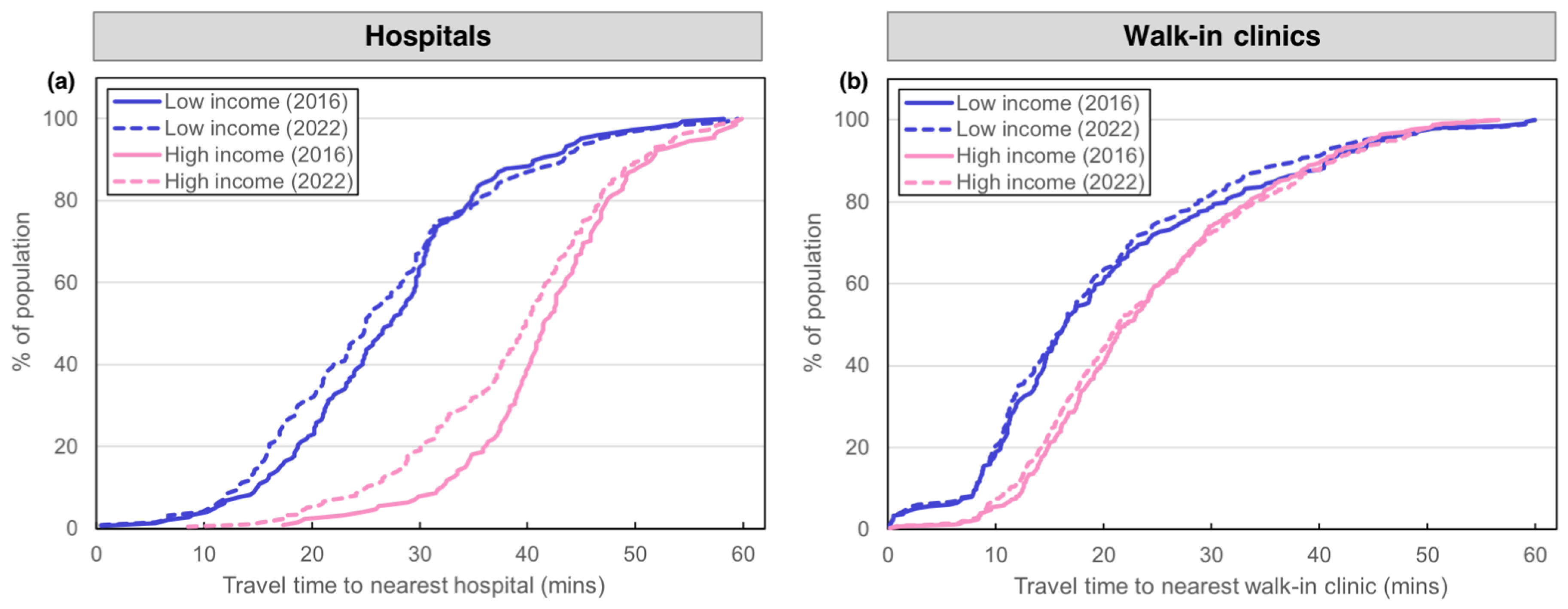
3.2.3. Accessibility to Nearest Facility
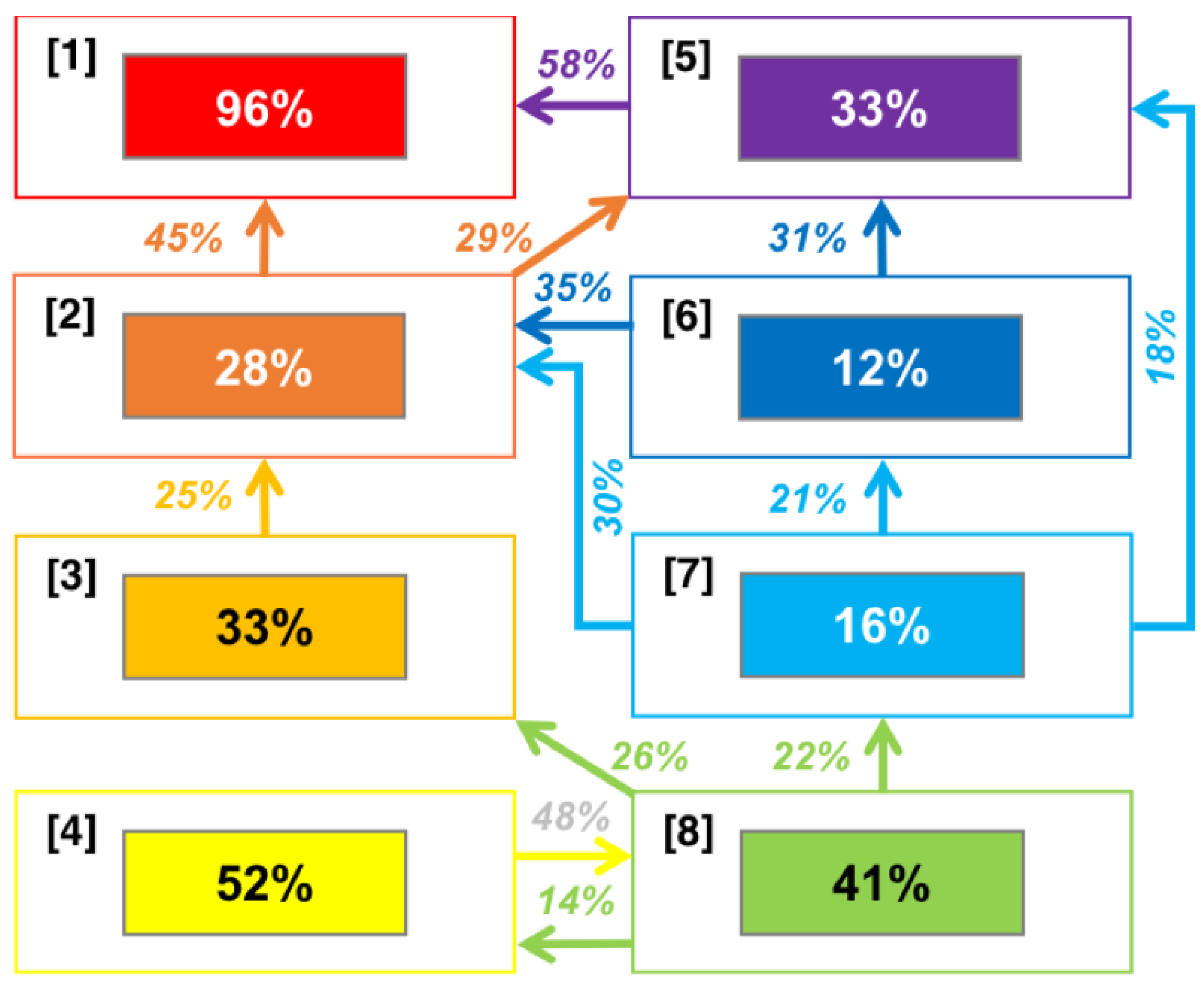
3.2.4. Cluster Change
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McKinsey Global Institute. Smart Cities: Digital Solutions for a More Livable Future. 2018. Available online: https://www.mckinsey.com/~/media/mckinsey/industries/capital%20projects%20and%20infrastructure/our%20insights/smart%20cities%20digital%20solutions%20for%20a%20more%20livable%20future/mgi-smart-cities-full-report.ashx (accessed on 1 July 2018).
- Smart Cities Council. Smart Cities Readiness Guide; Smart Cities Council: Reston, VA, USA, 2015. [Google Scholar]
- Thrift, N. The promise of urban informatics: Some speculations. Environ. Plan. A 2014, 46, 1263–1266. [Google Scholar] [CrossRef]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 461, 912–913. [Google Scholar] [CrossRef] [PubMed]
- Stiglitz, J.E.; Sen, A.; Fitoussi, J.-P. Report by the Commission on the Measurement of Economic Performance and Social Progress; Government of France: Paris, France, 2009. [Google Scholar]
- United Nations Commission on Science and Technology for Development. Smart Cities and Infrastructure; United Nations Commission on Science and Technology for Development: Budapest, Hungary, 2015. [Google Scholar]
- United Nations. 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2017. [Google Scholar]
- European Commission. The European Union 2020 Strategy; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Batty, M.; Axhausen, K.W.; Giannotti, F.; Pozdnoukhov, A.; Bazzani, A.; Wachowicz, M.; Ouzounis, G.; Portugali, Y. Smart cities of the future. Eur. Phys. J. Spec. Top. 2012, 214, 481–518. [Google Scholar] [CrossRef]
- Batty, M. Big data, smart cities and city planning. Dialogues Hum. Geogr. 2013, 3, 274–279. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 24, 7301–7306. [Google Scholar] [CrossRef] [PubMed]
- World Bank. Tracking SDG7: The Energy Progress Report; World Bank: Washington, DC, USA, 2018. [Google Scholar]
- Cohen, B.; Kietzmann, J. Ride on: Business models for the sharing economy. Organ. Environ. 2014, 27, 279–296. [Google Scholar] [CrossRef]
- Perera, C.; Liu, C.H.; Jayawardena, S. The emerging internet of things marketplace from an industrial perspective: A survey. IEEE Trans. Emerg. Top. Comput. 2015, 3, 585–589. [Google Scholar] [CrossRef]
- Neutens, T. Accessibility, equity and health care: Review and research directions for transport geographers. J. Transp. Geogr. 2015, 43, 14–27. [Google Scholar] [CrossRef]
- Apparicio, P.; Abdelmajid, M.; Riva, M.; Shearmur, R. Comparing alternative approaches to measuring the geographical accessibility of urban health services: Distance types and aggregation-error issues. Int. J. Health Geogr. 2008, 7, 7. [Google Scholar] [CrossRef]
- Bissonnette, L.; Wilson, K.; Bell, S.; Shah, T.I. Neighbourhoods and potential access to health care: The role of spatial and aspatial factors. Health Place 2012, 18, 841–853. [Google Scholar] [CrossRef]
- Hiscock, R.; Pearce, J.; Blakely, T.; Witten, K. Is neighborhood access to health care provision associated with individual-level utilization and satisfaction? Health Serv. Res. 2008, 43, 2183–2200. [Google Scholar] [CrossRef] [PubMed]
- Hickford, A.J.; Nicholls, R.J.; Otto, A.; Hall, J.W.; Blainey, S.P.; Tran, M.; Barua, P. Creating an ensemble of future strategies for national infrastructure provision. Futures 2015, 66, 13–24. [Google Scholar] [CrossRef]
- Dai, D. Black residential segregation, disparities in spatial access to health care facilities, and late-stage breast cancer diagnosis in metropolitan Detroit. Health Place 2010, 16, 1038–1052. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, N.; Winkleby, M.; Skog, L.; Szulkin, R.; Sundquist, K. Differences in neighborhood accessibility to health-related resources: A nationwide comparison between deprived and affluent neighborhoods in Sweden. Health Place 2011, 17, 132–149. [Google Scholar] [CrossRef] [PubMed]
- Frank, L.; Mayaud, J.R.; Hong, A.; Fisher, P.; Kershaw, S. Unmet demand for walkable transit-oriented neighborhoods in a mid-sized Canadian community: Market and planning implications. J. Plan. Educ. Res. 2019. in print. [Google Scholar] [CrossRef]
- Wegener, M. The future of mobility in cities: Challenges for urban modelling. Transp. Policy 2013, 29, 275–282. [Google Scholar] [CrossRef]
- Weiss, D.J.; Nelson, A.; Gibson, H.S.; Temperley, W.; Peedell, S.; Lieber, A.; Hancher, M.; Poyart, E.; Belchior, S.; Fullman, N.; et al. A global map of travel time to cities to assess inequalities in accessibility in 2015. Nature 2018, 553, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Pereira, R.H.M. Transport legacy of mega-events and the redistribution of accessibility to urban destinations. Cities 2018. [Google Scholar] [CrossRef]
- Mayaud, J.R.; Tran, M.; Pereira, R.H.M.; Nuttall, R. Future access to essential services in a growing smart city: The case of Surrey, British Columbia. Comput. Environ. Urban Syst. 2018. [Google Scholar] [CrossRef]
- Fusco, G.; Colombaroni, C.; Isaenko, N. Short-term speed predictions exploiting big data on large urban road networks. Transp. Res. Part C Emerg. Technol. 2016, 73, 183–201. [Google Scholar] [CrossRef]
- Lopez-Behar, D.; Tran, M.; Mayaud, J.R.; Froese, T.; Herrera, O.E.; Merida, W. Putting electric vehicles on the map: A policy agenda for residential charging infrastructure in Canada. Energy Res. Soc. Sci. 2019, 50, 29–37. [Google Scholar] [CrossRef]
- Schwanen, T. Geographies of transport II: Reconciling the general and the particular. Prog. Hum. Geogr. 2017, 41, 355–364. [Google Scholar] [CrossRef]
- Toch, E.; Lerner, B.; Ben-Zion, E. Knowledge & Information Systems. 2018, pp. 1–23. Available online: https://www.springer.com/computer/information+systems+and+applications/journal/10115 (accessed on 15 June 2018).
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer: Berlin, Germany, 2001. [Google Scholar]
- Johnsson, M. Applications of Self-Organizing Maps. InTech Open, 2012. Available online: https://www.intechopen.com/books/applications-of-self-organizing-maps (accessed on 2 July 2018).
- Unglert, K.; Radić, V.; Jellinek, A.M. Principal component analysis vs. self-organizing maps combined with hierarchical clustering for pattern recognition in volcano seismic spectra. J. Volcanol. Geotherm. Res. 2016, 320, 58–74. [Google Scholar] [CrossRef]
- Ashpole, I.; Washington, R. Intraseasonal variability and atmospheric controls on daily dust occurrence frequency over the central and western Sahara during the boreal summer. J. Geophys. Res. Atmos. 2013, 118, 12915–12926. [Google Scholar] [CrossRef]
- Sohn, K. Feature mapping the Seoul metro station areas based on a self-organizing map. J. Urban Technol. 2014, 20, 23–42. [Google Scholar] [CrossRef]
- Hagenauer, J.; Helbich, M. A comparative study of machine learning classifiers for modeling travel mode choice. Expert Syst. Appl. 2017, 78, 273–282. [Google Scholar] [CrossRef]
- Mahrsi, M.K.; Côme, E.; Oukhellou, L.; Verleysen, M. Clustering smart card data for urban mobility analysis. IEEE Trans. Intell. Transp. Syst. 2017, 18, 712–728. [Google Scholar] [CrossRef]
- Skupin, A.; Hagelman, R. Visualizing demographic trajectories with self-organizing maps. GeoInformatica 2005, 9, 159–179. [Google Scholar] [CrossRef]
- Yan, J.; Thill, J. Visual data mining in spatial interaction analysis with self-organizing maps. Environ. Plan. B Plan. Des. 2009, 36, 466–486. [Google Scholar] [CrossRef]
- Arribas-Bel, D.; Kourtit, K.; Nijkamp, P. Benchmarking of world cities through Self-Organizing Maps. Cities 2013, 31, 248–257. [Google Scholar] [CrossRef]
- Arribas-Bel, D.; Nijkamp, P.; Scholten, H. Multidimensional urban sprawl in Europe: A self-organizing map approach. Comput. Environ. Urban Syst. 2011, 35, 263–275. [Google Scholar] [CrossRef]
- Lucas, K. Transport and social exclusion: Where are we now? Transp. Policy 2012, 20, 105–113. [Google Scholar] [CrossRef]
- Darcy, S. The politics of disability and access: The Sydney 2000 Games experience. Disabil. Soc. 2003, 18, 737–757. [Google Scholar] [CrossRef]
- City of Surrey. Sustainability Charter 2.0. 2016. Available online: http://www.surrey.ca/community/3568.aspx (accessed on 23 January 2018).
- Statistics Canada. 2017. Available online: http://www12.statcan.gc.ca/ (accessed on 23 January 2018).
- SimplyAnalytics. Census 2016 Current Estimates Data; Census 2022 Projected Estimates. DemoStats Database, 2017. Available online: http://simplyanalytics.com/ (accessed on 30 January 2018).
- SimplyAnalytics. Data Providers, Definitions and Methodology Information. 2017. Available online: https://simplyanalytics.zendesk.com/hc/en-us/articles/115003011663-Data-Providers-Definitions-and-Methodology-Information (accessed on 23 January 2018).
- Barrington-Leigh, C.; Millard-Ball, A. The world’s user-generated road map is more than 80% complete. PLoS ONE 2017, 12, e0180698. [Google Scholar] [CrossRef] [PubMed]
- Siqueira-Gay, J.; Giannotti, M.; Sester, M. Learning spatial inequalities: A clustering approach. In Proceedings of the XVIII Brazilian Symposium on Geoinformatics, Salvador, Brazil, 4–6 December 2017. [Google Scholar]
- Cirillio, P. Are your data really Pareto distributed? Physica A 2013, 392, 5947–5962. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis. In Monographs on Statistics and Applied Probability; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Hsieh, W.W. Machine Learning Methods in the Environmental Sciences: Neural Networks and Kernels; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. The comparison of dendrograms by objective methods. Taxon 1962, 11, 33–40. [Google Scholar] [CrossRef]
- Fazlollahia, S.; Girardinb, L.; Maréchalb, F. Clustering urban areas for optimizing the design and the operation of district energy systems. In Proceedings of the 24th European Symposium on Computer Aided Process Engineering, Budapest, Hungary, 15–18 June 2014. [Google Scholar]
- Hooper, P.; Knuiman, M.; Bull, F.; Jones, E.; Giles-Corti, B. Are we developing walkable suburbs through urban planning policy? Identifying the mix of design requirements to optimise walking outcomes from the ‘Liveable Neighbourhoods’ planning policy in Perth, Western Australia. Int. J. Behav. Nutr. Phys. Act. 2015, 12, 63. [Google Scholar] [CrossRef]
- Liu, L.; Peng, Z.; Wu, H.; Jiao, H.; Yu, Y.; Zhao, J. Fast identification of urban sprawl based on k-means clustering with population density and local spatial entropy. Sustainability 2018, 10, 2683. [Google Scholar] [CrossRef]
- Radić, V.; Cannon, A.J.; Menounos, B.; Gi, N. Future changes in autumn atmospheric river events in British Columbia, Canada, as projected by CMIP5 global climate models. J. Geophys. Res. Atmos. 2015, 120, 9279–9302. [Google Scholar] [CrossRef]
- Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J. Self-organizing map in Matlab: The SOM Toolbox. In Proceedings of the MATLAB DSP Conference, Espoo, Finland, 1 February 1999; pp. 16–17. [Google Scholar]
- Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J. SOM Toolbox for Matlab 5: Technical Report; Report A57; Helsinki University of Technology: Espoo, Finland, 2000. [Google Scholar]
- Open Trip Planner. 2017. Available online: https://github.com/opentripplanner/OpenTripPlanner (accessed on 3 November 2017).
- Wachs, M.; Kumagai, T. Physical accessibility as a social indicator. Socioecon. Plan. Sci. 1973, 7, 327–456. [Google Scholar] [CrossRef]
- Boisjoly, G.; El-Geneidy, A.M. How to get there? A critical assessment of accessibility objectives and indicators in metropolitan transportation plans. Transp. Policy 2017, 55, 38–50. [Google Scholar] [CrossRef]
- Schuenemann, K.C.; Cassano, J.J. Changes in synoptic weather patterns and Greenland precipitation in the 20th and 21st centuries: 1. Evaluation of late 20th century simulations from IPCC models. J. Geophys. Res. 2009, 114, DS20113. [Google Scholar] [CrossRef]
- Cosco, T.; Brayne, C.; Howse, K. Healthy ageing, resilience, and wellbeing. Epidemiol. Psychiatr. Sci. 2017, 26, 579. [Google Scholar] [CrossRef] [PubMed]
- Loo, B.P.Y.; Wing, W.; Lam, Y. Geographic accessibility around health care facilities for elderly residents in Hong Kong: A microscale walkability assessment. Environ. Plan. B Plan. Des. 2012, 39, 629–646. [Google Scholar]
- Lutz, W.; Sanderson, W.; Scherbov, S. The coming acceleration of global population ageing. Nature 2008, 451, 716–719. [Google Scholar] [CrossRef]
- Cosco, T.D.; Cooper, R.; Kuh, D.; Stafford, M. Socioeconomic inequalities in resilience and vulnerability among older adults: A population-based birth cohort analysis. Int. Psychogeriatr. 2018, 30, 695–703. [Google Scholar] [CrossRef]
- Hager, K.; Rauh, J.; Rid, W. Agent-based modeling of traffic behavior in growing metropolitan areas. Transp. Res. Procedia 2015, 10, 306–315. [Google Scholar] [CrossRef]
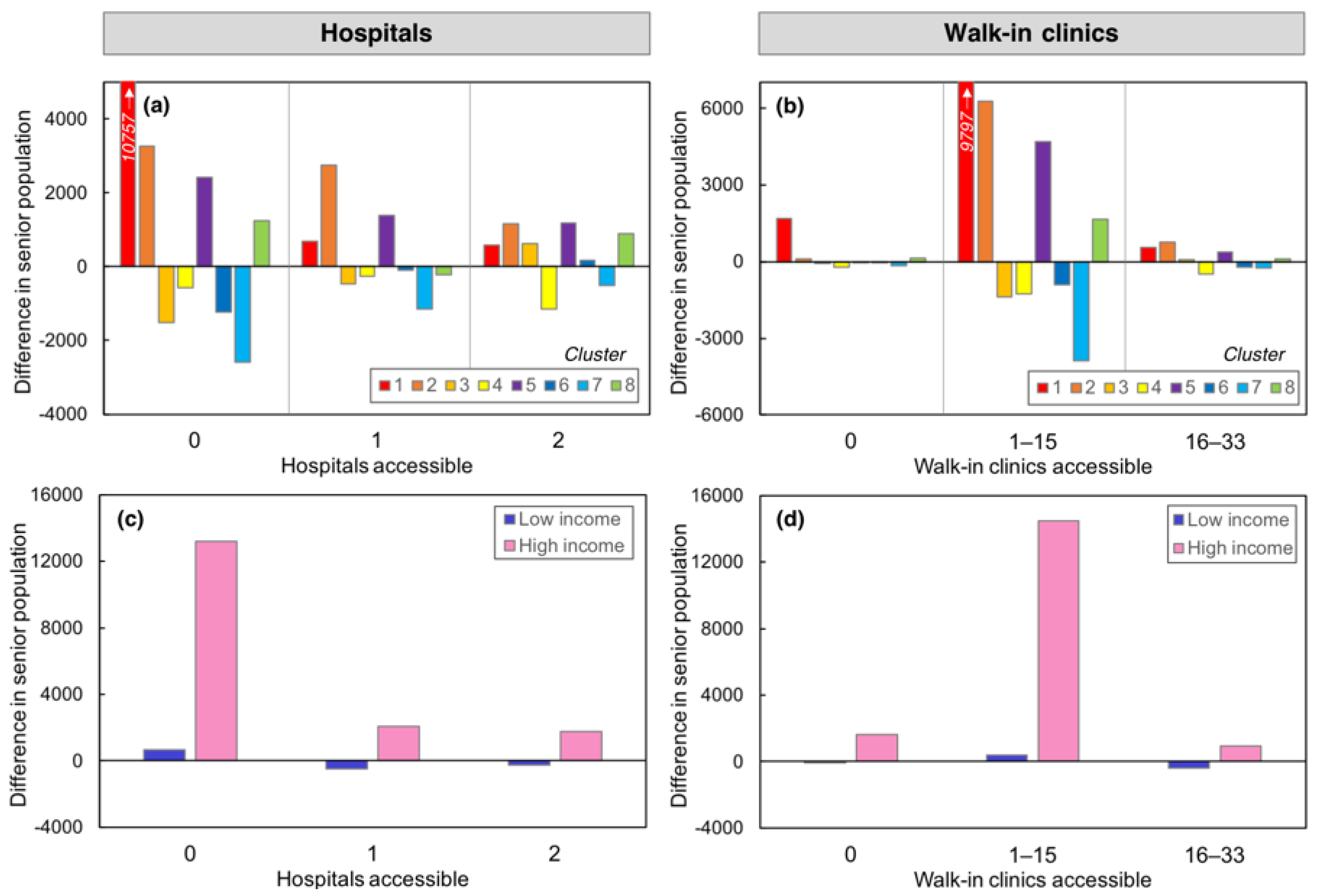
| Scenario | Net Difference | Intra-Pattern Variability Component | Pattern Frequency Component | Combined Term | ||
|---|---|---|---|---|---|---|
| Hospitals | Access = 0 | Seniors | 11,775 | 5317 | 6031 | 426 |
| Total pop. | 27,575 | −16,454 | 47,389 | −3359 | ||
| Access > 0 | Seniors | 5595 | 11,710 | −5650 | −464 | |
| Total pop. | 16,495 | 56,801 | −44,311 | 4005 | ||
| Walk-in clinics | Access = 0 | Seniors | 1429 | −110 | 1392 | 148 |
| Total pop. | 2620 | −6091 | 10,277 | −1565 | ||
| Access > 0 | Seniors | 15,941 | 17,137 | −1011 | −186 | |
| Total pop. | 41,450 | 46,438 | −7199 | 2211 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayaud, J.R.; Anderson, S.; Tran, M.; Radić, V. Insights from Self-Organizing Maps for Predicting Accessibility Demand for Healthcare Infrastructure. Urban Sci. 2019, 3, 33. https://doi.org/10.3390/urbansci3010033
Mayaud JR, Anderson S, Tran M, Radić V. Insights from Self-Organizing Maps for Predicting Accessibility Demand for Healthcare Infrastructure. Urban Science. 2019; 3(1):33. https://doi.org/10.3390/urbansci3010033
Chicago/Turabian StyleMayaud, Jerome R., Sam Anderson, Martino Tran, and Valentina Radić. 2019. "Insights from Self-Organizing Maps for Predicting Accessibility Demand for Healthcare Infrastructure" Urban Science 3, no. 1: 33. https://doi.org/10.3390/urbansci3010033
APA StyleMayaud, J. R., Anderson, S., Tran, M., & Radić, V. (2019). Insights from Self-Organizing Maps for Predicting Accessibility Demand for Healthcare Infrastructure. Urban Science, 3(1), 33. https://doi.org/10.3390/urbansci3010033





