1. Introduction
The concepts of
distribution function (
) and
probability density (
) of a
stochastic (or
random)
variable (
with realizations
; notice the notational convention to underline stochastic variables—the Dutch convention) are central in Kolmogorov’s foundation of probability in 1933 [
1,
2] and its applications. (Here, we adhere to the original Kolmogorov’s terms, noting that in the English literature
is also known as the cumulative distribution function.) Their estimation, based on a sample of
, is crucial in most applications.
The standard estimate of
was again introduced by Kolmogorov [
3], who termed it the
empirical distribution, and is still in common use [
4], sometimes under the name
sample distribution function. Denoting
the
ith
order statistic in a sample of size
, i.e., the
ith smallest of the
variables arranged in increasing order (
), the standard estimate is:
where
is the number of the values in the observed sample that do not exceed
(an integer). The function
has a staircase form with discontinuities at each of the observations
(see
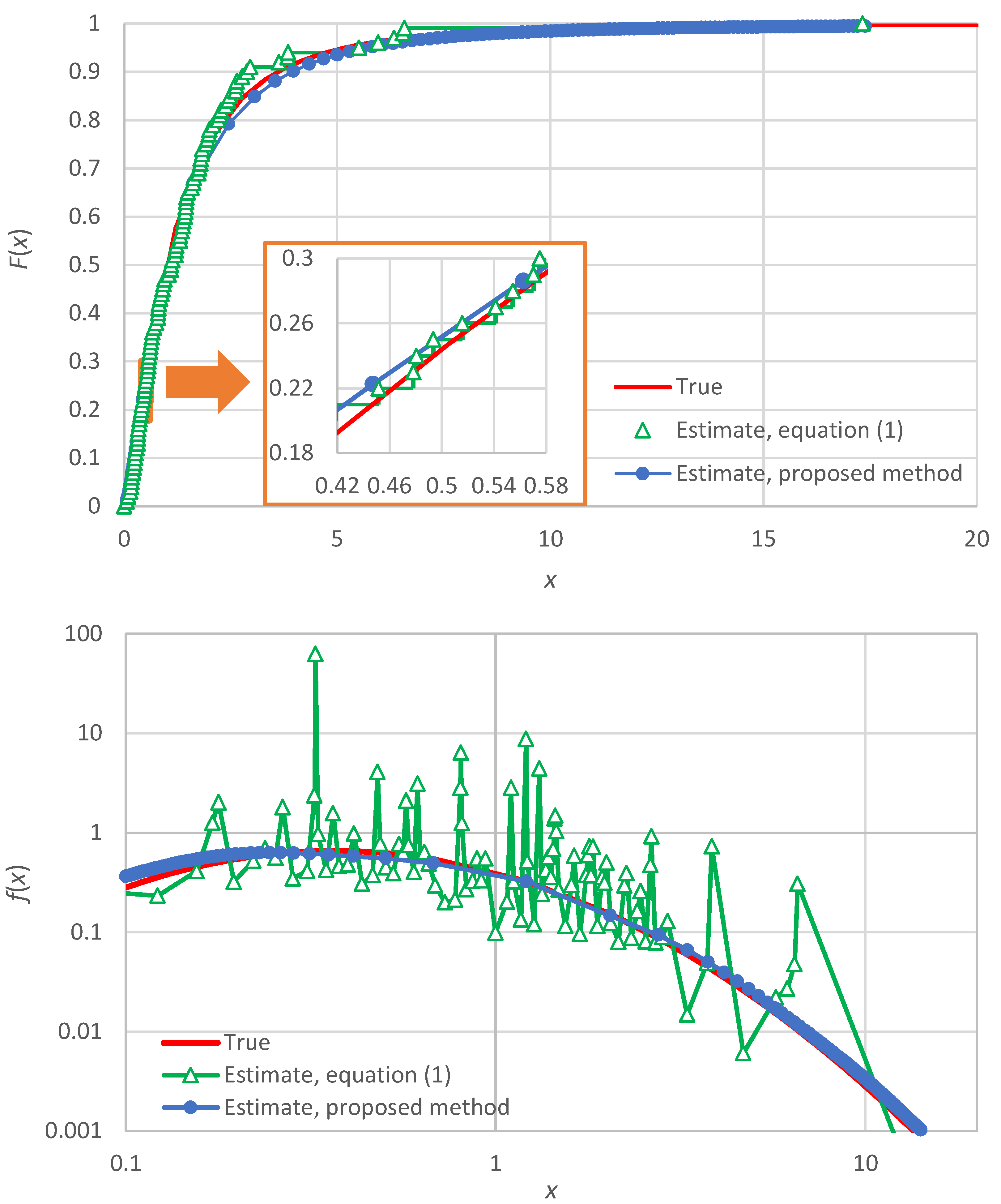
Appendix A for an illustration and more details). If
is a continuous variable, almost certainly the values
are distinct and the jump of
at
equals
. Apparently then, the representation of the continuous
by the discontinuous
is not ideal. This representation has two additional problems, i.e., (a) for
the resulting
is 0, and (b) for
the resulting
is 1. Both these are problematic results if the variable
is unbounded.
Both the latter problems are usually tackled with the notion of so-called
plotting positions (e.g., [
5])—a rather unsatisfactory name. There is a variety of plotting position formulae, each of which is a modification of Equation (1) by adding one or two constants in the numerator and/or the denominator. A review of these formulae and their justification is provided by Koutsoyiannis (2022) [
6], along with a set of new proposed ones, derived using the theoretical properties of order statistics.
One could also think to tackle the discontinuity problem by replacing the staircase function by some type of interpolation (e.g., linear or logarithmic). However, the thus resulting function would again be too rough for practical applications. In particular, a rough function, where the roughness is a statistical sampling effect rather than an intrinsic property of the distribution function, cannot support reliable estimation of derivatives. Since the density
is the first derivative of the distribution
, the above framework cannot be used to estimate the former. An illustration of the roughness of
and
, if the former is estimated from Equation (1) and the latter by the numerical derivative of the former, is provided in
Appendix A (in particular, in
Figure A1).
Methods for a detailed estimation of the probability density at different points
are lacking. Instead, a gross estimation based on the histogram constitutes the standard representation of the density. Yet, the estimation of the density is necessary for several tasks, e.g., those involving hazard (where the hazard function is defined as
; see [
7]) or entropy (where entropy is the expectation of
properly standardized; see
Section 3.3).
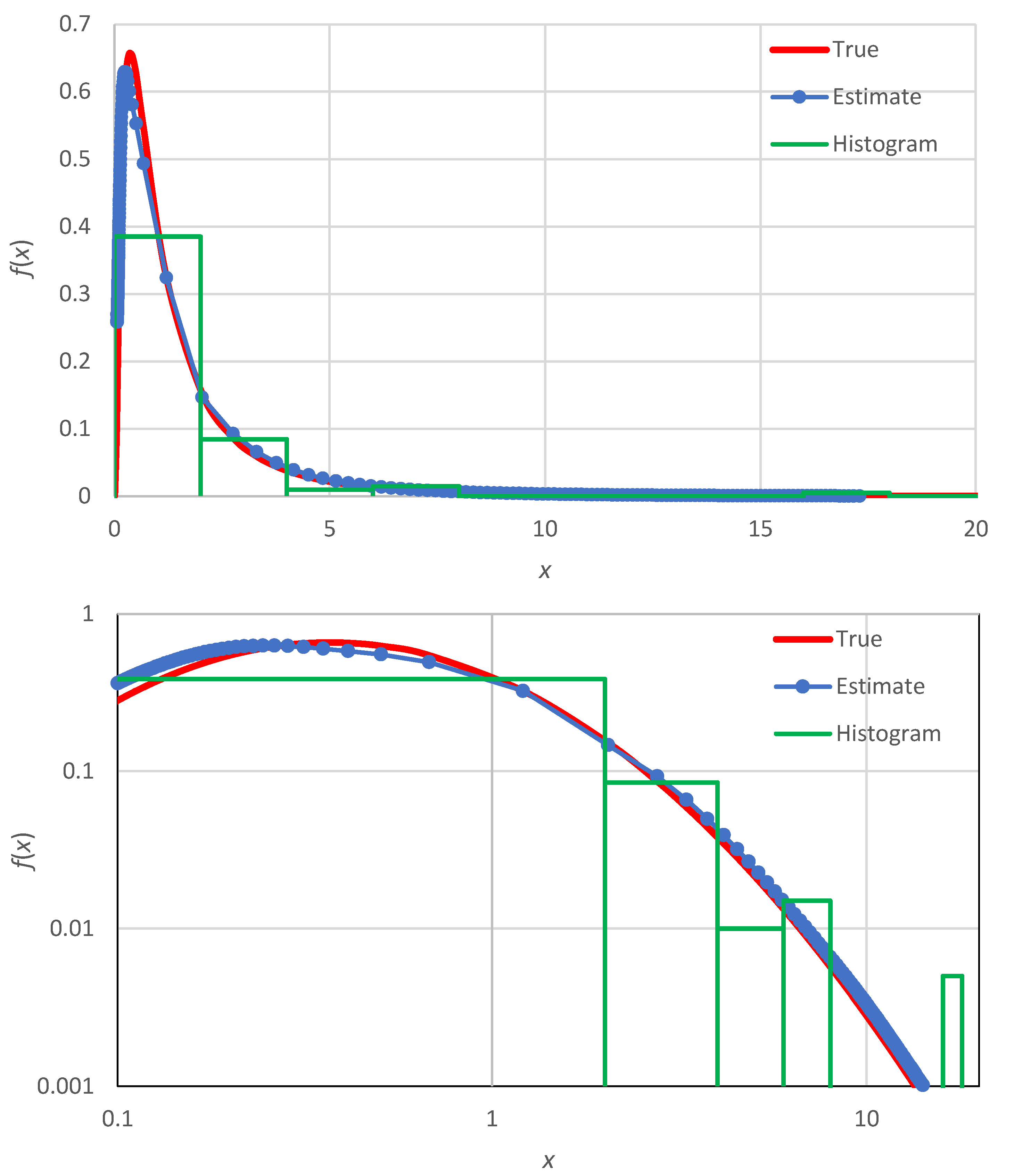
The histogram representation is constructed by choosing (a) an interval
that contains all observations (often called the range) and (b) a number
of equally spaced bins, so that the width of the bins is
The number
is usually small, typically chosen by the old Sturges’ rule [
8]:
For example, for a sample size
, this results in
. The underlying rationale for the rule and comparisons with additional rules are provided by Scott [
9]. Once
are chosen, the density estimate is
The entire framework for the construction of histogram entails subjectivity, and lacks detail and accuracy.
As an alternative to constructing a smooth empirical density function, Rosenblatt [
10] and Parzen [
7] proposed the use of kernel smoothing. They have been followed by several researchers who developed the method further [
11,
12,
13,
14]. This is regarded as a non-parametric method, but it uses a specified kernel function which contains parameters, where both the function expression and its parameters are arbitrarily chosen by the user. Typical kernel functions include uniform, triangular, quadratic (Epanechnikov), biweight, triweight, normal, and even atomic kernels [
15,
16]. While the methods of this type may provide a smooth function, their reliability is questionable, and the results are affected by a great deal of subjectivity owing to user choices. These characteristics are illustrated in
Appendix A (in particular, in
Figure A2).
Here, we propose a new method of estimation of the probability density based on the concept of
knowable moments, abbreviated as
K-moments. As shown in [
6] (pp. 147–249) and summarized in the next section, the noncentral K-moment of order
,
, can: (a) yield a reliable and unbiased estimate
from a sample, up to order
equal to the sample size
, and (b) be assigned a value of return period, or equivalently distribution function estimate,
. In addition, the sequence of estimates
form a smooth function which can be used in estimating the probability density at a large number of points (as opposed to the roughness implied by Equation (1)—or other versions thereof based on plotting positions and eventually on order statistics—and as illustrated in
Figure A1 of
Appendix A). The estimate
is based on the notion of order statistics but, contrary to their standard use, where only one sample value is used at a time, the K-moment framework combines many order statistics simultaneously, thus converting a rough arrangement to smooth, without involving any subjectively chosen kernel function.
4. Discussion
The method is described above in its minimal configuration. Improvements are possible in several ways, e.g., to take into account possible dependence of the consecutive variables (i.e., when we do not have an observed sample but a time series), or to use more accurate representations of the relationship between K-moments and their corresponding values of distribution functions. These issues are studied in Koutsoyiannis [
6] (pp. 147–249)—but not for the density estimation.
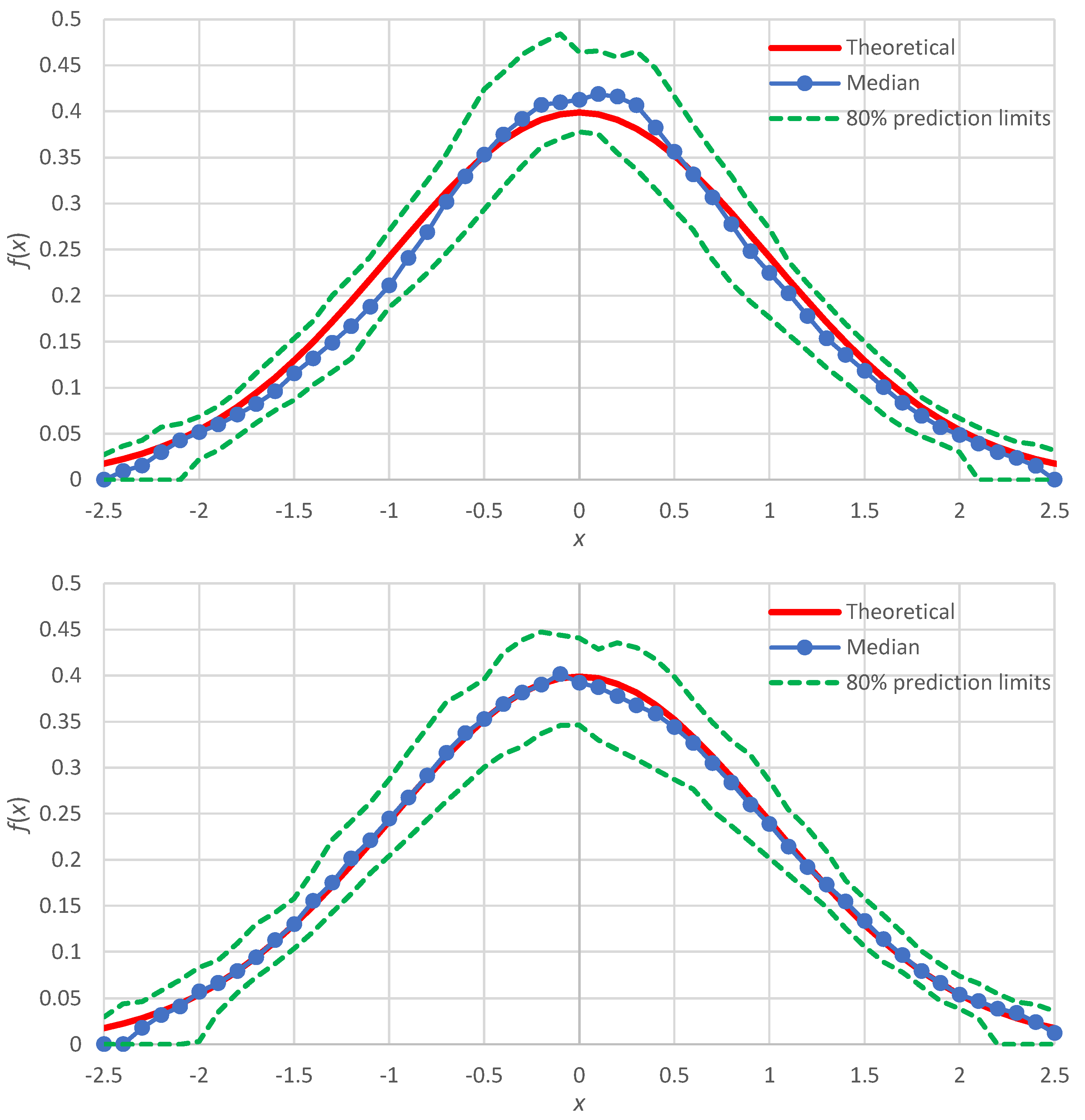
Here, we discuss the case of improvement of the distribution function estimation for the normal distribution, for which the simulation results (
Figure 3) showed slight discrepancies. As shown in [
6] (pp. 209–213), the more accurate representation of the Λ-coefficients for the normal distribution are
where for the normal distribution
. In this case, we find:
In addition, noticing that the points plotted around
are at greater distances to each other than the other points, we can use non-integer values of
between 1 and 2. Repeating the Monte Carlo simulation with these two modifications, we get the results shown in
Figure 6 (lower panel), which are in better agreement with the true density than those of the minimal version, also reproduced in
Figure 6 (upper panel).
Even if we use the minimal version, it is possible and sometimes useful to calculate
for non-integer order
. In this case, we can even find (see derivation in
Appendix B) an analytical expression for the probability density estimate, which for the noncentral K-moments is
where
and
is given by Equation (18). It is reminded that
denotes the
nth harmonic number. Similar equations can be developed for the tail K-moments.
Notice in Equations (48) and (49) that the lower limit of the sum is not the non-integer p but its floor . This means that the functions and will not be fully continuous, but only left continuous. However, the discontinuities are practically negligible for .
A final note is that the proposed method, in addition to providing point estimates
, can also produce interval estimates of
by means of confidence limits determined by Monte Carlo simulation. These differ from the prediction limits of
Section 3.2, which were constructed for a known true distribution function that was used to generate several (in our case 100) realizations of samples. For the confidence limits, the true distribution is assumed unknown and the simulation is made from the estimate
, which is determined at the points
and
The generation from this distribution is easy: the values are generated as
, where
is a random number from the uniform distribution in [0, 1]. The inverse function
is determined by interpolation (and occasionally extrapolation) from the sequence of points
, with the sequence of
being
. The interpolation is better made in terms of the quantity
instead of
.
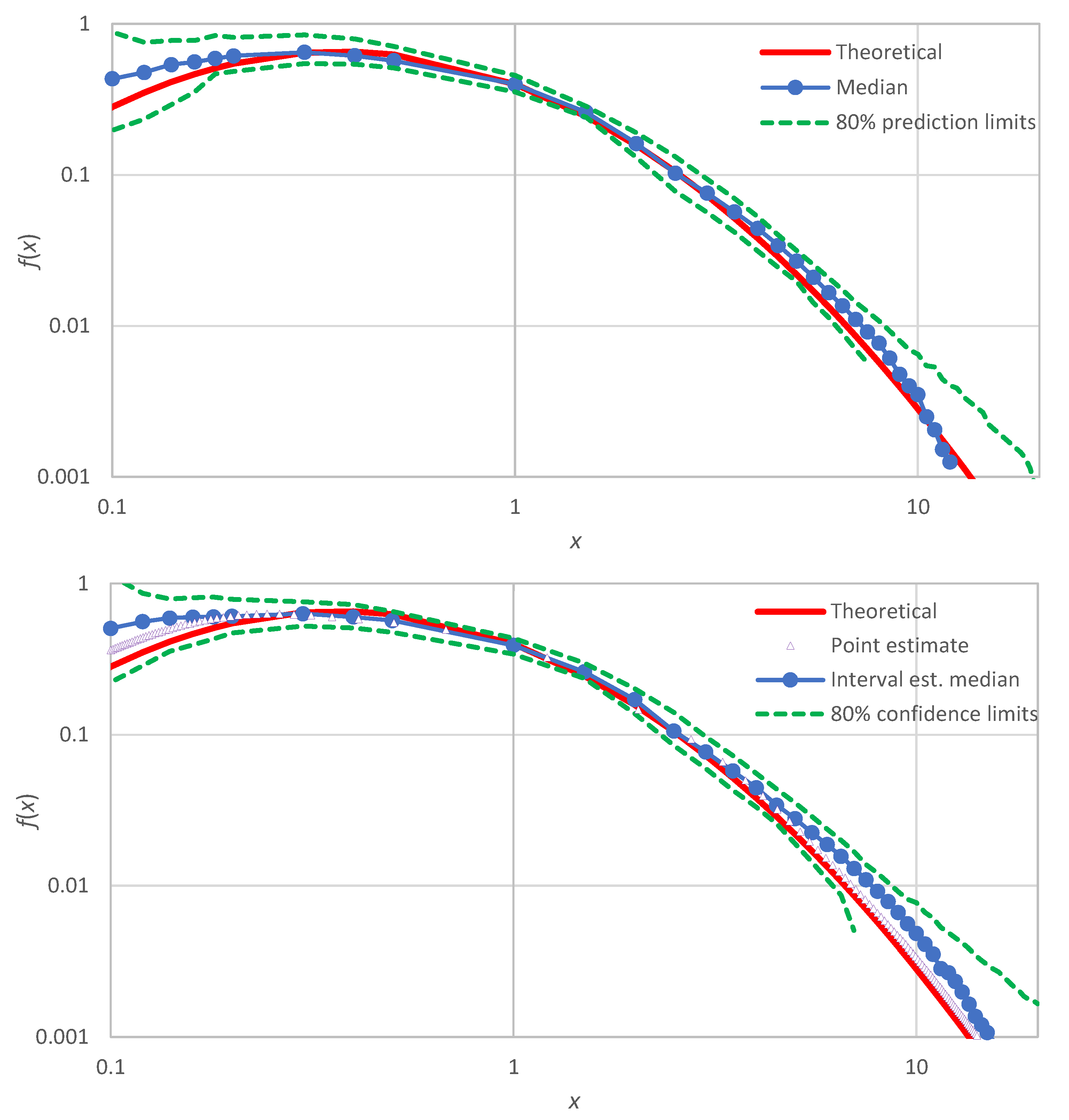
An illustration for the example of
Figure 1 (lognormal distribution) is shown in
Figure 7 (lower panel), where the produced confidence band is also compared with uncertainty band defined by the prediction limits of the lognormal distribution (upper panel of
Figure 7). We observe that: (a) the confidence band (lower panel) has about the same width as the uncertainty band (upper panel), and (b) the true distribution, which was not used in the Monte Carlo simulation of the lower panel, is contained within the produced confidence band—as it should.
5. Conclusions
For continuous stochastic variables, the proposed framework is an improved, detailed and smooth alternative to the widely used concept of the histogram, which provides only a gross representation of the probability density. The proposed framework is based on the concept of knowable moments (K-moments) and its characteristics that make possible the estimate of the probability density are:
The ability to reliably estimate from a sample, moments of high order, up to the sample size.
The ability to assign values of the distribution function to each estimated value of K-moment.
The smoothness of the estimated values, which are linear combinations of a number of observations, rather than based on a single observation as in other approaches.
The latter characteristic is crucial in estimating the probability density, which is the first derivative of the distribution function.
Prominent characteristics of the proposed method of density estimation, confirmed by several applications of the method for a variety of distribution functions, are:
The faithful representation of the true density, both in the body and the tails of the distribution.
The dense and smooth shape, owing to the ability to estimate values of the density at very many points (even for any arbitrary point) within the range of the available observations.
The low uncertainty of estimates.
The ability to provide both point and interval estimates (confidence limits), with the latter becoming possible by Monte Carlo simulation.
The simplicity of the calculations, which can be made in a typical spreadsheet environment.
Specifically, the calculations include the following steps, which summarize the numerical part of the proposed method.
We sort the observed sample in ascending order.
We calculate the estimates from Equations (17) and (18).
We estimate the coefficient from Equation (24) and calculate from Equation (30).
We assume the tail indices of the distribution and choose values of
and
from
Table 3 (see [
6] (pp. 209–213), for additional distributions).
We calculate the estimates and from Equations (28) and (32) for all derived in step 2. (By plotting the tails and in double logarithmic graphs, we check whether the empirically estimated tail indices agree with those assumed in Step 4 and, if not, we repeat steps 4 and 5 with new estimates).
We calculate the estimates of from Equation (33).
These calculations are illustrated in the
Supporting Information, which contains a spreadsheet accompanying this paper. This gives a full-scale application of the method, related to the construction of
Figure 1.
A problem of the method is that it requires one to have an idea of the type of the true distribution, in terms of its upper- and lower-tail indices, in order to estimate the asymptotic Λ-coefficients (). If the sample size is large, the K-moments can support the estimation of these tail indices (cf. points steps 4 and 5 above). However, for small samples () their estimation becomes problematic and higher uncertainty is induced. This issue requires further investigation.