Scarce Data in Intelligent Technical Systems: Causes, Characteristics, and Implications
Abstract
1. Introduction
- A closer look into the causes and implications of scarce data is provided. A typology is presented which categorises the subtypes of scarce data.
- An overview of data augmentation, transfer learning, and information fusion methods is given.
- A combination of machine learning and fusion techniques is discussed and further research efforts in this area are motivated.
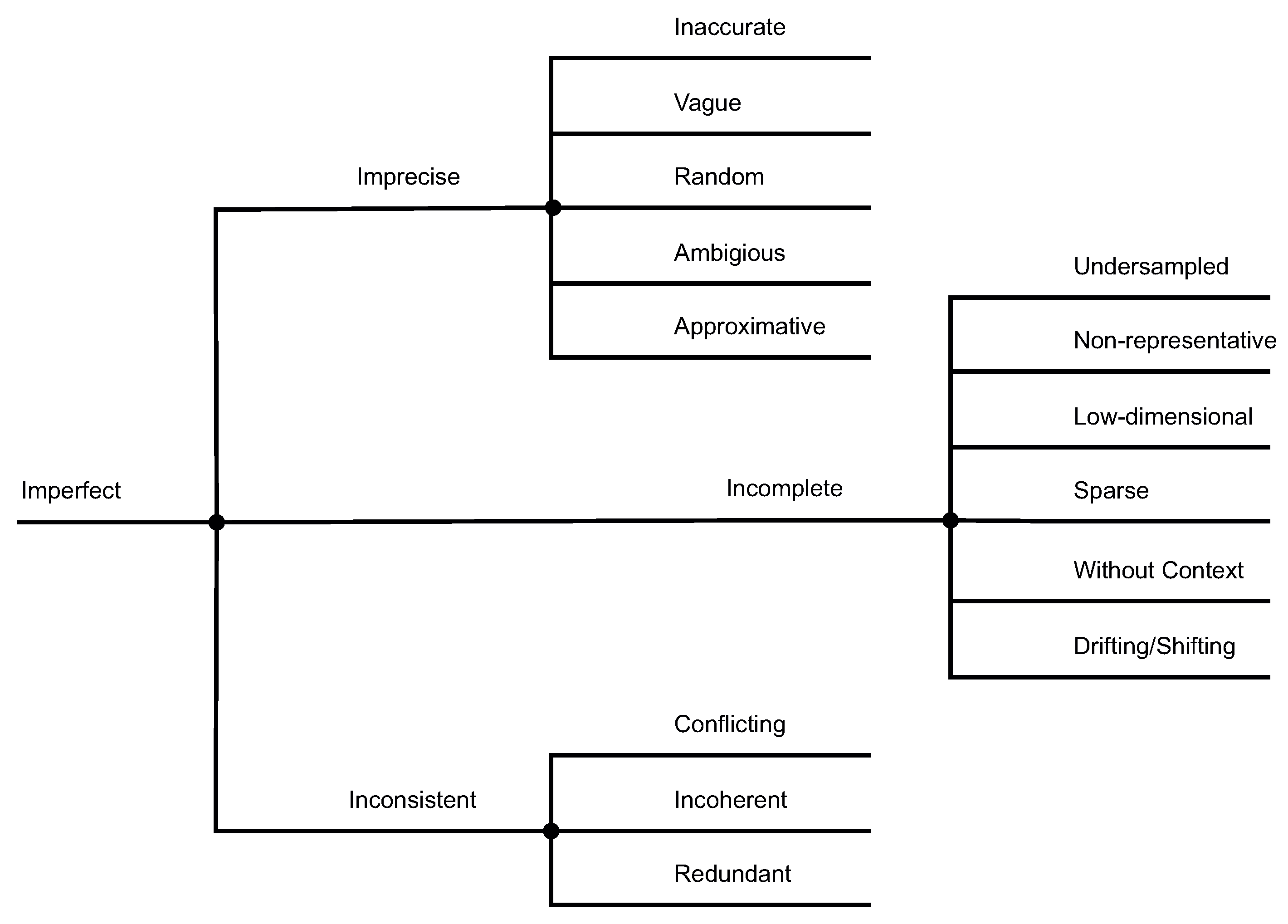
2. A Typology of Scarce Data
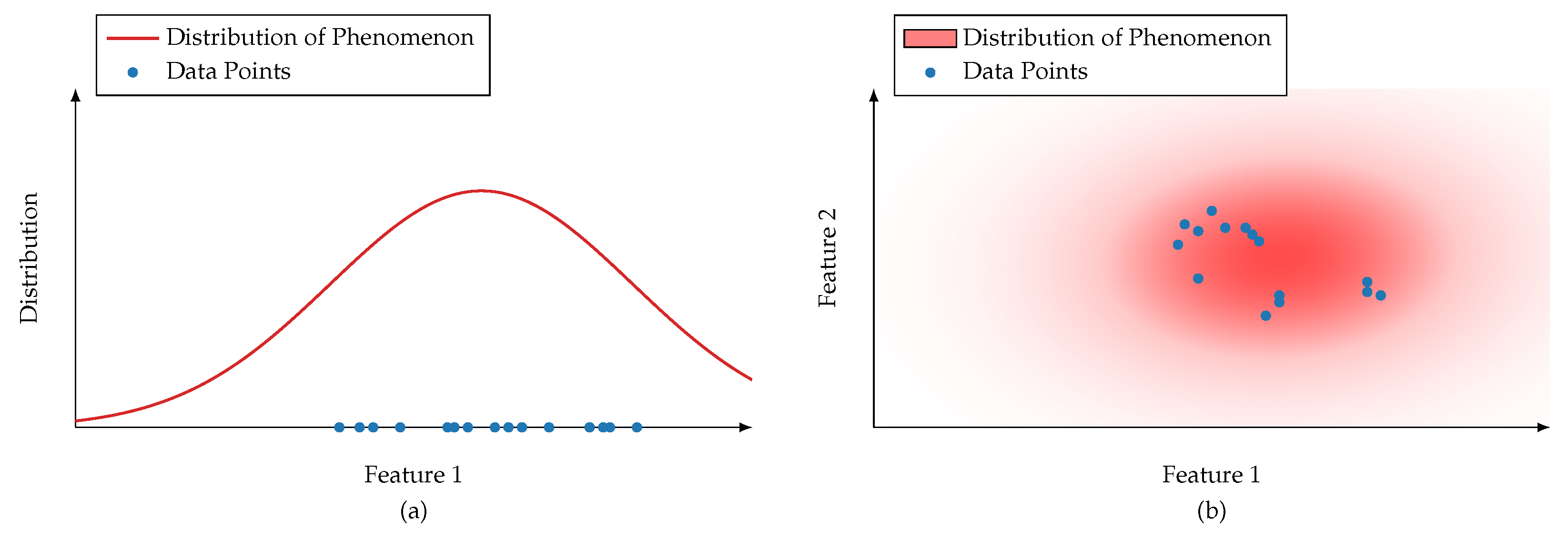
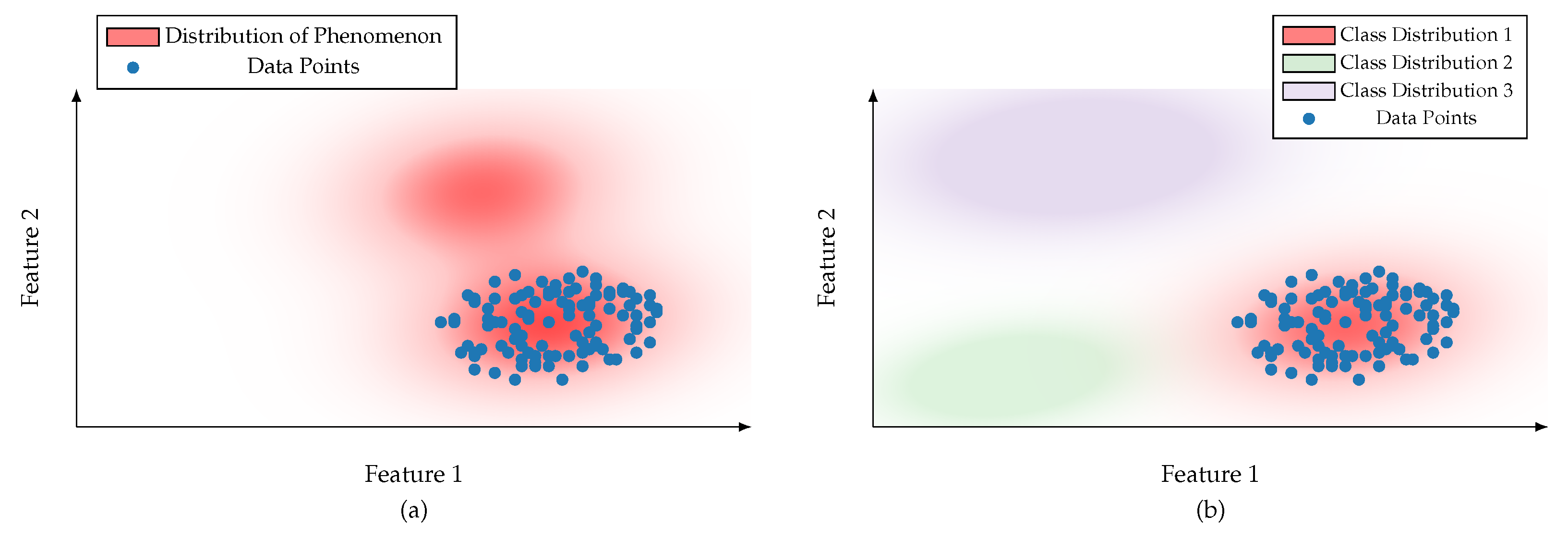
- Sensors are not available or limited in their functionality. They are technically infeasible, too costly, or not obtainable. The engineering effort to design and plan sensor systems is too complex or too expensive. The sensors’ properties are limited, for example, their sampling rate or operating range.
- The observation period or sampling size is insufficient. Observations do not cover certain concepts or phenomena (Data does not capture the Black Swan [18]). The operation of a sensor is too costly, takes too much time, or is destructive.
- Blind ignorance of human engineers prevents all potential data from being obtained. Missing knowledge about real-world phenomena or the availability of sensors limits the amount of data gathered.
3. An Overview of Methods for Working with Scarce Data
3.1. Transfer Learning
3.2. Data Augmentation
3.3. Information Fusion
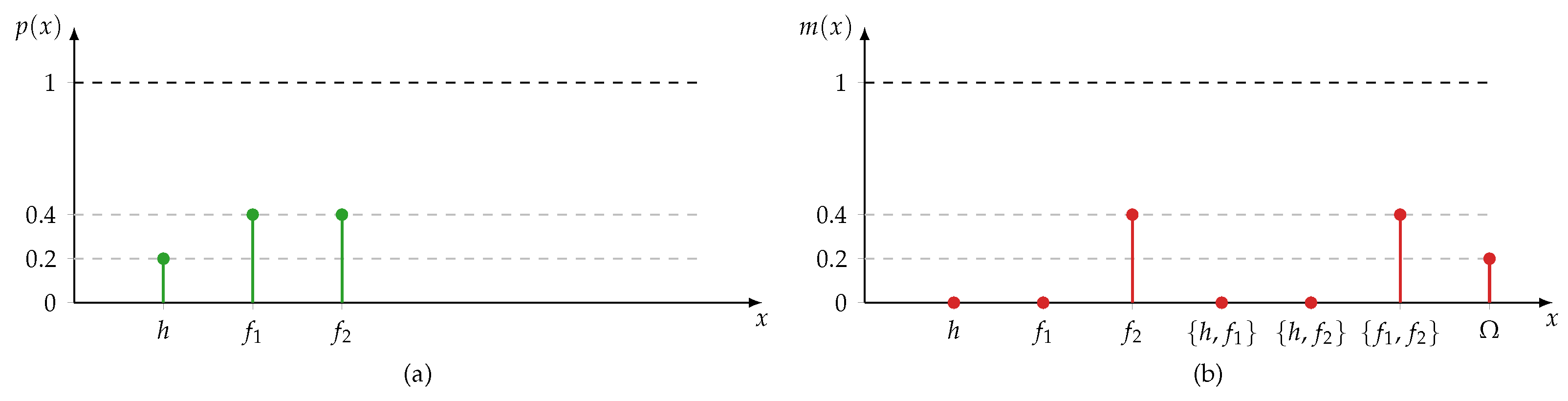
3.3.1. Dempster-Shafer Theory
3.3.2. Fuzzy Set Theory
3.3.3. Possibility Theory
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DST | Dempster-Shafer theory of evidence |
| FST | Fuzzy set theory |
| PosT | Possibility theory |
| ProbT | Probability theory |
References
- Sharp, M.; Ak, R.; Hedberg, T. A survey of the advancing use and development of machine learning in smart manufacturing. J. Manuf. Syst. 2018, 48, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.D.P.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Babbar, R.; Schölkopf, B. Data scarcity, robustness and extreme multi-label classification. Mach. Learn. 2019, 108, 1329–1351. [Google Scholar] [CrossRef]
- Wang, Q.; Farahat, A.; Gupta, C.; Zheng, S. Deep time series models for scarce data. Neurocomputing 2021, 456, 504–518. [Google Scholar] [CrossRef]
- Shu, J.; Xu, Z.; Meng, D. Small Sample Learning in Big Data Era. arXiv 2018, arXiv:1808.04572. [Google Scholar]
- Qi, G.J.; Luo, J. Small Data Challenges in Big Data Era: A Survey of Recent Progress on Unsupervised and Semi-Supervised Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2168–2187. [Google Scholar] [CrossRef]
- Adadi, A. A survey on data–efficient algorithms in big data era. J. Big Data 2021, 8, 24. [Google Scholar] [CrossRef]
- Andriyanov, N.A.; Andriyanov, D.A. The using of data augmentation in machine learning in image processing tasks in the face of data scarcity. J. Phys. Conf. Ser. 2020, 1661, 012018. [Google Scholar] [CrossRef]
- Hutchinson, M.L.; Antono, E.; Gibbons, B.M.; Paradiso, S.; Ling, J.; Meredig, B. Overcoming data scarcity with transfer learning. arXiv 2017, arXiv:1711.05099. [Google Scholar]
- Chen, Z.; Liu, Y.; Sun, H. Physics-informed learning of governing equations from scarce data. Nat. Commun. 2021, 12, 6136. [Google Scholar] [CrossRef] [PubMed]
- Vecchi, E.; Pospíšil, L.; Albrecht, S.; O’Kane, T.J.; Horenko, I. eSPA+: Scalable Entropy-Optimal Machine Learning Classification for Small Data Problems. Neural Comput. 2022, 34, 1220–1255. [Google Scholar] [CrossRef] [PubMed]
- Bhouri, M.A.; Perdikaris, P. Gaussian processes meet NeuralODEs: A Bayesian framework for learning the dynamics of partially observed systems from scarce and noisy data. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20210201. [Google Scholar] [CrossRef]
- Dubois, D.; Liu, W.; Ma, J.; Prade, H. The basic principles of uncertain information fusion. An organised review of merging rules in different representation frameworks. Inf. Fusion 2016, 32, 12–39. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Klir, G.J. Uncertainty Modeling and Analysis in Engineering and the Sciences; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Lohweg, V.; Voth, K.; Glock, S. A possibilistic framework for sensor fusion with monitoring of sensor reliability. In Sensor Fusion; Thomas, C., Ed.; IntechOpen: London, UK, 2011. [Google Scholar]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Taleb, N.N. The Black Swan: The Impact of the Highly Improbable; Incerto, Random House Publishing Group: New York, NY, USA, 2007. [Google Scholar]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Huang, Z.; Lam, H.; Zhang, H. Quantifying Epistemic Uncertainty in Deep Learning. arXiv 2021, arXiv:2110.12122. [Google Scholar]
- Bengs, V.; Hüllermeier, E.; Waegeman, W. Pitfalls of Epistemic Uncertainty Quantification through Loss Minimisation. arXiv 2022, arXiv:2203.06102. [Google Scholar]
- Smithson, M. Ignorance and Uncertainty: Emerging Paradigms; Cognitive science; Springer: New York, NY, USA; Heidelberg, Germany, 1989. [Google Scholar]
- Smets, P. Imperfect Information: Imprecision and Uncertainty. In Uncertainty Management in Information Systems: From Needs to Solutions; Motro, A., Smets, P., Eds.; Springer: New York, NY, USA, 1997; pp. 225–254. [Google Scholar]
- Bosu, M.F.; MacDonell, S.G. A Taxonomy of Data Quality Challenges in Empirical Software Engineering. In Proceedings of the 2013 22nd Australian Software Engineering Conference, Melbourne, VIC, Australia, 4–7 June 2013; pp. 97–106. [Google Scholar]
- Rogova, G.L. Information quality in fusion-driven human-machine environments. In Information Quality in Information Fusion and Decision Making; Bossé, É., Rogova, G.L., Eds.; Springer: Cham, Switzerland, 2019; pp. 3–29. [Google Scholar]
- Raglin, A.; Emlet, A.; Caylor, J.; Richardson, J.; Mittrick, M.; Metu, S. Uncertainty of Information (UoI) Taxonomy Assessment Based on Experimental User Study Results; Human-Computer Interaction. Theoretical Approaches and Design, Methods; Kurosu, M., Ed.; Springer: Cham, Switzerland, 2022; pp. 290–301. [Google Scholar]
- Jousselme, A.L.; Maupin, P.; Bosse, E. Uncertainty in a situation analysis perspective. In Proceedings of the Sixth International Conference of Information Fusion, Cairns, QSL, Australia, 8–11 July 2003; Volume 2, pp. 1207–1214. [Google Scholar]
- de Almeida, W.G.; de Sousa, R.T.; de Deus, F.E.; Daniel Amvame Nze, G.; de Mendonça, F.L.L. Taxonomy of data quality problems in multidimensional Data Warehouse models. In Proceedings of the 2013 8th Iberian Conference on Information Systems and Technologies (CISTI), Lisbon, Portugal, 19–22 June 2013; pp. 1–7. [Google Scholar]
- Krause, P.; Clark, D. Representing Uncertain Knowledge: An Artificial Intelligence Approach; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Huber, W.A. Ignorance Is Not Probability. Risk Anal. 2010, 30, 371–376. [Google Scholar] [CrossRef]
- Kim, Y.; Bang, H. Introduction to Kalman Filter and Its Applications: 2. In Introduction and Implementations of the Kalman Filter; Govaers, F., Ed.; IntechOpen: London, UK, 2018. [Google Scholar]
- Calude, C.; Longo, G. The deluge of spurious correlations in big data. Found. Sci. 2017, 22, 595–612. [Google Scholar] [CrossRef]
- Horenko, I. On a Scalable Entropic Breaching of the Overfitting Barrier for Small Data Problems in Machine Learning. Neural Comput. 2020, 32, 1563–1579. [Google Scholar] [CrossRef] [PubMed]
- Snidaro, L.; Herrero, J.G.; Llinas, J.; Blasch, E. Recent Trends in Context Exploitation for Information Fusion and AI. AI Mag. 2019, 40, 14–27. [Google Scholar] [CrossRef]
- Gama, J.; Žliobaitė, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A Survey on Concept Drift Adaptation. ACM Comput. Surv. 2014, 46, 44:1–44:37. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. Meta-learning framework with applications to zero-shot time-series forecasting. arXiv 2020, arXiv:2002.02887. [Google Scholar] [CrossRef]
- Mihalkova, L.; Huynh, T.N.; Mooney, R.J. Mapping and Revising Markov Logic Networks for Transfer Learning; AAAI: Menlo Park, CA, USA, 2007. [Google Scholar]
- Niculescu-Mizil, A.; Caruana, R. Inductive Transfer for Bayesian Network Structure Learning. In Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics, San Juan, Puerto Rico, 21–24 March 2007; Meila, M., Shen, X., Eds.; PMLR Proceedings of Machine Learning Research: New York City, NY, USA, 2007; Volume 2, pp. 339–346. [Google Scholar]
- Yao, S.; Kang, Q.; Zhou, M.; Rawa, M.J.; Abusorrah, A. A survey of transfer learning for machinery diagnostics and prognostics. Artif. Intell. Rev. 2022. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, Y.; Chua, T.S.; Schiele, B. Meta-Transfer Learning for Few-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wang, Z.; Dai, Z.; Poczos, B.; Carbonell, J. Characterizing and Avoiding Negative Transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Zhang, W.; Deng, L.; Zhang, L.; Wu, D. A Survey on Negative Transfer. IEEE/CAA J. Autom. Sin. 2022, 9, 1. [Google Scholar] [CrossRef]
- Geirhos, R.; Rubisch, P.; Michaelis, C.; Bethge, M.; Wichmann, F.A.; Brendel, W. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Dekhtiar, J.; Durupt, A.; Bricogne, M.; Eynard, B.; Rowson, H.; Kiritsis, D. Deep learning for big data applications in CAD and PLM – Research review, opportunities and case study. Emerg. Ict Concepts Smart Safe Sustain. Ind. Syst. 2018, 100, 227–243. [Google Scholar] [CrossRef]
- Židek, K.; Lazorík, P.; Piteľ, J.; Hošovský, A. An Automated Training of Deep Learning Networks by 3D Virtual Models for Object Recognition. Symmetry 2019, 11, 496. [Google Scholar] [CrossRef]
- Židek, K.; Lazorík, P.; Piteľ, J.; Pavlenko, I.; Hošovský, A. Automated Training of Convolutional Networks by Virtual 3D Models for Parts Recognition in Assembly Process. In ADVANCES IN MANUFACTURING; Trojanowska, J., Ciszak, O., Machado, J.M., Pavlenko, I., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2019; Volume 13, pp. 287–297. [Google Scholar]
- Perez, L.; Wang, J. The effectiveness of data augmentation in image classification using deep learning. arXiv 2017, arXiv:1712.04621. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Feng, S.Y.; Gangal, V.; Wei, J.; Chandar, S.; Vosoughi, S.; Mitamura, T.; Hovy, E. A Survey of Data Augmentation Approaches for NLP. arXiv 2021, arXiv:2105.03075. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M.; Furht, B. Text Data Augmentation for Deep Learning. J. Big Data 2021, 8, 101. [Google Scholar] [CrossRef] [PubMed]
- Bayer, M.; Kaufhold, M.A.; Reuter, C. A Survey on Data Augmentation for Text Classification. ACM Computing Surveys 2022, accept. [Google Scholar] [CrossRef]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time Series Data Augmentation for Deep Learning: A Survey. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Virtual, 19–27 August 2021; International Joint Conferences on Artificial Intelligence Organization: Menlo Park, CA, USA, 2021. [Google Scholar]
- Parente, A.P.; de Souza Jr, M.B.; Valdman, A.; Mattos Folly, R.O. Data Augmentation Applied to Machine Learning-Based Monitoring of a Pulp and Paper Process. Processes 2019, 7, 958. [Google Scholar] [CrossRef]
- Shi, D.; Ye, Y.; Gillwald, M.; Hecht, M. Robustness enhancement of machine fault diagnostic models for railway applications through data augmentation. Mech. Syst. Signal Process. 2022, 164, 108217. [Google Scholar] [CrossRef]
- Dao, T.; Gu, A.; Ratner, A.J.; Smith, V.; de Sa, C.; Ré, C. A Kernel Theory of Modern Data Augmentation. arXiv 2018, arXiv:1803.06084. [Google Scholar]
- Antoniou, A.; Storkey, A.; Edwards, H. Data Augmentation Generative Adversarial Networks. arXiv 2017, arXiv:1711.04340. [Google Scholar]
- Jain, N.; Manikonda, L.; Hernandez, A.O.; Sengupta, S.; Kambhampati, S. Imagining an Engineer: On GAN-Based Data Augmentation Perpetuating Biases. arXiv 2018, arXiv:1811.03751. [Google Scholar]
- Hall, D.; Llinas, J. Multisensor Data Fusion. In Handbook of Multisensor Data Fusion; Electrical Engineering & Applied Signal Processing Series; Hall, D., Llinas, J., Eds.; CRC Press: Boca Raton, FL, USA, 2001; Volume 3. [Google Scholar]
- Mönks, U. Information Fusion Under Consideration of Conflicting Input Signals; Technologies for Intelligent Automation; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bloch, I.; Hunter, A.; Appriou, A.; Ayoun, A.; Benferhat, S.; Besnard, P.; Cholvy, L.; Cooke, R.; Cuppens, F.; Dubois, D.; et al. Fusion: General concepts and characteristics. Int. J. Intell. Syst. 2001, 16, 1107–1134. [Google Scholar] [CrossRef]
- Dubois, D.; Everaere, P.; Konieczny, S.; Papini, O. Main issues in belief revision, belief merging and information fusion. In A Guided Tour of Artificial Intelligence Research: Volume I: Knowledge Representation, Reasoning and Learning; Marquis, P., Papini, O., Prade, H., Eds.; Springer: Cham, Switzerland, 2020; pp. 441–485. [Google Scholar]
- Denœux, T.; Dubois, D.; Prade, H. Representations of uncertainty in artificial intelligence: Probability and possibility. In A Guided Tour of Artificial Intelligence Research: Volume I: Knowledge Representation, Reasoning and Learning; Marquis, P., Papini, O., Prade, H., Eds.; Springer: Cham, Switzerland, 2020; pp. 69–117. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Salicone, S.; Prioli, M. Measuring Uncertainty within the Theory of Evidence; Springer Series in Measurement Science and Technology; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Shafer, G. Dempster’s rule of combination. Int. J. Approx. Reason. 2016, 79, 26–40. [Google Scholar] [CrossRef]
- Yager, R.R. On the dempster-shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Campos, F. Decision Making in Uncertain Situations: An Extension to the Mathematical Theory of Evidence. Ph.D. Thesis, Dissertation.Com., Boca Raton, FL, USA, 2006. [Google Scholar]
- Polikar, R. Ensemble Learning. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: New York, NY, USA, 2012; pp. 1–34. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. WIREs Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Learning. In Machine Learning; Springer: Singapore, 2021; pp. 181–210. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mönks, U.; Petker, D.; Lohweg, V. Fuzzy-Pattern-Classifier training with small data sets. Information Processing and Management of Uncertainty in Knowledge-Based Systems. Theory and Methods; Hüllermeier, E., Kruse, R., Hoffmann, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 426–435. [Google Scholar]
- Bocklisch, S.F. Prozeßanalyse mit unscharfen Verfahren, 1st ed.; Verlag Technik: Berlin, Germany, 1987. [Google Scholar]
- Bocklisch, S.F.; Bitterlich, N. Fuzzy Pattern Classification—Methodology and Application—. In Fuzzy-Systems in Computer Science; Kruse, R., Gebhardt, J., Palm, R., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1994; pp. 295–301. [Google Scholar]
- Holst, C.A.; Lohweg, V. A conflict-based drift detection and adaptation approach for multisensor information fusion. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Torino, Italy, 1–4 September 2018; pp. 967–974. [Google Scholar]
- Holst, C.A.; Lohweg, V. Improving majority-guided fuzzy information fusion for Industry 4.0 condition monitoring. In Proceedings of the 2019 22nd International Conference on Information Fusion (FUSION), IEEE, Ottawa, ON, Canada, 2–5 July 2019. [Google Scholar]
- Holst, C.A.; Lohweg, V. A redundancy metric set within possibility theory for multi-sensor systems. Sensors 2021, 21, 2508. [Google Scholar] [CrossRef]
- Holst, C.A.; Lohweg, V. Designing Possibilistic Information Fusion—The Importance of Associativity, Consistency, and Redundancy. Metrology 2022, 2, 180–215. [Google Scholar] [CrossRef]
- Aizerman, M.A.; Braverman, E.M.; Rozonoer, L.I. Theoretical foundations of the potential function method in pattern recognition learning. Autom. Remote Control 1964, 25, 821–837. [Google Scholar]
- Lohweg, V.; Diederichs, C.; Müller, D. Algorithms for hardware-based pattern recognition. EURASIP J. Appl. Signal Process. 2004, 2004, 1912–1920. [Google Scholar] [CrossRef]
- Hempel, A.J. Netzorientierte Fuzzy-Pattern-Klassifikation nichtkonvexer Objektmengenmorphologien. Ph.D. Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2011. [Google Scholar]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Solaiman, B.; Bossé, É. Possibility Theory for the Design of Information Fusion Systems; Information Fusion and Data Science; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Dubois, D.; Prade, H. Practical methods for constructing possibility distributions. Int. J. Intell. Syst. 2016, 31, 215–239. [Google Scholar] [CrossRef]
- Wang, G.; Li, W.; Aertsen, M.; Deprest, J.; Ourselin, S.; Vercauteren, T. Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks. Neurocomputing 2019, 338, 34–45. [Google Scholar] [CrossRef]
- Diez-Olivan, A.; Del Ser, J.; Galar, D.; Sierra, B. Data fusion and machine learning for industrial prognosis: Trends and perspectives towards Industry 4.0. Inf. Fusion 2019, 50, 92–111. [Google Scholar] [CrossRef]
- Blasch, E.; Sullivan, N.; Chen, G.; Chen, Y.; Shen, D.; Yu, W.; Chen, H.M. Data fusion information group (DFIG) model meets AI+ML. In Signal Processing, Sensor/Information Fusion, and Target Recognition XXXI; Kadar, I., Blasch, E.P., Grewe, L.L., Eds.; SPIE: Bellingham, WA, USA, 2022; Volume 12122, p. 121220N. [Google Scholar]
- Holzinger, A.; Dehmer, M.; Emmert-Streib, F.; Cucchiara, R.; Augenstein, I.; Del Ser, J.; Samek, W.; Jurisica, I.; Díaz-Rodríguez, N. Information fusion as an integrative cross-cutting enabler to achieve robust, explainable, and trustworthy medical artificial intelligence. Inf. Fusion 2022, 79, 263–278. [Google Scholar] [CrossRef]
- Holst, C.A.; Lohweg, V. Feature fusion to increase the robustness of machine learners in industrial environments. at-Automatisierungstechnik 2019, 67, 853–865. [Google Scholar] [CrossRef]
- Kondo, R.E.; de Lima, E.D.D.; Freitas Rocha Loures, E.D.; Santos, E.A.P.D.; Deschamps, F. Data Fusion for Industry 4.0: General Concepts and Applications. In Proceedings of the 25th International Joint Conference on Industrial Engineering and Operations Management—IJCIEOM, Novi Sad, Serbia, 15–17 July 2019; Anisic, Z., Lalic, B., Gracanin, D., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 362–373. [Google Scholar]
- Denœux, T.; Masson, M.H. Dempster-Shafer Reasoning in Large Partially Ordered Sets: Applications in Machine Learning. In Integrated Uncertainty Management and Applications; Huynh, V.N., Nakamori, Y., Lawry, J., Inuiguchi, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 39–54. [Google Scholar]
- Hui, K.H.; Ooi, C.S.; Lim, M.H.; Leong, M.S. A hybrid artificial neural network with Dempster-Shafer theory for automated bearing fault diagnosis. J. Vibroengineering 2016, 18, 4409–4418. [Google Scholar] [CrossRef]
- Peñafiel, S.; Baloian, N.; Sanson, H.; Pino, J.A. Applying Dempster–Shafer theory for developing a flexible, accurate and interpretable classifier. Expert Syst. Appl. 2020, 148, 113262. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. From possibilistic rule-based systems to machine learning—A discussion paper. In Scalable Uncertainty Management; Davis, J., Tabia, K., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 35–51. [Google Scholar]

| Authors | Focus | Builds | Relies on | Details Subcategories of Incompleteness |
|---|---|---|---|---|
| upon | Incompleteness | |||
| Smithson [22] | Ignorance | - | yes | Partially. Incompleteness is subcategorised into Uncertainty (including Vagueness, Probability, Ambiguity) and Absence. Absence of information is not further detailed. |
| Smets [23] | Imperfection | - | yes | No |
| Krause and Clark [29] | Uncertainty | - | yes | No |
| Ayyub and Klir [15] | Ignorance | [22] | yes | Partially. Similar to Smithson. |
| Bosu and MacDonell [24] | Data Quality | - | yes | No |
| Rogova [25] | Information Quality | [23] | yes | No |
| Raglin et al. [26] | Uncertainty | - | yes | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holst, C.-A.; Lohweg, V. Scarce Data in Intelligent Technical Systems: Causes, Characteristics, and Implications. Sci 2022, 4, 49. https://doi.org/10.3390/sci4040049
Holst C-A, Lohweg V. Scarce Data in Intelligent Technical Systems: Causes, Characteristics, and Implications. Sci. 2022; 4(4):49. https://doi.org/10.3390/sci4040049
Chicago/Turabian StyleHolst, Christoph-Alexander, and Volker Lohweg. 2022. "Scarce Data in Intelligent Technical Systems: Causes, Characteristics, and Implications" Sci 4, no. 4: 49. https://doi.org/10.3390/sci4040049
APA StyleHolst, C.-A., & Lohweg, V. (2022). Scarce Data in Intelligent Technical Systems: Causes, Characteristics, and Implications. Sci, 4(4), 49. https://doi.org/10.3390/sci4040049







