Stress Evaluation Method by Neutron Diffraction for HCP-Structured Magnesium Alloy
Abstract
:1. Introduction
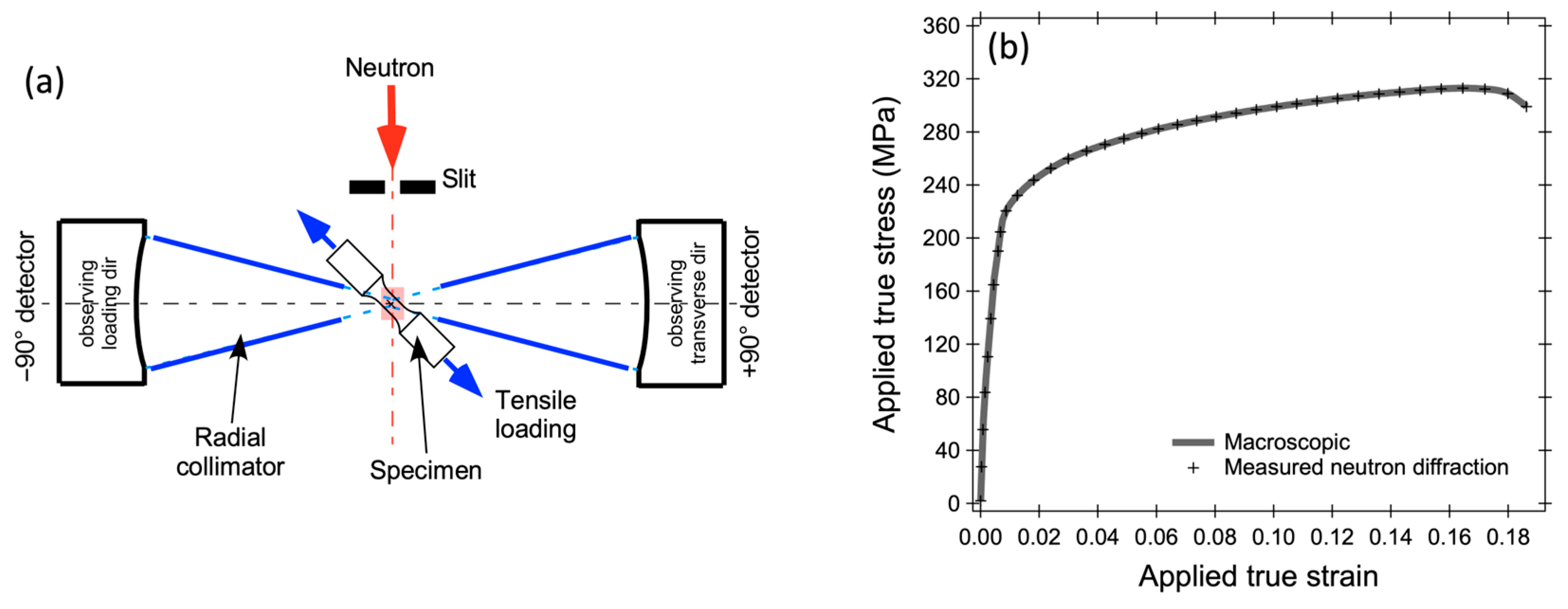
2. Materials and Methods
3. Results and Discussion
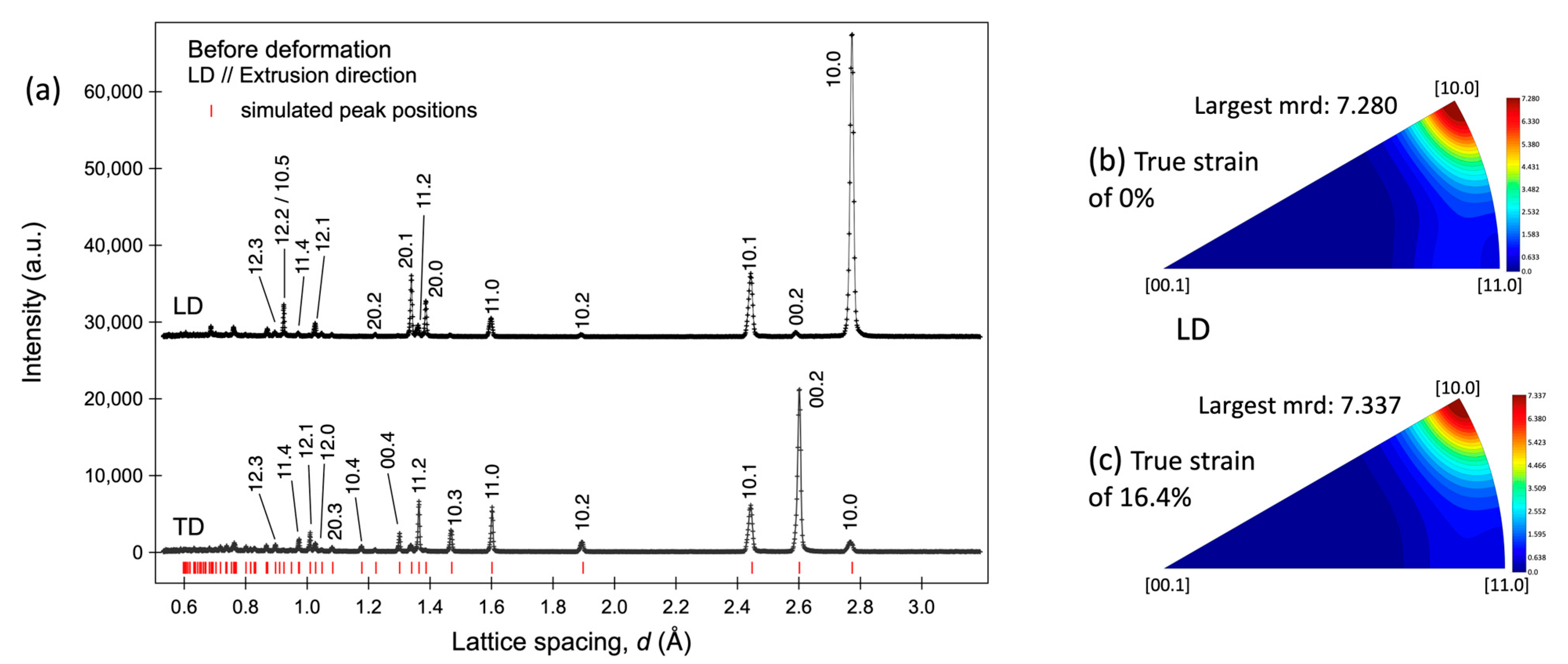
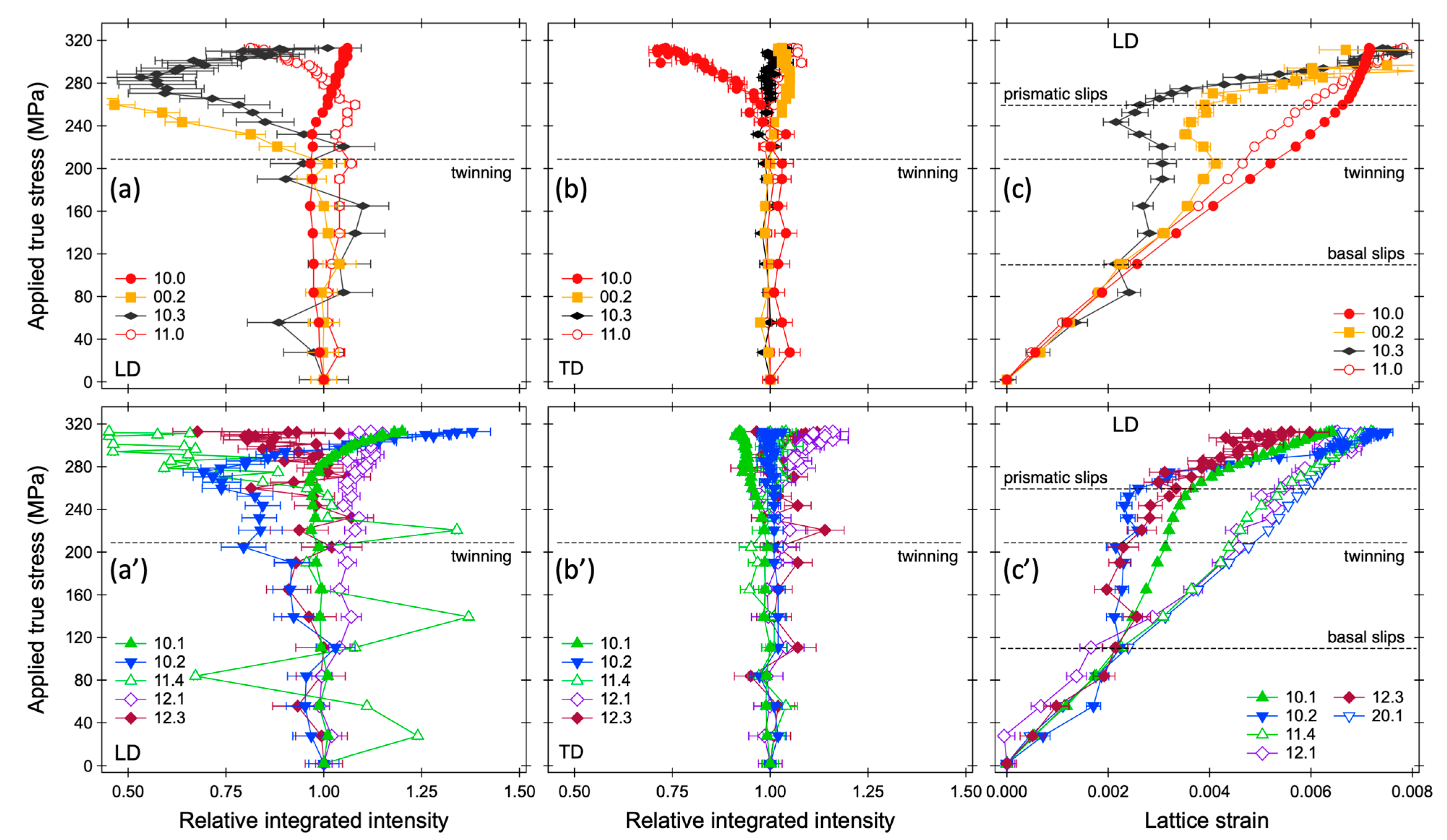
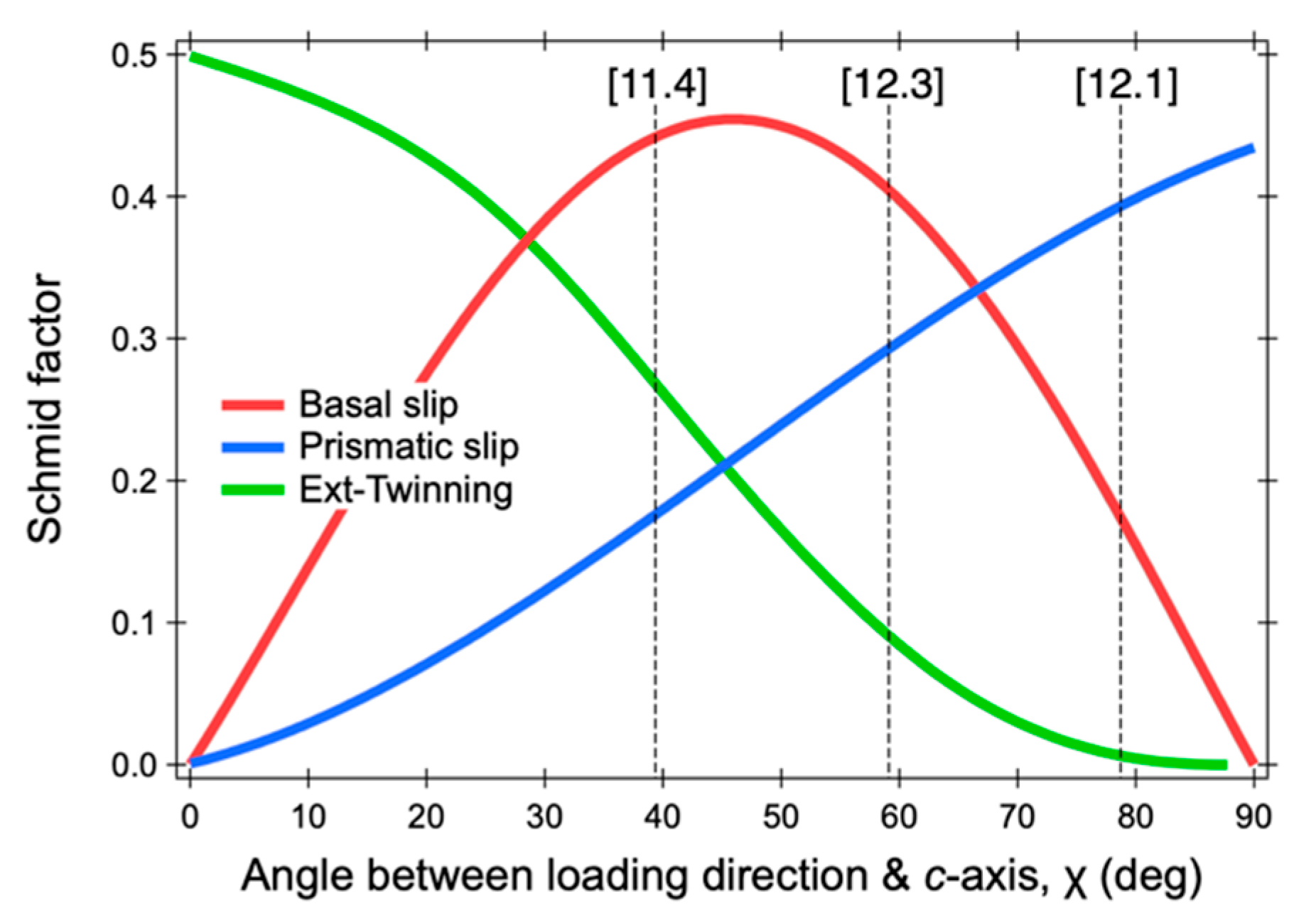
3.1. Responses of [hk.l] Orientations
3.2. Conventional Procedures for Evaluations of Phase Strain and Phase Stress
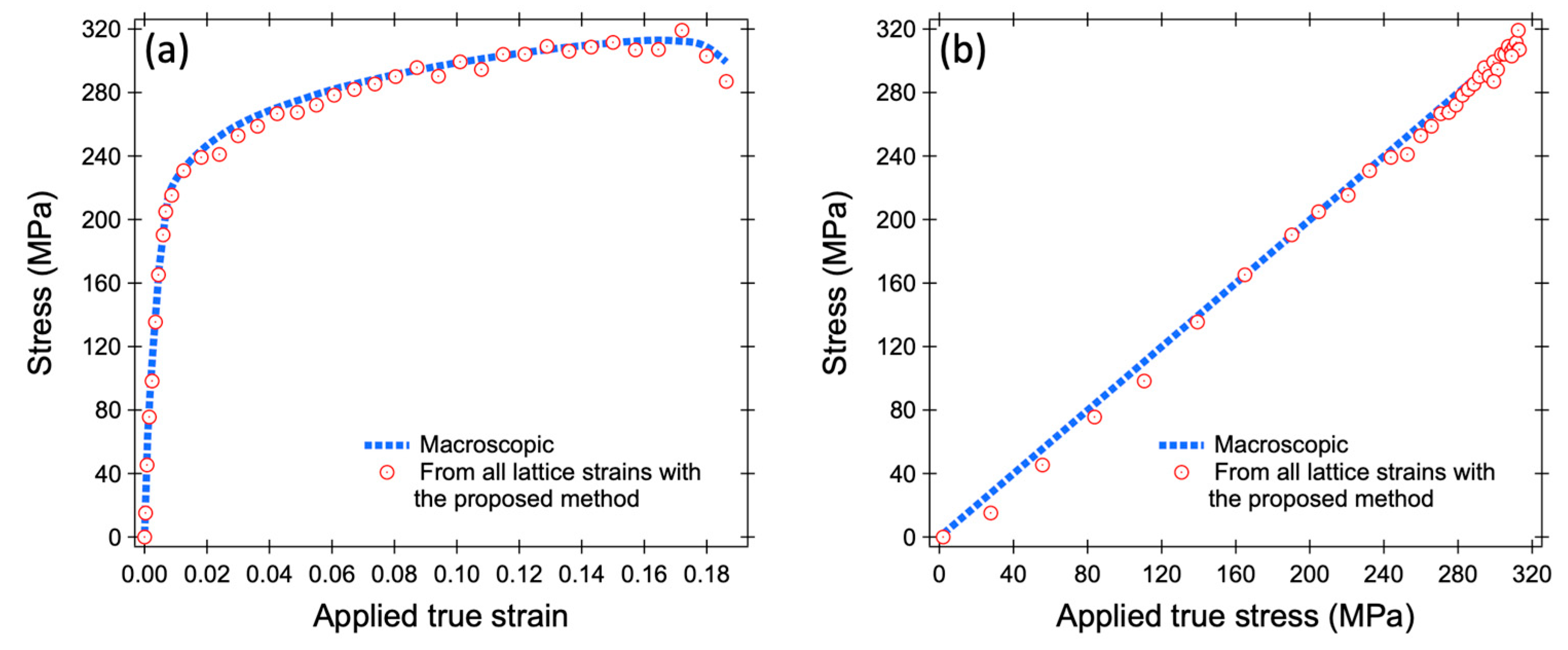
3.3. New Procedure for Phase Stress Evaluation
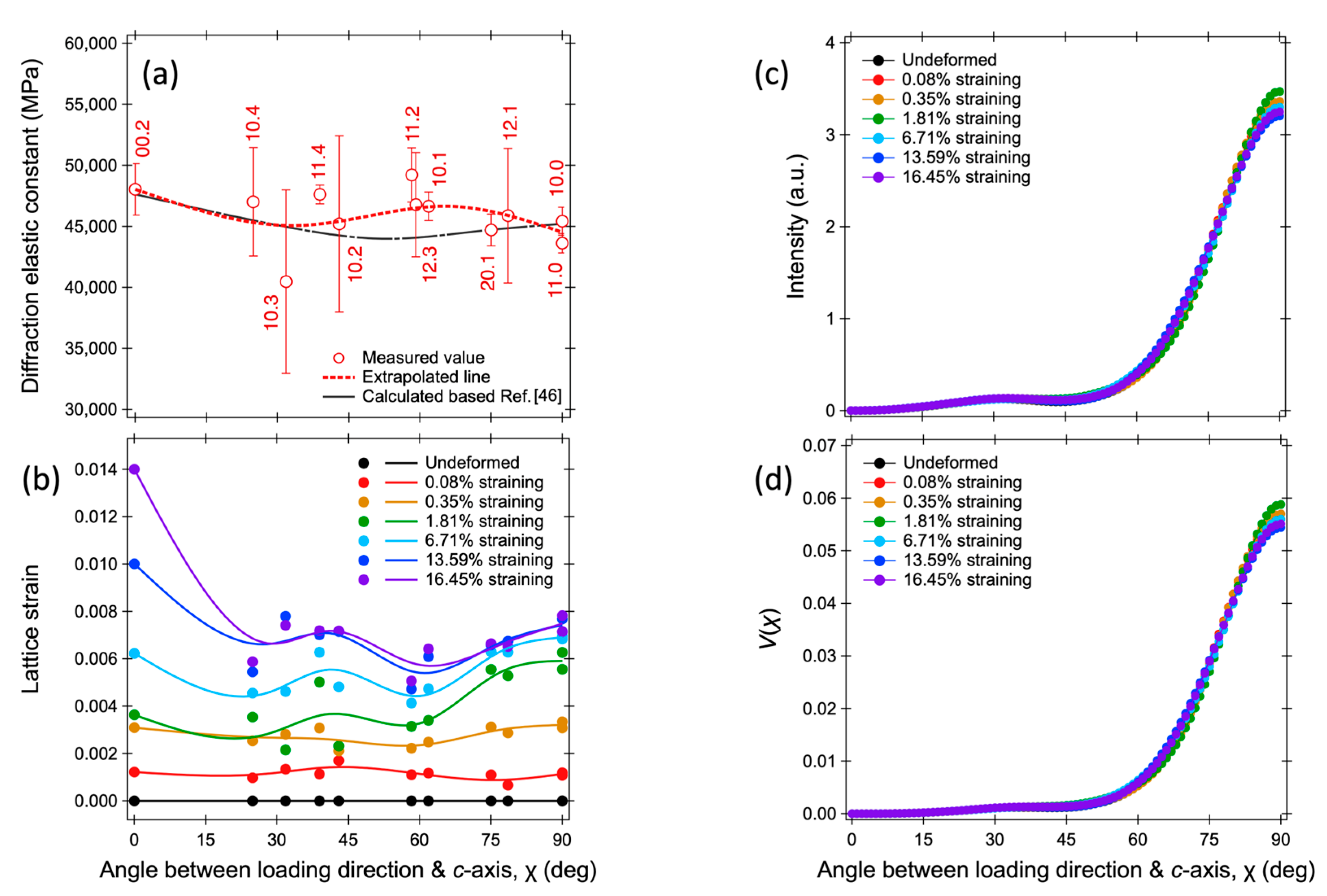
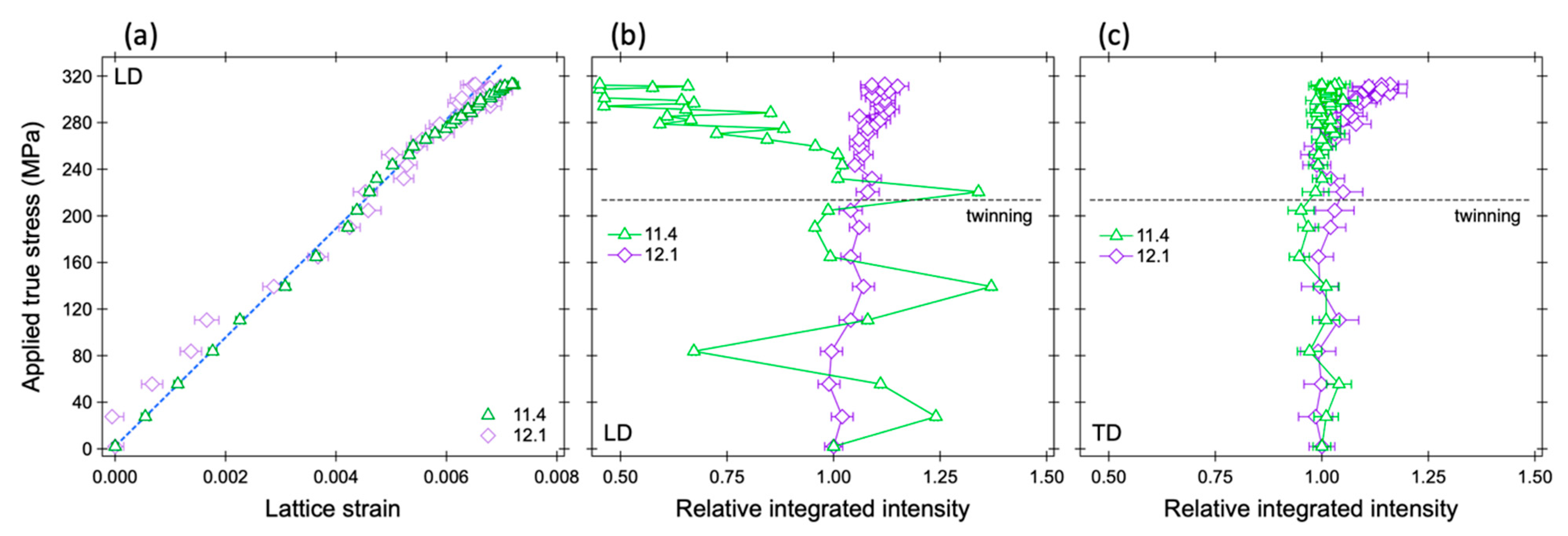
3.4. The Lattice Strain of Particular Grain for Phase Stress
4. Conclusions
- The increases in the lattice strains with respect to the applied true stress after yielding largely vary among [hk.l] grains. Some [hk.l] grains have little or no increase in lattice strain, making it difficult to use the conventional procedures for determining the average phase strain by using lattice constants or by averaging several lattice strains.
- Our newly proposed procedure of stress evaluation from the lattice strains shows very high accuracy and reliability by weighting the volume fraction of [hk.l] grains and evaluating them in many [hk.l] orientations in addition to multiplication by the diffraction elastic constant.
- The conventionally recommended 12.3 peak for stress measurement of HCP-structured materials should be used with caution for the evaluation of stresses of HCP-structured engineering parts due to the huge stress relaxation in 12.3 oriented grains by basal slip.
- We recommend to use the 12.1 peak for stress evaluation when multiple hk.l peaks cannot be obtained simultaneously. The lattice strain value evaluated from the 12.1 peak shows a good linear relationship with the applied true stress for the whole deformation region.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joost, W.J.; Krajewski, P.E. Towards magnesium alloys for high-volume automotive applications. Scr. Mater. 2017, 128, 107–112. [Google Scholar] [CrossRef]
- Agnew, S.R. Wrought magnesium: A 21st century outlook. JOM 2004, 56, 20–21. [Google Scholar] [CrossRef]
- Kawamura, Y.; Hayashi, K.; Inoue, A.; Masumoto, T. Rapidly Solidified Powder Metallurgy Mg97Zn1Y2Alloys with Excellent Tensile Yield Strength above 600 MPa. Mater. Trans. 2001, 42, 1172–1176. [Google Scholar] [CrossRef]
- Blum, W.; Zhang, P.; Watzinger, B.; Grossmann, B.V.; Haldenwanger, H.G. Comparative study of creep of the die-cast Mg-alloys AZ91, AS21, AS41, AM60, and AE42. Mater. Sci. Eng. A 2001, 319–321, 735–740. [Google Scholar] [CrossRef]
- Itoi, T.; Inazawa, T.; Yamasaki, M.; Kawamura, Y.; Hirohashi, M. Microstructure and mechanical properties of Mg-Zn-Y alloy sheet prepared by hot-rolling. Mater. Sci. Eng. A 2013, 560, 216–223. [Google Scholar] [CrossRef]
- Noyan, I.C. Equilibrium Conditions for the Average Stresses Measured By X-rays. Metall. Trans. A Phys. Metall. Mater. Sci. 1983, 14, 1907–1914. [Google Scholar] [CrossRef]
- Harjo, S.; Tomota, Y.; Ono, M. Measurements of thermal residual elastic strains in ferrite–austenite Fe–Cr–Ni alloys by neutron and X-ray diffractions. Acta Mater. 1998, 47, 353–362. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Z.; Zhuang, W.; Peng, H. Effects of pre-strain on the surface residual stress and corrosion behavior of an Al-Zn-Mg-Cu alloy plate. Mater. Charact. 2020, 160, 110129. [Google Scholar] [CrossRef]
- Hutchings, M.T. Neutron diffraction measurement of residual stress fields-the engineer’s dream come true? Neutron News 1992, 3, 14–19. [Google Scholar] [CrossRef]
- Nishida, S.; Nishino, S.; Sekine, M.; Oka, Y.; Harjo, S.; Kawasaki, T.; Suzuki, H.; Morii, Y.; Ishii, Y. Analysis of Residual Stress in Steel Bar Processed by Cold Drawing and Straightening. Mater. Trans. 2021, 62, 667–674. [Google Scholar] [CrossRef]
- Harjo, S.; Tsuchida, N.; Abe, J.; Gong, W. Martensite phase stress and the strengthening mechanism in TRIP steel by neutron diffraction. Sci. Rep. 2017, 7, 15149. [Google Scholar] [CrossRef]
- Harjo, S.; Gong, W.; Aizawa, K.; Kawasaki, T.; Yamasaki, M. Strengthening of αMg and long-period stacking ordered phases in a Mg-Zn-Y alloy by hot-extrusion with low extrusion ratio. Acta Mater. 2023, 255, 119029. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress. Part 1—Measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Koyanagi, Y.; Ueta, S.; Kawasaki, T.; Harjo, S.; Cho, K.; Yasuda, H.Y.H.Y. Investigation of strengthening mechanism in Ni–38Cr-3.8Al alloy with fine lamellar structure by in situ neutron diffraction analysis. Mater. Sci. Eng. A 2020, 773, 138822. [Google Scholar] [CrossRef]
- Daymond, M.R.; Bourke, M.A.M.; Von Dreele, R.B.; Clausen, B.; Lorentzen, T. Use of Rietveld refinement for elastic macrostrain determination and for evaluation of plastic strain history from diffraction spectra. J. Appl. Phys. 1997, 82, 1554–1562. [Google Scholar] [CrossRef]
- Harjo, S.; Kawasaki, T.; Grazzi, F.; Shinohara, T.; Tanaka, M. Neutron diffraction study on full-shape Japanese sword. Materialia 2019, 7, 100377. [Google Scholar] [CrossRef]
- Muránsky, O.; Carr, D.G.; Barnett, M.R.; Oliver, E.C.; Šittner, P. Investigation of deformation mechanisms involved in the plasticity of AZ31 Mg alloy: In situ neutron diffraction and EPSC modelling. Mater. Sci. Eng. A 2008, 496, 14–24. [Google Scholar] [CrossRef]
- Muránsky, O.; Barnett, M.R.; Carr, D.G.; Vogel, S.C.; Oliver, E.C. Investigation of deformation twinning in a fine-grained and coarse-grained ZM20 Mg alloy: Combined in situ neutron diffraction and acoustic emission. Acta Mater. 2010, 58, 1503–1517. [Google Scholar] [CrossRef]
- Gong, W.; Aizawa, K.; Harjo, S.; Zheng, R.; Kawasaki, T.; Abe, J.; Kamiyama, T.; Tsuji, N. Deformation behavior of as-cast and as-extruded Mg97Zn1Y2 alloys during compression, as tracked by in situ neutron diffraction. Int. J. Plast. 2018, 111, 288–306. [Google Scholar] [CrossRef]
- Woo, W.; Choo, H.; Prime, M.B.; Feng, Z.; Clausen, B. Microstructure, texture and residual stress in a friction-stir-processed AZ31B magnesium alloy. Acta Mater. 2008, 56, 1701–1711. [Google Scholar] [CrossRef]
- Turski, M.; Paradowska, A.; Zhang, S.Y.; Mortensen, D.; Fjaer, H.; Grandfield, J.; Davis, B.; Delorme, R. Validation of predicted residual stresses within direct chill cast magnesium alloy slab. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2012, 43, 1547–1557. [Google Scholar] [CrossRef]
- Brown, D.W.; Agnew, S.R.; Bourke, M.A.M.; Holden, T.M.; Vogel, S.C.; Tomé, C.N. Internal strain and texture evolution during deformation twinning in magnesium. Mater. Sci. Eng. A 2005, 399, 1–12. [Google Scholar] [CrossRef]
- Prevey, P.S. X-Ray Diffraction Residual Stress Techniques. In Materials Characterization; ASM International: Almere, The Netherlands, 1986; pp. 380–392. [Google Scholar] [CrossRef]
- Harjo, S.; Ito, T.; Aizawa, K.; Arima, H.; Abe, J.; Moriai, A.; Iwahashi, T.; Kamiyama, T. Current Status of Engineering Materials Diffractometer at J-PARC. Mater. Sci. Forum. 2011, 681, 443–448. [Google Scholar] [CrossRef]
- Nakajima, K.; Kawakita, Y.; Itoh, S.; Abe, J.; Aizawa, K.; Aoki, H.; Endo, H.; Fujita, M.; Funakoshi, K.; Gong, W.; et al. Materials and Life Science Experimental Facility (MLF) at the Japan Proton Accelerator Research Complex II: Neutron Scattering Instruments. Quantum Beam Sci. 2017, 1, 9. [Google Scholar] [CrossRef]
- Máthis, K.; Drozdenko, D.; Németh, G.; Harjo, S.; Gong, W.; Aizawa, K.; Yamasaki, M.; Kawamura, Y. In-situ Investigation of the Microstructure Evolution in Long-Period-Stacking-Ordered (LPSO) Magnesium Alloys as a Function of the Temperature. Front. Mater. 2019, 6, 270. [Google Scholar] [CrossRef]
- Harjo, S.; Aizawa, K.; Gong, W.; Kawasaki, T. Neutron diffraction monitoring of as-cast Mg97Zn1Y2 during compression and tension. Mater. Trans. 2020, 61, 828–832. [Google Scholar] [CrossRef]
- Ito, T.; Nakatani, T.; Harjo, S.; Arima, H.; Abe, J.; Aizawa, K.; Moriai, A. Application Software Development for the Engineering Materials Diffractometer, TAKUMI. Mater. Sci. Forum. 2010, 652, 238–242. [Google Scholar] [CrossRef]
- Kawasaki, T.; Nakamura, T.; Gong, W.; Oikawa, K. Testing of time-of-flight neutron diffraction imaging using a high-resolution scintillator detector with wavelength-shifting fibers. Phys. B Condens. Matter 2018, 551, 460–463. [Google Scholar] [CrossRef]
- Mao, W.; Gong, W.; Kawasaki, T.; Harjo, S. Effect of deformation-induced martensitic transformation on nonuniform deformation of metastable austenitic steel. Mater. Sci. Eng. A 2022, 837, 142758. [Google Scholar] [CrossRef]
- Oishi-Tomiyasu, R.; Yonemura, M.; Morishima, T.; Hoshikawa, A.; Torii, S.; Ishigaki, T.; Kamiyama, T. Application of matrix decomposition algorithms for singular matrices to the Pawley method in Z-Rietveld. J. Appl. Crystallogr. 2012, 45, 299–308. [Google Scholar] [CrossRef]
- Xu, P.; Harjo, S.; Ojima, M.; Suzuki, H.; Ito, T.; Gong, W.W.; Vogel, S.C.; Inoue, J.; Tomota, Y.Y.; Aizawa, K.; et al. High stereographic resolution texture and residual stress evaluation using time-of-flight neutron diffraction. J. Appl. Crystallogr. 2018, 51, 746–760. [Google Scholar] [CrossRef]
- Wenk, H.-R.; Lutterotti, L.; Vogel, S.C. Rietveld texture analysis from TOF neutron diffraction data. Powder Diffr. 2010, 25, 283–296. [Google Scholar] [CrossRef]
- Lutterotti, L.; Matthies, S.; Wenk, H.-R.; Schultz, A.S.; Richardson, J.W. Combined texture and structure analysis of deformed limestone from time-of-flight neutron diffraction spectra. J. Appl. Phys. 1997, 81, 594–600. [Google Scholar] [CrossRef]
- Gong, W.; Zheng, R.; Harjo, S.; Kawasaki, T.; Aizawa, K.; Tsuji, N. In-situ observation of twinning and detwinning in AZ31 alloy. J. Magnes. Alloy. 2022, 10, 3418–3432. [Google Scholar] [CrossRef]
- Harjo, S.; Gong, W.; Aizawa, K.; Kawasaki, T.; Yamasaki, M.; Mayama, T.; Kawamura, Y. Effect of Extrusion Ratio in Hot-Extrusion on Kink Deformation during Compressive Deformation in an αMg/LPSO Dual-Phase Magnesium Alloy Monitored by In Situ Neutron Diffraction. Mater. Trans. 2023, 64, 766–773. [Google Scholar] [CrossRef]
- Čapek, J.; Máthis, K.; Clausen, B.; Stráská, J.; Beran, P.; Lukáš, P. Study of the loading mode dependence of the twinning in random textured cast magnesium by acoustic emission and neutron diffraction methods. Mater. Sci. Eng. A 2014, 602, 25–32. [Google Scholar] [CrossRef]
- Agnew, S.R. Deformation Mechanisms of Magnesium Alloys; Woodhead Publishing Limited: Thorston, UK, 2012. [Google Scholar] [CrossRef]
- Liu, M.; Diercks, P.; Manzoni, A.; Čížek, J.; Ramamurty, U.; Banhart, J. Positron annihilation investigation of thermal cycling induced martensitic transformation in NiTi shape memory alloy. Acta Mater. 2021, 220, 117298. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the ductility of magnesium alloys. Part I: “Tension” twins. Mater. Sci. Eng. A 2007, 464, 1–7. [Google Scholar] [CrossRef]
- Pawley, G.S. Unit-cell refinement from powder diffraction scans. J. Appl. Crystallogr. 1981, 14, 357–361. [Google Scholar] [CrossRef]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure refinement. Acta Crystallogr. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Asoo, K.; Tomota, Y.Y.; Harjo, S.; Okitsu, Y. Tensile behavior of a trip-aided ultra-fine grained steel studied by neutron diffraction. ISIJ Int. 2011, 51, 145–150. [Google Scholar] [CrossRef]
- Fukuda, K.; Tomota, Y.; Harjo, S.; Gong, W.; Woo, W.; Seong, B.S.S.; Kuwahara, Y.; Ikuta, F. Residual stresses in steel rod with collar formed by partial diameter-enlarging technique. Mater. Sci. Technol. 2017, 33, 172–180. [Google Scholar] [CrossRef]
- Paddea, S.; Francis, J.A.; Paradowska, A.M.; Bouchard, P.J.; Shibli, I.A. Residual stress distributions in a P91 steel-pipe girth weld before and after post weld heat treatment. Mater. Sci. Eng. A 2012, 534, 663–672. [Google Scholar] [CrossRef]
- Kröner, E. Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls. Z. Phys. 1958, 151, 504–518. [Google Scholar] [CrossRef]
- Slutsky, L.J.; Garland, C.W. Elastic constants of magnesium from 4.2°K to 300°K. Phys. Rev. 1957, 107, 972–976. [Google Scholar] [CrossRef]
- Clausen, B.; Tomé, C.N.; Brown, D.W.; Agnew, S.R. Reorientation and stress relaxation due to twinning: Modeling and experimental characterization for Mg. Acta Mater. 2008, 56, 2456–2468. [Google Scholar] [CrossRef]
- Agnew, S.R.; Mulay, R.P.; Polesak, F.J.; Calhoun, C.A.; Bhattacharyya, J.J.; Clausen, B. In situ neutron diffraction and polycrystal plasticity modeling of a Mg-Y-Nd-Zr alloy: Effects of precipitation on individual deformation mechanisms. Acta Mater. 2013, 61, 3769–3780. [Google Scholar] [CrossRef]
- Hielscher, R.; Schaeben, H. A novel pole figure inversion method: Specification of the MTEX algorithm. J. Appl. Crystallogr. 2008, 41, 1024–1037. [Google Scholar] [CrossRef]
- Ungár, T.; Stoica, A.D.; Tichy, G.; Wang, X.L. Orientation-dependent evolution of the dislocation density in grain populations with different crystallographic orientations relative to the tensile axis in a polycrystalline aggregate of stainless steel. Acta Mater. 2014, 66, 251–261. [Google Scholar] [CrossRef]
- Xie, Q.; Yan, Z.; Yu, D.; An, K.; Yan, X.; Yin, S.; Gillham, B.; Wu, X.; Yang, P.; Zhao, Z.; et al. Crystallographic orientation and spatially resolved damage for polycrystalline deformation of a high manganese steel. Acta Mater. 2022, 226, 117628. [Google Scholar] [CrossRef]
- Tomota, Y.; Ojima, M.; Harjo, S.; Gong, W.; Sato, S.; Ungár, T. Dislocation densities and intergranular stresses of plastically deformed austenitic steels. Mater. Sci. Eng. A 2019, 743, 32–39. [Google Scholar] [CrossRef]
- Yu, M.; Cui, Y.; Wang, J.; Chen, Y.; Ding, Z.; Ying, T.; Llorca, J.; Zeng, X. Critical resolved shear stresses for slip and twinning in Mg-Y-Ca alloys and their effect on the ductility. Int. J. Plast. 2023, 162, 103525. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harjo, S.; Gong, W.; Kawasaki, T. Stress Evaluation Method by Neutron Diffraction for HCP-Structured Magnesium Alloy. Quantum Beam Sci. 2023, 7, 32. https://doi.org/10.3390/qubs7040032
Harjo S, Gong W, Kawasaki T. Stress Evaluation Method by Neutron Diffraction for HCP-Structured Magnesium Alloy. Quantum Beam Science. 2023; 7(4):32. https://doi.org/10.3390/qubs7040032
Chicago/Turabian StyleHarjo, Stefanus, Wu Gong, and Takuro Kawasaki. 2023. "Stress Evaluation Method by Neutron Diffraction for HCP-Structured Magnesium Alloy" Quantum Beam Science 7, no. 4: 32. https://doi.org/10.3390/qubs7040032
APA StyleHarjo, S., Gong, W., & Kawasaki, T. (2023). Stress Evaluation Method by Neutron Diffraction for HCP-Structured Magnesium Alloy. Quantum Beam Science, 7(4), 32. https://doi.org/10.3390/qubs7040032





