Clonogenic Survival RBE Calculations in Carbon Ion Therapy: The Importance of the Absolute Values of α and β in the Photon Dose-Response Curve and a Strategy to Mitigate Their Anticorrelation
Abstract
1. Introduction
- (1)
- Study the effect of αref/βref on the RBE of 12C ions calculated with the MCF MKM.
- (2)
- Investigate the effect of the absolute value of αref and βref on the RBE of 12C ions computed using the MCF MKM in the case of two clinically relevant values of αref/βref (2 and 10 Gy).
- (3)
- Explore the possibility of mitigating the anticorrelation between αref and βref by means of an MKM-based LQM fit of published in vitro photon survival curves. The RBE values predicted with the MCF MKM in combination with the αref and βref obtained with this MKM-based LQM fit are compared with the RBE values computed using the published αref and βref values obtained by other authors fitting the same survival curve. A benchmark of the RBE against corresponding in vitro data for irradiations with 12C ions is also included.
2. Materials and Methods
2.1. Relative Biological Effectiveness
2.2. Mayo Clinic Florida Microdosimetric Kinetic Model (MCF MKM)
2.2.1. Historical Background
2.2.2. MCF MKM Formalism
2.2.3. MCF MKM Parameters
2.3. Effect of αref/βref on the Calculated RBE for 12C Ions
2.4. Effect of the Absolute Values of αref and βref on the Calculated RBE for 12C Ions
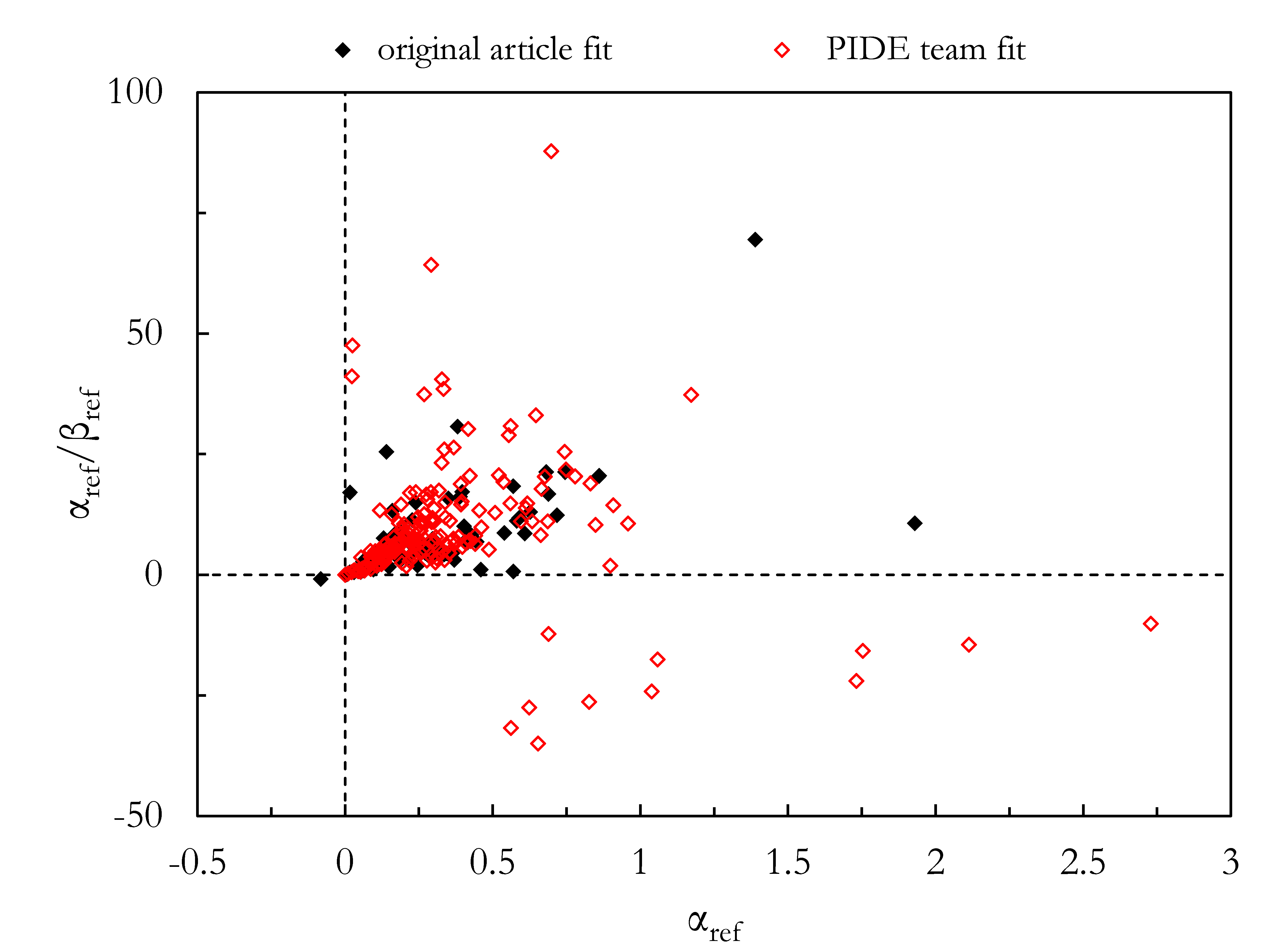
2.5. MKM-Based Fit of the Photon Survival Curve
2.6. Effect of Different Fits of the Same Photon Survival Curve on the Calculated RBE for 12C Ions
2.7. Computer Simulations
3. Results
3.1. Effect of αref/βref on the Calculated RBE for 12C Ions
3.2. Effect of the Absolute Values of αref and βref on the Calculated RBE for 12C Ions
3.3. Effect of Different Fits of the Same Photon Survival Curve on the Calculated RBE for 12C Ions
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| α | linear term of the linear-quadratic model of clonogenic survival |
| α0 | α in the limit of the lineal energy y → 0 |
| αref | α for the reference photon exposure |
| β | quadratic term of the linear-quadratic model of clonogenic survival |
| β0 | β in the limit of the lineal energy y → 0 |
| βref | β for the reference photon exposure |
| A-172 cell line | human glioblastoma cells |
| BED | biologically effective dose [37] |
| DNA | deoxyribonucleic acid |
| LEM | local effect model [8] |
| LEM IV | fourth version of the local effect model [30] |
| LET | linear energy transfer |
| LQM | linear-quadratic model of clonogenic survival [32] |
| M/10 cell line | human mammary epithelial cells |
| MCF | Mayo Clinic Florida, Jacksonville, Florida, United States of America |
| MCF MKM | Mayo Clinic Florida microdosimetric kinetic model [23] |
| MKM | microdosimetric kinetic model [25] |
| modified MKM | modified microdosimetric kinetic model [9] |
| PHITS | Particle and Heavy Ion Transport code System [57] |
| PIDE | Particle Irradiation Data Ensemble [53] |
| RBE | relative biological effectiveness |
| RBES | in vitro clonogenic cell survival RBE for the surviving fraction S (Equation (4)) |
| rd | mean radius of the subnuclear domains |
| Rn | mean radius of the cell nucleus |
| U-87 cell line | human glioblastoma cells |
| U-251MG cell line | human astrocytoma cells |
| y | lineal energy |
References
- Wilson, R.R. Radiological use of fast protons. Radiology 1946, 47, 487–491. [Google Scholar] [CrossRef] [PubMed]
- Durante, M.; Paganetti, H. Nuclear physics in particle therapy: A review. Rep. Prog. Phys. 2016, 79, 096702. [Google Scholar] [CrossRef] [PubMed]
- Facoetti, A.; Barcellini, A.; Valvo, F.; Pullia, M. The Role of Particle Therapy in the Risk of Radio-induced Second Tumors: A Review of the Literature. Anticancer Res. 2019, 39, 4613–4617. [Google Scholar] [CrossRef] [PubMed]
- Scholz, M. Effects of Ion Radiation on Cells and Tissues. Radiat. Eff. Polym. Biol. Use 2003, 162, 95–155. [Google Scholar]
- Ando, K.; Kase, Y. Biological characteristics of carbon-ion therapy. Int. J. Radiat. Biol. 2009, 85, 715–728. [Google Scholar] [CrossRef]
- Tinganelli, W.; Durante, M. Carbon Ion Radiobiology. Cancers 2020, 12, 3022. [Google Scholar] [CrossRef]
- Kanai, T.; Furusawa, Y.; Fukutsu, K.; Itsukaichi, H.; Eguchi-Kasai, K.; Ohara, H. Irradiation of mixed beam and design of spread-out Bragg peak for heavy-ion radiotherapy. Radiat. Res. 1997, 147, 78–85. [Google Scholar] [CrossRef]
- Scholz, M.; Kellerer, A.M.; Kraft-Weyrather, W.; Kraft, G. Computation of cell survival in heavy ion beams for therapy. The model and its approximation. Radiat. Environ. Biophys. 1997, 36, 59–66. [Google Scholar] [CrossRef]
- Kase, Y.; Kanai, T.; Matsumoto, Y.; Furusawa, Y.; Okamoto, H.; Asaba, T.; Sakama, M.; Shinoda, H. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams. Radiat. Res. 2006, 166, 629–638. [Google Scholar] [CrossRef]
- Kanai, T.; Endo, M.; Minohara, S.; Miyahara, N.; Koyama-ito, H.; Tomura, H.; Matsufuji, N.; Futami, Y.; Fukumura, A.; Hiraoka, T.; et al. Biophysical characteristics of HIMAC clinical irradiation system for heavy-ion radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 1999, 44, 201–210. [Google Scholar] [CrossRef]
- Jakel, O.; Kramer, M.; Karger, C.P.; Debus, J. Treatment planning for heavy ion radiotherapy: Clinical implementation and application. Phys. Med. Biol. 2001, 46, 1101–1116. [Google Scholar] [CrossRef] [PubMed]
- Inaniwa, T.; Kanematsu, N.; Matsufuji, N.; Kanai, T.; Shirai, T.; Noda, K.; Tsuji, H.; Kamada, T.; Tsujii, H. Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the National Institute of Radiological Sciences, Japan. Phys. Med. Biol. 2015, 60, 3271–3286. [Google Scholar] [CrossRef] [PubMed]
- Inaniwa, T.; Suzuki, M.; Hyun Lee, S.; Mizushima, K.; Iwata, Y.; Kanematsu, N.; Shirai, T. Experimental validation of stochastic microdosimetric kinetic model for multi-ion therapy treatment planning with helium-, carbon-, oxygen-, and neon-ion beams. Phys. Med. Biol. 2020, 65, 045005. [Google Scholar] [CrossRef] [PubMed]
- Yagi, M.; Tsubouchi, T.; Hamatani, N.; Takashina, M.; Maruo, H.; Fujitaka, S.; Nihongi, H.; Ogawa, K.; Kanai, T. Commissioning a newly developed treatment planning system, VQA Plan, for fast-raster scanning of carbon-ion beams. PLoS ONE 2022, 17, e0268087. [Google Scholar] [CrossRef]
- Puck, T.T.; Marcus, P.I. Action of X-rays on mammalian cells. J. Exp. Med. 1956, 103, 653–666. [Google Scholar] [CrossRef]
- Brix, N.; Samaga, D.; Belka, C.; Zitzelsberger, H.; Lauber, K. Analysis of clonogenic growth in vitro. Nat. Protoc. 2021, 16, 4963–4991. [Google Scholar] [CrossRef]
- Kanai, T.; Matsufuji, N.; Miyamoto, T.; Mizoe, J.; Kamada, T.; Tsuji, H.; Kato, H.; Baba, M.; Tsujii, H. Examination of GyE system for HIMAC carbon therapy. Int. J. Radiat. Oncol. Biol. Phys. 2006, 64, 650–656. [Google Scholar] [CrossRef]
- Paganetti, H. Relating the proton relative biological effectiveness to tumor control and normal tissue complication probabilities assuming interpatient variability in alpha/beta. Acta Oncol. 2017, 56, 1379–1386. [Google Scholar] [CrossRef]
- Abolfath, R.; Helo, Y.; Bronk, L.; Carabe, A.; Grosshans, D.; Mohan, R. Renormalization of radiobiological response functions by energy loss fluctuations and complexities in chromosome aberration induction: Deactivation theory for proton therapy from cells to tumor control. Eur. Phys. J. D 2019, 73, 1–22. [Google Scholar] [CrossRef]
- Kase, Y.; Kanai, T.; Matsufuji, N.; Furusawa, Y.; Elsasser, T.; Scholz, M. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation. Phys. Med. Biol. 2008, 53, 37–59. [Google Scholar] [CrossRef]
- Karger, C.P. Peschke, RBE and related modeling in carbon-ion therapy. Phys. Med. Biol. 2017, 63, 01TR02. [Google Scholar] [CrossRef] [PubMed]
- Beltran, C.; Amos, R.A.; Rong, Y. We are ready for clinical implementation of Carbon Ion Radiotherapy in the United States. J. Appl. Clin. Med. Phys. 2020, 21, 6–9. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Beltran, C.J.; Furutani, K.M. The Mayo Clinic Florida microdosimetric kinetic model of clonogenic survival: Formalism and first benchmark against in vitro and in silico data. Phys. Med. Biol. 2022, 67, 185013. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Beltran, C.J.; Furutani, K.M. The Mayo Clinic Florida Microdosimetric Kinetic Model of Clonogenic Survival: Application to Various Repair-Competent Rodent and Human Cell Lines. Int. J. Mol. Sci. 2022, 23, 12491. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.B. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat. Res. 1994, 140, 366–374. [Google Scholar] [CrossRef]
- Loncol, T.; Cosgrove, V.; Denis, J.M.; Gueulette, J.; Mazal, A.; Menzel, H.G.; Pihet, P.; Sabattier, R. Radiobiological Effectiveness of Radiation Beams with Broad LET Spectra: Microdosimetric Analysis Using Biological Weighting Functions. Radiat. Prot. Dosim. 1994, 52, 347–352. [Google Scholar] [CrossRef]
- Hawkins, R.B. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET. Radiat. Res. 2003, 160, 61–69. [Google Scholar] [CrossRef]
- Parisi, A.; Sato, T.; Matsuya, Y.; Kase, Y.; Magrin, G.; Verona, C.; Tran, L.; Rosenfeld, A.; Bianchi, A.; Olko, P.; et al. Development of a new microdosimetric biological weighting function for the RBE(10) assessment in case of the V79 cell line exposed to ions from (1)H to (238)U. Phys. Med. Biol. 2020, 65, 235010. [Google Scholar] [CrossRef]
- Friedrich, T.; Durante, M.; Scholz, M. Modeling cell survival after photon irradiation based on double-strand break clustering in megabase pair chromatin loops. Radiat. Res. 2012, 178, 385–394. [Google Scholar] [CrossRef]
- Elsasser, T.; Weyrather, W.K.; Friedrich, T.; Durante, M.; Iancu, G.; Kramer, M.; Kragl, G.; Brons, S.; Winter, M.; Weber, K.J.; et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: Direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int. J. Radiat. Oncol. Biol. Phys. 2010, 78, 1177–1183. [Google Scholar] [CrossRef]
- Mairani, A.; Bohlen, T.T.; Dokic, I.; Cabal, G.; Brons, S.; Haberer, T. Modelling of cell killing due to sparsely ionizing radiation in normoxic and hypoxic conditions and an extension to high LET radiation. Int. J. Radiat. Biol. 2013, 89, 782–793. [Google Scholar] [CrossRef] [PubMed]
- McMahon, S.J. The linear quadratic model: Usage, interpretation and challenges. Phys. Med. Biol. 2018, 64, s01TR01. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T.; Scholz, U.; Elsasser, T.; Durante, M.; Scholz, M. Systematic analysis of RBE and related quantities using a database of cell survival experiments with ion beam irradiation. J. Radiat. Res. 2013, 54, 494–514. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Beltran, C.J.; Furutani, K.M. The effect of fitting the reference photon dose-response on the clonogenic survival predicted with the Mayo Clinic Florida microdosimetric kinetic model in case of accelerated ions. Radiat. Prot. Dosim. 2022; in press. [Google Scholar]
- Rorvik, E.; Fjaera, L.F.; Dahle, T.J.; Dale, J.E.; Engeseth, G.M.; Stokkevag, C.H.; Thornqvist, S.; Ytre-Hauge, K.S. Exploration and application of phenomenological RBE models for proton therapy. Phys. Med. Biol. 2018, 63, 185013. [Google Scholar] [CrossRef]
- Fowler, J.F. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol. 1989, 62, 679–694. [Google Scholar] [CrossRef]
- Fowler, J.F. 21 years of biologically effective dose. Br. J. Radiol. 2010, 83, 554–568. [Google Scholar] [CrossRef]
- Jones, B.; Carabe-Fernandez, A.; Dale, R.G. Calculation of high-LET radiotherapy dose required for compensation of overall treatment time extensions. Br. J. Radiol. 2006, 79, 254–257. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Watanabe, R.; Kase, Y.; Tsuruoka, C.; Suzuki, M.; Furusawa, Y.; Niita, K. Analysis of cell-survival fractions for heavy-ion irradiations based on microdosimetric kinetic model implemented in the particle and heavy ion transport code system. Radiat. Prot. Dosim. 2011, 143, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Scholz, M. Calculation of RBE for normal tissue complications based on charged particle track structure. Bull. Cancer Radiother. 1996, 83, 50s–54s. [Google Scholar] [CrossRef]
- Mein, S.; Klein, C.; Kopp, B.; Magro, G.; Harrabi, S.; Karger, C.P.; Haberer, T.; Debus, J.; Abdollahi, A.; Dokic, I.; et al. Assessment of RBE-Weighted Dose Models for Carbon Ion Therapy Toward Modernization of Clinical Practice at HIT: In Vitro, In Vivo, and in Patients. Int. J. Radiat. Oncol. Biol. Phys. 2020, 108, 779–791. [Google Scholar] [CrossRef] [PubMed]
- Rossi, H.H.; Zaider, M. Microdosimetry and Its Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Hawkins, R.B. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET. Med. Phys. 1998, 25, 1157–1170. [Google Scholar] [CrossRef]
- Sato, T.; Furusawa, Y. Cell survival fraction estimation based on the probability densities of domain and cell nucleus specific energies using improved microdosimetric kinetic models. Radiat. Res. 2012, 178, 341–356. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Li, C.; Qiu, R.; Wu, Z. A modified microdosimetric kinetic model for relative biological effectiveness calculation. Phys. Med. Biol. 2017, 63, 015008. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Furutani, K.M.; Beltran, C.J. On the calculation of the relative biological effectiveness of ion radiation therapy using a biological weighting function, the microdosimetric kinetic model (MKM) and subsequent corrections (non-Poisson MKM and modified MKM). Phys. Med. Biol. 2022, 67, 095014. [Google Scholar] [CrossRef]
- McMahon, S.J.; McNamara, A.L.; Schuemann, J.; Paganetti, H.; Prise, K.M. A general mechanistic model enables predictions of the biological effectiveness of different qualities of radiation. Sci. Rep. 2017, 7, 10790. [Google Scholar] [CrossRef]
- Yokota, H.; Vandenengh, G.; Hearst, J.E.; Sachs, R.K.; Trask, B.J. Evidence for the Organization of Chromatin in Megabase Pair-Sized Loops Arranged along a Random-Walk Path in the Human G0/G1 Interphase Nucleus. J. Cell Biol. 1995, 130, 1239–1249. [Google Scholar] [CrossRef]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA double-stranded breaks induce histone H2AX phosphorylation on serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef]
- Paganetti, H. Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer. Phys. Med. Biol. 2014, 59, R419–R472. [Google Scholar] [CrossRef]
- Tilly, N.; Johansson, J.; Isacsson, U.; Medin, J.; Blomquist, E.; Grusell, E.; Glimelius, B. The influence of RBE variations in a clinical proton treatment plan for a hypopharynx cancer. Phys. Med. Biol. 2005, 50, 2765–2777. [Google Scholar] [CrossRef]
- McNamara, A.L.; Schuemann, J.; Paganetti, H. A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data. Phys. Med. Biol. 2015, 60, 8399–8416. [Google Scholar] [CrossRef]
- Friedrich, T.; Pfuhl, T.; Scholz, M. Update of the particle irradiation data ensemble (PIDE) for cell survival. J. Radiat. Res. 2021, 62, 645–655. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T.; Durante, M.; Scholz, M. Comments on the paper “Modelling of cell killing due to sparsely ionizing radiation in normoxic and hypoxic conditions and an extension to high LET radiation” by A. Mairani et al. Int. J. Radiat. Biol. 89(10), 2013, 782–793. Int. J. Radiat. Biol. 2015, 91, 127–128. [Google Scholar] [CrossRef] [PubMed]
- Tsuboi, K.; Tsuchida, Y.; Nose, T.; Ando, K. Cytotoxic effect of accelerated carbon beams on glioblastoma cell lines with p53 mutation: Clonogenic survival and cell-cycle analysis. Int. J. Radiat. Biol. 1998, 74, 71–79. [Google Scholar] [CrossRef]
- Belli, M.; Bettega, D.; Calzolari, P.; Cherubini, R.; Cuttone, G.; Durante, M.; Esposito, G.; Furusawa, Y.; Gerardi, S.; Gialanella, G.; et al. Effectiveness of monoenergetic and spread-out bragg peak carbon-ions for inactivation of various normal and tumour human cell lines. J. Radiat. Res. 2008, 49, 597–607. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Iwamoto, Y.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Abe, S.-i.; Kai, T.; Tsai, P.-E.; Matsuda, N.; Iwase, H.; et al. Features of Particle and Heavy Ion Transport code System (PHITS) version 3.02. J. Nucl. Sci. Technol. 2018, 55, 684–690. [Google Scholar] [CrossRef]
- Sato, T.; Watanabe, R.; Niita, K. Development of a calculation method for estimating specific energy distribution in complex radiation fields. Radiat. Prot. Dosim. 2006, 122, 41–45. [Google Scholar] [CrossRef]
- Tsuda, S.; Sato, T.; Takahashi, F.; Satoh, D.; Sasaki, S.; Namito, Y.; Iwase, H.; Ban, S.; Takada, M. Systematic measurement of lineal energy distributions for proton, He and Si ion beams over a wide energy range using a wall-less tissue equivalent proportional counter. J. Radiat. Res. 2012, 53, 264–271. [Google Scholar] [CrossRef] [PubMed]
- Takada, K.; Sato, T.; Kumada, H.; Koketsu, J.; Takei, H.; Sakurai, H.; Sakae, T. Validation of the physical and RBE-weighted dose estimator based on PHITS coupled with a microdosimetric kinetic model for proton therapy. J. Radiat. Res. 2018, 59, 91–99. [Google Scholar] [CrossRef]
- Hu, N.; Tanaka, H.; Takata, T.; Endo, S.; Masunaga, S.; Suzuki, M.; Sakurai, Y. Evaluation of PHITS for microdosimetry in BNCT to support radiobiological research. Appl. Radiat. Isot. 2020, 161, 109148. [Google Scholar] [CrossRef]
- Parisi, A.; Van Hoey, O.; Mégret, P.; Vanhavere, F. Microdosimetric specific energy probability distribution in nanometric targets and its correlation with the efficiency of thermoluminescent detectors exposed to charged particles. Radiat. Meas. 2019, 123, 1–12. [Google Scholar] [CrossRef]
- Parisi, A.; Dabin, J.; Schoonjans, W.; Van Hoey, O.; Mégret, P.; Vanhavere, F. Photon energy response of LiF:Mg,Ti (MTS) and LiF:Mg,Cu,P (MCP) thermoluminescent detectors: Experimental measurements and microdosimetric modeling. Radiat. Phys. Chem. 2019, 163, 67–73. [Google Scholar] [CrossRef]
- Parisi, A.; Struelens, L.; Vanhavere, F. Nanoscale calculation of the relative efficiency of 7LiF:Mg,Ti (MTS-7) and 7LiF:Mg,Cu,P (MCP-7) thermoluminescent detectors for measuring electrons and positrons. J. Phys. Conf. Ser. 2020, 1662, 012025. [Google Scholar] [CrossRef]
- Parisi, A.; Olko, P.; Swakoń, J.; Horwacik, T.; Jabłoński, H.; Malinowski, L.; Nowak, T.; Struelens, L.; Vanhavere, F. A new method to predict the response of thermoluminescent detectors exposed at different positions within a clinical proton beam. Radiat. Meas. 2020, 133, 106281. [Google Scholar] [CrossRef]
- Parisi, A.; Sawakuchi, G.; Granville, D.; Yukihara, E.G. Microdosimetric modeling of the relative efficiency of Al2O3:C (Luxel, blue emission) optically stimulated luminescent detectors exposed to ions from 1H to 132Xe. Radiat. Meas. 2022, 150, 106678. [Google Scholar] [CrossRef]
- Hirata, Y.; Sato, T.; Watanabe, K.; Ogawa, T.; Parisi, T.; Uritani, A. Theoretical and experimental estimation of the relative optically stimulated luminescence efficiency of an optical-fiber-based BaFBr:Eu detector for swift ions. J. Nucl. Sci. Technol. 2022, 59, 915–924. [Google Scholar] [CrossRef]
- Parisi, A.; Struelens, L.; Vanhavere, F. Comparison between the results of a recently-developed biological weighting function (V79-RBE(10)BWF) and thein vitroclonogenic survival RBE(10)of other repair-competent asynchronized normoxic mammalian cell lines and ions not used for the development of the model. Phys. Med. Biol. 2021, 66, 235006. [Google Scholar]
- Inaniwa, T.; Suzuki, M.; Furukawa, T.; Kase, Y.; Kanematsu, N.; Shirai, T.; Hawkins, R.B. Effects of dose-delivery time structure on biological effectiveness for therapeutic carbon-ion beams evaluated with microdosimetric kinetic model. Radiat. Res. 2013, 180, 44–59. [Google Scholar] [CrossRef] [PubMed]
- Inaniwa, T.; Kanematsu, N.; Suzuki, M.; Hawkins, R.B. Effects of beam interruption time on tumor control probability in single-fractionated carbon-ion radiotherapy for non-small cell lung cancer. Phys. Med. Biol. 2015, 60, 4105–4121. [Google Scholar] [CrossRef] [PubMed]
- McMahon, S.J. Proton RBE models: Commonalities and differences. Phys. Med. Biol. 2021, 66, 04NT02. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.B. Mammalian cell killing by ultrasoft X rays and high-energy radiation: An extension of the MK model. Radiat. Res. 2006, 166, 431–442. [Google Scholar] [CrossRef]
- Chaudhary, P.; Marshall, T.I.; Perozziello, F.M.; Manti, L.; Currell, F.J.; Hanton, F.; McMahon, S.J.; Kavanagh, J.N.; Cirrone, G.A.; Romano, F.; et al. Relative biological effectiveness variation along monoenergetic and modulated Bragg peaks of a 62-MeV therapeutic proton beam: A preclinical assessment. Int. J. Radiat. Oncol. Biol. Phys. 2014, 90, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Joiner, M.C.; Marples, B.; Lambin, P.; Short, S.C.; Turesson, I. Low-dose hypersensitivity: Current status and possible mechanisms. Int. J. Radiat. Oncol. Biol. Phys. 2001, 49, 379–389. [Google Scholar] [CrossRef] [PubMed]
- Matsuya, Y.; Sasaki, K.; Yoshii, Y.; Okuyama, G.; Date, H. Integrated Modelling of Cell Responses after Irradiation for DNA-Targeted Effects and Non-Targeted Effects. Sci. Rep. 2018, 8, 4849. [Google Scholar] [CrossRef] [PubMed]
- Garcia, L.M.; Leblanc, J.; Wilkins, D.; Raaphorst, G.P. Fitting the linear-quadratic model to detailed data sets for different dose ranges. Phys. Med. Biol. 2006, 51, 2813–2823. [Google Scholar] [CrossRef]
- Astrahan, M. Some implications of linear-quadratic-linear radiation dose-response with regard to hypofractionation. Med. Phys. 2008, 35, 4161–4172. [Google Scholar] [CrossRef] [PubMed]


| Cell Line | Rn [µm] | rd [µm] | LQM Fit | αref [Gy−1] | βref = β0 [Gy−2] | αref/βref [Gy] | α0 [Gy−1] |
|---|---|---|---|---|---|---|---|
| A-172 | 5.7 [34] | 0.3 [34] | original article [55] | 0.405 | 0.0588 | 6.89 | 0.328 |
| PIDE team [53] | 0.310 | 0.0888 | 3.49 | 0.194 | |||
| MKM-based | 0.428 | 0.0544 | 7.87 | 0.357 | |||
| M/10 | 4.7 [24] | 0.29 [24] | original article [56] | 0.300 | 0.0680 | 4.41 | 0.205 |
| PIDE team [53] | 0 | 0.1120 | 0 | −0.156 | |||
| MKM-based | 0.288 | 0.0785 | 3.67 | 0.178 | |||
| U-251MG | 4.9 [24] | 0.29 [24] | original article [55] | 0.031 | 0.0551 | 0.56 | −0.046 |
| PIDE team [53] | 0 | 0.0609 | 0 | −0.085 | |||
| MKM-based | 0.0635 | 0.0455 | 1.39 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parisi, A.; Beltran, C.J.; Furutani, K.M. Clonogenic Survival RBE Calculations in Carbon Ion Therapy: The Importance of the Absolute Values of α and β in the Photon Dose-Response Curve and a Strategy to Mitigate Their Anticorrelation. Quantum Beam Sci. 2023, 7, 3. https://doi.org/10.3390/qubs7010003
Parisi A, Beltran CJ, Furutani KM. Clonogenic Survival RBE Calculations in Carbon Ion Therapy: The Importance of the Absolute Values of α and β in the Photon Dose-Response Curve and a Strategy to Mitigate Their Anticorrelation. Quantum Beam Science. 2023; 7(1):3. https://doi.org/10.3390/qubs7010003
Chicago/Turabian StyleParisi, Alessio, Chris J. Beltran, and Keith M. Furutani. 2023. "Clonogenic Survival RBE Calculations in Carbon Ion Therapy: The Importance of the Absolute Values of α and β in the Photon Dose-Response Curve and a Strategy to Mitigate Their Anticorrelation" Quantum Beam Science 7, no. 1: 3. https://doi.org/10.3390/qubs7010003
APA StyleParisi, A., Beltran, C. J., & Furutani, K. M. (2023). Clonogenic Survival RBE Calculations in Carbon Ion Therapy: The Importance of the Absolute Values of α and β in the Photon Dose-Response Curve and a Strategy to Mitigate Their Anticorrelation. Quantum Beam Science, 7(1), 3. https://doi.org/10.3390/qubs7010003









