3D Visualized Characterization of Fracture Behavior of Structural Metals Using Synchrotron Radiation Computed Microtomography
Abstract
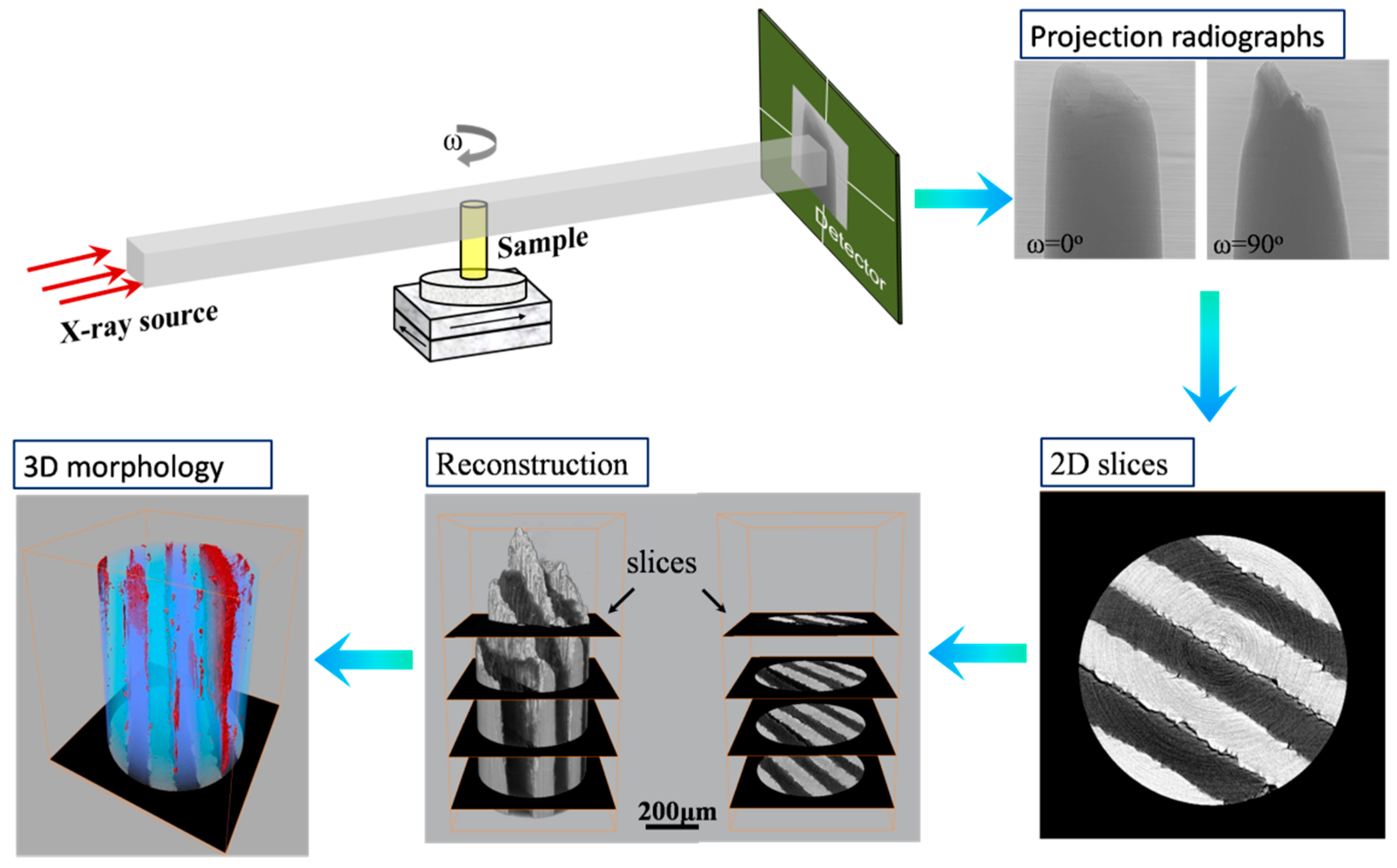
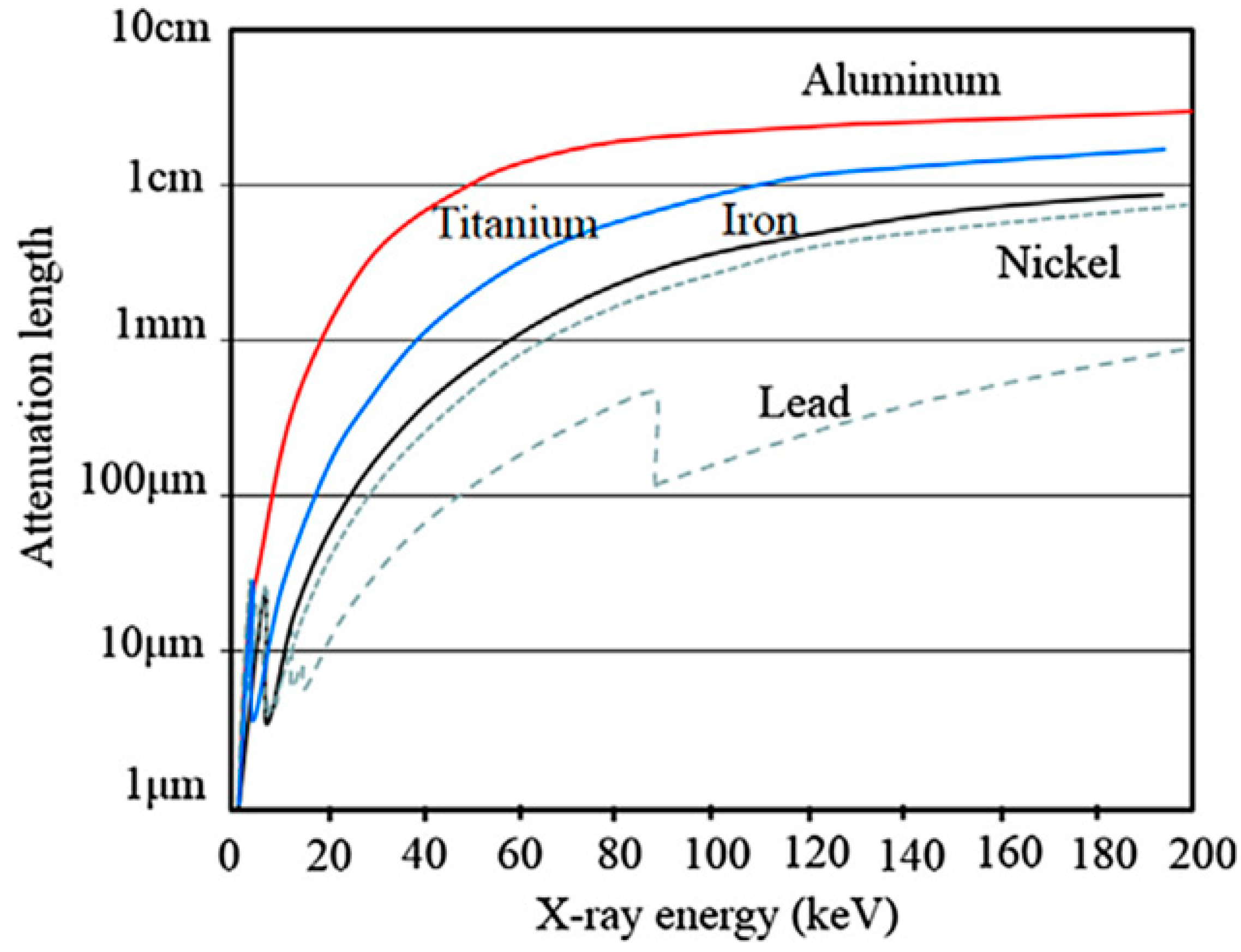
1. Introduction
2. 3D Characterization of Fracture Behavior for Metal Matrix Composites Using SR-μCT
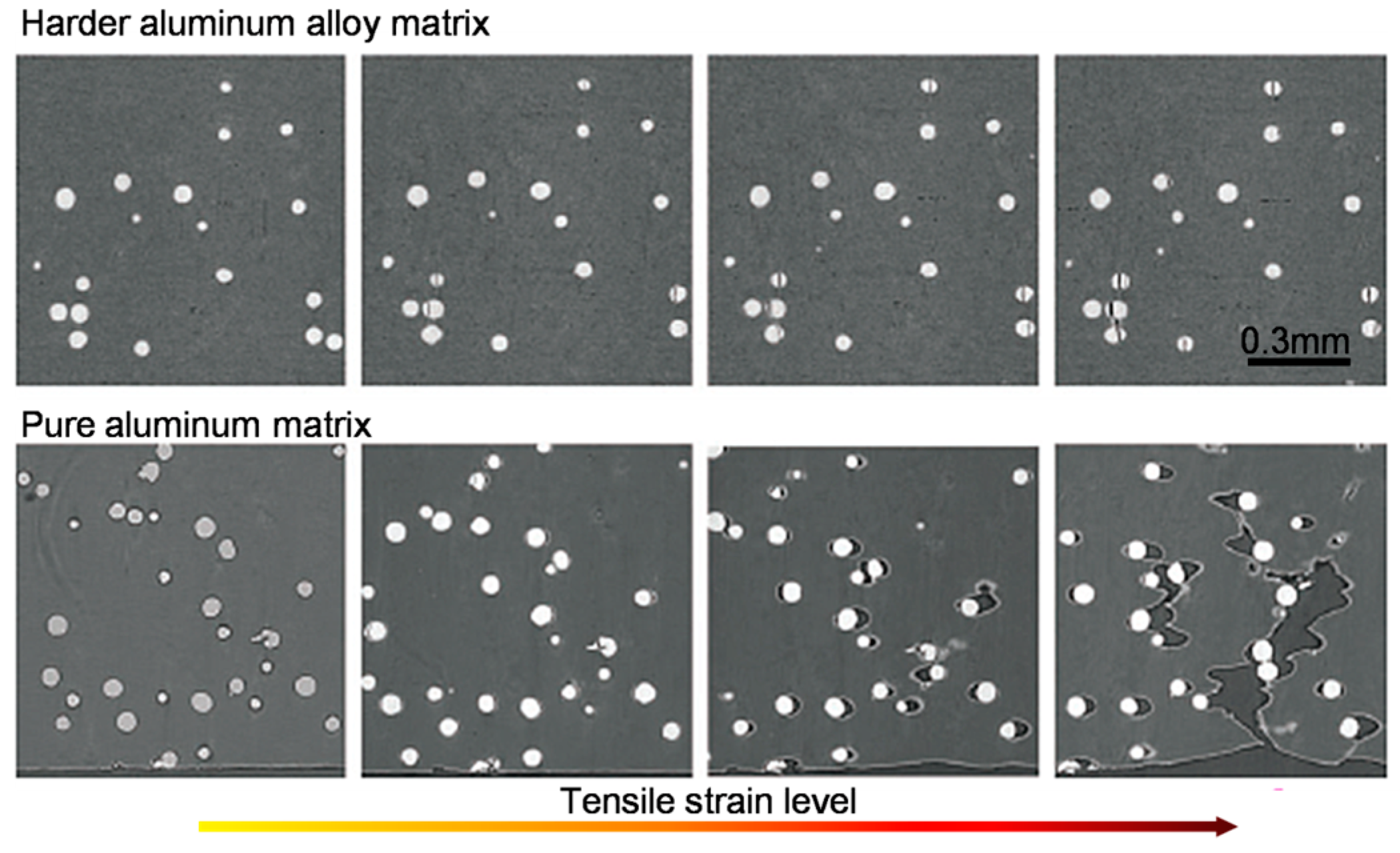
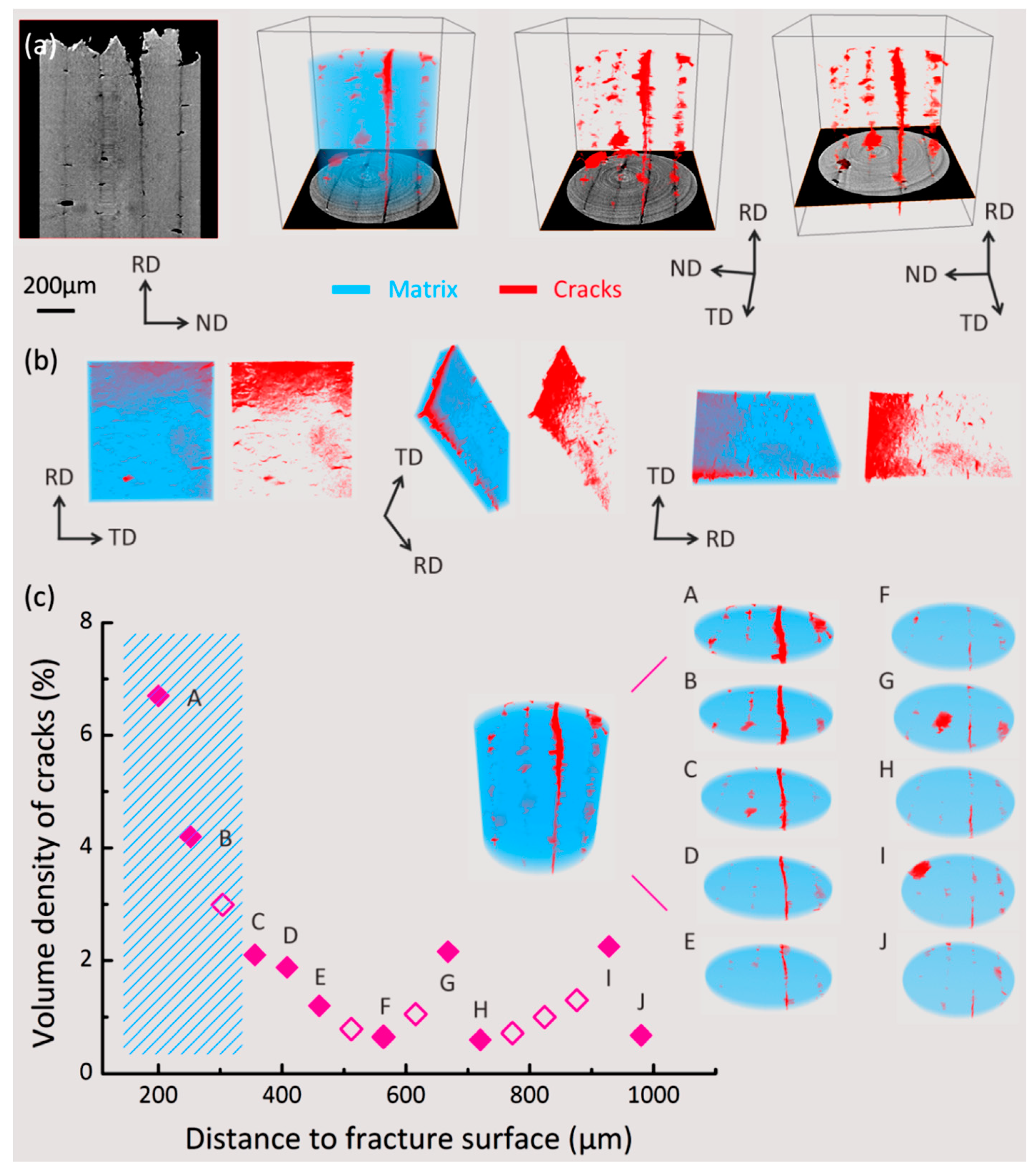
2.1. Particle-Reinforced Aluminum Matrix Composites
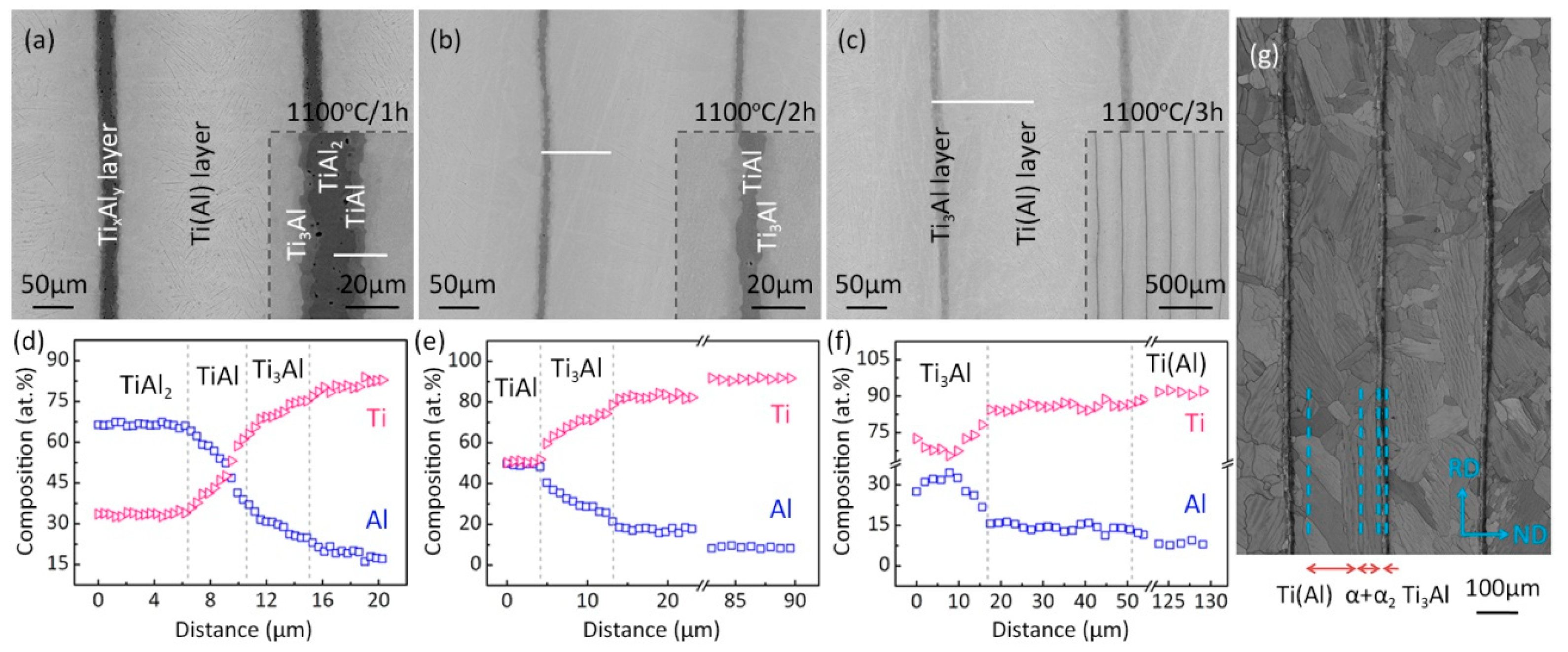
2.2. Layered α2-Ti3Al/α-Ti Composite
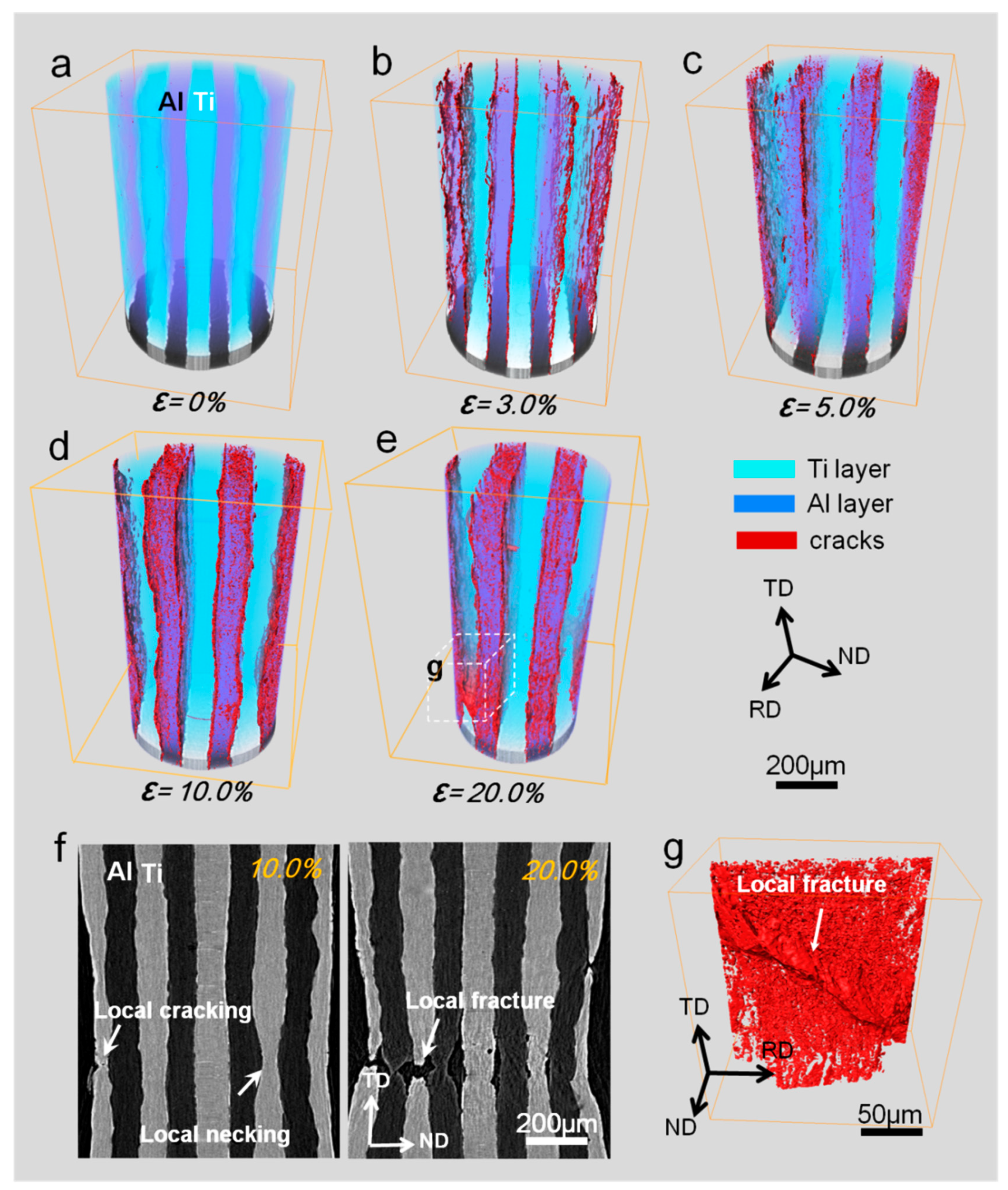
2.3. Layered Ti/Al Metal Composites
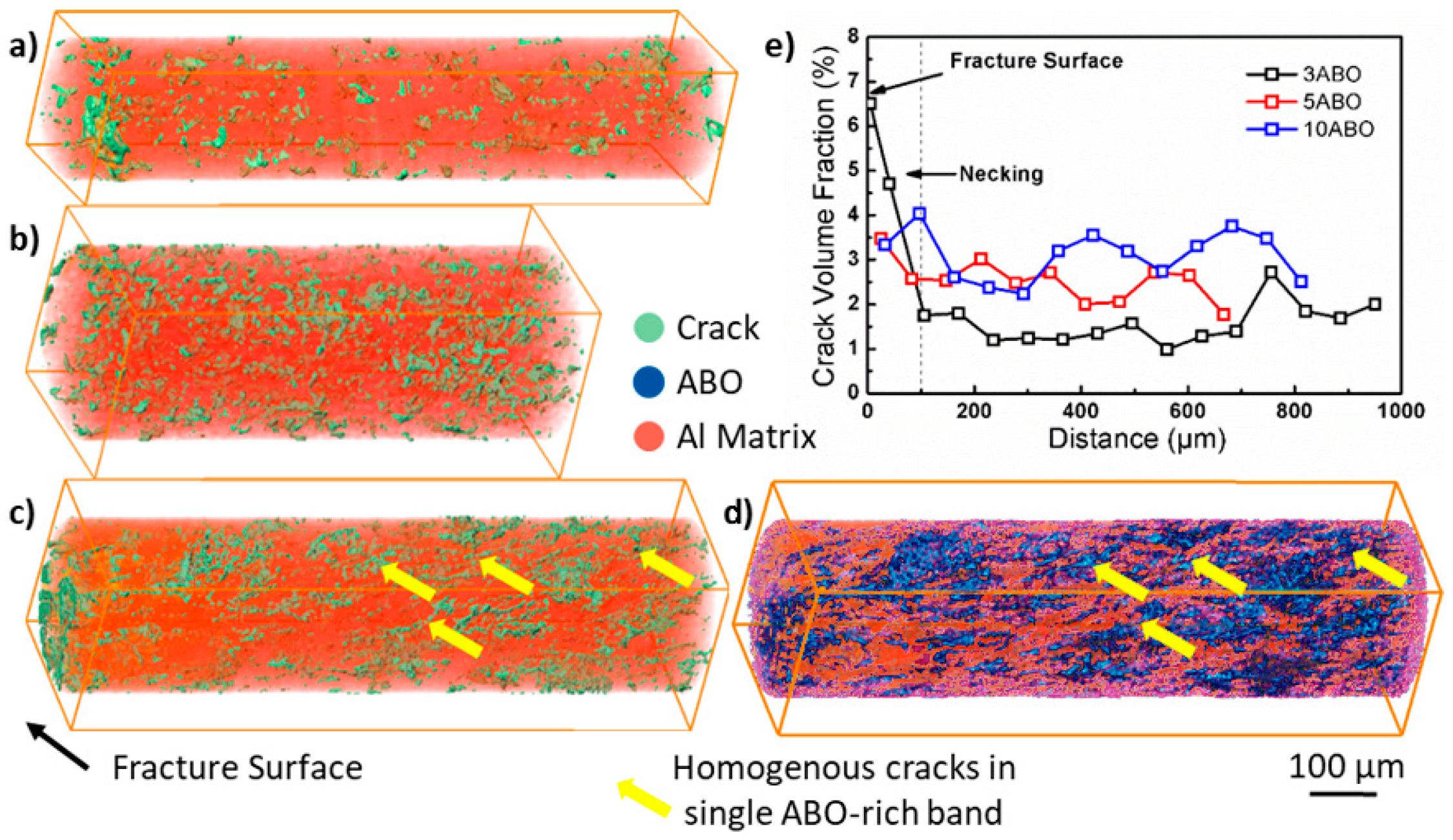
2.4. Al/Al18B4O33 Composites
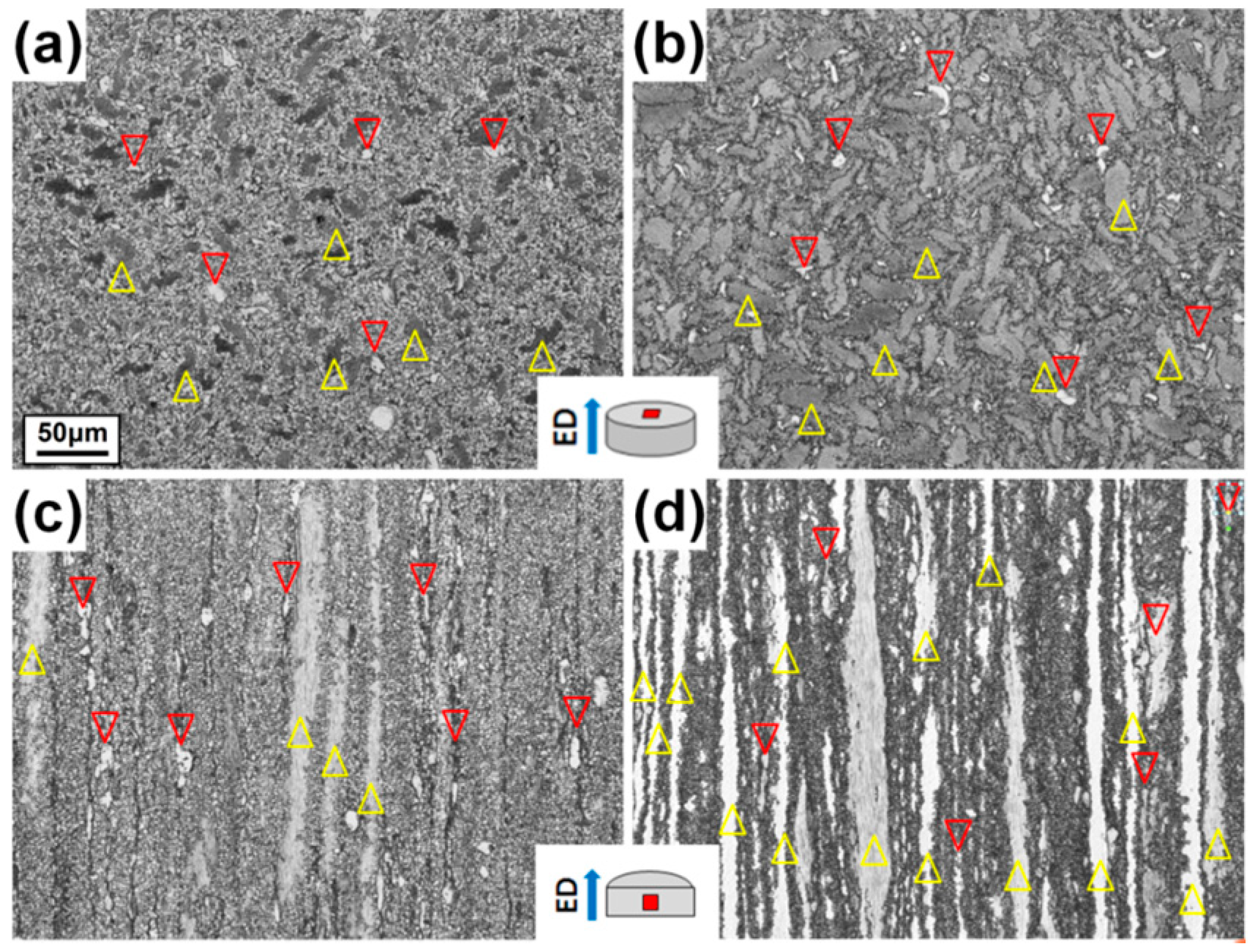
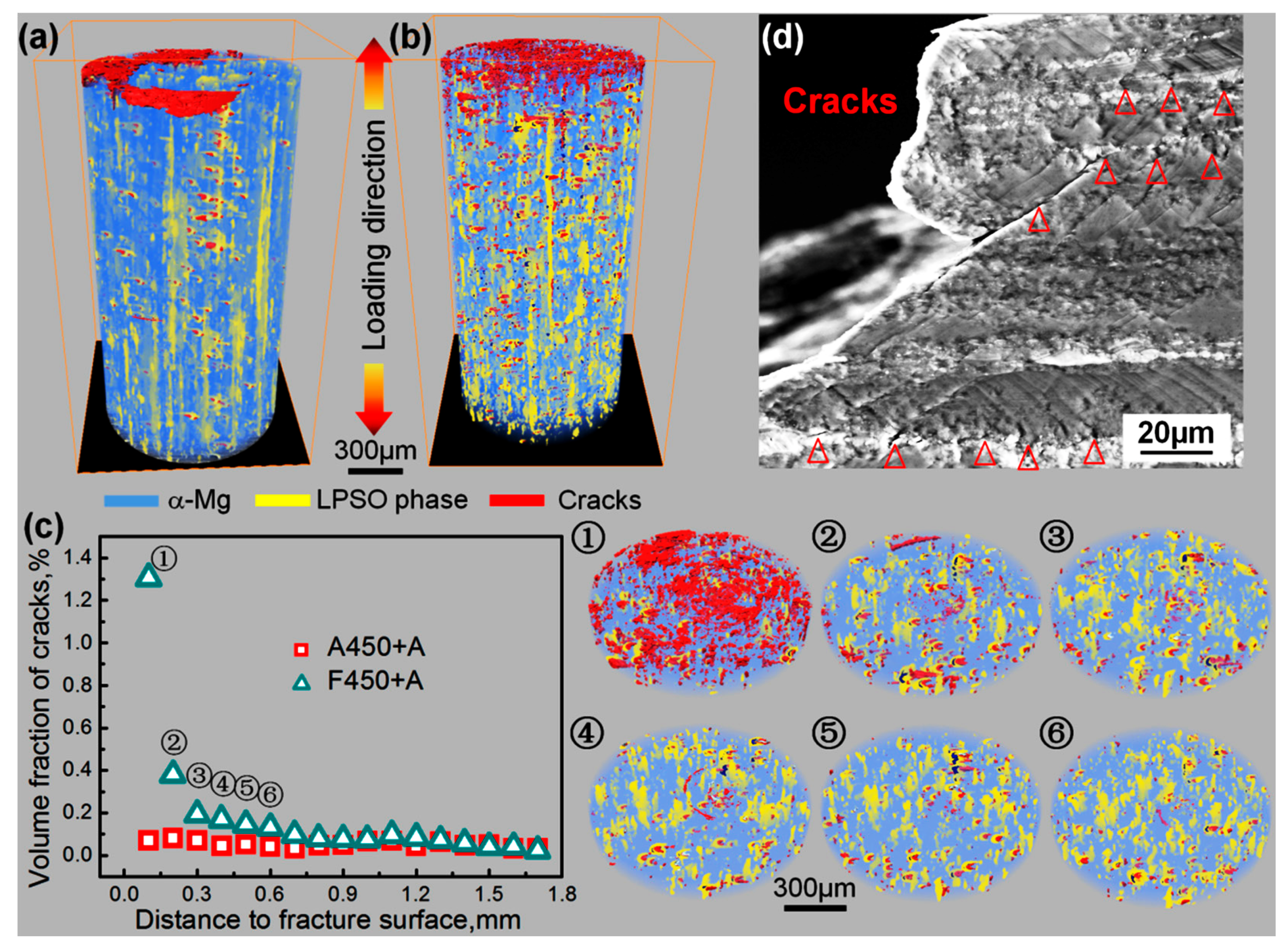
2.5. Long Period Stacking Ordered (LPSO) Phase Containing Mg Alloy
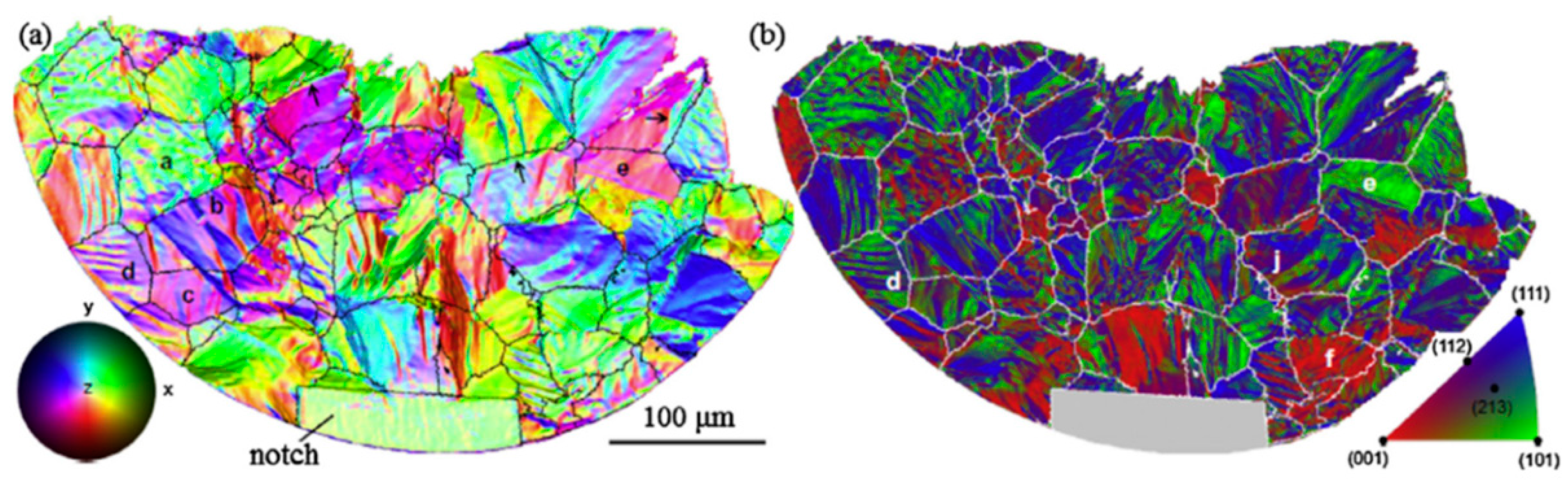
2.6. Grain Mapping with Diffraction Contrast Tomography (DCT)
3. Summary and Future Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Wu, S.C.; Hu, Y.N.; Duan, H.; Yu, C.; Jiao, H.S. On the fatigue performance of laser hybrid welded high Zn 7000 alloys for next generation railway components. Int. J. Fatigue 2016, 91, 1–10. [Google Scholar] [CrossRef]
- Gao, Y.K.; Li, X.B.; Yang, Q.X.; Yao, M. Influence of surface integrity on fatigue strength of 40CrNi2Si2MoVA steel. Mater. Lett. 2007, 61, 466–469. [Google Scholar] [CrossRef]
- Withers, P.J. Fracture mechanics by three-dimensional crack-tip synchrotron X-ray microscopy. Philos. Trans. R. Soc. A 2015, 373, 20130157. [Google Scholar] [CrossRef] [PubMed]
- Stock, S.R. Recent advances in X-ray microtomography applied to materials. Int. Mater. Rev. 2013, 53, 129–181. [Google Scholar] [CrossRef]
- Wu, S.C.; Yu, C.; Zhang, W.H.; Fu, Y.N.; Helfen, L. Porosity induced fatigue damage of laser welded 7075-T6 joints investigated via synchrotron X-ray microtomography. Sci. Technol. Weld. Join. 2015, 20, 11–19. [Google Scholar] [CrossRef]
- Hounsfield, G.N. Computerized transverse axial scanning (tomography): Part I. Description of system. Br. J. Radiol. 1973, 46, 1016–1022. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.C.; Xiao, T.Q.; Withers, P.J. The imaging of failure in structural materials by synchrotron radiation X-ray microtomography. Eng. Fract. Mech. 2017, 182, 127–156. [Google Scholar] [CrossRef]
- Stock, S.R. X-ray microtomography of materials. Int. Mater. Rev. 2013, 44, 141–164. [Google Scholar] [CrossRef]
- Wang, T.; Xu, J.; Xiao, T.; Xie, H.; Li, J.; Li, T.; Cao, Z. Evolution of dendrite morphology of a binary alloy under an applied electric current: An in situ observation. Phys. Rev. E 2010, 81, 042601. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Cao, F.; Zhou, P.; Kang, H.; Chen, Z.; Fu, Y.; Xiao, T.; Huang, W.; Yuan, Q. Study on diffusion behavior and microstructural evolution of Al/Cu bimetal interface by synchrotron X-ray radiography. J. Alloys Compd. 2014, 616, 550–555. [Google Scholar] [CrossRef]
- Kamitsubo, H. Spring 8 program. J. Synchrotron Radiat. 1997, 5, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Fan, G.H.; Geng, L.; Cao, G.J.; Du, Y.; Wu, H.; Zhang, T.T.; Kang, H.J.; Wang, T.M.; Du, G.H.; et al. Revealing extraordinary tensile plasticity in layered Ti-Al metal composite. Sci. Rep. 2016, 6, 38461. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Fan, G.H.; Nakata, T.; Liang, X.; Chi, Y.Q.; Qiao, X.G.; Cao, G.J.; Zhang, T.T.; Huang, M.; Miao, K.S.; et al. Deformation behavior of ultra-strong and ductile Mg-Gd-Y-Zn-Zr alloy with bimodal structure. Metall. Mater. Trans. A 2018, 49, 1931–1947. [Google Scholar] [CrossRef]
- Sasov, A.; Pauwels, B.; Bruyndonckx, P.; Liu, X.; McNulty, I.; Eyberger, C.; Lai, B. New lens-free X-ray source for laboratory nano-CT with 50-nm spatial resolution. AIP Conf. Proc. 2011, 1365, 140–143. [Google Scholar]
- Cloetens, P.; Barrett, R.; Baruchel, J.; Guigay, J.P.; Schlenker, M. Phase objects in synchrotron radiation hard X-ray imaging. J. Phys. D Appl. Phys. 1996, 29, 133–146. [Google Scholar] [CrossRef]
- Marrow, T. High resolution X-ray tomography of short fatigue crack nucleation in austempered ductile cast iron. Int. J. Fatigue 2004, 26, 717–725. [Google Scholar] [CrossRef]
- Garces, G.; Morris, D.G.; Muñoz-Morris, M.A.; Perez, P.; Tolnai, D.; Mendis, C.; Stark, A.; Lim, H.K.; Kim, S.; Shell, N.; et al. Plasticity analysis by synchrotron radiation in a Mg97Y2Zn1 alloy with bimodal grain structure and containing LPSO phase. Acta Mater. 2015, 94, 78–86. [Google Scholar] [CrossRef]
- Fu, H.; Ge, B.; Xin, Y.; Wu, R.; Fernandez, C.; Huang, J.; Peng, Q. Achieving high strength and ductility in magnesium alloys via densely hierarchical double contraction nanotwins. Nano Lett. 2017, 17, 6117–6124. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Toda, H.; Hara, H.; Kobayashi, M.; Kobayashi, T.; Sugiyama, D.; Kuroda, N.; Uesugi, K. Three-dimensional visualization of the interaction between fatigue crack and micropores in an aluminum alloy using synchrotron X-ray microtomography. Metall. Mater. Trans. A 2007, 38, 1774–1785. [Google Scholar] [CrossRef]
- Kabir, M.; Bulpett, R. A study of fatigue failure initiation in high cycle high-pressure automotive applications and conventional rotating bending fatigue testing. Int. J. Fatigue 2007, 29, 1966–1970. [Google Scholar] [CrossRef]
- Wu, S.C.; Yu, C.; Yu, P.S.; Buffière, J.Y.; Helfen, L.; Fu, Y.N. Corner fatigue cracking behavior of hybrid laser AA7020 welds by synchrotron X-ray computed microtomography. Mater. Sci. Eng. A 2016, 651, 604–614. [Google Scholar] [CrossRef]
- Pannemaecker, A.; Fouvry, S.; Brochu, M.; Buffiere, J.Y. Identification of the fatigue stress intensity factor threshold for different load ratios R: From fretting fatigue to C(T) fatigue experiments. Int. J. Fatigue 2016, 82, 211–225. [Google Scholar] [CrossRef]
- Landis, E.N.; Nagy, E.N.; Keane, D.T. Microstructure and fracture in three dimensions. Eng. Fract. Mech. 2003, 70, 911–925. [Google Scholar] [CrossRef]
- Zhu, M.L.; Xuan, F.Z.; Tu, S.T. Observation and modeling of physically short fatigue crack closure in terms of in-situ SEM fatigue test. Mater. Sci. Eng. A 2014, 618, 86–95. [Google Scholar] [CrossRef]
- Dezecot, S.; Maurel, V.; Buffiere, J.; Szmytka, F.; Koster, A. 3D characterization and modeling of low cycle fatigue damage mechanisms at high temperature in a cast aluminum alloy. Acta Mater. 2017, 123, 24–34. [Google Scholar] [CrossRef]
- Dezecot, S.; Buffiere, J.Y.; Koster, A.; Maurel, V.; Szmytka, F.; Charkaluk, E.; Dahdah, N.; El Bartali, A.; Limodin, N.; Witz, J.F. In situ 3D characterization of high temperature fatigue damage mechanisms in a cast aluminum alloy using synchrotron X-ray tomography. Scr. Mater. 2016, 113, 254–258. [Google Scholar] [CrossRef]
- Maire, E.; Carmona, V.; Courbon, J.; Ludwig, W. Fast X-ray tomography and acoustic emission study of damage in metals during continuous tensile tests. Acta Mater. 2007, 55, 6806–6815. [Google Scholar] [CrossRef]
- Baaklini, G.Y.; Bhatt, R.T.; Eckel, A.J.; Engler, P.; Rauser, R.W.; Castelli, M.G. X-ray microtomography of ceramic and metal matrix composites. Mater Eval. 1995, 53, 1040–1044. [Google Scholar]
- Sinclair, R.; Preuss, M.; Maire, E.; Buffiere, J.Y.; Bowen, P.; Withers, P.J. The effect of fibre fractures in the bridging zone of fatigue cracked Ti–6Al–4V/SiC fibre composites. Acta Mater. 2004, 52, 1423–1438. [Google Scholar] [CrossRef]
- Silva, C.M.; Snead, L.L.; Hunn, J.D.; Specht, E.D.; Terrani, K.A.; Katoh, Y. Application of X-ray microcomputed tomography in the characterization of irradiated nuclear fuel and material specimens. J. Microsc. 2015, 260, 163–174. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Fan, G.; Huang, M.; Geng, L.; Cui, X.; Xie, H. Deformation behavior of brittle/ductile multilayered composites under interface constraint effect. Int. J. Plast. 2017, 89, 96–109. [Google Scholar] [CrossRef]
- Wu, H.; Fan, G.; Jin, B.C.; Geng, L.; Cui, X.; Huang, M. Fabrication and mechanical properties of TiBw/Ti-Ti(Al) laminated composites. Mater. Des. 2016, 89, 697–702. [Google Scholar] [CrossRef]
- Wu, H.; Jin, B.C.; Geng, L.; Fan, G.; Cui, X.; Huang, M. Ductile-phase toughening in TiBw/Ti-Ti3Al metallic-intermetallic laminate composites. Metall. Mater. Trans. A 2015, 46, 3803–3807. [Google Scholar] [CrossRef]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Science 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.L.; Jiang, P.; Chen, L.; Yuan, F.P.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. USA 2014, 111, 7197–7201. [Google Scholar] [CrossRef] [PubMed]
- Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Fan, G.; Yu, T.; Hansen, N.; Geng, L.; Huang, X. Laminated Ti-Al composites: Processing, structure and strength. Mater. Sci. Eng. A 2016, 673, 572–580. [Google Scholar] [CrossRef]
- Huang, M.; Xu, C.; Fan, G.; Maawad, E.; Gan, W.; Geng, L.; Lin, F.; Tang, G.; Wu, H.; Du, Y.; et al. Role of layered structure in ductility improvement of layered Ti-Al metal composite. Acta Mater. 2018, 153, 235–249. [Google Scholar] [CrossRef]
- Akatsu, T.; Suzuki, M.; Tanabe, Y.; Yasuda, E. Effects of whisker content and dimensions on the R-curve behavior of an alumina matrix composite reinforced with silicon carbide whiskers. J. Mater. Res. 2001, 16, 1919–1927. [Google Scholar] [CrossRef]
- Papazian, J.M.; Adler, P.N. Tensile properties of short fiber-reinforced SiC/Al composites: Part I. Effects of matrix precipitates. Metall. Trans. A 1990, 21, 401–410. [Google Scholar] [CrossRef]
- Selvakumar, S.; Dinaharan, I.; Palanivel, R.; Ganesh Babu, B. Characterization of molybdenum particles reinforced Al6082 aluminum matrix composites with improved ductility produced using friction stir processing. Mater. Charact. 2017, 125, 13–22. [Google Scholar] [CrossRef]
- Tzamtzis, S.; Barekar, N.S.; Hari Babu, N.; Patel, J.; Dhindaw, B.K.; Fan, Z. Processing of advanced Al/SiC particulate metal matrix composites under intensive shearing-A novel Rheo-process. Compos. Part A Appl. Sci. Manuf. 2009, 40, 144–151. [Google Scholar] [CrossRef]
- Nie, C.Z.; Gu, J.J.; Liu, J.L.; Zhang, D. Production of boron carbide reinforced 2024 aluminum matrix composites by mechanical alloying. Mater. Trans. 2007, 48, 990–995. [Google Scholar] [CrossRef]
- Wu, H.; Fan, G.; Huang, M.; Geng, L.; Cui, X.; Chen, R.; Peng, G. Fracture behavior and strain evolution of laminated composites. Compos. Struct. 2017, 163, 123–128. [Google Scholar] [CrossRef]
- Fan, G.; Geng, L.; Wu, H.; Miao, K.; Cui, X.; Kang, H.; Wang, T.; Xie, H.; Xiao, T. Improving the tensile ductility of metal matrix composites by laminated structure: A coupled X-ray tomography and digital image correlation study. Scr. Mater. 2017, 135, 63–67. [Google Scholar] [CrossRef]
- Miao, K.; Li, D.; Tang, G.; Xu, C.; Geng, L.; Zhang, J.; Leng, X.; Kang, H.; Wang, T.; Yan, S.; et al. High elongation achieved by band-like distribution of reinforcements in aluminum matrix composites. Mater. Charact. 2018, 144, 42–47. [Google Scholar] [CrossRef]
- Williams, J.J.; Flom, Z.; Amell, A.A.; Chawla, N.; Xiao, X.; De Carlo, F. Damage evolution in SiC particle reinforced Al alloy matrix composites by X-ray synchrotron tomography. Acta Mater. 2010, 58, 6194–6205. [Google Scholar] [CrossRef]
- Xu, C.; Nakata, T.; Qiao, X.G.; Zheng, M.Y.; Wu, K.; Kamado, S. Ageing behavior of extruded Mg–8.2 Gd–3.8 Y–1.0 Zn–0.4 Zr (wt.%) alloy containing LPSO phase and γ′ precipitates. Sci. Rep. 2017, 7, 43391. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.H.; Yang, Z.Q.; Ma, X.L. Strengthening and toughening mechanisms in Mg–Zn–Y alloy with a long period stacking ordered structure. Acta Mater. 2010, 58, 4760–4771. [Google Scholar] [CrossRef]
- Chen, T.; Chen, Z.; Shao, J.; Wang, R.; Mao, L.; Liu, C. Evolution of LPSO phases in a Mg-Zn-Y-Gd-Zr alloy during semi-continuous casting, homogenization and hot extrusion. Mater. Des. 2018, 152, 1–9. [Google Scholar] [CrossRef]
- Garces, G.; Munoz-Morris, M.A.; Morris, D.G.; Jimenez, J.A.; Perez, P.; Adeva, P. The role of extrusion texture on strength and its anisotropy in a Mg-base alloy composed of the Long-Period-Structural-Order phase. Intermetallics 2014, 55, 167–176. [Google Scholar] [CrossRef]
- Randle, V. Overview no. 127 the role of the grain boundary plane in cubic polycrystals. Acta Mater. 1998, 46, 1459–1480. [Google Scholar] [CrossRef]
- Johnson, G.; King, A.; Honnicke, M.G.; Marrow, J.; Ludwig, W. X-ray diffraction contrast tomography: A novel technique for three-dimensional grain mapping of polycrystals. II. The combined case. J. Appl. Crystallogr. 2010, 41, 310–318. [Google Scholar] [CrossRef]
- King, A.; Johnson, G.; Engelberg, D.; Ludwig, W.; Marrow, J. Observations of intergranular stress corrosion cracking in a grain-mapped polycrystal. Science 2008, 321, 382–385. [Google Scholar] [CrossRef] [PubMed]
- Herbig, M.; King, A.; Reischig, P.; Proudhon, H.; Lauridsen, E.M.; Marrow, J. 3-D growth of a short fatigue crack within a polycrystalline microstructure studied using combined diffraction and phase-contrast X-ray tomography. Acta Mater. 2011, 59, 590–601. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Huang, M.; Wu, H.; Miao, K.; Tang, G.; Xie, H.; Xiao, T.; Kang, H.; Wang, T.; Geng, L.; et al. 3D Visualized Characterization of Fracture Behavior of Structural Metals Using Synchrotron Radiation Computed Microtomography. Quantum Beam Sci. 2019, 3, 5. https://doi.org/10.3390/qubs3010005
Xu C, Huang M, Wu H, Miao K, Tang G, Xie H, Xiao T, Kang H, Wang T, Geng L, et al. 3D Visualized Characterization of Fracture Behavior of Structural Metals Using Synchrotron Radiation Computed Microtomography. Quantum Beam Science. 2019; 3(1):5. https://doi.org/10.3390/qubs3010005
Chicago/Turabian StyleXu, Chao, Meng Huang, Hao Wu, Kesong Miao, Guangze Tang, Honglan Xie, Tiqiao Xiao, Huijun Kang, Tongmin Wang, Lin Geng, and et al. 2019. "3D Visualized Characterization of Fracture Behavior of Structural Metals Using Synchrotron Radiation Computed Microtomography" Quantum Beam Science 3, no. 1: 5. https://doi.org/10.3390/qubs3010005
APA StyleXu, C., Huang, M., Wu, H., Miao, K., Tang, G., Xie, H., Xiao, T., Kang, H., Wang, T., Geng, L., & Fan, G. (2019). 3D Visualized Characterization of Fracture Behavior of Structural Metals Using Synchrotron Radiation Computed Microtomography. Quantum Beam Science, 3(1), 5. https://doi.org/10.3390/qubs3010005





