Abstract
Since the late 1970s, MnSi has played a major role in developing the theory of helical magnets in non-centrosymmetric materials showing the Dzyaloshinsky-Moriya interaction (DMI). With a long helimagnetic pitch of 175 Å as compared to the lattice d-spacing of 4.55 Å, it was ideal for performing neutron studies, especially as large single crystals could be grown. A (B-T)-phase diagram was measured, and in these studies, under the application of a field of about 180 mT perpendicular to the scattering vector Q, a so-called A-phase in the B-T phase diagram was found and first interpreted as a re-orientation of the magnetic helix. After the surprising discovery of the skyrmion lattice in the A-phase in 2009, much interest arose due to the rigidity of the skyrmionic lattice, which is only loosely bound to the crystal lattice, and therefore only relatively small current densities can already induce a motion of this lattice. A very interesting approach to even better understand the complex structures in the phase diagram is to measure and model the spin excitations in MnSi. As the helimagnetic state is characterized by a long pitch of about 175 Å, the associated characteristic excitations form a band structure due to Umklapp scattering and can only be observed at very small Q with energies below 1 meV. Similarly, the excitations of the skyrmion lattice are very soft and low-energetic. We investigated the magnons in MnSi in the whole (B,T)-phase diagram starting in the single-k helimagnetic state by applying a small magnetic field, B = 100 mT. This way, the complexity of the magnon spectrum is significantly reduced, allowing for a detailed comparison of the data with theory, resulting in a full theoretical understanding of the spin system of MnSi in all its different magnetic phases.
1. What Makes MnSi So Interesting?
Helical magnets are currently of high interest because they serve as model systems for complex magnetic ordering, yielding interesting properties such as multiferroicity and the appearance of stable magnetic vortices (i.e. skyrmions), to name a few. The interplay of the various energy scales often leads to magnetic ordering, exhibiting a periodicity that is incommensurate with the lattice and to magnetic Brillouin zones that are much smaller than the chemical ones.
A prominent example showing incommensurate helical ordering is MnSi, which is a non-centrosymmetric itinerant magnet with a P23 structure and a lattice spacing of a = 4.55 Å. The (B-T)-phase diagram is shown on the left of Figure 1. It exhibits a large variety of different phases, such as single-handed helical and conical ordering, a field-polarized and paramagnetic state, as well as a non-trivial topological spin state (A-phase), i.e., a skyrmion phase.
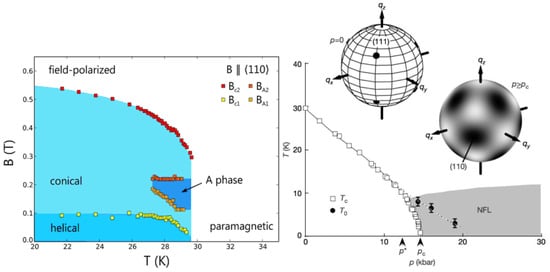
Figure 1.
(Left) The (B-T)-phase diagram of MnSi. The A-phase contains the skyrmion lattice (reproduced from [1], © by the American Association for the Advancement of Science (AAAS). (Right) The (T-P)-phase diagram of MnSi. The grey shaded area designates the non-Fermi-liquid phase (NFL). The spheres show directions of strong elastic neutron intensity in reciprocal space (reproduced from [2], © by Springer Nature).
In this article, we show how the concept of a skyrmionic crystal developed from the neutron-scattering experiments and the measurement of the anomalous Hall effect. Furthermore, we will show the behavior of magnetic excitations (magnons) in all parts of the phase diagram of MnSi. Together with a mean-field theory of the dynamics in MnSi, this leads to a very detailed understanding of the experimentally observed spectra.
2. How Everything Began
Somewhat surprisingly, despite the discovery of the helimagnetic state in the 1970s [3,4], initial research focused on the investigation of the magnetic excitations in the field-polarized phase of MnSi (see Figure 1) because MnSi represents, beside NiAl, one of the best realizations of a weak itinerant ferromagnet due to the large difference between the ordered and the paramagnetic moments. In his seminal works, Ishikawa et al. succeeded in mapping out the spectrum of the spin waves, the Stoner excitations, and the paramagnetic scattering up to room temperature [4]. In parallel, the (B,T)-phase diagram (see Figure 1) of MnSi was determined [5].
Theoretical explanations were based on the early theory of Bak and Jensen [6], who proposed an explanation of the phase diagram of MnSi based on the Dzyaloshinsky-Moriya interaction (DMI) originating from non-centrosymmetry. We now understand the appearance of most of the magnetic phases in MnSi to be a generic property of the hierarchy of the various energy scales appearing in these B20 compounds. As for the helical ground state, the ferromagnetic exchange interaction corresponds to the strongest scale and leads to a preference for parallel spin alignment. The much weaker Dzyaloshinsky-Moriya interaction favors a perpendicular alignment of the spins. The competition between the two leads to the formation of a spin spiral with a large pitch of Å. The DMI is the leading term (second-order) in spin-orbit coupling (SOC), which is a relativistic correction. It is a consequence of the crystal structure (P23), which lacks inversion symmetry. Finally, very weak crystal field effects (fourth-order SOC), representing the lowest energy scale, pin the wave vectors of the helix to point along the space diagonals of the cubic unit cell (a = 4.558 Å) of MnSi with Å.
It was Shirane et al. who, for the first time, investigated the effect of the single-handed helimagnetic phase in MnSi on the cross-section of polarized neutrons [7], followed by the work of Sorensen [8]. Roessli et al. [9] demonstrated the appearance of chiral correlations due to the single-handedness of helical ordering in the paramagnetic phase.
In 2004, Pfleiderer et al. discovered the appearance of a non-Fermi-liquid phase under the application of pressure above 14.6 kbar [2]. Most interestingly, the intensity of the magnetic satellite peaks due to the magnetic ordering vanished, and scattering in the {110} directions in small-angle neutron-scattering appeared. The origin of these peaks and the excitations stabilizing or destabilizing the non-Fermi-liquid phase (NFL) phase are not known at present. At this time, the phase diagram of MnSi and the (T-P)-regime was established as well (see Figure 1).
There is an interesting feature in the (B-T) phase diagram—the so-called “A-phase”—which has been investigated with ultrasonic absorption experiments [10] and magnetoresistance measurements [5]. Lebech at al. [11] studied this pocket in the phase diagram the first time by using small-angle scattering experiments. The experiments were performed with a field perpendicular to the momentum transfer of the neurons—the so-called “scattering vector Q” —and showed a disappearance of the magnetic intensity when entering the A-phase in the phase diagram. This was interpreted as a re-orientation of the magnetic helix out of the scattering plane [12], but Lebech had already pointed out that the diffraction pattern in this phase could probably not be explained by pure helical modulation of the spin structure [11].
3. From the Neutron Small-Angle Scattering Results to the Skyrmion Interpretation
In 2009, extensive small-angle neutron scattering experiments were performed in all phases of MnSi [1,13]. Most of these experiments were performed with fields perpendicular to Q, but some of these measurements were also performed along Q. Apart from the A-phase, the results confirmed the picture described above with the hierarchy of the three interactions. However, in the A-phase, when applying B parallel to Q, a six-fold geometry showed up independent of the orientation of the underlying crystal. This result has been explained as the formation of a skyrmion lattice. Theoretically, it can be described by a three-fold Q-structure with Q = 0, which has a local minimum of the free energy inside the A-phase. Due to thermal fluctuations, this structure is stabilized in a global minimum in the A-phase. This leads to the picture of a hexagonal vortex-like skyrmion lattice or crystal in MnSi. The concept of skyrmions originated from Skyrme [14], who used it to describe the low-energy dynamics of mesons and baryons. Bogdanov, Hubert, and Yablonskii [15,16,17] then used the name “skyrmion” to describe vortex-like states in condensed-matter physics, and in 2002, Bogdanov et al. [18] introduced the notation of chiral skyrmions, which is what we simply call “skyrmions” today.
The topological nature of the skyrmions and their interaction with electrons are described in terms of the (fictitious) emergent electromagnetic fields [19,20,21,22], E and B. Taken together, E and B account for the Berry phase that the spin of a conduction electron accumulates when following the magnetic texture adiabatically. As the integral of over a surface describes the solid angle , the emergent magnetic flux of each skyrmion is accurately given by one (negative) flux quantum [19]:
Interestingly, skyrmions are therefore characterized by a non-zero winding number indicating a different topical structure from classical magnetic systems. Experimental consequences have been detected directly in terms of an additional (topological) contribution to the Hall signal and an emergent electric field, providing evidence for the motion of the skyrmions [19,23,24]. The measurements of this motion show that the skyrmions are only loosely bound to the lattice of the underlying crystal, and that with current densities which are three orders of magnitude smaller than in usual magnetic structures, the lattice can start moving [24]. This is due to the rigidity of the lattices involved and the large periodicity, which leads to an efficient decoupling of the magnetic and atomic lattices.
As the topologically quantized winding number, or, equivalently, the quantized magnetic flux has to change when two skyrmions merge, decay of a skyrmion is only possible via a monopole interaction, meaning that these structures are thus strongly stabilized. Due to the topological nature of the winding number, this is, in fact, only possible by a singular field configuration for which the local magnetization vanishes at a point in space. Hence, when two ingoing skyrmions merge, there must be a singular field configuration, a hedgehog defect with a winding number of +1, which creates one quantum of emergent magnetic flux. The point of coalescence therefore carries a quantized emergent magnetic charge—that is, it is an emergent magnetic monopole. Similarly, when an ingoing single skyrmion line splits into two, an anti-monopole with winding number is located at the point of separation.
The stability and high mobility of the skyrmions made these structures ideal candidates for quantum-computing storage devices; therefore, several hundreds of publications have dealt with such topological, protected multi-q structures in metals, semimetals, and isolators in bulk materials since the discovery of the skyrmion crystal in MnSi. They were found in thin films and isolators, and even more complex systems will be discussed.
4. Magnons in MnSi
So far, we have only dealt with the structure within the different magnetic phases of MnSi; however, there are also magnetic excitations of the spirals and the skyrmion lattice, which shed light on the dynamics of these spin systems. Exciting these modes requires a very small energy transfer even at a relatively large q. It turns out that most of the interesting physics takes place below 1 meV excitation energy, which were thus missed by the early experiments and is now reinvestigated with modern instruments with an adequate momentum and energy resolution.
As for the structure in each of the magnetic phases, typical excitations can be found, and we will explain their dynamics in the following subsections going with increasing magnetic fields from the helical, over the conical, and into the ferromagnetic phase. We also measured the excitations of the skyrmion crystal, assuming the skyrmion to be a 3-q phase-coupled superposition of helical spirals.
4.1. Helimagnons
The dispersion of the excitations of the magnetic spiral in the multi-domain helimagnetic phase was first mapped out by Janoschek et al. [25] in zero-field where the magnetic domains aligned along the <111> directions. The resulting spectra were complex superpositions of the contributions of 4 chiral domains. Janoschek et al. successfully described the dispersions in terms of a universal Ginzburg-Landau theory which depends only on known macroscopic material parameters. The helical ground state is obtained by a minimization of the free-energy functional [26]:
with the magnetization being the order parameter. The free energy consists of the exchange interaction J, favoring a parallel magnetization, and the Dzyaloshinsky-Moriya interaction (DMI) D, favoring a perpendicular alignment, resulting in a spiral with the pitch length Å. The anisotropy terms then aligns the spiral along the <111> direction. Recently, Schwarze et al. [26] performed measurements at Q = 0 for all magnetic phases in MnSi, FeCoSi and CuOSeO using microwaves. For an adequate description of the measurements, the theory had to be modified () to include a dipolar magnetic term and a cubic anisotropy; the first term being essential for a realistic description of the spectra, and the latter term giving a small correction.
In order to follow-up on the detailed dependence of the helimagons on momentum Q and the B-field, we induced a single-domain state which was achieved by application of a small magnetic field of approximately B = 100 mT (see Kugler et al. [27]). This procedure allowed to directly identify the individual bands of the theoretically proposed band structure (see Figure 2) for finite Q. We showed that the theory required further refinements by introducing a higher-order correction term in the free energy, with the unit vector n pointing along the magnetization M and being the stiffness density [27]. Fitting the data yields, for the dimensionless constant A, the value , providing an excellent description of the data. MnSi can therefore be viewed as a one-dimensional helimagnetic crystal. The low-energy bands are basically equivalent to the physics of particles trapped in a one-dimensional potential. This result is highly relevant because the skyrmions in MnSi are related particles that are trapped by a similar potential and stabilized on the energy scales of the helimagnetic state.
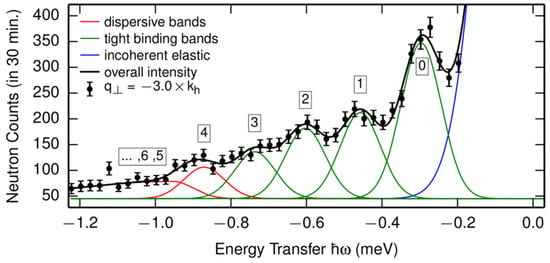
Figure 2.
The figure (reproduced from [27], © by the American Physical Society, USA) shows an energy scan measured at T = 20 K and for a fixed reduced momentum transfer q perpendicular to the wave vector of the helix. Five bands are readily resolved and can be parametrized using a multi-Gaussian spectrum. The elastic peak appears due to incoherent scattering.
4.2. Conical and in the Field-Polarized Phase
The dispersion branches in the field-polarized ferromagnetic phase were originally mapped out by Ishikawa et al. [4,28]; however, they were only at momentum transfers as they performed experiments using thermal triple-axis spectroscopy, thus restricting the accessible energies to a range well above 1 meV. In a recent study, we succeeded in quantitatively verifying the helimagnon model [29] under the application of magnetic fields, starting from the helimagnetic-conical phase transition at B, moving up to the second critical field B [30] at much smaller momentum transfer and energies. Observing the transition from the band structure in the helical and conical phases towards a single mode in the field-polarized ferromagnetic phase, we demonstrated an excellent agreement of the theoretically predicted helimagnon energies and their spectral weights.
Figure 3 shows the field dependence of the helimagnons for momentum transfers parallel (left-hand side) and perpendicular (right-hand side) to the helix wave vector . The perpendicular momentum transfer leads to the band structure, which condenses toward a single field-polarized magnon with an increasing magnetic field. A peculiarity resulting from the non-centrosymmetric space group of MnSi shows up for momentum transfers parallel to the helix. Here, the spectral weights begin to reshuffle in an asymmetric way with an increasing field [30], as the magnons are created with a different weight factor as they are annihilated. In the field-polarized phase, all the dispersion branches which lose spectral weight on increasing fields do not exist anymore. This leads to the extreme situation where field-polarized magnons are created with a different energy as they are annihilated [31].
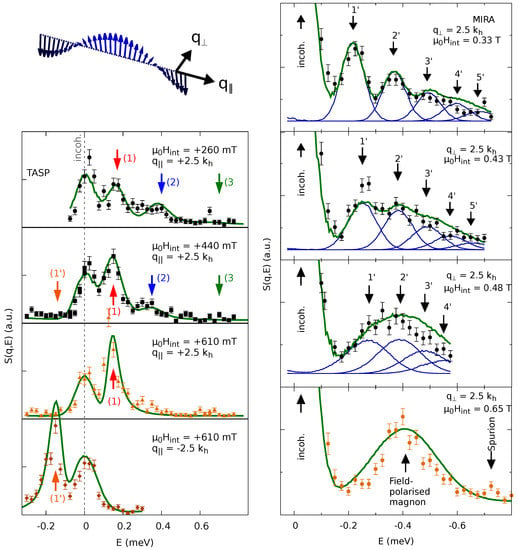
Figure 3.
The figure (reproduced from [30], © by the American Physical Society, USA) shows the field-dependent evolution of the helimagnon excitations for the reduced momentum transfer q parallel (left) and q perpendicular (right) to the helix in units of the spiral pitch.
4.3. Skyrmion Phase
The magnons in the skyrmion phase were first discovered by M. Janoschek [25] and are currently being mapped out and described theoretically, both for the reciprocal [32] and the non-reciprocal dispersion relation [33,34]. The magnons comprise very complicated spectra [29] which cannot be resolved individually using current spectrometers. Interestingly, the distribution of spectral weights imposes a dispersion-like pattern onto the densely-packed branches. The weight factors themselves are within the resolution limits of neutron spectroscopy. At Q = 0, the spectral weights condense at three distinct energies, which have been identified as a clockwise, counter-clockwise, and breathing motion of the skyrmion vortex [26]. While these magnons at finite Q possess a still lower spin-wave stiffness than in the conical phase, we recently found that the magnons of both phases share the same asymmetric phenomena as the magnons in the conical phase, where the spectral weight for creating a magnon in the skyrmion phase is markedly different than for annihilation as long as the momentum transfer is along the normal of the skyrmion plane [33].
Figure 4 shows typical scans of the magnons in the skyrmion phase. Similar to the conical phase, the spectral weights show a strong non-reciprocity for momentum transfers along the axis of the skyrmion plane. Here, the spectral weights are asymmetric, with respect to a change of momentum transfer or rotation of the external field by 180 degrees.
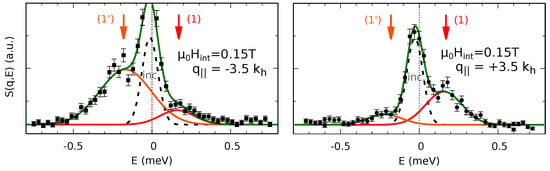
Figure 4.
The figure (reproduced from [33], © by the American Institute of Physics, USA) shows the non-reciprocal nature of the skyrmion dynamics for momentum transfers along the skyrmion axis. The lines are Gaussian fits.
5. Conclusions
Even though MnSi has now been measured for 50 years and has altered our understanding of helimagnetic systems with long spiral pitches several times, it is still a very interesting material for learning more about the structure and dynamics of incommensurate magnets. Here, we have shown how MnSi became a prototype for helimagnetic systems and how the dynamics in this phase can be understood from the hierarchy of the three energy scales involved. We further reviewed the discovery of the skyrmions, which gave a huge boost in the understanding and use of topological spin systems in the last decade. So far, the magnetic system is only fully understood in regard to ambient pressure, meaning that there is still a lot to learn for the development of the spin system with increasing pressure up to the critical pressure at 14.6 kbar, where the long-reaching interactions break down and only paramagnetic behavior survives. What is particularly of interest is the question of how much the low-pressure phases of the helimagnetic and skyrmionic phase contribute to the development of the non-Fermi liquid phase in MnSi.
Author Contributions
Writing—original draft, R.G. and T.W.; Writing—review & editing, R.G.
Acknowledgments
We acknowledge very helpful discussions with P. Böni und S. Mühlbauer. This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) under the project GE971/5-1 and GE971/5-2. This work is based on experiments performed at the MIRA instrument operated by Heinz Maier-Leibnitz Zentrum (MLZ), Technische Universität München, Germany [35] and on experiments performed at the TASP instrument operated by Paul Scherrer Institute, Switzerland [36].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DMI | Dzyaloshinsky-Moriya interaction |
| SOC | Spin-orbit coupling |
References
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral Magnet. Science 2009, 323, 5916. [Google Scholar] [CrossRef] [PubMed]
- Pleiderer, C.; Reznik, D.; Pintschovius, L.; Löhneysen, H.; M, M.G.; Rosch, A. Partial order in the non-Fermi-liquid phase of MnSi. Nature 2004, 427, 227. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, Y.; Shirane, G.; Tarvin, J.A.; Koghi, M. Magnetic excitations in the weak intinerant ferromagnet MnSi. Phys. Rev. B 1977, 16, 4956. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Noda, Y.; Fincher, C.; Shirane, G. Low-energy paramagnetic spin fluctuations in the weak itinerant ferromagnet MnSi. Phys. Rev. B 1982, 25, 254. [Google Scholar] [CrossRef]
- Kadowaki, K.O.; Date, M. Magnetization and Magnetoresistance of MnSi. I. J. Phys. Sot. Jpn. 1982, 51, 2433. [Google Scholar] [CrossRef]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 12, L881–L885. [Google Scholar] [CrossRef]
- Shirane, G.; Cowley, R.; Majkrazk, C.; Sokoloff, J.; Pagonis, B.; Perry, C.; Ishikawa, Y. Spiral magnetic correlation in cubic MnSi. Phys. Rev. B 1983, 28, 6251. [Google Scholar] [CrossRef]
- Sorensen, S.A. Neutron Scattering Studies of Modulated Magnetic Structures. Ph.D. Thesis, Riso National Laboratory, Roskilde, Denmark, 1999. [Google Scholar]
- Roessli, B.; Böni, P.; Fischer, W.; Endoh, Y. Chiral Fluctuations in MnSi above the Curie Temperature. Phys. Rev. Lett. 2002, 88, 237204. [Google Scholar] [CrossRef] [PubMed]
- Komatsubara, T.; Kusaka, S.; Ishikawa, Y. Proceedings of the 6th International Conference on Internal Friction and Ultrasonic Attenuation in Solids; University of Tokyo Press: Tokyo, Japan, 1977; Volume 1, p. 237. [Google Scholar]
- Lebech, B.; Harris, P.; Mortensen, K.; Greorgy, C.; Boenhof, N.; Jermey, M.; Brown, S. Magentic phase diagram of MnSi. J. Magn. Magn. Mater. 1995, 140, 119–120. [Google Scholar] [CrossRef]
- Grigoriev, S.V.; Maleyev, S.V.; Okorokov, A.I.; Chetverikov, Y.O.; Eckerlebe, H. Field-induced reorientation of the spin helix in MnSi near Tc. Phys. Rev. B 2006, 73, 224440. [Google Scholar] [CrossRef]
- Pfleiderer, C.; Neubauer, A.; Muehlbauer, S.; Jonietz, F.; Janoschek, M.; Legl, S.; Ritz, R.; Muenzer, W.; Franz, C.; Niklowitz, P.; et al. Quantum order in the chiral magnet MnSi. J. Phys. Condensed Matter 2009, 21, 164215–164221. [Google Scholar] [CrossRef] [PubMed]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101–103. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Bogdanov, A.; Hubert, A. The stability of vortex-like structures in uniaxial ferromagnets. J. Magn. Magn. Mater. 1999, 195, 182–192. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Rößler, U.K.; Wolf, M.; Müller, K.H. Magnetic structures and reorientation transitions in noncentrosymmetric uniaxial antiferromagnets. Phys. Rev. B 2002, 66, 214410. [Google Scholar] [CrossRef]
- Schulz, T.; Ritz, R.; Bauer, A.; Halder, M.; Wagner, M.; Franz, C.; Pfleiderer, C.; Everschor, K.; Garst, M.; Rosch, A. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 2012, 8, 301–304. [Google Scholar] [CrossRef]
- Volovik, G. Linear momentum in ferromagnets. J. Phys. C Solid State Phys. 1987, 20, L83. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.S.L. Generalization of the Landau-Lifshitz-Gilbert Equation for Conducting Ferromagnets. Phys. Rev. Lett. 2009, 102, 086601. [Google Scholar] [CrossRef] [PubMed]
- Zang, J.; Mostovoy, M.; Han, J.H.; Nagaosa, N. Dynamics of Skyrmion Crystals in Metallic Thin Films. Phys. Rev. Lett. 2011, 107, 136804. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [PubMed]
- Ritz, R.; Halder, M.; M, M.W.; C, C.F.; Bauer, A.; Pfleiderer, C. Formation of a topological non-Fermi liquid in MnSi. Nature 2013, 497, 231. [Google Scholar] [CrossRef] [PubMed]
- Janoschek, M.; Jonietz, F.; Link, P.; Pfleiderer, C.; Böni, P. Helimagnons in the skyrmion lattice of MnSi. J. Phys. Conf. Ser. 2010, 200, 032026. [Google Scholar] [CrossRef]
- Schwarze, T.; Waizner, J.; Garst, M.; Bauer, A.; Stasinopoulos, I.; Berger, H.; Pfleiderer, C.; Grundler, D. Universal helimagnon and skyrmion excitations in metallic, semiconducting and insulating chiral magnets. Nat. Mater. 2015, 14, 478. [Google Scholar] [CrossRef] [PubMed]
- Kugler, M.; Brandl, G.; Waizner, J.; Janoschek, M.; Georgii, R.; Bauer, A.; Seemann, K.; Rosch, A.; Pfleiderer, C.; Böni, P.; et al. Band Structure of Helimagnons in MnSi Resolved by Inelastic Neutron Scattering. Phys. Rev. Lett. 2015, 115, 097203. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, Y.; Noda, Y.; Uemura, Y.J.; Majkrzak, C.F.; Shirane, G. Paramagnetic spin fluctuations in the weak itinerant-electron ferromagnet MnSi. Phys. Rev. B 1985, 31, 5884. [Google Scholar] [CrossRef]
- Garst, M.; Waizner, J.; Grundler, D. Collective spin excitations of helices and magnetic skyrmions: Review and perspectives of magnonics in non-centrosymmetric magnets. J. Phys. D Appl. Phys. 2017, 50, 293002. [Google Scholar] [CrossRef]
- Weber, T.; Waizner, J.; Tucker, G.S.; Georgii, R.; Kugler, M.; Bauer, A.; Pfleiderer, C.; Garst, M.; Böni, P. Field dependence of nonreciprocal magnons in chiral MnSi. Phys. Rev. B 2018, 97, 224403. [Google Scholar] [CrossRef]
- Sato, T.J.; Okuyama, D.; Hong, T.; Kikkawa, A.; Taguchi, Y.; Arima, T.h.; Tokura, Y. Magnon dispersion shift in the induced ferromagnetic phase of noncentrosymmetric MnSi. Phys. Rev. B 2016, 94, 144420. [Google Scholar] [CrossRef]
- Fobes, D.; Weber, T.; Waizner, J.; Kugler, M.; Bauer, A.; Georgii, R.; Link, P.; Ehlers, G.; Bewley, R.; Pfleiderer, C.; et al. Spin Excitations of the Skyrmion Lattice in MnSi. In Proceedings of the Bulletin of the American Physical Society, Los Angeles, CA, USA, 5–9 March 2018. [Google Scholar]
- Weber, T.; Waizner, J.; Tucker, G.S.; Beddrich, L.; Skoulatos, M.; Georgii, R.; Bauer, A.; Pfleiderer, C.; Garst, M.; Böni, P. Non-reciprocal magnons in non-centrosymmetric MnSi. AIP Adv. 2018, 8, 101328. [Google Scholar] [CrossRef]
- Weber, T.; Steffens, P.; Bauer, A.; Böni, P.; Garst, M. Polarisation-Dependence of the Spin Excitations of the Skyrmion Lattice in MnSi. ILL Reports 79803 and 80215. 2018; Unpublished work. [Google Scholar]
- Georgii, R.; Weber, T.; Brandl, G.; Skoulatos, M.; Janoschek, M.; Mühlbauer, S.; Pfleiderer, C.; Böni, P. The multi-purpose three-axis spectrometer (TAS) MIRA at FRM II. Nuclear Instrum. Methods Phys. Res. Sect. A 2017. [Google Scholar] [CrossRef]
- Semadeni, F.; Roessli, B.; Böni, P. Three-axis spectroscopy with remanent benders. Phys. B Condensed Matter 2001, 297, 152–154. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).