Influence of Concentration Fluctuations on Relaxation Processes in Spin Glasses
Abstract
1. Introduction
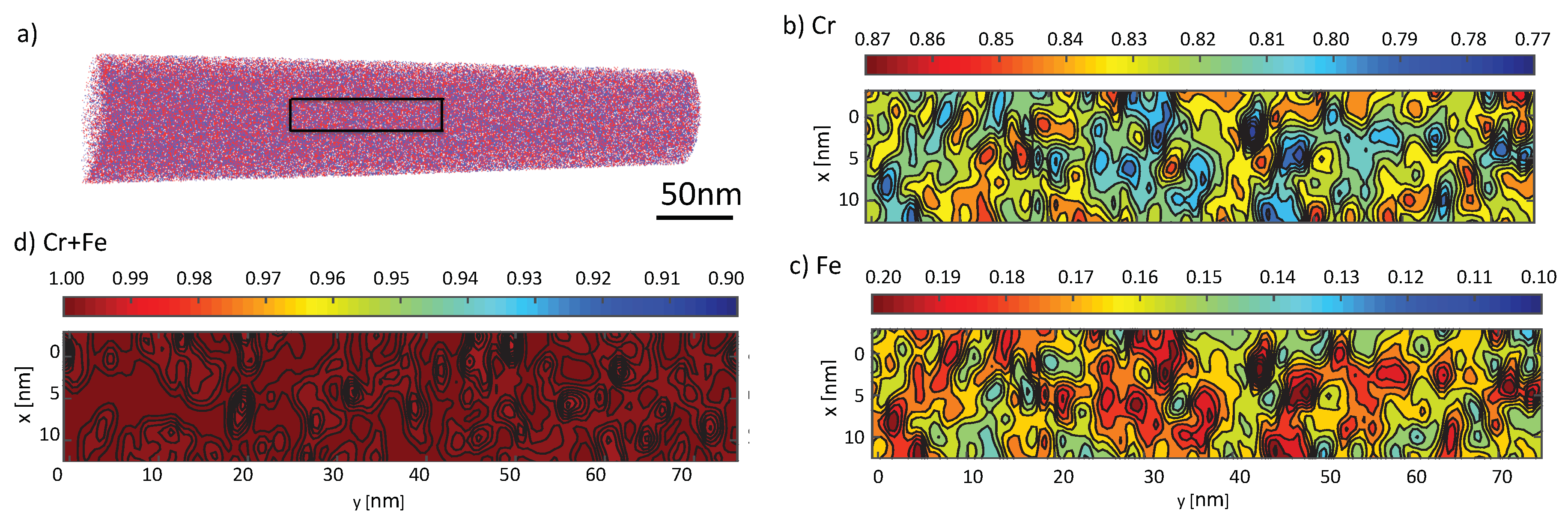
2. Experimental Details
3. Generalized Spin Glass Relaxation Model Based on Weron
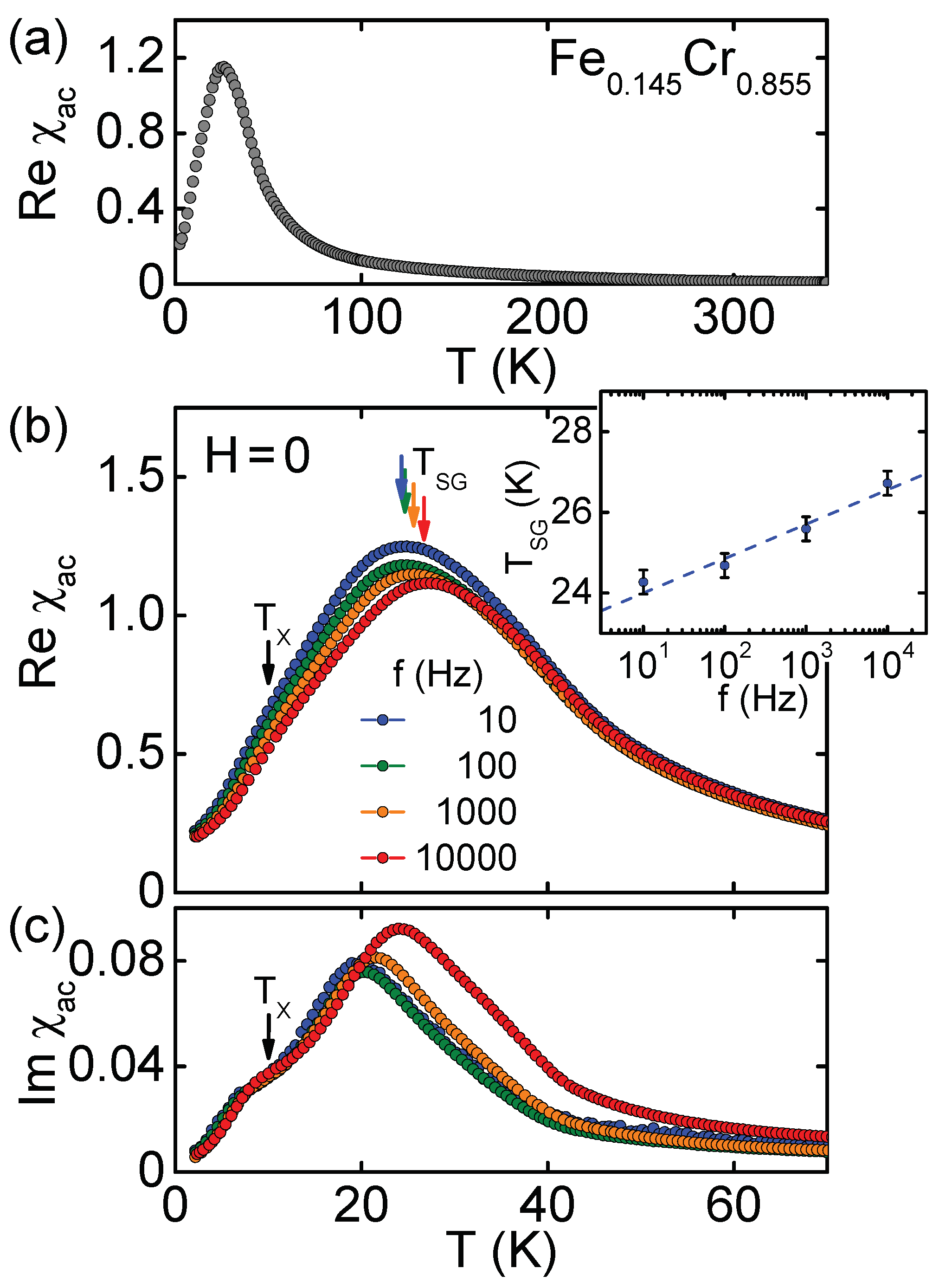
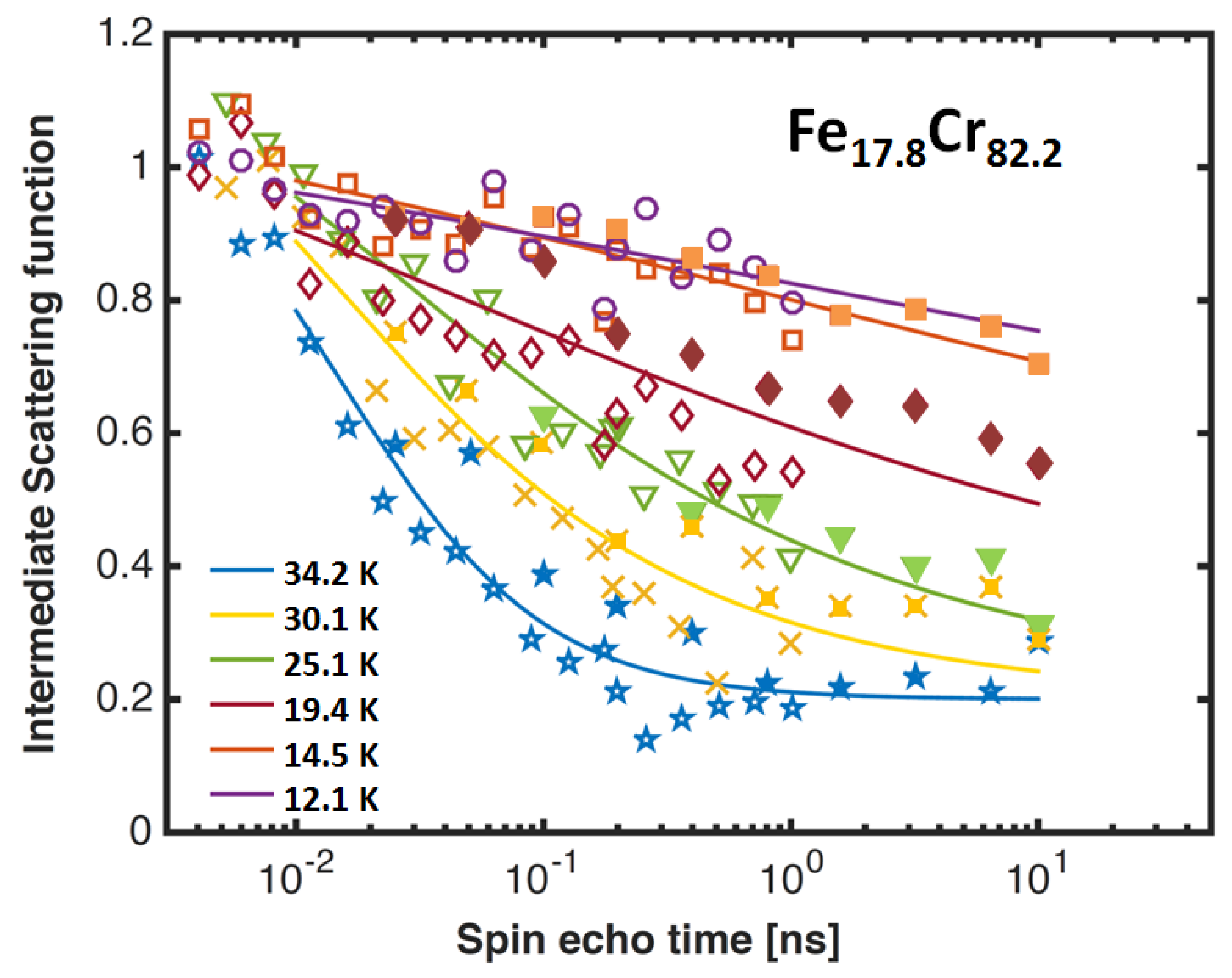
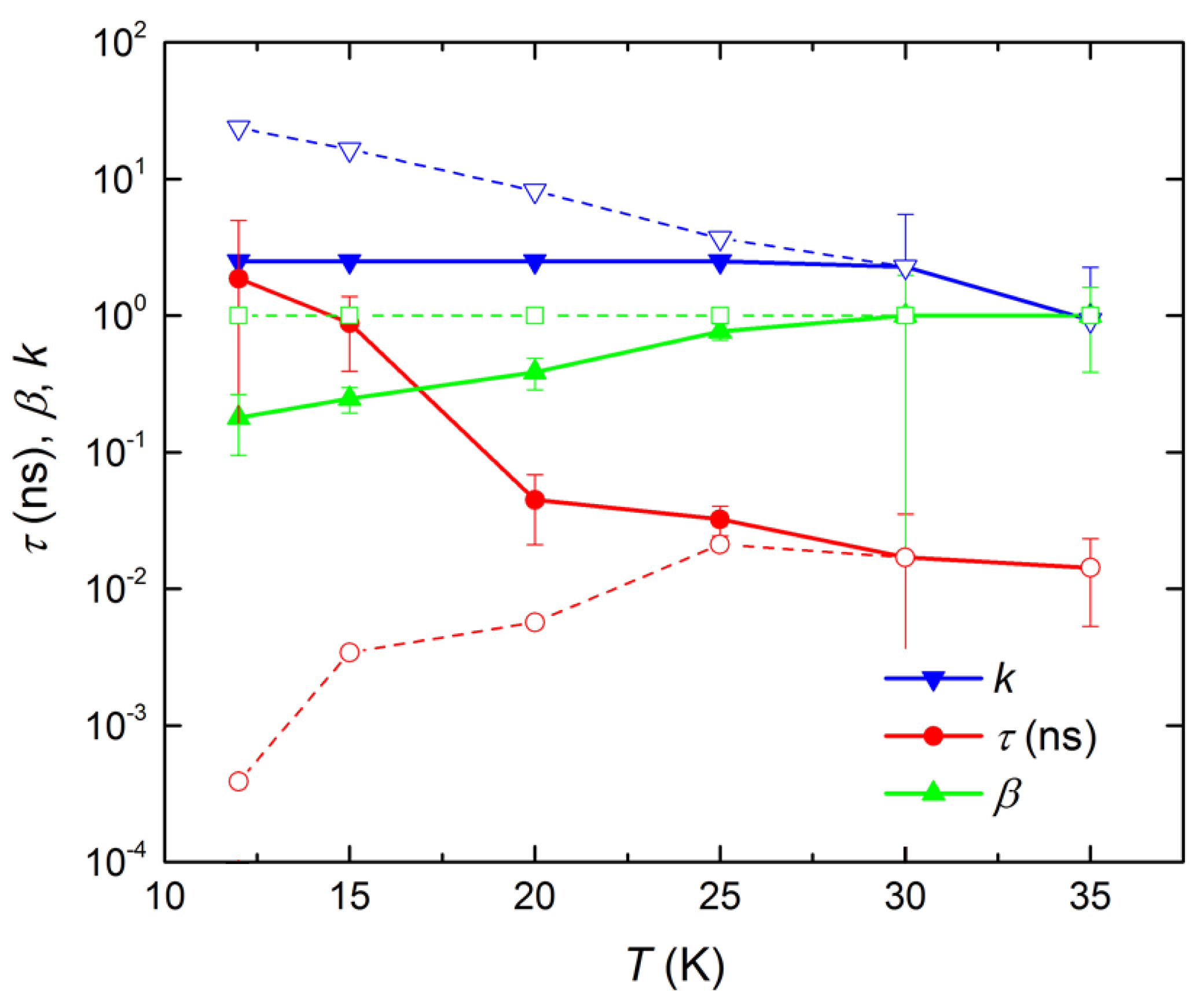
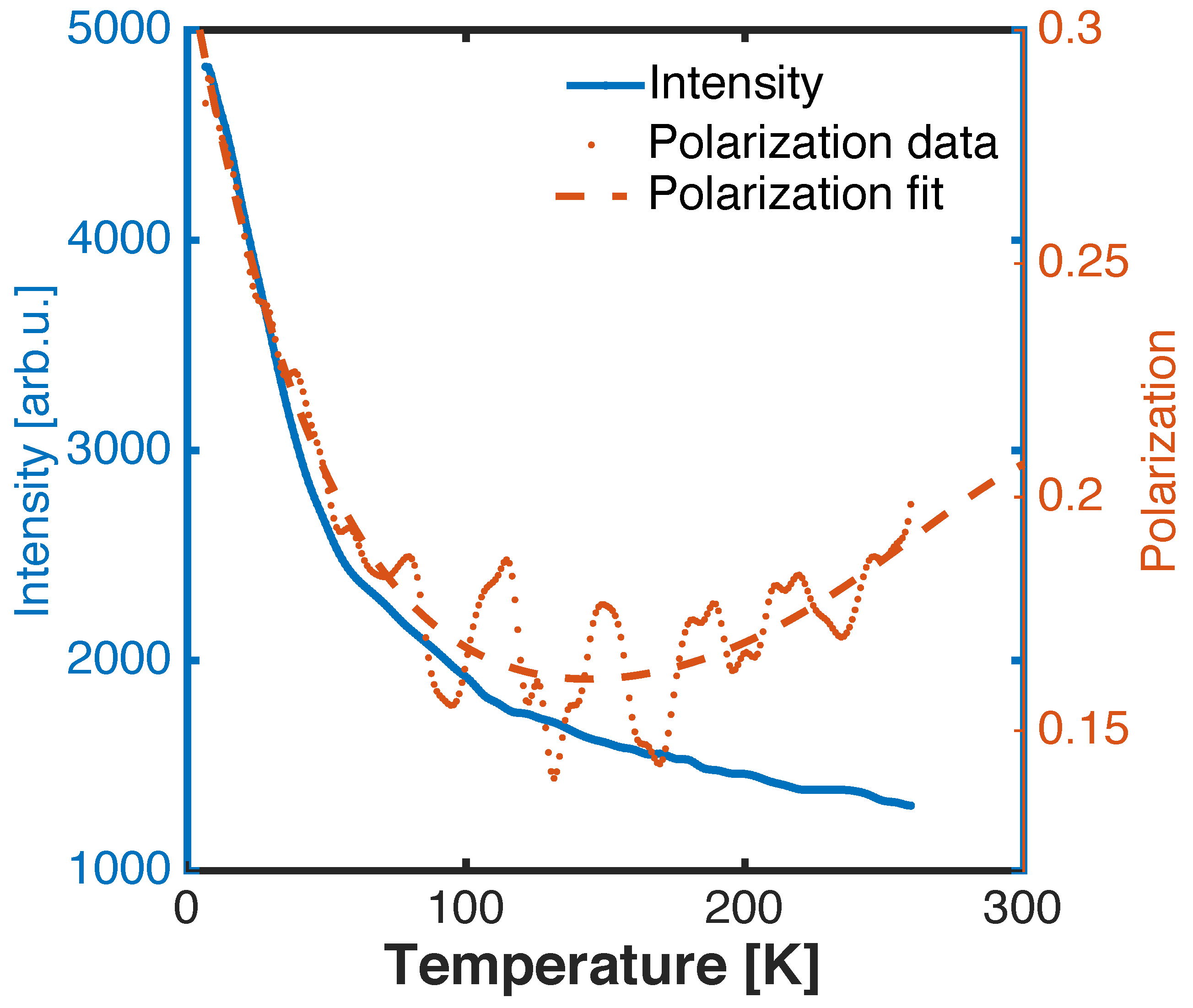
4. Results
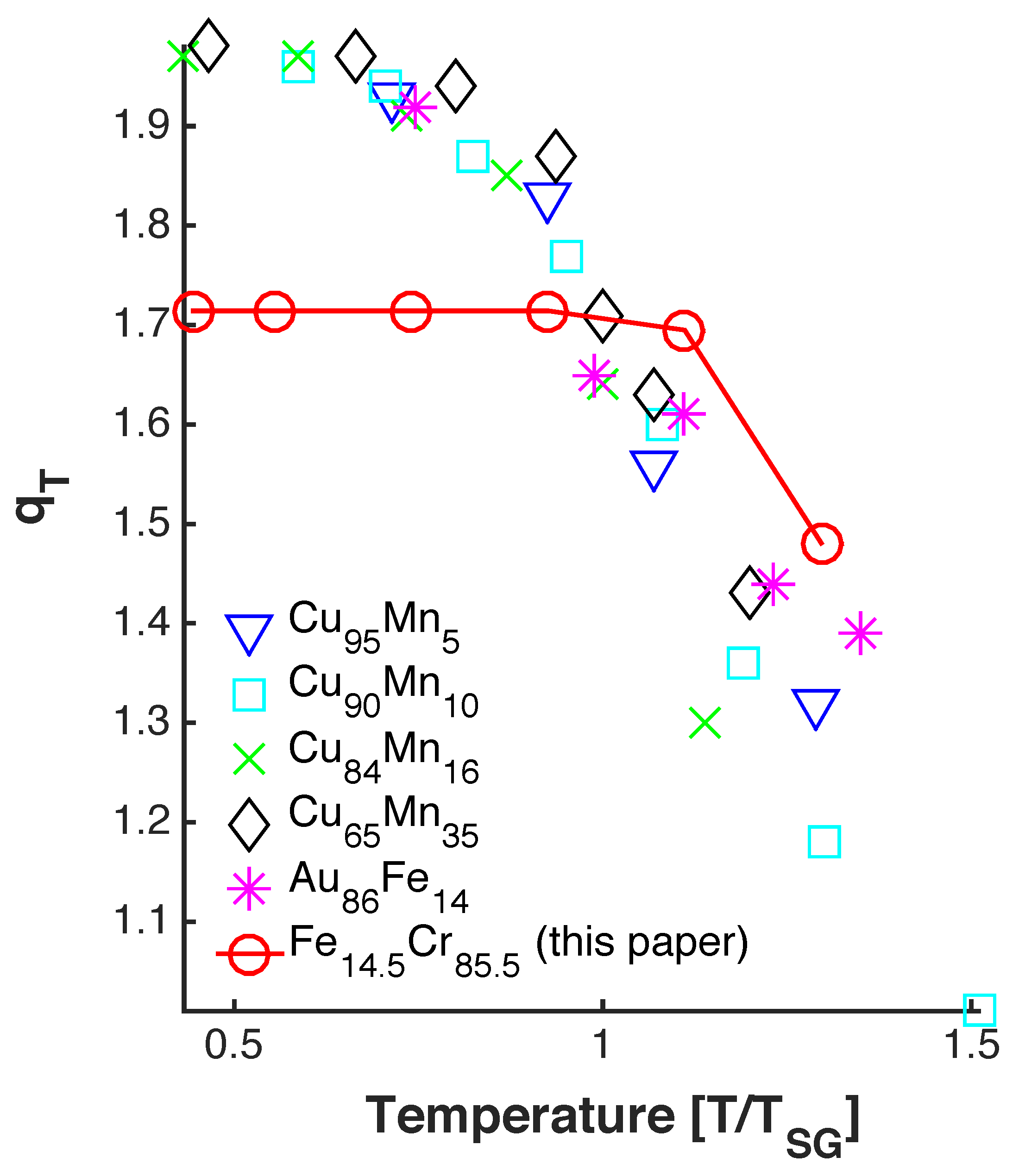
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| APT | atom probe tomography |
| FRM II | Forschungs Reaktor München II (research neutron source Heinz Maier-Leibnitz) |
| FWHM | full width at half maximum |
| ISF | intermediate scattering function |
| J-NSE | Jülich Neutron Spin Echo spectrometer |
| KNMF | Karlsruhe Nano Micro Facility |
| N(R)SE | neutron (resonance) spin echo |
| NSE | neutron spin echo |
| PM | paramagnetic |
| PPMS | physical property measurement system |
| RESEDA | REsonance Spin Echo spectrometer for Diverse Applications |
| RF | radio frequency |
| SET | spin echo time |
| SG | spin glass |
References
- Ramirez, A.P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 1994, 24, 453–480. [Google Scholar] [CrossRef]
- Bao, W.; Raymond, S.; Shapiro, S.M.; Motoya, K.; Fåk, B.; Erwin, R.W. Unconventional Ferromagnetic and Spin-Glass States of the Reentrant Spin Glass Fe0.7Al0.3. Phys. Rev. Lett. 1999, 82, 4711–4714. [Google Scholar] [CrossRef]
- Murani, A.P.; Tholence, J.L. Spin Dynamics of a Binary Alloy (Spin Glass). Solid State Commun. 1977, 22, 25–28. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Yamazaki, T.; Harshman, D.R.; Senba, M.; Ansaldo, E.J. Muon-spin relaxation in AuFe and CuMn spin glasses. Phys. Rev. B 1985, 31, 546–563. [Google Scholar] [CrossRef]
- Pickup, R.M.; Cywinski, R.; Pappas, C.; Farago, B.; Fouquet, P. Generalized Spin-Glass Relaxation. Phys. Rev. Lett. 2009, 102, 097202. [Google Scholar] [CrossRef] [PubMed]
- Weron, K. How to obtain the universal response law in the Jonscher screened hopping model for dielectric relaxation. J. Phys. Condens. Matter 1991, 3, 231–233. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-Mechanical Foundation of the Ubiquity of Lévy Distributions in Nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef] [PubMed]
- Gabay, M.; Toulouse, G. Coexistence of Spin-Glass and Ferromagnetic Orderings. Phys. Rev. Lett. 1981, 47, 201–204. [Google Scholar] [CrossRef]
- Gault, B.; Moody, M.P.; Cairney, J.M.; Ringer, S.P. Atom Probe Microscopy; Springer: New York, NY, USA, 2012; ISBN 978-1-4614-3436-8. [Google Scholar]
- Larson, D.J.; Prosa, T.J.; Ulfig, R.M.; Geiser, B.P.; Kelly, T.F. Local Electrode Atom Probe Tomography; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-8721-0. [Google Scholar]
- Miller, M.K. Atom Probe Tomography; Springer: Boston, MA, USA, 2014; ISBN 978-1-4615-4281-0. [Google Scholar]
- Burke, S.K.; Cywinski, R.; Davis, J.R.; Rainford, B.D. The evolution of magnetic order in CrFe alloys. II. Onset of ferromagnetism. J. Phys. F 1983, 13, 451–470. [Google Scholar] [CrossRef]
- Häussler, W.; Böni, P.; Klein, M.; Schmidt, C.J.; Schmidt, U.; Groitl, F.; Kindervater, J. Detection of high frequency intensity oscillations at RESEDA using the CASCADE detector. Rev. Sci. Instrum. 2011, 82, 045101. [Google Scholar] [CrossRef]
- Holderer, O.; Monkenbusch, M.; Schätzler, R.; Kleines, H.; Westerhausen, W.; Richter, D. The JCNS neutron spin-echo spectrometer J-NSE at the FRM II. Meas. Sci. Technol. 2008, 19, 034022. [Google Scholar] [CrossRef]
- IVAS-Software. Available online: https://www.cameca.com/service/software/ivas (accessed on 20 November 2018).
- Brouers, F.; Sotolongo-Costa, O. Universal relaxation in nonextensive systems. Europhys. Lett. 2003, 62, 808–814. [Google Scholar] [CrossRef]
- Fincher, C.R., Jr.; Shapiro, S.M.; Palumbo, A.H.; Parks, R.D. Spin-Wave Evolution Crossing From the Ferromagnetic to Spin-Glass Regime of FexCr1−x. Phys. Rev. Lett. 1980, 45, 474–477. [Google Scholar] [CrossRef]
- Shapiro, S.M.; Fincher, C.R., Jr.; Palumbo, A.C.; Parks, R.D. Anomalous spin-wave behavior in the magnetic alloy FexCr1−x. Phys. Rev. B 1981, 24, 6661–6674. [Google Scholar] [CrossRef]
- Halpern, O.; Holstein, T. On the Passage of Neutrons Through Ferromagnets. Phys. Rev. 1941, 59, 960–981. [Google Scholar] [CrossRef]
- Kittel, C. Einführung in die Festkörperphysik; Oldenbourg Verlag: München, Germany, 2002. [Google Scholar]
- Miller, M.K.; Hyde, J.M.; Hetherington, M.G.; Cerezo, A.; Smith, G.D.W.; Elliott, C.M. Spinodal Decomposition in Fe-Cr Alloys: Experimental Study at the Atomic Level and Comparison with computer Models—I. Introduction and Methology. Acta Metall. Mater. 1995, 43, 3385–3401. [Google Scholar] [CrossRef]
| (ns) | 12.1 K | Error | (ns) | 14.5 K | Error | (ns) | 19.4 K | Error |
|---|---|---|---|---|---|---|---|---|
| 0.00409 | 1.02276 | 0.06006 | 0.00409 | 1.05768 | 0.05938 | 0.00409 | 0.98686 | 0.05903 |
| 0.00602 | 1.00878 | 0.05935 | 0.00602 | 1.09378 | 0.06067 | 0.00602 | 1.06622 | 0.06179 |
| 0.00813 | 0.96591 | 0.05791 | 0.00813 | 1.01485 | 0.05781 | 0.00813 | 0.95992 | 0.05795 |
| 0.01145 | 0.92834 | 0.0538 | 0.01145 | 0.92272 | 0.05197 | 0.01145 | 0.82503 | 0.05063 |
| 0.01617 | 0.91736 | 0.05504 | 0.01617 | 0.97386 | 0.05513 | 0.01617 | 0.88892 | 0.05423 |
| 0.02253 | 0.93979 | 0.05484 | 0.02253 | 0.88035 | 0.05109 | 0.02253 | 0.79933 | 0.05037 |
| 0.03181 | 0.91483 | 0.05615 | 0.03181 | 0.90611 | 0.05406 | 0.03181 | 0.77239 | 0.05158 |
| 0.04465 | 0.85836 | 0.05449 | 0.04465 | 0.88378 | 0.0536 | 0.04465 | 0.74521 | 0.05102 |
| 0.06279 | 0.97755 | 0.06212 | 0.06279 | 0.95468 | 0.05939 | 0.06279 | 0.71707 | 0.05341 |
| 0.08888 | 0.87447 | 0.05982 | 0.08888 | 0.87917 | 0.0582 | 0.08888 | 0.72044 | 0.05503 |
| 0.12548 | 0.92691 | 0.06301 | 0.12548 | 0.90804 | 0.06025 | 0.12548 | 0.7405 | 0.05691 |
| 0.17724 | 0.78653 | 0.05843 | 0.17724 | 0.76687 | 0.05573 | 0.17724 | 0.5812 | 0.05268 |
| 0.19732 | 0.87647 | 0.06422 | 0.19732 | 0.90613 | 0.0629 | 0.19732 | 0.63119 | 0.05613 |
| 0.26199 | 0.93792 | 0.06647 | 0.26199 | 0.84559 | 0.06081 | 0.26199 | 0.66925 | 0.05729 |
| 0.36492 | 0.8335 | 0.0552 | 0.36492 | 0.84718 | 0.05369 | 0.36492 | 0.62548 | 0.04892 |
| 0.51595 | 0.89125 | 0.05869 | 0.51595 | 0.8401 | 0.05497 | 0.51595 | 0.52864 | 0.048 |
| 0.71752 | 0.85023 | 0.07396 | 0.71752 | 0.79749 | 0.06927 | 0.71752 | 0.55169 | 0.06368 |
| 1.01391 | 0.79711 | 0.07074 | 1.01391 | 0.73849 | 0.06605 | 1.01391 | 0.54046 | 0.06272 |
| 0.02529 | 0.92578 | 0.0217 | 0.02543 | 0.91805 | 0.02341 | |||
| 0.04978 | 0.90893 | 0.02173 | 0.04989 | 0.90867 | 0.02357 | |||
| 0.0998 | 0.92581 | 0.02124 | 0.1003 | 0.8605 | 0.02246 | |||
| 0.19972 | 0.8752 | 0.01941 | 0.19945 | 0.74776 | 0.0202 | |||
| 0.39854 | 0.86228 | 0.01845 | 0.39976 | 0.71885 | 0.0191 | |||
| 0.79839 | 0.83665 | 0.01753 | 0.79888 | 0.66614 | 0.01803 | |||
| 1.59816 | 0.7778 | 0.01495 | 1.59894 | 0.64925 | 0.01571 | |||
| 3.19855 | 0.7861 | 0.01559 | 3.19747 | 0.64314 | 0.0161 | |||
| 6.39774 | 0.76103 | 0.01594 | 6.39856 | 0.59164 | 0.01658 | |||
| 9.9985 | 0.70518 | 0.02048 | 9.99848 | 0.55466 | 0.0217 | |||
| 0.00526 | 1.09754 | 0.06667 | 0.00525 | 0.96771 | 0.0617 | 0.00409 | 1.01164 | 0.06198 |
| 0.00754 | 1.03817 | 0.06788 | 0.00765 | 1.00928 | 0.06715 | 0.00602 | 0.88442 | 0.05747 |
| 0.01079 | 0.99185 | 0.06757 | 0.01082 | 0.92648 | 0.06523 | 0.00813 | 0.89517 | 0.05781 |
| 0.01512 | 0.88966 | 0.06278 | 0.01508 | 0.88101 | 0.06266 | 0.01145 | 0.73806 | 0.04983 |
| 0.02125 | 0.80296 | 0.05852 | 0.02125 | 0.66394 | 0.05382 | 0.01617 | 0.61188 | 0.04774 |
| 0.03002 | 0.85592 | 0.06467 | 0.02987 | 0.59078 | 0.05516 | 0.02253 | 0.49692 | 0.04387 |
| 0.04216 | 0.67408 | 0.05884 | 0.04217 | 0.60437 | 0.0567 | 0.03181 | 0.44948 | 0.04482 |
| 0.05965 | 0.8016 | 0.06767 | 0.05955 | 0.57911 | 0.05997 | 0.04465 | 0.42374 | 0.04469 |
| 0.08404 | 0.58313 | 0.06082 | 0.08394 | 0.50844 | 0.05899 | 0.06279 | 0.36484 | 0.04685 |
| 0.11873 | 0.60005 | 0.06782 | 0.11872 | 0.4726 | 0.06416 | 0.08888 | 0.28966 | 0.04716 |
| 0.16803 | 0.57163 | 0.08267 | 0.16771 | 0.42479 | 0.0778 | 0.12548 | 0.25518 | 0.04778 |
| 0.19188 | 0.60791 | 0.09113 | 0.19179 | 0.37019 | 0.0829 | 0.17724 | 0.27402 | 0.04849 |
| 0.25498 | 0.50625 | 0.07413 | 0.25486 | 0.36084 | 0.07005 | 0.19732 | 0.21112 | 0.05007 |
| 0.355 | 0.56178 | 0.06561 | 0.35483 | 0.30882 | 0.059 | 0.26199 | 0.14018 | 0.04911 |
| 0.50215 | 0.51515 | 0.07345 | 0.50191 | 0.22345 | 0.06644 | 0.36492 | 0.1709 | 0.04189 |
| 0.70143 | 0.49382 | 0.10095 | 0.70109 | 0.41314 | 0.09901 | 0.51595 | 0.19155 | 0.04417 |
| 0.9911 | 0.41238 | 0.09801 | 0.99062 | 0.28469 | 0.09488 | 0.71752 | 0.19639 | 0.05956 |
| 0.09993 | 0.62805 | 0.02397 | 0.02534 | 0.75225 | 0.02896 | 1.01391 | 0.18747 | 0.05861 |
| 0.20028 | 0.61087 | 0.02242 | 0.04913 | 0.66412 | 0.02883 | 0.02533 | 0.58292 | 0.03211 |
| 0.39978 | 0.48247 | 0.02087 | 0.09842 | 0.58733 | 0.02762 | 0.05043 | 0.56945 | 0.03201 |
| 0.79925 | 0.49432 | 0.02003 | 0.19907 | 0.43724 | 0.02542 | 0.09976 | 0.38865 | 0.03089 |
| 1.59864 | 0.44597 | 0.01732 | 0.40046 | 0.45993 | 0.02417 | 0.19893 | 0.34034 | 0.02876 |
| 3.19816 | 0.40069 | 0.01767 | 0.79944 | 0.3529 | 0.02284 | 0.39957 | 0.29977 | 0.02729 |
| 6.3974 | 0.41392 | 0.01823 | 1.59859 | 0.34077 | 0.01993 | 0.79908 | 0.2258 | 0.02593 |
| 9.99879 | 0.31263 | 0.02397 | 3.19825 | 0.34015 | 0.02046 | 1.59863 | 0.21929 | 0.02263 |
| 6.39851 | 0.36829 | 0.02118 | 3.19827 | 0.23321 | 0.0233 | |||
| 9.99884 | 0.29178 | 0.02805 | 6.3991 | 0.21245 | 0.02436 | |||
| 9.99846 | 0.28799 | 0.03217 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagner, J.N.; Häußler, W.; Holderer, O.; Bauer, A.; Shapiro, S.M.; Böni, P. Influence of Concentration Fluctuations on Relaxation Processes in Spin Glasses. Quantum Beam Sci. 2018, 2, 26. https://doi.org/10.3390/qubs2040026
Wagner JN, Häußler W, Holderer O, Bauer A, Shapiro SM, Böni P. Influence of Concentration Fluctuations on Relaxation Processes in Spin Glasses. Quantum Beam Science. 2018; 2(4):26. https://doi.org/10.3390/qubs2040026
Chicago/Turabian StyleWagner, Julia N., Wolfgang Häußler, Olaf Holderer, Andreas Bauer, Stephen M. Shapiro, and Peter Böni. 2018. "Influence of Concentration Fluctuations on Relaxation Processes in Spin Glasses" Quantum Beam Science 2, no. 4: 26. https://doi.org/10.3390/qubs2040026
APA StyleWagner, J. N., Häußler, W., Holderer, O., Bauer, A., Shapiro, S. M., & Böni, P. (2018). Influence of Concentration Fluctuations on Relaxation Processes in Spin Glasses. Quantum Beam Science, 2(4), 26. https://doi.org/10.3390/qubs2040026






