On the Robustness of the MnSi Magnetic Structure Determined by Muon Spin Rotation
Abstract
1. Introduction
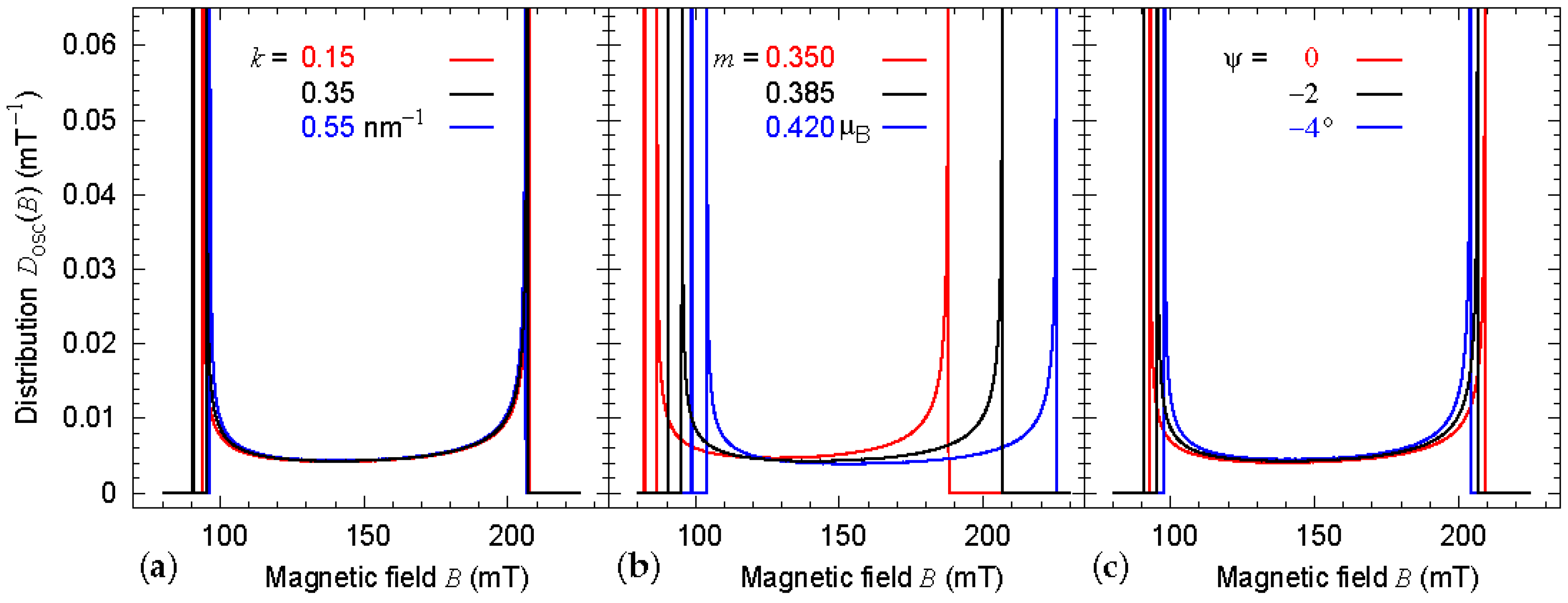
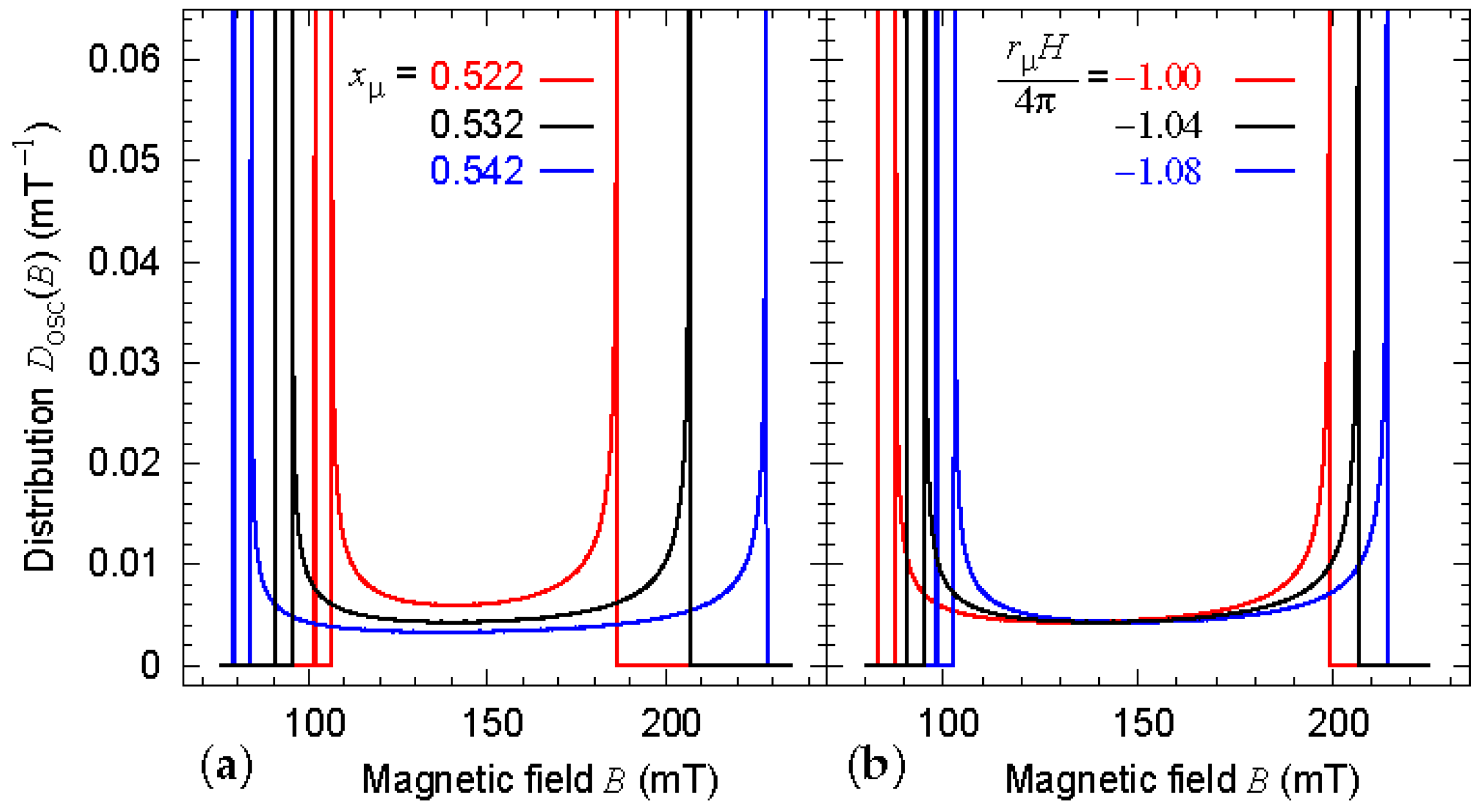
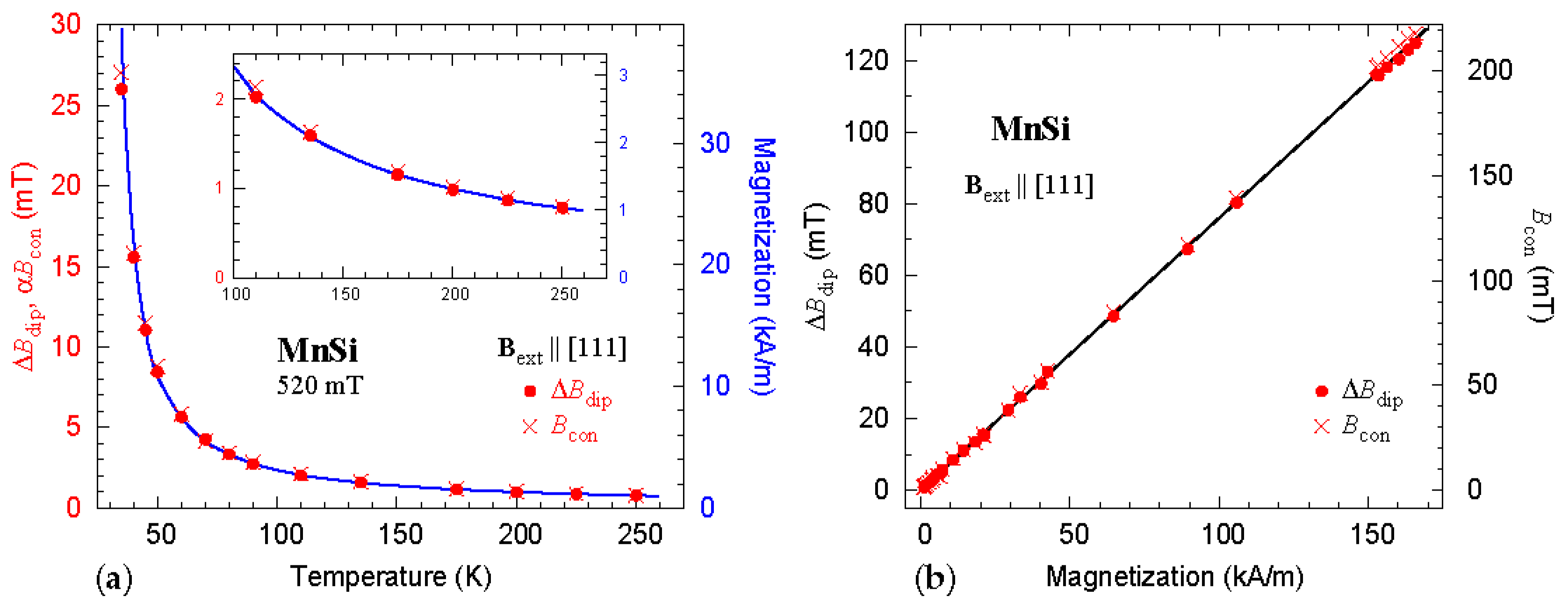
2. Parameter Dependence of the Field Distribution
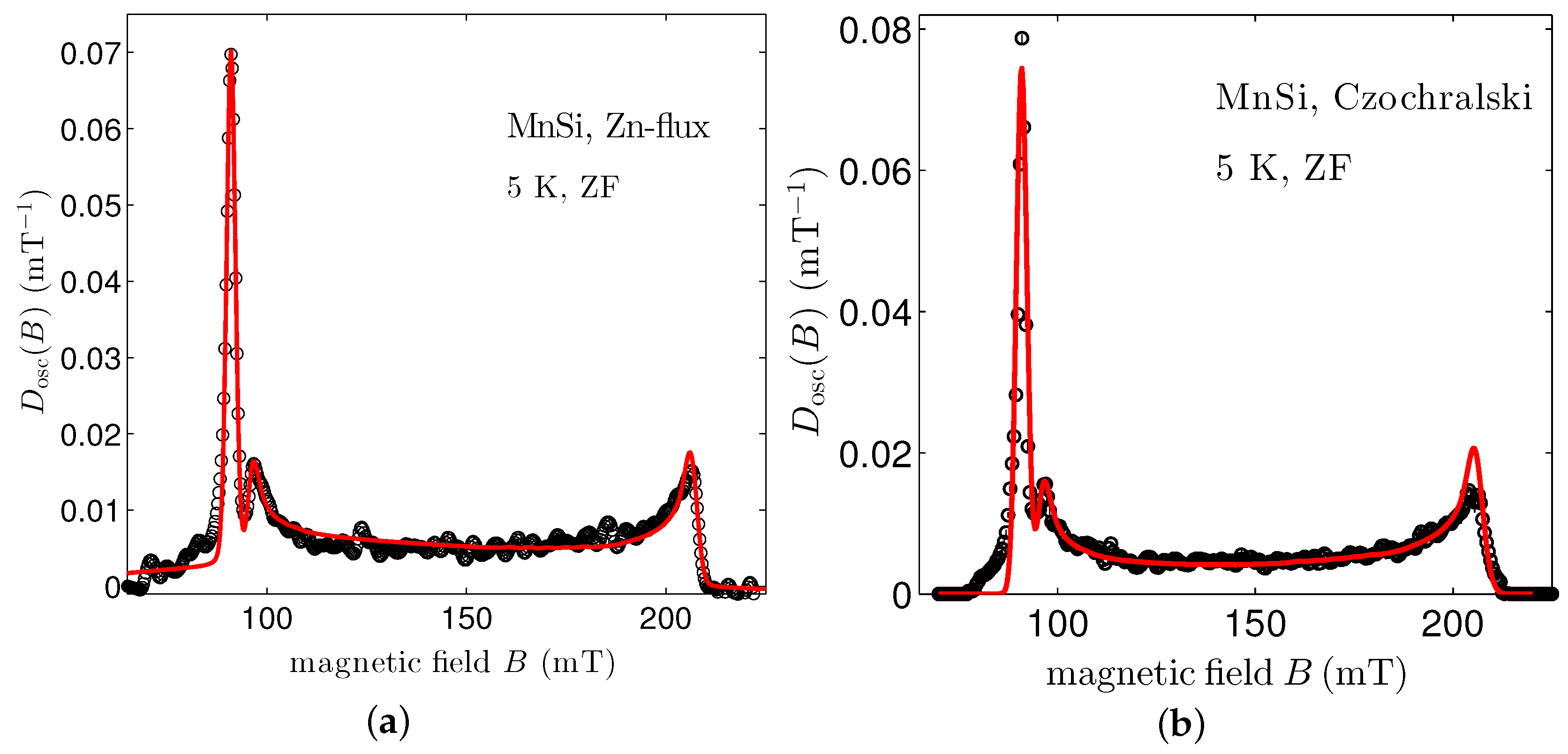
3. Specimen Dependence of the Zero-Field Spectrum
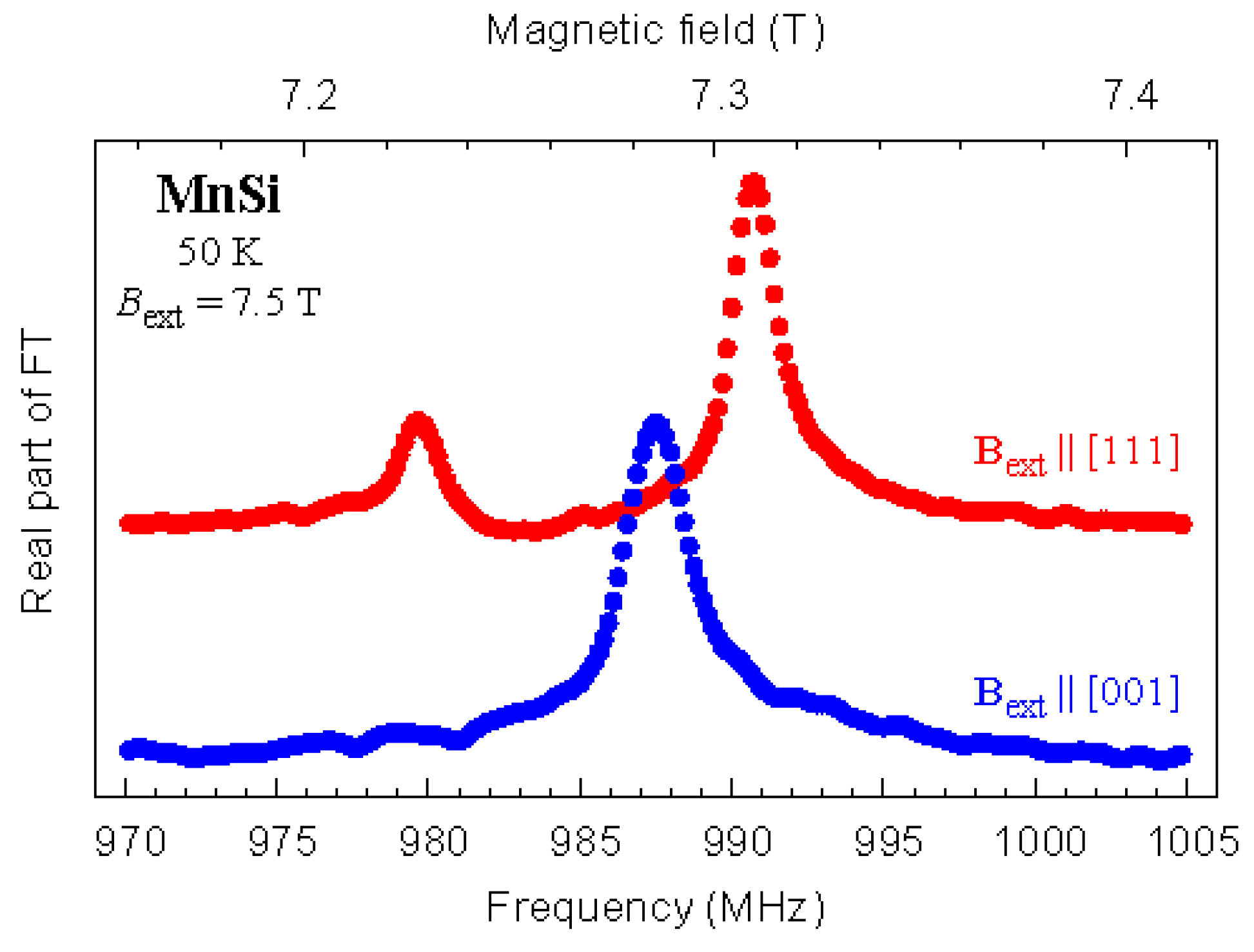
4. Testing the Possibility of a Muon-Induced Effect
5. Materials and Methods
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Borén, B. Röntgenuntersuchung der Legierungen von Silizium mit Chrom, Mangan, Kobalt und Nickel. Arkiv Kemi Miner. Geol. 1933, 11A, 1–28. [Google Scholar]
- Williams, H.J.; Wernick, J.H.; Sherwood, R.C.; Wertheim, G.K. Magnetic Properties of the Monosilicides of Some 3d Transition Elements. J. Appl. Phys. 1966, 37, 1256. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Tajima, K.; Bloch, D.; Roth, M. Helical spin structure in manganese silicide MnSi. Solid State Commun. 1976, 19, 525–528. [Google Scholar] [CrossRef]
- Ishida, M.; Endoh, Y.; Mitsuda, S.; Ishikawa, Y.; Tanaka, M. Crystal Chirality and Helicity of the Helical Spin Density Wave in MnSi. II. Polarized Neutron Diffraction. J. Phys. Soc. Jpn. 1985, 54, 2975–2982. [Google Scholar] [CrossRef]
- Pfleiderer, C.; Julian, S.R.; Lonzarich, G.G. Non-Fermi liquid nature of the normal state of itinerant-electron ferromagnets. Nature 2001, 414, 427–430. [Google Scholar] [CrossRef] [PubMed]
- Pfleiderer, C.; Reznik, D.; Pintschovius, L.; von Löhneysen, H.; Garst, M.; Rosch, A. Partial order in the non-Fermi-liquid phase of MnSi. Nature 2004, 427, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion Lattice in a Chiral Magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Amato, A.; Dalmas de Réotier, P.; Andreica, D.; Yaouanc, A.; Suter, A.; Lapertot, G.; Pop, I.M.; Morenzoni, E.; Bonfà, P.; Bernardini, F.; De Renzi, R. Understanding the μSR spectra of MnSi without magnetic polarons. Phys. Rev. B 2014, 89, 184425. [Google Scholar] [CrossRef]
- Dalmas de Réotier, P.; Maisuradze, A.; Yaouanc, A.; Roessli, B.; Amato, A.; Andreica, D.; Lapertot, G. Determination of the zero-field magnetic structure of the helimagnet MnSi at low temperature. Phys. Rev. B 2016, 93, 144419. [Google Scholar] [CrossRef]
- Dalmas de Réotier, P.; Maisuradze, A.; Yaouanc, A.; Roessli, B.; Amato, A.; Andreica, D.; Lapertot, G. Unconventional magnetic order in the conical state of MnSi. Phys. Rev. B 2017, 95, 180403(R). [Google Scholar] [CrossRef]
- Bertaut, E.F. On group theoretical techniques in magnetic structure analysis. J. Magn. Magn. Mater. 1981, 24, 267–278. [Google Scholar] [CrossRef]
- Hahn, T. (Ed.) International Tables for Crytallography, 5th ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Bonfà, P.; Onuorah, I.J.; De Renzi, R. Introduction and a quick look at MUESR, the Magnetic structure and mUon Embedding Site Refinement suite. JPS Conf. Proc. 2018, 21, 011052. [Google Scholar] [CrossRef]
- Yaouanc, A.; Dalmas de Réotier, P.; Gubbens, P.C.M.; Sakarya, S.; Lapertot, G.; Hillier, A.D.; King, P.J.C. Testing the self-consistent renormalization theory for the description of the spin-fluctuation modes of MnSi at ambient pressure. J. Phys. Condens. Matter. 2005, 17, L129. [Google Scholar] [CrossRef]
- Andreica, D.; Dalmas de Réotier, P.; Yaouanc, A.; Amato, A.; Lapertot, G. Absence of magnetic phase separation in MnSi under pressure. Phys. Rev. B 2010, 81, 060412(R). [Google Scholar] [CrossRef]
- Fåk, B.; Sadykov, R.A.; Flouquet, J.; Lapertot, G. Pressure dependence of the magnetic structure of the itinerant electron magnet MnSi. J. Phys. Condens. Matter. 2005, 17, 1635. [Google Scholar] [CrossRef]
- Miyake, A.; Villaume, A.; Haga, Y.; Knebel, G.; Salce, B.; Lapertot, G.; Flouquet, J. Pressure Collapse of the magnetic ordering in MnSi via thermal expansion. J. Phys. Soc. Jpn. 2009, 78, 044703. [Google Scholar] [CrossRef]
- Pedrazzini, P.; Jaccard, D.; Lapertot, G.; Flouquet, J.; Inada, Y.; Kohara, H.; Ōnuki, Y. Probing the extended non-Fermi liquid regimes of MnSi and Fe. Physica B 2006, 378–380, 165–166. [Google Scholar] [CrossRef]
- Dalmas de Réotier, P.; Yaouanc, A.; Maisuradze, A. New insights for the description of magnetic correlations inferred from μSR. J. Phys. Conf. Ser. 2014, 551, 012005. [Google Scholar] [CrossRef]
- Maisuradze, A.; Yaouanc, A.; Dalmas de Réotier, P. Reverse Monte Carlo Algorithm and Maximum Entropy Principle for the Analysis of Positive Muon Spin Rotation and Relaxation Spectra. JPS Conf. Proc. 2018, 21, 011053. [Google Scholar] [CrossRef]
- Bauer, A.; Neubauer, A.; Franz, C.; Münzer, W.; Garst, M.; Pfleiderer, C. Quantum phase transitions in single-crystal Mn1−xFexSi and Mn1−xCoxSi: Crystal growth, magnetization, ac susceptibility, and specific heat. Phys. Rev. B 2010, 82, 064404. [Google Scholar] [CrossRef]
- Pfleiderer, C.; Böni, P.; Franz, C.; Keller, T.; Neubauer, A.; Niklowitz, P.G.; Schmakat, P.; Schulz, M.; Huang, Y.K.; Mydosh, J.A.; et al. Search for Electronic Phase Separation at Quantum Phase Transitions. J. Low Temp. Phys. 2010, 161, 167–181. [Google Scholar] [CrossRef]
- Goko, T.; Arguello, C.J.; Hamann, A.; Wolf, T.; Lee, M.; Reznik, D.; Maisuradze, A.; Khasanov, R.; Morenzoni, E.; Uemura, Y.J. Restoration of quantum critical behavior by disorder in pressure-tuned (Mn,Fe)Si. npj Quantum Mater. 2017, 2, 44. [Google Scholar] [CrossRef]
- Bleaney, B. Enhanced nuclear magnetism. Physica 1973, 69, 317–329. [Google Scholar] [CrossRef]
- Kayzel, F.; Franse, J.J.M.; Gubbens, P.C.M.; Moolenaar, A.A.; Dalmas de Réotier, P.; Yaouanc, A.; Bonville, P.; Imbert, P.; Pari, P. Quasi-static spin dynamics in the Van-Vleck paramagnet PrNi5. Hyperfine Interact. 1994, 85, 275–280. [Google Scholar] [CrossRef]
- Feyerherm, R.; Amato, A.; Grayevsky, A.; Gygax, F.; Kaplan, N.; Schenck, A. Crystal electric field next to a hydrogen-like interstitial μ+ in PrNi5. Z. Phys. B 1995, 99, 3–13. [Google Scholar] [CrossRef]
- Mulders, A.M.; Yaouanc, A.; Dalmas de Réotier, P.; Gubbens, P.C.M.; Moolenaar, A.A.; Fåk, B.; Ressouche, E.; Prokeš, K.; Menovsky, A.A.; Bushow, K.H.J. PrRu2Si2: A giant anisotropic induced magnet with a singlet crystal-field ground state. Phys. Rev. B 1997, 56, 8752. [Google Scholar] [CrossRef]
- Tashma, T.; Amato, A.; Grayevsky, A.; Gygax, F.N.; Pinkpank, M.; Schenck, A.; Kaplan, N. Electronic changes induced by μ+ in PrIn3: Muon-spin-rotation observation and crystalline-electric-field model calculation. Phys. Rev. B 1997, 56, 9397. [Google Scholar] [CrossRef]
- MacLaughlin, D.E.; Ohta, Y.; Machida, Y.; Nakatsuji, S.; Luke, G.M.; Ishida, K.; Heffner, R.H.; Shu, L.; Bernal, O.O. Weak quasistatic magnetism in the frustrated Kondo lattice Pr2Ir2O7. Physica (Amsterdam) 2009, 404B, 667–670. [Google Scholar] [CrossRef]
- Foronda, F.R.; Lang, F.; Möller, J.S.; Lancaster, T.; Boothroyd, A.T.; Pratt, F.L.; Giblin, S.R.; Prabhakaran, D.; Blundell, S.J. Anisotropic Local Modification of Crystal Field Levels in Pr-Based Pyrochlores: A Muon-Induced Effect Modeled Using Density Functional Theory. Phys. Rev. Lett. 2015, 114, 017602. [Google Scholar] [CrossRef] [PubMed]
- Julien, M.H. Magnetic order and superconductivity in La2−xSrxCuO4: A review. Physica B 2003, 329–333, 693–696. [Google Scholar] [CrossRef]
- Amato, A. Heavy-fermion systems studied by μSR technique. Rev. Mod. Phys. 1997, 69, 1119. [Google Scholar] [CrossRef]
- Onuorah, I.J.; Bonfà, P.; De Renzi, R. Muon contact hyperfine field in metals: A DFT calculation. Phys. Rev. B 2018, 97, 174414. [Google Scholar] [CrossRef]
- Schenck, A.; Gygax, F.N. Magnetic materials studied by muon spin rotation spectroscopy. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 9. [Google Scholar]
- Dalmas de Réotier, P.; Yaouanc, A. Muon spin rotation and relaxation in magnetic materials. J. Phys. Condens. Matter. 1997, 9, 9113. [Google Scholar] [CrossRef]
- Kalvius, G.M.; Noakes, D.R.; Hartmann, O. μSR studies of rare-earth and actinide magnetic materials. In Handbook on the Physics and Chemistry of Rare Earths; Gschneidner, K.A., Eyring, L., Lander, G.H., Eds.; North-Holland: Amsterdam, The Netherlands, 2001; Volume 32. [Google Scholar]
- Yaouanc, A.; Dalmas de Réotier, P. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Lancaster, T.; Williams, R.C.; Thomas, I.O.; Xiao, F.; Pratt, F.L.; Blundell, S.J.; Loudon, J.C.; Hesjedal, T.; Clark, S.J.; Hatton, P.D.; et al. Transverse field muon-spin rotation signature of the skyrmion-lattice phase in Cu2OSeO3. Phys. Rev. B 2015, 91, 224408. [Google Scholar] [CrossRef]
| Sample | m () | (degrees) | (-) | (nm) |
|---|---|---|---|---|
| Czochralski | ||||
| Zn-flux |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalmas de Réotier, P.; Yaouanc, A.; Amato, A.; Maisuradze, A.; Andreica, D.; Roessli, B.; Goko, T.; Scheuermann, R.; Lapertot, G. On the Robustness of the MnSi Magnetic Structure Determined by Muon Spin Rotation. Quantum Beam Sci. 2018, 2, 19. https://doi.org/10.3390/qubs2030019
Dalmas de Réotier P, Yaouanc A, Amato A, Maisuradze A, Andreica D, Roessli B, Goko T, Scheuermann R, Lapertot G. On the Robustness of the MnSi Magnetic Structure Determined by Muon Spin Rotation. Quantum Beam Science. 2018; 2(3):19. https://doi.org/10.3390/qubs2030019
Chicago/Turabian StyleDalmas de Réotier, Pierre, Alain Yaouanc, Alex Amato, Alexander Maisuradze, Daniel Andreica, Bertrand Roessli, Tatsuo Goko, Robert Scheuermann, and Gérard Lapertot. 2018. "On the Robustness of the MnSi Magnetic Structure Determined by Muon Spin Rotation" Quantum Beam Science 2, no. 3: 19. https://doi.org/10.3390/qubs2030019
APA StyleDalmas de Réotier, P., Yaouanc, A., Amato, A., Maisuradze, A., Andreica, D., Roessli, B., Goko, T., Scheuermann, R., & Lapertot, G. (2018). On the Robustness of the MnSi Magnetic Structure Determined by Muon Spin Rotation. Quantum Beam Science, 2(3), 19. https://doi.org/10.3390/qubs2030019





