Abstract
The three-point bending behavior of a single Au nanowire deformed by an atomic force microscope was monitored by coherent X-ray diffraction using a sub-micrometer sized hard X-ray beam. Three-dimensional reciprocal-space maps were recorded before and after deformation by standard rocking curves and were measured by scanning the energy of the incident X-ray beam during deformation at different loading stages. The mechanical behavior of the nanowire was visualized in reciprocal space and a complex deformation mechanism is described. In addition to the expected bending of the nanowire, torsion was detected. Bending and torsion angles were quantified from the high-resolution diffraction data.
1. Introduction
In recent years, low-dimensional materials were intensively investigated revealing superior properties for nanostructures compared to their bulk counterparts. In particular, quasi one-dimensional objects such as nanowires and nanotubes were regarded as potential candidates for future sensors, optoelectronics or nano-electromechanical systems [1,2,3,4,5]. For the development of reliable future devices based on nanomaterials, knowledge and understanding of mechanical properties at the nanoscale are of paramount interest. Pioneered by Uchic et al. [6], mechanical tests on micro- and nanostructures demonstrated increasing yield strengths with decreasing structure size reaching the ultimate limit of the material for defect scarce nanowires. This trend became known in literature as “smaller is stronger”. More recently, in situ experimental techniques were developed that are compatible with scanning and transmission electron microscopy or synchrotron X-ray diffraction techniques providing access to the evolution of the deformation during mechanical loading [7,8,9,10,11]. Such in situ experiments demonstrated, for instance, pseudo-elastic behavior by reversible twinning/de-twinning of Au nanowires [12] and the activation of unexpected slips systems [13,14]. Transmission electron microscopy allows for following the evolution of strain and defects inside the specimen [15]. However, electron transparent samples are needed and the limited available space strongly restricts the sample environment for in situ experiments.
These limitations do not necessarily apply to synchrotron-based X-ray diffraction techniques, thanks to both the comparatively large space at synchrotron beamlines and to the penetration of hard X-rays in matter. At third generation synchrotron sources, Bragg coherent X-ray diffraction imaging (BCDI) was developed, which is a lens-less imaging technique that gives access to the displacement field in a sample with an unprecedented accuracy of 1 pm [16,17]. In addition to BCDI, white beam Laue microdiffraction was proven to provide invaluable information on the crystal orientation and rotation rendering possible the evaluation of the elastic and plastic deformation of a specimen without the need for rocking the sample [18]. However, while the spatial resolution of Laue microdiffraction is essentially given by the beam size, BCDI provides spatial resolutions in the order of 10 nm. Considering its distinct advantage, it may seem surprising that very few in situ experiments have been reported combining mechanical testing and coherent X-ray diffraction [19,20]. This might be partly due to the fact that BCDI requires the rocking of the sample in the order of one degree, which may induce vibrations that are detrimental during nanomechanical tests. Cornelius et al. demonstrated 3D reciprocal space mapping of micrometric SiGe islands by scanning the energy of the incident X-ray beam, thus avoiding any sample movements and possible vibrations during data acquisition [21]. While BCDI data recorded by standard rocking scans are almost routinely inverted into real space images, Cha et al. were the first to demonstrate the inversion of Bragg coherent X-ray diffraction images recorded by the energy scanning technique [22].
In the present work, suspended Au nanowires were bent in a three-point bending configuration using the custom-built scanning force microscope “SFINX” (Marseille, France) [23]. The deformation was monitored by Bragg coherent X-ray diffraction employing the energy scanning approach [21]. The sub-micrometer sized beam illuminated the volume under the SFINX-tip, as well as regions next to it, which are strongly affected by the applied force. The use of a two-dimensional photon-counting detector and the energy scanning method allowed for the measurement of the three-dimensional intensity distribution in reciprocal space in the vicinity of the Au 111 Bragg peak. The mechanical behavior of the nanosized gold crystal was inferred from lattice strain measurements demonstrating the plastic character of the deformation. The obtained results were in good agreement both with previous works on similar nanowires and finite element calculations for quasi one-dimensional objects of the same size [24]. Moreover, the presented approach allows for following in detail the structural changes in the gold nanocrystal during bending. This study does not attempt to invert the coherent diffraction data but rather emphasizes the experimental procedures and 3D visualization of the Au nanowire lattice behavior under an external mechanical load. It contributes to the understanding of the deformation mechanisms of nanoscale objects and lattice distortions at low forces.
2. Materials and Methods
Gold nanowires were grown by vapor phase deposition on carbon coated tungsten substrates under ultrahigh vacuum conditions [25]. For bending experiments, the as-grown nanowires were transferred onto a Si wafer that was patterned with micro-trenches. Some of the randomly distributed nanowires crossed a micro-trench resulting in the formation of nano-bridges enabling mechanical tests in a three-point bending configuration. According to previous characterizations, the nanowires grow along the [110] direction and lie down on one of their (111) side facets [24]. To avoid any sliding during three-point bending tests, the suspended nanowires were glued at their contact points with the Si substrate by carbon deposition from the residual gas in a Scanning Electron Microscopy (SEM) chamber. The mechanical tests were performed using the custom built in situ AFM “SFINX” which was installed at the upgraded ID01 beamline at the European Synchrotron (ESRF) in Grenoble (France) where the incident 9 keV X-ray beam was focused down to 350 nm (V) × 700 nm (H) using a tungsten Fresnel zone plate. The coherent part of the incident beam was selected by closing slits in front of the focusing optics to 300 µm (V) × 80 µm (H) matching the lateral coherence lengths at the upgraded beamline. The diffracted signal was recorded by a two-dimensional MAXIPIX (ESRF, Grenoble, France) detector with a pixel size of 55 × 55 µm2, which was mounted 1260 mm downstream from the sample position. Further details of the experimental setup and the X-ray beam focusing at the ID01 beamline can be found in [26,27].
Prior to in situ three-point bending tests, the SFINX-tip and the nanofocused X-ray beam were aligned with respect to a pre-selected Au nanowire by optical microscopy, rendering a precision of a few micrometers followed by AFM imaging and scanning X-ray diffraction mapping using the K-mapping approach available at the ID01 beamline where the sample is continuously scanned through the beam and the diffraction yield at a selected Bragg peak is monitored [10]. Ordinary three-dimensional reciprocal space maps (3D-RSMs) were recorded along the suspended part of the nanowire in steps of 500 nm by rocking the sample by ±0.6°, thus covering 1.8 nm−1 along Qz.
For in situ three-point bending tests, the SFINX-tip was first positioned a few micrometers above the center of the suspended Au nanowire and then lowered with a speed of 5 nm/s. Simultaneously, 2D coherent X-ray diffraction patterns were recorded with an exposure time of 1 s. Considering the time needed for the read-out of all detectors and motor positions and saving the data, a coherent 2D X-ray diffraction pattern was stored every 4 s (corresponding to a movement of 20 nm of the SFINX-tip). At pre-defined loading steps, 3D reciprocal space maps of the deformed nanowire were recorded by scanning the energy of the incident X-ray beam by ±100 eV. The covered Q-range was limited to 0.6 and 0.25 nm−1 in the vertical and horizontal direction in reciprocal space, respectively, by the chromaticity of the Fresnel zone plate and its focal depth [28].
3. Results
A scanning electron micrograph of a suspended Au nanowire is presented in Figure 1a illustrating the experimental geometry with the contact point of the SFINX-tip marked by a cross, the X-ray beam focal spot represented by a full dot and the direction of the incident X-ray beam indicated by an arrow. The corresponding scanning X-ray diffraction map recorded at the Au 111 Bragg peak is displayed in Figure 1b. The positions along the nanowire with lower diffraction intensity correlated with the positions where the nanowire crossed the Si ridges. The lack of diffraction intensity originated from the deformation of the Au nanowire at the Si support, which was probably caused by the preparation procedure (see Supplementary Materials).
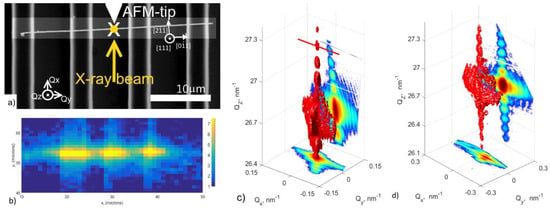
Figure 1.
(a) Scanning electron microscopy image of selected Au nanowire. The yellow full dot represents the X-ray beam focus while the yellow arrow indicates the direction of the incident X-ray beam. (b) Scanning X-ray diffraction map of the sample recorded at the Au 111 Bragg peak. Three-dimensional iso-surface of the intensity distribution around the Au 111 Bragg peak of the gold nanowire recorded by rocking scan (c) before and (d) after the three-point bending test (sample detector distance has been changed). AFM = Atomic Force Microscopy.
A typical 3D-RSM of the Au 111 Bragg peak measured by ordinary rocking scans far from the clamping points is shown in Figure 1c. The Bragg reflection was located at Qz = 26.7 nm−1 containing a large number of characteristic size oscillations from which the width and the thickness of the nanowire was inferred to be 155 and 57 nm, respectively. The good agreement of the experimental Qz value with the theoretical Au 111 Bragg position as well as the good visibility of the size oscillations demonstrated the strain-free state of the suspended part of the nanowire. The fact that the 3D-RSM was very narrow in the third direction (along Qy) was caused by the length of the nanowire, which is much larger than the area illuminated by the X-ray beam.
Three-dimensional iso-intensity surface representations at 73% of the maximum intensity of 3.7 × 104 cps together with two-dimensional cuts in the three different Q-directions of the same nanowire at different states of deformation are displayed in Figure 2. The results for the pristine nanowire are shown in Figure 2a. Due to the smaller Q-range covered by the energy scan compared to ordinary rocking scans, only the central peak together with the first size oscillations were observed (see Figure 1c,d and Figure 2a,f, respectively, for the pristine nanowire and unloaded nanowire). The slight differences observed when comparing reciprocal space maps and calculated from rocking or energy scans may be attributed to an unavoidable slight offset in the measurement position along the nanowire. Despite both this difference and the smaller Q-range covered by the E-scan, structural changes induced by mechanical deformations using the SFINX-tip were observable, as demonstrated in the following. When loading the nanowire with the SFINX-tip, the shape of the Bragg peak changed immediately after creating contact. The diffraction signal at smaller Qx values, corresponding to about 20% of the total diffraction intensity, became elongated (Figure 2b) and the volume fraction as well as the width increased further both in the Qx and in the Qy direction and it moved along Qx with increasing load (Figure 2c). The Bragg peak eventually split into an ellipsoidal and a broad diffuse peak whereas the latter moved along Qy with further load (Figure 2d,e). The broad peak probably originates from the fact that the X-ray beam probes a segment of a few hundred nanometers of the nanowire which exhibits both a continuum of bending angles and a comparatively large strain distribution at the loading point reaching from compressive to tensile strain. The sharper and less intense Bragg peak is related to nanowire parts which are relatively far from the loading point and which are illuminated by the tails of the X-ray beam. These nanowire parts are not affected by the actual three-point bending test resulting in a Bragg reflection that remains stable in reciprocal space throughout the nano-mechanical test.
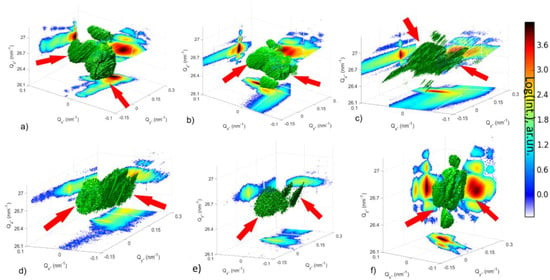
Figure 2.
Three-dimensional iso-surfaces of diffraction intensity at different loading stages during the in situ three-point bending test recorded using energy scans: (a) pristine nanowire, (b–e) under increasing load, (f) unloaded nanowire. The arrows highlight the two parts of the Bragg peak that separate from each other during loading of the nanowire.
The peak center positions and the full width at half maximum (FWHM) of the Bragg peak were evaluated by fitting the 2D cuts of the coherent 3D diffraction patterns shown in Figure 2 with a Gaussian. Since the Bragg peak moves exclusively in the Qx–Qy plane, the peak displacement was evaluated at the same Qz for all deformation stages. The relative movements of the diffraction signals in reciprocal space are summarized in Figure 3a. When the SFINX-tip touched the nanowire, the Bragg peak shifted by +0.032 and −0.06 nm−1 along Qx and Qy, respectively. With increasing load, it then reversed its course along both Q-directions moving essentially along Qy. At the highest load, the Bragg peak shifted by +0.028 nm−1 along Qx and +0.32 nm−1 along Qy with respect to its initial position. After complete unloading, the diffuse Bragg peak did not return to its initial position and the shape of the Bragg peak was different from the shape prior to the nano-mechanical test (see Figure 2f). It consisted of more pronounced size oscillations which were also confirmed by a rocking scan performed after unloading (Figure 1d), thus, demonstrating good agreement of the two techniques.
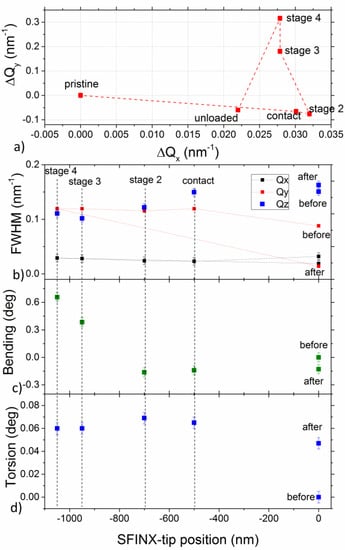
Figure 3.
(a) Displacement and (b) full width of half maximum (FWHM) of the Au 111 Bragg peak in reciprocal space during the in situ three-point bending test. (c) Bending and (d) torsion of the nanowire during the nano-mechanical test inferred from the displacement of the Au 111 Bragg peak is shown in part (a).
The FWHM of the diffraction peak, which is presented in Figure 3b, was obtained by fitting the intensity distribution in reciprocal space by Gaussians in all three Q directions. The most significant changes of the peak width were along Qy, as well as along Qz while the variations along Qx were negligible as already observed in the three-dimensional representation of the Bragg peak in Figure 2a–f.
In the following, the changes observed in the in situ 3D coherent X-ray diffraction patterns are discussed with respect to the actual deformation of the nanowire including torsion and bending. While displacements of the Bragg peak along Qy originated mainly from an in-plane bending, movements along Qx were caused by nanowire torsion. The results are summarized in Figure 3c,d. Here, bending was the dominating deformation process reaching values of up to 0.7° at the highest load. Assuming that the X-ray beam was perfectly centered around the loading position, the nanowire bending profile was symmetric, i.e., the diffraction peak position is fixed along Qy and the measurement is insensitive to the bending but only to bending gradients. The fact that finite bending was observed, this indicated a slightly imperfect alignment of the nano-focused X-ray beam with respect to the SFINX-tip. After unloading, a residual upward bending of −0.15° remained, which might have originated from sticking the SFINX-tip to the nanowire during retraction thus pulling the nanowire upwards. The aforementioned FWHM of the Bragg peak along Qy actually translated to a distribution of bending angles in the illuminated nanowire part that increased to a range of 0.25° at the highest load and then diminished to 0.14° after unloading. This bending gradient originated from the fact that the focused X-ray beam was positioned at the loading point, thus probing the nanowire curvature below the SFINX-tip and nanowire parts next to the contact point (according to beam size). In addition to the bending, the nanowire was also twisted during the nano-mechanical test probably because of a slight misalignment of the SFINX-tip with respect to the center of the nanowire width, thus inducing a torque [18]. The torsion was induced as soon as the SFINX-tip touched the nanowire and then stayed rather constant during the loading process. Finite element method simulations revealed that nanowire torsion was highly sensitive to any misalignment of the SFINX-tip with respect to the center of the nanowire width inducing a torque [14]. While misalignments of 50 nm resulted in twisting of several degrees, torsion angles <0.1° reported in the present work evidenced an excellent alignment of the SFINX-tip with respect to the center of the nanowire width. However, the torsion was about one order of magnitude smaller than the bending at the highest load. After unloading, the nanowire stayed twisted by about 0.05°. The residual bending and torsion may have originated either from a slipping of the nanowire in the carbon glue used for fixation or from plastic deformation during the three-point bending test. As demonstrated by in situ Laue micro-diffraction experiments, plasticity sets in close to the camping positions where the highest stresses are expected and which are far from the actual X-ray beam focus and thus, could not be detected in the present work [14]. The increased peak width along Qz by about 0.04 nm−1 compared to the pristine state suggested a strain gradient within the bent nanowire. Considering that the pristine nanowire was free of strain gradients and taking into account the beam divergence of 0.018° the strain gradient at the highest load was estimated to be 0.18% across the nanowire thickness of 57 nm.
4. Discussion
In previous works, we reported about in situ three-point bending tests on Au nanowires monitored by Laue micro-diffraction, which also revealed bending and torsion [24]. However, the resolution in reciprocal space which strongly depends on the sample-detector distance is much larger for coherent diffraction than for standard Laue diffraction where the sample-detector distance is one to two orders of magnitude smaller. This higher resolution in reciprocal space facilitates the detection of bending and torsion angles as small as 0.01° while for Laue micro-diffraction the limit is typically of the order of 0.1°. The additional use of energy scans instead of ordinary rocking scans avoids possible vibrations induced by moving diffractometer motors that typically hamper in situ nano-mechanical tests in combination with coherent diffraction. Despite the limited energy scan range, due to the chromaticity of the used focusing optics, the main signal of the Bragg peak as well as the first order of the size fringes were accessible, thus visualizing the three-dimensional deformation of the illuminated nanowire volume during the three-point bending test. This limited range in reciprocal space, however, hindered the reconstruction of the real space image and strain field within the nanowire by phase retrieval algorithms. This clearly underlines the importance of achromatic focusing optics, like Kirkpatrick-Baez mirrors, or an integration of energy-dependent positioning for their chromatic counterparts as used in our study. To finally achieve a complete picture of objects exposed to external stimuli such as mechanical loading, novel scanning techniques have to be developed that allow for the displacement of the coherent X-ray beam on the sample surface and therefore the mapping of the complete structure instead of one singular position only. This kind of beam scanning method has been demonstrated for Laue micro-diffraction, where the beam focus is displaced on the sample by laterally scanning the KB mirrors separately [29]. Moreover, it is necessary that modified phase retrieval algorithms take into account the dilatation of the effective pixel size when varying the energy of the incident X-ray beam. More brilliant hard X-ray beams are desirable to reduce the measurement time and hence to increase the stability of the experimental setup during the actual measurement. Thus, latter point should be resolved with the upgrade of existing third generation sources like the European Synchrotron Radiation Facility and the Advance Photon source to extremely brilliant sources (EBS) within the coming year(s). With the development of these mandatory accessories, the rapidly growing field of coherent diffraction imaging could integrate energy scanning Bragg coherent X-ray diffraction imaging (E-BCDI) as a tool for in situ mechanical testing.
5. Conclusions
In conclusion, in situ three-point bending tests on gold nanowires were monitored by coherent X-ray diffraction using sub-micrometer focused hard X-ray beams. The diffraction patterns provided detailed structural information on a selected gold nanowire. Energy scanning was employed to record three-dimensional reciprocal space maps at different stages of deformation. For reconstruction of the whole picture of a nanowire’s lattice behavior during bending, 3D-reciprocal space maps are very helpful, considering the complexity of the mechanical test with lattice strain, torsion and bending. Our approach was made possible thanks to the implementation of energy scanning. The present work constitutes a proof of feasibility. With a few technical improvements on the beamline side, we expect it to become a routine technique for the study of the elastic and plastic behavior of individual nanostructures.
Supplementary Materials
The following are available online at http://www.mdpi.com/2412-382X/2/4/24/s1, Figure S1: (a) Scanning electron microscopy image of the selected Au nanowire before the in situ three-point bending test. (b) Au 111 Bragg peak position recorded along the nanowire in steps of 1 µm. Reciprocal space maps recorded (c) at the left-hand side Si support, (d) at the center of the suspended Au nanowire and (e) at the right-hand side Si support, Figure S2: SEM image of gold nanowire lying across Si trenches overlaid with the Au 311 Laue spot measured along the nanowire.
Author Contributions
Investigation, T.C., Z.R., A.D., C.L.; formal analysis, A.D., T.C.; writing—original draft preparation, A.D.; writing—review and editing, T.W.C.; validation, R.Z.; methodology, G.A.C., T.S.; visualization, F.L.; resources, G.R.; supervision, O.T.
Funding
This work was funded by the French National Research Agency through the project ANR-11-BS10-01401 MecaniX.
Acknowledgments
The authors are grateful to ESRF for allocating beamtime at the ID01 beamline.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gall, Z.; Zhong, X.; Schulman, D.; Kang, M.; Razavieh, A.; Mayer, T. Titanium dioxide nanowire sensor array integration on CMOS platform using deterministic assembly. Nanotechnology 2017, 28, 265501. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Myers, A.; Malhotra, A.; Lin, F.; Bozkurt, A.; Muth, J.; Zhu, Y. A Wearable Hydration Sensor with Conformal Nanowire Electrodes. Adv. Healthc. Mater. 2017, 6, 1601159. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Qu, Y.; Das Gupta, T.; Darga, A.; Nguyên, D.; Page, A.; Rossi, M.; Ceriotti, M.; Sorin, F. Semiconducting Nanowire-Based Optoelectronic Fibers. Adv. Mater. 2017, 2017 29, 1700681. [Google Scholar] [CrossRef]
- Shainline, J.; Buckley, S.; Mirin, R.; Nam, S. Superconducting Optoelectronic Circuits for Neuromorphic Computing. Phys. Rev. Appl. 2017, 7, 034013. [Google Scholar] [CrossRef]
- Mercier de Lépinay, L.; Pigeau, B.; Besga, B.; Vincent, P.; Poncharal, P.; Arcizet, O. A universal and ultrasensitive vectorial nanomechanical sensor for imaging 2D force field. Nat. Nanotechnol. 2017, 12, 156. [Google Scholar] [CrossRef] [PubMed]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample dimensions influence strength and crystal plasticity. Science 2004, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Clark, J.; Ihli, J.; Schenk, A.; Kim, Y.; Kulak, A.; Campbell, J.; Nisbet, G.; Meldrum, F.; Robinson, I. Three-dimensional imaging of dislocation propagation during crystal growth and dissolution. Nat. Mater. 2015, 14, 780–784. [Google Scholar] [CrossRef] [PubMed]
- Hintsala, E.; Kiener, D.; Jackson, J.; Gerberich, W. In-situ measurements of free-standing, ultra-thin film crackingin bending. Exp. Mech. 2015, 55, 1681–1690. [Google Scholar] [CrossRef]
- Zou, Y.; Wheeler, J.; Ma, H.; Okle, P.; Spolenak, R. Nanocrystaline high-entropy alloys: A new paradigm in high-temperature strength and stability. Nano Lett. 2017, 17, 1569–1574. [Google Scholar] [CrossRef] [PubMed]
- Chahine, G.A.; Zoellner, M.H.; Richard, M.I.; Guha, S.; Reich, C.; Zaumseil, P.; Capellini, G.; Schroeder, T.; Schülli, T.U. Strain and lattice orientation distribution in SiN/Ge complementary metal-oxide-semiconductor compatible light emitting microstructures by quick X-ray nano-diffraction microscopy. Appl. Phys. Lett. 2015, 106, 071902. [Google Scholar] [CrossRef]
- Cornelius, T.W.; Thomas, O. Progress of in-situ synchrotron X-ray diffraction studies on the mechanical behavior of materials at small scale. Prog. Mater. Sci. 2018, 94, 384–434. [Google Scholar] [CrossRef]
- Lee, S.; Im, J.; Yoo, Y.; Bitzek, E.; Kiener, D.; Richter, G.; Kim, B.; Oh, S.H. Reversible cyclic deformation mechanism of gold nanowires by twinning-detwinning transition evidenced from in-situ TEM. Nat. Commun. 2014, 5, 3033. [Google Scholar] [CrossRef] [PubMed]
- Maaß, R.; Van Petegem, S.; Ma, D.; Zimmermann, J.; Grolimund, D.; Roters, F.; Van Swygenhoven, H.; Raabe, D. Smaller is stronger: The effect of strain hardening. Acta Mater. 2009, 57, 5996–6005. [Google Scholar] [CrossRef]
- Ren, Z.; Cornelius, T.W.; Leclere, C.; Davydok, A.; Micha, J.-S.; Robach, O.; Ullrich, O.; Richter, G.; Thomas, O. Three-point bending behavior of Au nanowires studied by in situ Laue microdiffraction. J. Appl. Phys. 2018, in press. [Google Scholar] [CrossRef]
- Bouscaud, D.; Morawiec, A.; Pesci, R.; Berveiller, S.; Patoor, E. Strain resolution of scanning electron microscopy based Kossel microdiffraction. J. Appl. Cryst. 2014, 47, 1699–1707. [Google Scholar] [CrossRef]
- Oku, T. Direct analysis of advanced nanomaterials by high-resolution electron microscopy. Nanotechnol. Rev. 2012, 1, 389–425. [Google Scholar] [CrossRef]
- Biermanns, A.; Breuer, S.; Trampert, A.; Davydok, A.; Geelhaar, L.; Pietsch, U. Strain accomodation in Ga-assisted GaAs nanowires grown on silicon (111). Nanotechnology 2012, 23, 305703. [Google Scholar] [CrossRef] [PubMed]
- Labat, S.; Richard, M.-I.; Dupraz, M.; Gailhanou, M.; Beutier, G.; Verdier, M.; Mastropietro, F.; Cornelius, T.W.; Schülli, T.U.; Eymery, J.; et al. Inversion domain boundaries in GaN wires revealed by coherent bragg imaging. ACS Nano 2015, 9, 9210–9216. [Google Scholar] [CrossRef] [PubMed]
- Dupraz, M.; Beutier, G.; Cornelius, T.W.; Parry, G.; Ren, Z.; Labat, S.; Richard, M.-I.; Chahine, G.A.; Kovalenko, O.; Boissieu, M.D.; et al. 3D imaging of a dislocation loop at the onset of plasticity in an indented nanocrystal. Nano Lett. 2017, 17, 6696–6701. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.; Cornelius, T.W.; Labat, S.; Lauraux, F.; Richard, M.-I.; Richter, G.; Blanchard, N.; Gianola, D.C.; Thomas, O. In-situ bragg coherent X-ray diffraction during tensile testing of an individual Au nanowire. J. Appl. Cryst. 2018, 51, 781–788. [Google Scholar] [CrossRef]
- Cornelius, T.W.; Davydok, A.; Jacques, V.L.R.; Grifone, R.; Schülli, T.; Richard, M.-I.; Beutier, G.; Verdier, M.; Metzger, T.H.; Pietsch, U.; et al. In-situ three-dimensional reciprocal-space mapping during mechanical deformation. J. Synchrotron Radiat. 2012, 19, 688–694. [Google Scholar] [CrossRef] [PubMed]
- Cha, W.; Ulvestad, A.; Allain, M.; Chamard, V.; Harder, R.; Leake, S.J.; Maser, J.; Fuoss, P.H.; Hruszekewycz, S.O. Three dimensional variable-wavelength X-ray bragg coherent diffraction imaging Phys. Rev. Lett. 2016, 117, 225501. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Mastropietro, F.; Langlais, S.; Davydok, A.; Richard, M.-I.; Thomas, O.; Dupraz, M.; Verdier, M.; Beutier, G.; Boesecke, P.; et al. Scanning force microscope for in situ nanofocused X-ray diffraction studies. J. Synchrotron Radiat. 2014, 21, 1128–1133. [Google Scholar] [CrossRef] [PubMed]
- Leclere, C.; Cornelius, T.W.; Ren, Z.; Davydok, A.; Micha, J.-S.; Robach, O.; Richter, G.; Belliard, L. Thomas O. In-situ bending of an Au nanowire monitored by micro Laue diffraction. J. Appl. Cryst. 2015, 48, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Richter, G.; Hillerich, K.; Gianola, D.S.; Mönig, R.; Kraft, O.; Volkert, C.A. Ultrahigh strength single crystalline nanowhiskers grown by physical vapor deposition. Nano Lett. 2009, 9, 3048–3052. [Google Scholar] [CrossRef] [PubMed]
- Leake, S.J.; Favre-Nicolin, V.; Zatterin, E.; Richard, M.-I.; Fernandez, S.; Chahine, G.; Zhou, T.; Boesecke, P.; Djazouli, H.; Schülli, T.U. Coherent nanoscale X-ray probe for crystal interrogation at ID01, ESRF—The European Synchrotron. Mater. Des. 2017, 119, 470–471. [Google Scholar] [CrossRef]
- Schülli, T.U.; Leake, S.J. X-ray nanobeam diffraction imaging of materials. Curr. Opin. Solid State Mater. Sci. 2018. [Google Scholar] [CrossRef]
- Mastropietro, F.; Carbone, D.; Diaz, A.; Eymery, J.; Sentenac, A.; Metzger, T.H.; Chamard, V.; Favre-Nicolin, V. Coheren X-ray wavefront reconstruction of a partially illuminated Fresnel zone plate. Opt. Express 2011, 19, 19223. [Google Scholar] [CrossRef] [PubMed]
- Leclere, C.; Cornelius, T.W.; Ren, Z.; Robach, O.; Micha, J.-S.; Davydok, A.; Ullrich, O.; Richter, G.; Thomas, O. KB-scanning of X-ray beam for Laue microdiffraction on accelero-phobic samples: Application to in situ mechanically loaded nanowires. J. Synchrotron Radiat. 2016, 23, 1395–1400. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).